تُعَدّ ملاءمة المربعات الصغرى الخطية التي ذكرناها في المقال السابق مثالًا عن الانحدار regression، وهو المشكلة الأكثر عمومية لمسألة ملاءمة النماذج المختلفة مع أي نوع من البيانات، علمًا أنّ استخدام مصطلح الانحدار regression هو مصادفة تاريخية فهو مرتبط بالمعنى الأصلي للكلمة الأجنبية ارتباطًا غير مباشر ليس إلا، ويتمثَّل هدف تحليل الانحدار في وصف العلاقة بين مجموعة واحدة من المتغيرات التي تُدعى بالمتغيرات التابعة dependent variables ومجموعة أخرى من البيانات والتي تُدعى بالمتغيرات التوضيحية explanatory variables أو المتغيرات المستقلة independent.
استخدمنا في المقال السابق عمر الأم على أساس متغير توضيحي للتنبؤ بوزن الطفل على أساس متغير تابع، علمًا أنّ الانحدار البسيط simple regression هو الحالة التي توجد فيها متغير تابع واحد فقط ومتغير توضيحي واحد فقط، وسنتناول في هذا المقال الانحدار المتعدد multiple regression الذي يحوي أكثر من متغير توضيحي، لكن إذا كان هناك أكثر من متغير تابع واحد، فسيكون الانحدار من نوع الانحدار متعدد المتغيرات multivariate regression، وإذا كانت العلاقة بين المتغير التوضيحي والمتغير التابع خطيةً، فسيكون الانحدار من نوع الانحدار الخطي linear regression، فإذا كان مثلًا المتغير التابع y والمتغيران التوضيحيان هما x1 وx2، فيمكننا صياغة نموذج الانحدار الخطي كما يلي:
| y = β0 + β1 x1 + β2 x2 + ε |
حيث يكون β0 هو نقطة التقاطع وβ1 هو المُعامِل المرتبط بالمتغير x1 ويكون β2 هو الوسيط المرتبط بالمتغير x2، في حين يكون ε هو الراسب residual (أو الباقي) الناتج عن إما تباين عشوائي أو عوامل أخرى غير معروفة، فإذا كان لدينا متسلسلةً من قيم متسلسلةً من قيم y ومتسلسلتَين من `x1 و x2، فسيكننا إيجاد المُعامِلات β0 وβ1 وβ2 التي تقلل من مجموع ε2، وتُدعى هذه العملية بالمربعات الصغرى العادية ordinary least squares.
يُعَدّ هذا الحساب مشابهًا لـ thinkstats2.LeastSquare لكنه معمَّم للتعامل مع أكثر من متغير توضيحي واحد، وللمزيد من التفاصيل يمكنك زيارة صفحة ويكيبيديا، كما توجد الشيفرة الخاصة بهذا المقال في regression.py.
الحزمة StatsModels
تناولنا في المقال السابق التابع thinkstats2.LeastSquares، الذي يُعَدّ تنفيذًا للانحدار الخطي البسيط وهو مصمم ليكون سهل القراءة؛ أما بالنسبة للانحدار المتعدد multiple regression، فسننتقل للتعامل مع الحزمة StatsModels وهي حزمة بايثون تزودنا بعدة أشكال من الانحدار بالإضافة إلى عدة تحليلات أخرى، علمًا أنه ستكون هذه الحزمة مثبتةً لديك في حال كنت تستخدم أناكوندا Anaconda، وإلا فقد تضطر إلى تثبيتها، حيث سننفِّذ النموذج الذي تناولناه في الفصل السابق على أساس مثال على ذلك لكن باستخدام الحزمة StatsModels:
import statsmodels.formula.api as smf live, firsts, others = first.MakeFrames() formula = 'totalwgt_lb ~ agepreg' model = smf.ols(formula, data=live) results = model.fit()
توفِّر الحزمة statsmodels واجهتَين من نوع واجهات برمجة التطبيقات APIs، حيث تستخدِم المعادلة formula الخاصة بواجهة برمجة التطبيقات السلاسل strings لتحديد المتغيرات التابعة والمتغيرات التوضيحية، كما تستخدِم صيغة قواعدية syntax تُدعى patsy، تكون مهمة العامِل ~ في هذا المثال فصل المتغير التابع عن المتغيرات التوضيحية بحيث يضع المتغير التابع في الجهة اليسرى والمتغيرات التوضيحية في الجهة اليمنى.
يأخذ التابع smf.ols السلسلة formula وإطار البيانات live ويُعيد كائن OLS الذي يمثِّل النموذج علمًا أنّ تسمية ols اختصار لمصطلح المربعات الصغرى العادية ordinary least squares؛ أما التابع fit فهو يلائم النموذج مع البيانات ويُعيد الكائن RegressionResults الذي يحتوي على النتائج، علمًا أنّ النتائج متوافرة على صورة سمات attributes، وتكون params هي سلسلة Series تحوِّل أسماء المتغيرات إلى معامِلاتها لكي نحصل على الميل ونقطة التقاطع كما في الشيفرة التالية:
inter = results.params['Intercept'] slope = results.params['agepreg']
المعامِلان المقدَّران هما 6.83 و0.0175 أي تمامًا مثل LeastSquares. تُعَدّ pvalues سلسلةً Series تحول أسماء المتغيرات إلى القيمة الاحتمالية المرتبطة بها لكي نتحقق فيما إن كان الميل المقدَّر ذا دلالة إحصائية:
slope_pvalue = results.pvalues['agepreg']
القيمة الاحتمالية p-value المرتبطة بالمتغير agepreg هي 5.7e-11 أي أقل من 0.001 كما هو متوقع تمامًا.
يحتوي results.rsquared على R2 التي تبلغ قيمتها 0.0047، ويزودنا results بـ f_pvalue وهي القيمة الاحتمالية المرتبطة بالنموذج بأكمله بصورة مشابهة لاختبار فيما إن كان R2 ذي دلالة إحصائية، كما يزودنا results بـ resid وهو متسلسلة من الرواسب، وبـ fittedvalues وهو متسلسلة من القيم الملاءمة المقابلة لـ agepreg، كما يزودنا الكائن results بالدالة summary() التي تمثُِل النتائج بصيغة مقروءة.
print(results.summary())
لكن تطبع هذه الدالة الكثير من المعلومات التي لا تهمنا حاليًا، لذا سنستخدِم دالةً أبسط تُدعى SummarizeResults، إليك نتائج هذا النموذج كما يلي:
Intercept 6.83 (0) agepreg 0.0175 (5.72e-11) R^2 0.004738 Std(ys) 1.408 Std(res) 1.405
يُعَدّ Std(ys) الانحراف المعياري للمتغير التابع، وهو جذر متوسط مربع الخطأ RMSE نفسه إذا خمّنت أوزان الولادات بدون متغيرات توضيحية؛ أما Std(res) فهو الانحراف المعياري للرواسب وهو خطأ الجذر التربيعي المتوسط RMSE إذا كانت تخميناتك مبينةً على عمر الأم، حيث أنّ عمر الأم -كما رأينا سابقًا- لا يقدِّم أيّ تحسين جوهري إلى التنبؤات.
الانحدار المتعدد
رأينا في مقال دوال التوزيع التراكمي Cumulative distribution functions ميل الأطفال الأوائل ليكونوا أقل وزنًا من بقية الأطفال، ويُعَدّ هذا التأثير ذا دلالة إحصائية لكنه نتيجةً غريبةً بسبب عدم وجود آلية واضحة تتسبب في جعل الأطفال الأوائل أقل وزنًا من غيرهم، لذا قد نتساءل فيما إذا كانت هذه العلاقة زائفةً spurious.
يوجد تفسير محتمل لهذا التأثير في الواقع، فقد رأينا اعتماد وزن الطفل عند الولادة على عمر الأم، لذا قد نتوقع أنّ أمهات الأطفال الأوائل أصغر عمرًا من غيرهن، ويمكننا التحقق مما إن كان هذا التفسير معقولًا من خلال بعض العمليات الحسابية ثم سنستخدِم الانحدار المتعدد لإجراء تحقيق أكثر دقة، لذا سنرى في البداية حجم الفرق في الوزن ما يلي:
diff_weight = firsts.totalwgt_lb.mean() - others.totalwgt_lb.mean()
عادةً ما يكون الأطفال الأوائل أخف وزنًا من غيرهم بمقدار 0.125 رطلًا أو 2 أوقية أو ما يعادل 0.1 كيلوغرامًا؛ أما الفرق في الأعمار فهو:
diff_weight = firsts.totalwgt_lb.mean() - others.totalwgt_lb.mean()
أي أن أمهات الأطفال الأوائل أصغر من أمهات بقية الأطفال بـ 3.59 عامًا، حيث يمكننا الحصول على الفرق في وزن الطفل عند الولادة على أساس دالة العمر عن طريق تشغيل النموذج الخطي مرةً أخرى:
results = smf.ols('totalwgt_lb ~ agepreg', data=live).fit() slope = results.params['agepreg']
يقدَّر الميل بـ 0.0175 رطلًا في العام الواحد، فإذا أجرينا عملية جداء بين الميل والفرق في الأعمار، فسنحصل على الفرق المتوقَّع في وزن الطفل عند الولادة للأطفال الأوائل وبقية الأطفال والناتج عن عمر الأم:
slope * diff_age
النتيجة هي 0.063 وتساوي نصف الفرق المرصود، لذا نستنتج مبدئيًا أنه يمكن تفسير الفرق الملحوظ في وزن الطفل عند الولادة بالاختلاف في عمر الأم، كما يمكننا استكشاف هذه العلاقات بطريقة منهجية باستخدام الانحدار المتعدد كما يلي:
live['isfirst'] = live.birthord == 1 formula = 'totalwgt_lb ~ isfirst' results = smf.ols(formula, data=live).fit()
ينشئ السطر الأول من الشيفرة السابقة عمودًا جديدًا باسم isfirst وقيمته البوليانية صحيحية True للأطفال الأوائل وخاطئة false ما عدا ذلك، ثم نستخدِم العمود isfirst على أساس متغير توضيحي لكي نلائم نموذجًا، وإليك النتائج كما يلي:
Intercept 7.33 (0) isfirst[T.True] -0.125 (2.55e-05) R^2 0.00196
تعامِل ols العمود isfirst على أنه متغير فئوي categorical variable نظرًا لأنه من النوع البولياني boolean، أي أن القيم تندرج في فئتين هما True وFalse ولا ينبغي معاملتها على أساس أعداد، علمًا أن المعامِلات المقدَّرة estimated parameter هي التأثير على وزن الطفل عند الولادة في حال كانت قيمة isfirst هي true، لذا تكون النتيجة المقدَّرة بـ -0.125 رطل هي الفرق في وزن الطفل عند الولادة بين الأطفال الأوائل وبقية الأطفال.
يملك الميل slope ونقطة التقاطع intercept دلالةً إحصائيةً، أي أنه من غير المحتمل حدوث التأثير صدفةً، لكن قيمة R2 الخاصة بالنموذج صغيرةً، مما يعني أنّ isfirst لا يمثِّل جزءًا كبيرًا من التباين في وزن الطفل عند الولادة، كما تتشابه النتائج مع النتائج التي ظهرت مع agepreg كما يلي:
Intercept 6.83 (0) agepreg 0.0175 (5.72e-11) R^2 0.004738
تملك المعامِلات -كما ذكرنا سابقًا- دلالةً إحصائيةً لكن قيمة R2 منخفضةً، كما تؤكِّد هذه النماذج النتائج التي رأيناها بالفعل، لكن يمكننا الآن ملاءمة نموذج واحد يتضمن كلا المتغيرين بحيث نحصل على ما يلي باستخدام المعادلة totalwgt_lb ~ isfirst + agepreg:
Intercept 6.91 (0) isfirst[T.True] -0.0698 (0.0253) agepreg 0.0154 (3.93e-08) R^2 0.005289
إنّ قيمة المعامِل isfirst أصغر بحوالي النصف في النموذج المشترك، مما يعني أنه يتم حساب جزء من التأثير الظاهر للعمود isfirst بواسطة agepreg، كما أن القيمة الاحتمالية للعمود isfirst هي حوالي 2.5% وهي على حدود الدلالة الإحصائية، لكن قيمة R2 في هذا النموذج أعلى بقليل، أي أنّ المتغيرين معًا يمثلان تباينًا أكبر من التباين الذي يمثله كل منهما بمفرده في وزن المواليد ولكن الفرق ليس بكبير.
العلاقات اللاخطية
قد تكون المساهمة التي قدمها agepreg لاخطيةً، لذا قد نفكر في إضافة متغير يصف العلاقة وصفًا أفضل، ويتمثل أحد الخيارات في إنشاء عمود آخر باسم agepreg2 يحتوي على مربعات الأعمار كما يلي:
live['agepreg2'] = live.agepreg**2 formula = 'totalwgt_lb ~ isfirst + agepreg + agepreg2'
يمكننا ملاءمة قطع مكافئ parabola ملائمةً فعالةً عن طريق تقدير المعامِلَين agepreg وagepreg2 كما يلي:
Intercept 5.69 (1.38e-86) isfirst[T.True] -0.0504 (0.109) agepreg 0.112 (3.23e-07) agepreg2 -0.00185 (8.8e-06) R^2 0.007462
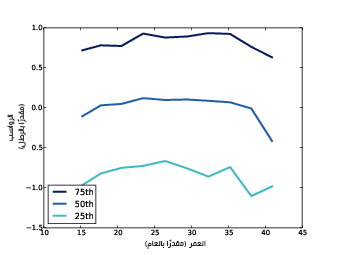
لدينا المعامِل agepreg2 سالبًا لذا ينحني القطع المكافئ إلى الأسفل، وهذا متوافق تمامًا مع شكل الخطوط في الشكل 10.2 في هذا الفصل، ويمثِّل النموذج التربيعي quadratic model للمعامِل agepreg2 تباينًا أكبر في وزن الطفل عند الولادة، كما أنّ isfirst أصغر في هذا النموذج ولم يعُد ذا دلالة إحصائية.
يُعَدّ استخدام متغيرات محسوبة مثل agepreg2 طريقةً شائعةً لملاءمة كثيرات الحدود ودوال أخرى مع البيانات، ولا تزال هذه العملية مندرجةً تحت نوع الانحدار الخطي لأن المتغير التابع هو دالة خطية للمتغيرات التوضيحية بغض النظر عما إذا كانت بعض المتغيرات تمثِّل دوالًا لاخطيةً لغيرها، كما يلخِّص الجدول التالي نتائج تحليلات الانحدار هذه:
| isfirst | agepreg | agepreg2 | R2 | |
|---|---|---|---|---|
| النموذج الأول | -0.125 * | - | - | 0.002 |
| النموذج الثاني | - | 0.0175 * | - | 0.0047 |
| النموذج الثالث | -0.0698 (0.025) | 0.0154 * | - | 0.0053 |
| النموذج الرابع | -0.0504 (0.11) | 0.112* | -0.00185 * | 0.0075 |
تمثِّل أعمدة هذا الجدول المتغيرات التوضيحية بالإضافة إلى مُعامِل التحديد R2، حيث تُعَدّ كل خانة من الجدول معامِلًا مقدَّرًا وإما قيمةً احتماليةً بين قوسين أو قيمةً احتماليةً بجانبها علامة نجمية * تشير إلى أن القيمة الاحتمالية أقل من 0.001.
نستنتج مما سبق أنّ الاختلاف الواضح في وزن الطفل عند الولادة هو بسبب الفرق في عمر الأم بصورة جزئية على الأقل، إذ يصغر تأثير isfirst عندما نضيف عمر الأم إلى النموذج، وقد يكون التأثير المتبقي هو بسبب الصدفة فقط، ويكون عمر الأم في هذا المثال متغير تحكم control variable حيث أن إضافة المتغير agepreg إلى النموذج "يتحكم" بالفرق في العمر بين أمهات الأطفال الأوائل وأمهات بقية الأطفال مما يجعل عزل تأثير isfirst ممكنًا إذا وجد.
التنقيب في البيانات
لم نستخدِم حتى الآن سوى نماذج الانحدار لتفسير التأثيرات، فقد اكتشفنا في القسم السابق أن الفرق الواضح في وزن الطفل عند الولادة ناتج عن فرق في عمر الأم، لكن قيم R2 لهذه النماذج هي قيم منخفضة جدًا، مما يعني أن قوتها التنبؤية ضئيلة، لذا سنحاول إيجاد طريقة أفضل في هذا المقال.
لنفترض أنّ أحد زملائك يتوقع ولادة طفله في الوقت القريب القادم وهناك لعبة تخمين في المكتب لتوقُّع وزن الطفل عند الولادة، فإذا افترضنا الآن أنه لديك رغبةً كبيرةً في ربح هذه اللعبة، ما الذي يمكنك أن تفعله لتحسين احتمال فوزك؟ تحتوي مجموعة بيانات المسح الوطني لنمو الأسرة على 244 متغير لكل حالة حمل وحوالي 3087 متغير لكل مستجيب، فقد يكون لبعض هذه المتغيرات قوةً تنبؤيةً، لذا لِمَ لا نجربها جميعًا لنعلم أي منها هو الأكثر فائدةً؟
تُعَدّ عملية اختبار المتغيرات في جدول الحَمل عمليةً سهلةً، لكن سيتوجب علينا مطابقة كل حالة حمل مع مستجيب إذا أردنا استخدام متغيرات جدول المستجيبين، ويمكننا نظريًا المرور على صفوف جدول الحمل ومن ثم استخدام المتغير caseid لإيجاد المستجيب الموافق لحالة الحمل ثم نسخ القيم من جدول المستجيبين إلى جدول حالات الحمل لكن ستتطلب هذه العملية وقتًا كبيرًا.
يوجد خيار أفضل وهو عملية الضم join المُعرَّفة في لغة الاستعلامات المهيكلة SQL، كما يمكنك الاطلاع على مقال الدمج بين الجداول في SQL لمزيد من المعلومات حول لمزيد من المعلومات حول العملية، علمًا أنّ التنفيذ البرمجي لهذه العملية هنا هو على صورة إطار بيانات، لذا يمكننا إجراءها كما يلي:
live = live[live.prglngth>30] resp = chap01soln.ReadFemResp() resp.index = resp.caseid join = live.join(resp, on='caseid', rsuffix='_r')
يحدِّد السطر الأول سجلات حالات الحمل التي تزيد مدتها عن 30 أسبوعًا بافتراض أنّ لعبة التخمين في المكتب قد بدأت قبل عدة أسابيع من موعد الولادة، في حين يقرأ السطر التالي ملف المستجيبين، وتكون النتيجة هي إطار بيانات يحوي فهارس صحيحة integer، لكننا استبدلنا resp.caseid مكان resp.index من أجل البحث عن المستجيبين بكفاءة عالية.
استُدعِي التابع join في live وهو يمثِّل الجدول الأيسر، ومرِّر respالذي يمثِّل الجدول الأيمن؛ أما الوسيط المحجوز on فيشير إلى المتغير المستخدَم لمطابقة الصفوف من الجدولين، وتظهر في هذا المثال بعض أسماء الجداول في الجدولين، لذا يجب توفير المتغير rsuffix الذي يُعَدّ سلسلةً نصيةً string والتي ستُضاف إلى نهاية أسماء الأعمدة المتكررة في الجدول الأيمن، فقد يحتوي مثلًا كلا الجدولين على عمود باسم race يرمز لعِرق المستجيب، وبالتالي ستحتوي نتيجة الضم على عمود باسم race وعمود باسم race_r.
يُعَدّ التنفيذ البرمجي لبانداز pandas سريعًا، حيث لا يستغرق ضم جداول المسح الوطني لنمو الأسرة أكثر من ثانية واحدة وباستخدام حاسوب عادي، ويمكننا الآن البدء باختبار المتغيرات.
t = [] for name in join.columns: try: if join[name].var() < 1e-7: continue formula = 'totalwgt_lb ~ agepreg + ' + name model = smf.ols(formula, data=join) if model.nobs < len(join)/2: continue results = model.fit() except (ValueError, TypeError): continue t.append((results.rsquared, name))
يمكننا إنشاء نموذج لكل متغير ثم حساب R2 وإضافة النتيجة إلى قائمة، كما تحتوي النماذج كلها على agepreg نظرًا لأننا نعلم مسبقًا أنها تمتلك بعض القوة التنبؤية، كما تحققنا أن لكل لمتغير توضيحي بعض التباين، وإلا لن يكون من الممكن الاعتماد على نتائج الانحدار، وتحققنا أيضًا من عدد المرات التي رُصد فيها كل نموذج، فلا يمكن أن تكون المتغيرات التي تحتوي على عدد كبير من قيم nans جيدةً للتنبؤ.
لم يُطبَّق على معظم هذه المتغيرات أيّ عملية تنظيف للبيانات، حيث أن بعضها مرمَّز بطريقة غير مناسبة كثيرًا للانحدار الخطي، ونتيجة لهذا فقد نتجاهل بعض المتغيرات التي قد تكون مفيدةً إذا نُقّيَت تنقيةً صحيحةً، لكن ربما سنجد بعض المتغيرات التي يحتمل أن تكون مناسبة للتنبؤ.
التنبؤ
تتمثل الخطوة التالية في فرز النتائج وتحديد المتغيرات التي تنتج أعلى قيم R2:
t.sort(reverse=True) for mse, name in t[:30]: print(name, mse)
يُعَدّ totalwgt_lb أول متغير على القائمة ثم birthwgt_lb، لكن من الواضح أنه لا يمكننا استخدام وزن الطفل عند الولادة لتوقع الوزن نفسه، كما يملك المتغير prglngth قوةً تنبؤيةً مفيدةً، لكننا سنفترض أثناء تعاملنا مع لعبة التخمين في المكتب أنّ مدة الحمل وبقية المتغيرات ذات الصلة غير معروفة بعد.
يُعَدّ babysex أول متغير تنبؤي مفيد والذي يشير إلى جنس الطفل فيما إذا هو ذكر أو أنثى، ويكون الصبيان في مجموعة بيانات المسح الوطني لنمو الأسرة أكبر وزنًا بحوالي 0.3 رطلًا -أي 0.13 كيلوغرامًا تقريبًا-، لذا سنتمكن من استخدام جنس المولود في التنبؤ إذا افترضنا أنه معروف.
يشير المتغير race الذي إلى عِرق المستجيب فيما إذا هو أسود البشرة أو أبيض البشرة أو غير ذلك، وقد يكون العِرق إشكاليًا إن تعاملنا معه على أساس متغير توضيحي، لكن يرتبط المتغير race في بيانات المسح الوطني لنمو الأسرة بالعديد من المتغيرات الأخرى بما في ذلك الدخل والعوامل الاجتماعية والاقتصادية الأخرى، علمًا أنه في نموذج الانحدار كان العِرق متغيرًا وكيلًا proxy variable، لذلك غالبًا ما تكون الارتباطات الظاهرة مع العِرق ناتجةً عن عوامل أخرى بصورة جزئية على الأقل.
يكون المتغير التالي في القائمة هو nbrnaliv والذي يشير إلى ما إذا كان الحمل قد أدى إلى ولادة متعددة -أي ولادة توأم من طفلين أو أكثر-، وعادةً ما يكون التوأم من طفلين أو ثلاث أطفال أقل وزنًا من غيرهم، لذا فقد يساعدنا معرفة فيما إذا كان زميلنا الافتراضي يتوقع ولادة توأم؛ أما المتغير paydu فيشير إلى ما إذا كان المستجيب يمتلك منزله أم لا، وهو أحد المتغيرات التي تتعلق بالدخل بالإضافة إلى عدة متغيرات أخرى والتي توضح أنها تنبؤية، ويكون الدخل والثروة في مجموعة بيانات مثل المسح الوطني لنمو الأسرة مرتبطَين بكل شي تقريبًا، حيث يرتبط الدخل في هذا المثال بالحمية الغذائية والصحة والعناية الصحية وعوامل أخرى من المرجح أن تؤثِّر على وزن الطفل عند الولادة.
توجد متغيرات أخرى في القائمة لكنها أمور لن نعرفها إلا في وقت لاحق مثل bfeedwks والذي يمثِّل عدد الأسابيع التي رضع فيها الطفل رضاعةً طبيعيةً، وعلى الرغم أنه لا يمكننا استخدام هذه المتغيرات للتنبؤ إلا أنك قد ترغب في التكهن بالأسباب التي قد يرتبط فيها المتغير bfeedwks مع الوزن عند الولادة، وقد تلجأ في بعض الأحيان إلى البدء بنظرية ومن ثم اختبارها باستخدام بيانات معينة، وفي بعض الأحيان قد تبدأ ببيانات ومن ثم تبحث عن نظريات ممكنة.
سنستعرِض في هذا القسم الطريقة الثانية والتي تدعى التنقيب في البيانات data mining، ومن مزايا التنقيب في البيانات هو اكتشاف أنماط غير متوقعة، لكن الخطر هو أنه قد تكون العديد من الأنماط المُكتشَفة عشوائيةً أو زائفةً، وقد اختبرنا بعد تحديد المتغيرات التوضيحية المحتمَلة بعض النماذج واستقرَّينا على هذا النموذج:
formula = ('totalwgt_lb ~ agepreg + C(race) + babysex==1 + ' 'nbrnaliv>1 + paydu==1 + totincr') results = smf.ols(formula, data=join).fit()
تستخدِم هذه المعادلة formula صياغة syntax لم نرها بعد مثل C(race) التي تطلب من محلل الصيغة باتسي Patsy معاملة العِرق على أساس متغير فئوي على الرغم أنه مرمَّز بصورة عددية، كما يكون ترميز المتغير babysex هو 1 للذكر و2 للأنثى، لكن إذا كتبنا babysex==1، فسيتحول المتغير إلى النوع البولياني ليصبح True للذكر وfalse للأنثى، وبالمثل يكون nbrnaliv> 1 هو True للولادات المتعددة ويكون paydu == 1 هو True للمستجيبين الذين يمتلكون منازلهم، علمًا أن المتغير totincr مرمز عدديًا من 1-14، حيث تمثِّل كل زيادة حوالي 5000 دولارًا أمريكيًا في الدخل السنوي، لذا يمكننا التعامل مع هذه القيم على أنها عددية ونعبِّر عنها بوحدات من 5000 دولارًا أمريكيًا، وإليك نتائج النموذج كما يلي:
Intercept 6.63 (0) C(race)[T.2] 0.357 (5.43e-29) C(race)[T.3] 0.266 (2.33e-07) babysex == 1[T.True] 0.295 (5.39e-29) nbrnaliv > 1[T.True] -1.38 (5.1e-37) paydu == 1[T.True] 0.12 (0.000114) agepreg 0.00741 (0.0035) totincr 0.0122 (0.00188)
من المفاجئ أن المعامِلات المقدَّرة للعِرق أكبر مما توقعنا خاصةً وأن المتغير التحكم هو الدخل، علمًا أن الترميز هو 1 لذوي البشرة السوداء و2 لذوي البشرة البيضاء و3 غير ذلك، إذًا يكون أطفال الأمهات ذوات البشرة السوداء أقل وزنًا من الأطفال الذي ينتمون إلى عروق أخرى بحوالي 0.27 - 0.36 رطلًا -أي بين 0.12 - 0.16 كيلوغرامًا-، وكما رأينا سابقًا فقد يميل الصبيان لأن يكونوا أكثر وزنًا بحوالي 0.3 رطلًا -أي 0.13 كيلوغرامًا تقريبًا-؛ أما التوائم سواءً اثنين أو أكثر فتكون أقل وزنًا بحوالي 1.4 رطلًا -أي 0.6 كيلوغرامًا تقريبًا-.
الأشخاص الذين يمتلكون منازلهم يلدون أطفالًا أكثر وزنًا بحوالي 0.12 رطلًا -أي 0.05 كيلوغرامًا تقريبًا- حتى عندما يكون متغير التحكم هو الدخل، ويكون معامِل عمر الأم هنا أقل من الذي رأيناه في جزئية الانحدار المتعدد في هذا المقال، مما يشير إلى أن بعض المتغيرات الأخرى مرتبطةً بالعمر، بما في ذلك على الأرجح paydu وtotincr.
نستنتج أنّ هذه المتغيرات ذو دلالة إحصائية ولبعضها قيمة احتمالية منخفضة جدًا، لكن قيمة R2 هي 0.06 فقط وهو مقدار صغير جدًا، كما أن قيمة جذر متوسط مربع الخطأ RMSE هي 1.27 رطل -أي حوالي 0.57 كيلوغرام- بدون استخدام النموذج؛ أما في حال استخدمنا النموذج فستنخفض القيمة إلى 1.23 رطل -أي حوالي 0.55 كيلوغرام-، أي لم تتحسن فرصتك في الفوز بلعبة التخمين تسحنًا كبيرًا.
الانحدار اللوجستي
وردت في أمثلتنا السابقة عدة متغيرات توضيحية، كان بعضها عدديًا وبعضها الآخر فئويًا بما فيها البولياني، لكن المتغير التابع كان دائمًا عدديًا، لذا يمكن تعميم الانحدار الخطي ليكون قادرًا على التعامل مع أنواع أخرى من المتغيرات التابعة، فإذا كان المتغير التابع بوليانيًا، فسيُدعى النموذج المعمم بالانحدار اللوجستي logistic regression؛ أما إذا كان المتغير التابع عددًا صحيحًا ويمثِّل تعدادًا، فسيُدعى بانحدار بواسون Poisson regression.
دعنا نضع تباينًا على سيناريو لعبة التخمين في المكتب على أساس مثال عن الانحدار اللوجستي، حيث سنفترض أنّ صديقتك حامل وتريد توقُّع فيما إذا كان المولود صبيًا أو بنتًا، إذ يمكنك عندها استخدام البيانات الخاصة بالمسح الوطني لنمو الأسرة لإيجاد العوامل المؤثرة على نسبة الجنس التي عُرِّفت عادةً على أنها احتمال كون المولود صبيًا، فإذا كان المتغير التابع من النوع العددي، بحيث يكون 0 إذا كان المولود بنتًا و1 إذا كان صبيًا على سبيل المثال، ويمكنك عندها تطبيق طريقة المربعات الصغرى العادية لكن سنواجه عندها بعض المشاكل، وقد يكون النموذج الخطي مثل هذا:
| y = β0 + β1 x1 + β2 x2 + ε |
حيث يكون y هو المتغير التابع وتكون x1 وx2 هي متغيرات توضيحية، أي يمكننا الآن إيجاد المعامِلات التي تقلل من الرواسب residuals، لكن مشكلة هذه الطريقة أنها تنتج تنبؤات يصعب تفسيرها.
نظرًا للمعامِلات المقدَّرة وقيم كل من x1 وx2، فقد يتنبأ النموذج أنّ y=0.5، لكن القيم الوحيدة ذات المعنى للمتغير y هي 0 و1، وقد يكون من المغري تفسير نتيجة مثل هذه على أنها احتمال، فقد نقول مثلًا أنّ المستجيب صاحب القيم المعينة للمتغيرَين x1 وx2 لديه فرصة 50% في إنجاب صبي، لكن من الممكن أن يتنبأ هذا النموذج بـy=1.1 أو y= -0.1، إلا أنّ هذه الاحتمالات غير صالحة.
يتجنب الانحدار اللوجستي هذه المشكلة عن طريق التعبير عن التنبؤات على صورة أرجحية odds بدلًا من الاحتمالات، وإذا لم يكن لديك فكرةً مسبقةً عن الأرجحية، فسنقول لك أنّ "الأرجحية لصالح" odds in favor حدث ما هي نسبة احتمال حدوثه إلى احتمال عدم حدوثه، فإذا اعتقدنا أنّ للفريق فرصة فوز بنسبة 75%، فسنقول أنّ الأرجحية لصالحهم هي 3 على 1 لأن فرصة الفوز هي ثلاثة أضعاف فرصة الخسارة، ويمثِّل كل من الأرجحية والاحتمال المعلومات نفسها لكن بطرق مختلفة، كما يمكننا حساب يمكننا حساب الأرجحية إذا كان لدينا احتمال ما باستخدام هذه المعادلة:
o = p / (1-p)
أما إذا كان لدينا قيمة الأرجحية لصالح، فيمكننا تحويلها إلى احتمال باستخدام هذه المعادلة:
p = o / (o+1)
يعتمد الانحدار اللوجستي على النموذج التالي:
| logo = β0 + β1 x1 + β2 x2 + ε |
يمثِّل o الأرجحية لصالح نتيجة ما، حيث يكون o هو الأرجحية لصالح ولادة صبي مثلًا، ولنفترض أنه لدينا المعامِلات المقدَّرةβ0 وβ1وβ2 والتي سنشرحها بعد قليل، ولنفترض أنه لدينا قيم x1 وx2، حيث يمكننا عندها حساب القيمة المتوقعة لـ logo ثم تحويلها إلى احتمال كما يلي:
o = np.exp(log_o) p = o / (o+1)
لذا يمكننا في سيناريو لعبة التخمين في المكتب حساب الاحتمال التنبؤي لولادة صبي، لكن كيف يمكننا تقدير المعامِلات؟
تقدير المعاملات
لا يحتوي الانحدار الخطي على حل منغلق الشكل على عكس الانحدار الخطي، لذا يمكن حله عن طريق تخمين حل أولي ومن ثم تحسينه في كل تكرار، حيث أنّ الهدف المعتاد هو إيجاد تقدير الاحتمال الأعظم maximum-likelihood estimate -أو MLE اختصارًا- وهو مجموعة من المعامِلات التي تزيد من احتمالية البيانات، ولنفترض مثلًا أنه لدينا البيانات التالية:
>>> y = np.array([0, 1, 0, 1]) >>> x1 = np.array([0, 0, 0, 1]) >>> x2 = np.array([0, 1, 1, 1])
نبدأ بالتخمينات الأولية وهي β0= -1.5 و β1=2.8و β2=1.1:
>>> beta = [-1.5, 2.8, 1.1]
ثم نحسب log_o لكل صف بمفرده:
>>> log_o = beta[0] + beta[1] * x1 + beta[2] * x2 [-1.5 -0.4 -0.4 2.4]
بعد ذلك نحول الأرجحية اللوغاريتمية إلى احتمالات:
>>> o = np.exp(log_o) [ 0.223 0.670 0.670 11.02 ] >>> p = o / (o+1) [ 0.182 0.401 0.401 0.916 ]
لاحظ أنه عندما يكونlog_o أكبر من الصفر، تكون قيمة o أكبر من الواحد، وتكون قيمة p أكبر من 0.5.
تكون احتمالية likelihood خرج ما هي p عندما يكون 1==y وتكون 1-p عندما يكون 0==y، ولنفترض مثلًا أنه اعتقدنا أن احتمال probability ولادة صبي هي 0.8 وكان الخرج هو ولادة صبي، فستكون الاحتمالية likelihood هي 0.8، وإذا كان الخرج فتاةً، فستتكون الاحتمالية 0.2، كما يمكننا إجراء الحسابات كما يلي:
>>> likes = y * p + (1-y) * (1-p) [ 0.817 0.401 0.598 0.916 ]
تكون الاحتمالية الإجمالية للبيانات هي ناتج ضرب قيم likes:
>>> like = np.prod(likes) 0.18
تكون احتمالية البيانات 0.18 في حال اعتمدنا قيم بيتا beta هذه، علمًا أن هدف الانحدار اللوجستي هو إيجاد المعامِلات التي تزيد من هذه الاحتمالية، ولإجراء هذا تستخدِم معظم الحِزم حلًا تكراريًا مثل تابع نيوتن Newton’s method، كما يمكنك زيارة صفحة ويكيبيديا للمزيد من التفاصيل.
التنفيذ implementation
تزودنا StatsModels بتنفيذ برمجي للانحدار اللوجستي ويُدعى logit وسُمي باسم الدالة التي تحول الاحتمال إلى الأرجحية اللوغاريتمية log odds، كما سنبحث عن متغيرات تؤثِّر على نسبة الجنس لتوضيح استخدامه.، وسنُعيد تحميل بيانات المسح الوطني لنمو الأسرة وسنختار حالات الحمل التي تجاوزت مدتها 30 أسبوع:
live, firsts, others = first.MakeFrames() df = live[live.prglngth>30]
لكن أحد شروط logit هو أن يكون المتغير التابع ثنائيًا binary عوضًا بدلًا من النوع البولياني boolean، لذا فقد أنشأنا عمودًا جديدًا باسم boy باستخدام astype(int) لتحويل القيم إلى قيم ثنائية صحيحة binary integers:
df['boy'] = (df.babysex==1).astype(int)
يُعَدّ عمر الوالدَين وترتيب الولادة والعِرق والحالة الاجتماعية عواملًا مؤثرةً في نسبة الجنس، كما يمكننا استخدام الانحدار اللوجستي من أجل التحقق فيما إذا كانت تظهر هذه التأثيرات في بيانات المسح الوطني لنمو الأسرة، حيث سنبدأ أولًا من عمر الأم:
import statsmodels.formula.api as smf model = smf.logit('boy ~ agepreg', data=df) results = model.fit() SummarizeResults(results)
تأخذ الدالتان logit وols الوسائط نفسها وهي عبارة عن معادلة بصيغة Patsy بالإضافة إلى إطار بيانات، وتكون نتيجة الدالة logit هي كائن Logit يمثِّل النموذج، حيث يتضمن سمتين بحيث تحتوي السمة الأولى endog على المتغير الداخلي endogenous variable وهو اسم آخر للمتغير التابع؛ أما السمة الثانية exog فتحتوي على المتغيرات الخارجية exogenous variables وهو اسم آخر للمتغيرات التوضيحية، وبما أنهما مصفوفتَي نمباي NumPy arrays، فقد يكون من الأفضل في بعض الأحيان تحويلها إلى أُطر بيانات DataFrames:
endog = pandas.DataFrame(model.endog, columns=[model.endog_names]) exog = pandas.DataFrame(model.exog, columns=model.exog_names)
تكون نتيجة model.fit كائن BinaryResults يشبه كائن RegressionResults الذي ينتج من ols، وإليك تلخيص للنتائج كما يلي:
Intercept 0.00579 (0.953) agepreg 0.00105 (0.783) R^2 6.144e-06
وجدنا أن المعامِل الخاص بـ ageprep موجب الذي يشير إلى أنه من المرجح ولادة الأمهات الأكبر سنًا صبيانًا، لكن القيمة الاحتمالية هي 0.783 التي تعني أنه يمكن أن يكون التأثير الواضح ناتجًا عن الصدفة، ولا ينطبق مُعامِل التحديد R2 على الانحدار اللوجستي لكن يوجد عدة بدائل وتُدعى قيم R2 الوهمية أي pseudo-R2، إذ يمكن أن تكون هذه القيم مفيدةً لموازنة النماذج، وإليك على سبيل المثال نموذج يتضمن عدة عوامل يُقال أنها مرتبطة بنسبة الجنس:
formula = 'boy ~ agepreg + hpagelb + birthord + C(race)' model = smf.logit(formula, data=df) results = model.fit()
يتضمن هذا النموذج عمر الأب عند الولادة hpagelb إلى جانب عمر الأم أيضًا، ويمثِّل المتغير birthord ترتيب ولادة الطفل؛ أما العِرق فهو متغير فئوي، وإليك ما نتج كما يلي:
Intercept -0.0301 (0.772) C(race)[T.2] -0.0224 (0.66) C(race)[T.3] -0.000457 (0.996) agepreg -0.00267 (0.629) hpagelb 0.0047 (0.266) birthord 0.00501 (0.821) R^2 0.000144
ليس لأي من هذه المعامِلات المُقدَّرة دلالة إحصائية، وعلى الرغم أن قيمة R2 الوهمية أعلى بقليل إلا أنه من المحتمل أن يكون هذا صدفةً.
الدقة Accuracy
أكثر ما يهمنا في سيناريو لعبة التخمين في المكتب هو دقة النموذج، وهي عبارة عن عدد التنبؤات الصحيحة موازنةً مع ما نتوقعه صدفةً، ونظرًا لأن عدد الصبيان يفوق عدد الإناث في بيانات المسح الوطني لنمو الأسرة، فيمكننا تحديد الاستراتيجية الأساسية على أنها تخمين ولادة صبي في كل مرة، وبذلك تكون دقة النموذج هي نسبة الصبيان:
actual = endog['boy'] baseline = actual.mean()
يكون المتوسط mean هو نسبة الصبيان وقيمته 0.507 بما أنه رُمِّز المتغير actual بترميز ثنائي صحيح binary integers، وإليك طريقة حساب دقة النموذج كما يلي:
predict = (results.predict() >= 0.5)
true_pos = predict * actual
true_neg = (1 - predict) * (1 - actual)
يُعيد results.predict مصفوفة نمباي NumPy array تحتوي على الاحتمالات والتي نقربها إلى 0 أو 1، علمًا أنه ينتج 1 عن عملية جداء مع المتغير actual إذا توقعنا ولادة صبي وأصبنا التوقُّع، في حين ينتج 0 في غير ذلك، لذا يشير المتغير true_pos إلى true positives أي الإيجابيات الصحيحة، كما يشير المتغير true_neg إلى الحالات التي نتوقع فيها ولادة بنت ويصيب توقعنا، وبلتالي تكون الدقة هي نسبة التخمينات الصحيحة:
acc = (sum(true_pos) + sum(true_neg)) / len(actual)
ظهرت النتيجة 0.512 وهي أفضل بقليل من القيمة الأساسية 0.507، لكن عليك ألا تأخذ هذه النتيجة على محمل الجد لأننا استخدَمنا البيانات نفسها في عمليتَي بناء واختبار النموذج، لذا قد لا يمتلك النموذج قوةً تنبؤيةً على البيانات الجديدة، لكن دعنا على أيّ حال نستخدِم النموذج للتبنؤ في لعبة التخمين في المكتب ولنفترض أنّ عمر صديقتك 35 عامًا وذات بشرة بيضاء وعمر زوجها 39 عامًا وأنها حامل بطفلهما الثالث:
columns = ['agepreg', 'hpagelb', 'birthord', 'race'] new = pandas.DataFrame([[35, 39, 3, 2]], columns=columns) y = results.predict(new)
إذا أردنا استدعاء results.predict لحالة حمل جديدة، فسيتوجب علينا إنشاء إطار بيانات DataFrame يحوي عمودًا لكل متغير في النموذج وتكون النتيجة في هذه الحالة 0.52، لذا يجب عليك تخمين ولادة صبي، لكن إذا حسَّن النموذج من فرصك في الفوز، فسيكون الفارق ضئيلًا جدًا.
التمارين
يوجد الحل الخاص بنا في chap11soln.ipynb.
تمرين 1
لنفترض أن ولادة طفل أحد زملائك في العمل قد اقتربت وقررت المشاركة في لعبة التخمين في المكتب لتوقع موعد الولادة، فإذا افترضنا أنّ التخمينات قد حصلت في الأسبوع الثلاثين من الحمل، فما هي المتغيرات التي ستستخدِمها لتحقيق أفضل تنبؤ؟ يجب أن يقتصر استخدامك للمتغيرات على المتغيرات المعلومة قبل الولادة وتلك التي من المرجح أن تكون معروفةً عند المشاركين في لعبة المكتب.
تمرين 2
تقترح فرضية تريفرز-ويلارد Trivers-Willard hypothesis اعتمادية نسبة الجنس بالنسبة للعديد من الثدييات على حالة الأم، أي تعتمد على عوامل مثل عمر الأم وحجمها وصحتها وحالتها الاجتماعية، كما يمكنك الاطلاع على صفحة ويكيبيديا للمزيد من التفاصيل.، حيث أظهرت بعض الدراسات وجود هذا التأثير ضمن البشر لكن النتائج مختلطة، إذ أجرينا اختبارات على بعض المتغيرات المتعلِّقة بهذه العوامل لكننا لم نجد أي تأثير ذا دلالة إحصائية على نسبة الجنس.
اختبر المتغيرات الأخرى في ملفات الحمل والمستجيبِين باستخدام طريقة التنقيب عن البيانات، وذلك على أساس تمرين على ما سبق، هل وجدت بعد ذلك أيّ عوامل لها تأثير كبير؟
تمرين 3
يمكنك استخدام انحدار بواسون Poisson regression إذا كانت القيمة التي تريد التنبؤ بها تعدادًا، علمًا أنّ تنفيذ انحدار بواسون البرمجي موجود في StatsModels مع دالة اسمها poisson، وهي تعمل بالطريقة نفسها التي تعمل فيها الدالتين ols وlogit، لذا دعنا نستخدِم هذه الدالة على أساس تمرين لما سبق للتنبؤ بعدد أطفال امرأة معيّنة في بيانات المسح الوطني لنمو الأسرة، حيث أن اسم المتغير الذي يمثل عدد الأطفال هو numbabes.
لنفترض أنك قابلت امرأةً تبلغ من العمر 35 عامًا سوداء البشرة وخريجة جامعية يتجاوز دخل أسرتها السنوي 75 ألف دولار، فكم تتوقع أن يكون عدد أطفالها؟
تمرين 4
يمكنك استخدام الانحدار اللوجستي متعدد الحدود multinomial logistic regression إذا أردت تنبؤ قيمة فئوية، علمًا أنّ تنفيذه البرمجي في StatsModels مع دالة اسمها mnlogit، لذا دعنا نستخدِم هذه الدالة على أساس تمرين لما سبق لتخمين فيما إذا كانت المرأة متزوجة أو أرملة أو منفصلة عن زوجها أو أنها لم تتزوج على الإطلاق، علمًا أنّ اسم المتغير الذي يمثل الحالة الزوجية في المسح الوطني لنمو الأسرة هو rmarital.
لنفترض أنك قابلت امرأةً تبلغ من العمر 25 عامًا بيضاء البشرة وأنهت دراسة المرحلة الثانوية لكنها لم تدرس في المرحلة الجامعية ودخل أسرتها السنوي حوالي 45 ألف دولار، ما هو احتمال أن تكون متزوجة أو أرملة، …إلخ؟
ترجمة -وبتصرف- للفصل Chapter 11 Regression analysis من كتاب Think Stats: Exploratory Data Analysis in Python.











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.