توجد الشيفرة الخاصة بهذا المقال في ملف estimation.py.
لعبة التقدير
ستكون بداية هذا المقال مع لعبة، حيث سنعطيك توزيعًا ومهمتك هي تخمين ماهية هذا التوزيع، كما سنزوِّدك بتلميحَين هما أنّ التوزيع طبيعي، وأن هناك عينةً عشوائيةً منه:
[-0.441, 1.774, -0.101, -1.138, 2.975, -2.138]
برأيك ما هو معامل المتوسط μ لهذا التوزيع؟
يمكننا استخدام متوسط العينة x̄ على أساس تقدير لـ μ، حيث يكون متوسط العينة في هذا المثال هو 0.155 أي x̄=0.155، لذا من المنطقي قولنا أنّ μ=0.155، حيث تدعى هذه العملية بالتقدير estimation، وتُدعى الإحصائية التي استخدمناها -أي متوسط العينة- بالمقدِّر estimator.
في الواقع يُعَدّ استخدام متوسط العينة لتقدير واضحًا لدرجة أنه من الصعب علينا تخيل وجود بديل منطقي، لكننا سنعدِّل اللعبة الآن عن طريق إضافة قيم شاذة outliers، ويكون التوزيع الجديد توزيعًا طبيعيًا أيضًا، وإليك عينةً جمَعها مسّاح غير موثوق به يضع الفاصلة العشرية في المكان الخطأ أحيانًا:
[-0.441, 1.774, -0.101, -1.138, 2.975, -213.8]
ما هو تقديرك لقيمة μ؟ إذا استخدمت متوسط العينة في عملية التقدير، فسيكون تخمينك هو 35.12-، لكن هل هذا هو الخيار الأفضل؟ وما هي البدائل؟
تُعَدّ عملية تحديد القيم الشاذة والتخلص منها ومن ثم حساب متوسط العينة لما تبقى هي إحدى هذه البدائل، كما يمكننا استخدام الوسيط median على أساس مُقدِّر، لكن يعتمد تحديد المُقدِّر الأفضل على الظروف مثل ما إذا كانت هناك قيم شاذة، وعلى الهدف مثل هل تحاول تقليل الأخطاء أو زيادة فرصتك في الحصول على الإجابة الصحيحة؟
يقلل متوسط العينة من متوسط الخطأ التربيعي mean squared error - أو MSE اختصارًا- إذا لم تكن هناك أيّ قيم شاذة، أي إذا لعبنا اللعبة ذاتها عدة مرات وحسبنا الخطأ x̄-μ، فسيقِل متوسط العينة.
| MSE = |
|
∑(x − µ)2 |
حيث أنّ m هو عدد مرات لعبك للعبة التقدير، ومن المهم التفريق بينها وبين n حجم العينة المستخدَم في حساب x̄، وإليك الدالة التي تحاكي لعبة التقدير ومن ثم تحسب خطأ الجذر التربيعي المتوسط RSME وهو الجذر التربيعي لمتوسط الخطأ التربيعي:
def Estimate1(n=7, m=1000): mu = 0 sigma = 1 means = [] medians = [] for _ in range(m): xs = [random.gauss(mu, sigma) for i in range(n)] xbar = np.mean(xs) median = np.median(xs) means.append(xbar) medians.append(median) print('rmse xbar', RMSE(means, mu)) print('rmse median', RMSE(medians, mu))
نؤكد على أنّ n هو حجم العينة وm هو عدد مرات لعب اللعبة، في حين يكون means قائمة التقديرات المبنية على x̄ ويكون medians قائمة وسطاء medians، وفيما يلي الدالة التي تحسب خطأ الجذر التربيعي المتوسط RSME:
def RMSE(estimates, actual): e2 = [(estimate-actual)**2 for estimate in estimates] mse = np.mean(e2) return math.sqrt(mse)
تُعَدّ estimates قائمة التقديرات وactual القيمة الفعلية التي يتم تقديرها، لكن في التطبيق العملي تكون قيمة actual غير معروفة، إذ لسنا بحاجة إلى تقديرها في حال كنا نعرفها مسبقًا، حيث أن الغرض من هذه التجربة هو موازنة أداء المقدِّرات.
ظهرت نتيجة خطأ الجذر التربيعي المتوسط لمتوسط العينة 0.41 عندما نفّذنا هذه الشيفرة، مما يعني أنه إذا استخدمنا x̄ لتقدير متوسط هذا التوزيع بناءً على عينة تحوي 7 قيم أي n=7، فيجب علينا التوقع أن يكون الخطأ وسطيًا 0.41، وفي حال استخدام الوسيط median من أجل تقدير المتوسط فستنتج لدينا قيمة للخطأ الجذر التربيعي المتوسط، وهي 0.53، مما يعني أنه وعلى الأقل بالنسبة لهذا المثال ينتج عن x̄ خطأ الجذر التربيعي المتوسط الأدنى.
يُعَدّ تقليل الخطأ التربيعي المتوسط MSE خاصيةً جيدةً لكنها ليست الاستراتيجية الأفضل في كل الأوقات، فلنفترض مثلًا أننا نقدِّر توزيع سرعات الرياح في موقع بناء، فإذا كان التقدير مرتفعًا جدًا، فقد نبالغ في بناء الهيكل مما يزيد من تكلفته، لكن إذا كان التقدير منخفضًا للغاية، فقد ينهار البناء بسبب عدم الحذر أثناء البناء، كما أنّ تقليل الخطأ التربيعي المتوسط MSE ليس أفضل استراتيجية ممكنة، وذلك لأن التكلفة في حال كانت دالة خطأ ليست متناظرةً.
افترض أيضًا أننا ألقينا ثلاثة أحجار نرد سداسية الجوانب وطلبنا أن تتوقع مجموع الناتج الكلي، فإذا كان تقديرك صحيحًا تمامًا، فستحصل على جائزة؛ وإلا فلن تحصل على أيّ شيء، لذا تكون القيمة التي تقلل الخطأ التربيعي المتوسط MSE في هذه الحالة هي 10.5، لكن سيكون هذا تخمينًا سيئًا لأنه لا يمكن أن يكون مجموع الأرقام التي ظهرت على أحجار النرد الثلاثة 10.5 في أي حال من الأحوال، وبالنسبة لهذه اللعبة أنت تريد مُقدِّرًا لديه أعلى فرصة ليكون صحيحًا وهو مُقدِّر الاحتمال الأعظم maximum likelihood estimator -أو MLE اختصارًا-، فإذا اخترت 10 أو 11، فستكون فرصتك في الفوز هي 1 من 8 وهذا أفضل ما يمكنك الوصول إليه.
خمن التباين
إليك هذا التوزيع الطبيعي المألوف:
[-0.441, 1.774, -0.101, -1.138, 2.975, -2.138]
ما هي برأيك قيمة التباين σ2 الخاصة بالتوزيع السابق؟ بالطبع يُعَد الخيار الواضح هو استخدام تباين العينة S2 على أساس مُقدِّر estimator.
| S2 = |
|
∑(xi − x)2 |
لكن يكون S2 مقدِّرًا مناسبًا بالنسبة للعينات الضخمة إلا أنه يميل إلى أن يكون منخفضًا جدًا بالنسبة للعينات الصغيرة، حيث تطلق عليه تسمية المقدِّر المتحيز biased بسبب هذه الخاصية المؤسفة، لكن يكون المقدِّر غير متحيز unbiased إذا كان الخطأ المتوقع الكلي -أو المتوسط- هو 0 وذلك بعد عدة تكرارات للعبة التقدير، وتوجد لحسن الحظ إحصائية بسيطة أخرى غير متحيزة للتباين σ2 كما يلي:
| Sn−12 = |
|
∑(xi − x)2 |
إذا كنت تريد شرحًا عن سبب تحيز S2 وبرهانًا على عدم تحيز Sn-12 ، فيمكنك الاطلاع على الانحياز المقدر.
تتمثل أكبر مشكلة لهذا المُقدِّر في كون الاسم والرمز غير متناسقَين، حيث يمكن أن يشير الاسم "تباين العينة" إلى S2 أو Sn-12، كما أن فإن الرمز S2 يستخدَم للمصطلحين، وفيما يلي دالة تُحاكي لعبة التقدير وتختبر أداء كل من S2 وSn-12:
def Estimate2(n=7, m=1000): mu = 0 sigma = 1 estimates1 = [] estimates2 = [] for _ in range(m): xs = [random.gauss(mu, sigma) for i in range(n)] biased = np.var(xs) unbiased = np.var(xs, ddof=1) estimates1.append(biased) estimates2.append(unbiased) print('mean error biased', MeanError(estimates1, sigma**2)) print('mean error unbiased', MeanError(estimates2, sigma**2))
يشير n إلى حجم العينة وm إلى عدد مرات لعب اللعبة، كما يحسب التابع np.var المقدار S2 اقتراضيًا، إلى جانب أنه يمكن أن يحسب Sn-12 إذا زُوِّد بالوسيط ddof=1 الذي يشير إلى "درجة حرية دلتا"، وعلى الرغم من أنه لن نشرح هذا المصطلح إلا أنه يمكنك معرفة تفاصيله عن طريق الاطلاع على صفحة درجة الحرية على ويكيبيديا.
يحسب التابع MeanError متوسط الفرق بين التقديرات والقيمة الفعلية:
def MeanError(estimates, actual): errors = [estimate-actual for estimate in estimates] return np.mean(errors)
كان متوسط خطأ S2 عندما نفّذنا هذه الشيفرة هو -0.13، وكما هو متوقع، يميل المُقدِّر المتحيز إلى أن يكون منخفضًا للغاية، كما كانت قيمة Sn-12 هي 0.014 أي أقل بعشر مرات، وكلما ازدادت قيمة m توقعنا مقاربة متوسط خطأ Sn-12 من الصفر.
تُعَدّ خاصتَي الخطأ التربيعي المتوسط MSE والتحيز bias والخواص المشابهة توقعات للمدى الطويل وهي مبنية على عدة تكرارات للعبة التقدير، بحيث يمكننا موازنة المُقدِّرات والتحقق فيما إذا كان لها خصائصًا مرغوبًا بها أم لا عن طريق تشغيل عمليات محاكاة مثل الموجودة في هذا المقال، لكنك لا تحصل إلا على تقدير واحد حينما تطبق المُقدِّر على البيانات الحقيقية، إذ لن يكون قولنا بأنّ التقدير غير متحيز ذا أهمية أو معنى، وذلك لأن خاصية عدم التحيز هي خاصية المُقدِّر لا التقدير، وتكون الخطوة التالية بعد اختيارك المُقدِّر الذي يمتلك الخصائص المناسبة لك واستخدامه لتوليد التقدير هي توصيف عدم استقرار التقدير الذي سنتناوله في القسم التالي.
توزيعات أخذ العينات sampling distributions
لنفترض أنك عالم تهتم بدراسة الغوريلا في محمية للحياة البرية مثلًا، وتريد معرفة متوسط وزن أنثى حيوان الغوريلا في هذه المحمية، لكن سيتوجب عليك تهدئتها أولًا، وهذا أمر خطير ومُكلف وقد يضر بصحة الحيوان نفسه، لكن إذا كان الحصول على المعلومات أمرًا هامًا، فقد يكون من المقبول وزن تسعة منها إذا افترضنا أنّ العدد الكامل للمحمية معلوم مسبقًا ويمكننا عندها اختيار عينة تمثيلية للإناث البالغات، كما يمكننا استخدام متوسط العينة x̄ لتقدير متوسط عدد الحيوانات المجهولين μ.
قد تجد عند وزن 9 إناث أن x̄=90 kg وأن الانحراف المعياري للعينة هو S = 7.5 kg، حيث أن متوسط العينة هو مُقدِّر غير متحيز للمقدار μ ويقلل متوسط الخطأ التربيعي MSE على المدى الطويل، لذا إن كنت تريد الخروج بتقدير واحد يلخص النتيجة، فيمكنك اختيار القيمة 90 kg، لكن ما مدى ثقتك بهذا التقدير؟ إذا وزنت 9 إناث فقط n=9 من أصل عدد كبير، فقد لا يكون الحظ حليفك، فربما تكون قد اخترت أكثر الإناث وزنًا -أو أقلها وزنًا- عن طريق الصدفة وحسب.
يُعرَف تباين التقدير الناتج عن الاختيار العشوائي بخطأ أخذ العينات sampling error، حيث يمكننا حساب خطأ أخذ العينات عن طريق محاكاة عملية أخذ العينات بقيم افتراضية للمقدارين σ وμ، ومن ثم مراقبة مدى تباين x̄، كما سنستخدِم تقديرات كلًا من x̄ وS لعدم معرفتنا القيم الفعلية للمقدارين σ وμ، لذا يكون السؤال المطروح هو إذا كانت القيمة الفعلية هي σ=90 kg وμ = 7.5 kg ونفّذنا التجربة عدة مرات، فكيف سيتغير المتوسط المُقدَّر x̄؟ إليك الدالة التي تجيب عن هذا السؤال:
def SimulateSample(mu=90, sigma=7.5, n=9, m=1000): means = [] for j in range(m): xs = np.random.normal(mu, sigma, n) xbar = np.mean(xs) means.append(xbar) cdf = thinkstats2.Cdf(means) ci = cdf.Percentile(5), cdf.Percentile(95) stderr = RMSE(means, mu)
تُعَدّ كلًا من mu وsigma قيمًا افتراضيةً للمعامِلات، وn هي حجم العينة أي عدد إناث الغوريلا التي وزناها، وm هي عدد المرات التي ننفِّذ فيها المحاكاة.
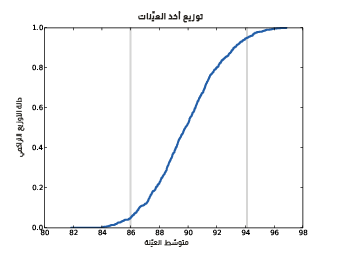
يوضِّح الشكل السابق توزيع أخذ عينات x̄ مع مجال الثقة.
نختار في كل تكرار n قيمةً من التوزيع الطبيعي مع المعامِلات المعطاة ونحسب متوسط العينة xbar وننفِّذ 1000 محاكاةً للتجربة، ثم نحسب توزيع التقديرات cdf، ويُظهر الشكل السابق النتيجة ويُدعى هذا التوزيع بتوزيع أخذ العينات sampling distributions للمُقدِّر، وهو يُظهر مدى تنوّع التقديرات إذا نفّذنا التجربة عدة مرات.
تقترب قيمة متوسط توزيع أخذ العينات من القيمة الافتراضية للمقدار μ، مما يعني أن التجربة تعطي الإجابة الصحيحة وسطيًا، حيث أنّ أقل نتيجة بعد 1000 محاولة هي 82 كيلوغرامًا وأعلى قيمة هي 98 كيلوغرامًا، ويشير هذا المجال إلى احتمالية ابتعاد التقدير عن القيمة الحقيقية بمقدار 8 كيلوغرام.
توجد طريقتان شائعتان لتلخيص توزيع أخذ العينات وهما:
- الخطأ المعياري standard error -أو SE اختصارًا-: هو مقياس لمدى توقعنا أن يكون التقدير بعيدًا عن القيمة الحقيقية وسطيًا، حيث نحسب الخطأ x̄-μ لكل تجربة محاكاة ومن ثم نحسب خطأ الجذر التربيعي المتوسط RSME، إذ تكون قيمة الخطأ في هذا المثال 2.5 كيلو غرامًا.
- lمجال الثقة confidence interval -أو IC اختصارًا-: هو مجال يتضمن جزءًا من توزيع أخذ العينات، أي مجال الثقة 90% مثلًا هو المجال من المئين رقم 5 5th percentile إلى المئين رقم 95 95th percentile؛ أما في هذا المثال فيكون مجال الثقة 90% هو (94 ,86) كيلوغرامًا.
غالبًا ما تكون الأخطاء المعيارية ومجالات الثقة مصدرًا للالتباس كما يلي:
- غالبًا ما يحصل خلط بين الخطأ المعياري والانحراف المعياري، لذا تذكَّر أنّ الانحراف المعياري يصف التباين في عينة مُقاسة، حيث يكون الانحراف المعياري لوزن إناث الغوريلا في هذا المثال هو 7.5 كيلو غرامًا؛ أما الخطأ المعياري فيصف التباين في التقدير، حيث يكون الخطأ المعياري للمتوسط بناءً على عينة من 9 قياسات هي 2.5 كيلو غرامًا، كما يمكنك تذكُّر الفرق بين المفهومين عن طريق حفظ القاعدة التي تقول أنه كلما ازداد حجم العينة، صغر الخطأ المعياري، على عكس الانحراف المعياري الذي لا يقل.
- غالبًا ما يعتقد الأشخاص أنه هناك احتمال بنسبة 90% لوقوع المعامِل الفعلي في مجال الثقة، لكن هذا ليس صحيحًا لأنه سيتوجب عليك استخدام التوابع البايزية -ويمكنك الاطلاع على كتابنا Think Bayes- في حال كنت تريد تقديم ادّعاءً من هذا القبيل، كما يجيب توزيع أخذ العينات عن سؤال آخر، فهو يمنحك معلومات عن مدى تغير التقدير إذا كررت التجربة، لذا تستطيع من خلاله معرفة ما إذا كان التقدير هذا موثوقًا أم لا.
من المهم أن تتذكر أن مجالات الثقة confidence intervals والأخطاء المعيارية standard errors تحسب خطأ أخذ العينات sampling error فقط، أي أنها لا تحسب سوى الأخطاء الناتجة عن معاينة جزء من العدد الكلي وحسب، كما لا يأخذ توزيع العينات في الحسبان مصادر الخطأ الأخرى خاصةً تحيز أخذ العينات sampling bias وخطأ القياس measurement error وهما موضوعا القسم التالي.
تحيز أخذ العينات sampling bias
إذا افترضنا أنك تريد معرفة متوسط أوزان النساء في المدينة التي تعيش فيها بدلًا عن وزن الغوريلات في محمية طبيعية، فسيكون من غير المرجح السماح لك باختيار عينة تمثيلية من النساء وتسجيل أوزانهن، لذا ستحتاج إلى بديل وسيكون البديل البسيط هو أخذ العينات عن طريق المكالمة الهاتفية telephone sampling، أي يمكنك اختيار أرقام عشوائية من دليل الهاتف ومن ثم الاتصال وسؤال امرأة بالغة عن وزنها.
تملك طريقة أخذ العينات عن طريق المكالمة الهاتفية بالطبع قيودًا وحدودًا واضحةً، أي تُعَدّ هذه الطريقة مثلًا محدودةً بالأشخاص الذين يملكون أرقامًا هاتفية ومسجلةً في دليل الهاتف، لذا فهي تستبعد الأشخاص الذين لا يملكون هواتفًا -أي مَن قد يكونوا أفقر من المتوسط- ومَن رقمه ليس مسجلًا -أي مَن قد يكونوا أثرى من المتوسط-، كما أنه إذا اتصلت على المنازل في النهار، فسيكون احتمال إيجاد الأشخاص الذين يمتلكون عملًا احتمالًا ضعيفًا إلى حد ما، وإذا لم تسأل سوى أول مَن يجيب على الهاتف، فسيكون احتمال أخذ عينة من الأشخاص الذين يشتركون معه في الهاتف ضعيفًا أيضًا.
ستتأثر نتيجة المسح هذا بطريقة أو بأخرى إذا وُجدت بعض العوامل، مثل الدخل والحالة الوظيفية وعدد أفراد الأسرة التي تُعَدّ أمورًا متعلقةً بالوزن -ومن المنطقي أن تكون كذلك-، حيث تُدعى هذه المشكلة بتحيز أخذ العينات sampling bias لأنها خاصية من عملية أخذ العينات، كذلك فإنّ عملية أخذ العينات مُعرّضة لما يُعرَف بالاختيار الذاتي self-selection الذي يُعَدّ نوعًا من أنواع تحيز أخذ العينات.
اقتباستوضيح: الاختيار الذاتي في الإحصاء أو البحث هو تحيز ناتج عن أن الأشخاص يستطيعون أن يرفضوا الإجابة عن السؤال المطروح، أي أنهم يختارون فيما إن كانوا سينتمون إلى مجموعة المشاركين أم لا، حيث أنه من الجائز أن يرفض البعض الإجابة عن السؤال، لذا ستتأثر النتائج إذا كان احتمال الرفض متعلقًا بالوزن.
أخيرًا، قد تكون النتائج غير دقيقة في حال سألت الأشخاص عن وزنهم بدلًا من قيامك أنت بعملية الوزن، حيث سترى في أفضل الحالات -أي إذا كان المستجيبون متعاونِين- أنه قد يلجأ المشاركون إلى تقريب وزنهم من أقرب قيمة عليا صحيحة أو أقرب قيمة دنيا صحيحة إن كانت لديهم بعض المشاكل المتعلقة بالثقة أو عدم الراحة تجاه وزنهم الفعلي، فضلًا عن أنّ بعض المستجيبين لا يكونون متعاونِين كثيرًا، وتُعَدّ هذه الأخطاء في الدقة أمثلةً عن الخطأ في القياس measurement error، وفي حال كان تقريرك يحوي قيمةً مُقدَّرةً، فقد يكون من المفيد حساب الخطأ المعياري أو مجال الثقة أو كلاهما معًا، وذلك من أجل تحديد خطأ أخذ العينات sampling error، ولكن من المهم أيضًا التذكُّر أنّ خطأ أخذ العينات هو أحد مصادر الخطأ -أي ليس المصدر الوحيد-، وغالبًا لا يكون المصدر الأكبر.
التوزيعات الأسية
دعنا نلعب لعبة التقدير مرةً أخرى، بحيث يكون التوزيع هنا توزيعًا أسيًا، وإليك عينةً منه:
[5.384, 4.493, 19.198, 2.790, 6.122, 12.844]
برأيك ما هو معامِل λ الخاص بهذا التوزيع؟
تقول القاعدة إنه بصورة عامة فإن متوسط التوزيع الأسي هو 1/λ، لذا إذا عكسنا العملية فقد نختار:
L=1/ x̄
يُعَدّ L مُقدِّرًا للـ λ كما أنه ليس مقدرًا عاديًا بل هو مُقدِّر الاحتمال الأعظم maximum likelihood estimator -أو MLE اختصارًا-، ويمكنك قراءة المزيد من المعلومات عنه في صفحة الويكيبيديا، فإذا كنت ترغب بزيادة فرصتك إلى أعلى حد ممكن في تخمين λ تخمينًا دقيقًا، فعليك اللجوء إلى L، لكننا نعلم أنه في حال وجود قيم شاذة، فلن يكون x̄ متينًا؛ لذا من المتوقع أن يكون للمقدر L المشكلة ذاتها، كما يمكننا اختيار بديل بناءً على وسيط العينة sample median، حيث أن الصيغة الرياضية لوسيط التوزيع الأسي هو ln(2)/λ، لذا إذا عكسنا العملية، فيمكننا تعريف مُقدِّر كما يلي:
Lm=ln(2)/m
حيث m وسيط العينة sample median.
يمكننا إجراء محاكاة لعملية أخذ العينات إذا أردنا اختبار أداء هذه المُقدِّرات، وإليك الشيفرة الموافقة كما يلي:
def Estimate3(n=7, m=1000): lam = 2 means = [] medians = [] for _ in range(m): xs = np.random.exponential(1.0/lam, n) L = 1 / np.mean(xs) Lm = math.log(2) / thinkstats2.Median(xs) means.append(L) medians.append(Lm) print('rmse L', RMSE(means, lam)) print('rmse Lm', RMSE(medians, lam)) print('mean error L', MeanError(means, lam)) print('mean error Lm', MeanError(medians, lam))
كان خطأ الجذر التربيعي المتوسط RMSE للمقدر L هو 1.1 عندما نفَّذنا هذه التجربة من أجل λ=2 ؛ أما بالنسبة للمُقدِّر Lm المبني على الوسيط median-based، فإن خطأ الجذر التربيعي المتوسط RMSE هو 1.8، وفي الواقع لا يمكننا الاستنتاج من هذه التجربة ما إذا كان L يقلل من الخطأ التربيعي المتوسط MSE أم لا، لكن يبدو لنا أن L هو على الأقل أفضل من Lm، لكن لسوء الحظ يبدو أنّ المُقدِّران متحيزان، حيث أن الخطأ المتوسط للـ L هو 0.33 والخطأ المتوسط للمقدر Lm هو 0.45، ولا يتقارب أيّ منهما إلى الصفر مع ازدياد قيمة m، وبالتالي يتضح أنّ x̄ هي مُقدِّر غير متحيز لمتوسط التوزيع 1/λ، في حين L ليس مُقدِّرًا غير متحيز لـ λ.
التمارين
قد يكون من المفيد لك أخذ نسخة من الملف estimation.py على أساس نقطة انطلاق لهذه التمارين، مع العلم أنّ الحلول موجودة في chap08soln.py.
تمرين 1
استخدمنا في هذا المقال كلًا من x̄ والوسيط من أجل تقدير μ، ووجدنا أنّ الخطأ التربيعي المتوسط الأدنى ينتج عن x̄، كما استخدمنا S2 وSn-12 لتقدير الانحراف المعياري σ ووجدنا أنّ S2 متحيز وأنّ Sn-12 غير متحيز، لذا وانطلاقًا من هذا نفِّذ بعض التجارب المماثلة لترى فيما إذا كان x̄ والوسيط هي تقديرات متحيزة للمتوسط μ، وتحقق فيما إذا كان ينتج عن S2 أو Sn-12 خطأً تربيعيًا متوسطًا أدنى أم لا.
تمرين 2
لنفترض أنك رسمت عينةً تحوي 10 قيم أي n=10 وبتوزيع أسي، بحيث يكون λ=2.
نفِّذ محاكاةً لهذه التجربة 1000 مرة وارسم توزيع أخذ العينات للتقدير L، واحسب الخطأ المعياري للتقدير ومجال الثقة 90%، ثم كرر التجربة مع تغيير قيمة n بضع مرات، وارسم مخطط الخطأ المعياري مقابل n.
تمرين 3
عادةً ما يكون الوقت بين الأهداف في رياضات مثل الهوكي وكرة القدم أسيًا، لذا يمكنك تقدير معدل تسجيل الفريق للأهداف عن طريق رصد عدد الأهداف التي يسجلونها في مباراة ما، حيث تختلف عملية التقدير هذه اختلافًا صغيرًا عن عملية أخذ عينات من الوقت بين الأهداف، لذا سنرى التطبيق العملي لهذا.
اكتب دالةً تأخذ معدل تسجيل الأهداف lam والذي وحدة قياسه أهداف لكل مباراة، ثم حاكي مباراةً بتوليد الوقت بين الأهداف إلى أن يتخطى الوقت زمن مباراة واحدة، ومن ثم تُعيد هذه الدالة عدد الأهداف المسجلة، واكتب دالةً أخرى تُحاكي عدة مباريات وتسجِّل تقديرات لـ lam، ثم تحسب خطأ المتوسط وخطأ الجذر التربيعي المتوسط RMSE.
برأيك هل تُعَدّ هذه الطريقة في إنشاء تقدير متحيزة؟ ارسم توزيع أخذ العينات sampling distribution الذي يحوي التقديرات ومجال الثقة 90%؛ ما هو الخطأ المعياري في هذه الحالة؟ وكيف تؤثر زيادة قيم lam على خطأ أخذ العينات sampling error؟
ترجمة -وبتصرف- للفصل Chapter 8 Estimate analysis من كتاب Think Stats: Exploratory Data Analysis in Python.
اقرأ أيضًا
- المقال السابق: العلاقات بين المتغيرات الإحصائية وكيفية تنفيذها في بايثون
- المقال التالي: اختبار الفرضيات الإحصائية
- البرمجة بلغة بايثون











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.