تُعَدّ السلسلة الزمنية time series تسلسلًا sequence من القياسات المأخوذة من نظام والمتغيرة بمرور الزمن، ومن الأمثلة الشهيرة "مخطط عصا الهوكي" الذي يُظهر متوسط درجة الحرارة في العالم مع مرور الوقت، كما يمكنك الاطلاع على صفحة ويكيبيديا للمزيد من المعلومات، حيث أنّ مصدر المثال الذي نناقشه في هذا المقال هو البيانات المتاحة من موقع kaggle والتي تُعطي بيانات مبيعات الأفوكادو للأعوام 2015-2020 في الولايات المتحدة الأمريكية وذلك لكل من نوعي الأفوكادو العادي Conventional والأفوكادو العضوي Organic.
نأمل أن تجدوا هذا المقال مثيرًا للاهتمام. توجد الشيفرة الخاصة بهذا المقال في الرابط على Google Colab أو يمكنك تنزيلها من المرفقات.
استيراد وتنظيف البيانات
توجد البيانات المستخدمة في موقع Kaggle كما أرفقناها في نهاية المقال، وتُعَدّ الشيفرة التالية مسؤولةً عن قراءتها على هيئة إطار بيانات بانداز pandas DataFrame:
transactions = pandas.read_csv('avocado.csv', parse_dates=[0])
حيث أنّ مهمة الوسيط parse_dates هي الإشارة إلى الدالة read_csv لتفسير القيم الموجودة في العمود رقم 0 (العمود الأول) على أساس تواريخ ومن ثم تحويلها إلى كائنات datetime64 من نوع نمباي NumPy، كما يحتوي إطار البيانات DataFrame على سطر لكل عملية مبيع مسجلة بالإضافة إلى الأعمدة التالية:
-
average_price: السعر الوسطي مقدرًا بالدولار. -
total_volume: الحجم الكلي المُباع. -
type: نوع الأفوكادو: عادي أم عضوي. -
date: تاريخ عملية المبيع. -
year: عام المبيع. -
geography: الولاية والمدينة.
علمًا أنّ كل عملية مبيع هي حدث في الزمن، لذا يمكننا معاملة مجموعة البيانات هذه على أساس سلسلة زمنية time series، لكن المسافة الزمنية بين الأحداث غير متساوية، إذ يتراوح عدد عمليات المبيع المسجلة بين 0 إلى عدة عشرات يوميًا، حيث تتطلب الكثير من طرق تحليل سلاسل البيانات أن تكون الأزمنة بين الأحداث متساويةً أو على الأقل فإن الأمور أكثر بساطةً إن كانت الأزمنة متساويةً، ومن أجل توضيح هذه الطرق قسَّمنا مجموعة البيانات هذه إلى مجموعات حسب الكمية ومن ثم حوَّلنا كل مجموعة إلى سلسلة تتباعد فيها الأحداث تباعدًا متساويًا عن بعضها وذلك عن طريق حساب متوسط السعر اليومي.
def GroupByTypeAndDay(transactions): groups = transactions.groupby('type') dailies = {} for name, group in groups: dailies[name] = GroupByDay(group) return dailies
علمًا أن groupby هو تابع خاص بأُطر البيانات وهو يُعيد كائن GroupBy باسم groups، حيث يُستخدم الكائن groups في حلقة for ليمر مرورًا تكراريًا على أسماء المجموعات وأُطر البيانات التي تمثِّلها، وبما أنّ للنوع احتمالين هما عادي أو عضوي، فسينتج مجموعتين تحمل هذه الأسماء -أي عادي وعضوي-، حيث تمر الحلقة مرورًا تكراريًا على المجموعات وتستدعي التابع GroupByDay الذي يحسب متوسط السعر اليومي ويُعيد إطار بيانات جديد:
def GroupByDay(transactions, func=np.mean): grouped = transactions[['date', 'average_price']].groupby('date') daily = grouped.aggregate(func) daily['date'] = daily.index start = daily.date[0] one_year = np.timedelta64(1, 'Y') daily['years'] = (daily.date - start) / one_year return daily
يُعَدّ المعامِل transactions إطار بيانات ويحتوي على العمودين date وaverage_price، لذا سنحدِّد هذين العمودين ومن ثم نجمِّعهما على أساس التاريخ، وتكون النتيجة هي grouped التي تُعَدّ خريطةً map تحوِّل كل تاريخ إلى إطار بيانات يحتوي على الأسعار التي أُبلِغ عنها في ذلك التاريخ المحدَّد، ويُعَدّ aggregate تابع تجميع GroupB يمر مرورًا تكراريًا على المجموعات ويطبق دالةً على كل عمود من المجموعة، وفي حالتنا هذه لا يوجد سوى عمود واحد هو average_price الذي يمثِّل السعر الوسطي.
تُخزَّن البيانات في هذه الأُطر على أساس كائنات نمباي NumPy من نوع datetime64 والتي تمثَّل على أساس أعداد صحيحة حجمها 46 بتًا -أي 64-bit integers- بالنانو ثانية، لكن سيكون من المناسب التعامل في بعض التحليلات القادمة مع وحدات قياس زمنية مألوفة أكثر بالنسبة للبشر مثل السنوات، أي يُضيف التابع GroupByDay عمودًا اسمه date عن طريق نسخ الفهرس ومن ثم يُضيف العمود years الذي يحتوي على عدد السنوات التي مرت منذ أول عملية مبيع وهو عدد عشري، كما يحتوي إطار البيانات الناتج على average_price الذي يمثِّل السعر الوسطي بالدولار والعمود date الذي يمثِّل التاريخ وyears.
رسم المخططات
تكون نتيجة GroupByTypeAndDay خريطةً map تحوِّل كل نوع إلى إطار بيانات يحتوي على الأسعار اليومية، وإليك الشيفرة التي استخدمناها لرسم السلسلتين الزمنيتين:
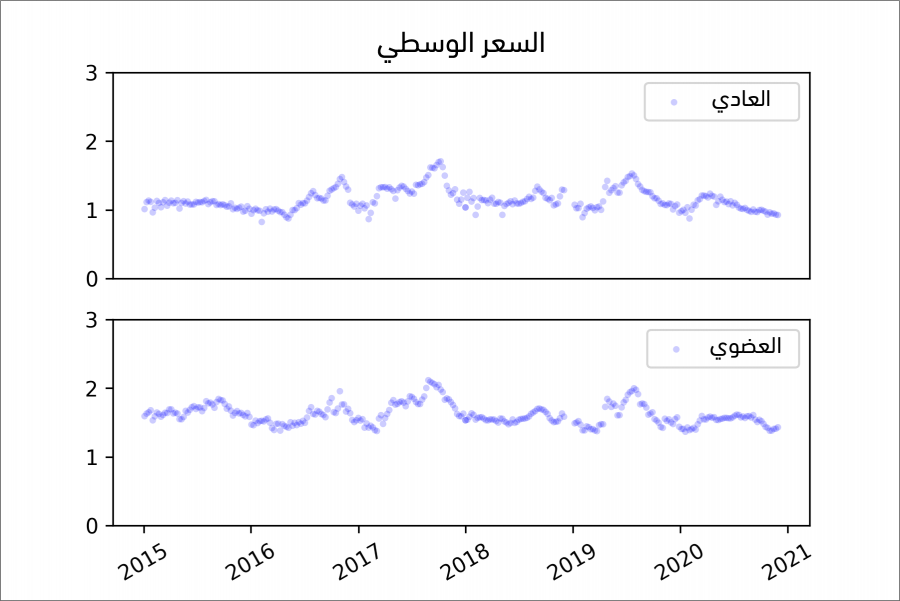
thinkplot.PrePlot(rows=2) for i, (name, daily) in enumerate(dailies.items()): thinkplot.SubPlot(i+1) title = 'Average Price' if i == 0 else '' thinkplot.Config(ylim=[0, 3], title=title) thinkplot.Scatter(daily.average_price, s=10, label=name) if i == 1: pyplot.xticks(rotation=30) else: thinkplot.Config(xticks=[])
تشير الدالة PrePlot في حال وجود الوسيط rows=2 إلى أننا سنرسم مخططين فرعيين في السطرين، حيث تمر الحلقة مرورًا تكراريًا على أطر البيانات وتنشئ مخطط انتشار لكل إطار، ومن الشائع رسم السلاسل الزمنية مع قطع مستقيمة تصل بين النقطة والأخرى، لكن توجد في هذه الحالة العديد من نقاط البيانات والأسعار متغيرةً تغيرًا كبيرًا، لذا لن يكون من المفيد إضافة القطع المستقيمة، وبما أن التواريخ موجودة على محور x -أي المحور الأفقي-، فسنستخدِم pyplot.xticks للتدوير بمقدار 30 درجة، وبذلك نجعلها مقروءةً أكثر.
يوضِّح الشكل السابق سلسلةً زمنيةً تمثِّل متوسط السعر اليومي، وذلك بالنسبة للنوع العادي والنوع العضوي، كما يُظهر الشكل السابق النتيجة، حيث نرى صفةً واضحةً في هذه المخططات وهي وجود بعض الفجوات الزمنية ، فمن المحتمل أنّ جمع البيانات في ذلك الوقت كان متوقفًا أو أنَّ البيانات غير متوافرة، لكننا سنفكر لاحقًا في طرق للتعامل مع هذه البيانات المفقودة على أية حال.
يبدو لنا من النظر إلى المخطط أنّ أسعار الأفوكادو وصلت لذروتها في عام 2017 ثم عاودت بالتذبذب إلا أن أسعار الأفوكادو العضوي حافظت دائماً على ارتفاعها مقارنة بالأفوكادو العادي.
الانحدار الخطي
على الرغم من وجود توابع خاصة بتحليل السلاسل الزمنية، إلا أنّ الطريقة الأبسط التي تحل الكثير من المسائل تتمثل في تطبيق أدوات ذات غرض عام مثل الانحدار الخطي، إذ تأخذ الدالة التالية إطار بيانات للأسعار اليومية وتحسب ملائمة مربعات صغرى، ومن ثم تُعيد النموذج والكائنات الناتجة من StatsModels:
def RunLinearModel(daily): model = smf.ols('average_price ~ years', data=daily) results = model.fit() return model, results
يمكننا المرور مرورًا تكراريًا على النوعين المختلفين (العادي والعضوي) وملاءمة نموذج لكل منها:
dailies = GroupByTypeAndDay(transactions)
for name, daily in dailies.items():
model, results = RunLinearModel(daily)
print(results.summary()
إليك النتائج:
| النوع | نقطة التقاطع | الميل | R2 |
|---|---|---|---|
| عادي | 1.1348 | 0.0034 | 0.001 |
| عضوي | 1.6690 | 0.0183- | 0.044 |
تشير قيم الميل المُقدَّرة إلى انخفاض سعر الأفوكادو العضوي قليلًا (2 سنتًا) في كل سنة ضمن الفترة الزمنية التي رُصدَت الأسعار فيها؛ أما الأفوكادو العادي فقد ارتفع سعره قليلًا (أقل من 1 سنتًا في كل سنة)، علمًا أن التقديرات هذه ذات دلالة إحصائية وقيمها الاحتمالية صغيرة جدًا.
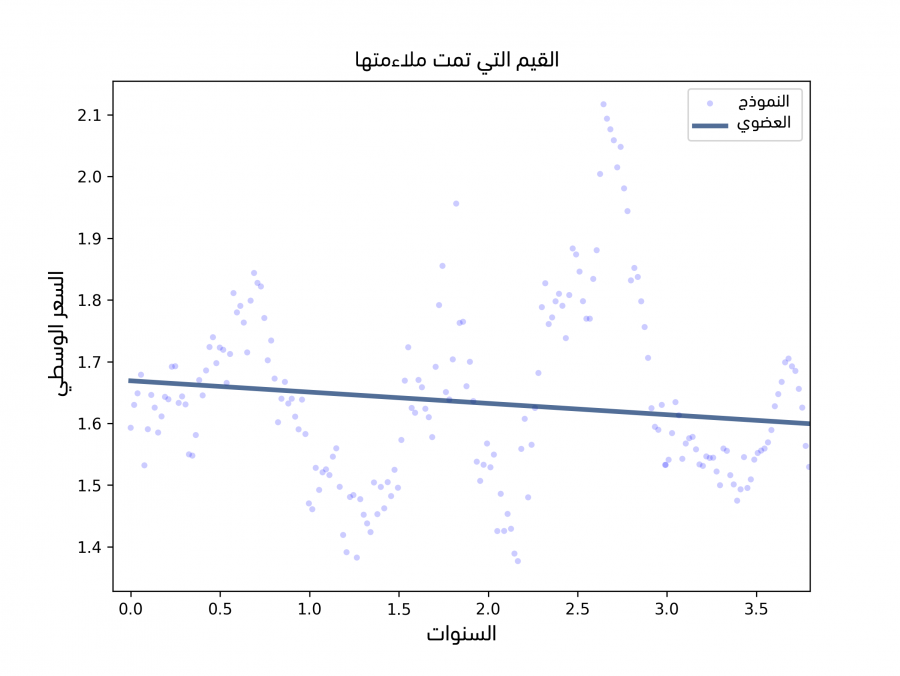
إنّ قيمة R2 هي 0.044 للأفوكادو العضوي أي أن الزمن بصفته متغير توضيحي يمثِّل 4% من التباين المرصود في السعر، لكن يكون التغير في السعر أصغر والتباين في الأسعار أقل بالنسبة للأفوكادو العادي، لذا فإن قيم R2 أصغر لكنها ما زالت ذات دلالة إحصائية، وترسم الشيفرة التالية الأسعار المرصودة والقيم الملاءمة:
def PlotFittedValues(model, results, label=''): years = model.exog[:,1] values = model.endog thinkplot.Scatter(years, values, s=15, label=label) thinkplot.Plot(years, results.fittedvalues, label='model' )
يحتوي model على exog وendog كما رأينا في قسم سابق في مقال الانحدار الإحصائي regression، حيث أنهما مصفوفتا نمباي NumPy تحتويان على المتغيرات الخارجية -أي التوضيحية- والمتغيرات الداخلية -أي التابعة-.
يوضِّح الشكل السابق سلسلةً زمنيةً للأسعار اليومية، بالإضافة إلى ملاءمة مربعات صغرى خطية linear least squares fit، كما تُنشئ الدالة PlotFiitedValues مخططًا انتشاريًا لنقاط البيانات ورسمًا خطيًا للقيم الملائمة، ويُظهر الشكل السابق نتائج الأفوكادو العضوي، حيث يبدو أنّ النموذج يلائم البيانات ملاءمةً جيدةً ولكن الانحدار الخطي ليس الخيار الأفضل لهذه البيانات:
- أولًا: ما من سبب يدفعنا للتوقُّع أنّ الاتجاه الذي استمر فترةً طويلةً هو خط أو دالة بسيطة، والذي يحدِّد الأسعار عمومًا هو العرض والطلب وكلاهما يختلف بمرور الزمن بطرق لا يمكن التنبؤ بها.
- ثانيًا: يعطي نموذج الانحدار الخطي وزنًا متساويًا لكل البيانات سواءً البيانات الحديثة أو السابقة، لكن يجب علينا إعطاء البيانات الحديثة وزنًا أكبر.
- أخيرًا: تقول إحدى الفرضيات حول الانحدار الخطي أنّ الرواسب residuals هي ضجيج غير مترابط، لكن غالبًا ما تكون هذه الفرضية غير صحيحة في حال تعاملنا مع سلاسل زمنية لأن القيم المتتالية مترابطة.
يقدِّم القسم التالي بديلًا أفضل للتعامل مع بيانات السلاسل الزمنية.
المتوسطات المتحركة
تعتمد معظم السلاسل الزمنية على افتراض النمذجة عادةً والذي يقول أنّ السلسلة المرصودة هي ناتج جمع المكوِّنات الثلاثة التالية:
- الاتجاه: هو دالة ملساء -أي منتظمة- تخزِّن التغييرات المستمرة.
- الموسمية: هو تباين دوري، وقد يتضمن دورات يومية أو أسبوعية أو شهرية أو سنوية.
- الضجيج: التباين العشوائي حول الاتجاه طويل الأمد.
يُعَدّ الانحدار أحد طرق استخراج الاتجاه من سلسلة معينة تمامًا كما رأينا في القسم السابق، لكن يوجد بديل آخر في حال لم يكن الاتجاه دالةً بسيطةً وهو المتوسط المتحرك moving average، حيث يقسِّم المتوسط المتحرك السلسلة إلى مناطق متداخلة تُدعى نوافذ windows ومن ثم يحسب متوسط القيم في كل نافذة window.
يُعَدّ المتوسط المتدحرج rolling mean الذي يحسب متوسط القيم في كل نافذة من أبسط أنواع المتوسطات المتحركة، فإذا كان حجم النافذة 3 مثلًا، فسيحسب المتوسط المتدحرج متوسط القيم من 0 إلى 2 ومن 1 إلى 3 ومن 2 إلى 4 وهكذا دواليك، كما يُبين المثال التالي:
df=pandas.DataFrame(np.arange(10)) roll_mean = df.rolling(3).mean() print(roll_mean) nan, nan, 1, 2, 3, 4, 5, 6, 7, 8
نلاحظ أنّ أول قيمتين هما nan -أي ليس عددًا-؛ أما القيمة التالية فهي متوسط العناصر الثلاث الأولى أي 0 و1 و2، والقيمة التالية هي متوسط 1 و2 و3، وهكذا، حيث يتعين علينا التعامل مع القيم المفقودة في البداية وقبل تطبيق rolling على بيانات الأفوكادو، ونلاحظ في الواقع في الفترة المرصودة وجود عدة أيام لم يُبلَّغ فيها عن أيّ عمليات مبيع لنوع معين أو أكثر من نوع -أي النوع العادي أو العضوي- من الأفوكادو.
لم تكن هذه التواريخ موجودةً في أيّ من أُطر البيانات التي استخدمناها سابقًا، حيث كان الفهرس يتخطى الأيام التي لا تحتوي على أية بيانات، لكن بالنسبة للتحليل التالي، فنحتاج إلى تمثيل البيانات المفقودة تمثيلًا صريحًا، حيث يمكننا إنجاز ذلك عن طريق إعادة فهرسة reindexing إطار البيانات:
dates = pandas.date_range(daily.index.min(), daily.index.max()) reindexed = daily.reindex(dates)
يحسب السطر الأول من الشيفرة السابقة مجال التواريخ الذي يتضمن تاريخ كل الأيام من بداية فترة رصد عمليات المبيع حتى اليوم الأخير؛ أما السطر الثاني فينشئ إطار بيانات جديد يحتوي على كل البيانات الموجودة في daily بالإضافة إلى الأسطر التي تحتوي على جميع التواريخ ذات القيمة nan، حيث يمكننا الآن رسم المتوسط المتجدد كما يلي:
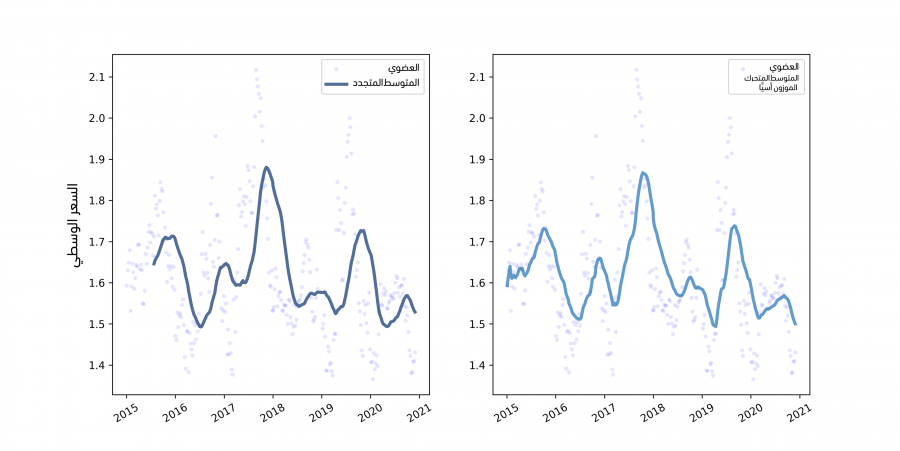
roll_mean = reindexed.average_price.rolling(30).mean() thinkplot.Plot(roll_mean.index, roll_mean,label="rolling mean") thinkplot.config(xlabel='date', ylabel='average-price') thinkplot.show()
حجم النافذة هنا هو 30، لذا فإن كل قيمة في roll_mean هي متوسط 30 قيمة من reindexed.average-price.
يوضِّح الشكل السابق الأسعار اليومية والمتوسط المتدحرج rolling mean في الجهة اليسرى والمتوسط المتحرك الموزون أسيًا exponentially-weighted moving average في الجهة اليمنى، كما يُظهر الشكل السابق الموجود في الجهة اليسرى النتيجة، حيث يبدو أن المتوسط المتدحرج قد أتقن تنظيم smoothing الضجيج واستخرج الاتجاه.
البديل هو **المتوسط المتحرك الموزون أسيًا exponentially-weighted moving average -أو EWMA اختصارًا-، والذي يتمتع بميزتين اثنتين، حيث يمكننا استنتاج الميزة الأولى من الاسم، أي يحسب متوسطًا موزونًا يكون فيه لأحدث قيمة أعلى وزن؛ أما القيم السابقة فتنخفض قيمتها انخفاضًا أسيًا، والميزة الثانية هي أنّ تنفيذ بانداز pandas للمتوسط المتحرك الموزون أسيًا يعالِج القيم المفقودة بإتقان أكبر.
ewm=reindexed['average_price'].ewm(span=30).mean() thinkplot.Plot(ewm)
يتوافق المعامِل span تقريبًا مع حجم نافذة متوسط متحرك، كما أنه يتحكم في مدى سرعة انخفاض الأوزان، لذا فهو يحدِّد عدد النقاط التي تقدِّم مساهمةً كبيرةً لكل متوسط من المتوسطات، ويُظهر الشكل السابق الموجود في الجهة اليمنى المتوسط المتحرك الموزون أسيًا EWMA الخاص بالبيانات نفسها، وهو يشبه المتوسط المتدحرج rolling mean في الحالات التي يكون كلاهما معرَّفًا، إلا أنه لا يحتوي على أي قيم مفقودة، لذا فمن السهل التعامل معه، ونلاحظ أنّ القيم تحتوي على ضجيج في بداية السلسلة الزمنية لأنها مبنية على عدد أقل من نقاط البيانات.
ewm=reindexed['average_price'].ewm(span=30).mean() thinkplot.Plot(ewm, label="ewma") thinkplot.config(xlabel='date', ylabel='average-price') thinkplot.show()
القيم المفقودة
ستكون الخطوة التالية بعد أن حدَّدنا توجه السلسلة الزمنية هي البحث في كل موسم على حدة، فالموسم هو فترة أسبوع أو يوم أو سنة أو …إلخ، أي ليس بالضرورة موسم كما يشير الاسم، فهو سلوك دوري، وغالبًا ما تكون السلاسل الزمنية التي تستند إلى السلوك البشري دورات يومية أو أسبوعية أو شهرية أو سنوية، لذا سنقدِّم في القسم التالي طُرقًا لاختبار المواسم لكنها لا تعمل جيدًا في حال وجود قيم مفقودة، لذا علينا حل هذه المشكلة أولًا، حيث توجد طريقة سهلة وشائعة يمكننا من خلالها ملء البيانات المفقودة وهي استخدام متوسط متحرك، حيث يزودنا تابع السلسلة fillna بتنفيذ ملائم جدًا لمتطلباتنا:
reindexed.average_price.fillna(ewm, inplace=True)
عندما تكون قيمة reindexed.average_price هي nan، فسيستبدلها التابع fillna بالقيم الموافقة من ewm، حيث تشير الراية inplace إلى التابع fillna لكي يعدل السلسلة الحالية بدلًا من إنشاء سلسلة جديدة، وإحدى مساوئ هذه الطريقة هي أنها تقلل من قيمة الضجيج في السلسلة، لكن يمكننا حل هذه المشكلة عن طريق إضافة الرواسب التي طُبِّق عليها أخذ عينات:
resid = (reindexed.average_price - ewm).dropna() fake_data = ewm + thinkstats2.Resample(resid, len(reindexed)) reindexed.average_price.fillna(fake_data, inplace=True)
يحتوي المتغير resid على قيم الرواسب، لكن لا يحتوي على الأيام التي يكون فيها average_price أي السعر الوسطي هو nan، كما يحتوي fake_data على مجموع المتوسط المتحرك وعينة عشوائية من الرواسب، وأخيرًا، يستبدل التابع fillna قيم fake_data بقيم من nan.
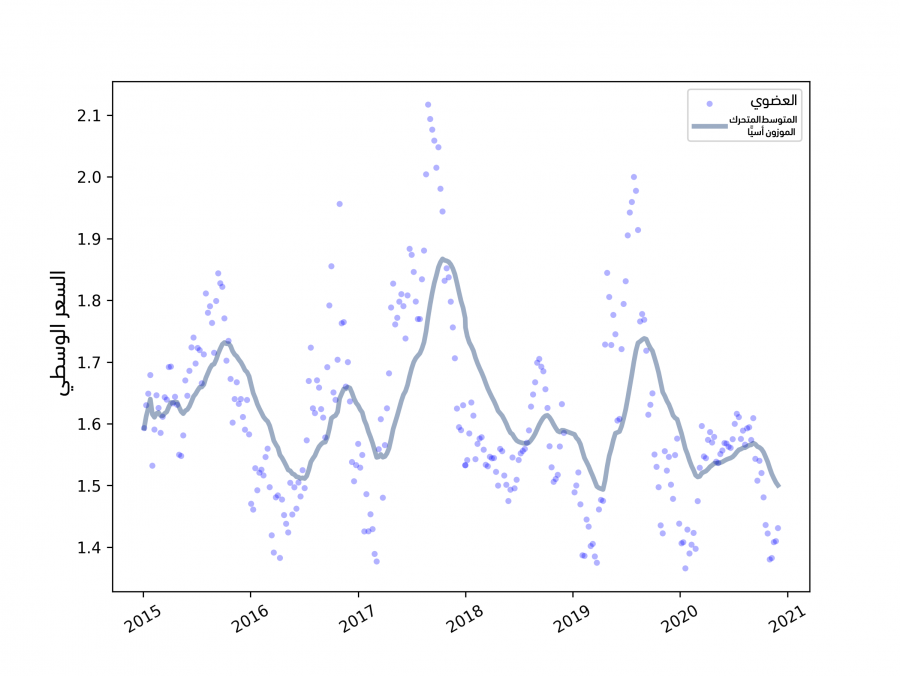
يوضِّح الشكل السابق الأسعار اليومية بعد ملء القيم ويُظهر النتيجة، حيث تشبه البيانات المملوءة القيم الفعلية من الناحية البصرية، وبما أنّ الرواسب التي تطُبِّق عليها إعادة أخذ عينات هي قيم عشوائية، فستكون النتائج مختلفةً في كل مرة، لذا سنرى لاحقًا طريقةً لوصف الخطأ الذي نتج عن القيم المفقودة.
الارتباط التسلسلي
قد تتوقع أن تجد أنماطًا متكررةً لأن الأسعار تتغيَّر يوميًا، فإذا كان السعر مرتفعًا يوم الاثنين، فقد تتوقع أن يكون مرتفعًا للأيام القليلة التالية، وإذا كان منخفضًا، فقد تتوقع أن يبقى منخفضًا، حيث يُدعى هذا النمط الارتباط التسلسلي serial correlation لأن كل قيمة مترابطة مع القيمة التالية في السلسلة، ويمكنك إزاحة السلسلة الزمنية بمقدار قدره تأخير lag من أجل حساب الارتباط التسلسلي ومن ثم حساب الارتباط بين السلسلة المزاحة والسلسلة الأصلية:
def SerialCorr(series, lag=1): xs = series[lag:] ys = series.shift(lag)[lag:] corr = thinkstats2.Corr(xs, ys) return corr
تكون قيم التأخير الأول nan بعد أول إزاحة، لذا فقد استخدمنا شريحةً لإزالتها قبل حساب Corr، فإذا طبقنا SerialCorr على بيانات الأسعار الأولية بقيمة تأخير 1، فسنجد أنَّ الارتباط التسلسلي 0.26 للأفوكادو العضوي و 0.39 للأفوكادو العادي، كما نتوقَّع رؤية ارتباط تسلسلي قوي في حال كانت السلسلة الزمنية ذا اتجاه طويل الأمد، فإذا كانت الأسعار تنخفض على سبيل المثال، فسنتوقع رؤية قيم النصف الأول من السلسلة أعلى من المتوسط، وقيم النصف الثاني من السلسلة أقل من المتوسط، ومن المثير للاهتمام رؤية فيما إذا كان الارتباط مستمرًا إذا لم نأخذ الاتجاه بالحسبان، إذ يمكننا مثلًا حساب راسب المتوسط المتحرك الموزون أسيًا ومن ثم حساب ارتباطه التسلسلي كما يلي:
ewm=reindexed['average_price'].ewm(span=30).mean() resid = reindexed.average_price - ewm corr = thinkstats2.SerialCorr(resid, 1)
تكون الارتباطات التسلسلية للبيانات التي أهملنا فيها الاتجاه في حال كانت قيمة التأخير 1 أي lag=1 هي 0.89 بالنسبة للأفوكادو العضوي، والقيمة 0.86 بالنسبة للأفوكادو العادي، كما تُعَدّ قيمًا كبيرة مما يشير إلى وجود ترابط تسلسلي يومي جيد، حيث سننفِّذ التحليل مرةً أخرى مع قيم تأخير مختلفة وذلك للتحقق من وجود موسمية أسبوعية أو شهرية أو سنوية، وإليك نتائج التحليل:
| التأخير | العادي | العضوي |
|---|---|---|
| 1 | 0.86 | 0.89 |
| 7 | 0.29 | 0.37 |
| 30 | -0.18 | -0.33 |
| 300 | 0.33 | -0.5 |
سنُجري في القسم التالي اختبارات لنعلم ما إذا كانت هذه الارتباطات ذات دلالة إحصائية (ليست ذات دلالة إحصائية)، ولكن يمكننا مبدئيًا استنتاج أنه لا توجد أنماط موسمية كبيرة في السلسلة، فعلى الأقل لا توجد أنماط بوجود هذه التأخيرات.
الارتباط الذاتي
ستضطر إلى اختبار جميع القيم إذا اعتقدت بوجود ارتباط تسلسلي في سلسلة زمنية ما لكنك لست متأكدًا من قيم التأخير التي يجب عليك اختبارها، حيث تُعَدّ دالة الارتباط الذاتي autocorrelation function دالةً تحوِّل التأخير lag إلى ارتباط تسلسلي بتأخير مُعطى، كما يُعَدّ الارتباط الذاتي والارتباط التسلسلي وجهَين لعملة واحدة، أي أنهما يشيران إلى المفهوم ذاته لكن غالبًا يُستخدَم الارتباط الذاتي عندما تكون قيمة التأخير مختلفةً عن 1، كما تزودنا StatsModels التي استخدمناها في الانحدار الخطي في المقال السابق بدوال لتحليل السلاسل الزمنية مثل acf التي تحسب دالة الارتباط الذاتي كما يلي:
import statsmodels.tsa.stattools as smtsa acf = smtsa.acf(filled.resid, nlags=365)
تحسب الدالة acf الارتباطات التسلسلية مع قيم تأخير بين 0 وnlags، وتكون النتيجة مصفوفةً من الارتباطات، فإذا حددنا الأسعار اليومية للأفوكادو العضوي واستخرجنا قيم الارتباطات في حال كانت قيم التأخير هي 1 و 7 و 30 و 365، فسيمكننا عندها التأكُّد من إنتاج الدالتين acf وSerialCorr النتائج نفسها تقريبًا:
>>> acf[0], acf[1], acf[7], acf[30], acf[365] 1.000, 0.859, 0.286, -0.176, 0.000
تحسب الدالة acf ارتباط السلسلة مع نفسها إذا كانت قيمة التأخير 0 أي lag=0، علمًا أن الارتباط في هذه الحالة هو 1 دائمًا.
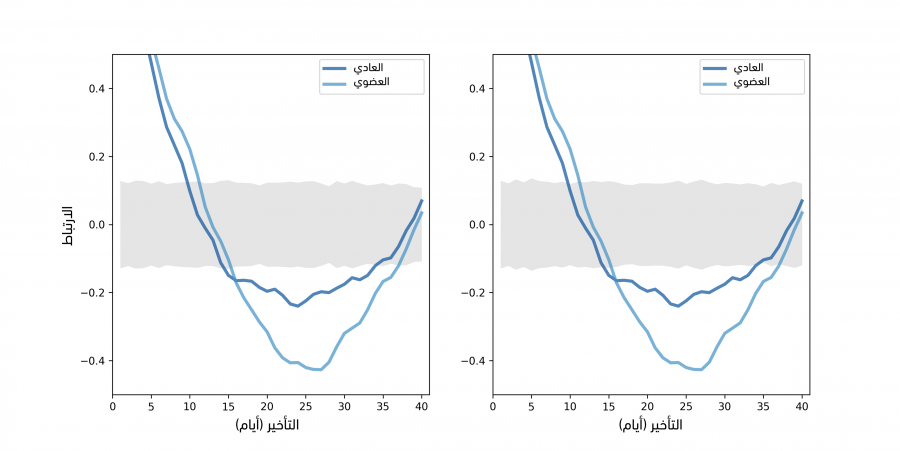
يوضِّح الشكل السابق دالة الارتباط الذاتي للأسعار اليومية في الجهة اليسرى؛ أما في الجهة اليمنى فيوضِّح الأسعار اليومية إذا أجرينا محاكاةً لموسمية أسبوعية، حيث يُظهر الشكل السابق في الجهة اليسرى دوال الارتباط الذاتي للأفوكادو العادي والعضوي وذلك من أجل nlags=40، حيث تُظهر المنطقة الرمادية التباين الطبيعي الذي نتوقعه إذا لم يكن هناك أي ارتباط ذاتي فعلي، علمًا أن القيم التي تقع خارج هذا المجال هي ذات دلالة إحصائية وقيمتها الاحتمالية p-value هي أقل من 5%، وبما أن معدل الإيجابية الكاذبة هو 5% ونحن في طور حساب 120 ارتباطًا (بمعدل 40 تأخير لكل سلسلة من السلسلتين الزمنيتين)، فسنتوقع رؤية 6 نقاط خارج هذه المنطقة وفي الواقع يوجد أكثر من 6 نقاط، لذا نستنتج أنه لا يمكننا تفسير أيّ ارتباط ذاتي في السلسلة على أنه حدث بمحض الصدفة فحسب.
حسبنا المناطق الرمادية عن طريق إعادة أخذ عينات الرواسب (ويمكنك الاطلاع على شيفرتنا في في الرابط وتُدعى الدالة SimulateAutocorrelation)، ولرؤية كيف تبدو دالة الارتباط الذاتي في حال وجود موسمية من نوع ما، ولَّدنا بيانات محاكاة وذلك عن طريق إضافة دورة أسبوعية، ففي حال كان الطلب على الأفوكادو أعلى في العطل الأسبوعية، فقد نتوقع أن يكون السعر أعلى، حيث حدَّدنا التواريخ التي تصادف يومي الجمعة والسبت ومن ثم أضفنا قيمةً عشوائيةً مُختارةً من توزيع منتظم بين 0$ و 2$ على السعر وذلك من أجل محاكاة هذا التأخير.
def AddWeeklySeasonality(daily): frisat = (daily.index.dayofweek==4) | (daily.index.dayofweek==5) fake = daily.copy() fake.average_price[frisat] += np.random.uniform(0, 2, frisat.sum()) return fake
يُعَدّ frisat سلسلةً بوليانيةً، بحيث تكون القيمة True ليومي الجمعة والسبت، كما يُعَدّ fake إطار بيانات جديد وهو نسخة من إطار البيانات daily بعد أن أجرينا عليه تعديل إضافة قيم عشوائية إلى average_price.frisat.sum وهو العدد الكلي لأيام الجمعة والسبت التي ظهرت، أي عدد القيم التي سيتوجب علينا توليدها.
يُظهر الشكل السابق في الجهة اليمنى دوال الارتباط الذاتي للأسعار مع موسمية محاكاة، حيث نرى كما هو متوقَّع أن الارتباطات أعلى في حال كان التأخير من مضاعفات العدد 7، كما تكون الارتباطات لنوعي الأفوكادو ليست ذات دلالة إحصائية لأن الرواسب هنا كبيرة ومن المفترض أن يكون التأخير أكبر ليكون مرئيًا في وسط كل هذا الضجيج.
التنبؤ
يمكن استخدام تحليل السلاسل الزمنية لاكتشاف أو شرح سلوك الأنظمة التي تتغير بمرور الزمن، كما يمكن استخدامها لتوليد تنبؤات، كما يمكن استخدام الانحدار الخطي الذي تناولناه في قسم الانحدار الخطي في هذا المقال لتوليد تنبؤات أيضًا، حيث يزودنا الصنف RegressionResults بالدالة predict التي تأخذ إطار بيانات يحتوي على المتغيرات التوضيحية ويُعيد تسلسلًا من التنبؤات، وإليك الشيفرة الموافقة كما يلي:
def GenerateSimplePrediction(results, years): n = len(years) inter = np.ones(n) d = dict(Intercept=inter, years=years) predict_df = pandas.DataFrame(d) predict = results.predict(predict_df) return predict
يُعَدّ results كائنًا من الصنف RegressionResults، ويُعَدّ years تسلسلًا من قيم الزمن التي نريد استنباط تنبؤاتها، كما تبني الدالة إطار بيانات وتمرره إلى الدالة predict وتُعيد النتيجة، فإذا كان ما نريد هو تنبؤ وحيد وأفضل ما في الإمكان فقط، فستكون مهمتنا قد انتهت هنا، لكن من المهم حساب الخطأ في معظم الأحيان، أي نريد بكلمات أخرى معرفة دقة التنبؤ المحتملة، كما يجب علينا أخذ مصادر الخطأ الثلاثة هذه بالحسبان:
- خطأ أخذ العينات: يكون التنبؤ هنا مبنيًا على المعامِلات المُقدَّرة التي تعتمد على التبيان العشوائي في العينة، حيث نتوقَّع تغيُّر التقديرات إذا أجرينا التجربة مرةً ثانيةً.
- التباين العشوائي: ستتغير البيانات المرصودة قرب الاتجاه طويل الأمد حتى لو كانت المعاملات المُقدَّرة دقيقةً تمامًا، ونتوقع استمرار هذا التباين في المستقبل أيضًا.
- خطأ النمذجة: لدينا أدلةً تثبت أنّ الاتجاه طويل الأمد ليس خطيًا، لذا فإن التنبؤات مبنية على نموذج خطي سيفشل عاجلًا أم آجلًا.
من مصادر الخطأ الأخرى التي يجب علينا أخذها بالحسبان هي الحوادث المستقبلية غير المتوقعة مثل تأثر أسعار المنتجات الزراعية بالطقس وتأثر جميع الأسعار بالقوانين والسياسات، ومن الصعب حساب أخطاء النمذجة والأخطاء المستقبلية غير المتوقعة، ومن السهل التعامل مع خطأ أخذ العينات والتباين العشوائي لذا سنبدأ بهذين النوعين.
استخدمنا إعادة أخذ العينات كما فعلنا في قسم الرواسب في مقال المربعات الصغرى الخطية في بايثون بهدف حساب خطأ أخذ العينات، وكما هي العادة فهدفنا هو استخدام عمليات الرصد الفعلية لإجراء محاكاة لما يمكن أن يحدث إذا أجرينا التجربة مرةً أخرى، حيث أنّ عمليات المحاكاة مبنية على افتراض أن المعاملات المقدَّرة صحيحة، لكن قد تكون الرواسب العشوائية مختلفةً، وإليك الدالة التي تجري عمليات المحاكاة:
def SimulateResults(daily, iters=101): model, results = RunLinearModel(daily) fake = daily.copy() result_seq = [] for i in range(iters): fake.average_price = results.fittedvalues + thinkstats2.Resample(results.resid) _, fake_results = RunLinearModel(fake) result_seq.append(fake_results) return result_seq
يُعَدّ daily إطار بيانات يحتوي على الأسعار المرصودة، وiters هو عدد عمليات المحاكاة التي يجب تشغيلها، كما تستخدِم الدالة SimulateResults الدالة RunLinearModel من قسم الانحدار الخطي الموجود في هذا المقال، وذلك من أجل تقدير ميل القيم المرصودة ونقطة تقاطعها، كما تولِّد الدالة مجموعة بيانات مزيفة في كل تكرار من الحلقة عن طريق إعادة أخذ عينات الرواسب وإضافتها إلى القيم الملائمة، ومن ثم تشغِّل نموذجًا خطيًا على البيانات المزيفة وتخزِّن الكائن RegresssionResults، في حين تكون الخطوة القادمة هنا هي استخدام النتائج التي أجرينا عليها محاكاةً من أجل توليد تنبؤات:
def GeneratePredictions(result_seq, years, add_resid=False): n = len(years) d = dict(Intercept=np.ones(n), years=years, years2=years**2) predict_df = pandas.DataFrame(d) predict_seq = [] for fake_results in result_seq: predict = fake_results.predict(predict_df) if add_resid: predict += thinkstats2.Resample(fake_results.resid, n) predict_seq.append(predict) return predict_seq
تأخذ الدالة GeneratePredictions تسلسل النتائج من الخطوة السابقة، بالإضافة إلى القيم years والتي هي تسلسل من القيم العشرية التي تحدِّد المجال الذي يجب علينا توليد تنبؤات له، كما تأخذ هذه الدالة الوسيط add_resid الذي يخبرنا فيما إذا كان يجب إضافة رواسب مُعاد أخذ عيناتها إلى التنبؤ المباشر، حيث تمر GeneratePredictions مرورًا تكراريًا على التسلسل RegressionResults وتولِّد تسلسلًا من التنبؤات.
وأخيرًا إليك الشيفرة التي ترسم مجال الثقة 90% للتنبؤات:
def PlotPredictions(daily, years, iters=101, percent=90): result_seq = SimulateResults(daily, iters=iters) p = (100 - percent) / 2 percents = p, 100-p predict_seq = GeneratePredictions(result_seq, years, True) low, high = thinkstats2.PercentileRows(predict_seq, percents) thinkplot.FillBetween(years, low, high, alpha=0.3, color='gray') predict_seq = GeneratePredictions(result_seq, years, False) low, high = thinkstats2.PercentileRows(predict_seq, percents) thinkplot.FillBetween(years, low, high, alpha=0.5, color='gray')
تستدعي الدالة PlotPredictions دالة GeneratePredictions مرتين، مرةً إذا كان add_resid=True ومرةً أخرى إذا كان add_resid=False، كما تستخدِم PercentileRows لتحديد المئين 95 والمئين 5 لكل سنة، وترسم أخيرًا منطقةً رماديةً بين الحدَّين.
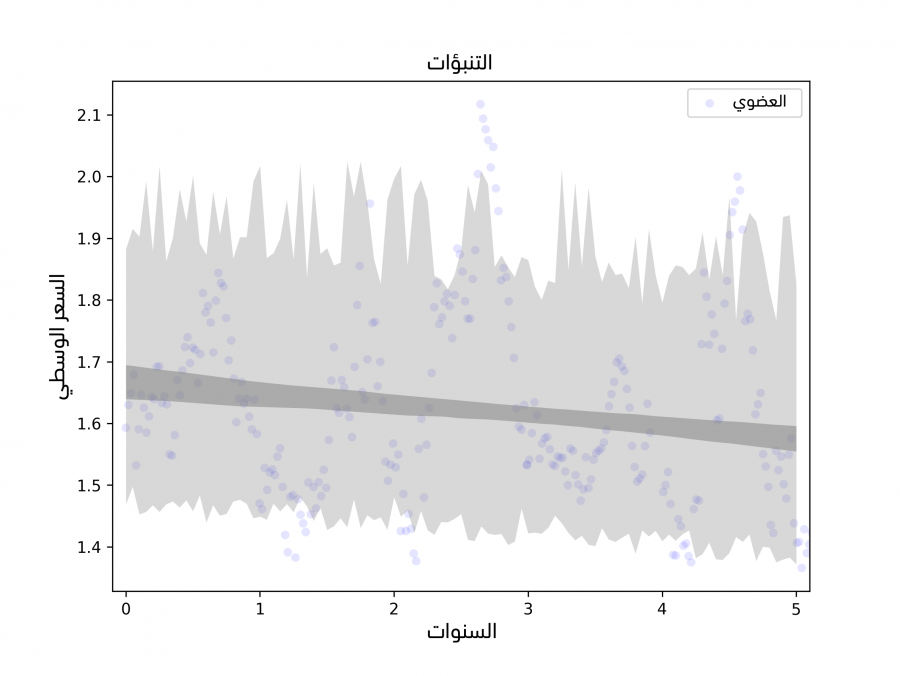
يُظهر الشكل السابق النتيجة، حيث تمثِّل المنطقة الرمادية الداكنة 90% من مجال الثقة لخطأ أخذ العينات، أي عدم اليقين بشأن الميل المقدَّر ونقطة التقاطع بسبب أخذ العينات،
تُظهر المنطقة فاتحة اللون مجال ثقة 90% لخطأ التنبؤ وهو نتيجة جمع التباين العشوائي مع خطأ أخذ العينات.
تحسب هاتان المنطقتان خطأ أخذ العينات والتباين العشوائي وليس خطأ النمذجة، فمن الصعب عمومًا حساب خطأ النمذجة، لكن يمكننا في هذه الحالة معالجة مصدر خطأ واحد على الأقل وهو الأحداث الخارجية غير المتوقعة، فنموذج الانحدار مبني على افتراض أنّ النظام ثابت stationary، أي أن معامِلات النموذج لا تتغير بمرور الزمن، خاصةً الميل ونقطة التقاطع بالإضافة إلى توزيع الرواسب.
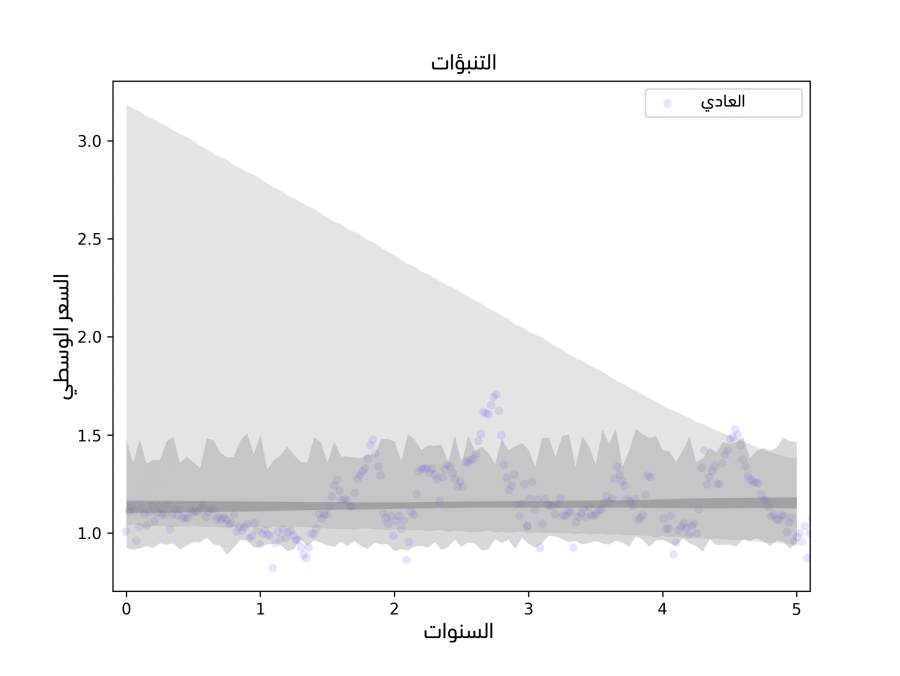
لكن سيبدو لنا بالنظر إلى المتوسطات المتحركة في الشكل 12.5 أنّ الميل يتغير مرةً واحدةً على الأقل خلال فترة الرصد، وسيبدو تباين الرواسب في النصف الأول أكبر من تباينه في النصف الثاني، ونتيجةً لذلك نقول أنّ المعاملات تعتمد على الفترة التي نرصد فيها عمليات البيع، ولرؤية مدى تأثير هذا على التنبؤات يمكننا توسيع SimulateResults لاستخدام فترات الرصد لكن مع تغيير موعد بدء الرصد وانتهائه.
يوضِّح الشكل السابق التنبؤات المبنية على الملاءمة الخطية ويُظهِر التباين الناتج عن فترة الرصد، كما يُظهر النتيجة من أجل الأفوكادو العادي، في حين تُظهر المنطقة الرمادية الفاتحة اللون مجال الثقة الذي يحتوي على عدم اليقين الناتج عن خطأ أخذ العينات، وكذلك يحتوي على التباين العشوائي والتباين في فترة الرصد، علمًا أنّ ميل النموذج المبني على الفترة الكلية موجب، مما يدل على أنّ الأسعار آخذة في الارتفاع، لكن تُظهر الفترة الأحدث أدلةً على انخفاض الأسعار، لذا فإن ميل النماذج المبنية على البيانات الأحدث سالب، وبالتالي تتضمن أوسع فترة تنبؤية إمكانية خفض الأسعار خلال العام المقبل.
لقراءة أكثر تفصيلا
يُعَدّ تحليل السلاسل الزمنية موضوعًا كبيرًا، ولا يتناول هذا المقال سوى جزء يسير منه، إذ يُعَدّ الانحدار الذاتي autoregression من الأدوات الهامة للتعامل مع السلاسل الزمنية، لكنا لم نذكره في هذا المقال، ويعود ذلك إلى أنه قد تبين أنه ليس مفيدًا للبيانات التي عملنا معها، لكن سيؤهلك فهمك للمواد الموجودة في هذا المقال لتعلُّم الانحدار الذاتي، كما يمكننا اقتراح مصدر يتناول موضوع تحليل السلاسل الزمنية وهو تحليل البيانات باستخدام أدوات مفتوحة المصدر، أروايلي ميديا، 2011 (Data Analysis with Open Source Tools, O’Reilly Media, 2011) للكاتب فيليب جارنيت Philipp Janert، حيث يُعَدّ المقال الذي يتحدث فيه عن تحليل السلاسل الزمنية استمرارًا لهذا المقال.
تمارين
إليك التمارين التالية لحلها والتدرب عليها، وانتبه إلى أننا تصرفنا في النص أثناء ترجمته لذا لن تكون الحلول في الملف chap12soln.py في مستودع الشيفرات ThinkStats2 على GitHub صالحة.
تمرين 1
يملك النموذج الخطي الذي استخدمناه في هذا المقال عيبًا واضحًا وهو أنه خطي، وما من سبب يدفعنا للتوقُع أن تغير الأسعار سيبقى خطيًا بمرور الوقت، حيث يمكننا إضافة مرونة إلى النموذج عن طريق إضافة مصطلح تربيعي كما فعلنا في قسم العلاقات اللاخطية في المقال الماضي.
استخدم نموذجًا تربيعيًا لملاءمة السلسلة الزمنية للأسعار اليومية، واستخدم هذا النموذج لتوليد التنبؤات، لكن سيكون عليك في البداية كتابة نسخة من RunLinearModel لتستطيع تشغيل هذا النموذج التربيعي، وبعد ذلك يمكنك توليد التنبؤات عن طريق إعادة استخدام الشيفرة التي استخدمناها في هذا المقال.
تمرين 2
اكتب تعريفًا للصنف SerialCorrelationTest يرث الصنف HypothesisTest من القسم HypothesisTest الموجود في مقال اختبار الفرضيات الإحصائية، بحيث يأخذ سلسلةً series وتأخيرًا lag على أساس وسيطين، ومن ثم يحسب الارتباط التسلسلي للسلسلة مع التأخير المُعطى، ثم يحسب الصنف القيمة الاحتمالية p-value للارتباط المرصود.
استخدم هذا الصنف لتعلم ما إذا كان الارتباط التسلسلي ذا دلالة إحصائية أم لا، واختبرأيضًا الرواسب للنموذج التربيعي والنموذج الخطي (إذا حللت التمرين السابق).
تمرين 3
يمكننا توسيع نموذج المتوسط المتحرك الموزون أسيًا EWMA لتوليد التنبؤات باستخدام عدة طرق، ومن أبسطها اتباع الخطوات التالية:
-
احسب المتوسط المتحرك الموزون أسيًا EWMA للسلسلة الزمنية، ومن ثم استخدِم النقطة الأخيرة على أساس نقطة تقاطع
inter. -
احسب المتوسط المتحرك الموزون أسيًا EWMA للفروق بين العناصر المتتالية في السلسلة الزمنية، ومن ثم استخدِم النقطة الأخيرة على أساس ميل
slope. -
احسب
inter+slope * dtللتنبؤ بالقيم المستقبلية، حيث أنّdtهو الفرق بين زمن التنبؤ وزمن آخر عملية رصد.
استخدِم هذه الطريقة لتوليد تنبؤات لمدة سنة بعد آخر عملية رصد، وإليك بعض التلميحات:
-
استخدِم
timeseries.FillMissingلملء القيم المفقودة قبل إجراء هذا التحليل لكي يكون الزمن بين العناصر المتتالية متسقًا. -
استخدِم
Series.diffلحساب الفرق بين العناصر المتتالية. -
استخدِم
reindexلتوسيع فهرس إطار البيانات في المستقبل. -
استخدِم
fillnaلوضع القيم التي تنبأت بها في إطار البيانات.
ترجمة وبتصرف للفصل Chapter 12 Time series Analysis من كتاب Think Stats: Exploratory Data Analysis in Python.
الملف المرفق dataset.zip.












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.