توجد الشيفرة الخاصة بهذا المقال في الملف linear.py.
ملاءمة المربعات الصغرى
تقيس معاملات الترابط قوة وإشارة العلاقة لكنها لا تقيس الميل slope، إذ توجد عدة طرق لتقدير الميل وأكثر هذه الطرق شيوعًا هي ملاءمة المربعات الصغرى الخطية linear least squares fit، حيث تُعَدّ الملاءمة الخطية linear fit خطًا ينمذج العلاقة بين المتغيرات؛ أما ملاءمة المربعات الصغرى least squares فتقلل الخطأ التربيعي المتوسط mean squared error -أو MSE اختصارًا- بين الخط والبيانات.
لنفترض أنه لدينا متسلسلةً من النقاط ys، ونريد التعبير عنها على أساس دالة من متسلسلة أخرى xs، فإذا كانت هناك علاقةً خطيةً بين xs وys مع نقطة تقاطع inter وميل slope، فسنتوقع عندها y ليكون inter + slope * x، علمًا أنّ هذا التوقع تقريبي فحسب أي ليس دقيقًا إلا إذا كان الترابط مثاليًا، وتكون الصيغة الرياضية للانحراف العمودي عن الخط أو ما يُعرف بالراسب residual هي:
res = ys - (inter + slope * xs)
قد تكون الرواسب ناتجةً عن عوامل عشوائية مثل الخطأ في القياس أو عوامل غير عشوائية وغير معروفة، فإذا حاولنا مثلًا توقّع الوزن من دالة الطول، فستشمل عوامل غير معروفة الحمية الغذائية والتمارين الرياضية ونوع الجسم، وإذا لم يكن حسابنا للمعامِلَين inter وslope صحيحًا، فستكون الرواسب أكبر، لذا من المنطقي أن تكون المعاملات التي نريدها هي تلك التي تقلل من الرواسب.
قد نحاول تقليل القيمة المطلقة للرواسب أو مربعها أو مكعبها، لكن الخيار الأكثر شيوعًا واستخدامًا هو تقليل مجموع مربعات الرواسب sum(res**2)، لكن لمَ تُعَدّ هذه الطريقة هي الأشيع؟ هناك ثلاث أسباب وجيهة وسبب أقل أهمية لذلك كما يلي:
- يعامِل التربيع الرواسب الموجبة والسالبة بالطريقة نفسها، وهي ميزة مفيدة لنا في أغلب الأحيان.
-
يُعطي التربيع وزنًا -أي ترجيحًا- أكبر للرواسب الكبيرة، لكن ليس للدرجة التي تتسبب فيها هذه الميزة بهيمنة الرواسب الأكبر دائمًا. *إذا لم تكن الرواسب مترابطةً وإذا كان توزيعها طبيعيًا مع متوسط قدره 0 وتباين ثابت لكن غير معروف، فستكون ملاءمة المربعات الصغرى هي نفسها مُقدِّر الاحتمال الأعظم maximum likelihood estimator -أو MLE اختصارًا- لكل من
interوslope، ويمكنك زيارة صفحة ويكيبيديا لمزيد من المعلومات. -
يمكن حساب قيم
interوslopeالتي تقلل من الرواسب المربعة بكفاءة.
يُعَدّ السبب الأخير منطقيًا حينما كانت كفاءة الحسابات أهم من اختيار الطريقة الأنسب للمشكلة التي نحاول حلها لكن الأمر لم يعُد كذلك، لذلك يجدر التفكير فيما إذا كانت الرواسب المربّعة هي ما نريد تقليله أم لا، ولنفترض مثلًا أنك تحاول التنبؤ بقيم ys باستخدام xs، فقد يكون تخمين القيم المرتفعة جدًا أفضل -أو أسوأ- من تخمين القيم المنخفضة جدًا، وقد نرغب في هذه الحالة في حساب بعض من دوال الكلفة لكل راسب من الرواسب ثم تقليل الكلفة الإجمالية sum(cost(res))، ومع ذلك يُعَدّ حساب ملاءمة المربعات الصغرى سريعًا وسهلًا وغالبًا ما يكون جيدًا بدرجة كافية.
التنفيذ
يزود المستودع thinkstats2 بدوال بسيطة توضِّح المربعات الصغرى الخطية، إليك الشيفرة الموافقة لذلك كما يلي:
def LeastSquares(xs, ys): meanx, varx = MeanVar(xs) meany = Mean(ys) slope = Cov(xs, ys, meanx, meany) / varx inter = meany - slope * meanx return inter, slope
يأخذ التابع LeastSquares متسلسلتين هما xs وys ويُعيد المعامِلَين المُقدِّرَين inter وslop، كما يمكنك الاطلاع على مزيد من التفاصيل حول آلية عمله عن طريق زيارة صفحة ويكيبيديا، كما يزود المستودع thinkstats2 بالتابع FitLine أيضًا، حيث يأخذ المعامِلَين inter وslope ويُعيد الخط الملائم للمتسلسلة xs، وإليك الشيفرة الموافقة لذلك كما يلي:
def FitLine(xs, inter, slope): fit_xs = np.sort(xs) fit_ys = inter + slope * fit_xs return fit_xs, fit_ys
يمكننا استخدام هذه الدوال لحساب ملاءمة المربعات الصغرى لوزن الولادات على أساس دالة لعمر الأم:
live, firsts, others = first.MakeFrames() live = live.dropna(subset=['agepreg', 'totalwgt_lb']) ages = live.agepreg weights = live.totalwgt_lb inter, slope = thinkstats2.LeastSquares(ages, weights) fit_xs, fit_ys = thinkstats2.FitLine(ages, inter, slope)
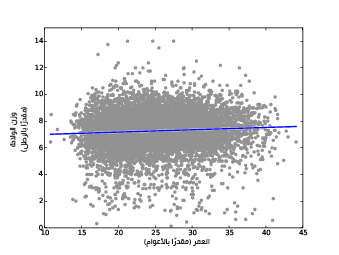
تبلغ قيمة نقطة التقاطع المقدَّرة والميل المقدَّر 6.8 رطلًا -أي حوالي 3.08 كيلوغرامًا- و0.017 رطلًا في العام الواحد -أي حوالي 0.007 كيلوغرامًا في العام الواحد-، ومن الصعب تفسير هذه القيم بهذه الصورة، حيث تُعَدّ نقطة التقاطع الوزن المتوقع للطفل إذا كان عمره أمه 0 عام، وهذا ليس منطقيًا في سياقنا، والميل صغير جدًا بحيث لا يمكن فهمه بسهولة.
غالبًا ما يكون من المفيد البدء بنقطة التقاطع عند متوسط x بدلًا من البدء بنقطة التقاطع من القيمة 0 أي x=0، لذا يكون متوسط العمر في هذه الحالة هو 25 تقريبًا ومتوسط وزن الطفل للأم التي يبلغ عمرها 25 عامًا هو 7.3 رطلًا -أي حوالي 3.31 كيلوغرامًا-، بذلك يكون الميل 0.27 رطلًا في العام الواحد أي حوالي 0.12 كيلوغرامًأ- أو 0.17 رطلًا كل 10 أعوام -أي حوالي 0.07 كيلوغرامًا كل 10 أعوام-.
يوضِّح الشكل السابق مخطط انتشار أوزان الولادات وعمر الأم مع ملاءمة خطية، ومن الجيد النظر إلى شكل مثل هذا بهدف تقييم ما إذا كانت العلاقة خطيةً أم لا وما إذا كان الخط الملائم يبدو نموذجًا جيدًا للعلاقة أم لا.
الرواسب
يُعَدّ رسم الرواسب اختبارًا مفيدًا أيضًا، كما يزودنا المستودع thinkstats2 بدالة تحسب الرواسب، إليك الشيفرة الموافقة لذلك كما يلي:
def Residuals(xs, ys, inter, slope): xs = np.asarray(xs) ys = np.asarray(ys) res = ys - (inter + slope * xs) return res
تأخذ الدالة Residuals متسلسلتين هما xs وys، ومعامِلَين مُقدِّرَين هما inter وslope وتُعيد الفروق بين القيم الفعلية والخط الملائم.
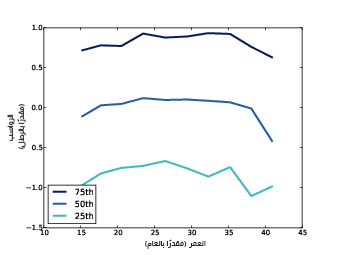
يوضِّح الشكل السابق رواسب الملاءمة الخطية.
جمعنا المستجيبين حسب العمر وحسبنا قيم المئين في كل مجموعة تمامًا من أجل رسم مخططات للرواسب كما رأينا في قسم توصيف العلاقات في المقال السابق، حيث يوضِّح الشكل السابق المئين 25 -أي 25th percentile- والمئين 50 -أي 50th percentile- والمئين 75 -أي 75th percentile- للرواسب الموجودة في كل مجموعة، وكما هو متوقع فإن الوسيط median يقارب الصفر والانحراف الربيعي interquartile range هو حوالي رطلين -أي حوالي 0.9 كيلوغرامًا-، لذا يمكننا تخمين وزن الطفل بخطأ قدره رطلًا واحدًا بحوالي 50% من المرات إذا علمنا عمر الأم مسبقًا.
تكون هذه الخطوط في الوضع المثالي مسطحةً ويشير هذا إلى أن الرواسب عشوائية ومتوازية وإلى أن المجموعات متساوية فيما بينهما من حيث تباين الرواسب -أي أن قيم الرواسب متساوية بالنسبة لكل المجموعات-، حيث أن الخطوط قريبة من التوازي وهذا أمر جيد، لكن يوجد بعض الانحناءات في هذه الخطوط مما يدل على أن العلاقة لاخطية، ومع ذلك تُعَدّ الملاءمة الخطية نموذجًا بسيطًا ربما يكون جيدًا بما يكفي لبعض الأغراض.
التقدير
يُعَدّ المعامِلان slope وinter تقديرَين بناءً على عينة ما، وهما عُرضة للتحيز في أخذ العينات sampling bias تمامًا مثل التقديرات الأخرى، وكذلك فهما عُرضة للخطأ في القياس measurement error والخطأ في أخذ العينات sampling error، حيث أن التحيُز في أخذ العينات -كما ناقشنا في مقال التقدير Estimation الإحصائي في بايثون- ناتج عن أخذ عينات غير تمثيلية non-representative sampling، والخطأ في القياس ناتج عن أخطاء في جمع وتسجيل البيانات؛ أما الخطأ في أخذ العينات فهو نتيجة لقياس عينة ما بدلًا من قياس السكان بأكملهم.
سنطرح السؤال التالي من أجل تقييم الخطأ في أخذ العينات: ما مقدار التباين الذي نتوقعه في التقديرات إذا أجرينا هذه التجربة مرةً أخرى؟ حيث سنجيب عن هذا السؤال عن طريق إجراء عدة تجارب محاكاة ومن ثم حساب توزيعات أخذ العينات للتقديرات، وقد طبقنا محاكاةً للتجارب عن طريق إعادة أخذ عينات البيانات، أي نعامل حالات الحمل المرصودة كما لو أنها تمثل السكان جميعهم ومن ثم سحبنا عينات مع الاستبدال من العينة المرصودة، وإليك الشيفرة الموافقة لذلك كما يلي:
def SamplingDistributions(live, iters=101): t = [] for _ in range(iters): sample = thinkstats2.ResampleRows(live) ages = sample.agepreg weights = sample.totalwgt_lb estimates = thinkstats2.LeastSquares(ages, weights) t.append(estimates) inters, slopes = zip(*t) return inters, slopes
تأخذ الدالة SamplingDistributions إطار بيانات DataFrame بسطر واحد لكل ولادة حية، ويمثِّل المتغير iter عدد التجارب التي سنحاكيها، كما تستخدِم ResampleRows لإعادة أخذ العينات الخاصة بحالات الحمل المرصودة، حيث أننا تطرقنا سابقًا إلى SampleRows التي تختار أسطرًا عشوائية من إطار بيانات، كما يزودنا المستودع thinkstats2 بالدالة ResampleRows التي تُعيد عينةً حجمها بحجم العينة الأصلية كما يلي:
def ResampleRows(df): return SampleRows(df, len(df), replace=True)
استخدمنا العينات المُحاكاة لتقدير المِعاملات بعد عملية إعادة أخذ العينات، إذ تكون النتيجة متسلسلتين هما نقط التقاطع المُقّدَّرة والميول المقدَّرة، كما لخصنا توزيعات أخذ العينات عن طريق طباعة فاصل الثقة والخطأ المعياري، وإليك الشيفرة الموافقة لذلك كما يلي:
def Summarize(estimates, actual=None): mean = thinkstats2.Mean(estimates) stderr = thinkstats2.Std(estimates, mu=actual) cdf = thinkstats2.Cdf(estimates) ci = cdf.ConfidenceInterval(90) print('mean, SE, CI', mean, stderr, ci)
يأخذ التابع Summarize متسلسلةً من التقديرات والقيمة الفعلية، حيث تطبع تقديرات المتوسط والخطأ المعياري وفاصل الثقة 90%؛ أما بالنسبة لنقطة التقاطع فيكون تقدير المتوسط هو 6.83 مع خطأ معياري قدره 0.07 وفاصل ثقة 90% هو (6.71- 6.94)؛ أما الميل المُقدَّر فشكله أكثر تراصًا وإحكامًا، حيث أن قيمته هي 0.0174 وقيمة الخطأ المعياري 0.0028، وقيمة فاصل الثقة هي (0.0126 - 0.0220)، وفي الواقع الفرق بين النهاية المنخفضة والمرتفعة من فاصل الثقة هو الضعف، لذا يجب اعتباره تقديرًا تقريبيًا.
يمكننا حساب كل الخطوط الملائمة إذا أردنا رسم أخطاء أخذ العينات للتقديرات، لكن إذا أردنا أن يكون تمثيل البيانات أقل تفاوتًا، فيمكننا رسم فاصل الثقة 90% لكل عمر، إليك الشيفرة الموافقة لذلك كما يلي:
def PlotConfidenceIntervals(xs, inters, slopes, percent=90, **options): fys_seq = [] for inter, slope in zip(inters, slopes): fxs, fys = thinkstats2.FitLine(xs, inter, slope) fys_seq.append(fys) p = (100 - percent) / 2 percents = p, 100 - p low, high = thinkstats2.PercentileRows(fys_seq, percents) thinkplot.FillBetween(fxs, low, high, **options)
يمثِّل المتغير xs متسلسلةً لعمر الأم؛ أما inters وslopes فهما معامِلَين مقدَّرَين ولَّدهما التابع SamplingDistributions، في حين يشير المتغير percent إلى فاصل الثقة الذي نريد رسمه، كما يولِّد التابع PlotConfidenceIntervals الخط الملائم لكل زوج من inter وslope ويخزن النتائج في متسلسلة fys_seq، ومن ثم يستخدِم PercentileRows لتحديد مئين العلوي والسفلي من y لكل قيمة x؛ أما بالنسبة لفاصل الثقة 90% فيحدد التابع المئين 5 -أي 5th percentile- والمئين 95 -أي 95th percentile-، كما يرسم التابع FillBetween مضلعًا يملأ الفراغ بين خطين اثنين.
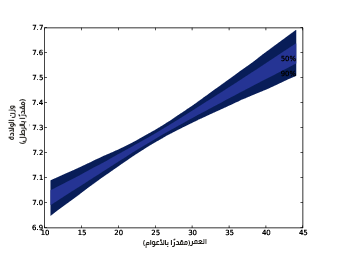
يُظهِر الشكل السابق فاصلي الثقة 50% و90% التباين في الخط الملائم الناتج عن الخطأ في أخذ عينات inter وslope، كما يوضِّح فاصلي الثقة 50% و90% للمنحنيات الملائمة لأوزان الولادات على أساس دالة عمر الأم؛ أما العرض الرأسي للمنطقة فيمثِّل تأثير الخطأ في أخذ العينات، حيث أن التأثير أصغر على القيم التي تقارب المتوسط mean وأكبر على القيم المتطرفة extremes.
حسن الملاءمة
يمكننا قياس جودة النموذج الخطي أو ما يُعرَف بحُسن الملائمة goodness of fit بعدة طرق، وإحدى أبسط هذه الطرق هي الانحراف المعياري للرواسب، فإذا استخدمت نموذجًا خطيًا للتنبؤ، فسيكونStd(res) هو خطأ الجذر التربيعي المتوسط -أو RMSE اختصارًا- لتنبؤاتك.
يكون خطأ الجذر التربيعي المتوسط مثلًا لتخمينك هو 1.14 رطلًا -أي حوالي 0.5 كيلوغرامًا- إذا استخدمت عمر الأم لتخمين وزن الطفل، وإذا خمنت وزن الطفل دون معرفة عمر الأم، فسيكون خطأ الجذر التربيعي المتوسط لتخمينك هو Std(ys) أي 1.14 رطل، لذا لا تؤدي معرفة عمر الأم في مثالنا هذا إلى تحسين التنبؤ إلى حد كبير، كما يمكننا قياس حُسن الملاءمة عن طريق مُعامِل التحديد coefficient of determination أيضًا، علمًا أنه يرمز له R2 ويدعى مربع R:
def CoefDetermination(ys, res): return 1 - Var(res) / Var(ys)
يُعَدّ Var(res) الخطأ التربيعي المتوسط -أو MSE اختصارًا- لتنبؤاتك باستخدام النموذج؛ أما الخطأ التربيعي المتوسط للتنبؤات بدون استخدام النموذج فهو Var(ys)، لذا فإن نسبتها هي الجزء المتبقي من الخطأ التربيعي المتوسط إذا استخدمتَ النموذج، وR2 هو جزء الخطأ التربيع المتوسط الذي يحذفه النموذج، حيث أنّ قيمة R2 بالنسبة لوزن الولادة وعمر الأم هو 0.0047 أي أن عمر الأم يتنبأ بنصف 1% من التباين في وزن الولادة.
توجد علاقة بسيطة بين مُعامِل ترابط بيرسون وبين مُعامِل التحديد وهي تحدَّد بالعلاقة R2=ρ2، فإذا كان ρ مثلًا 0.8 أو 0.8-، فسيكون R2=0.64، وعلى الرغم أنه غالبًا ما يُستخدَم كل من ρ وR2 لتحديد قوة علاقة، إلا أنه ليس من السهل تفسير هذين المقدارين من حيث القوة التنبؤية، كما يكون أفضل تمثيل لجودة التنبؤ برأينا هو Std(res) خاصةً إذا مُثِّل بالعلاقة مع Std(ys)، فعندما يتحدث الأشخاص مثلًا عن صلاحية اختبار سات SAT -وهو اختبار موحد للالتحاق بالجامعات في الولايات المتحدة الأمريكية-، فإنهم غالبًا ما يتحدثون عن الارتباطات بين درجات سات ومقاييس الذكاء الأخرى.
يوجد - وقفًا لإحدى الدراسات- ارتباط بيرسون ρ=0.72 بين درجات اختبار سات ومعدل اختبار الذكاء IQ، وقد يبدو هذا الارتباط قويًا لكن R2=ρ=0.52، لذا فإن درجات سات لا تمثِّل سوى 52% من التباين في اختبار الذكاء IQ، كما وُحِّد معدل اختبار الذكاء IQ بالمعادلة Std(ys)=15، لذا يكون:
>>> var_ys = 15**2 >>> rho = 0.72 >>> r2 = rho**2 >>> var_res = (1 - r2) * var_ys >>> std_res = math.sqrt(var_res) 10.4096
لذا يقلل استخدام نتيجة اختبار سات لتوقع معدل الذكاء IQ من معدل خطأ الجذر التربيعي المتوسط RMSE بحيث يصبح 10.4 نقطة بعد أن كان 15 نقطة، أي ينتج عن ارتباط 0.72 انخفاضًا في خطأ الجذر التربيعي المتوسط بنسبة 31% فقط، فإذا رأيتَ ارتباطًا مذهلًا، فتذكَّر أن R2 هو مؤشر أفضل للانخفاض في الخطأ التربيعي المتوسط MSE، وكذلك يكون الانخفاض في خطأ الجذر التربيعي المتوسط RMSE مؤشرًا أفضل للقوة التنبؤية.
اختبار نموذج خطي
يُعَدّ تأثير عمر الأم على وزن الولادة صغيرًا وتُعَدّ قوته التنبؤية صغيرةً، لذا هل من الممكن أن تكون العلاقة الظاهرة ناتجةً عن الصدفة؟ هناك عدة طرق يمكننا من خلالها اختبار نتيجة الملاءمة الخطية linear fit.
يتمثَّل أحد الخيارات في اختبار كون الانخفاض الظاهر في الخطأ التربيعي المتوسط ناتجًا عن الصدفة، وفي هذه الحالة تكون إحصائية الاختبار هي R2 وفرضية العدم هنا هي أنه لا توجد علاقة بين المتغيرات، كما يمكننا محاكاة فرضية العدم عن طريق التبديل permutation كما فعلنا في قسم اختبار الارتباط في المقال السابق عندما اختبرنا الارتباط بين عمر الأم ووزن الولادة.
يكافئ الاختبار أحادي الجانب للمقدار R2 للاختبار ثنائي الجانب لارتباط بيرسون ρ في الواقع نظرًا لأن R2=ρ2، وقد أجرينا هذا الاختبار سابقًا ووجدنا أنّ القيمة الاحتمالية أصغر من 0.001 أي p<0.001، لذا نستنتج أن للعلاقة الظاهرة بين عمر الأم ووزن الولادة دلالة إحصائية.
توجد طريقة أخرى لاختبار فيما إن كان الميل slope الظاهر ناجمًا عن الصدف فحسب، إذ تقول فرضية العدم في هذا الحالة أنّ الميل صفر، ويمكننا في هذه الحالة نمذجة أوزان الولادات على أساس تباينات عشوائية حول قيمة المتوسط الخاصة بهم، وإليك HypothesisTest خاص بهذا النموذج كما يلي:
class SlopeTest(thinkstats2.HypothesisTest): def TestStatistic(self, data): ages, weights = data _, slope = thinkstats2.LeastSquares(ages, weights) return slope def MakeModel(self): _, weights = self.data self.ybar = weights.mean() self.res = weights - self.ybar def RunModel(self): ages, _ = self.data weights = self.ybar + np.random.permutation(self.res) return ages, weights
البيانات هنا مُمثَّلة بمتسلسلتين هما ages يمثِّل الأعمار وweights يمثِّل الأوزان، وتكون إحصائية الاختبار test statistic هنا الميل المُقدَّر بواسطة LeastSquares، في حين يكون نموذج فرضية العدم ممثَّلًا بمتوسط أوزان جميع الأطفال وبالانحرافات عن المتوسط، كما يمكننا توليد بيانات مُحاكاة عن طريق تبديل الانحرافات وإضافة هذه الانحرافات إلى المتوسط، وإليك الشيفرة التي تنفِّذ اختبار الفرضية كما يلي:
live, firsts, others = first.MakeFrames() live = live.dropna(subset=['agepreg', 'totalwgt_lb']) ht = SlopeTest((live.agepreg, live.totalwgt_lb)) pvalue = ht.PValue()
تكون القيمة الاحتمالية هنا أقل من 0.001، أي على الرغم من أن الميل المُقدَّر صغير إلا أنه من غير المرجح أن يكون ناجمًا عن الصدفة، ويُعَدّ تقدير القيم الاحتمالية عن طريق إجراء محاكاة لفرضية العدم تقديرًا صحيحًا تمامًا لكن يوجد بديل أبسط من هذه الطريقة، علمًا أننا حسبنا توزيع أخذ العينات الخاص بالميل في قسم التقدير في هذا المقال، لذا افترضنا أنّ الميل المرصود صحيح ثم حاكينا تجاربًا عن طريق إعادة أخذ العينات resampling.
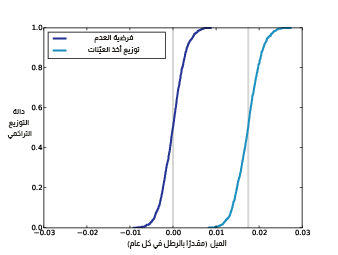
يوضِّح الشكل التالي توزيع أخذ العينات للميل من قسم التقدير في هذا المقال، ويوضح أيضًا توزيع الميول المولَّدة في ظل فرضية العدم، كما يتركَّز توزيع أخذ العينات حول الميل المقدَّر وهو 0.017 رطلًا في العام الواحد، في حين تتركز الميول تحت فرضية العدم حول القيمة 0، لكن بخلاف ذلك فإن التوزيعات متطابقة وهي متماثلة أيضًا لأسباب سنراها في قسم لاحق في مقال لاحق.
يوضِّح الشكل السابق توزيع أخذ العينات للميل المُقدَّر وتوزيع الميول المولَّدة في ظل فرضية العدم، حيث أن الخطوط العمودية هي عند القيمة 0 والميل المرصود هو 0.017 رطل في العام الواحد، لذا يمكننا تقدير القيمة الاحتمالية بطريقتين هما:
- حساب احتمال تخطي قيمة الميل في ظل فرضية العدم لقيمة الميل المرصود.
- حساب احتمال انخفاض قيمة الميل في توزيع أخذ العينات عن الصفر، فإذا كان الميل المُقدَّر سالبًا، فسنحسب احتمال زيادة قيمة الميل في توزيع أخذ العينات عن الصفر.
يُعَدّ الخيار الثاني خيارًا أسهل لأننا عادةً نريد حساب توزيع أخذ العينات للمعامِلات على أي حال، كما يُعَدّ تقديرًا تقريبيًا جيدًا إلا في حال كان حجم العينة صغيرًا وكان توزيع الرواسب متجانفًا skewed، وحتى حينها يكون هذا الخيار جيدًا بما فيه الكفاية لأنه ليس من الضروري أن تكون القيم الاحتمالية دقيقةً، وإليك الشيفرة التي تقدِّر القيمة الاحتمالية للميل باستخدام توزيع أخذ العينات:
inters, slopes = SamplingDistributions(live, iters=1001) slope_cdf = thinkstats2.Cdf(slopes) pvalue = slope_cdf[0]
وجدنا مجدَّدًا أنّ القيمة الاحتمالية أصغر من 0.001 أي p<0.001.
إعادة أخذ العينات مع الأوزان
عامَلنا في هذا الكتاب بيانات المسح الوطني لنمو الأسرة NSFG على أنها عينة تمثيلية، لكنها ليس تمثيلية كما ذكرنا في مقال تحليل البيانات الاستكشافية لإثبات النظريات الإحصائية، حيث تعمَّد هذا المسح الإفراط في أخذ عينات عدة مجموعات من أجل زيادة احتمال ظهور نتائج ذات دلالة إحصائية، أي بهدف تحسين قوة الاختبارات التي تخص هذه المجموعات.
يُعَدّ تصميم الإحصائية هذا مفيدًا لعدة أغراض لكنه يعني أنه لا يمكننا استخدام العينة لتقدير قيم عامة السكان من دون حساب عملية أخذ العينات، كما تحوي بيانات المسح الوطني لنمو الأسرة متغيرًا يُدعى finalwgt لكل مستجيب بحيث يشير إلى عدد الأشخاص الذي يمثلهم هذا المستجيب، وتُدعى هذه القيمة بوزن أخذ العينات sampling weight أو الوزن فقط، فإذا أجريت مسحًا لمائة ألف مستجيب في بلد يحوي 300 مليون نسمة، فسيمثل كل مستجيب 3000 شخص، وإذا بالغت في أخذ عينات مجموعة ما بعامِل 2 -أي الضعف-، فسيكون لكل شخص في المجموعة ذات العينات المبالغة بها وزنًا أقل، أي حوالي 1500.
يمكننا استخدام إعادة أخذ العينات إذا أردنا تصحيح المبالغة في أخذ العينات oversampling، أي يمكننا سحب عينات من المسح باستخدام الاحتمالات المتناسبة مع أوزان أخذ العينات، ثم يمكننا توليد توزيعات أخذ العينات sampling distributions والأخطاء المعيارية standard errors ومجالات الثقة confidence intervals، حيث سنقدِّر مثلًا قيمة متوسط وزن الولادة مع وبدون أوزان أخذ العينات.
رأينا في قسم التقدير في هذا المقال التابع ResampleRows الذي يختار أسطرًا من إطار بيانات معطيًا كل الأسطر الاحتمال نفسه؛ أما الآن فسيتوجب علينا إجراء ذات العمليات لكن مع استخدام احتمالات متناسبة مع أوزان أخذ العينات، في حين يأخذ التابع ResampleRowsWeighted إطار بيانات ويَعيد أخذ عينات resamples الأسطر حسب الوزن في المتغير finalwgt، ثم يُعيد إطار البيانات الذي يحتوي على الأسطر التي أُجري عليها عملية إعادة أخذ عينات.
def ResampleRowsWeighted(df, column='finalwgt'): weights = df[column] cdf = Cdf(dict(weights)) indices = cdf.Sample(len(weights)) sample = df.loc[indices] return sample
يُعَدّ المتغير weights سلسلةً Series، ويؤدي تحويلها إلى قاموس dictionary إلى إنشاء خريطة map من الفهارس إلى الأوزان، علمًا أنّ القيم في cdf هي فهارس والاحتمالات متناسبة مع الأوزان؛ أما indicies فهي متسلسلة sequence من أسطر تحوي فهارس، ويمثِّل sample إطار بيانات يحتوي على الأسطر المُحدَّدة، وقد يظهر السطر نفسه أكثر من مرة لأننا نستخدِم عينات مع الاستبدال، كما يمكننا الآن موازنة تأثير إعادة أخذ العينات مع الأوزان وبدونها، حيث نولِّد توزيعات أخذ العينات بدون أوزان (أي دون إعطاء ترجيح) كما يلي:
estimates = [ResampleRows(live).totalwgt_lb.mean() for _ in range(iters)]
أما مع أوزان (أي مع ترجيح) فيصبح كما يلي:
estimates = [ResampleRowsWeighted(live).totalwgt_lb.mean() for _ in range(iters)]
يلخص الجدول التالي النتائج:
| متوسط أوزان الولادات (مقدرةً بالرطل) | الخطأ المعياري | فاصل الثقة 90% | |
|---|---|---|---|
| بدون أوزان | 7.27 | 0.014 | (7.24, 7.29) |
| مع أوزان | 7.35 | 0.014 | (7.32, 7.37) |
يُعَدّ أثر الترجيح في هذا المثال صغيرًا لكنه غير مهمل، ويكون الفرق في المتوسطين المُقدَّرَين مع ترجيح وبدون ترجيح هو 0.08 رطلًا تقريبًا -أي حوالي 0.03 كيلوغرامًا- أو 1.3 أوقيةً، وهذا الفرق أكبر بكثير من الخطأ المعياري للتقدير الذي تبلغ قيمته 0.014 رطلًا -أي حوالي 0.006 كيلوغرامًا-، مما يعني أنّ الفرق لم يحدث صدفةً.
تمارين
يوجد حل هذا التمرين في chap10soln.ipynb.
تمرين 1
استخدِم البيانات الخاصة بنظام مراقبة عوامل المخاطر السلوكية BRFSS واحسب ملاءمة المربعات الصغرى الخطية للوغاريتم الوزن مقابل الطول.
ما هي أفضل طريقة لتمثيل المعامِلات المُقدَّرة لنموذج مثل هذا، أي نموذج طُبق التحويل اللوغاريتم على أحد متغيراته؟ وإلى أي مدى سيساعدك على معرفة وزن شخص ما في حال كنت تحاول تخمينه؟
يُفرِط نظام مراقبة العوامل السلوكية في أخذ العينات لبعض المجموعات تمامًا مثل المسح الوطني لنمو الأسرة ويزودنا بوزن أخذ العينات لكل مستجيب، حيث أنّ اسم متغير هذه الأوزان في بيانات نظام مراقبة العوامل السلوكية هو finalwt.
استخدم إعادة أخذ العينات resampling مع الأوزان وبدونها من أجل تقدير متوسط أطوال المستجيبين في نظام مراقبة العوامل السلوكية، بالإضافة إلى الخطأ المعياري للمتوسط وفاصل الثقة 90%، وإلى أي مدى يؤثر الترجيح الصحيح على التقديرات؟
ترجمة -وبتصرف- للفصل Chapter 10 Linear least squares analysis من كتاب Think Stats: Exploratory Data Analysis in Python.
اقرأ أيضًا
- العلاقات بين المتغيرات الإحصائية وكيفية تنفيذها في بايثون
- نمذجة التوزيعات Modelling distributions في بايثون
- دوال الكثافة الاحتمالية في بايثون









أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.