توجد الشيفرة الخاصة بهذا المقال في الملف hypothesis.py.
الطريقة الكلاسيكية في اختبار الفرضيات
لاحظنا عند استكشاف بيانات المسح الوطني لنمو الأسرة NSFG تأثيرات واضحةً منها الفرق بين الأطفال الأوائل وبقية الأطفال، ولم نشكك في صحتها حتى الآن، لذا سنخصص هذا المقال لاختبار صحة الآثار التي ظهرت من عدمها، حيث سنتطرق إلى سؤال أساسي وهو: في حال رأينا تأثيرات في عينة ما، فهل من المرجح أن تظهر هذه التأثيرات في عينة أكبر؟ فقد نرى فرقًا على سبيل المثال في متوسط مدة الحمل للأطفال الأوائل وبقية الأطفال في المسح الوطني لنمو الأسرة، ونود معرفة ما إذا كان هذا التأثير يعكس اختلافًا حقيقيًا في مدة حمل النساء في الولايات المتحدة الأمريكية أم أنه قد يظهر في العينة عن طريق الصدفة.
يمكننا صياغة هذا السؤال بعدة طرق، منها اختبار فرضيات العدم عند فيشر Fisher null hypothesis testing ونظرية قرار نيمان بيرسون Neyman-Pearson decision theory، والاستدلال البايزي Bayesian inference، كما يُعَدّ ما سنقدِّمه في هذا المقال مجموعةً فرعيةً من الطرق الثلاث المذكورة آنفًا وهي ما يستخدِمه معظم الأشخاص في الممارسات العملية وسنسميها الطريقة الكلاسيكية في اختبار الفرضيات classical hypothesis testing.
الهدف من الطريقة الكلاسيكية في اختبار الفرضيات هو الإجابة على السؤال التالي: إذ كان لدينا عينةً ما وهناك تأثير ظاهر فيها، فما هو احتمال رؤية مثل هذا التأثير عن طريق الصدفة؟ إليك كيف نجيب على هذا السؤال:
- تتمثل الخطوة الأولى في تحديد حجم التأثير الظاهر وذلك عن طريق اختيار إحصائية اختبار test statistic، حيث أنّ التأثير الظاهر في مثال المسح الوطني لنمو الأسرة هو فرق في مدة الحمل بين الأطفال الأوائل وبقية الأطفال، لذا فمن المنطقي أن تكون إحصائية الاختبار هي فرق المتوسطات means بين المجموعتين.
- تتمثل الخطوة الثانية في تعريف فرضية عدم null hypothesis، وهي نموذج للنظام مبنية على افتراض أن التأثير الظاهر ليس حقيقيًا، وتكون فرضية العدم في مثال المسح الوطني لنمو الأسرة هي أنه لا يوجد فرق بين الأطفال الأوائل وبقية الأطفال، أي أنّ توزيع مدة الحمل للأطفال الأوائل هو توزيع مدة الحمل لبقية الأطفال نفسه.
- تتمثل الخطوة الثالثة في حساب القيمة الاحتمالية p-value، وهي احتمال وجود التأثير الظاهر في حال كانت فرضية العدم صحيحة، حيث نحسب الفرق الفعلي في المتوسطين في مثال المسح الوطني لنمو الأسرة، ومن ثم نحسب احتمال وجود الفارق بالحجم نفسه أو وجود فارق أكبر وذلك في ظل وجود فرضية العدم.
- تتمثّل الخطوة الأخيرة في أنها تفسير النتيجة، حيث إذا كانت القيمة الاحتمالية منخفضةً فيُقال عن التأثير أنه ذات دلالة إحصائية statistically significant، أي أنه من غير المحتمل أن يكون قد ظهر بمحض الصدفة، حيث يمكننا في هذه الحالة استنتاج أنه من المرجح ظهور هذا التأثير في عينة أكبر.
يتشابه منطق هذه العملية مع البرهان بالتناقض، أي لإثبات تعبير رياضي A، سنفترض مؤقتًا أنّ A خاطئ، فإذا أدى هذا الافتراض إلى تناقض، فسنستنتج أنّ A صحيحة، وبالمثل لاختبار فرضية مثل "هذا التأثير حقيقي"، سنفترض مؤقتًا أنها خاطئة وهذه هي فرضية العدم، حيث نحسب احتمال التأثير الظاهر بناءً على هذا الافتراض وهذه هي القيمة الاحتمالية p-value، فإذا كانت هذه القيمة الاحتمالية منخفضةً، فسنستنتج أنه من المرجح أن تكون فرضية العدم صحيحة.
الصنف HypothesisTest
يزوِّدنا المستودع thinkstats2 بالصنف Hypothesis والذي يمثِّل بنية الطريقة الكلاسيكية في اختبار الفرضيات، إليك تعريفه كما يلي:
class HypothesisTest(object): def __init__(self, data): self.data = data self.MakeModel() self.actual = self.TestStatistic(data) def PValue(self, iters=1000): self.test_stats = [self.TestStatistic(self.RunModel()) for _ in range(iters)] count = sum(1 for x in self.test_stats if x >= self.actual) return count / iters def TestStatistic(self, data): raise UnimplementedMethodException() def MakeModel(self): pass def RunModel(self): raise UnimplementedMethodException()
يُعَدّ الصنف HypothesisTest صنفًا مجردًا وهو صنف أب أيضًا، حيث يزوِّدنا بتعريفات كاملة لبعض التوابع وتوابع نائبة عن أخرى place-keepers، كما ترث الأصناف الأبناء المبنية على الصنف HypothesisTest التابعين _init_ وPValue، كما تزوِّدنا بالتوابع TestStatistic وRunModel وقد تزودنا اختياريًا بالتابع MakeModel.
يأخذ التابع _init_ البيانات بأي صيغة مناسبة، ويستدعي التابع MakeModel الذي يبني تمثيلًا لفرضية العدم، ومن ثم يمرر البيانات إلى التابع TestStatistics الذي يحسب حجم التأثير في العينة، كما يحسب التابع PValue احتمال التأثير الظاهر في ظل فرضية العدم، ويأخذ المتغير iters على أساس معامِل له، حيث يمثل هذا المتغير عدد مرات تكرار المحاكاة.
يولد السطر الأول البيانات التي تمت محاكاتها ويحسب إحصائيات الاختبار test statistics ويخزنها في test_stats، حيث تكون النتيجة جزءًا من العناصر في test_stats مساويًا لإحصائية الاختبار المرصودة self.actual أو أكبر منها، ولنفترض مثلًا أننا رمينا قطعة نقود 250 مرة وظهر لنا الشعار 140 مرة وظهرت لنا الكتابة 110 مرات، فقد نشك أنّ العملة منحازة بناءً على هذه النتيجة أي منحازة لظهور الشعار، ولاختبار هذه الفرضية يمكننا حساب احتمال وجود مثل هذا الفرق إذا كانت قطعة النقود عادلة:
class CoinTest(thinkstats2.HypothesisTest): def TestStatistic(self, data): heads, tails = data test_stat = abs(heads - tails) return test_stat def RunModel(self): heads, tails = self.data n = heads + tails sample = [random.choice('HT') for _ in range(n)] hist = thinkstats2.Hist(sample) data = hist['H'], hist['T'] return data
يُعَدّ المعامِل data زوجًا من الأرقام الصحيحة يحوي عدد مرات ظهور الشعار والكتابة، كما تكون إحصائية الاختبار هي الفرق المطلق بينهما لذا فإن قيمة self.actual هي 30، في حين ينفِّذ التابع RunModel محاكاةً لرمي قطع النقود بافتراض أن القطعة عادلة، حيث يولِّد عينةً من 250 رمية ويستخدِم Hist لحساب عدد مرات ظهور الشعار والكتابة ويُعيد زوجًا من الأعداد الصحيحة، ولا يتعيّن علينا الآن سوى إنشاء نسخة من CoinTest واستدعاء التابع PValue كما يلي:
ct = CoinTest((140, 110)) pvalue = ct.PValue()
النتيحة هي 0.07 تقريبًا أي إذا كانت قطعة النقود عادلةً، فسنتوقَّع وجود فارق بحجم 30 حوالي 7% من المرات، لذا كيف يمكننا تفسير هذه النتيجة؟ تكون 5% هي عتبة الأهمية الإحصائية اصطلاحيًا، وإذا كانت القيمة الاحتمالية p-value هي أقل من 5% يكون التأثير ذا دلالة إحصائية statistically significant وإلا لا يكون ذا دلالة إحصائية، لكن يُعَدّ اختيار 5% اختيارًا اعتباطيًا، وكما سنرى لاحقًا فإن القيمة الاحتمالية تعتمد على اختيار الاختبار الإحصائي ونموذج فرضية العدم، لذلك لا يجب افتراض أنّ القيم الاحتمالية هي مقاييس دقيقة.
نوصي بتفسير القيم الاحتمالية وفقًا لحجمها، أي إذا كانت القيمة الاحتمالية أقل من 1% فمن غير المرجح أن يكون التأثير بمحض الصدفة؛ أما إذا كانت أكبر من 10%، فيمكننا القول أنّ التأثير ربما قد ظهر بمحض الصدفة؛ أما بالنسبة للقيم بين 1% و10% فلا يمكن عدّها حديةً، لذا فقد استنتجنا في هذا المثال أنّ البيانات لا تقدِّم دليلًا قويًا على انحياز العملة أو عدم انحيازها.
اختبار الفرق في المتوسطين
يُعَدّ الفرق بين متوسطي مجموعتين اثنتين من أكثر التأثيرات التي يجري اختبارها. حيث وجدنا في بيانات المسح الوطني لنمو الأسرة أنّ متوسط مدة حمل الأطفال الأوائل أكبر بقليل، ومتوسط الوزن عند ولادة الأطفال الأوائل أقل بقليل، وسنرى الآن فيما إذا كانت هذه التأثيرات ذات دلالة إحصائية، كما تتمثَّل فرضية العدم في هذه الأمثلة في تطابق توزيعي المجموعتين، وتتمثَّل إحدى طرق نمذجة فرضية العدم في التبديل permutation، وهو عبارة عن خلط قيم الأطفال الأوائل وبقية الأطفال ومعاملة المجموعتين على أنهما مجموعة واحدة كبيرة، وإليك الشيفرة الموافقة لذلك كما يلي:
class DiffMeansPermute(thinkstats2.HypothesisTest): def TestStatistic(self, data): group1, group2 = data test_stat = abs(group1.mean() - group2.mean()) return test_stat def MakeModel(self): group1, group2 = self.data self.n, self.m = len(group1), len(group2) self.pool = np.hstack((group1, group2)) def RunModel(self): np.random.shuffle(self.pool) data = self.pool[:self.n], self.pool[self.n:] return data
تُعَدّ data زوجًا من المتسلسلات، أي متسلسلة sequence لكل مجموعة، وتكون إحصائية الاختبار هي الفرق المطلق في المتوسطين؛ أما MakeModel فيسجل حجمي المجموعتين n وm ويجمعهما في مصفوفة نمباي NumPy واحدة باسم self.pool، كما يحاكي RunModel فرضية العدم عن طريق خلط القيم المجمَّعة وتقسيمها إلى مجموعتين بحيث يكون حجم الأولى n والثانية m، وكما هو الحال دائمًا تكون القيمة التي يعيدها التابع RunModel بصيغة البيانات المرصودة نفسها، وإليك شيفرة اختبار الفرق في مدة الحمل كما يلي:
live, firsts, others = first.MakeFrames() data = firsts.prglngth.values, others.prglngth.values ht = DiffMeansPermute(data) pvalue = ht.PValue()
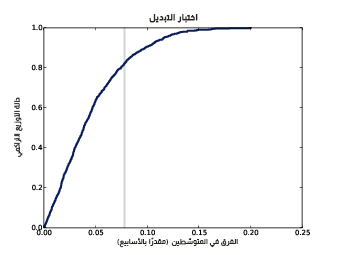
يقرأ التابع MakeFrames بيانات المسح الوطني لنمو الأسرة ويعيد أُطر بيانات DataFrames تمثِّل جميع الولادات الحية للأطفال الأوائل وبقية الأطفال، حيث نستخرِج مدة حالات الحمل على شكل مصفوفات نمباي NumPy ونمررها على أساس بيانات إلى DiffMeansPermute ثم نحسب القيمة الاحتمالية p-value، وتكون النتيجة 0.17 تقريبًا أي أننا نتوقع رؤية فارقًا حجمه بحجم التأثير المرصود حاولي 17% من المرات، لذا نستنتج أنه ليس للتأثير دلالةً إحصائيةً.
يوضِّح الشكل السابق دالة التوزيع التراكمي CDF للفرق في متوسط الحمل في ظل فرضية العدم.
يزودنا الصنف HypothesisTest بالتابع PlotCdf الذي يرسم توزيع إحصائية الاختبار وكذلك فهو يرسم خطًا رماديًا يدل على حجم التأثير المرصود.
ht.PlotCdf() thinkplot.Show(xlabel='test statistic', ylabel='CDF')
يُظهِر الشكل السابق النتيجة، حيث تتقاطع دالة التوزيع التراكمي مع الفرق المرصود عند 0.83 وهو مكمِّل complement القيمة الاحتمالية وهي 0.17.
اقتباستوضيح: لحساب مكمل قيمة ما complement نطرح هذه القيمة من 1، حيث يكون المكمِّل في المثال السابق 1-0.17=0.83
إذا نفَّذنا التحليل نفسه لأوزان الولادات حيث أن القيمة الاحتمالية المحسوبة هي 0، فلن تسفر المحاكاة بعد 100 محاولة عن تأثير بحجم الفرق المرصود أبدًا، فالفرق المرصود هو 0.12 رطلًا أي ما يعادل حوالي 0.05 كيلوغرامًا، ونقول عندها أنّ القيمة الاحتمالية أصغر من 0.001 أي p<0.001 ونستنتج أنّ الفرق في أوزان الولادات ذو دلالة إحصائية statistically significant.
إحصائيات اختبار أخرى
يعتمد اختيار أفضل إحصائية اختبار على السؤال الذي نحاول تناوله، فإذا كان السؤال المطروح مثلًا هو عن كَون مدة حمل الأطفال الأوائل مختلفةً عن بقية الأطفال فمن المنطقي حساب الفرق المطلق في المتوسطين كما فعلنا في القسم السابق، وإذا كنا نعتقد لسبب ما أنه من المرجح أن تتأخر ولادة الأطفال الأوائل، نستخدم إحصائية الاختبار بدلًا من القيمة المطلقة للفرق، وإليك إحصائية الاختبار كما يلي:
class DiffMeansOneSided(DiffMeansPermute): def TestStatistic(self, data): group1, group2 = data test_stat = group1.mean() - group2.mean() return test_stat
يرث الصنف DiffMeansOneSided التابعين MakeModel وRunModel من DiffMeansPermute والفرق الوحيد هو أن TestStatistic لا يأخذ القيمة المطلقة للفرق، كما يندرج هذا الاختبار تحت نوع الاختبارات أحادية الجانب one-sided لأن هذا الاختبار يحسب جانبًا واحدًا فقط من توزيع الفروق، في حين يستخدِم الاختبار السابق الجانبين، لذا فهو ثنائي الجانب two-sided.
تكون القيمة الاحتمالية في هذه النسخة من الاختبار هي 0.09، في حين تكون القيمة الاحتمالية للاختبار أحادي الجانب عمومًا هي حوالي نصف القيمة الاحتمالية للاختبار ثنائي الجانب وذلك اعتمادًا على شكل التوزيع، وتُعَدّ الفرضية أحادية الجانب التي تقول أنّ الأطفال الأوائل يولدون متأخرين هي أكثر دقة من الفرضية ثنائية الجانب، لذا تكون القيمة الاحتمالية أصغر، لكن ليس للفرق أيّ دلالة إحصائية حتى بالنسبة للفرضية الأقوى.
يمكننا استخدام إطار العمل ذاته لاختبار وجود فرق في الانحراف المعياري، وقد رأينا في قسم سابق في مقال دوال الكتلة الاحتمالية في بايثون دليلًا على أنه من المرجح ولادة الأطفال الأوائل مبكرين أو متأخرين وأقل احتمالًا أن يولدوا في الوقت المحدد، لذا قد نفترض أنّ الانحراف المعياري أعلى، وإليك الشيفرة التي تنفِّذ الاختبار كما يلي:
class DiffStdPermute(DiffMeansPermute): def TestStatistic(self, data): group1, group2 = data test_stat = group1.std() - group2.std() return test_stat
يُعَدّ هذا اختبارًا أحادي الجانب، إذ لا تقول الفرضية إن قيمة الانحراف المعياري للأطفال الأوائل مختلفة عن القيمة الاحتمالية فحسب بل تحدد أن قيمتها أعلى، حيث أن القيمة الاحتمالية هي 0.09 أي ليس لها دلالة إحصائية.
اختبار الارتباط
يمكن لإطار العمل هذا أن يختبر الارتباطات أيضًا، ففي مجموعة بيانات المسح الوطني لنمو الأسرة مثلًا يكون الارتباط بين عمر الأم وبين أوزان الولادات هو حوالي 0.07، أي يبدو أن الأمهات الأكبر عمرًا يلدن أطفالًا أكثر وزنًا، لكن هل يمكن لهذا التأثير أن يكون بسبب الصدفة؟
استخدمنا ارتباط بيرسون لإحصائية الاختبار هذه، علمًا أن ارتباط سبيرمان مناسب أيضًا. حيث يمكن إجراء اختبار أحادي الجانب إذا توقَّعنا لسبب ما أن الارتباط موجب، لكن بما أنه لا يوجب سبب لنعتقد هذا سنُجري اختبارًا ثنائي الجانب باستخدام قيمة الارتباط المطلقة، وتقول فرضية العدم أنه لا يوجد ارتباط بين عمر الأم ووزن الولادة، وإذا خلطنا القيم المرصودة فيمكننا محاكاة عالَم يكون فيه توزيع عمر الأمهات مساويًا لوزن الولادات لكن لا تكون المتغيرات متعلقة ببعضها:
class CorrelationPermute(thinkstats2.HypothesisTest): def TestStatistic(self, data): xs, ys = data test_stat = abs(thinkstats2.Corr(xs, ys)) return test_stat def RunModel(self): xs, ys = self.data xs = np.random.permutation(xs) return xs, ys
يُعَدّ المتغير data زوجًا من المتسلسلات sequences، حيث يحسب TestStatistic القيمة المطلقة لارتباط بيرسون، أما RunModel فهو يخلط قيم المصفوفة xs ويعيد البيانات المُحاكاة، وإليك الشيفرة التي تقرأ البيانات وتنفِّذ الاختبار كما يلي:
live, firsts, others = first.MakeFrames() live = live.dropna(subset=['agepreg', 'totalwgt_lb']) data = live.agepreg.values, live.totalwgt_lb.values ht = CorrelationPermute(data) pvalue = ht.PValue()
استخدمنا dropna في هذه الشيفرة مع الوسيط subset لحذف الأسطر التي لا تحوي أحد المتغيرات التي نحتاجها، وتكون قيمة الارتباط الفعلي هي 0.07 والقيمة الاحتمالية المحسوبة هي 0 وبعد حوالي 1000 تكرار يكون أكبر ارتباط مُحاكى هو 0.04، لذا على الرغم من صغر الارتباط المرصود إلا أنه ذو دلالة إحصائية، كما يُعَدّ هذا المثال بمثابة تذكير بأنّ كَون التأثير ذا دلالة إحصائية فلا يعني دائمًا أنه مهم في الناحية العملية، وإنما يعني فقط أنه من غير المرجح أن يكون قد ظهر بمحض الصدفة فقط.
اختبار النسب
لنفترض أنك تدير منتدى ترفيهي وشككت في يوم من الأيام أنك أحد الزبائن يستخدِم قطعة نرد ملتوية، أي أنه يُتلاعب بها لكي يكون احتمال ظهور أحد الوجوه أكبر من احتمال ظهور الوجوه الأخرى، لذا تقبض على المتهم وتصادر قطعة النرد لكن يتعيّن عليك عندها إثبات غشه، حيث ترمي قطعة النرد 60 مرة وتحصل على النتائج الموضحة بالجدول التالي:
| القيمة | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| التردد (عدد مرات التكرار) | 8 | 9 | 19 | 5 | 8 | 11 |
نتوقع ظهور كل قيمة 10 مرات وسطيًا، وفي مجموعة البيانات هذه تظهر القيمة 3 أكثر من المتوقع وتظهر القيمة 4 أقل من المتوقع، لكن هل لهذه الفروق دلالة إحصائية؟ يمكننا اختبار هذه الفرضية عن طريق حساب التردد المتوقع لكل قيمة، والفرق بين الترددات المتوقعة والترددات المرصودة والفرق المطلق الكلي، بحيث نتوقع في هذا المثال ظهور كل وجه 10 مرات من أصل 60 مرة، وتكون الانحرافات عن هذا التوقع هي: 2- و1- و9 و5- و2- و1، لذا فإن الفرق المطلق الكلي هو 20، إذًا كم مرة سنرى مثل هذا الاختلاف صدفةً؟ إليك نسخة من الصنف HypothesisTest تجيبنا عن هذا السؤال كما يلي:
class DiceTest(thinkstats2.HypothesisTest): def TestStatistic(self, data): observed = data n = sum(observed) expected = np.ones(6) * n / 6 test_stat = sum(abs(observed - expected)) return test_stat def RunModel(self): n = sum(self.data) values = [1, 2, 3, 4, 5, 6] rolls = np.random.choice(values, n, replace=True) hist = thinkstats2.Hist(rolls) freqs = hist.Freqs(values) return freqs
تُمثَّل هذه البيانات على صورة قائمة من الترددات حيث أن القيم المرصودة هي: [8, 9, 19, 5, 8, 11] والترددات المتوقعة هي 10 لكل القيم، كما أن إحصائية الاختبار هي مجموع الفروق المطلقة؛ أما فرضية العدم فتقول أن قطعة النرد عادلة، لذا سنحاكي هذه الفرضية عن طريق أخذ عينات عشوائية من القيم values، ويستخدِم التابع RunModel الصنف Hist لحساب وإعادة قائمة الترددات، كما تكون القيمة الاحتمالية للبيانات هي 0.13 أي أنه إذا كانت قطعة النرد عادلةً، فسنتوقع ظهور الانحراف الكلي المرصود أو قيمة انحراف أكبر من المتوقعة لتكون حوالي 13% من المرات، لذا ليس للتأثير الظاهر دلالة إحصائية.
اختبارات مربع كاي
استخدمنا في القسم السابق الانحراف الكلي على أساس اختبار إحصائي، لكن يشيع استخدام إحصائية مربع كاي لاختبار النسب، وتكون الصيغة الرياضية لمربع كاي كما يلي:
| χ2 = |
|
|
حيث Oi هي الترددات المرصودة وEi هي الترددات المتوقعة، وفيما يلي شيفرة بايثون الموافقة:
class DiceChiTest(DiceTest): def TestStatistic(self, data): observed = data n = sum(observed) expected = np.ones(6) * n / 6 test_stat = sum((observed - expected)**2 / expected) return test_stat
يعطي تربيع الانحرافات -بدلًا من أخذ القيم المطلقة- وزنًا أكبر للانحرافات الكبيرة، إذ يوحِّد standardizes التقسيم على expected الانحرافات على الرغم أنه ليس لها في هذه الحالة أثر لأن الترددات المتوقَّعة متساوية فيما بينها، وتكون القيمة الاحتمالية في حال استخدام إحصائية مربع كاي مساويةً لـ 0.04 وهي أصغر بكثير من 0.13 والتي حصلنا عليها عندما استخدمنا الانحراف الكلي، فإذا أخذنا العتبة 5% على محمل الجد، فسننظر للتأثير على أنه ذو دلالة إحصائية، لكن يمكننا القول إذا أخذنا الاختبارَين بالحسبان فستكون النتائج حديةً borderline، وعلى الرغم أنه لن نستبعد احتمال أن يكون النرد ملتويًا، إلا أننا لن نُدين المتهم بالغش.
يوضِّح هذا المثال نقطة مهمة وهي اعتمادية القيمة الاحتمالية على اختيار إحصائية الاختبار وعلى اختيار نموذج فرضية العدم، وفي بعض الأحيان تحدِّد هذه الاختيارات ما إذا كان التأثير ذا دلالة إحصائية أم لا، وللمزيد من المعلومات حول اختبار مربع كاي يمكنك زيارة صفحة ويكيبيديا.
عودة إلى الأطفال الأوائل
ألقينا نظرة في بداية المقال على مدة حالات الحمل للأطفال الأوائل وبقية الأطفال واستنتجنا أن الفروق الظاهرة في المتوسط mean والانحراف المعياري standard deviation ليست ذا دلالة إحصائية، لكن رأينا في قسم سابق في مقال دوال الكتلة الاحتمالية في بايثون فروقًا واضحةً في توزيع مدة الحمل خاصةً في المجال بين 35 إلى 43 أسبوع، كما يمكننا استخدام اختبار مبني على إحصائية مربع كاي لنتحقق فيما إذا كانت هذه الفروق ذات دلالة إحصائية أم لا، وتجمع الشيفرة هذه عدة عناصر من الأمثلة السابقة:
class PregLengthTest(thinkstats2.HypothesisTest): def MakeModel(self): firsts, others = self.data self.n = len(firsts) self.pool = np.hstack((firsts, others)) pmf = thinkstats2.Pmf(self.pool) self.values = range(35, 44) self.expected_probs = np.array(pmf.Probs(self.values)) def RunModel(self): np.random.shuffle(self.pool) data = self.pool[:self.n], self.pool[self.n:] return data
تُمثَّل هذه البيانات على أساس قائمتي مدة حمل، وفرضية العدم هي أنّ العينتين مأخوذتان من التوزيع ذاته، كما ينمذج التابع MakeModel التوزيع عن طريق تجميع العينتَين باستخدام hstack، ومن ثم يولِّد التابع RunModel البيانات المُحاكاة عن طريق خلط العينة المجمَّعة وقسمها إلى جزئين اثنين، كما يُعرِّف MakeModel المتغير values وهو مجال الأسابيع الذي سنستخدمه، والمتغير expected_probs وهو احتمال كل قيمة في التوزيع المجمَّع، وفيما يلي الشيفرة التي تحسب إحصائية الاختبار:
# class PregLengthTest: def TestStatistic(self, data): firsts, others = data stat = self.ChiSquared(firsts) + self.ChiSquared(others) return stat def ChiSquared(self, lengths): hist = thinkstats2.Hist(lengths) observed = np.array(hist.Freqs(self.values)) expected = self.expected_probs * len(lengths) stat = sum((observed - expected)**2 / expected) return stat
يحسب TestStatistics إحصائية مربع كاي للأطفال الأوائل وبقية الأطفال وتحسب مجموعها، في حين يأخذ التابع ChiSquared متسلسلةً من مدة الحمل ويحسب مدرَّجه التكراري histogram ويحسب observed التي هي قائمة من الترددات الموافقة للقيم self.values، كما يضرب ChiSquared الاحتمالات المحسوبة مسبقًا expected_probs بحجم العينة لحساب قائمة الترددات المتوقعة ويُعيد إحصائية مربع كايstat.
تكون إحصائية مربع كاي الكليّة لبيانات المسح الوطني لنمو الأسرة هي 102 وليس لهذه القيمة معنى لوحدها، لكن بعد 1000 تكرار تكون قيمة أكبر إحصائية اختبار مولدة في ظل فرضية العدم 32، وبالتالي نستنتج أنه من غير المرجح أن تكون إحصائية مربع كاي مرصودةً في ظل فرضية العدم -أي من غير المرجح أن تكون مرصودة بافتراض أن فرضية العدم صحيحة-، لذا فإن التأثير الظاهر ذو دلالة إحصائية، كما يوضح هذا المثال وجود قيود على اختبارات مربع كاي، فهي تشير إلى وجود اختلاف بين المجموعتين، لكنها لا تذكر أي معلومة محددة حول ماهية الاختلاف.
الأخطاء
يكون التأثير ذا دلالة إحصائية في الطريقة الكلاسيكية في اختبار الفرضيات إذا كانت القيمة الاحتمالية أقل من عتبة معينة وغالبًا ما تكون 5%، كما يثير هذا النهج سؤالين هما:
- إذا كان التأثير قد ظهر صدفةً، فما هو احتمال أن نعده ذو دلالة إحصائية؟ يدعى هذا الاحتمال بمعدل السلبية الكاذبة false negative rate.
- إذا كان التأثير حقيقيًا، فما احتمال فشل اختبار الفرضية؟ يدعى هذا الاحتمال بمعدل الإيجابية الكاذبة false positive rate.
من السهل نسبيًا حساب معدل الإيجابية الكاذبة، فهو 5% إذا كانت العتبة 5%، وإليك السبب كما يلي:
- إذا لم يكن هناك تأثير حقيقي، فستكون فرضية العدم صحيحةً، لذا يمكننا حساب توزيع إحصائية الاختبار عن طريق محاكاة فرضية العدم، وندعو هذا التوزيع CDFT.
-
نحصل على إحصائية اختبار
tمأخوذة من CDFT في كل مرة ننفِّذ فيها تجربة، ومن ثم نحسب القيمة الاحتمالية التي هي احتمال تجاوز قيمة عشوائية مأخوذة من CDFT الإحصائيةt، أي 1-CDFT(t). -
إذا كانت CDFT(t) أكبر من 95%، فستكون القيمة الاحتمالية أصغر من 5% وذلك إذا تجاوزت
tالمئين 95 -أي 95th percentile، وكم مرة تتجاوز قيمة مختارة ما من CDFT المئين 95؟ حوالي 5% من المرات الكلية.
لذا إن أدّيت اختبار فرضية واحدًا مع عتبة 5%، فستتوقع حصول إيجابية كاذبة مرة واحدة من كل 20 مرة.
القوة
يعتمد معدل السلبية الكاذبة على حجم التأثير الفعلي الذي لا يكون معلومًا عادةً، لذا فمن الصعب حسابه، لكن يمكننا حساب المعدل عن طريق حساب معدل مشروط بحجم تأثير افتراضي، فإذا افترضنا مثلًا أن الفارق المرصود بين المجموعتين دقيقًا، فيمكننا استخدام العينات المرصودة على أساس نموذج للسكان ومن ثم استخدام البيانات المُحاكاة من أجل تنفيذ اختبارات الفرضيات كما يلي:
def FalseNegRate(data, num_runs=100): group1, group2 = data count = 0 for i in range(num_runs): sample1 = thinkstats2.Resample(group1) sample2 = thinkstats2.Resample(group2) ht = DiffMeansPermute((sample1, sample2)) pvalue = ht.PValue(iters=101) if pvalue > 0.05: count += 1 return count / num_runs
يأخذ التابع FalseNegRate بيانات على صورة متسلسلتين بحيث يكون لكل مجموعة متسلسلة، إذ يحاكي التابع تجربةً في كل تكرار من الحلقة عن طريق سحب عينة عشوائية من كل مجموعة وتنفيذ اختبار فرضية، ومن ثم يتحقق التابع من النتيجة ويحسب عدد مرات السلبية الكاذبة، في حين يأخذ التابع Resample متسلسلةً ويسحب عينةً من الطول نفسه مع استبدال كما يلي:
def Resample(xs): return np.random.choice(xs, len(xs), replace=True)
إليك الشيفرة التي تختبر مدة حالات الحمل:
live, firsts, others = first.MakeFrames() data = firsts.prglngth.values, others.prglngth.values neg_rate = FalseNegRate(data)
تكون النتيجة حوالي 70%، أي نتوقع أن تؤدي تجربة بحجم العينة هذا إلى اختبار سلبي 70% من المرات إذا كان الفرق الفعلي في متوسط مدة الحمل 0.078 أسبوعًا، لكن غالبًا ما تُقدَّم هذه النتيجة بالطريقة المعاكسة أي نتوقع أن تؤدي تجربة بحجم العينة هذا إلى اختبار إيجابي 30% من المرات إذا كان الفرق الفعلي في متوسط مدة الحمل 0.078 أسبوعًا، حيث يدعى معدل الإيجابية الصحيحة هذا بقوة power الاختبار، أو يدعى أحيانًا بحساسية sensitivity الاختبار، إذ تعكس هذه التسمية قدرة الاختبار على تحديد تأثير بحجم معين مُعطى سابقًا. كان احتمال أن يعطي الاختبار نتيجةً إيجابيةً في هذا المثال هو 30% -في حال كان الفرق هو 0.078 أسبوعًا كما ذكرنا سابقًا-، وتقول القاعدة العامة أنه تُعَدّ قوة 80% قيمةً مقبولةً، لذلك يمكننا القول أنّ هذا الاختبار كان ضعيفًا أو يفتقر للقوة underpowered، وبصورة عامة لا يعني اختبار الفرضية السلبي negative hypothesis test أنه لا يوجد فرق بين المجموعات، وإنما يقترح أنه إذا كان هناك فارقًا، فهو صغير جدًا لتحديده باستخدام حجم العينة هذا.
التكرار
تُعَدّ عملية اختبار الفرضيات الموضحة في هذا المقال ليست ممارسة جيدة بالمعنى الدقيق للكلمة.
أولًا، أدينا عدة اختبارات، حيث أنك إذا نفَّذت اختبار فرضية واحد، فسيكون احتمال ظهور إيجابية كاذبة هو 1 من 20 وقد يكون هذا مقبولًا، لكن إن أجريت 20 اختبارًا تتوقع ظهور إيجابية كاذبة مرة واحدة على الأقل في معظم الأوقات.
ثانيًا، استخدمنا مجموعة البيانات ذاتها لعمليتي الاستكشاف والاختبار، وإذا استكشفتَ مجموعة بيانات ضخمة ووجدت تأثيرًا مفاجئًا ثم اختبرته لتعرف فيما إذا كان ذا دلالة إحصائية أم لا، فسيكون من المرجح توليد إيجابية كاذبة.
يمكنك ضبط عتبة القيمة الاحتمالية للتعويض عن الاختبارات المتعددة، كما هو وارد في صفحة ويكيبيديا، أو يمكنك معالجة كلا المشكلتين عن طريق تقسيم البيانات باستخدام مجموعة للاستكشاف ومجموعة أخرى للاختبار، كما تكون بعض هذه الممارسات إجباريةً في بعض المجالات أو مستحسنَةً على الأقل، لكن من الشائع أيضًا معالجة هذه المشاكل ضمنيًا عن طريق تكرار النتائج المنشورة، وعادةً ما تُعَدّ الورقة البحثية الأولى التي تقدم نتيجة جديدة أنها استكشافية exploratory، كما تُعَدّ الأوراق اللاحقة التي تكرر النتيجة باستخدام بيانات جديدة أنها مؤكِدة confirmatory.
صدف وأن أتُيحت لنا الفرصة لتكرار النتائج في هذا المقال، حيث أن النسخة الأولى من الكتاب مبنية على الدورة السادسة من المسح الوطني لنمو الأسرة التي صدرت عام 2002، لكن أصدرت مراكز السيطرة على الأمراض والوقاية منها CDC في الشهر 10 من عام 2010 بيانات إضافية مبنية على المقابلات التي أجريت بين عامي 2006-2010، كما يحتوي nsfg2.py على تعليمات برمجية لقراءة هذه البيانات وتنظيفها، حيث يكون في مجموعة البيانات الجديدة ما يلي:
- الفرق في متوسط مدة الحمل هو 0.16 أسبوع وله دلالة إحصائية وقيمته الاحتمالية أصغر من 0.001 أيp<0.001 موازنةً بفارق 0.078 أسبوع في مجموعة البيانات الأصلية.
- الفرق في وزن الولادة هو 0.17 رطل مع قيمة احتمالية أصغر من 0.001 أي p<0.001 موازنةً بفارق 0.12 رطل في مجموعة البيانات الأصلية.
- الارتباط بين وزن الولادة وعمر الأم هو 0.08 مع قيمة احتمالية أصغر من 0.001 أي p<0.001 موازنةً بفارق 0.07.
- اختبار مربع كاي فهو ذو دلالة إحصائية مع قيمة احتمالية أصغر من 0.001 أي p<0.001 كما كان في مجموعة البيانات الأصلية.
باختصار، تكررت التأثيرات في مجموعة البيانات الجديدة والتي تمتعت بدلالة إحصائية في مجموعة البيانات الأصلية، وكذلك فإن الفرق في طول الحمل أكبر في مجموعة البيانات الجديدة وهو ذو دلالة إحصائية أيضًا مع أنه لم يكن ذا دلالة إحصائية في مجموعة البيانات الأصلية.
تمارين
يوجد حل التمارين في chap09soln.py.
تمرين 1
تزداد قوة اختبار الفرضية كلما ازداد حجم العينة، أي أنه من المرجح أن يكون موجبًا إن كان التأثير حقيقيًا، والعكس صحيح فعندما ينقص حجم العينة يصبح من غير المرجح أن يكون الاختبار موجبًا حتى ولو كان التأثير حقيقيًا، وللتحقق من هذا الأمر نفِّذ الاختبارات التي ذكرناها في هذا المقال على مجموعات فرعية من بيانات المسح الوطني لنمو الأسرة، علمًا أنه يمكنك استخدام thinkstats2.SampleRows لاختيار مجموعة فرعية عشوائية من الأسطر في إطار بيانات.
ماذا سيكون مصير القيم الاحتمالية لهذه الاختبارات عندما ينقص حجم العينة؟ وما هو أصغر حجم عينة ينتج عنه اختبار إيجابي؟
تمرين 2
أجرينا في قسم اختبار الفرق في المتوسطين محاكاةً لفرضية العدم عن طريق التبديل permutation، أي أننا عاملنا القيم المرصودة على أساس جمع السكان ومن ثم قسمنا الأشخاص إلى مجموعتين عشوائيًا، كما يوجد بديل آخر وهو استخدام العينة لتقدير توزيع السكان ومن ثم سحب عينة عشوائية من هذا التوزيع، وتدعى هذه العملية بإعادة أخذ عينات resampling، حيث أنه هناك عدة طرق لإعادة أخذ العينات، وإحدى أبسط هذه الطريق هي سحب عينة مع استبدال with replacement من القيم المرصودة كما فعلنا في قسم "القوة".
اكتب صنفًا class باسم DiffMeansResample يرث من الصنف DiffMeansPermute وأعِد تعريف التابع RunModel لتنفيذ إعادة أخذ عينات resampling بدلًا من التبديل permutation، ثم استخدم هذا النموذج لاختبار الفروق في مدة الحمل ووزن الولادة، وما مدى تأثير النموذج على النتائج؟
ترجمة -وبتصرف- للفصل Chapter 9 Hypothesis testing analysis من كتاب Think Stats: Exploratory Data Analysis in Python.









أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.