قد تظن عندما تتابع دورةً تدريبيةً أو تقرأ كتابًا في علم البيانات، أنك تملكت من المطلوب لتنفيذ مشروعًا كاملًا في تعلّم الآلة، لكن لن تكون لديك الخبرة الكافية بالضرورة لتكامل جميع أجزاء ومراحل تطوير نظام تعلّم آلة لحل مسألة حقيقية على أرض الواقع. ربما يُشكّل تنفيذك المشروع الأول تحديًا كبيرًا لكن إتمامك له بنجاح سيمنحك الثقة والخبرة اللازمتين لتنفيذ مشاريع لاحقة بعدها. تعرض هذه السلسلة من المقالات آلية تسلسل خطوات معالجة مسائل تعلّم الآلة عبر القيام بتنفيذ مشروع متكامل مع بيانات حقيقية.
نعمل وفق المنهجية العامة المتبعة عادةً في مسائل تعلّم الآلة خطوةً بخطوة وفق ما يلي:
- تنظيف البيانات وتنسيقها.
- استكشاف وتحليل البيانات.
- هندسة الميزات واختيار المناسب منها.
- اعتماد مقاييس الأداء وموازنة نماذج التعلّم وفقها.
- ضبط قيم المعاملات الفائقة لنموذج التعلّم الأفضل.
- تقويم النموذج الأفضل باستخدام مجموعة بيانات الاختبار.
- تفسير وشرح نتائج النموذج.
- عرض الاستنتاجات وتوثيق العمل.
نُنفذ فيما يلي كل خطوة من الخطوات السابقة مع بيان تكامل كل خطوة مع الخطوة التالية لها، حيث نعرض في هذه المقالة الخطوات الثلاث الأولى ونتابع في مقالات لاحقة الخطوات المتبقية، ويُمكن الحصول على الشيفرة الكاملة للمشروع من هذا المستودع.
اقتباسنفذّ كاتب المقال هذا المشروع بصفة اختبار قبول لوظيفة في شركة ناشئة، وأُسندت الوظيفة الشاغرة له بالنتيجة، إلا أن المدير التنفيذي للشركة استقال ولم تتابع الشركة الناشئة العمل. ويبدو أن الأمور تجري هكذا في الشركات الناشئة.
تعريف المسألة
قبل البدء بالعمل البرمجي لابدّ من فهم المسألة ومعاينة البيانات المتاحة. نحلل في هذا المشروع ومعالجة بيانات الطاقة لمدينة نيويورك والمنشورة للعموم.
يهدف المشروع إلى تحليل بيانات الطاقة للوصول إلى نموذج متعلّم يُمكنه التنبؤ بمعامل نجمة الطاقة Energy Star Score الذي يعتمده برنامج نجمة الطاقة وهو برنامج تديره وكالة حماية البيئة الأمريكية ووزارة الطاقة الأمريكية لتعزيز كفاءة الطاقة. كما يجب في النهاية تفسير النتائج لمعرفة العوامل التي يُمكنها التأثير في هذا المعامل.
تحوي البيانات المتاحة قيم معامل نجمة الطاقة، مما يعني أن المسألة المطروحة هي مسألة تعلّم آلة من نمط موجه عبر الانحدار supervised regression machine learning:
- تعليم موجه Supervised: تحوي البيانات المتاحة الميزات والنتيجة معًا، لذلك تدريب نموذج يتعلّم الربط بين هذه الميزات والنتيجة هو المطلوب في هذا النمط.
- عبر الانحدار Regression: لأن المعامل المطلوب هو قيمة رقمية حقيقية.
نهدف إلى بناء نموذج تعلّم دقيق يُمكنه التنبؤ بقيمة قريبة من القيمة الحقيقية لمعامل نجمة الطاقة، ويجب أن تكون نتائج النموذج المبني قابلةً للتفسير والفهم أيضًا. توجّه هذه الأهداف قراراتنا المتخَذة لاحقًا أثناء تحليلنا البيانات وبناء النموذج.
تنظيف البيانات
تُعَد عمليات تنظيف البيانات وتنسيقها في البداية من العمليات الأساسية، إذ أن بيانات العالم الحقيقة غالبًا ما تكون ناقصةً وتحوي العديد من القيم المتطرفة (بخلاف مجموعات بيانات التدريب المُعدّة لأهداف تعليمية مثل mtcars وiris). حيث تكون بيانات العالم الحقيقية في فوضى كبيرة، مما يستلزم تنظيفها وإعادة تشكيلها قبل البدء بتحليلها. قد تبدو مهمة تنظيف البيانات غير ممتعة إلا أنها ضرورية في جميع مسائل العالم الحقيقي.
نبدأ أولًا بتحميل البيانات ضمن إطار من البيانات DataFrame من مكتبة Pandas ومن ثم عرضها:
import pandas as pd import numpy as np # قراءة البيانات وتحميلها ضمن إطار من البيانات data = pd.read_csv('data/Energy_and_Water_Data_Disclosure_for_Local_Law_84_2017__Data_for_Calendar_Year_2016_.csv') # إظهار الجزء الأعلى من إطار البيانات data.head()
يظهر لنا أولًا:
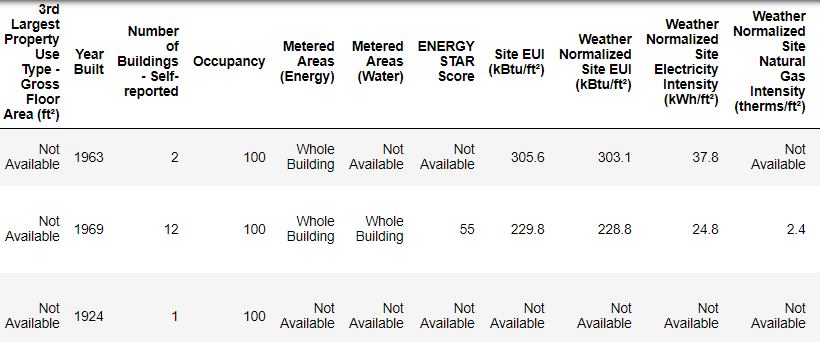
يُظهِر الشكل مجموعةً جزئيةً من البيانات والتي تحوي 60 عمودًا، مما يطرح المسألة الأولى التالية: نريد التنبؤ بمعامل نجمة الطاقة Energy Star Score، إلا أننا لا نعرف أي عمود من الأعمدة يوافق هذا المعامل. قد تكون عدم معرفة معاني الأعمدة في بعض المسائل غير مهمة ويُمكن بناء نماذج دقيقة إلا أنه في حالتنا، وبما أن المطلوب تفسير النتائج فيجب فهم معاني بعض الأعمدة على الأقل.
لم يُرد كاتب المقال عندما كُلّف بالعمل على هذا المشروع، سؤال أحد عن معاني الأعمدة، إلا أنه عندما تمعن في اسم الملف:
قرر البحث عن القانون المدعو بـ Local Law 84، مما قاده إلى هذه الصفحة التي تفرض على جميع مباني مدينة نيويورك اعتبارًا من حجم معين، تقديم تقرير عن استهلاك الطاقة فيها. وبمزيد من البحث توصل إلى تعريفات جميع الأعمدة.
يجب بدء العمل بتأن وروية دائمًا وعدم نسيان أي أمر قد يكون هامًا مثل معاينة اسم الملف، إذ لا نحتاج عمليًا لدراسة جميع الأعمدة، إلا أنه يجب أن نفهم معامل نجمة الطاقة والموصّف على أساس نسبة مئوية (رقم صحيح بين 1 و100) لتقييم استهلاك الطاقة في سنة معينة، والذي يُقدّر لكل بناء في مدينة نيويورك، وهو مقياس نسبي يُستخدم لموازنة كفاءة الطاقة في المباني.
بعد حل المسألة الأولى نلتفت إلى المسألة الثانية وهي مشكلة القيم الناقصة، إذ تحوي البيانات المتاحة عبارة غير متوفر Not Available في الكثير من الخلايا التي لا تُعرَف قيمتها، ستُجبِر هذه القيمة النصية بايثون على تخزين العمود (ولو كان عمودًا رقميًا) كائن مثلًا object وذلك لأن مكتبة Pandas تعد جميع قيم العمود نصية بمجرد وجود قيمة نصية واحدة ضمن هذا العمود، ويُمكن معاينة نوع بيانات الأعمدة باستخدام طريقة إطار البيانات dataframe.info:
# معاينة بيانات الأعمدة والقيم غير الناقصة data.info()
ويكون الناتج:
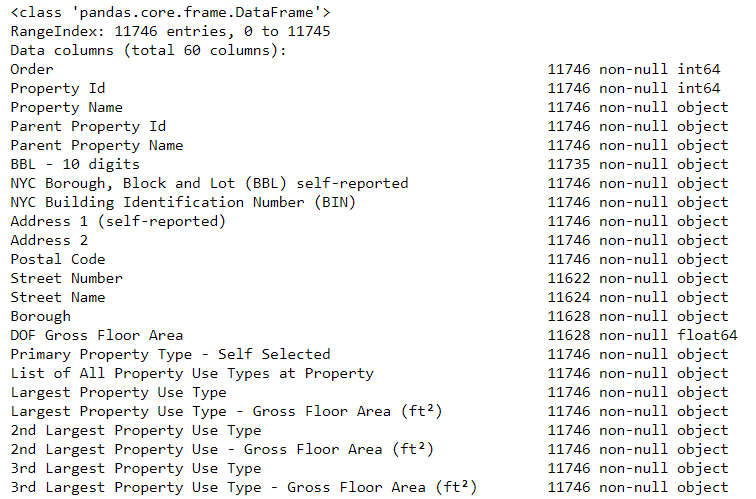
تُخزّن الكثير من الأعمدة الرقمية مثل كائن object مشابه للمساحة بالأقدام المربعة ft2، مما يستلزم تحويلها إلى رقم حقيقي float كي نستطيع إنجاز عمليات التحليل المطلوبة والتي لا يُمكن تطبيقها على السلاسل النصية.
سنعرض فيما يلي شيفرة بايثون التي تحول السلسلة النصية Not Available إلى القيمة np.nan "ليس رقمًا" not a number والتي يُمكن معاملتها مثل الأرقام ومن ثم تحويل العمود الموافق إلى نمط البيانات عدد حقيقي float:
# استبدال القيم الناقصة data = data.replace({'Not Available': np.nan}) # المرور على الأعمدة عمودًا عمودًا for col in list(data.columns): # اختيار الأعمدة التي يجب أن تكون رقميةً if ('ft²' in col or 'kBtu' in col or 'Metric Tons CO2e' in col or 'kWh' in col or 'therms' in col or 'gal' in col or 'Score' in col): # تحويل نمط البيانات إلى عدد data[col] = data[col].astype(float)
بعد الانتهاء من تعديل الأعمدة المناسبة إلى أرقام، ننتقل لمعاينة البيانات.
البيانات الناقصة والمتطرفة
من المشاكل الشائعة أيضًا وجود العديد من القيم الناقصة في البيانات لأسباب عديدة. يجب حذف هذه القيم أو إيجاد طريقة لملئها بقيم متوقعة قبل بناء نموذج التعلّم، لنبدأ أولًا بتحديد حجم هذه المشكلة لكل عمود (يُمكن العودة لرابط المشروع من أجل الحصول على الشيفرة).
نُظهر الجدول التالي والذي يحسب نسبة القيم الناقصة لكل عمود باستخدام الشيفرة الموجودة في هذا السؤال من موقع Stack Overflow.
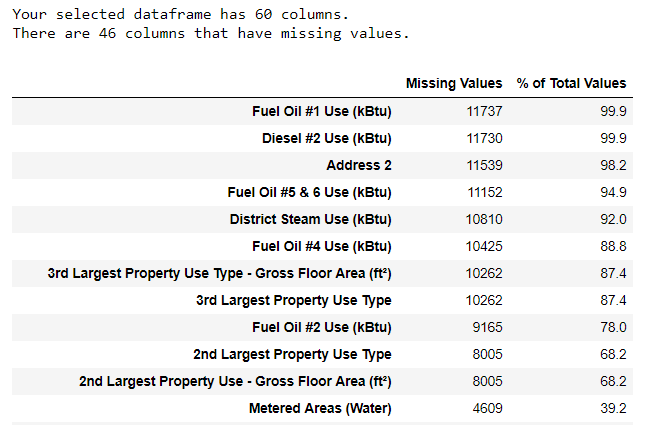
يجب توخي الحذر عند حذف عمود يحوي نسبةً كبيرةً من القيم الناقصة إذ قد يكون مفيدًا لنموذج التعلّم المطلوب. تعتمد العتبة والتي من فوقها نحذف العمود على المسألة المطروحة (تجد في هذا الرابط مناقشة لمسألة العتبة) وفي مشروعنا سنحذف أي عمود يحوي أكثر من 50% قيمًا ناقصةً.
نحذف القيم المتطرفة أيضًا في هذه المرحلة والتي يُمكن أن تظهر في البيانات نتيجة أخطاء طباعية أو أخطاء في الوحدات units المستخدمة، لكن يجب الملاحظة أنها في بعض الأحيان قد تكون صحيحةً إلا أنها بعيدةً كثيرًا عن باقي القيم. سنحذف القيم بالاعتماد على تعريف القيم المتطرفة البعيدة التالي:
- أقل من الربع الأول – 3 * الانحراف الربيعي.
- فوق الربع الثالث + 3 * الانحراف الربيعي.
يُمكن العودة للمشروع للاطلاع على شيفرة حذف الأعمدة والقيم المتطرفة.
في نهاية هذه المرحلة، بقي لدينا أكثر من 11000 مبنىً مع 49 ميزةً.
تحليل البيانات الاستكشافي
بعد الانتهاء من المرحلة السابقة الضرورية جدًا رغم صعوبتها بعض الشيء، يُمكن لنا الانتقال إلى مرحلة تحليل البيانات الاستكشافي، والذي نعني به تطبيق بعض الحسابات الاحصائية ورسم بعض المخططات بهدف إيجاد الاتجاهات العامة trends والمتطرفات anomalies والأنماط patterns والعلاقات relationships الموجودة ضمن البيانات. وباختصار يُعدّ الهدف من هذه المرحلة هو استكشاف المعلومات المُضمّنة في البيانات والتي يُمكن لها لعب دورًا مهمًا في توجيه خياراتنا عند بناء نماذج التعلّم، مثلًا: من هي الميزات الأكثر ارتباطًا مع الهدف؟
نعمل عادةً هذه الخطوة بشكل تدريجي، أي نبدأ من نظرة عامة كلية قد تقودنا في بعض الأحيان إلى التركيز على بيانات محدّدة معينة.
رسم متغير وحيد
هدفنا التنبؤ بمعامل نجمة الطاقة (ندعوه 'score' في بياناتنا)، لذلك من الطبيعي البدء باستكشاف توزع هذا المعامل، وبالطبع فأسهل شيء يُمكن اللجوء له هو رسم المدرج التكراري Histogram، والذي يسمح بمعاينة توزع متغير لاسيما أنه يُمكن إنجاز ذلك بسهولة باستخدام المكتبة matplotlib كما يلي:
import matplotlib.pyplot as plt # المدرج التكراري لمعامل نجمة الطاقة plt.style.use('fivethirtyeight') plt.hist(data['score'].dropna(), bins = 100, edgecolor = 'k') plt.xlabel('Score'); plt.ylabel('Number of Buildings') plt.title('Energy Star Score Distribution')
ويكون الناتج ما يلي:
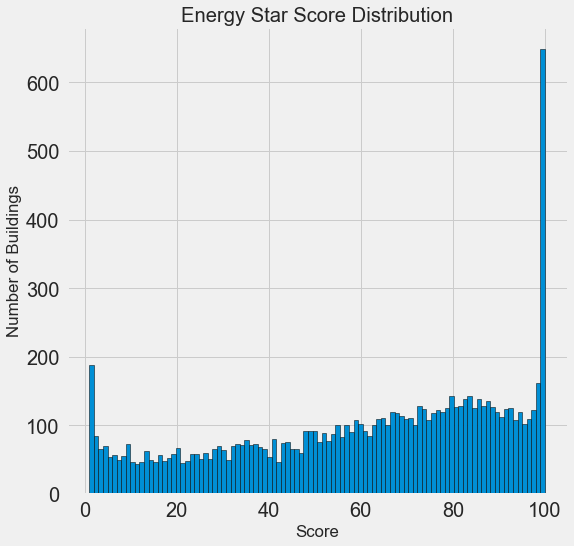
يُظهِر هذا المدرج التكراري الملاحظة التالية المثيرة للانتباه: بالرغم من أن مُعامل نجمة الطاقة هو نسبة مئوية، أي يُفترض تشكيل توزيعًا منتظمًا تقريبًا، إذ يوجد اختلاف كبير بين عدد الأبنية ذات معامل يساوي 100 وعدد الأبنية ذات معامل يساوي 1، أي أنه كلما كان معامل نجمة الطاقة كبيرًا كانت كفاءة الطاقة أفضل.
إذا عُدنا إلى تعريف معامل نجمة الطاقة فسنجد أنه تقدير نسبي يُعطيه الأشخاص مما يُفسّر الظاهرة السابقة، لربما كان الطلب من سكان الأبنية تقدير استهلاكهم من الطاقة يشابه الطلب من طلاب صف تقويم أنفسهم في امتحان ما، وبالنتيجة فإننا نعتقد أن هذا المعيار غير موضوعي لقياس كفاءة الطاقة في الأبنية.
يُمكن التحري عن السبب في اختلاف قيم المعيار بين الأبنية عن طريق إيجاد الميزات المشتركة بين الأبنية التي لها تقريبًا نفس قيم المعيار؛ إلا أننا لن نفعل ذلك لأن مهمتنا هي التنبؤ بقيم هذا المعيار وليس إيجاد طرق أفضل لتقويم طاقة الأبنية. سنضع في تقريرنا النهائي ملاحظاتنا عن التوزيع غير المنتظم إلا أننا سنركز على مسألة التنبؤ.
إيجاد العلاقات
تهدف مرحلة تحليل البيانات الاستكشافية أساسًا إلى إيجاد العلاقات الكامنة بين الميزات وبين المعامل الهدف، حيث تكون الميزات المترابطة مع الهدف مفيدةً جدًا لنموذج التعلّم، لأنه يُمكن استخدامها في عملية التنبؤ بالهدف.
يُمكن رسم مخطط الكثافة لاستكشاف تأثير متغير فئوي (يأخذ مجموعةً مُحدّدةً من القيم) على الهدف وذلك باستخدام المكتبة seaborn، ويُمكن النظر لمخطط الكثافة مثل تنعيم للمدرج التكراري لأنه يُظهر توزع متغير وحيد أيضًا.
يُمكن تلوين مخطط الكثافة حسب الفئة لنرى كيف يؤثر المتغير الفئوي على التوزيع، حيث ترسم الشيفرة التالية مخططات الكثافة لمعامل الطاقة ملون حسب نوع المبنى (يقتصر على أنواع المباني التي تحتوي على أكثر من 100 سطر بيانات):
# إنشاء قائمة من الأبنية التي لها أكثر من 10 قياس
types = data.dropna(subset=['score'])
types = types['Largest Property Use Type'].value_counts()
types = list(types[types.values > 100].index)
# رسم توزيع المعامل وفق فئة البناء
figsize(12, 10)
# رسم كل بناء
for b_type in types:
# اختيار فئة البناء
subset = data[data['Largest Property Use Type'] == b_type]
# رسم مخطط الكثافة لمعامل الطاقة
sns.kdeplot(subset['score'].dropna(),
label = b_type, shade = False, alpha = 0.8);
# عنونة المخطط
plt.xlabel('Energy Star Score', size = 20); plt.ylabel('Density', size = 20);
plt.title('Density Plot of Energy Star Scores by Building Type', size = 28);
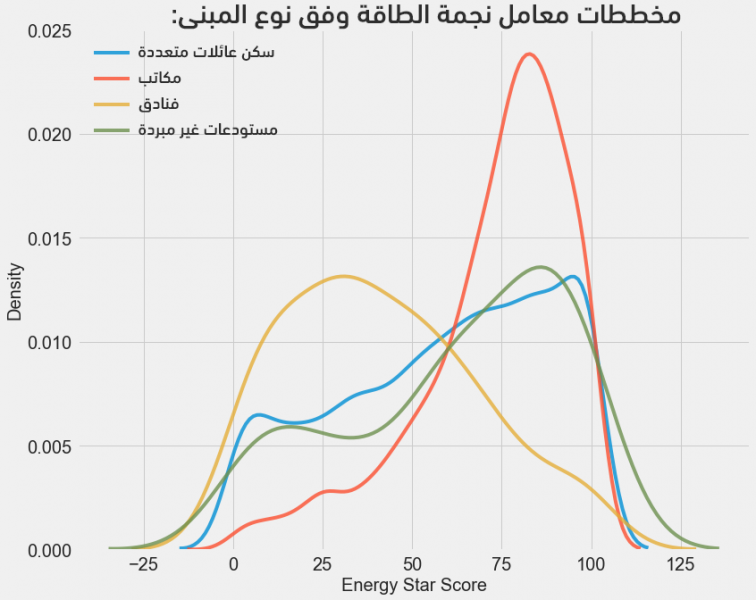
ويكون الناتج مخططات الكثافة حسب نوع البناء (الأزرق للمنازل السكنية، والأحمر للمكاتب، أما الأصفر فللفنادق، بينما الأخضر فالمستودعات غير المبردّة):
تُبرهن المخططات أعلاه على أن نوع المبنى يؤثر كثيرًا في معامل نجمة الطاقة، إذ يكون لمباني المكاتب معاملات عالية بينما تأخذ الفنادق القيم الأدنى، مما يستلزم تضمين نوع المبنى في نموذج التعلّم لأنه يؤثر بوضوح على الهدف بصفة متغير فئوي، وسيتوجب علينا استخدام ترميز ساخن واحد one-hot.
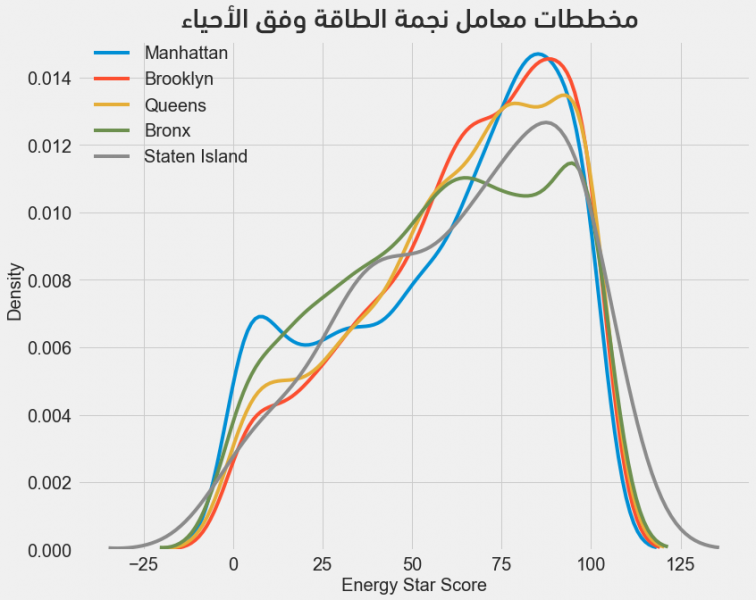
يُمكن تكرار العمل لدراسة العلاقة بين حي السكن ومعامل الطاقة حيث ينتج لدينا:
تُبرهن المخططات أعلاه عدم وجود تأثير كبير للحي على معامل نجمة الطاقة، ومع ذلك سنضمن الحي في نموذجنا نظرًا لوجود بعض الاختلافات الطفيفة بين الأحياء.
يُمكن استخدام معامل الارتباط لبيرسون Pearson لتحديد نوع العلاقات بين المتغيرات:
- القيمة 1 تعني علاقة تناسب طردي.
- القيمة -1 تعني تناسب عكسي.
- أما القيمة 0 تعني عدم وجود أي علاقة.
يُبين الشكل التالي بعض قيم معامل الارتباط لبيرسون:
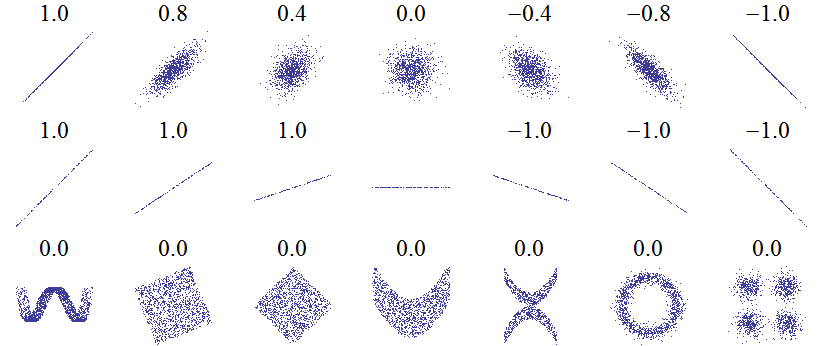
لا يكشف معامل الارتباط العلاقات غير الخطية وعلى الرغم من ذلك، فهو يبقى في البداية طريقةً جيدةً لاستكشاف ترابط المتغيرات مع بعضها البعض، يُمكن بسهولة إيجاد معاملات الارتباط باستخدام المكتبة Pandas:
# إيجاد قيم جميع الارتباطات وترتيبها تصاعديًا correlations_data = data.corr()['score'].sort_values()
يُبين الشكل التالي علاقات الارتباط الناتجة السلبية (على اليسار، تناسب عكسي) والإيجابية (على اليمين، تناسب طردي):
نلاحظ وجود العديد من الارتباطات السلبية (العكسية) بين الميزات ومعامل نجمة الطاقة الهدف. لنأخذ مثلًا الميزة EUI والتي هي كثافة استخدام الطاقة في المبنى أي الطاقة المستهلكة للمبنى مقسومًا على مساحة المبنى، بالطبع كلما كان هذا المقدار أصغر كانت الكفاءة أكبر (والتي يُعبّر عنها مقياس نجمة الطاقة).
رسم مخطط متغيرين
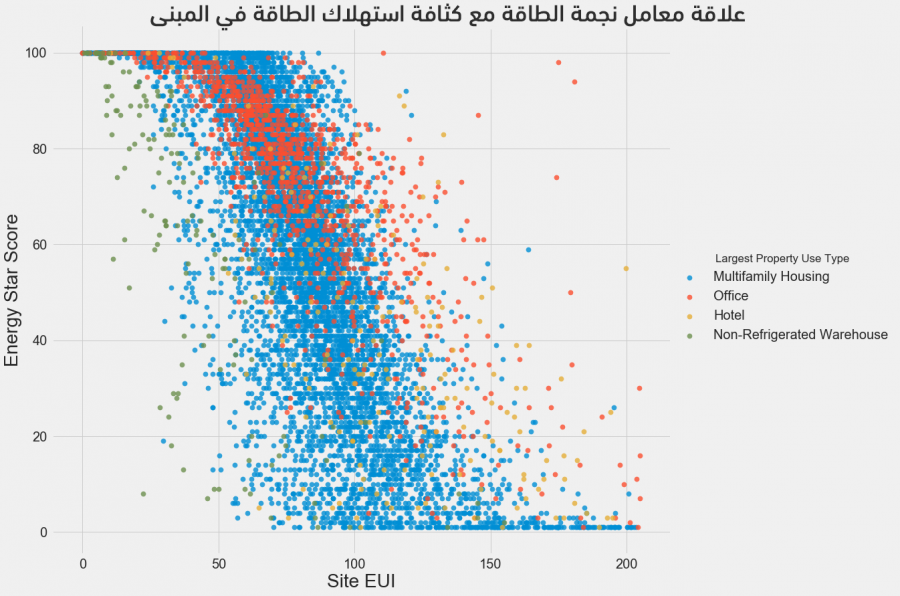
لمعاينة العلاقة بين متغيرين مستمرين (قيم رقمية حقيقية) يُمكن اللجوء إلى المخططات من النمط المبعثر scatterplots، كما يُمكن إضافة معلومات أخرى مثل المتغيرات الفئوية لتلوين نقاط المخطط، حيث يُبين المخطط التالي العلاقة بين كثافة استخدام الطاقة EUI ومعامل نجمة الطاقة ملونة حسب نوع البناء:
يُظهر هذا المخطط علاقةً عكسيةً بين كثافة استخدام الطاقة ومعامل نجمة الطاقة، فكلما انخفضت الكثافة ارتفع معامل نجمة الطاقة (يكون معامل الترابط حوالي -0.7).
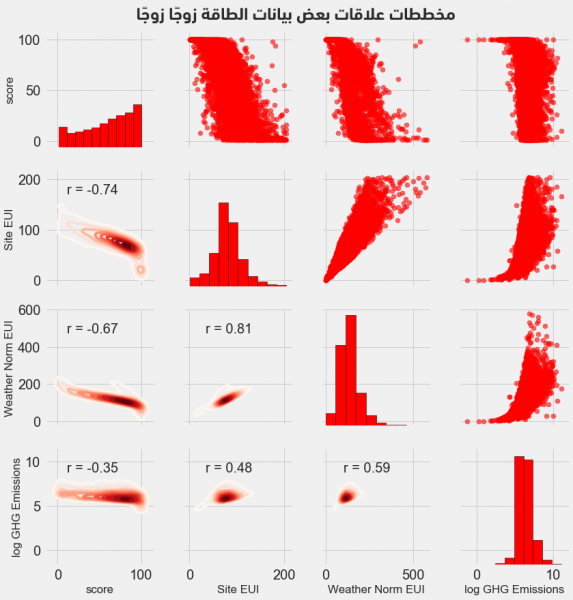
أخيرًا، لنرسم مخطط باريس Paris Plot، والذي يوفر أداةً ممتازةً لاستكشاف البيانات، إذ يُمكّننا من معاينة العلاقات بين عدة أزواج من المتغيرات إضافًة إلى توزيعات متغيرات وحيدة. سنستخدم مكتبة المعاينة seaborn والتابع PairGrid لرسم مخطط باريس وحيث نضع في المثلث العلوي المخططات المتناثرة وعلى القطر المدرجات التكرارية، بينما نضع مخططات كثافة النواة ثنائية الأبعاد 2D kernel density مع معاملات الترابط في المثلث السفلي.
# تحديد أعمدة المخطط plot_data = features[['score', 'Site EUI (kBtu/ft²)', 'Weather Normalized Source EUI (kBtu/ft²)', 'log_Total GHG Emissions (Metric Tons CO2e)']] # استبدال اللانهاية بليس رقمًا plot_data = plot_data.replace({np.inf: np.nan, -np.inf: np.nan}) # إعادة تسمية الأعمدة plot_data = plot_data.rename(columns = {'Site EUI (kBtu/ft²)': 'Site EUI', 'Weather Normalized Source EUI (kBtu/ft²)': 'Weather Norm EUI', 'log_Total GHG Emissions (Metric Tons CO2e)': 'log GHG Emissions'}) # حذف القيم غير الرقمية plot_data = plot_data.dropna() # تابع حساب معامل الارتباط بين عمودين def corr_func(x, y, **kwargs): r = np.corrcoef(x, y)[0][1] ax = plt.gca() ax.annotate("r = {:.2f}".format(r), xy=(.2, .8), xycoords=ax.transAxes, size = 20) # إنشاء كائن الشبكة grid = sns.PairGrid(data = plot_data, size = 3) # الأعلى هو المخطط المبعثر grid.map_upper(plt.scatter, color = 'red', alpha = 0.6) # القطر هو المدرج التكراري grid.map_diag(plt.hist, color = 'red', edgecolor = 'black') # الأسفل هو مخطط الارتباط والكثافة grid.map_lower(corr_func) grid.map_lower(sns.kdeplot, cmap = plt.cm.Reds) # العنوان الكلي للمخطط plt.suptitle('Pairs Plot of Energy Data', size = 36, y = 1.02)
فنحصل على المخططات التالية:
ننظر لتقاطع سطر المتغير الأول مع عمود المتغير الثاني لمعاينة التفاعل بين متغيرين، مثلًا: لمعاينة الارتباط بين كثافة الكهرباء وفق الطقس Weather Norm EUI والمعامل الهدف score، ننظر إلى تقاطع سطر Weather Norm EUI مع عمود score لنجد معامل ارتباط قيمته -0.67 أي أن العلاقة بينهما عكسيةً.
يُمكن أن يُساعد هذا المخطط إضافًة لمظهر المخطط السابق الرائع، في تحديد الميزات المفيدة في عملية النمذجة.
هندسة الميزات والاختيار
تختصر عملية هندسة الميزات وحسن اختيار المناسب منها الوقت اللازم لمعالجة مسائل تعلّم الآلة. لنبدأ أولًا بتعريف هاتين المهمتين:
- هندسة الميزات Feature engineering: وهي عملية استخراج أو إنشاء ميزات جديدة من البيانات الأساسية المتاحة، قد يستلزم ذلك إجراء بعض التحويلات على المتغيرات طبعًا، مثل إيجاد مربع القيمة أو اللوغاريتم الطبيعي لها، أو ترميز المتغيرات الفئوية لتُصبح قابلةً للاستخدام في النموذج. يُمكن النظر لهندسة الميزات عمومًا على أنها عملية إنشاء ميزات جديدة.
- اختيار الميزات Feature selection: وهو عملية اختيار الميزات الأنسب للنموذج، حيث نحذف عادةً الميزات غير المرتبطة مع الهدف كي نُساعد النموذج على التعميم الأفضل للبيانات الجديدة وللحصول على نموذج قابل للشرح والفهم. يُمكن النظر لاختيار الميزات بشكل عام على أنها عملية حذف الميزات غير المرتبطة مع الهدف والإبقاء على الميزات المهمة فقط.
يتعلّم نموذج تعلّم الآلة فقط من البيانات التي نُقدّمها له، لذا يُعدّ التأكد من أن البيانات تتضمن جميع الميزات الهامة أمرًا أساسيًا، وإذا لم نغذي النموذج بالبيانات الصحيحة، فإننا نعدّه ليفشل ولا يجب أن نتوقع منه أن يتعلّم عمليًا.
ننجز بمشروعنا في مرحلة هندسة الميزات بما يلي:
- ترميز المتغيرات الفئوية باستخدام ترميز ساخن واحد (ميزة الحي السكني وميزة نوع استخدام الملكية).
- إضافة اللوغاريتم الطبيعي للمتغيرات الرقمية.
يلزم استخدام هذا الترميز one-hot لتضمين متغير فئوي categorical variables في النموذج، إذ لا تفهم خوارزمية تعلّم الآلة بأن نوع البناء مكتبًا مثلًا، إذ يجب استخدام 1 إذا كان نوع البناء مكتبًا وإلا 0.
يُمكن أن تساهم إضافة ميزات جديدة ناتجة عن تطبيق بعض التوابع الرياضية على الميزات الرقمية في مساعدة النموذج على تعلّم العلاقات غير الخطية الموجودة ضمن البيانات، ومن الممارسات الشائعة حساب الجذر التربيعي أو القوة من مرتبة معينة أو اللوغاريتم الطبيعي، والتي تعتمد عادةً على التجربة أو المعرفة بمجال المسألة، ونضيف في مشروعنا اللوغاريتم الطبيعي لجميع الميزات الرقمية.
تختار الشيفرة التالية الميزات الرقمية ومن ثم يوجد اللوغاريتم الطبيعي لها ثم يختار الميزتين الفئويتين ويرمزهما ثم يدمج الكل، قد يبدو أن هذا يتطلب الكثير من الجهد لكن استخدام المكتبة Pandas يُسهّل العمل:
# نسخ البيانات الأولية features = data.copy() # اختيار الأعمدة الرقمية numeric_subset = data.select_dtypes('number') # إنشاء أعمدة جديدة للوغاريتم الطبيعي للأعمدة الرقمية for col in numeric_subset.columns: # تجاوز عمود معامل الطاقة if col == 'score': next else: numeric_subset['log_' + col] = np.log(numeric_subset[col]) # اختيار الأعمدة الفئوية categorical_subset = data[['Borough', 'Largest Property Use Type']] # ترميز واحد ساخن categorical_subset = pd.get_dummies(categorical_subset) # وصل إطاري العمل الناتجين # اضبط قيمة العمود على 1 لإنشاء عمود ربط features = pd.concat([numeric_subset, categorical_subset], axis = 1)
بعد هذه المعالجة سيكون لدينا أكثر من 11000 مبنى مع 110 عمود (ميزة)، حيث لن تكون كل هذه الميزات مفيدةً في عملية التنبؤ بمعامل الطاقة لذا نحذف بعضها.
اختيار الميزات
ترتبط العديد من الميزات مع بعضها البعض بصورة وثيقة مما يعني حصول تكرار عمليًا، إذ يُبين المخطط التالي مثلًا ترابط ميزة كثافة الطاقة Site EUI مع ميزة كثافة الكهرباء Weather Normalized Site EUI، وبقيمة ترابط عالية جدًا 0.997.
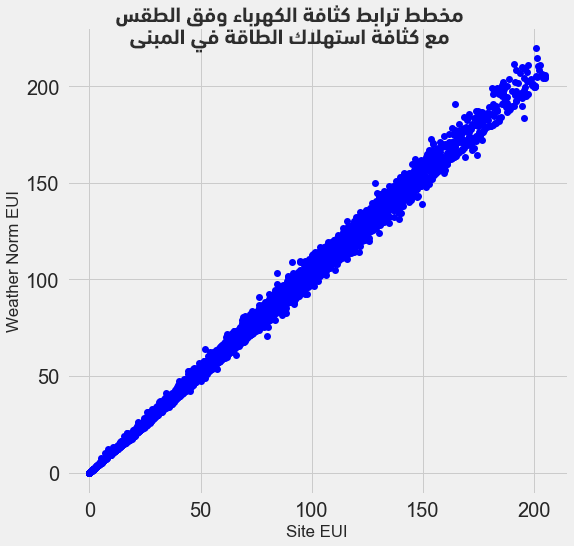
نحذف عادةً الميزات المترابطة مع بعضها كثيرًا تُدعى علاقة خطية متداخلة collinear، مما يُساعد على الحصول على نموذج تعلّم عام قابل للتفسير. حيث نشير هنا إلى الارتباط بين الميزات مع بعضها البعض وليس إلى ارتباط الميزات مع الهدف.
توجد العديد من الطرق لحساب علاقات التداخل الخطية بين الميزات، حيث يُمكن استخدام عامل تضخم التباين variance inflation factor. سنستخدم في هذا المشروع معامل الارتباط لإيجاد الميزات المترابطة ونحذف ميزةً من أجل كل ميزتين إذا كان معدل الارتباط بينهما أكبر من 0.6، حيث يمكنك الحصول على الشيفرة أيضًا.
لاحظ أن القيمة المعتمدة 0.6 هي قيمة تجريبية اختيرت بعد العديد من التجارب، لنتذكر أن تعلّم الآلة هو حقل تجريبي وغالبًا ما نجرب عدة تجارب ومحاولات لاختيار الأفضل.
أخيرًا وبعد مرحلة اختيار الميزات تبقى لدينا 64 عمودًا وهدفًا وحيدًا.
# حذف الأعمدة ذات القيم غير الرقمية features = features.dropna(axis=1, how = 'all') print(features.shape) (11319, 65)
إنشاء خط الأساس
بعد أن أنهينا مرحلة تنظيف البيانات وتحليل البيانات الاستكشافي وهندسة الميزات، الآن يجب تحديد خط الأساس المبدئي Baseline قبل البدء بعملية بناء النموذج، وهو عبارة عن تخمين يُستخدم للحكم فيما إذا كانت نتائج نموذج التعلّم مقبولةً أم لا.
يُمكن في مسائل الانحدار اعتماد القيمة الأوسط median للهدف والمحسوبة لبيانات اختبار الخط الذي يجب لنموذج التعلّم تجاوزه وهو عمليًا هدف سهل الوصول.
نستخدم متوسط الخطأ المطلق MAE mean absolute error، والذي يقيس متوسط الفروقات بالقيمة المطلقة بين تنبؤ النموذج والقيم الحقيقية. توجد العديد من المقاييس في الواقع إلا أنه يُمكن اتباع نصيحة اعتماد مقياس واحد دومًا إضافةً إلى أن حساب متوسط الخطأ المطلق سهل وقابل للشرح والتفسير.
قبل حساب خط الأساس يجب تقسيم البيانات إلى مجموعتين هما مجموعة التدريب ومجموعة الاختبار:
- مجموعة التدريب: وهي مجموعة البيانات التي نُقدّمها للنموذج ليتعلّم منها، حيث تتألف من مجموعة الميزات إضافةً إلى القيمة الهدف (معامل الطاقة في حالتنا).
- مجموعة الاختبار: تُستخدم هذه المجموعة لتقويم كفاءة نموذج التعلّم حيث نختبر النموذج المدرب مع هذه البيانات، ومن ثم نوازن جواب النموذج مع الجواب المعروف لدينا في هذه البيانات، مما يسمح لنا بحساب قيمة متوسط الخطأ المطلق.
نقسم البيانات إلى 70% للتدريب و30% للاختبار:
# تقسيم البيانات إلى 70% للتدريب و30% للاختبار X, X_test, y, y_test = train_test_split(features, targets, test_size = 0.3, random_state = 42)
يُمكن لنا الآن حساب خط الأساس:
# تابع حساب متوسط الخطأ المطلق def mae(y_true, y_pred): return np.mean(abs(y_true - y_pred)) baseline_guess = np.median(y) print('The baseline guess is a score of %0.2f' % baseline_guess) print("Baseline Performance on the test set: MAE = %0.4f" % mae(y_test, baseline_guess))
والذي يُعطي:
The baseline guess is a score of 66.00 Baseline Performance on the test set: MAE = 24.5164
مما يعني أن الخطأ من مرتبة 25% وهي عتبة سهلة التجاوز.
النتائج
استعرضنا في هذه المقالة الخطوات الثلاث الأولى لمعالجة مسألة تعلّم الآلة، بعد تحديد المشكلة نفعل ما يلي:
- تنظيف وتنسيق البيانات الخام المتاحة.
- تحليل استكشافي للبيانات بهدف التعرّف على البيانات.
- تطوير مجموعةً من الميزات للاستخدام في نموذج التعلّم.
وفي النهاية، أجرينا عملية تحديد خط الأساس الذي سيسمح لنا بقبول نموذج التعلّم أو رفضه.
نعرض في المقالة الثانية كيفية استخدام Scikit-Learn لتقييم نماذج التعلّم واختيار الأفضل منها، إضافةً إلى آليات معايرة المعاملات الفائقة للنموذج للوصول إلى نموذج أمثلي، وتعرض المقالة الثالثة كيفية تفسير النموذج وعرض النتائج.
ترجمة -وبتصرف- للمقال A Complete Machine Learning Project Walk-Through in Python: Part One لكاتبه Will Koehrsen.













أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.