المرجع الشامل إلى تعلم الخوارزميات للمبتدئين

6 يونيو 2023

https://academy.hsoub.com/programming/advanced/%D8%A7%D9%84%D8%AE%D9%88%D8%A7%D8%B1%D8%B2%D9%85%D9%8A%D8%A7%D8%AA/

لا شك تعلم الخوارزميات أحد النصائح المهمة التي وجهت لك إذا قررت تعلم البرمجة فكلمة خوارزمية تتردد كثيرًا في مجال البرمجة وغيرها من المجالات مثل الرياضيات والعلوم والمنطق وكل ما يتعلق بالحاسوب خصوصًا، فهي من أهم المفاهيم التي لا يمكن أن يستقيم لك تعلم البرمجة والرياضيات وعلوم الحاسب بدونها.

إذا كنت تتساءل ما هي الخوارزمية، وكيف أتعلم الخوازميات، وما أهمية الخوارزميات في علوم الحاسب وفي البرمجة بشكل خاص، وما هي أنواع الخوارزميات التي علي تعلمها، وكيف أكتب أفضل خوارزمية فهذه المقالة لك، حيث سنستعرض في سياقها كل ما تحتاج معرفته عن الخوارزميات، ونوفر لك مجموعة من المصادر التعليمية العربية الغنية التي تساعدك على تعلم رموز الخوارزميات وطرق حل الخوارزميات في الحاسوب بأفضل طريقة.

ما هي الخوارزمية؟

الخوارزمية algorithm هي مجموعة من التعليمات المرتبة لحل مشكلة ما في الرياضيات أو أي مشكلة تواجهك في الحياة اليومية خلال زمن محدد وعدد خطوات محدود.

ينبغي أن تكون خطوات وتعليمات الخوارزمية واضحة ومُرتّبة بحيث تنتهي بحل المشكلة. فكّر في الخوارزمية كما لو كانت وصفة طبخ، إذ تقدّم الوصفة طريقة تحضير وجبة ما خطوة بخطوة، ابتداءً بالمقادير الضرورية للوجبة، وحتى آخر خطوة من تحضير الوجبة وتقديمها.

ورغم أن مفهوم الخوارزميات يمكن أن يطبق في كل مجالات الحياة لكن تبرز أهمية الخوارزميات في علوم الحاسب بشكل خاص فهي تنظم عمل المبرمج وتعزز تفكيره المنطقي والرياضي وتمكنه من فهم المشكلات وتصورها بشكل أفضل قبل حلها وتطبيقها فعليًا على برامج حاسوبية مكتوبة بإحدى لغات البرمجة.

تاريخ الخوارزميات

تُعزى أقدم الخوارزميات المعروفة إلى البابليين، إذ عُثِر على أقدم لوح يحتوي تعليمات خوارزمية لإجراء عملية القسمة، ويعود تاريخه لسنة 2500 قبل الميلاد. وقد عثِر كذلك على خوارزميات حسابية تعود إلى المصريين القدامى تعود إلى سنة 1550 قبل الميلاد.

ازداد استخدام الخوارزميات في حقبة اليونان، حيث ظهرت الكثير من الخوارزميات الرياضية التي ما تزال تُستخدم حتى يومنا هذا، مثل خوارزمية قسمة إقليدس التي تحسب خارج وباقي عملية القسمة.

تطور مفهوم الخوارزميات في عصر الحضارة الإسلامية، إذ استخدم المسلمون الخوارزميات لحل المعادلات والمسائل الرياضية. ولعل أشهر هذه الخوارزميات هي خوارزمية حل المعادلات من الدرجة الثانية التي ذُكِرت في كتاب "حساب الجبر والمقابلة" لعالم الرياضيات المسلم محمد بن موسى الخوارزمي مؤسس علم الجبر، والذي تُنسب إليه كلمة خوارزمية في اللغة العربية، وكذلك الكلمة المقابلة لها في اللغات اللاتينية algorithm المُشتقة من الكلمة al-Khwārizmī، وهو الاسم الرومي للخوارزمي -وأيضًا كلمة الجبر algebra.

استخدم الأوروبيون كلمة algorithm للدلالة على القواعد والتقنيات التي استخدمها الخوارزمي لحل المعادلات الجبرية، ثمّ عُمِّم هذا المصطلح ليشمل أيّ مجموعة من القواعد والتقنيات الساعية لحل مشكلة ما.

استمر مفهوم الخوارزميات في التطور بعد الحقبة الإسلامية إبّان عصر النهضة، خصوصًا مع تطوّر أسس علم الحوسبة في القرن التاسع عشر وإنتاج أول خوارزمية يمكن تنفيذها على الحاسوب سنة 1840 على يد آدا لوفانس Ada Lovelace. ثمّ الصياغة النهائية لمفهوم الخوارزمية على يد آلان تورنغ Alan Turing عبر آلته الشهيرة آلة تورنغ (Turing machine).

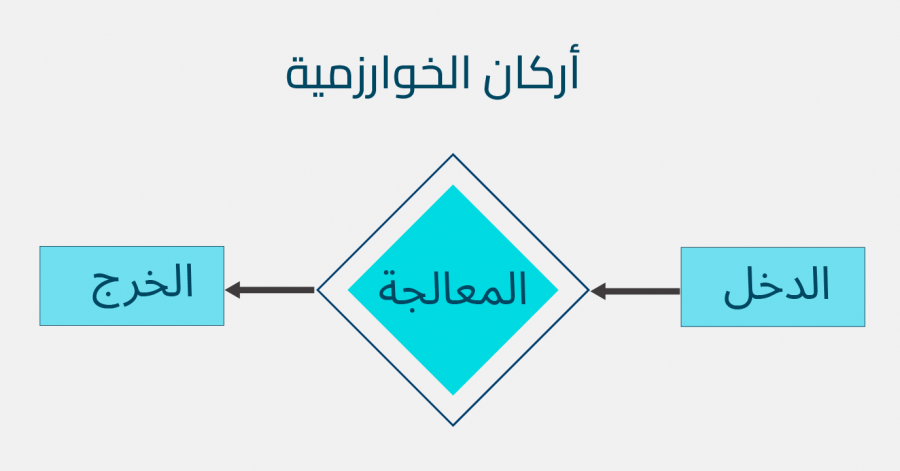
أركان الخوارزمية

تملك أي خوارزمية ثلاثة أركان رئيسية وهي:

الدخل أو المدخلات: تمثل البيانات أو الأشياء الضرورية والمطلوبة التي تعمل عليها الخوارزمية وإن كان الدخل مؤلفًا من عدة عناصر، فإنّ تعداد عناصره يسمى حجم الدخل، مثلًا إن كان الدخل عبارة عن مصفوفة أو سلسلة نصية مؤلفة من n عنصر، فإنّ حجم الدخل سيساوي n. لو عدنا إلى مثال الطبخ فإنّ دخل خوارزمية طهي وجبة معينة ستكون هي المقادير المُستخدمة لإعداد الوجبة.
متن الخوارزمية: تأخذ الخوارزمية الدخل، وتطبّق عليه سلسلة من خطوات المعالجة المتتابعة والمُحدّدة سلفًا. مثلًا، يشمل متن خوارزمية الطبخ كل عمليات تجهيز المقادير وإعدَادها وخطوات طهيها.
الخرج أو المُخرجات: بعد أن تنتهي الخوارزمية من تنفيذ كافة الخطوات، تُنتج لنا خرجًا يمثل حل المشكلة. مثلًا خرج خوارزمية طهي وجبة سيكون هو الوجبة نفسها جاهزة ومطهيّة.

على سبيل المثال إذا أردنا كتابة خوارزمية جداء عددين صحيحين ستكون أركان هذه الخوارزمية كالتالي:

الدخل: هو العددان الصحيحان المطلوب حساب ناتج جدائهما x, y
الخرج: هو ناتج الجداء z
متن الخوارزمية:
- الخطوة 1: ابدأ
- الخطوة 2: قم بالتصريح عن ثلاثة أعداد صحيحة x و y و z
- الخطوة 3: أدخل قيم المدخلات x و y
- الخطوة 4: اضرب قيم x بـ y
- الخطوة 5: خزّن ناتج الضرب في z
- الخطوة 6: اعرض قيمة z
- الخطوة 7: توقف

خطوات حل الخوارزميات

عندما تواجهك أي مشكلة وتريد كتابة خوارزمية لحلها عليك أن تفكر في العثور على إجابات للأسئلة التالية:

ما هو دخل الخوارزمية أي ما هي المعلومات التي أحتاج إلى الحصول عليها من المستخدم؟
ما هو خرج الخوارزمية أي ما هي المعلومات التي أحتاج لعرضها على المستخدم؟
ما هي الخطوات الرئيسية المطلوبة لحل هذه المشكلة؟
ما هو ترتيب تنفيذ هذه الخطوات؟
ما هي القرارات أو الشروط التي أحتاج مراعاتها عند معالجة المعلومات؟
هل هناك تعليمات بحاجة لأن أكررها عدة مرات؟

طرق تمثيل الخوارزميات

يمكنك ثمثيل الخوارزمية أو التعبير عنها بعدة طرق:

الطريقة الأولى من خلال الكلام المبعثر الذي يصف حل المشكلة بلغتك المحكية دون اتباع أي قواعد في الوصف.
الطريقة الثانية من خلال ما يسمى الشيفرة الوهمية أو الزائفة pseudocode وهي مجموعة من التعليمات التي تحاكي في طريقة كتابتها لغات البرمجة لكنها لا تلتزم بقواعد البرمجة التي يجب الالتزام بها عندما تكتب شيفرات برمجية فعلية.
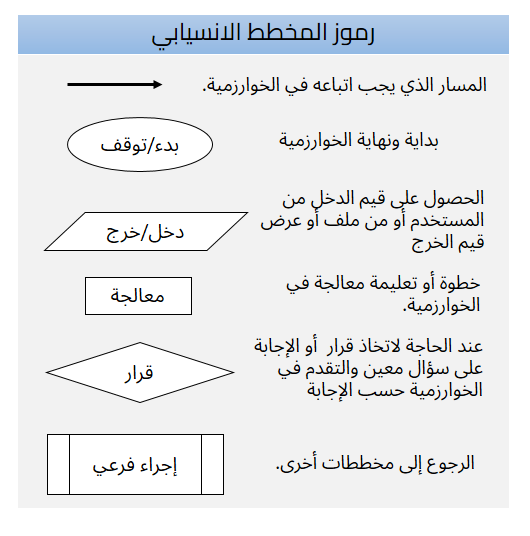
الطريقة الثالثة تسمى المخططات الانسيابية Flowcharts، والمخطط الانسيابي هو تمثيل رسومي للخوارزمية يرسم باستخدام أنواع مختلفة من الرموز لكل رمز غرض معين وهو في تقسيم المشكلة الكبيرة إلى مشاكل صغيرة سهلة الفهم ويعد طريقة مناسبة للتواصل بين الأشخاص غير التقنيين.

تتوافر عدة برامج مساعدة تساعدك على رسم المخططات الانسيابية، وللمزيد يمكنك مطالعة مقال كيفية رسم مخطط انسيابي Flowchart باستخدام PowerPoin.

مثال على استخدام الخوارزمية في حياتنا اليومية

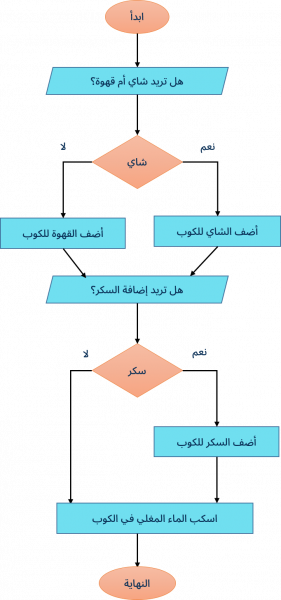
على سبيل المثال إذا طلب منك كتابة خوارزمية توضح طريقة التعامل مع آلة صنع القهوة والشاي ستكون الخطوات التي عليك اتباعها كالتالي:

معرفة إن كان الزبون يريد شرب الشاي أم القهوة
إضافة الشاي أو القهوة إلى الكوب
معرفة إن كان المستخدم يريد إضافة السكر للكوب
إذا كان الجواب نعم أضف السكر إلى الكوب
سكب الماء الساخن في الكوب

للتعبير عن هذه الخوارزمية باستخدام الشيفرة الزائفة سنكتب التالي:

START;
/Would you like Tea or Coffee?/;
if tea {
  Add Tea in cup;
} else {
  Add Coffee in cup;
}
/Would you like Sugar?/;
if Sugar {
  Add Sugar in cup;
}
Pour boiling water in cup
END;

وللتعبير عنها باستخدام المخطط الانسيابي سنرسم المخطط التالي:

أمثلة على الخوارزميات

لنفهم بشكل أفضل ما هي الخوارزميات دعنا نستعرض بعض الأمثلة الإضافية على خوارزميات لحل مسائل رياضية بسيطة ونتعرف على أركانها المختلفة وخطوات حلها ونعبر عنها بالطرق المختلفة.

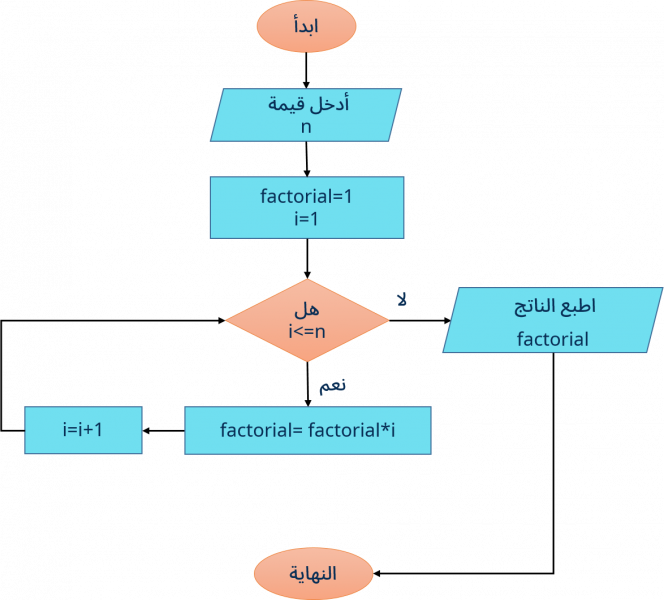
خوارزمية لحساب قيمة مضروب عدد

في الرياضيات المضروب factorial أو عاملي العدد الصحيح n الذي يعبر عنه بالشكل التالي n! هو جداء كل الأعداد الطبيعية المساوية أو الأصغر من n ما عدا الصفر ولكتابة خوارزمية تحل هذه المسألة الرياضية علينا اتباع الخطوات التالية:

الدخل: هو العدد الصحيح المطلوب حساب مضروبه n.
الخرج: هو ناتج المضروب factorial
المتن:
- الخطوة 1: إدخال العدد n المراد حساب مضروبه
- الخطوة 2: تعريف متغير مساعد وليكن i وهو عبارة عن عدد صحيح يأخذ قيمة متغيرة بين الواحد والعدد نفسه ويساعدنا على حساب القيمة المطلوبة.
- الخطوة 3: تهيئة المتغير factorial الذي يمثل القيمة المؤقتة للمضروب، والمتغير i الذي يمثل المرحلة التي نحن فيها أثناء تنفيذ الخوارزمية بالقيمة واحد أي نجعل factorial = 1 و i = 1
- الخطوة 4: إعادة تعيين قيم المتغير factorial بالقيمة factorial*i والمتغير بالقيمة i+1
- الخطوة 5: كرر الخطوة 3 حتى تصبح قيمة المتغير i أكبر تمامًا من n
- الخطوة 6: قم بإيقاف الخوارزمية وإعادة قيمة factorial التي تمثل مضروب العدد n

الصورة التالية توضح طريقة رسم المخطط الانسيابي لحل خوارزمية حساب مضروب عدد:

هل تعرف طرقًا أو أساليب أخرى لحل هذه المسألة؟ شاركنا إياها في قسم التعليقات أسفل المقال.

خوارزمية للعثور على أكبر عدد من بين ثلاثة أعداد

سنكتب حل هذه المسألة بأكثر من خوارزمية أو طريقة:

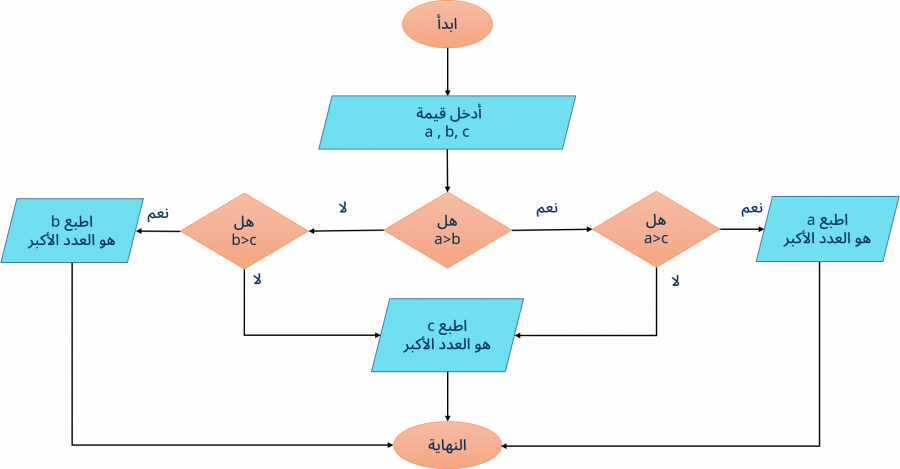
طريقة 1:

الدخل: 3 أرقام a و b و c
الخرج: العدد الأكبر من بينها a أو b أو c
المتن:
- الخطوة 1: أدخل الأرقام الثلاثة وخزنها في المتغيرات a و b و c على التوالي.
- الخطوة 2: تحقق من كون الرقم الأول a أكبر من الرقم الثاني b و الثالث c عندها اطبع أن a هو العدد الأكبر بين الكل وأنهي التنفيذ
- الخطوة 3: تحقق من كون b أكبر من a و c عندها اطبع أن b هو العدد الأكبر بين الكل وأنهي التنفيذ
- الخطوة 4: تحقق من كون c أكبر من a و b عندها اطبع أن c هو العدد الأكبر بين الكل وأنهي التنفيذ

الكود الزائف للتعبير عن خوارزمية أكبر عدد بين 3 أعداد:

Step-1 Start
Step-2 Read three numbers a,b,c
Step-3 If a>b then go to step-5
Step-4 IF b>c THEN
print b is largest
ELSE
print c is largest
ENDIF
GO TO Step-6
Step-5 IF a>c THEN
print a is largest
ELSE
print c is largest
ENDIF
Step-6 Stop

والمخطط الانسيابي للتعبير عن الخوارزمية هو كما يلي:

لعلك لاحظت أن الطريقة أعلاه تتطلب اختبار الكثير من الشروط حتى نصل لقرار حول العدد الأكبر من بين الأعداد الثلاثة، دعنا نحاول حلها بطريقة أبسط.

كما تلاحظ فإن خوارزمية مقارنة ثلاثة أعداد حتى نصل لقرار حول العدد الأكبر من بين الأعداد الثلاثة تطلبت إجراء خطوتين والمرور مرتين على كل عدد، ولكن ماذا لو كان لدينا 10 أعداد أو أكثر ستزداد الخطوات ومرات المرور على الأعداد وسيزاد زمن الحل وتعقده لذا من الأفضل أن نفكر بطريقة أفضل تمكننا من المرور مرة واحدة على الأعداد ومعرفة العدد الأكبر من بينها.

يمكن أن نخزن الأعداد في بنية واحدة مثل المصفوفة ثم نقرأها واحدًا تلو الآخر ونعتبر أن أول عدد هو الأكبر من بين كل الأعداد وكلما قرأنا عددًا جديدًا نقارنه بالذي قبله مباشرة فإن كان أكبر منه نبدل بينهما وإن كان أصغر منه أو يساويه لا نقوم بأي إجراء. لنطبق هذه الطريقة لإيجاد العدد الأكبر من بين ثلاثة أعداد

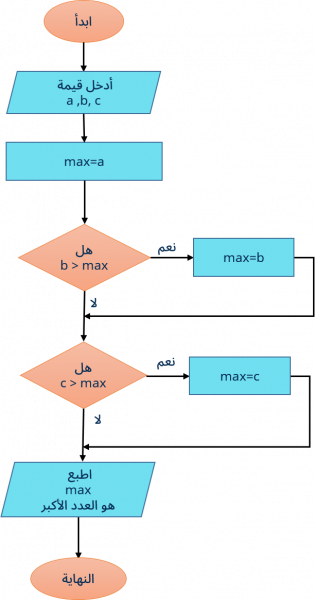
طريقة 2:

الدخل: 3 أرقام a و b و c
الخرج: max الذي يمثل العدد الأكبر
المتن:
- الخطوة 1: أدخل الأعداد الثلاثة وخزنها في a و b و c على التوالي
- الخطوة 3: افترض أن العدد الأول a هو الأكبر max = a
- الخطوة 4: إذا كان العدد الثاني b أكبر من max اجعل max = b
- الخطوة 5: إذا كان العدد الثالث c أكبر من أكبر من max اجعل max = c
- الخطوة 6: اعرض قيمة max

الكود الزائف للتعبير عن هذه الخوارزمية لإيجاد أكبر عدد من بين 3 أعداد:

Step-1 Start
Step-2 Read three numbers: a,b,c
Step-3 max = a
Step-4 IF b > max THEN
max = b
ENDIF
Step-5 IF c > max THEN
max = c
ENDIF
Step-6 print max
Step-7 Stop

والمخطط الانسيابي للتعبير عن الخوارزمية هو كما يلي:

Quote

هذه الطريقة هي ما نتبعه نحن البشر عادةً فإن طلب منك معرفة أكبر رقم من مجموعة أعداد فستمر عليها من البداية وحتى النهاية وتحفظ (تُخزن في ذاكرتك) العدد الأكبر الذي يمر معك لتقوله في النهاية.

هل لديك خوارزمية أخرى أفضل لحل هذه المسألة؟ يمكن أن تشاركنا إياها لنتناقش حولها.

كما تلاحظ فقد مررنا مرة واحدة على الأعداد وعرفنا أيها أكبر، وهذا لن يختلف لو كان لدينا قائمة تحوي 100 عدد أو أكثر، هذا المفهوم ببساطته يسمى بكفاءة الخوارزمية أو تعقيد الخوارزمية والذي يشار إليه برمز Big O وستجده دومًا في أي موضوع يتناول الخوارزميات، لأن من شروط كتابة الخوارزميات أن تكون ذات كفاءة وأقل تعقيدًا ممكنًا.

فكل الخوارزميات تعطي في النهاية الخرج الصحيح نفسه ولكن تتميز عن بعضها بكفاءة وكيفية وسرعة الوصول للخرج الصحيح، وهنا تبرز أهمية التفكير المنطقي وضرورة دراسة الخوارزميات وبنى المعطيات لمعرفة الحل الأكثر كفاءة لحل أي مسألة برمجية تواجهها وسنتحدث عن هذا الموضوع بالتفصيل تاليًا في فقرة "تحليل الخوارزميات".

تحويل الخوارزمية إلى برنامج حاسوبي

إن طرق تمثيل الخوارزمية مفهومة وواضحة لنا كبشر لكنها في الواقع غير قابلة للاستخدام والتطبيق على الحاسوب، لأنّ الخوارزميات خطط عامة ومجرّدة لحل المشاكل.

فإن أردنا استخدام الخوارزمية لحل مشكلة ما، فسيكون علينا ترجمتها أو التعبير عنها بإحدى لغات البرمجة كي يفهمها الحاسوب ويعيد لنا النتائج المطلوبة، هذه العملية تُسمّى تحقيق الخوارزمية أو تنفيذ الخوارزمية implementation وينتج عن تحويل الخوارزمية إلى إحدى لغات البرمجة شيفرة برمجية قابلة للتنفيذ execution على الحاسوب.

لنضرب مثالًا على ذلك سنحول الخوارزمية التي ذكرناها آنفًا والتي تحاول إيجاد أكبر عدد من بين ثلاثة أعداد إلى برنامج مكتوب بلغة بايثون حتى يتسنّى لنا تنفيذها على الحاسوب.

تنفيذ خوارزمية إيجاد أكبر عدد من بين ثلاثة أعداد في لغة بايثون

برنامج بايثون لإيجاد أكبر عدد من بين ثلاثة أعداد

a = int(input('a= '))
b = int(input('b= '))
c = int(input('c= '))
max = a
if b > max :
    max = b
if c > max :
    max = c
print(max, "هو العدد الأكبر")

يمكنك الآن تنفيذ هذه الشيفرة على أيّ حاسوب وستعمل كما هو متوقع. كما يمكنك بالطبع تحقيق الخوارزمية بأيّ لغة برمجة أخرى تريدها مثل C أو C++‎ أو جافا أو جافا سكريبت أو R …إلخ.

تمرين ما رأيك أن تجرب تحويل الخوارزمية السابقة إلى برنامج حاسوبي يطلب من المستخدم إدخال مجموعة أعداد تفصل بينها فراغات مثل 4 9 8 7 10 ليحللها البرنامج بتلك الخوارزمية ويعطي العدد الأكبر من بينها (مساعدة: ستحاول استعمال حلقات التكرار loops)

مجالات استخدام الخوارزميات

كانت الخوارزميات تُستخدم طوال آلاف السنوات من قبل علماء الرياضيات لحل المعادلات والمسائل الرياضية وما تزال إلى يومنا هذا. فالخوارزميات جزء لا يتجزأ من الرياضيات ابتداءً من حل المعادلات الجبرية، وحتى كتابة البراهين المنطقية.

وتستخدم الخوارزميات اليوم على نطاق واسع في مجال البرمجة وعلوم الحاسب، فالحاسوب ليس سوى آلة تنفذ الأوامر بكفاءة وسرعة على عكس البشر، الذين يفهمون المطلوب ويحللونه ويفكرون بأدمغتهم لوضع الخوارزميات ثم ينفذونها بواسطة الحاسوب. لذلك، تحتاج إلى تبسيط ووضع خوارزمية للحاسوب لينفذها لك بحذافيرها وبأفضل أداء ممكن.

وكل البرامج والتطبيقات وأنظمة التشغيل تعتمد على الخوارزميات وتستخدمها من أجل معالجة البيانات وإجراء الحسابات وحلّ مشكلات العمل كما تستخدم الخوارزميات في عدة مجالات أخرى مثل الفيزياء وتحليل اللغات والاقتصاد وغيرها من مناحي الحياة وهي تطبق اليوم في كل شيء نستخدمه من حولنا ومن أبرز الأمثلة على مجالات استخدام الخوارزميات في حياتنا اليومية نذكر:

خوارزميات التواصل الاجتماعي التي تتحكم فيما تراه على مواقع التواصل الاجتماعي خاصتك
خوارزميات محركات البحث التي تحسن عمليات البحث وتتنبأ بما سيكتبه المستخدمون.
خوارزميات كشف الجرائم باستخدام تقنيات التعرف على الوجه ورسم الخرائط التنبؤية لتوقع الجرائم واتخاذ الإجراءات لمنعها.
خوارزميات التشفير التي تقوم بتحويل نص مفهوم إلى نص غير مفهوم وتُستخدم لحماية البيانات المهمة بحيث لا يفهمها إلّا الأشخاص الذين وجهت إليهم.
خوارزميات التنبؤ بحالة الطقس ودرجة الحرارة بمساعدة البيانات السابقة وهي تفيد في عدة مجالات أهمها الزراعة والطيران والاتصالات والحروب.
خوارزميات تحديد مواعيد وصول الحافلات وجدولتها بأفضل طريقة.
خوارزميات تحديد مواقف السيارات المتاحة لمساعدة السائقين على العثور على وجهتم بسرعة وسهولة.
خوارزميات توجيه المركبات إلى أفضل طريق.
خوارزميات تعديل مسارات الصواريخ.

وغيرها الكثير من مجالات الحياة المختلفة في الاقتصاد والعلوم والإعلام وما شابه التي تلعب فيها الخوارزميات دورًا فعالًا وحيويًا، على سبيل المثال عرضت نيتفليكس جائزة قدرها مليون دولار لمن يطور خوارزميتها المستخدمة في اقتراح الأفلام والمسلسلات على الزوار ويجعلها أفضل بنسبة 10%.

مواصفات الخوارزمية الجيدة

قد تتساءل وهل هناك خوارزمية جيدة وأخرى ليست كذلك؟ وما الذي يجعل الخوارزمية جيدة؟ والجواب هو نعم فكما أنّ هناك وصفات طبخة سيئة ولا تنجح، فكذلك هناك خوارزميات سيئة وغير عملية ولا تصلح للتطبيق، فليست كل سلسلة متتابعة من الخطوات والتعليمات خوارزمية، بل لابد أن تتوفر فيها شروط خاصة تجعلها عملية وقابلة للتطبيق مثل:

الوضوح: ينبغي أن تكون كل خطوة من خطوات الخوارزمية واضحة ومفهومة ولا لبس فيها.
المحدودية: يجب أن تكون الخوارزمية محدودة، أي أن تكون خطواتها منتهية، وتُنفّذ في مدة زمنية منتهية. فإن كان عدد الخطوات غير منته، أو كان بإمكان إحدى الخطوات أن تستغرق مدة لا منتهية، فإنّها ليست خوارزمية.
البساطة والواقعية: ينبغي أن تكون الخوارزمية قابلة للتطبيق بالموارد والتقنيات المتاحة، ولا ينبغي أن تعتمد على تقنية مستقبلية أو غامضة.
قابلية التطبيق: يعني الاستقلالية عن لغات البرمجة أي لا ينبغي أن تكون الخوارزمية مرتبطة بلغة برمجة محددة، ويجب أن تكون مجردة وعامّة بحيث تركز على العمل الأساسي للبرنامج بدلًا من التركيز على خصائص لغة برمجة معينة وبعدها يمكن تطبيقها عبر أي لغة برمجة.
صحة النتائج: يجب أن تقوم الخوارزمية بتنفيذ المهمة المطلوبة منها دون أخطاء في التنفيذ أو عدم دقة في النتائج.
الكفاءة والفعالية: ينبغي أن تستخدم الخوارزمية أفضل الطرق لحل المشكلة بأسرع وقت تنفيذ أو ما يعرف بالتعقيد الزماني للخوارزمية وأقل مساحة ذاكرة أو ما يعرف بالتعقيد المكاني للخوارزمية.

هل أحتاج إلى معرفة الرياضيات لتعلم الخوارزميات؟

الجواب هو نعم ولا، وكي أوضح إجابتي أكثر ، فالخوارزميات تُستخدم أساسًا لحل مشاكل حسابية، مثل متوسط مجموعة من القيم، أو أقصر مسار بين نقطتين في شعبة، أو أسهل طريقة لرسم شكل هندسي، أو ترتيب عناصر مصفوفة. كل هذه المشاكل تنطوي على قدر من الرياضيات الأساسية، لذلك فالجواب هو نعم.

لكن إن كنت تقصد بمعرفة الرياضيات أنّه ينبغي أن تكون لك شهادة جامعية في الرياضيات، أو تكون لك معرفة عميقة أو حتى متوسطة بها، فالجواب سيكون لا لأنّ الخوارزميات لا تتطلب معرفة عميقة بمفاهيم الرياضيات.

تذكر أنّ الخوارزميات هي طرق عامة لحل المشاكل والمسائل الحسابية، لذلك فمقدار الرياضيات التي تحتاجها يتعلق بنوع المشكلة التي تريد حلها، إن كنت تريد حل مشكلة معقدة، مثل التنبؤ بالمناخ، فعلى الأرجح أنّ الخوارزمية ستكون معقدة وتحتاج إلى معرفة متقدمة بالرياضيات لكن لا تدع هذا يخيفك ويصدّك عن تعلم الخوارزميات، إذ أنّ معظم المسائل التي ستُواجهها هي مشاكل لا تحتاج إلا إلى معرفة بسيطة بأساسيات الرياضيات، مثل العمليات الحسابية البسيطة.

خلاصة القول هو أنك لا تحتاج إلى تعلم الرياضيات لكي تتعلم الخوارزميات، فما دمت تفهم كيف تجري العمليات الحسابية البسيطة، مثل الجمع والضرب، وبعض المفاهيم البسيطة، مثل المجموعات والدوال وطرق حل المعادلات فيمكنك أن تتعلم الخوارزميات بسهولة.

لكن النقطة الأهم هي الارتباط بين التفكير المنطقي أو طرق حل المشكلات وبين الخوارزميات والبرمجة، فالتفكير المنطقي هو بلا شك مهارة ضرورية للبشر عمومًا وللمبرمجين على وجه الخصوص ومن الضروري تعليمه للأطفال من سن مبكرة لمنحهم هذه المهارة المهمة والضرورية جدًا لنجاحهم في مستقبلهم المهني.

تحليل الخوارزميات

الخوارزمية هي في الأصل خطة لحل مشكلة حسابية فإن لم تكن تملك خطة مُسبقة لحل مشكلة معقدة، فستفشل محاولاتك على الأرجح لحل تلك المشكلة وحتى لو كانت المشكلة بسيطة، فقد يكون هناك العديد من الحلول، وبعض هذه الحلول أسرع وأكفأ من بعض.

من هنا تأتي أهمية تحليل الخوارزميات الذي يهتم بدراسة كفاءة الخوارزميات من ناحية الوقت والذاكرة التي يحتاجها تنفيذ الخوارزمية واختيار الحل الأبسط والأسرع والأقل استهلاكًا للموارد، أو بلغة الحوسبة، تريد أن تخفض تعقيد الخوارزمية Algorithms Complexity إلى أقصى حد ممكن.

يشمل تعقيد الخوارزمية كل الموارد الضرورية لحل المشكلة، إن كانت الخوارزمية خوارزميةَ طبخ، فإنّ تعقيدها سيكون الوقت والطاقة اللازمة لإعداد الوجبة. أما إن كانت الخوارزمية تسعى لحل مشكلة في الرياضيات، سيكون تعقيدها هو الوقت اللازم لإجراء خطوات الخوارزمية.

أما إن كانت الخوارزمية حاسوبية، فإنّ تعقيدها سيكون الوقت ومساحة الذاكرة الضروريان لتنفيذ خطوات الخوارزمية. لهذا السبب ابتكر العلماء فرعًا كاملًا في علم الخوارزميات مُخصّصًا لتقدير تعقيد الخوارزميات يُسمّى نظرية التعقيد، والذي يصنّف الخوارزميات إلى أصناف بحسب تعقيدها الزماني Time Complexity الذي يصف مقدار الوقت الذي يستغرقه تنفيذ الخوارزمية. وتعقيدها المكاني أو ما يسمى بتعقيد المساحة Space Complexity الذي يمثل عدد خلايا الذاكرة اللازمة لتنفيذ عمليات الخوارزمية مع استثناء المساحة المخصصة لدخل الخوارزمية.

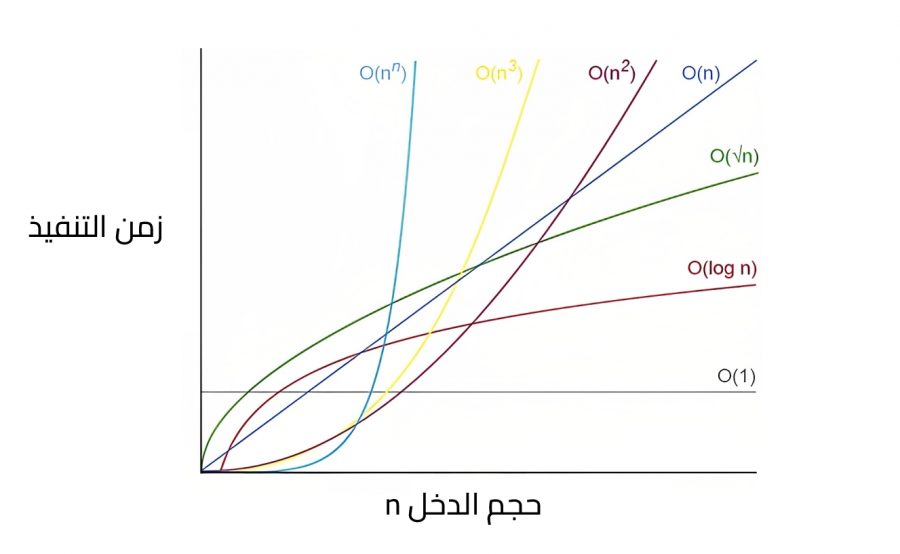
يتم التعبير عن تعقيد الخوارزمية بتدوين خاص يسمى Big O notation وهو طريقة لوصف تعقيد الخوارزمية الزمني باستخدام مصطلحات جبرية وأدنى هذه الأصناف هو الصنف O(1)‎، والذي يعني أنّ الخوارزمية تستغرق وقتا ثابتًا لحل المشكلة مهما كان حجم الدخل كما في خوارزمية معرفة كون العدد فردي أم زوجي مثلًا أو خوازرمية طباعة أول رقم من بين قائمة من الأرقام، أما الصنف O(n)‎ فَيعني أنّ مدة تنفيذ الخوارزمية متناسبة مع حجم الدخل n كما في خوارزمية حساب مضروب العدد وخوازمية إيجاد أكبر عدد من بين مجموعة من الأعداد.

وإليك قائمة مختصرة بأشهر أنواع تعقيد الخوارزميات وفق تدوين Big O ودلالة كل منها:

O(1)‎ تعقيد زمني ثابت: أي تستغرق الخوارزمية نفس الزمن مهما كان حجم الدخل.
O(n)‎ تعقيد زمني خطي: أي يتناسب زمن تنفيذ الخوارزمية بشكل خطي مع حجم الدخل، بمعنى آخر إذا كان حجم الدخل n فإن عدد الخطوات المطلوب لحلها سيكون n على الأكثر.
O(sqrt(n)) تعقيد جذر تربيعي: أي إذا كان حجم دخل الخوازرمية هو n سوف يتناسب زمن تنفيذ الخوارزمية مع الجذر التربيعي لقيمة الدخل.
O(n^c)‎ تعقيد كثير الحدود: يتناسب زمن تنفيذ الخوارزمية مع حجم الدخل مرفوع للأس c وله أنواع فقد يكون تعقيد زمني تربيعي O (n^²)‎ أي يتناسب زمن تنفيذ الخوارزمية مع مكعب حجم الدخل أو تعقيد زمني تكعيبي O(n^3)‎ أي يتناسب زمن تنفيذ الخوارزمية مع مكعب حجم الدخل.
O(log n)‎ تعقيد لوغاريتمي: تناسب زمن تنفيذ الخوارزمية مع لوغاريتم حجم الدخل.
O(n log n)‌‎ تعقيد لوغاريتمي خطي: وهو أبطأ قليلاً من الخطي
O(2^n)‎ تعقيد أسي: وفيه تتضاعف خطوات الخوارزمية بشكل أسي مع زيادة حجم الدخل.
O(n!)‎ تعقيد عاملي: أي يتناسب زمن الخوارزمية مع قيمة عاملي الدخل أي ضرب جميع الأعداد الصحيحة الموجبة الأصغر من قيمة الدخل.

يمكنك أن تجد حلًا للمشاكل بدون الخوارزميات، لكن من النادر أن يكون ذلك الحل الذي وجدته هو الحل الأفضل والأكفأ، وهذه فائدة تحليل الخوارزميات فهو يمكّنك من العثور على الحل الأمثل والأنسب والأقل استهلاكًا للموارد.

للمزيد من المعلومات أنصح بمطالعة مقال مدخل إلى تحليل الخوارزميات ومقال الدليل الشامل عن تعقيد الخوارزميات

أنواع الخوارزميات البرمجية

الخوارزميات هي خطط عامة لحل المشاكل وتتنوع أساليب وأنواع الخوارزميات بحسب الأسلوب الذي تتبعه الخوارزمية لحل المشكلة أو بحسب نوع المشكلة التي تحلها، وبناء على ذلك يمكن أن نجد أنواعًا مختلفة من الخوارزميات ومن أبرزها:

خوارزميات القوة الغاشمة Brute force algorithms : تحاول الخوارزميات من هذا النوع حل المشكلة بطريقة مباشرة وتمر بجميع الخيارات الممكنة حتى تتمكن من العثور على حل لهذه المشكلة.
الخوارزميات الجشعة Greedy algorithms: تحاول الخوارزميات الجشعة حل المشكلة خطوة فخطوة، بحيث تقترب رويدًا رويدًا من الحل العام للمشكلة.
خوارزميات البرمجة الديناميكية Dynamic Programming: تقسّم خوارزميات البرمجة الديناميكية المشكلة إلى مشاكل فرعية أبسط، ثمّ تحل تلك المشاكل الفرعية لاستنتاج الحل النهائي
خوارزميات فرق تسد Divide and conquer algorithms: تقسِّم خوارزميات فرِّق تسد المسألة إلى مسائل فرعية تشبه المسألة الأصلية، ثمّ تحلها وتدمج الحلول لتقديم حلٍّ المسألة الأصلية.
خوارزميات التعقب الخلفي Backtracking algorithms: تحاول خوارزميات التعقب الخلفي حل المشكلة تعاوديًا عبر بناء الحل تصاعديًا خطوة فخطوة، مع حذف الحلول التي لا تستجيب للقيود التي تفرضها المسألة المُراد حلها في أيّ وقت أثناء تنفيذ الخوارزمية.
خوارزميات الترتيب Sort algorithms: هي خوارزميات ترتب مجموعة من العناصر القائمة في ترتيب معين رقمي أو هجائي. والفرز هو أحد الخطوات الهامة في الخوارزميات الأكثر تعقيدًا، توجد عدة خوارزميات تمكننا من تحقيق عملية الفرز ولكل منها ميزاتها ومحدوديتها.
خوارزميات البحث Search algorithms: هي خوارزميات تقوم بتحديد موقع بيانات محددة بين مجموعة من البيانات أي أنها تبحث عن البيانات المخزنة ضمن بعض الهياكل أو بنى البيانات وتقوم باستردادها.
خوارزميات التعلم الآلي: هي خوارزميات تحاول التعلم بناءً على مجموعة من حالات اتخاذ القرار السابقة كي تتمكن من اتخاذ قرارات معقدة بناءً عليها.
خوارزميات التشفير: هي الخوارزميات التي تقوم بتحويل نص مقروء إلى نص غير مقروء يُعرف باسم النص المشفر بحيث يمكن للأطراف المصرح لهم فقط بفهم المعلومات الموجودة في هذا النص وهي خوارزميات هامة جدًا في مجال أمن البيانات الحساسة والحفاظ على الخصوصية.

كانت تلك بعض أنواع وتصنيفات الخوارزميات الأكثر شيوعًا وهناك بالطبع العديد من الخوارزميات الأخرى للعديد من الحالات المختلفة.

هناك أيضًا طرق أخرى يمكن تطبيقها بسهولة في التطبيقات مثل خوارزمية Dijkstra و Cycle Detection و Kruskal Minimum Spanning Trees فهي من الخوارزميات الأساسية للمبتدئين للتعلم منها.

أهمية الخوارزميات في البرمجة

هناك من قد يقول أنّ تعلم الخوارزميات تَرفٌ، وهو غير ضروري لكتابة البرامج والتطبيقات، وأنّه يمكن للمبرمج أن يكتب برامجه مباشرة دون الحاجة إلى مفاهيم الخوارزميات.

صحيح أنّه ليس عليك أن تكون خبيرًا في الخوارزميات لتَكون مبرمجًا، لكن لا يمكنك أن تكون مبرمجًا بارعًا ومحترفًا دون أن تتعلم فن تصميم الخوارزميات.

يوفر تعلم الخوارزميات للمبرمج العديد من الفوائد أبرزها:

القدرة على حل المشكلات بشكل أفضل
الاستخدام الفعال للموارد الحاسوبية
يوفر وقت البرمجة
يجعل منك مبرمجًا أفضل

لنناقش كل فائدة منها بمزيد من التفصيل ونتعرف كيف يسهم تعلم الخوارزميات في تعزيزها.

القدرة على حل المشكلات بشكل أفضل

سيحسن تعلمك لطرق حل الخوارزميات من قدرتك على حل المشكلات بصورة عامة والمشكلات البرمجية على وجه الخصوص، ويكسبك مرونة ذهنية في التفكير في الحلول ويساعدك لاحقًا في كتابة البرامج الحاسوبية المتنوعة أيًا كانت اللغة البرمجية المستخدمة خصوصًا بأنّ الخوارزميات مستقلة عن لغات البرمجة، لذا يمكنك استخدامها مهما كانت لغة البرمجة التي تعمل عليها.

الاستخدام الفعال للموارد

يضمن لك اختيار الخوارزمية الصحيحة الاستخدام المناسب للموارد مثل الذاكرة والتخزين والشبكة وغيرها. فلا يكفي أن تكون الفكرة التي بنيت عليها البرنامج أو التطبيق مفيدة ومبتكرة، ينبغي أن تكون عملية بحيث ينفّذها الحاسوب أو الجوال في وقت معقول وموارد محدودة، فما فائدة تطبيق رسم يحتاج دقيقة كاملة ليرسم مربعًا، وما فائدة برنامج يحتاج إلى 10 جيجابايت من الذاكرة ليعمل!

توفير وقت البرمجة

يوفر عليك تعلم الخوارزميات الكثير من الوقت، إذ أنّ معظم المشاكل والمسائل التي قد تعترضك أثناء كتابة البرامج لها حلول جاهزة على هيئة خوارزميات مُحسّنة وسريعة، ما يغنيك عن إعادة اختراع العجلة في كل مرة تعترضك مشكلة ما، لأنّ هناك من حلّها قبلك على الأرجح وأعدّها على هيئة خوارزمية وكل ما عليك فعله هو تحويلها إلى لغة البرمجة التي تستعملها ثم تنفّذها وقد لا تضطر حتى إلى تنفيذها فمعظم الخوارزميات الشهيرة والفعالة مثل خوارزميات البحث والفرز تدمج في لغات البرمجة بشكل مكتبات جاهزة يمكنك استخدامها في شيفراتك البرمجية.

الخوارزميات تجعل منك مبرمجًا أفضل

تعلم الخوارزميات سيجعلك مبرمجًا أفضل وأكثر احترافية، فسَواء كنت متخصصًا في تطبيقات الجوال أو تطبيقات سطح المكتب، أو في بناء المواقع أو تصميم الألعاب أو غيرها من مجالات البرمجة، فإنّ تعلم الخوارزميات سيوسع أفق تفكيرك البرمجي ويساعدك على تطوير برامج أجود وأسرع وأكثر موثوقية.

أهم مصادر تعلم الخوارزميات

هناك للأسف ضعف في المحتوى العربي التقني، هذا الضعف يظهر أكثر ما يظهر في مجالات الخوارزميات. ولسدّ هذا القصور في المحتوى العربي فقد وفرت أكاديمية حسوب العديد من مصادر التعلم القيمة باللغة العربية.

فنظرًا للأهمية الكبيرة للخوارزميات في كافة مجالات البرمجة، وفي غيرها من المجالات مثل الرياضيات والتنمية وغيرها، فقد وفرت لك أكاديمية حسوب دورة علوم الحاسب والتي تتضمن مسارات متعددة يحتاجها أي مبتدئ في تعلم البرمجة من أهمها مسار الخوارزميات وبنى المعطيات الذي يعلمك خطوة بخطوة كيفية كتابة الخوارزميات وتحليلها ويعرفك على أهم الخوارزميات التي تفيدك في عملك البرمجي مثل خوارزميات البحث والترتيب والخوارزميات الرياضية وخوارزميات الرسوم البيانية وغيرها الكثير.

كما نشرت الأكاديمية سلسلة الخوارزميات للمحترفين التي تشرح الخوارزميات بالتفصيل وتغطّي كافة مفاهيمها الأساسية مثل مفهوم التعقيد لتقدير الموارد التي تستهلكها البرامج كالوقت والذاكرة. إضافة إلى مفاهيم البرمجة الديناميكية، وبعض أنماط الخوارزميات العامة.

تلك السلسلة غنية بالأمثلة التطبيقية، إذ تستعرض الكثير من الخوارزميات لحل بعض المشاكل التقليدية في علم الحاسب خصوصًا تلك المتعلقة بالأشجار وترتيب المصفوفات والبحث، علاوة على طائفة من الخوارزميات المتنوعة في مجالات الجبر والهندسة ونظرية الأعداد.

كما أن السلسلة تنفذ الخوارزميات التي تستعرضها من خلال العديد من لغات البرمجة، فمهما كانت لغة البرمجة خاصتك، سواء كانت بايثون أو جافا أو C++/C أو #C‏‏ أو جافا سكريبت، فستجد أمثلة بهذه اللغات وغيرها في هذا الكتاب.

وستجد كذلك توثيقًا شاملًا عن الخوارزميات في موسوعة حسوب يضم توثيقات لأهم الخوارزميات المُستخدمة في البرمجة.

وننصحك كذلك بأن تشترك في قناة أكاديمية حسوب على يوتيوب وستجد فيها الكثير من الدروس المفيدة والمواضيع الشيقة حول البرمجة والخوارزميات والتفكير المنطقي وغيرها الكثير.

وأخيرًا إذا كنت تتساءل هل يجب علي كمبتدئ أن أتعلم الخوارزميات أولًا أم أتعلم إحدى لغات البرمجة أولًا فنصيحتي لك أن تبدأ كخطوة أولى بالتعرف على أساسيات البرمجة وبعد التمكن منها يمكنك البدء بتعلم الخوارزميات وتطوير تفكيرك البرمجي والخوارزمي على التوازي في رحلة التعلم حتى تصل للاحتراف في كليهما.

إذا أتقنت تعلم الأساسيات يمكن أن تنتقل لتعلم الأمور المتقدمة وستجد في قسم البرمجة ضمن وتحديدًا في قسم "مقالات برمجة متقدمة" في أكاديمية حسوب مجموعة متنوعة من المقالات المتقدمة التي تزيد معرفتك وخبرتك في مجال الخوارزميات وفي حال واجهك أي سؤال يمكنك طرحه في قسم الأسئلة والأجوبة في الأكاديمية.

الخلاصة

تعرفنا في مقال اليوم ما هي الخوارزمية وأهمية الخوارزميات في علوم الحاسب وهندسة البرمجيات، وتعرفنا على خطوات حل الخوارزمية وطرق التعبير عن الخوارزميات بالشيفرة الوهمية والمخططات الانسيابية ثم تحويلها بعد ذلك إلى برامج حاسوبية من خلال الأمثلة العملية البسيطة التي تناسب المبتدئين.

كما تعرفنا في الختام على أبرز الفوائد التي تجنيها كمبرمج من تعلم الخوارزميات، وأهم المراجع العربية التي تشرح الخوارزميات من الصفر للاحتراف، فإذا كنت تسعى لتكون مبرمجًا محترفًا فتعلم الخوارزميات أحد الأمور المهمة التي ينبغي أن تضعها في الحسبان لتساعدك على تحقيق هذا الهدف.