يُعَدّ تحليل البقاء survival analysis أحد طرق وصف مدة بقاء شيء ما، حيث يستخدَم لدراسة عمر الإنسان غالبًا، ولكنه ينطبق أيضًا على بقاء الأجهزة الميكانيكية والإلكترونية، أو قد يدل على الفترات الزمنية التي تسبق حدثًا ما.
فلربما قد رأيت سابقًا مصطلح "معدل البقاء على قيد الحياة لمدة 5 سنوات" إذا شُخِّص أحد معارفك بمرض خطير، وهو احتمال بقاء المريض على قيد الحياة لمدة 5 سنوات بعد التشخيص، علمًا أنّ هذا التقدير والإحصاءات ذات الصلة هي نتيجة لتحليل البقاء.
توجد الشيفرة الخاصة بهذا المقال في الملف survival.py، في مستودع الشيفرات ThinkStats2 على GitHub.
منحنيات البقاء
يُعَدّ منحني البقاء survival curve الذي يرمز له بـ S(t) المفهوم الأساسي في تحليل البقاء، كما يُعَدّ دالةً تحوِّل المدة t إلى احتمال البقاء أطول من t، ويُعَدّ حساب منحني البقاء سهلًا إذا علمت توزيع المدة أو مدة الحياة، حيث يمكن حساب المنحني عندها عن طريق حساب مكمل دالة التوزيع التراكمي كما يلي:
S(t)=1-CDF(t)
حيث يكون CDF(t) هو احتمال أن تكون مدة البقاء على قيد الحياة أقل أو تساوي t، ونعلم مثلًا في مجموعة بيانات المسح الوطني لنمو الأسرة مدة حالات الحمل التامة التي بلغ عددها 1189 حالة، حيث يمكننا قراءة هذه البيانات وحساب دالة التوزيع التراكمي كما يلي:
preg = nsfg.ReadFemPreg() complete = preg.query('outcome in [1, 3, 4]').prglngth cdf = thinkstats2.Cdf(complete, label='cdf')
يدل رمز الخرج 1 على ولادة حية، ويدل رمز الخرج 3 على ولادة جنين ميت، في حين يدل رمز الخرج 4 على حالة إجهاض لا إرادية -أي غير متعمدة من قبل الأم-، كما استبعدنا حالات الإجهاض المتعمدة وحالات الحمل خارج الرحم وحالات الحمل التي كانت مستمرة أثناء مقابلة المستجيبة وذلك لأغراض هذا التحليل، كما يأخذ تابع إطار البيانات query تعبيرًا بوليانيًا ويقيّمه لكل سطر، ومن ثم يحدِّد الأسطر التي ينتج عنها قيمة True.
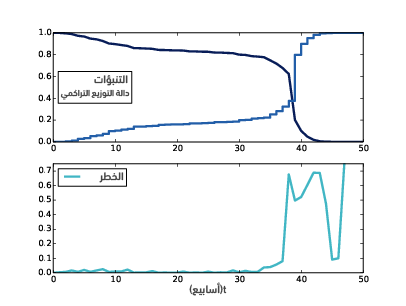
يوضِّح الشكل السابق دالة التوزيع التراكمي ومنحني البقاء لمدة الحمل في الأعلى؛ أما في الأسفل فيوضِّح منحني الخطر hazard curve، حيث عرّفنا كائنًا يغلِّف صنف Cdf وينفذ الواجهة:
class SurvivalFunction(object): def __init__(self, cdf, label=''): self.cdf = cdf self.label = label or cdf.label @property def ts(self): return self.cdf.xs @property def ss(self): return 1 - self.cdf.ps
يزودنا الصنف SurvivalFunction بخاصيتين اثنتين هما ts وهي تسلسل مدد الحياة وss التي هي منحني البقاء، إذ تُعَدّ الخاصية في لغة بايثون تابعًا يمكن استدعاؤه كما لو أنه متغير، كما يمكننا استنتاج الصنف SurvivalFunction عن طريق تمرير دالة التوزيع التراكمي لمدة الحياة كما يلي:
sf = SurvivalFunction(cdf)
كما يزودنا الصنف SurvivalFunction بالدالتين __getitem__ وProb اللتين تقيّمان منحني البقاء.
# class SurvivalFunction
def __getitem__(self, t):
return self.Prob(t)
def Prob(self, t):
return 1 - self.cdf.Prob(t)
يُعَدّ sf[13] على سبيل المثال نسبة حالات الحمل التي تجاوزت الثلث الأول من الحمل:
>>> sf[13] 0.86022 >>> cdf[13] 0.13978
نرى أنّ 86% من حالات الحمل تتجاوز الثلث الأول من الحمل؛ أما النسبة المتبقية 14% فهي لا تتجاوز هذه المدة، كما يزودنا الصنف SurvivalFunction بالدالة Render التي ترسم sf باستخدام الدوال الموجودة في المكتبة thinkplot:
thinkplot.Plot(sf)
يُظهر الشكل السابق الموجود في الأعلى النتيجة، حيث يكون المنحني مسطحًا تقريبًا بين الأسبوعين 13 و26، مما يدل على أن عدد قليل من حالات الحمل تنتهي في الثلث الثاني من الحمل، ويكون المنحني أكثر حدةً عند حوالي 39 أسبوعًا وهي أكثر فترات الحمل شيوعًا.
دالة الخطر
يمكننا اشتقاق دالة الخطر hazard function من منحني البقاء، حيث تُعَدّ دالة الخطر لمدة الحمل دالةً تحوِّل الزمن t إلى نسبة حالات الحمل التي تستمر حتى المدة t ومن ثم تنتهي عند t، ونقول بصورة أدق:
| λ(t) = |
|
يُعَدّ البسط نسبة مدة الحياة التي تنتهي عند t وهي تمثِّل أيضًا دالة الكثافة الاحتمالية عند t أي PMF(t)، كما يزودنا الصنف SurvivalFunction بالدالة MakeHazard التي تحسب دالة الخطر:
# class SurvivalFunction def MakeHazard(self, label=''): ss = self.ss lams = {} for i, t in enumerate(self.ts[:-1]): hazard = (ss[i] - ss[i+1]) / ss[i] lams[t] = hazard return HazardFunction(lams, label=label)
حيث يُعَدّ الكائن HazardFuntion مغلِفًا لسلسلة بانداز:
class HazardFunction(object): def __init__(self, d, label=''): self.series = pandas.Series(d) self.label = label
قد يكون d قاموسًا أو أيّ نوع آخر قادر على استنساخ سلسلة تتضمن سلسلةً أخرى، في حين يكون label سلسلةً نصيةً مستخدَمةً لتحديد HazardFunction عند رسمه، كما يزودنا HazardFunction بالدالة __getitem__، وبالتالي يمكننا تقييمه كما يلي:
>>> hf = sf.MakeHazard() >>> hf[39] 0.49689
لذا تنتهي حوالي 50% من بين جميع حالات الحمل التي تستمر حتى الأسبوع 39 في الأسبوع 39.
يُظهر الشكل السابق الموجود في الأسفل دالة الخطر hazard function لمدة الحمل، كما نرى أنّ دالة الخطر بعد الأسبوع 42 تصبح غير منتظمة لأنها مبنية على عدد صغير من الحالات، لكن بخلاف ذلك يكون شكل المنحني كما هو متوقع، بحيث يبلغ ذروته عند الأسبوع 30 تقريبًا ويصبح في الثلث الأول أعلى من الثلث الثاني، كما تُعَدّ دالة الخطر مفيدةً لوحدها، لكنها أيضًا أداةً مهمةً لتقدير منحنيات البقاء كما سنرى في القسم التالي.
استنتاج منحنيات البقاء
إذا علمت دالة التوزيع التراكمي CDF، فمن السهل حساب دالة البقاء ودالة الخطر، لكن من الصعب في كثير من المواقف الواقعية قياس توزيع مدة الحياة مباشرةً ويجب علينا استنتاجها، فلنفترض مثلًا أنك تراقب مجموعةً من المرضى لترى المدة التي بقوا فيها على قيد الحياة بعد التشخيص، وبما أنّ التشخيص لا يكون في اليوم نفسه لكل المرضى، فسيعيش بعض المرضى فترةً أطول من غيرهم في أي فترة من الزمن، وبالطبع نعلم مدة بقاء المرضى الذين تُوفوا، إلا أننا لا نعلم مدة بقاء المرضى الذين لا زالوا على قيد الحياة وإنما لدينا حدًا أدنى لمدة البقاء.
يمكننا حساب منحني البقاء إذا انتظرنا وفاة جميع المرضى، لكننا لن نستطيع الانتظار مدةً طويلةً إذا كنا بصدد تقييم فعالية دواء جديد، لذا نحتاج إلى تقدير منحنيات البقاء باستخدام معلومات غير مكتملة، وبالانتقال إلى مثال مُبهج، استخدمنا بيانات المسح الوطني لنمو الأسرة لحساب مدة بقاء المستجيبين بدون أول حالة زواج، أي المدة التي تسبق أول حالة زواج، بالطبع فإن المستجيبين هم من النساء كون الأسئلة تخص حالات الحمل، كما يتراوح مدى عمر المستجيبات بين 14 و 44 سنة، وبالتالي تزودنا مجموعة البيانات بلمحة عن النساء في مراحل مختلفة من حياتهن.
تتضمن مجموعة البيانات بالنسبة للنساء المتزوجات تاريخ أول زواج بالإضافة إلى عمر المرأة عندها؛ أما بالنسبة لغير المتزوجات فنحن نعلم عمر المستجيبة أثناء المسح لكننا لا نعلم متى ستتزوج أو أنها ستتزوج حتى، ونظرًا لأننا نعلم عمر أول حالة زواج لبعض النساء، فسيبدو لنا مغريًا استبعاد بقية النساء وحساب دالة التوزيع التراكمي للبيانات المعلومة، ولكنها فكرة سيئة لأن النتيجة ستكون في هذه الحالة مضللةً جدًا لسببين اثنين هما:
- سينتج عن هذا مبالغة في تمثيل النساء الأكبر عمرًا، لأنه من المرجح أن تكون هذه الفئة متزوجة أثناء إجراء المسح.
- سينتج مبالغة في تمثيل النساء المتزوجات.
سيؤدي هذا التحليل في الواقع إلى استنتاج مفاده أنّ جميع النساء يتزوجن، وهذا الأمر غير صحيح وضوحًا.
تقدير كابلان ماير
ليس من المفضل في هذا المثال تضمين حالات النساء غير المتزوجات وإنما هو أمر ضروري، وهو ما يقودنا إلى إحدى الخوارزميات الأساسية في تحليل البقاء والتي هي تقدير كابلان ماير Kaplan-Meier estimation.
تستند الفكرة العامة على استخدام البيانات لتقدير دالة الخطر ومن ثم تحويل دالة الخطر إلى منحني البقاء، وإذا أردنا تقدير تابع الخطر، فيمكننا من أجل كل عمر الأخذ في الحسبان: (1) عدد النساء اللواتي تزوجن في هذا العمر و(2) عدد النساء "المعرضات لخطر" الزواج، وهذا يتضمن النساء اللواتي لم يتزوجن من قبل، وإليك الشيفرة الموافقة كما يلي:
def EstimateHazardFunction(complete, ongoing, label=''): hist_complete = Counter(complete) hist_ongoing = Counter(ongoing) ts = list(hist_complete | hist_ongoing) ts.sort() at_risk = len(complete) + len(ongoing) lams = pandas.Series(index=ts) for t in ts: ended = hist_complete[t] censored = hist_ongoing[t] lams[t] = ended / at_risk at_risk -= ended + censored return HazardFunction(lams, label=label)
تُعَدّ complete أنها الحالات الكاملة التي رُصِدَت، وتكون في مثالنا هذا أعمار المستجيبات عندما تزوجن، في حين تُعَدّ ongoing أنها الحالات غير الكاملة وهي أعمار النساء غير المتزوجات في المسح.
نحسب بدايةً hist_complete، وهو دالة عدادة Counter تحوِّل العمر إلى عدد النساء المتزوجات في هذا العمر، كما نحسب hist_ongoing هو دالة عدادة Counter تحوِّل العمر إلى عدد النساء غير المتزوجات اللواتي قوبِلن في ذلك العمر؛ أما ts فهو اجتماع الأعمار التي تزوجت فيها المستجيبات والأعمار التي قوبلت فيها النساء غير المتزوجات مرتبًا ترتيبًا تصاعديًا، كما تتتبّع at_risk عدد المستجيبات المعرضات للخطر في كل عمر وهو العدد الكلي للمستجيبات، وتُخزن النتيجة في سلسلة Series بانداز Pandas والتي تحول كل عمر إلى دالة الخطر المقدَّرة في ذلك العمر.
نتعامل في كل مرور على الحلقة مع عمر واحد t ونحسب عدد الأحداث التي تنتهي عند t -أي عدد المستجيبات المتزوجات عند هذا العمر- وعدد الأحداث التي أوقِفت عند t -أي عدد النساء اللواتي قوبِلن عند t ولكن تواريخ زواجهن المستقبلية موقفة censored- ويشير مصطلح "أوقف" إلى أنّ البيانات غير متاحة بسبب عملية جمع البيانات، كما تُعَدّ دالة الخطر المُقدَّرة بأنها نسبة الحالات المعرَّضة للخطر والتي تنتهي عند t، ونطرح في نهاية الحلقة من at_risk عدد الحالات التي انتهت أو أوقفت عند t، ثم نمرِّر في النهاية lams إلى الباني HazardFunction ونُعيد النتيجة.
منحني الزواج
علينا تنظيف البيانات وتحويلها إذا أردنا اختبار هذه الدالة، علمًا أنّ المتغيرات التي نحتاجها من المسح الوطني لنمو الأسرة هي:
-
cmbirth: يوم ميلاد كل مستجيبة وهو معلوم في كل الحالات. -
cmintvw: تاريخ مقابلة كل مستجيبة وهو معلوم في كل الحالات. -
cmmarrhx: تاريخ أول حالة زواج للمستجيبة إذا كانت متزوجةً وكان التاريخ معلومًا. -
evrmarry: قيمة هذا المتغير 1 إذا كانت المستجيبة قد تزوجت قبل تاريخ المقابلة و0 بخلاف ذلك.
حيث أن المتغيرات الثلاثة الأولى مرمَّزة بنظام أشهر القرن وهو العدد الصحيح للأشهر منذ شهر 12 من عام 1899، أي يكون شهر القرن 1 هو شهر 1 من عام 1900، وسنقرأ في البداية ملف المستجيبات ونستبدل قيم cmmarrhx غير الصالحة كما يلي:
resp = chap01soln.ReadFemResp() resp.cmmarrhx.replace([9997, 9998, 9999], np.nan, inplace=True
ثم نحسب عمر كل مستجيبة عند الزواج وعند مقابلتها:
resp['agemarry'] = (resp.cmmarrhx - resp.cmbirth) / 12.0 resp['age'] = (resp.cmintvw - resp.cmbirth) / 12.0
ثم نستخرِج complete وهو عمر النساء المتزوجات عند زواجهن واللاتي لم تزلن متزوجات، وongoing وهو عمر النساء اللاتي لا يحققن ما سبق أثناء المقابلة:
complete = resp[resp.evrmarry==1].agemarry ongoing = resp[resp.evrmarry==0].age
سنحسب أخيرًا دالة الخطر:
hf = EstimateHazardFunction(complete, ongoing)
يُظهر الشكل 13.2 (الموجود في الجهة العليا) دالة الخطر المُقدَّرة، وهي منخفضة في فترة المراهقة ومرتفعة في العشرينات من العمر وتنخفض في الثلاثينات وتعود لترتفع في الأربعينات، لكن هذا ناتج عملية التقدير، حيث سينتج عن زواج عدد صغير من النساء خطرًا مقدَّرًا كبيرًا مع نقصان المستجيبات لمعرضات للخطر، لكن سيخفف منحني البقاء من هذا الضجيج.
تقدير منحني البقاء
يمكننا تقدير منحني البقاء عند حصولنا على دالة الخطر، حيث أنّ فرصة البقاء بعد الوقت t هو فرصة البقاء لكل الأوقات بدءًا من بداية الرصد حتى t، وهو ناتج الجداء التراكمي لدالة الخطر المكملة:
| [1−λ(0)] [1−λ(1)] … [1−λ(t)] |
يزودنا الصنف HazardFunction بالدالة MakeSurvival التي تحسب هذا الجداء:
# class HazardFunction: def MakeSurvival(self): ts = self.series.index ss = (1 - self.series).cumprod() cdf = thinkstats2.Cdf(ts, 1-ss) sf = SurvivalFunction(cdf) return sf
حيث أنّ ts هو تسلسل الأوقات التي قُدِّرت فيها دالة الخطر، وss هو ناتج الجداء التراكمي لدالة الخطر المكملة، وبالتالي فهو منحني البقاء، كما يتوجب علينا حساب مكمل ss ومن ثم إنشاء Cdf واستنساخ كائن SurvivalFunction وذلك بسبب الطريقة التي يُنفَّذ بها SurvivalFunction.
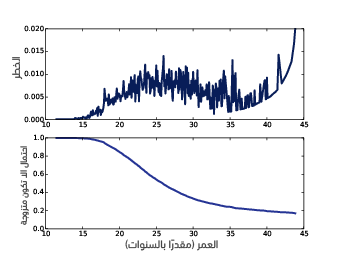
يوضَّح الشكل السابق الموجود في الأعلى دالة الخطر لعمر أول زواج؛ أما الذي في الأسفل فيوضَّح منحني البقاء، كما يُظهر الشكل السابق الموجود في الأسفل النتيجة، حيث يكون منحني البقاء أكثر حدةً بين العمرين 25 و35، وهو المدى الذي تتزوج فيه معظم النساء؛ أما بين العمرين 35 و45 فيكون المنحني مسطحًا تقريبًا، مما يشير إلى أنه من غير المرجح زواج النساء اللواتي لم يتزوجن قبل سن الخامس والثلاثين.
كان منحني ما مثل المنحني السابق أساس مقال شهير ظهر في مجلة عام 1986، فقد نُشر في مجلة نيوزويك Newsweek أن احتمال موت امرأة غير متزوجة عمرها 40 على يد قاتل أكبر من احتمال زواجها، وانتشرت هذه الإحصائيات انتشارًا واسعًا وأصبحت جزءًا من الثقافة الشعبية، لكنها كانت خاطئةً لأنها بُنيَت على تحليل خاطئ، واتضح أنهم على خطأ بسبب التغيرات الثقافية التي كانت جاريةً حينها واستمرت بعدها، لذا فقد نشرت مجلة نيوزويك Newsweek مقالًا آخرًا اعترفوا فيه بأنهم كانوا مخطئين، ونرى أنه من الأفضل قراءة المزيد عن هذا المقال والإحصائية المبنية عليه وردود الفعل لأنه سيذكِّرك بالالتزام الأخلاقي الذي يحتم عليك إجراء التحليل بعناية وتفسير النتائج بحيادية وعرضها على الجمهور بدقة وصدق.
فواصل الثقة
ينتج عن تحليل كابلان-ماير تقديرًا واحدًا لمنحني البقاء ولكنه مهم لحساب عدم اليقين الناتج عن التقدير، كما توجد ثلاثة مصادر محتملة للخطأ على أساس العادة وهي خطأ القياس measurement error وخطأ أخذ العينات sampling error وخطأ النمذجة modeling error، حيث يُعَدّ خطأ القياس في هذا المثال صغيرًا غالبًا، أي يعلم الأشخاص التاريخ الصحيح لولادتهم وإن كانوا قد تزوجوا بالإضافة إلى تاريخ الزواج، ويفترض أنهم قدَّموا هذه المعلومات بدقة، وإليك الشيفرة التي تحسب خطأ أخذ العينات عن طريق تطبيق إعادة أخذ العينات:
def ResampleSurvival(resp, iters=101): low, high = resp.agemarry.min(), resp.agemarry.max() ts = np.arange(low, high, 1/12.0) ss_seq = [] for i in range(iters): sample = thinkstats2.ResampleRowsWeighted(resp) hf, sf = EstimateSurvival(sample) ss_seq.append(sf.Probs(ts)) low, high = thinkstats2.PercentileRows(ss_seq, [5, 95]) thinkplot.FillBetween(ts, low, high)
تأخذ الدالة ResampleSurvival الوسيطَين resp وهو إطار بيانات المستجيبين وiters وهو عدد المرات التي يجب فيها إعادة أخذ العينات، ومن ثم تحسب ts وهو تسلسل الأعمار وهنا سنقيِّم منحني البقاء، كما تقوم الدالة ResampleSurvival بالخطوات التالية ضمن الحلقة:
-
تعيد أخذ عينات المستجيبين باستخدام
ResampleRowsWeighted، ورأينا هذا في قسم إعادة أخذ العينات مع الأوزان في مقال المربعات الصغرى الخطية في بايثون. -
تستدعي
EstimateSurvivalالتي تستخدِم العملية الموجودة في الأقسام السابقة بهدف تقدير منحني البقاء ومنحني الخطر. -
ثم تقيِّم منحني البقاء في كل عمر في
ts.
يُعَدّ ss_seq تسلسل منحنيات البقاء المقدَّرة، كما تأخذ الدالة PercentileRows هذا التسلسل وتحسب المئين الخامس والمئين الخامس والتسعين وتعيد فاصل الثقة 90% الخاص بمنحني البقاء.
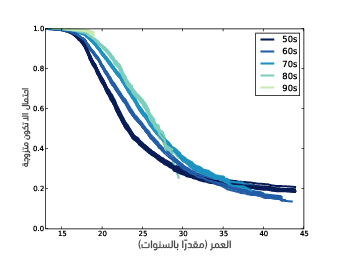
يوضِّح الشكل السابق منحني البقاء للعمر عند أول زواج الممثَّل بالخط الداكن وفاصل الثقة 90% المبني على إعادة أخذ العينات مع الأوزان والممثَّل بالخط الرمادي، كما يظهر الشكل السابق النتيجة ومنحني البقاء الذي قدَّرناه في القسم السابق، ويأخذ فاصل الثقة أوزان أخذ العينات بالحسبان على عكس المنحني المقدَّر الذي لا يضع الأوزان في حسبانه، علمًا أنَّ التناقض بينهما يشير إلى التأثير الكبير لأوزان أخذ العينات على التقدير وعلينا أخذ ذلك في الحسبان.
تأثيرات الفوج
يُعَدّ اعتماد الأجزاء المختلفة للمنحني المقدَّر على عدة مجموعات بأنه أحد تحديات تحليل البقاء، حيث أنّ جزء المنحني عند الوقت t مبني على المستجيبات اللاتي كان عمرهن t على الأقل أثناء المقابلة، لذا يحتوي الجزء الموجود في اليسار على بيانات جميع من شارك في المسح، في حين يحتوي الجزء الموجود في اليمين على المستجيبات الأكبر سنًا.
إذا لم تكن صفات المستجيبات ذات الصلة متغيرةً بمرور الوقت، فلا توجد مشكلة بالطبع، لكن يبدو في هذه الحالة أنّ أنماط الزواج متغيرة بالنسبة للنساء المولودات في أجيال مختلفة، كما يمكننا البحث في هذا التأثير عن طريق تصنيف المستجيبات إلى مجموعات بحسب عقد الميلاد، علمًا أنّ المجموعات المشابهة لهذه أي المعرفة بتاريخ ميلاد أو حدث مشابه تدعى الأفواج cohorts، في حين تدعى الفروق بين المجموعات تأثيرات الفوج cohort effects.
جمعنا بيانات الدورة السادسة من 2002 المستخدَمة في هذه السلسلة وبيانات الدورة السابعة من 2006-2010 المستخدَمة في قسم التكرار في مقال اختبار الفرضيات الإحصائية وبيانات الدورة الخامسة من 1995، حيث تحوي مجموعة البيانات كلها 30769 مستجيبةً، وذلك من أجل البحث في تأثيرات الفوج في بيانات الزواج في المسح الوطني لنمو الأسرة.
resp5 = ReadFemResp1995() resp6 = ReadFemResp2002() resp7 = ReadFemResp2010() resps = [resp5, resp6, resp7]
استخدمنا cmbirth من أجل كل إطار بيانات resp لحساب عقد ولادة كل مستجيبة:
month0 = pandas.to_datetime('1899-12-15') dates = [month0 + pandas.DateOffset(months=cm) for cm in resp.cmbirth] resp['decade'] = (pandas.DatetimeIndex(dates).year - 1900) // 10
حيث أن المتغير cmbirth مرمَّز ليدل على العدد الصحيح للأشهر التي مضت منذ شهر 12 من عام 1899، فتمثِّل month0 هذا التاريخ على أساس كائن ختم زمني Timestamp، كما نستنسخ DateOffset من أجل كل تاريخ ميلاد والذي يحتوي على أشهر القرن ونضيفه إلى month0 لتكون النتيجة تسلسلًا من الأختام الزمنية TimeStamps التي يجري تحوَّل إلى النوع DateTimeIndex، ونستخرج أخيرًا year الذي يمثِّل السنة ونحسب decades الذي يمثِّل العقد.
أعدنا أخذ العينات وصّنفنا المستجيبات حسب عقد الميلاد ورسمنا منحني البقاء وذلك لكي نحرص على أخذ أوزان أخذ العينات بالحسبان وإظهار التباين الناتج عن خطأ أخذ العينات أيضًا:
for i in range(iters): samples = [thinkstats2.ResampleRowsWeighted(resp) for resp in resps] sample = pandas.concat(samples, ignore_index=True) groups = sample.groupby('decade') EstimateSurvivalByDecade(groups, alpha=0.2)
تستخدِم بيانات الدورات الثلاثة للمسح الوطني لنمو الأسرة أوزانًا مختلفةً، لذا أعدنا أخذ عينات كل منها على حدة ثم استخدمنا concat لدمجها لتصبح إطار بيانات واحد، علمًا أنّ المعامِل ignore_index يشير إلى concat لكي لا يطابق المستجيبين حسب الفهرس وإنما ينشئ فهرسًا جديدًا من 0 إلى 30768، كما ترسم الدالة EstimateSurvivalByDecade منحنيات بقاء كل فوج.
def EstimateSurvivalByDecade(resp): for name, group in groups: hf, sf = EstimateSurvival(group) thinkplot.Plot(sf)
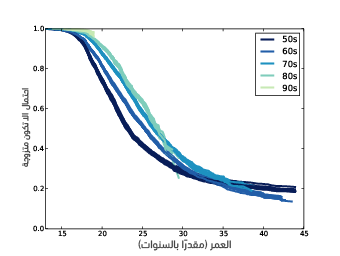
يوضِّح الشكل السابق منحنيات بقاء المستجيبات اللواتي ولدن ضمن عقود مختلفة، كما يظهر الشكل السابق النتائج ونرى عدة أنماط فيه وهي:
- النساء اللواتي ولدن في الخمسينيات هم أكثر من تزوج في عمر صغير، وكذلك فإن أفراد الفوج التالي تزوجن في عمر متأخر أكثر، والفوج التالي بعد الفوج السابق وهكذا، وبقوا على الأقل حتى عمر الثلاثين تقريبًا.
- تملك النساء اللواتي ولدن في ستينيات القرن الماضي نمطًا غريبًا، إذ تزوجت النساء هنا في عمر 25 بمعدل أبطأ من الفوج السابق، ولكن بعد عمر 25 أصبح معدل الزواج أسرع، لكن النساء في هذا الفوج تجاوزت فوج الخمسينيات عند عمر 32، واتضح أنَّ احتمال زواج النساء في عمر 44 هو المرجَّح، لكن النساء اللواتي ولدن في الستينيات بلغن عمر 25 بين عامَي 1985 و1995، ومن المغري اعتقاد أنّ المقال الذي ذكرناه منذ قليل قد تسبب في ازدياد حالات الزواج، لكنه تفسير رديء للغاية، ومع ذلك فإنه من المحتمل أن يكون المقال وردّ الفعل عليه مؤشرَين على حالة مزاجية أثرت على سلوك هذا الفوج.
- يملك فوج السبعينات نمطًا مشابهًا، حيث أن النساء هنا أقل احتمالًا لأن يتزوجن قبل عمر 25 إذا وازناه مع الأفواج السابقة، لكن هذا لهذا الفوج احتمالات مشابهة للأفواج السابقة فيما يخص الزواج عند عمر 35.
- احتمال أن زواج فوج الثمانينيات قبل 25 هو أقل من الفوج السابق، ولكن ما يحدث بعد ذلك هو غير واضح، وإذا أردنا بيانات أكثر، فعلينا الانتظار حتى الدورة التالية من المسح الوطني لنمو الأسرة.
يمكننا توليد بعض التنبؤات ريثما تصلنا البيانات.
الاستقراء الخارجي Extrapolation
ينتهي منحني البقاء لفوج السبعينات عند عمر 38 تقريبًا؛ أما فوج الثمانينات فينتهي منحني البقاء الخاص به عند سن 28، وبالطبع فإن بيانات فوج التسعينات نادرة جدًا، كما يمكننا استقراء هذه المنحنيات خارجيًا عن طريق استعارة بيانات من الفوج السابق، حيث يزودنا الصنف HazardFunction بالتابع Extend الذي ينسخ الذيل من HazardFunction أطول كما يلي:
# class HazardFunction def Extend(self, other): last = self.series.index[-1] more = other.series[other.series.index > last] self.series = pandas.concat([self.series, more])
يحتوي HazardFunction على سلسلة تحوِّل الوقت t إلى λ(t)، ويجد التابع Extend المتغير last وهو الفهرس الأخير في self.series،ثم يختار قيم من other التي تأتي بعد last ويضيفها إلى نهاية self.series، ويمكننا الآن توسيع HazardFunction الخاص بكل فوج وذلك بالاستعانة بقيم من الفوج السابق:
def PlotPredictionsByDecade(groups): hfs = [] for name, group in groups: hf, sf = EstimateSurvival(group) hfs.append(hf) thinkplot.PrePlot(len(hfs)) for i, hf in enumerate(hfs): if i > 0: hf.Extend(hfs[i-1]) sf = hf.MakeSurvival() thinkplot.Plot(sf)
حيث أن groups هو كائن GroupBy فيه معلومات المستجيبات مصنفة إلى مجموعات حسب عقد الولادة، كما تحسب الحلقة الأولى HazardFunction كل مجموعة، في حين توسِّع الحلقة الثانية كل HazardFunction بقيم من الفوج السابق له والذي قد يحتوي على قيم من المجموعة التي تسبقه أيضًا (أي قد يحتوي فوج الخمسينات على قيم من فوج الأربعينات وقد يحتوي فوج الأربعينات على قيم من فوج الثلاثينات وهكذا)، ثم تحوِّل كل HazardFunction إلى SurvivalFunction وترسمه.
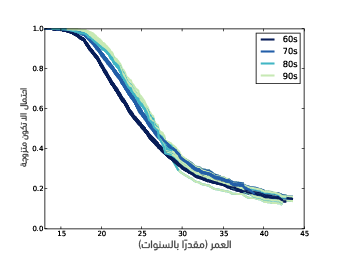
يوضِّح الشكل السابق منحنيات البقاء الخاصة بالمستجيبات اللواتي ولدن خلال عقود مختلفة، مع تنبؤات للأفواج اللاحقة، كما يُظهر الشكل السابق النتائج، وقد حذفنا فوج الخمسينات لجعل التنبؤات أكثر وضوحًا، وتقترح هذه النتائج أنه بحلول السن الأربعين ستتقارب الأفواج الأحدث مع فوج الستينيات وستمثل المستجيبات المتزوجات نسبةً تقل عن %20 من المجموع الكلي.
العمر المتبقي المتوقع
إذا كان لدينا منحني بقاء، فيمكننا حساب العمر المتبقي المتوقع على أساس دالة للعمر الحالي، أي إذا كان لدينا مثلًا منحني البقاء لطول الحمل من القسم الأول من هذا المقال، فيمكننا حساب الوقت المتوقع حتى حدوث المخاض والولادة، حيث تتمثل الخطوة الأولى في استخراج دالة الكثافة الاحتمالية PMF للأعمار، كما يزودنا الصنف SurvivalFunction بالتابع الذي يقوم بالمطلوب:
# class SurvivalFunction def MakePmf(self, filler=None): pmf = thinkstats2.Pmf() for val, prob in self.cdf.Items(): pmf.Set(val, prob) cutoff = self.cdf.ps[-1] if filler is not None: pmf[filler] = 1-cutoff return pmf
تذكر أنّ SurvivalFunction تحتوي على Cdf للعمر، وتنسخ الحلقة القيم والاحتمالات من Cdf إلى Pmf، كما تُعَدّ cutoff هي أعلى احتمال في Cdf، وهي 1 إذا كان Cdf كاملًا وأقل من 1 بخلاف ذلك، وإذا كان Cdf غير كامل، فسنُدخل القيمة المزوَّدة إلى filter لنكملها، لكن يُعَدّ Cdf لمدة الحمل كاملًا، لذا لا داع للقلق حول هذا الأمر؛ أما الخطوة التالية هنا فهي حساب العمر المتبقي المتوقع، حيث يعني المتوقع هنا المتوسط الحسابي، كما يزودنا SurvivalFunction بدالة تقوم بهذا أيضًا:
# class SurvivalFunction def RemainingLifetime(self, filler=None, func=thinkstats2.Pmf.Mean): pmf = self.MakePmf(filler=filler) d = {} for t in sorted(pmf.Values())[:-1]: pmf[t] = 0 pmf.Normalize() d[t] = func(pmf) - t return pandas.Series(d)
تأخذ RemainingLifetime الوسيط filterالذي يمرَّر إلى MakePmf وfunc وهو الدالة المستخدَمة لتلخيص توزيع العمر المتبقي؛ أما pmf فهي Pmf الأعمار المتبقية المستخرَجة من SurvivalFunction، وd هو قاموس يحتوي على النتائج وهو تحويل من العمر الحالي t إلى العمر المتبقي المتوقع.
تمر الحلقة مرورًا تكراريًا على القيم في Pmf، وهي تحسب التوزيع الشرطي للأعمار المتبقية لكل قيمة من t، باعتبار أنّ العمر المتبقي يتجاوز t، فإنها تنجز هذه المهمة عن طريق إزالة القيم من Pmf الواحدة تلو الأخرى ومن ثم إعادة توحيد renoramlizing القيم المتبقية، كما تستخدِم بعدها func لتلخيص التوزيع الشرطي وفي هذا المثال النتيجة هي مدة الحمل المتوسطة باعتبار أنّ المدة تتجاوز t، كما نحصل على متوسط مدة الحمل المتبقية عن طريق طرح t.
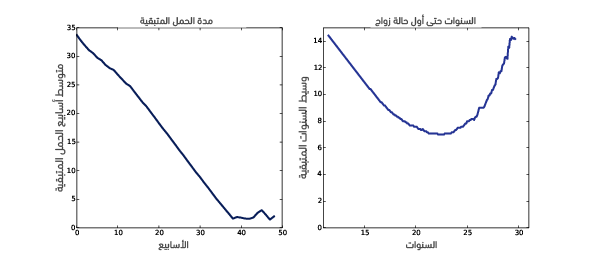
يوضِّح الشكل السابق مدة الحمل المتوقعة المتبقية في الجهة اليسرى؛ أما في الجهة اليمنى فيوضِّح السنوات حتى أول زواج، كما يُظهر الشكل السابق في الجهة اليسرى طول الحمل المتبقي المتوقع على أساس دالة للمدة الحالية، أي المدة المتبقية المتوقعة في الأسبوع 0 مثلًا هي حوالي 34 أسبوع، وهي أقل من طول الحمل الكامل -أي 39 أسبوع- لأن حالات الإجهاض التي حصلت في الثلث الأول قد خفضت من المتوسط.
ينخفض المنحني ببطء في الثلث الأول، وتكون المدة المتبقية المتوقعة بعد 13 أسبوع قد انخفضت 9 أسابيع لتصبح 25 أسبوع، بعد ذلك ينخفض بسرعة أكبر، وذلك بمعدل انخفاض أسبوع كامل في كل أسبوع جديد، في حين ينخفض المنحني حوالي أسبوع أو أسبوعين في الفترة ما بين الأسبوع 37 والأسبوع 42، وتكون المدة المتبقية المتوقعة في هذه الفترة ثابتةً، أي لا تصبح الوجهة أقرب مع مرور الأسابيع، وتدعى العمليات التي تحمل هذه الخاصية بعمليات بلا ذاكرة memoryless لأن ليس للماضي تأثير على التنبؤات، علمًا أنّ هذا السلوك هو الأساس الرياضي لجملة الممرضات الشهيرة التي تثير الغضب: اقترب موعد الولادة ومتوقع أن تلدي في أيّ يوم الآن.
يُظهر الشكل السابق في الجهة اليمنى الوقت الوسيط المتبقي حتى أول زواج على أساس دالة للعمر، حيث يكون الوسيط هو 14 عامًا بالنسبة لفتاة عمرها 11 عامًا، ويقل المنحني حتى عمر 22 حينما يصبح الوقت المتبقي الوسيط هو حوالي 7 سنوات، ويزداد مرةً أخرى بعدها وبحلول العمر 30 يعود إلى ما كان عليه أي 14 عامًا، ويمكننا استنادًا إلى هذه البيانات استنتاج أنّ للنساء صغيرات السن أعمارًا متبقيةً متناقصةً، وتدعى المكونات الميكانيكية المرتبطة بهذه الخاصية NBUE وهي اختصار لمِن المتوقع أن يكون الجديد أفضل من المستخدَم new better than used in expectation، أي من المتوقع بقاء الجزء الجديد فترةً أطول.
تملك النساء اللواتي تجاوزت أعمارهن 22 سنة وقتًا متبقيًا متزايدًا حتى أول زواج، وتدعى المكونات الميكانيكية المرتبطة بهذه الخاصية UBNE وهي اختصار لمِن المتوقع أن يكون المستخدَم أفضل من الجديد used better than new in expectation، أي من المتوقع أن يبقى الجزء المستخدَم فترةً أطول، إذ يُعَدّ الأطفال حديثو الولادة مثلًا ومرضى السرطان هم UBNE أيضًا لأن العمر المتوقع لديهم يزيد كلما طالت مدة حياتهم، فقد حسبنا الوسيط median في هذا المثال بدلًا من المتوسط mean لأن Cdf غير كامل، ويتوقع منحني البقاء أن نسبة 20% من المستجيبات لن يتزوجن قبل سن 44، وبما أن سن الزواج الأول لهؤلاء النساء غير معلوم وقد يكون غير موجود، فلن نتمكن من حساب المتوسط.
استبدلنا القيم غير المعلومة هنا بالقيمة np.inf وهي قيمة خاصة تمثِّل اللانهاية، أي أنها تجعل متوسط اللانهاية لكل الاعمار، لكن يبقى الوسيط محدَّدًا تمامًا طالما أنّ أكثر من 50% من الأعمار المتبقية نهائية، وهذا صحيح حتى عمر الثلاثين؛ أما بعدها فمن الصعب تحديد عمر متبقي متوقع له، وإليك الشيفرة التي تحسب وترسم هذه الدوال:
rem_life1 = sf1.RemainingLifetime() thinkplot.Plot(rem_life1) func = lambda pmf: pmf.Percentile(50) rem_life2 = sf2.RemainingLifetime(filler=np.inf, func=func) thinkplot.Plot(rem_life2)
حيث أن sf1 هو منحني البقاء لطول الحمل، ويمكن في هذه الحالة استخدام القيم الافتراضية للدالة RemainingLifetime؛ أما sf2 فهو منحني البقاء للعمر عند أول زواج، وfunc هو دالة تأخذ Pmf وتحسب وسيطها -أي المئين رقم 50-.
تمارين
يوجد الحل الخاص بهذا التمرين في chap13soln.py في مستودع الشيفرات ThinkStats2 على GitHub (وسائر ملفات التمارين).
تمرين 1
يحتوي المتغير cmdivorcx في الدورتين السادسة والسابعة من المسح الوطني لنمو الأسرة على تاريخ طلاق المستجيبين من أول حالة زواج، وهي مرمَّزة بطريقة أشهر القرن.
اقتباستوضيح: يوفِّر نظام أشهر القرن طريقةً سهلةً للعمل مع البيانات المرمزة حسب الشهر والسنة، وهي الطريقة الأساسية ترمَّز بها التواريخ في المسوح السكانية والصحية.
احسب مدة حالات الزواج التي انتهت بطلاق ومدة حالات الزواج المستمرة حتى الآن، وقدِّر منحني الخطر ومنحني البقاء لمدة الزواج، ثم استخدِم طريقة إعادة أخذ العينات resampling لمراعاة أوزان أخذ العينات، ثم وضِّح خطأ أخذ العينات بصريًا عن طريق رسم البيانات الناتجة عن عدة مرات أخذ عينات، علمًا أنه من الأفضل أن تفكِّر في تقسيم المستجيبين إلى مجموعات حسب عقد الولادة وربما حسب العمر عند أول حالة زواج.
ترجمة وبتصرف للمقال Chapter 13 Survival analysis analysis من كتاب Think Stats: Exploratory Data Analysis in Python.













أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.