قياس درجة تعقيد شيفرة بايثون باستخدام ترميز Big O

لتحديد ما هو تعقيد big O لجزء من الشيفرة الخاصة علينا إنجاز أربع مهام، هي: تحديد ما هي n، عدّ الخطوات في الشيفرة، إسقاط المراتب الدُنيا، وإسقاط المعاملات.

مثلًا، لنجد big O الخاص بالدالة readingList()‎:

def readingList(books):
    print('Here are the books I will read:')
    numberOfBooks = 0
    for book in books:
        print(book)
        numberOfBooks += 1
    print(numberOfBooks, 'books total.')

تذكر أن n تُمثل حجم بيانات الدخل التي تعمل عليها الشيفرة. تعتمد n في الدوال عادةً على المعامل، ومعامل الدالة readingList()‎ الوحيد هو books، لذا سيعطينا حجم books تصوّرًا جيدًا عن قيمة n، لأنه كلما زادت books يزداد وقت تنفيذ الدالة.

الآن، لنعدّ الخطوات في هذه الشيفرة، ولكن ما يمكننا أن نعدّه خطوة STEP مبهمًا إلى حد ما، لكننا سنتبّع سطر الشيفرة بمثابة قاعدة. لدى الحلقات عدد خطوات بعدد التكرارات مضروبًا بعدد أسطر الشيفرة في الحلقة، ولمعرفة ماذا يعني ذلك، هذا تعداد خطوات الشيفرة داخل الدالة readingList()‎:

def readingList(books):
    print('Here are the books I will read:')  # خطوة واحدة
    numberOfBooks = 0                         # خطوة واحدة
    for book in books:                        # ‫n مضروبًا بعدد الخطوات في هذه الحلقة
        print(book)                           # خطوة واحدة
        numberOfBooks += 1                    # خطوة واحدة
    print(numberOfBooks, 'books total.')      # خطوة واحدة

نعامل كل سطر من الشيفرة على أنه خطوة ما عدا حلقة for، إذ يُنفذ السطر مرةً لكل عنصر في books، ولأن n هي حجم books، يمكننا القول إنه ينفِّذ n خطوة. ليس هذا فقط بل إنه ينفِّذ كل الخطوات داخل الحلقة n مرة، لأن هناك خطوتان داخل الحلقة، يكون المجموع 2×n خطوة. يمكننا وصف خطواتنا على النحو التالي:

def readingList(books):
    print('Here are the books I will read:')  # خطوة واحدة
    numberOfBooks = 0                         # خطوة واحدة
    for book in books:                        #  ‫n مضروبًا 2 خطوة
        print(book)                           # خطوة معدودة مسبقًا
        numberOfBooks += 1                    #  خطوة معدودة مسبقًا
    print(numberOfBooks, 'books total.')      #خطوة واحدة

عندما نحسب عدد الخطوات الكلي، سنحصل على ‎1+1+1‎+(n×2)‎. يمكننا كتابة هذا التعبير على نحوٍ أبسط 2n+3.

ليس الهدف من big O حساب دقائق الأمور بل هو مؤشر عام، لذا نُسقط المراتب الأدنى من العد. المرتبة 2n+3 هي (2n) خطية و 3 هو ثابت. إذا ابقينا فقط أعلى مرتبة نحصل على 2n، ثم نُسقط المعاملات من المرتبة؛ ففي 2n المعامل هو 2، وبعد إسقاطه سيتبقى لنا n، وهذا يعطينا big O النهائي للدالة readingList()‎ الذي هو O(n)‎ أو تعقيد وقت خطي.

هذا الترتيب منطقي إذا فكرت فيه، فهناك عدة خطوات في الدالة الخاصة بنا، ولكن عمومًا إذا زادت قائمة books عشر مرات، يزداد وقت التنفيذ عشرة أضعاف أيضًأ. تغير زيادة books من 10 كتب إلى 100 كتاب الخوارزمية من 1 + (2 × 10) +1 + 1 أو 23 خطوة إلى 1 + (2 × 100) +1+ 1 أو 203 خطوات. الرقم 203 هو تقريبًا عشرة أضعاف 23، لذا يزداد وقت التنفيذ بالتناسب مع ازدياد n.

لماذا تكون المراتب الدنيا والمعاملات غير مهمة؟

نُسقط المراتب الأدنى من عد الخطوات لأنها تُصبح أقل أهمية مع ازدياد حجم n؛ فإذا زدنا قائمة books في الدالة السابقة readingList()‎ من 10 إلى 10,000,000,000 (10 مليار)، يزداد عدد الخطوات من 23 إلى 20,000,000,003 ولا تهم هذه الخطوات الثلاث الإضافية مع رقم كبير كهذا.

لا يشكّل معاملًا coefficient كبيرًا لمرتبة صغيرة مع ازدياد كمية البيانات أي فرق مقارنة مع المراتب الأعلى، فعند حجم n معين، ستكون المراتب الأعلى دائما أبطأ من المراتب الأدنى، مثلًا لنقل إنه لدينا quadraticExample()‎ الذي هو O(n²)‎ وفيه 3n² خطوة. لدينا أيضًا linearExample()‎ الذي هو O(n)‎ وفيه 1000n خطوة. لا يهم إذا كان المعامل 1000 أكبر من المعامل 3، فكلما زادت n ستكون بالنهاية العملية O(n²)‎ أبطأ من العملية الخطية O(n)‎. لا تهم الشيفرة تحديدًا ولكننا يمكن أن نفكر بها على النحو التالي:

def quadraticExample(someData):  # ‫n هو حجم someData
    for i in someData:           # ‫n خطوة
        for j in someData:       # ‫n خطوة
            print('Something')   # خطوة واحدة
            print('Something')   # خطوة واحدة
            print('Something')   # خطوة واحدة

def linearExample(someData):     #  ‫n هو حجم someData
    for i in someData:           #  ‫n خطوة
        for k in range(1000):    #  ‫1000 خطوة
            print('Something')   # خطوة معدودة مسبقًا

لدى الدالة linearExample()‎ معامل كبير (1000) مقارنة بالمعامل (3) الخاص بدالة quadraticExample. إذا كان حجم الدخل n هو 10، تظهر الدالة O(n²)‎ أسرع فقط في الخطوات ال 300 الخاصة به مقارنةً بخطوات الدالة O(n)‎ البالغ عددها 10000 خطوة.

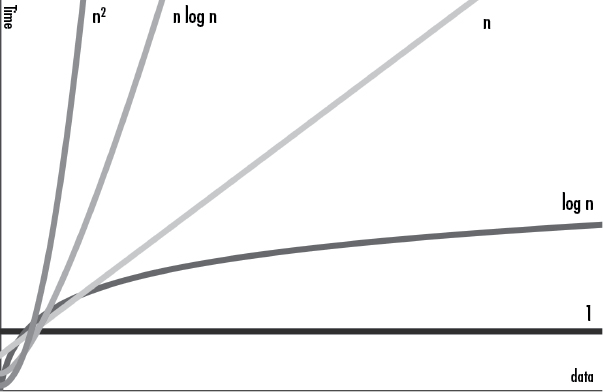
يهتم ترميز big O بصورةٍ أساسية بأداء الخوارزمية كلما تدرجت كمية العمل، فعندما يصل n إلى حجم 334 أو أكبر، ستكون الدالة quadraticExample()‎ دائمًا أبطأ من الدالة linearExample()‎، حتى لو كانت الدالة ()linearExample تتطلب 1,000,000n خطوة، ستصبح الدالة quadraticExample()‎ أبطأ عندما تصل n إلى 333,334. ستصبح العملية O(n²)‎ أبطأ من O(n)‎ أو المرتبة الأدنى. لمشاهدة ذلك لاحظ مخطط big O المبين بالشكل 3 التالي، الذي يبين كل مراتب ترميز big O. المحور X هو n حجم البيانات، والمحور y هو وقت التنفيذ اللازم لإنهاء العملية.

[الشكل 3: مخطط مراتب big O]

كما ترى، يزداد وقت التنفيذ بمعدل أسرع للمراتب الأعلى من المراتب الأدنى. على الرغم من أن المراتب الأدنى يمكن أن يكون لها معاملات أكبر مما يجعلها أكبر مؤقتًا من المراتب الأعلى، ستسبقهم المراتب الأعلى في النهاية.

أمثلة عن تحليل Big O

لنحدد مرتبة big O لبعض أمثلة الدوال، إذ سنستخدم في هذه الأمثلة المعامل المسمى books الذي هو قائمة سلسلة نصية لعناوين كتب.

تحسب دالة countBookPoints()‎ النتيجة score اعتمادًا على عدد books في قائمة الكتب، معظم الكتب قيمتها نقطة وبعض الكتب لكُتّاب معينين قيمتها نقطتين.

def countBookPoints(books):
    points = 0          # خطوة واحدة
    for book in books:  # ‫n خطوة مضروبًا بعدد تكرارات الحلقة
        points += 1     # خطوة واحدة 

    for book in books:                # ‫n خطوة مضروبًا بعدد تكرارات الحلقة
        if 'by Al Sweigart' in book:  # خطوة واحدة 
            points += 1               # خطوة واحدة
    return points                     # خطوة واحدة

يصبح عدد الخطوات ‎1+ (n × 1) + (n × 2) + 1 الذي يصبح 3n + 2 بعد جمع الحدود المتشابهة، وبعد إسقاط المراتب الأدنى والمعاملات يصبح O(n)‎ (تعقيد خطي)، حتى لو مررنا على books مرةً أو مرتين أو مليار مرة.

تستخدم كل الأمثلة حتى الآن حلقةً واحدةً بتعقيد خطي، ولكن هذه الحلقات تتكرر n مرة. سنرى في الأمثلة اللاحقة أن حلقة وحيدة في الشيفرة لا تُمثل تعقيدًا خطيًا بينما تمثّل حلقةً تمرّ على كل البيانات الخاصة بك ذلك.

تطبع دالة iLoveBooks()‎ جملة "I LOVE BOOKS!!!‎" أو "BOOKS ARE GREAT!!!‎" عشر مرات:

def iLoveBooks(books):
    for i in range(10):              #  ‫10 خطوات مضروبًا بعدد تكرارات الحلقة 
        print('I LOVE BOOKS!!!')     # خطوة واحدة
        print('BOOKS ARE GREAT!!!')  # خطوة واحدة

لدى هذه الدالة حلقة for ولكنها لا تمرّ على قائمة books وتجري عشرين خطوة مهما كان حجم books. يمكننا إعادة كتابة ذلك كما يلي: (1)20، وبعد إسقاط المعامل 20، يبقى لدينا O(1)‎ أو تعقيد زمن ثابت. هذا منطقي لأن الدالة تستغرق نفس زمن التنفيذ مهما كان n حجم قائمة books.

لاحقًا، لدينا الدالة cheerForFavoriteBook()‎ التي تبحث في قائمة books لإيجاد كتاب مفضل:

def cheerForFavoriteBook(books, favorite):
    for book in books:                            # ‫n خطوة مضروبًا بعدد تكرار الحلقة
        print(book)                               #  خطوة  واحدة
        if book == favorite:                      #  خطوة واحدة 
            for i in range(100):                  # ‫100 خطوة مضروبًا بعدد خطوات الحلقة
                print('THIS IS A GREAT BOOK!!!')  #  خطوة واحدة

تمرّ حلقة for book على قائمة books التي تتطلب n خطوة مضروبةً بعدد الخطوات داخل الحلقة، وتضم هذه الحلقة حلقة for i مضمّنة تتكرر مئة مرة، وهذا يعني أن حلقة for book تتكرر 102‎×n مرة أو 102n خطوة. سنجد بعد إسقاط المعامل أن cheerForFavoriteBook()‎ هي عملية O(n)‎ خطية. قد يكون المعامل 102 كبيرًا لكي يُهمل لكن خذ بالحسبان إذا لم تظهر favorite أبدًا في قائمة books ستُنفذ الدالة 1n خطوة فقط. يختلف تأثير المعاملات كثيرًا ولذا هي ليست ذات معنى كبير.

تبحث الدالة findDuplicateBooks()‎ في قائمة books (عملية خطية) مرةً لكل كتاب (عملية خطية أُخرى):

def findDuplicateBooks(books):
    for i in range(books):  # ‫n خطوة
        for j in range(i + 1, books):          #  ‫n خطوة
            if books[i] == books[j]:           #  خطوة واحدة
                print('Duplicate:', books[i])  #  خطوة واحدة

تمرّ حلقة for i على كل قائمة books وتُنفذ الخطوات داخل الحلقة n مرة. وتمرّ الحلقة for j على جزء من قائمة الكتب، على الرغم من أننا نُسقط المعاملات، لا تزال هذه العملية بتعقيد وقت خطي. هذا يعني أن حلقة for i تنجز n×n عملية أي n²، وهذا يعني أن الدالة findDuplicateBooks()‎ هي عملية بوقت تنفيذ متعدد الحدود polynomial time operation أي O(n²)‎.

لا تشير الحلقات المتداخلة Nested loops لوحدها أنها عمليات متعددة الحدود، ولكن الحلقات المتداخلة التي تكرر فيها الحلقات n مرة تُنتج n² خطوة، مما يدل على عملية O(n²)‎.

لنتابع على مثال أصعب؛ إذ تعمل عملية البحث الثنائي المذكورة سابقًا عن طريق البحث في منتصف القائمة المرتبة (سنسميها haystack) عن عنصر (سنسميه needle). إذا لم نجد needle هنا، سنكمل البحث في النصف التالي أو اللاحق من haystack اعتمادًا على أي نصف نتوقع فيه إيجاد needle فيه. نكرر هذه العملية عن طريق البحث عن الأنصاف الأصغر والأصغر حتى نجد needle أو ننهي العمل إذا لم تكن في haystack. لاحظ أن البحث الثنائي يعمل فقط مع العناصر في haystack مرتبة:

def binarySearch(needle, haystack):
    if not len(haystack):                        #  خطوة واحدة
        return None                             #  خطوة واحدة
    startIndex = 0                              #  خطوة واحدة
    endIndex = len(haystack) - 1                 #  خطوة واحدة

    haystack.sort()                              # عدد غير معلوم من الخطوات

    while start <= end:  #  عدد غير معلوم من الخطوات
        midIndex = (startIndex + endIndex) // 2  #  خطوة واحدة
        if haystack[midIndex] == needle:        #  خطوة واحدة
            # Found the needle.
            return midIndex                      #  خطوة واحدة
        elif needle < haystack[midIndex]:        #  خطوة واحدة
            # Search the previous half.
            endIndex = midIndex - 1              #  خطوة واحدة
        elif needle > haystack[mid]:             #  خطوة واحدة
            # Search the latter half.
            startIndex = midIndex + 1            #  خطوة واحدة

هناك سطرين في binarySearch()‎ ليس من السهل عدهما، إذ يعتمد ترميز big O الخاص باستدعاء الدالة haystack.sort()‎ على الشيفرة داخل وحدة sort()‎ الخاصة ببايثون. ليست هذه الشيفرة سهلة الإيجاد ولكن يمكنك معرفة ترميز big O على الإنترنت والذي هو O(n log n)‎. كل خوارزميات الترتيب العامة هي في أفضل الأحوال O(n log n)‎. سنغطي ترميز big O لعدد من التوابع والدوال الخاصة بلغة بايثون في فقرة "مراتب Big O لاستدعاءات الدوال العامة" لاحقًا في هذا الفصل.

حلقة while ليست بسيطة التحليل مثل حلقات for التي رأيناها، إذ علينا فهم خوارزمية البحث الثنائي لتحديد كم تكرار موجود في الحلقة. تغطي startIndex و endIndex قبل الحلقة كل مجال haystack وضُبطت midIndex في منتصف المجال. في كل تكرار لحلقة while يحصل واحد من شيئين:

إذا كان haystack[midIndex] == needle نعرف أننا وجدنا needle وتُعيد الدالة الفهرس needle في haystack.
إذا كان needle < haystack[midIndex]‎ أو needle > haystack[midIndex]‎ سيُنصّف المجال المُغطى من startIndex و endIndex، إما عن طريق تعديل startIndex أو endIndex.

عدد المرات التي يمكن تقسيم أي قائمة حجمها n إلى النصف هو log₂(n)‎. لذا، لدى حلقة while مرتبة big O هي O(log n)‎K ولكن لأن مرتبة O(n log n) ‎ في سطر haystack.sort()‎ هي أعلى من O(log n)‎، نسقط مرتبة O(log n)‎ الأدنى وتصبح مرتبة big O لكل الدالة binarySearch()‎ هي O(n log n)‎.

إذا ضمنا أن binarySearch()‎ ستُستدعى فقط على قائمة مرتبة من haystack، يمكننا إزالة السطر haystack.sort()‎ وجعل binarySearch()‎ دالة O(log n)‎. يحسّن هذا تقنيًا من كفاءة الدالة ولكن لا يجعل البرنامج أكثر كفاءة لأنه ينقل عمل الترتيب المطلوب إلى قسم آخر من البرنامج. تترك معظم تطبيقات البحث الثنائي خطوة الترتيب وبالتالي نقول أن خوارزميات البحث الثنائي لها تعقيد لوغاريتمي O(log n)‎.

مراتب Big O لاستدعاءات الدالة الشائعة

يجب أن يأخذ تحليل big O مرتبة big O بالحسبان لأي دالة يجري استدعاؤها. إذا كتبت دالةً يمكنك تحليل الشيفرة الخاصة بك، ولكن لمعرفة مرتبة big O لدوال وتوابع بايثون المضمّنة يجب عليك إرجاعها إلى قوائم.

تحتوي هذه القائمة مراتب big O لعمليات بايثون الشائعة لأنواع المتتاليات مثل السلاسل النصية والصفوف tuples والقوائم:

s[i] reading and s[i] = value assignment هي عمليات O(1)‎.
s.append(value)‎ هي عملية O(1)‎.
s.insert(i, value)‎ هي عملية O(n)‎. يحتاج إدخال قيم في متتالية (خاصة من المقدمة) إلى إزاحة كل القيم إلى الأعلى في الفهارس فوق i بمكان واحد في التسلسل.
s.remove(value)‎ هي عملية O(n)‎. يحتاج إزالة قيم في متتالية (خاصة من المقدمة) إلى إزاحة كل القيم إلى الأسفل في الفهارس فوق I بمكان واحد في التسلسل.
s.reverse()‎ هي عملية O(n)‎ لأنه يجب إعادة ترتيب كل عنصر في المتتالية.
s.sort()‎ هي عملية O(n log n)‎ لأن خوارزمية الترتيب الخاصة ببايثون هي O(n log n)‎.
value in s هي عملية O(n)‎ لأنه يجب التحقق من كل عنصر.
:for value in s عملية O(n)‎
len(s)‎ هي عملية O(n) ‎لأن بايثون يتابع كم عنصر موجود في المتتالية لذا لا يحتاج لإعادة عدهم عندما يُمرّر إلى len()‎

تحتوي هذه القائمة على مراتب big O لعمليات بايثون الشائعة أنواع الربط مثل القواميس والمجموعات sets والمجموعات الجامدة frozensets:

m[key] reading and m[key] = value assignment عمليات O(1)‎.
m.add(value)‎ عملية O(1)‎.
value in m عمليات O(1)‎ للقواميس التي هي أسرع باستخدام in مع المتتاليات.
for key in m: عملية O(n)‎.
len(m)‎ عملية O(1)‎ لأن بايثون يتابع كم عنصر موجود في الربط لذا لا يحتاج لإعادة عدهم عندما يمرر إلى len()‎.

على الرغم من أن القوائم تحتاج عمومًا إلى البحث عن كل العناصر من بدايتها حتى نهايتها، لكن القواميس تستخدم المفتاح لحساب العنوان والوقت اللازم للبحث عن قيمة المفتاح يبقى ثابتًا. يسمى هذا الاستدعاء خوارزمية التعمية Hashing Algorithm والعنوان يسمى التعمية hash. التعمية هي خارج نطاق هذا الكتاب ولكن يمكنك الاطلاع على مفهوم التعمية والدوال المرتبطة بها على موقع حسوب من خلال الرابط، إذ أنها السبب في جعل العديد من عمليات الربط بوقت ثابت O(1)‎. تستخدم المجموعات التعمية أيضًا لأن المجموعات هي قواميس بحقيقتها ولكن بوجود مفاتيح بدلًا من أزواج مفتاح-قيمة. لكن تحويل القائمة إلى مجموعة هو عملية بتعقيد O(n)‎ لذا لا يفيد تحويل القائمة إلى مجموعة ومن ثم الوصول إلى العناصر في تلك المجموعة.

تحليل Big O بنظرة سريعة

عندما تألف تنفيذ تحليل big O فأنت لست بحاجة لفعل كل الخطوات، إذ ستشاهد بعد فترة بعض الدلالات التي يمكن منها تحديد مرتبة big O بسرعة.

لاحظ أن n هي حجم البيانات التي تعمل عليها الشيفرة، هذه بعض القواعد العامة المُستخدمة:

إذا كانت الشيفرة لا تصل إلى أي بيانات هي O(1)‎.
إذا كانت الشيفرة تمر على البيانات تكون O(n)‎.
إذا كانت الشيفرة فيها حلقتين متداخلتين تمرّان على البيانات O(n²)‎.
لا تُعدّ استدعاءات الدالة خطوة واحدة بل هي عدد الخطوات داخل الدالة. راجع فقرة "مرتبة Big O لاستدعاءات الدالة العامة" في الأعلى.
إذا كانت للشيفرة عملية "فرّق تسد" التي تنصف البيانات تكون O(log n)‎.
إذا كانت للشيفرة عملية "فرّق تسد" التي تُنفذ مرة لكل عنصر في البيانات تكون O(n log n)‎.
إذا كانت الشيفرة تمر على كل مجموعة ممكنة من القيم في البيانات n تكون O(n²)‎ أو مرتبة أسية أُخرى.
إذا كانت الشيفرة تمر على كل تبديل (أي ترتيب) للقيم في البيانات تكون O(n!)‎.
إذا كانت الشيفرة تتضمن ترتيب البيانات تكون على الأقل O(n log n)‎.

هذه القيم هي نقطة انطلاق جيدة ولكن لا يوجد بديل لتحليل big O. تذكر أن مرتبة big O ليست الحكم النهائي على الشيفرة إذا ما كانت سريعة أو بطيئة أو فعّالة. لنرى الدالة waitAnHour()‎:

import time
def waitAnHour():
    time.sleep(3600)

تقنيًا هذه الدالة waitAnHour()‎ هي وقت ثابت O(1)‎، نفكّر دائمًا أن شيفرة الوقت الثابت سريعة، ولكن وقت تنفيذها هو ساعة. هل هذه الشيفرة فعّالة؟ لا، ولكن من الصعب تحسين برمجة دالة waitAnHour()‎ تستطيع أن تُنفذ بأسرع من ساعة. ترميز Big O ليس بديلًا عن تحليل الشيفرة الخاصة بك، وإنما الهدف منه هو إعطاؤك نظرةً عن أداء الشيفرة مع زيادة كمية البيانات المُدخلة.

لا يفيدنا Big O عندما تكون n صغيرة وعادة ما تكون n صغيرة

ربما ستكون متسرعًا لتحليل كل قطعة شيفرة تكتبها مع هذه المعلومات عن ترميز big O. قبل أن تستخدم المطرقة التي بيدك (شيفرة بايثون) لكل مسمار تراه، خذ بالحسبان أن ترميز big O يفيد أكثر عندما يكون هناك كميات كبيرة من البيانات لمعالجتها، وفي الواقع أغلب كميات البيانات هي صغيرة، وفي مثل تلك الحالات، لا يستحق إنشاء خوارزميات مُنمقة ومتطورة مع مراتب big O منخفضة ذلك العناء.

لدى مصمم لغة البرمجة جو Go روب بايك Rob Pike خمس قواعد عن البرمجة، واحدة منها هي: "الخوارزميات المنمّقة بطيئة عندما تكون 'n' صغيرة وبالعادة 'n' صغيرة". لن يواجه معظم مطورو البرمجيات مراكز بيانات كبيرة أو عمليات حسابية معقدة، بل برامج أبسط من ذلك، وفي هذه الحالات سيعطي تنفيذ الشيفرة مع محلًل معلومات profiler أدق عن أداء الشيفرة بدلًا من تحليل big O.

الخلاصة

خذ بالحسبان أن big O هي أداة تحليل مفيدة، ولكنها ليست بديل عن تنفيذ الشيفرة مع محلًل لمعرفة أين يوجد عنق الزجاجة، إذ تساعدك المعرفة بترميز big O وكيفية تباطؤ الشيفرة مع زيادة البيانات في تجنُّب كتابة الشيفرة في مراتب أبطأ من حاجتها.

ترجمة -وبتصرف- لقسم من الفصل Measuring Performance And Big O Algorithm Analysis من كتاب Beyond the Basic Stuff with Python.