بعد أساسيات بايثون ترميز Big O وحساب مراتب تعقيد الخوارزميات

بعد أن تعلمنا كيفية قياس سرعة البرامج في المقال السابق قياس أداء وسرعة تنفيذ شيفرة بايثون، سنتعلم كيفية قياس الزيادات النظرية theoretical increases في وقت التنفيذ runtime مع نمو حجم البيانات الخاصة بالبرنامج، ويُطلق على ذلك في علوم الحاسوب ترميز O الكبير big O notation.

ربما يشعر مطورو البرامج الذين ليس لديهم خلفية في علوم الحاسوب التقليدية بوجود نقص في معارفهم، على الرغم من كون المعرفة في علوم الحاسوب مفيدة، لكنه ليس مرتبط مباشرةً مع تطوير البرمجيات.

تُعدّ Big O نوعًا من خوارزميات التحليل التي تصف تعقيد الشيفرة مع زيادة عدد العناصر التي تعمل عليها. تصنف الشيفرة في مرتبة تصف عمومًا الوقت الذي تستغرقه الشيفرة لتُنفّذ، وكلما زادت تزيد كمية العمل الواجب إنجازه. يصف مطور لغة بايثون Python نيد باتشلدر Ned Batchelder خوارزمية big O بكونها تحليلًا لكيفية "تباطؤ الشيفرة كلما زادت البيانات" وهو عنوان حديثه في معرض PyCon 2018.

لننظر إلى المثال التالي: لنفترض أنه لديك كميةٌ معينةٌ من العمل الذي يستغرق ساعةً ليكتمل، فإذا تضاعفت كمية العمل، كم سيستغرق من الوقت؟ ربما تعتقد أنه سيستغرق ضعف المدة ولكن الجواب الصحيح هو: يعتمد الأمر على نوع العمل المُنجز.

إذا استغرقت ساعةً لقراءة كتاب قصير، فستستغرق أكثر أو أقل من ساعتين لقراءة كتابين قصيرين، وإذا كان بإمكانك ترتيب 500 كتاب أبجديًا، سيستغرق ترتيب 1000 كتاب أكثر من ساعتين لأنك ستبحث عن المكان المناسب لكل كتاب في مجموعة أكبر من الكتب. من ناحية أخرى، إذا أردت التأكد أن رف الكتب فارغ أو لا، لا يهم إذا كان هناك 0 أو 10 أو 1000 كتاب على الرف، فنظرةٌ واحدةٌ كافية لتعرف الجواب، إذ سيبقى وقت التنفيذ على حاله بغض النظر عن عدد الكتب الموجودة. يمكن أن يكون بعض الناس أسرع أو أبطأ في قراءة أو ترتيب الكتب أبجديًا ولكن تبقى هذه التوجهات العامة نفسها.

تصف خوارزمية big O هذه التوجهات، إذ يمكن أن تُنفذ الخوارزمية على حاسوب سريع أو بطيء ولكننا نستطيع استخدام big O لوصف كيفية عمل الخوارزمية عمومًا، بغض النظر عن العتاد الذي ينفذ هذه الخوارزمية. لا تستخدم big O وحدات معينة مثل الثواني أو دورات المعالج لوصف وقت تنفيذ الخوارزمية لأنها تختلف بين أجهزة الحاسوب ولغات البرمجة.

مراتب Big O

يُعرّف ترميز Big O عادةً المراتب التالية، التي تتراوح من المنخفضة -التي تصف الشيفرة التي لا تتباطأ كثيرًا كلما زادت البيانات- إلى المراتب العليا -التي تصف الشيفرة الأكثر تباطؤًا:

1. O(1)‎ وقت ثابت (أدنى مرتبة)
2. O(log n)‎ وقت لوغاريتمي
3. O(n)‎ وقت خطي
4. O(n log n)‎ وقت N-Log-N
5. O(n²)‎ وقت متعدد الحدود
6. O(2ⁿ)‎ وقت أسي
7. O(n!)‎ وقت عاملي (أعلى مرتبة)

لاحظ أن big O تستخدم حرف O كبير متبوعًا بقوسين يحتويان وصف المرتبة، إذ يمثّل حرف O الكبير المرتبة وتمثل n حجم دخل البيانات التي تعمل عليها الشيفرة. نلفظها "big oh of n" أو "big oh n".

لا تحتاج لفهم المعنى الدقيق لكلمات مثل لوغاريتمي أو حدودي لاستخدام صيغة big O، إذ سنصِف كل نوع بالتفصيل في الفقرة التالية ولكن هذا تبسيط لهم:

• خوارزميات O(1)‎ و O(log n)‎ سريعة
• خوارزميات O(n)‎ و O(n log n)‎ ليست سيئة
• خوارزميات O(n²)‎ و O(2ⁿ)‎ بطيئة يمكن طبعًا مناقشة العكس في بعض الحالات ولكن هذه التوصيفات هي قواعد جيدة عمومًا، فهناك مراتب أكثر من big O المذكورة هنا ولكن هذه هي الأعم. دعنا نتحدث عن أنواع المهام التي يصفها كل نوع من هذه المهام.

اصطلاح رف الكتب Bookshelf لمراتب Big O

سنستمر في المثال التالي لمراتب big O باستخدام مصطلح رف الكتب، إذ تمثّل n عدد الكتب في الرف ويصف ترميز Big O كيف أن المهام المختلفة تستغرق وقتًا أطول كلما زاد عدد الكتب.

تعقيد O(1)‎: وقت ثابت

معرفة "هل رف الكتب فارغ؟" هي عملية ذات وقت ثابت، إذ لا يهم عدد الكتب في الرف، فنظرةٌ واحدةٌ ستخبرنا ما إذا كان رف الكتب فارغ أم لا. يمكن أن يختلف عدد الكتب ولكن وقت التنفيذ يبقى ثابتًا، لأنه طالما رأينا كتابًا واحدًا على الرف يمكننا إيقاف البحث. القيمة n غير مهمة لسرعة تنفيذ المهمة لذا لا يوجد n في O(1)‎. يمكنك أيضًا رؤية الوقت الثابت مكتوبًا (O(c أحيانًا ‎.

تعقيد O(log n)‎: لوغاريتمي

اللوغاريتم هو عكس الأس، الأس 2⁴ أو 2×2×2×2 يساوي 16 ولكن اللوغاريتم log₂(16)‎ (تلفظ لوغاريتم أساس 2 للعدد 16) يساوي 4. نفترض في البرمجة قيمة الأساس 2 ولذلك نكتب O(log n)‎ بدلًا من O(log₂ n)‎.

البحث عن كتاب في رف كتب مرتب أبجديًا هي عملية لوغاريتمية الوقت؛ فمن أجل إيجاد كتاب واحد، يمكن التحقق من الكتاب في منتصف الرف، وإذا كان هو الكتاب المطلوب تكون قد انتهيت، وإذا لم يكن كذلك، يمكن تحديد إذا كان الكتاب قبل أو بعد الكتاب الذي في المنتصف. يقلل ذلك مجال البحث إلى النصف، ويمكنك تكرار هذه العملية مجددًا من خلال فحص الكتاب الذي في منتصف النصف الذي تتوقع فيه إيجاد الكتاب. نسمي ذلك خوارزمية بحث ثنائية binary search وهناك مثال على ذلك في "أمثلة عن ترميز Big O" لاحقًا.

عدد المرات التي تستطيع قسم مجموعة n كتاب للنصف هي log₂ n، في رف فيه 16 كتاب ستحتاج إلى 4 خطوات على الأكثر لإيجاد الكتاب الصحيح، لأن كل خطوة تقلل عدد الكتب التي يجب البحث فيها إلى النصف. يحتاج رف الكتب الذي فيه ضعف عدد الكتب فقط إلى خطوة إضافية واحدة للبحث عنه. إذا كان هناك 4.2 مليار كتاب في رف كتب مرتبة أبجديًا ستحتاج فقط إلى 32 خطوة لإيجاد كتاب معين.

تتضمن خوارزميات Log n عادةً خطوة فرّق تسد divide and conquer وتنطوي على اختيار نصف دخل n للعمل عليه وبعدها نصف آخر من ذلك النصف وهكذا دواليك. تتدرج عمليات log n جيدًا، إذ يمكن أن يزداد العمل n إلى الضعف ولكن سيزداد وقت التنفيذ خطوةً واحدةً فقط.

تعقيد O(n)‎: وقت خطي

تستغرق عملية قراءة كل الكتب على الرف وقتًا خطيًا؛ فإذا كانت الكتب بنفس الطول تقريبًا وضاعفت عدد الكتب على الرف، فسيستغرق ضعف الوقت تقريبًا لقراءة كل الكتب، ويزداد وقت التنفيذ بالتناسب مع عدد الكتب n.

تعقيد O(n log n)‎: وقت N-Log-N

ترتيب الكتب أبجديًا هي عملية تستغرق وقت n-log-n. هذه المرتبة هي ناتج ضرب وقتي التنفيذ O(n)‎ و O(log n)‎ ببعضهما. يمكن القول أن مهمة O(n log n)‎ هي مهمة O(log n)‎ مع تنفيذها n مرة. فيما يلي تفسير بسيط حول ذلك.

ابدأ بمجموعة كتب يجب ترتيبها أبجديًا ورف كتب فارغ، واتبع الخطوات في خوارزمية البحث الثنائي كما موضح في الفقرة السابقة "تعقيد O(log n)‎: زمن لوغاريتمي" لمعرفة مكان كل كتاب على الرف. هذه عملية O(log n)‎، ومن أجل ترتيب n كتاب أبجديًا وكان كل كتاب بحاجة إلى log n خطوة لترتيبه أبجديًا، ستحتاج n×log n أو n log n خطوة لترتيب كل مجموعة الكتب أبجديًا. إذا تضاعف عدد الكتب سيستغرق أكثر من ضعف الوقت لترتيبهم أبجديًا، لذا تتدرج خوارزميات n log n جيدًا.

خوارزميات الترتيب ذات الكفاءة، هي: O(n log n)‎، مثل ترتيب الدمج merge sort والترتيب السريع quicksort وترتيب الكومة heapsort وترتيب تيم Timsort (من اختراع تيم بيترز Tim Peters وهي الخوارزمية التي يستخدمها تابع sort()‎ الخاص ببايثون).

تعقيد O(n²)‎: وقت متعدد الحدود

التحقق من الكتب المكررة في رف كتب غير مرتب هي عملية تستغرق وقت حدودي polynomial time operation؛ فإذا كان هناك 100 كتاب يمكنك أن تبدأ بالكتاب الأول وتقارنه مع التسعة وتسعون الكتاب الباقين لمعرفة التشابه، ثم نأخذ ثاني كتاب ونتحقق بنفس الطريقة مثل باقي بقية الكتب التسعة وتسعون. خطوات التحقق من التكرار لكتاب واحد هي 99 (سنقرّب هذا الرقم إلى 100 الذي هو n في هذا المثال). يجب علينا فعل ذلك 100 مرة، مرةً لكل كتاب، لذا عدد خطوات التحقق لكل كتاب على الرف هو تقريبًا n×n أو n². (يبقى هذا التقريب n² صالحًا حتى لو كنا أذكياء ولم نكرر المقارنات).

يزداد وقت التنفيذ بازدياد عدد الكتب تربيعيًا. سيأخذ التحقق من التكرار لمئة كتاب 100×100 أو 10,000 خطوة، ولكن التحقق من ضعف هذه القيمة أي 200 كتاب سيكون 200×200 أو 40,000 خطوة، أي أربع مرات عمل أكثر.

وجد بعض الخبراء في كتابة الشيفرات الواقعية للعالم الحقيقي أن معظم استخدامات تحليل big O هي لتفادي كتابة خوارزمية O(n²)‎ عن طريق الخطأ، عند وجود خوارزمية O(n log n)‎ أو O(n)‎.

مرتبة O(n²)‎ هي عندما تبدأ الخوارزميات بالتباطؤ كثيرًا، لذا معرفة أن الشيفرة الخاصة بك في مرتبة O(n²)‎ أو أعلى يجب أن يجعلك تتوقف. ربما توجد خوارزمية مختلفة يمكنها حل المشكلة بصورةٍ أسرع، ويمكن في هذه الحالة أن يكون الإطلاع على قسم هيكلة البيانات والخوارزميات Data Structure and Algorithms -أو اختصارًا DSA- إما على أكاديمية حسوب مفيدًا.

نسمي أيضًا O(n²)‎ وقتًا تربيعيًا، ويمكن أن يكون لخوارزميات O(n³) وقتًا تكعيبيًا وهو أبطأ من O(n²)‎ أو وقتًا رباعيًا O(n⁴)‎ الذي هو أبطأ من O(n³)‎ أو غيره من الأوقات الزمنية متعددة الحدود.

تعقيد O(2ⁿ): وقت أسي

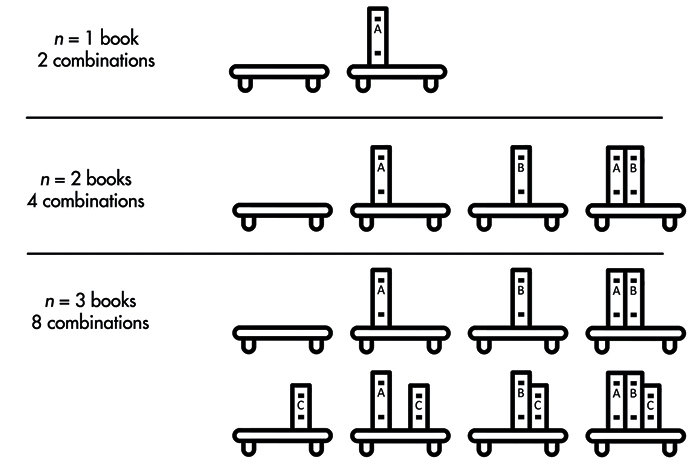
أخذ صور لرف الكتب مع كل مجموعة ممكنة من الكتب هو عملية تستغرق وقتًا أُسّيًا. انظر لهذا الأمر بهذه الطريقة، كل كتاب على الرف يمكن أن يكون في الصورة أو لا يكون. يبين الشكل 1 كل مجموعة ممكنة، إذ تكون n هي 1 أو 2 أو 3. إذا كانت n هي 1 هناك طريقين للتجميع، إذا كانت n هي 2 هناك أربعة صور ممكنة، الكتابان على الرف، أو الكتابان ليسا على الرف، أو الكتاب الأول موجود والثاني ليس موجودًا، أو الكتاب الأول ليس موجودًا والثاني موجود. إذا أضفنا كتابًا ثالثًا، نكون قد ضاعفنا مرةً ثانية العمل المُراد فعله، لذا يجب عليك النظر إلى كل مجموعة فرعية لكتابين التي تضم الكتاب الثالث (أربعة صور) وكل مجموعة فرعية لكتابين دون الكتاب الثالث (أربعة صور أُخرى أي 2³ أو 8 صور). يضاعف كل كتاب إضافي كمية العمل، فمن أجل n كتاب سيكون عدد الصور التي يجب أخذها (أي العمل الواجب فعله) هو 2ⁿ.

[الشكل 1: مجموعة الكتب الممكنة على رف كتب من أجل كتاب واحد أو اثنين أو ثلاث كتب]

يزداد وقت التنفيذ للمهام الأُسية بسرعة كبيرة. تحتاج ستة كتب إلى 2⁶ أو 32 صورة، ولكن 32 كتاب يحتاج 2³² أو أكثر من 4.2 مليار صورة. مرتبة O(2²) أو O(2³)‎ أو O(2⁴) وما بعدها هي مراتب مختلفة ولكنها كلها تحتوي تعقيدات وقت أُسّي.

تعقيد O(n!)‎: وقت عاملي

أخذ صورةٍ لكل ترتيب معين هي عملية تستغرق وقتًا عاملي. نطلق على كل ترتيب ممكن اسم التبديل permutation من أجل n كتاب. النتيجة هي ترتيب n!‎ أو n عاملي، فمثلًا 3‎!‎‎ هي 3×2×1 أو 6. يبين الشكل 2 كل التبديلات الممكنة لثلاثة كتب.

[الشكل 2: كل تبديلات !3 (أي 6) لثلاثة كتب على رف كتب]

لحساب ذلك بنفسك، فكر بكل التبديلات الممكنة بالنسبة إلى n كتاب. لديك n خيار ممكن للكتاب الأول وبعدها n-1 خيار ممكن للكتاب الثاني (أي كل كتاب ما عدا المكان الذي اخترته للكتاب الأول) وبعدها n-2 خيار ممكن للكتاب الثالث وهكذا دواليك. مع 6 كتب تكون نتيجة !6 هي 6×5×4×3×2×1 أو 720 صورة. إضافة كتاب واحد آخر يجعل عدد الصور المطلوبة !7 أو 5.040. حتى من أجل قيم n صغيرة، تصبح خوارزميات الوقت العاملي مستحيلة الإنجاز في وقت منطقي، فإذا كان لديك 20 كتاب ويمكنك ترتيبهم وأخذ صورة كل ثانية، فستحتاج إلى وقت أكثر من عمر الكون للانتهاء من كل تبديل.

واحدة من مشاكل O(n!)‎ المعروفة هي معضلة مندوب المبيعات المسافر، إذ يجب على مندوب المبيعات أن يزور n مدينة ويريد حساب المسافة المقطوعة لكل مراتب n!‎ الممكنة والتي يمكنه زيارتها، إذ يستطيع من تلك الحالات إيجاد أقصر طريق، ومن أجل منطقة بعدد كبير من المدن تصبح هذه المهمة مستحيلة الإنجاز في وقت منطقي. لحسن الحظ هناك خوارزميات مُحسنة لإيجاد طريق قصير (ولكن ليس من المضمون أن يكون الأقصر) بطريقة أسرع من O(n!)‎.

يحسب ترميز Big O الحالات الأسوأ

يحسب Big O أسوأ حالة ممكنة لأي مهمة، إذ يحتاج إيجاد كتاب معين في رف كتب غير مُنظم مثلًا أن تبدأ من أحد الأطراف وتتحقق من الكتب حتى تجد الكتاب المطلوب. يمكن أن تكون محظوظًا ويكون الكتاب المطلوب هو أول كتاب تتحقق منه، ولكن ربما تكون سيء الحظ ويكون الكتاب الذي تريده هو آخر كتاب تتحقق منه، أو قد لا يكون موجودًا على الرف إطلاقًا. لذلك، في أفضل الحالات لا يهم إذا كان هناك مليارات الكتب التي يجب البحث فيها لأنك ستجد الكتاب الذي تريده مباشرةً، لكن هذا التفاؤل ليس مفيدًا في خوارزميات التحليل. تصف Big O ماذا يحصل في الحالات الأسوأ حظًا، أي إذا كان لديك n كتاب يجب عليك البحث في كل الكتب، ففي هذا المثال يزداد وقت التنفيذ بنفس معدل ازدياد عدد الكتب.

يستخدم بعض المبرمجين ترميز big Omega لوصف الحالة الأفضل للخوارزمية، فمثلًا تعمل خوارزمية ‎Ω(n)‎ بكفاءة خطية في أفضل حالاتها وفي الحالة الأسوأ ربما تستغرق وقتًا أطول. تواجه بعض الخوارزميات حالات محظوظة جدًا، يحيث لا تعمل أي شيء، مثل إيجاد مسار الطريق لمكان أنت أصلًا فيه.

يصف ترميز Big Theta الخوارزميات التي لها الترتيب نفسه في أسوأ وأفضل الحالات، فمثلًا تصف ‎Θ(n)‎ خوارزميةً لديها كفاءة خطية في أحسن وأسوأ الحالات، أي أنها خوارزمية O(n)‎ وكذلك ‎Ω(n)‎. لا يُستخدم هذين الترميزين كثيرًا مثل استخدام big O ولكن تجدر معرفتهما.

يُعد سماع الناس يتحدثون عن "big O الحالة الوسطية" عندما يعنون big Theta أو "big O الحالة الفُضلى" عندما يعنون big Omega أمرًا شائعًا رغم أنه متناقض؛ إذ تصف big O الحالة الأسوأ لوقت تنفيذ الخوارزمية تحديدًا، ولكن حتى لو كانت كلماتهم خاطئة لا تزال تفهم المعنى بغض النظر.

العمليات الرياضية الكافية للتعامل مع Big O

إذا كان علم الجبر لديك ضعيفًا فمعرفة العمليات الرياضية التالية أكثر من كافي عند التعامل مع big O:

• الضرب: تكرار الإضافة أي 2×4=8 هو مثل 2+2+2+2=8، وفي حال المتغيرات يكون n+n+n هو 3‎×n.
• ترميز الضرب: يهمل ترميز الجبر عادةً إشارة ×، لذا 2‎×n تُكتب 2n ومع الأرقام 3×2 تُكتب (3)2 أو ببساطة 6.
• خاصية الضرب بالعدد 1: ضرب أي عدد بالرقم 1 يُنتج الرقم نفسه أي 5=x1‏5 و42 =x1‏42 أو عمومًا n×1=n
• توزيع الضرب على الجمع: (3×2) + (3×2) = (4+3)2x كل طرف من المعادلة يساوي 14 أي عمومًا a(b+c) = ab+ac
• الأس: تكرار الضرب 16= 2⁴ (تُلفظ "2 مرفوعة للقوة الرابعة تساوي 16") مثل 2×2×2×2= 16 هنا تكون 2 هي الأساس و 4 هي الأس. باستخدام المتغيرات n×n×n×n هي n⁴. يُستخدم في بايثون المعامل ** على سبيل المثال 2**4 تساوي 16.
• الأس الأول يساوي الأساس: 2= 2¹ و 9999=9999¹ وبصورةٍ عامة n¹=n
• الأس 0 يساوي 1: 1= 2⁰ و 1=9999⁰ وبصورةٍ عامة n⁰=1
• المعاملات: عوامل الضرب في 3n²+4n+5 المعاملات هي 3 و4 و5. يمكنك معرفة أن 5 هي معامل لأن 5 يمكن أن يُعاد كتابتها بالشكل (1)5 وأيضًا يمكن إعادة كتابتها 5n⁰.
• اللوغاريتمات: عكس الأس. لأن 16=2⁴ نعرف أن log₂(16)=4. نفول لوغاريتم الأساس 2 للعدد 16 هو 4. نستخدم في بايثون دالة math.log()‎ إذ math.log(16, 2)‎ تساوي إلى 4.0.

يتطلب حساب big O تبسيط العمليات عن طريق جمع الحدود المتشابهة؛ والحد هو مجموعة من الأرقام والمتغيرات مضروبة مع بعضها، ففي 3n²+4n+5 تكون الحدود هي 3n² و4n و5، إذ أن الحدود المتشابهة لديها نفس المتغير مرفوعًا لنفس القوة. في التعبير 3n²+4n+6n+5 الحدان 4n و6n هما متشابهان بإمكاننا التبسيط وإعادة الكتابة كالتالي 3n²+10n+5.

خذ بالحسبان أنه يمكن كتابة 3n²+5n+4 على النحو التالي 3n²+5n+4(1)‎، إذ تطابق الحدود في هذا التعبير مرتبات big O التالية O(n²)‎ و O(n)‎ و O(1)‎. سيفيد هذا لاحقًا عندما نُسقط المعاملات في حسابات big O.

ستفيد هذه التذكرة عندما تحاول معرفة big O لقطعة من الشيفرة، ولكن لن تحتاجها بعد أن تنتهي من "تحليل Big O بنظرة سريعة" في المقال التالي. مفهوم big O بسيط ويمكن أن يفيد حتى لو لم تتبع القواعد الرياضية بصرامة.

الخلاصة

يُعد ترميز Big O من أكثر المفاهيم انتشارًا في علم الحواسيب للمبرمجين، وهو بحاجة لبعض المفاهيم في الرياضيات لفهمه، ولكن يمكن للمفهوم الأساسي، ألا وهو معرفة أن الشيفرة ستبطأ كلما زادت البيانات، أن يصف الخوارزميات دون الحاجة إلى أرقام كبيرة لحسابها.

هناك سبع مراتب لترميز big O، وهي: O(1)‎ أو الوقت الثابت، الذي يصف الشيفرة التي لا تتغير مع زيادة البيانات؛ و O(log n)‎ أو الوقت اللوغاريتمي الذي يصف الشيفرة التي تزداد بخطوة كلما تضاعف عدد البيانات بمقدار n؛ و O(n)‎ أو الوقت الخطي، الذي يصف الشيفرة التي تتباطأ يتناسب مع زيادة حجم البيانات بمقدار n؛ و O(n log n)‎ أو وقت n-log-n، الذي يصف الشيفرة التي هي أبطأ من O(n)‎ والعديد من خوارزميات الترتيب لديها هذه المرتبة.

المراتب الأعلى هي أبطأ لأن وقت تنفيذها يزداد بصورةٍ أسرع من زيادة حجم دخل البيانات. يصف الوقت الحدودي O(n²)‎ الشيفرة التي يزداد وقت تنفيذها بتربيع الدخل n. ليست المراتب O(2ⁿ)‎ أو الوقت الأسّي، و O(n!)‎ أو الوقت العاملي شائعة جدًا، ولكنها تأتي مع المجموعات والتبديلات على الترتيب.

ترجمة -وبتصرف- لقسم من الفصل Measuring Performance And Big O Algorithm Analysis من كتاب Beyond the Basic Stuff with Python.

اقرأ أيضًا

• المقال السابق: قياس أداء وسرعة تنفيذ شيفرة بايثون -تحليل الخوارزميات
• تعقيد الخوارزميات Algorithms Complexity
• دليل شامل عن تحليل تعقيد الخوارزمية