النظام الثنائي هو نظام عددي يكون أساس العدد فيه 2، ويمثل المعلومات بحالتين متنافيتين لا ثالث لهما، ويتكون العدد الثنائي من عناصر تسمى بِتات bits بحيث يمكن أن يكون كل بت بإحدى الحالتين المحتمَلتَين، واللتين نمثلهما عمومًا بالرقمين 1 و 0.
نظرية النظام الثنائي
النظام الثنائي هو نظام يكون فيه الأساس هو العدد 2 ليمثل المعلومات بحالتين متنافيتين، ويتكون العدد الثنائي من عناصر تسمى بِتّات، إذ يمكن أن يكون كل بِتّ بإحدى الحالتين المحتمَلتين واللتين نمثِّلهما عمومًا بالرقمين 1 و 0، ويمكننا القول أنهما تمثِّلان القيمتَين الصحيحة والخاطئة؛ أما من الناحية الكهربائية، فقد تمثَّل الحالتين بجهد كهربائي مرتفع ومنخفض أو مثل زر التشغيل والإيقاف.
نبني الأعداد الثنائية بالطريقة نفسها التي نبني بها الأعداد في نظامنا التقليدي العشري الذي يكون فيه الأساس هو العدد 10، لكن بدلاً من منزلة الآحاد ومنزلة العشرات ومنزلة المئات، …إلخ، لدينا منزلة الواحد ومنزلة الاثنين ومنزلة الأربعة ومنزلة الثمانية، …إلخ، أي كما هو موضح في الجدول التالي:
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 2... |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | … |
لنمثِّل العدد 203 على سبيل المثال في الأساس العشري، إذ نعلم أننا نضع الرقم 3 في منزلة الآحاد، والرقم 0 في منزلة العشرات والرقم 2 في منزلة المئات، ويمثَّل هذا من خلال الأُسس exponents كما في الجدول التالي:
| 100 | 101 | 102 |
|---|---|---|
| 3 | 0 | 2 |
أو نمثلها بطريقة أخرى:
2x 102 + 3 x 100 = 200 + 3 = 203
لنمثِّل العدد نفسه بالنظام الثنائي، إذ سيكون لدينا الجدول التالي:
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
ويكافئ هذا:
27 + 26 + 23 + 21 + 20 = 128 + 64 + 8 + 2 + 1 = 203
أسس الحوسبة
قد تتساءل كيف لعدد بسيط أن يكون الأساس الذي بنيَت عليه كل الأمور المذهلة التي يستطيع الحاسوب تنفيذها، ورغم صعوبة تصديق ذلك إلا أنها الحقيقة، إذ يحتوي المعالج الموجود في حاسوبك على مجموعة معقدة -لكنها محدودة في النهاية- من التعليمات instructions التي يمكن تنفيذها على قيم مثل الجمع والضرب، …إلخ، إذ يُسنَد عدد إلى كل تعليمة من هذه التعليمات بصورة أساسية، حتى يمثَّل برنامج كامل بسلسلة من الأعداد فقط، أي أضف هذا إلى ذاك، اضرب بذاك، قسّم عليه، وهكذا، فإذا كان المعالج مثلًا يعلم أنّ العملية 2 هي الجمع، فإنّ العدد 252 قد يعني "اجمع 5 و 2 وخزِّن الناتج في مكان ما"، وتُعَدّ العمليات في الواقع أعقد بكثير طبعًا، إذ سنتناولها في فصل معمارية الحاسوب لاحقًا، لكن باختصار هذا هو الحاسوب.
كان بمقدور المرء في عهد البطاقات المثقَّبة punch-cards أن يرى بعينه الواحدات والأصفار التي تكوِّن مسار البرنامج من خلال النظر إلى الثقوب الموجودة على البطاقة، طبعًا تحوّل ذلك اليوم إلى آلية التخزين السريع والدقيق بواسطة قطبية الجزيئات الممغنطة الصغيرة مثل الأشرطة tapes أو الأقراص disks، والذي أتاح لنا حمل كميات هائلة تفوق التصور من البيانات في جيوبنا.
إنّ ترجمة هذه الأعداد إلى خدمات تنفع البشرية هي ما يجعل الحاسوب نافعًا لهذه الدرجة، وتتكوّن الشاشات مثلًا من ملايين البكسلات pixels المنفصلة، وكل منها صغير لدرجة لا تميّزه عين الإنسان، لكنها تكوِّن صورةً مكتملةً عندما تكون مجتمعةً، إذ يحتوي كل بكسل عمومًا على عناصر محدَّدة من الأحمر والأخضر والأزرق التي تكوِّن اللون الذي يعرضه، وبالتأكيد يمكن تمثيل هذه القيم بالأعداد التي بالطبع يمكن تمثيلها بالنظام الثنائي، وبالتالي يمكن تقسيم أيّ صورة إلى ملايين النقاط الفردية، وتُمثَّل كل نقطة بمجموعة من ثلاث قيم تمثِّل قيم الأحمر والأخضر والأزرق للبكسل، وبالتالي عندما يكون لدينا سلسلة طويلة من هذه الأعداد وتكون مُصاغةً بصورة صحيحة، فستتمكن أجهزة الفيديو في حاسوبك من تحويل هذه الأعداد إلى إشارات كهربائية لتشغيل وإيقاف البكسلات الفردية لعرض صورة.
سنبني بيئة الحوسبة الحديثة بأكملها في الكتاب بدءًا من اللبنة الأساسية هذه، أي من القاعدة إلى القمة إذا صح التعبير.
البتات bits والبايتات byts
يمكننا بصورة أساسية تمثيل أيّ شيء بعدد كما تحدثنا في الفقرات السابقة، ويمكن تحويله إلى النظام الثنائي وإجراء عمليات عليه بواسطة الحاسوب، إذ سنحتاج على الأقل لتمثيل جميع أحرف الأبجدية مثلًا إلى توليفات مختلفة وكافية لتمثيل جميع المحارف الصغيرة lower case والمحارف الكبيرة upper case والأعداد وعلامات الترقيم إلى جانب بعض الأمور الإضافية، ويعني هذا أننا ربما سنحتاج إلى حوالي 80 توليفة مختلفة.
إذا كان لدينا بِتّان، فيمكننا تمثيل 4 توليفات فريدة محتملة وهي 00 01 10 11؛ أما إذا كان لدينا ثلاث بِتّات، فيمكننا تمثيل 8 توليفات مختلفة، وبصورة عامة، إذا كان لدينا عدد n من البِتّات يمكننا تمثيل 2n توليفة فريدة.
تمنحنا 8 بِتّات 28 = 256 تمثيلًا فريدًا، وهذا عدد أكثر من كاف للتوليفات الأبجدية التي نحتاجها، كما أننا ندعو كل 8 بِتّات ببايت، كما أنّ حجم المتغير من نوع char هو بايت واحد في لغة C.
أسكي ASCII
يستطيع أيّ شخص اختلاق رابط بين الأحرف والأعداد عشوائيًا بما أنّ البايت يمكنه تمثيل أيّ قيمة بين 0 و 255، فقد تقرِّر الشركة المصنعة لبطاقات الفيديو مثلًا أنّ رقم 1 يمثل المحرف 'A'، لذا عندما ترسَل القيمة 1 إلى بطاقة الفيديو، ستعرض المحرف 'A' بحالته الكبيرة على الشاشة، وقد تقرِّر الشركة المصنعة للطابعة لسبب ما أن الرقم 1 يمثل 'z' بالحالة الصغيرة، وبالتالي سيتطلب عرض وطباعة الشيء نفسه تحويلات معقدة، ولتجنب حدوث ذلك ابتُكِرت الشيفرة المعيارية الأميركية لتبادل المعلومات American Standard Code for Information Interchange -أو ASCII اختصارًا-، وهذه الشيفرة مبنية على 7 بتات 7-bit code، أي توجد 27 أو 128 شيفرةً متاحةً.
ينقسم مجال الشيفرات إلى جزأين رئيسيين هما الشيفرات الغير قابلة للطباعة والشيفرات القابلة للطباعة، إذ تكون المحارف القابلة للطباعة مثل الأحرف الكبيرة والصغيرة والأعداد وعلامات الترقيم، في حين تكون المحارف الغير قابلة للطباعة مخصصةً للتحكم وتنفيذ عمليات مثل محارف الإرجاع carriage-return، أي العودة إلى بداية السطر الحالي دون النزول إلى السطر التالي، أو رن جرس الطرفية عند ورود المحرف Bell أو شيفرة القيمة الفارغة NULL الخاصة التي لا تمثل شيئًا على الإطلاق.
تكفي المحارف 127 الفريدة للغة الإنجليزية الأميركية، لكنها تصبح محدودةً جدًا عندما يريد المرء تمثيل المحارف السائدة في اللغات الأخرى وخاصةً اللغات الآسيوية التي قد تحتوي على عدة آلاف من المحارف الفريدة، وللحد من ذلك، تنتقل الأنظمة الحديثة من شيفرة أسكي إلى يونيكود Unicode التي تستخدِم ما يصل إلى 4 بايتات لتمثل محرفًا، وهذا يفسح مجالًا أكبر بكثير.
التكافؤ Parity
يبقى بت واحد من البايت فائضًا بما أنّ شيفرة الأسكي مبنية على 7 بتات فقط، ويمكن الاستفادة منه في تحقيق التكافؤ parity، إذ يُعَدّ شكلًا بسيطًا من أشكال التحقق من الأخطاء، فتخيّل حاسوبًا يستخدِم بطاقات مثقبة في عملية الإدخال، بحيث يمثِّل وجود الثقب البِتّ 1 وغيابه يمثل البِتّ 0، وستؤدي أية تغطية غير مقصودة لثقب ما إلى قراءة قيمة غير صحيحة وستتسبب في سلوك غير معرَّف.
يتيح التكافؤ إجراء فحص بسيط للبِتّات المؤلِّفة للبايت للتأكد من أنها قُرِئت بصورة صحيحة، ويمكننا تنفيذ التكافؤ الفردي أو الزوجي باستخدام البِتّ الفائض الذي نَعدّه بِتّ التكافؤ، فإذا كان عدد الواحدات في المعلومات المخزَّنة على البِتّات السبعة فرديًا، فسيضبط بت التكافؤ ويكون حينها التكافؤ فرديًا odd parity، وإذا كان عددها زوجيًا، فلا يضبط بِتّ التكافؤ؛ أما التكافؤ الزوجي Even parity، فهو عكس ذلك، فإذا كان عدد الواحدات زوجي، فسيُضبط بِتّ التكافؤ على الرقم 1، وبهذه الطريقة سينتج عن تغيّر بِتّ واحد خطأ تكافؤ يمكن اكتشافه.
الحواسيب ذات أنظمة 16 و 32 و 64 بت
لا تتسع جميع الأعداد في بايت أو مجموعة محددة من البايتات، فبفرض أن كان رصيدك المصرفي كبيرًا مثلًا فهو يحتاج إلى مجال أوسع مما يمكن أن يتسع في بايت واحد لتمثيله، وتتألف المعماريات الحديثة في الحواسيب حاليًا من أنظمة 32 بت على الأقل، وهذا يعني أنها تعمل مع 4 بايتات في وقت واحد عند المعالجة والقراءة أو الكتابة على الذاكرة، ونشير آنذاك إلى كل 4 بايتات بالكلمة word، وهذا مشابه للغة حيث تكوِّن الأحرف -أو البتات- الكلمات في جملة ما، والفارق في الحاسوب عن اللغة أنه تكون كل الكلمات بالحجم نفسه، وهو حجم المتغير من نوع int في اللغة C الذي يساوي 32 بِتّ، أما معماريات 64 بت الحديثة، يضاعف حجم عمل المعالج إلى 8 بايت بدلًا من 4 في معماريات 32 بت.
كيلوبايت وميغابايت وغيغابايت
تتعامل الحواسيب مع عدد كبير من البايتات وهذا ما يجعلها شديدة القوة، وبالتالي نحتاج إلى وسيلة للتحدث عن أعداد ضخمة من البايتات، والوسيلة البديهية لذلك هي استخدام بادئات نظام الوحدات الدولي International System of Units -أو SI اختصارًا- كما هو متّبع في معظم المجالات العلمية الأخرى، إذ يشير الكيلو مثلًا إلى 103 أو 1000 وحدة، بحيث يكون الكيلوغرام الواحد هو 1000 غرام.
يُعَدّ 1000 عددًا تقريبيًا round جيدًا في الأساس العشري، لكنه يمثَّل في النظام الثنائي بـ 1111101000 وهو ليس عددًا تقريبيًا، لكن 1024 أو 210 هو عدد تقريبي والذي يمثَّل في النظام الثنائي بـ 10000000000، وهو قريب جدًا من الكيلو في النظام العشري، أي العدد 1000 قريب من العدد 1024، وبالتالي أصبح 1024 بايت بطبيعة الحال يُعرَف بالكيلوبايت؛ أما الوحدة التالية في نظام الوحدات الدولي، فهي ميغا mega المقابلة لقيمة 106، كما تستمر البادئات بالازدياد بمقدار 103 المقابلة للتجميع المعتاد المكون من ثلاثة أرقام عند كتابة أعداد كبيرة، كما يصادف مجددًا أن تكون 220 قريبةً من تحديد نظام الواحدات الدولي للميغا في النظام العشري، أي 1048576 بدلًا من 1000000، فعند زيادة واحدات النظام الثنائي بالقوى من مضاعفات 10 تبقى قريبةً وظيفيًا من قيمة النظام العشري في نظام الواحدات الدولي، مع أنه يحيد قليلًا كل عامل متزايد عن دلالة أساس نظام الواحدات الدولي، وبالتالي فإنّ وحدات النظام العشري في نظام الواحدات الدولي قريبة بما يكفي على قيم النظام الثنائي، وقد شاع استخدامها لتلك القيم.
| الاسم | معامل النظام الثنائي | بايت | معامل النظام العشري القريب | بايت في النظام العشري |
|---|---|---|---|---|
| 1 كيلوبايت | 210 | 1024 | 103 | 1000 |
| 1 ميغابايت | 220 | 1.048.576 | 106 | 1.000.000 |
| 1 غيغابايت | 230 | 1.073.741.824 | 109 | 1.000.000.000 |
| 1 تيرابايت | 240 | 1.099.511.627.776 | 1012 | 1.000.000.000.000 |
| 1 بيتابايت | 250 | 1.125.899.906.842.624 | 1015 | 1.000.000.000.000.000 |
| 1 إكسابايت | 260 | 1.152.921.504.606.846.976 | 1018 | 1.000.000.000.000.000.000 |
قد يفيدك ترسيخ معامِلات النظام الثنائي في ذاكرتك كثيرًا في الربط السريع للعلاقة بين عدد البِتّات والأحجام التي يفهمها الإنسان، إذ يمكننا بسرعة مثلًا حساب إمكانية حاسوب بنظام 32 بِتّ أن يعالج ما يصل إلى 4 غيغابايت من الذاكرة من خلال ملاحظة إعادة التركيب (4) 22 + 230، وبالمثل يمكن أن تعالِج قيمة 64 بِتّ ما يصل إلى 16 إكسابايت، أي 260 + 24، كما يمكنك حساب ضخامة هذا العدد، ولتأخذ فكرةً عن مدى ضخامته، فيمكنك حساب المدة التي ستستغرقها في العد إلى 264 إذا عددت رقمًا واحدًا كل ثانية.
كيلوبت وميغابت وغيغابت
سيشار إلى السعات غالبًا بالبِتّات بدلًا من البايتات إلى جانب الارتباك الذي يحدث نتيجة العبء المفرط لتحويل واحدات نظام الواحدات الدولي SI بين النظامَين الثنائي والعشري، ويحدث هذا عمومًا عند التحدث في مجال الشبكات أو أجهزة التخزين، فربما لاحظت أنّ اتصال ADSL لديك يشار إليه بقيمة مثل 1500 كيلوبِت في الثانية، إن العملية الحسابية بسيطة، إذ نضرب بالعدد 1000 للكيلو ثم نقسِّم على 8 لنحوِّله إلى بايت ثم نقسِّمه على العدد 1024 لنحوله إلى كيلوبايت، وبالتالي تكون 1500 كيلوبِت في ثانية = 183 كيلوبايت في الثانية.
أقرَّت هيئة نظام الواحدات الدولي هذه الاستخدامات المزدوجة وحددت بادئات فريدةً للاستخدام الثنائي، إذ تقابل 1024 بايت بموجب المعيار كيبي بايت kibibyte، وهو اختصار للكيلوبايت الثنائي kilo binary byte وتُختصر بـ KiB؛ أما البادئات الأخرى، فلها بادئة مماثلة مثل ميبي بايتس MiB، ويمنع العرف المتَّبع إلى حد كبير استخدام هذه المصطلحات، لكنك قد تراها في بعض المؤلَّفات.
التحويل
يُعّدّ استخدام الحاسوب الطريقة الأسهل للتحويل بين الأنظمة، فبعد كل شيء هذا ما يبرع فيه. ومع ذلك، فمن المفيد معرفة كيفية إجراء التحويلات يدويًا.
تُعَدّ القسمة المتكررة الطريقة الأسهل للتحويل بين الأنظمة، بحيث نقسِّم ناتج القسمة بصورة متكررة على الأساس إلى أن يصبح ناتج القسمة صفرًا مع تدوين الباقي في كل خطوة، ثم ندوِّن الباقي بالعكس، أي نبدأ من الأسفل ونلحق العدد بالجهة اليمين في كل مرة، وسنذكر مثالًا للتوضيح، كما سيكون الأساس 2 نظرًا لأننا نحوِّل إلى النظام الثنائي.
| عملية القسمة | النتيجة | الباقي | اتجاه قراءة الباقي |
|---|---|---|---|
| 2 ÷ 20310 | 101 | 1 | |
| 2 ÷ 10110 | 50 | 1 | ↑ |
| 2 ÷ 5010 | 25 | 0 | ↑ |
| 2 ÷ 2510 | 12 | 1 | ↑ |
| 2 ÷ 1210 | 6 | 0 | ↑ |
| 2 ÷ 610 | 3 | 0 | ↑ |
| 2 ÷ 310 | 1 | 1 | ↑ |
| 2 ÷ 110 | 0 | 1 | ↑ |
ابدأ بقراءة الباقي من الأسفل وأضف كل عدد منه إلى اليمين لتحصل على النتيجة 11001011، وقد وجدنا فعلًا أنّ هذه القيمة في النظام الثنائي هي 203 في النظام العشري.
العمليات البوليانية Boolean Operations
اكتشف جورج بول عالم الرياضيات مجالًا كاملًا في الرياضيات يسمى جبر بُول Boolean Algebra، وعلى الرغم من أنّ اكتشافاته كانت في منتصف القرن التاسع عشر، إلا أنها أصبحت لاحقًا أساسيات علوم الحاسوب، ويُعَدّ جبر بول هو موضوع واسع النطاق، لذا سنتناول في هذا الكتاب بعض مبادئه الأساسية فقط حتى تستطيع بدء رحلة التعلم.
تأخذ العمليات البوليانية ببساطة دخلًا معينًا وتنتج خرجًا معينًا حسب قاعدة معينة، وأبسط عملية بوليانية مثلًا هي not، وهي تعكس قيمة معامِل operand الدخل؛ أما المعامِلات الأخرى، فتأخذ عادةً دخلين وتنتج خرجًا واحدًا.
يسهل تذكر العمليات البوليانية الأساسية المستخدَمة في علوم الحاسوب وقد أدرجناها في هذا الفصل، ومثلناها بجداول الحقيقة truth tables التي تبيِّن بمظهر بسيط جميع المدخلات والمخرجات المحتمَلة، ويقابل مصطلح حقيقي true القيمة 1 في النظام الثنائي.
معامل Not
تمثَّل عادةً بالرمز !، وهي تعكس قيمة الدخل فتحول 0 إلى 1 و 1 إلى 0.
| الدخل | الخرج |
|---|---|
| 1 | 0 |
| 0 | 1 |
معامل And
تذكَّر العبارة التالية: "تكون النتيجة حقيقيةً إذا كان الدخل الأول حقيقيًا و الدخل الثاني حقيقيًا" لكي يسهل عليك تذكُّر آلية عمل معامل and.
| الدخل الأول | الدخل الثاني | الخرج |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
معامل Or
تذكَّر العبارة التالية: "تكون النتيجة حقيقيةً إذا كان الدخل الأول حقيقيًا أو الدخل الثاني حقيقيًا" لكي يسهل عليك تذكُّر آلية عمل معامل or .
| الدخل الأول | الدخل الثاني | الخرج |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
معامل أو الحصرية Exclusive Or
تختصَر عبارة معامل أو الحصرية Exclusive Or بـ xor وهي حالة خاصة من معامِل or، بحيث يكون الخرج حقيقيًا عندما يكون أحد المدخَلين فقط حقيقيًا، وستدهشك الحيل المميزة التي يستطيع هذا المعامِل تنفيذها، لكنها ليست مستخدَمةً كثيرًا في النواة.
| الدخل الأول | الدخل الثاني | الخرج |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
استخدام العمليات البوليانية في الحواسيب
قد يصعب عليك تصديق أنّ أساس كل ما ينفِّذه حاسوبك هو تلك المعامِلات التي تحدثنا عنها، فالجامع النصفي half adder مثلًا هو أحد أنواع الدارات التي تتكون من العمليات البوليانية التي تجمع البِتّات، وقد سُمّي الجامع النصفي لأنه لا يعالج البتات الفائضة، وستبدأ في بناء كيان يجمع أعداد ثنائية طويلة من خلال وضع أكثر من جامع نصفي معًا، ثم أضف إليه بعض الذواكر الخارجية وستكون قد بنيت حاسوبًا.
تنفَّذ العمليات البوليانية من الناحية الإلكترونية في بوابات gates مصنوعة من الترانزستورات transistors، لذا لا بد أنك سمعت عن عدد الترانزستورات transistor counts وقانون مور وغيرها، وكلما زاد عدد الترانزستورات زاد عدد البوابات وزاد عدد الأشياء التي يمكنك جمعها، كما ستحتاج لبناء الحاسوب الحديث إلى عدد هائل من البوابات وعدد هائل من الترانزستورات، إذ تحتوي بعض معالِجات إيتانيوم Itanium الحديثة على حوالي 460 مليون ترانزستور.
العمل بالنظام الثنائي في اللغة C
توجد واجهة مباشرة لجميع المعامِلات التي ذكرناها في اللغة C، ويشرح الجدول التالي هذه المعامِلات:
| المعامل | اصطلاحه في اللغة C |
|---|---|
| not | ! |
| and | & |
| or | \ |
| xor | ^ |
نطبّق هذه المعامِلات على المتغيرات لتعديل البِتّات ضمن المتغير، ولكن يجب علينا أولًا أن نتناول شرحًا للترميز الست العشري قبل أن نستعرض أمثلةً عن ذلك.
النظام الست عشري Hexadecimal
يشير النظام الست عشري إلى نظام أساسه العدد 16، والسبب الوحيد لاستخدامنا هذا النظام في علوم الحاسوب هو أنه يسهِّل على الإنسان التفكير في الأرقام الثنائية، إذ يسهِّل عدم تعامل الحواسيب إلا مع النظامَين الثنائي والست عشري على الإنسان محاولته التعامل مع الحاسوب.
لكن لماذا اختير الأساس 16؟ إن الخيار الطبيعي هو الأساس 10 لأننا معتادون على التفكير في الأساس 10 حسب نظامنا العددي اليومي، لكن الأساس 10 لا يتوافق كثيرًا مع النظام الثنائي؛ إذ نحتاج إلى أربع بتات لتمثيل 10 عناصر مختلفة في النظام الثنائي، لكن تلك الأربع بتات توفر لنا ست عشرة توليفة محتمَلة، لذا نحن أمام احتمالين؛ إما أن نختار الطريقة شديدة التعقيد المتمثلة في محاولة التحويل بين النظام العشري والثنائي، أو أن نختار الطريقة السهلة وننشئ نظامًا عدديًا أساسه العدد 16 وهو النظام الست عشري.
يستخدِم النظام الست عشري الأعداد القياسية في النظام العشري مع إضافة الأحرف A B C D E F التي تشير إلى الأعداد 10 11 12 13 14 15، مع الانتباه إلى بدء العدّ من الصفر، فمتى ما رأيت عددًا مسبوقًا بـ 0x، فاعلم أنه يدل على عدد ست عشري، وكما ذكرنا أنه سنحتاج إلى أربع بتات بالضبط لتمثيل 16 نمط مختلف في النظام الثنائي، لذا يمثِّل كل عدد ست عشري أربع بتات بالضبط، ويجب أن تعدّه تمرينًا لتتعلم الجدول التالي عن ظهر قلب.
| النظام الست عشري | النظام الثنائي | النظام العشري |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
بالطبع لا يوجد سبب للتوقف عن متابعة النمط (مثل تحديد G للقيمة 16)، ولكن القيم الستة عشرة هي موازنة ممتازة بين تقلبات الذاكرة البشرية وعدد البتات التي يستخدمها الحاسوب، كما ستجد أيضًا الأساس 8 مستخدَمًا أحيانًا في سماحيات الملفات في أنظمة يونكس مثلًا، ونمثِّل ببساطة أعدادًا أكبر من البتات بأعداد أكثر، إذ يمكن مثلًا تمثيل متغير يتألف من ستة عشر بت بالقيمة 0xAB12، وما عليك سوى تحويل كل رقم على حدى وفقًا للجدول السابق ثم جمع القيم معًا لتجد مقابلها في النظام الثنائي، أي لتكون القيمة المقابلة للقيمة 0xAB12 هي العدد الذي يتألف من 16 بت في النظام الثنائي 1010101100010010، كما نستطيع التحويل من النظام الثنائي إلى النظام الست عشري بعكس تلك العملية، كما نستطيع الاستعانة بنهج القسمة المتكررة ذاته لتغيير أساس أي عدد، فلإيجاد قيمة العدد 203 بالنظام الست عشري مثلًا:
| عملية القسمة | النتيجة | الباقي | اتجاه قراءة الباقي |
|---|---|---|---|
| 16 ÷ 20310 | 12 | 11 (0xB) | |
| 16 ÷ 1210 | 0 | 12 (0xC) | ↑ |
لذا تكون قيمة 203 في النظام الست عشري هي 0xCB
الاستخدام العملي للأنظمة العددية
سنطلع فيما يلي على الاستخدام العملي للأنظمة العددية وما النتائج العملية التي ممكن أن نحصل عليها.
استخدام النظام الثنائي في الشيفرات البرمجية
تُعَدّ برمجة حاسوب بلغات عالية المستوى high level دون معرفة أيّ شيء عنه هو أمر عملي بحت على الرغم من أنّ النظام الثنائي هو اللغة الأساسية لكل حاسوب، وعلى أية حال نهتم ببعض مبادئ النظام الثنائي الأساسية والمستخدَمة بصورة متكررة بالنسبة شيفرة البرمجية منخفضة المستوى low level code التي سنتناولها.
التقنع والرايات
سنشرح مفهوم عمليتي التقنع والرايات وكيفية تطبيقهما عمليًا على الأنظمة العددية.
التقنع Masking
من المهم غالبًا جعل البنى والمتغيرات تحجز مساحةً بأكثر طريقة فعالة ممكنة في الشيفرة البرمجية منخفضة المستوى، وقد يتضمن هذا في بعض الحالات تعبئة packing متغيرين -يكونان مرتبطين ببعضهما عمومًا- بمتغير واحد بطريقة فعالة.
تذكَّر أنّ كل بِتّ يمثل حالتين، فإذا علمنا مثلًا أنّ للمتغير 16 حالة محتمَلة فقط، فيمكن تمثيله بـ 4 بِتّات، أي 24 = 16 قيمةً فريدةً، لكن أصغر نوع يمكننا التصريح عنه في اللغة C هو 8 بتات وهو نوع char أي محرف، فإما نهدر أربع بتات، أو نجد طريقةً نستخدِم فيها تلك البتات الفائضة، ويمكننا تحقيق ذلك بسهولة من خلال عملية التقنُّع التي تتبع قواعد العمليات المنطقية لاستخراج القيم وهي موضَّحة في الصورة التالية.
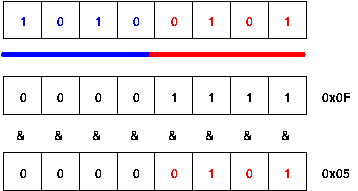
نحتفظ بقيمتَين منفصلتين تتألفان من 4 بِتّات داخل محرف واحد يتألف من 8 بِتّات، إذ نُعِدّ البِتّات الأربعة الأولى (الزرقاء) قيمةً واحدةً والبِتَات الأربعة الأخيرة (الحمراء) قيمةً أخرى، وقد ضبطنا القناع على تعيين قيمة البتات الأربعة الأخيرة 1 (0x0F) لاستخراج البِتّات الأربعة السفلية، وبما أنّ المعامِل and المنطقي سيضبط البت إلى 1 فقط إذا كانت قيمة كلا البتّين 1، فستخفي البِتّات التي ضبطنا قيمتها على 0 في القناع وهي البتات التي لا تهمنا بصورة فعالة.
(التقنُّع)
نقلب القناع للحصول على البِتّات الأربعة الأولى (الزرقاء)، أي نضبط البِتّات الأربعة الأولى على القيمة 1 والبتات الأربعة الأخيرة على القيمة 0، وستلاحظ أنّ نتيجة هذا ستكون 0000 1010 أو 0xA0 في النظام الست عشري، على حين أننا نريد فعلًا أن نعتبر هذه القيمة الفريدة المؤلفة من 4 بتات 1010 أي 0x0A، ولوَضع هذه البتات في الموضع الصحيح نستخدِم المعامِل right shift أربع مرات، والذي سيمنحنا القيمة النهائية 1010 0000.
1 #include <stdio.h> #define LOWER_MASK 0x0F #define UPPER_MASK 0xF0 5 int main(int argc, char* argv[]) { /* قيمتان بحجم 4 بتات مخزنتان في متغير بحجم 8 بتات */ 10 char value = 0xA5; char lower = value & LOWER_MASK; char upper = (value & UPPER_MASK) >> 4; printf("Lower: %x\n", lower); 15 printf("Upper: %x\n", upper); }
يتطلب ضبط البِتّات المعامِل or المنطقي، لكن سنستخدم الأصفار 0 بدلًا من استخدام الواحدات 1 على أساس قناع، كما ننصحك برسم مخطط مشابه للصورة السابقة والعمل على ضبط البِتّات بواسطة المعامِل or المنطقي.
الرايات flags
يتضمن البرنامج غالبًا عددًا كبيرًا من المتغيرات التي توجد فقط بصيغة رايات flags في شروط معينة، فآلة الحالات state machine مثلًا هي خوارزمية تتنقل عبر عدد من الحالات المختلفة، لكنها لا تتواجد إلا في حالة واحدة فقط في المرة الواحدة، ولنقل أنه لديها 8 حالات مختلفة، إذ نستطيع بسهولة التصريح عن 8 متغيرات مختلفة، بحيث يكون هناك متغير واحد لكل حالة، لكن في كثير من الحالات يفضَّل التصريح عن متغير واحد مؤلف من 8 بتات وتعيين راية لكل بِتّ للإشارة إلى حالة معينة.
تُعَدّ الرايات حالةً خاصةً من التقنُّع، لكن يمثِّل كل بِتّ حالةً بوليانيةً معينةً، أي تشغيل أو إيقاف، كما يمكن لمتغير مؤلَّف من عدد n من البتات أن يحمل العدد n من الرايات المختلفة، ويُعَدّ نموذج الشيفرة البرمجية التالي هو مثال نموذجي على استخدام الرايات، وستلحظ اختلافات في هذه الشيفرة البرمجية الأساسية في معظم الأحيان.
1 #include <stdio.h> /* * تعريف كافة الرايات الثمانية المحتمَلة لمتغير بحجم 8 بتات 5 * الاسم النظام الست عشري النظام الثنائي */ #define FLAG1 0x01 /* 00000001 */ #define FLAG2 0x02 /* 00000010 */ #define FLAG3 0x04 /* 00000100 */ 10 #define FLAG4 0x08 /* 00001000 */ /* ... وهكذا */ #define FLAG8 0x80 /* 10000000 */ int main(int argc, char *argv[]) 15 { char flags = 0; /* متغير بحجم 8 بتات */ /* ضبط الرايات بمعامل orالمنطقي */ flags = flags | FLAG1; /* ضبط الراية الأولى */ 20 flags = flags | FLAG3; /* ضبط الراية الثالثة /* تحقق من الرايات بالمعامل and المنطقي. إذا كانت الراية مضبوطة بالقيمة 1 * سيرجع المعامل and قيمة 1 * if مما سيحقق الشرط الوارد في */ 25 if (flags & FLAG1) printf("FLAG1 set!\n"); /* سيكون هذا بالطبع غير صحيح */ if (flags & FLAG8) 30 printf("FLAG8 set!\n"); /* تحقق من عدة رايات بواسطة or المنطقي * سيمرر هذا لأن الراية الأولى مضبوطة */ if (flags & (FLAG1|FLAG4)) 35 printf("FLAG1 or FLAG4 set!\n"); return 0; }
ترجمة -وبتصرف- للقسم Binary — the basis of computing من الفصل Chapter 2. Binary and Number Representation من كتاب Computer Science from the Bottom Up.












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.