إلكونت جافاسكريبت هياكل البيانات: الكائنات والمصفوفات في جافاسكريبت

اقتباس

لقد سئلت مرتين من قبل أني لو أَدخلتُ إلى الآلة أرقامًا خاطئةً فهل سأحصل على إجابات صحيحة؟ وإني في الحقيقة لعاجز عن فهم هذا الخلط في الفِكر الذي يجعل العقل يثير مثل هذا السؤال. ـــ تشارلز بابج Charles Babbage، مقاطع من حياة فيلسوف (1864).

تشكل الأعداد، والقيم البوليانية، والسلاسل، الذرات التي تُبنى منها هياكل البيانات في مجال هندسة البرمجيات وعلوم الحاسوب، وستحتاج عند عملك في البرمجة إلى أكثر من ذرة واحدة، إذ تسمح لنا الكائنات objects بتجميع القيم -بما في ذلك الكائنات الأخرى-، من أجل بناء هياكل أكثر تعقيدًا.

كانت البرامج التي أنشأناها حتى الآن في فصول هذه السلسلة محدودة إذ عملت فقط على أنواع بسيطة من البيانات، وسنتحدّث في هذا المقال عن الهياكل الأساسية للبيانات، كما ستعرف بنهايته ما يكفيك للبدء بكتابة برامج مفيدة، وسنمر فيه على بعض الأمثلة الواقعية نوعًا ما، متعرضين للمفاهيم أثناء تطبيقها على المشاكل المطروحة، كما سنبني الشيفرة التوضيحية غالبًا على الدوال والروابط التي شُرحت من قبل.

الإنسان المتحول إلى سنجاب

يتوهم سمير أنه يتحوّل إلى قارض فروي صغير ذو ذيل كثيف، وذلك من حين لآخر، وغالبًا بين الساعة الثامنة والعاشرة مساءً. وهو سعيد نوعًا ما لأنه غير مصاب بالنوع الشائع للاكتيريا السريرية classic lycanthropy، أو الاستذئاب -وهي حالة تجعل الشخص يتوهم أنه يتحول إلى حيوان، ويكون ذئبًا في الغالب-، فالتحول إلى سنجاب أهون من التحول إلى ذئب! إذ ليس عليه القلق إلا من أن يؤكل من قطة جاره، بدلاً من خشية أكل جاره بالخطأ.

لقد قرر إغلاق أبواب غرفته ونوافذها في الليل، ووضع بعض حبات البندق على الأرض، وذلك بعد مرتين من إيجاد نفسه يستيقظ على غصن رقيق غير مستقر في شجرة بلوط، عاري الجسد مشوش الذهن.

ولعلّ ذلك تكفّل بمسألتي القطة وشجرة البلوط، غير أنّ سمير يريد معالجة نفسه من حالته هذه بالكليّة، وقد لاحظ أنّ حالات التحول تلك غير منتظمة، فلا بد من وجود شيء ما يستفزها أو يبدؤها، وقد ظن لفترة أنّ شجرة البلوط هي السبب، إذ حدثت بضع مرات بجانبها، لكن تبين له أنّ تجنب أشجار البلوط لم يوقف المشكلة.

رأى سمير أن يغّير منهجه في التفكير إلى سلوك علمي، فبدأ بتسجيل يومي لكل ما يفعله في اليوم وما إن كان قد تحوّل أم لا، وهو يأمل بهذه البيانات حصر الظروف التي تؤدي إلى التحولات. والآن، بإسقاط ما سبق على موضوع هذا المقال، فأول شيء يحتاجه هو بنية بيانات لتخزين هذه المعلومات، أليس كذلك؟

مجموعات البيانات

إذا أردت العمل مع كميات كبيرة من البيانات الرقمية، فعليك أولًا إيجاد طريقة لتمثيلها في ذاكرة الحواسيب، فعلى سبيل المثال، إذا أردنا تمثيل تجميعة من الأرقام 2، و3، و5، و7، و11، فسنستطيع حل الأمر بأسلوب مبتكر باستخدام السلاسل النصية -إذ لا حد لطول السلسلة النصية، وعليه نستطيع وضع بيانات كثيرة فيها- واعتماد ‎"2 3 5 7 11"‎ على أنه التمثيل الخاص بنا، لكن هذا منظور غريب ومستهجن، إذ يجب استخراج الأعداد بطريقة ما، وإعادة تحويلها إلى أعداد من أجل الوصول إليها.

توفر جافاسكربت بدلًا من السلوك السابق، نوع بيانات يختص بتخزين سلاسل القيم، وهو المصفوفة array، والتي تُكتب على أساس قائمة من القيم بين قوسين مربعين، ومفصولة بفاصلات إنجليزية Comma، انظر كما يلي:

let listOfNumbers = [2, 3, 5, 7, 11];
console.log(listOfNumbers[2]);
// → 5
console.log(listOfNumbers[0]);
// → 2
console.log(listOfNumbers[2 - 1]);
// → 3

كذلك تَستخدِم الصيغة التي نحصل بها على العناصر داخل مصفوفة ما، الأقواس المربعة أيضًا، حيث يأتي قوسان مربعان بعد تعبير ما مباشرةً، ويحملان بينهما تعبيرًا آخرًا، إذ يبحثان في التعبير الأيسر عن عنصر يتوافق مع الفهرس index المعطى في التعبير المحصور بينهما.

الفهرس الأول للمصفوفة هو الصفر وليس الواحد، لذا يُسترد العنصر الأول باستخدام listOfNumbers[0]‎، وإن كنت جديدًا على علوم الحاسوب، فسيمر وقت قبل اعتياد بدء العد على أساس الصفر، وهو تقليد قديم في التقنية وله منطق مبني عليه، لكن كما قلنا، ستأخذ وقتك لتتعود عليه؛ ولتريح نفسك، فكر في الفهرس على أنه عدد العناصر التي يجب تخطيها بدءًا من أول المصفوفة.

الخصائص

رأينا في الفصول السابقة بعض التعبيرات المثيرة للقلق، مثل: myString.lengthالتي نحصل بها على طول السلسلة النصية، وMath.max التي تشير إلى الدالة العظمى، حيث تصل هذه تعبيرات إلى خصائص قيمة ما. ففي الحالة الأولى نصل إلى خاصية الطول للقيمة الموجودة في myString، أما في الثانية فسنصل إلى الدالة العظمى max في كائن Math، وهو مجموعة من الثوابت والدوال الرياضية.

تحتوي جميع قيم جافاسكربت تقريبًا على خصائص، باستثناء null، وundefined، إذ ستحصل على خطأ إذا حاولت الوصول إلى خاصية إحدى هذه القيم.

null.length;
// → TypeError: null has no properties

الطريقتان الرئيسيتان للوصول إلى الخصائص في جافاسكربت، هما: النقطة .، والأقواس المربعة []، حيث تصل كل من value.x، وvalue[x]‎ مثلًا، إلى خاصية ما في value، لكن ليس إلى الخاصية نفسها بالضرورة، ويكمن الفرق في كيفية تفسير x، فحين نستخدم النقطة فإن الكلمة التي تليها هي الاسم الحرفي للخاصية؛ أما عند استخدام الأقواس المربعة فيُقيَّم التعبير الذي بين الأقواس للحصول على اسم الخاصية.

في حين تجلب value.x خاصيةً اسمها x لـ value، فستحاول value[x]‎ تقييم التعبير x، وتستخدم النتيجة -المحوَّلة إلى سلسلة نصية- على أساس اسم للخاصية، لذا فإن كنت على علم بأنّ الخاصية التي تريدها تحمل الاسم "color"، فتقول value.color؛ أما إن أردت استخراج الخاصية المسماة بالقيمة المحفوظة في الرابطة i، فتقول value‎.

واعلم أنّ أسماء الخصائص ما هي إلا سلاسل نصية، فقد تكون أي سلسلة نصية، لكن صيغة النقطة لا تعمل إلا مع الأسماء التي تبدو مثل أسماء رابطات صالحة. فإذا أردت الوصول إلى خاصية اسمها "2" أو "John Doh"، فيجب عليك استخدام الأقواس المربعة: value[2]‎، أو value ["John Doh"]‎.

تُخزَّن العناصر في المصفوفة على أساس خصائص لها، باستخدام الأعداد على أساس أسماء للخصائص، وبما أنك لا تستطيع استخدام الصياغة النقطية مع الأرقام، وتريد استخدام رابطة تحمل الفهرس، فيجب عليك استخدام صيغة الأقواس للوصول إليها.

تخبرنا خاصية length للمصفوفة كم عدد العناصر التي تحتوي عليها، واسم الخاصية ذاك هو اسم رابطة صالح، كما نعرِّف اسمه مسبقًا، لذلك نكتب array.length للعثور على طول المصفوفة، وذلك أسهل من كتابة array["length"]‎.

التوابع Methods

تحتوي قيم السلاسل النصية وقيم المصفوفات على عدد من الخصائص التي تحمل قيمًا للدالة، إضافةً إلى خاصية length، كما في المثال التالي:

let doh = "Doh";
console.log(typeof doh.toUpperCase);
// → function
console.log(doh.toUpperCase());
// → DOH

كل سلسلة لها خاصية toUpperCase، إذ تعيد عند استدعائها نسخةً من السلسلة التي تم فيها تحويل جميع الأحرف إلى أحرف كبيرة. وبالمثل، تسير خاصية toLowerCase في الاتجاه العكسي. ومن المثير أنّ الدالة لديها وصول لسلسلة "Doh" النصية، وهي القيمة التي استدعينا خاصيتها، رغم أن استدعاء toUpperCase لا يمرر أي وسائط، وسننظر في تفصيل كيفية حدوث ذلك في المقال السادس.

تسمى الخصائص التي تحتوي على دوال توابعًا للقيم المنتمية إليها، فمثلًا، يُعَد toUpperCase تابعًا لسلسلة نصية، ويوضح المثال التالي تابعَيْن يمكنك استخدامهما للتعامل مع المصفوفات:

let sequence = [1, 2, 3];
sequence.push(4);
sequence.push(5);
console.log(sequence);
// → [1, 2, 3, 4, 5]
console.log(sequence.pop());
// → 5
console.log(sequence);
// → [1, 2, 3, 4]

يضيف تابع push قيمًا إلى نهاية مصفوفة ما؛ أما تابع pop فيفعل العكس تمامًا، حيث يحذف القيمة الأخيرة في المصفوفة ويعيدها. وهذه الأسماء السخيفة هي المصطلحات التقليدية للعمليات على المكدِّس stack، والمكدِّس في البرمجة هو أحد هياكل البيانات التي تسمح لك بدفع القيم إليها وإخراجها مرة أخرى بالترتيب المعاكس، بحيث يُبتدأ بإزالة العنصر الذي أضيف آخر مرة، وذلك استنادًا على منطق "آخرهم دخولًا أولهم خروجًا". ولعلك تذكر دالة مكدس الاستدعاءات من المقال السابق الذي يشرح الفكرة نفسها.

الكائنات Objects

بالعودة إلى سمير المتحوِّل، فيمكن تمثيل مجموعة من المدخلات اليومية للسجل بمصفوفة، لكن مدخلات التسجيلات تلك فيها أكثر من مجرد عدد أو سلسلة نصية، فكل إدخال يحتاج إلى تخزين قائمة بالأنشطة، وقيمة بوليانية توضح ما إذا كان سمير قد تحول إلى سنجاب أم لا، ونحن نود تجميع ذلك في قيمة واحدة، ثم نضع تلك القيم المجمعة في مصفوفة من مدخلات السجل، وبما أن القيم التي من نوع object هي مجرد تجميعات عشوائية من الخصائص، فيمكن إنشاء كائن باستخدام الأقواس في صورة تعبير. انظر كما يلي:

let day1 = {
  squirrel: false,
  events: ["work", "touched tree", "pizza", "running"]
};
console.log(day1.squirrel);
// → false
console.log(day1.wolf);
// → undefined
day1.wolf = false;
console.log(day1.wolf);
// → false

لدينا قائمة بالخصائص داخل الأقواس مفصولة بفواصل إنجليزية ,، ولكل خاصية اسم متبوع بنقطتين رأسيتين وقيمة، وحين يُكتب كائن في عدة أسطر، فإن وضع إزاحة بادئة له كما في المثال يجعل قراءته أيسر، والخصائص التي لا تحتوي أسماؤها على أسماء رابطات صالحة أو أرقام صالحة، يجب وضعها داخل علامتي اقتباس. انظر كما يلي:

let descriptions = {
  work: "Went to work",
  "touched tree": "Touched a tree"
};

هذا يعني أن الأقواس لها معنيان في جافاسكربت، فهي تبدأ بكتلة من التعليمات البرمجية إن جاءت في بداية تعليمة ما؛ أما إذا جاءت في موضع آخر، فستصف كائنًا ما. ولعلّ من حسن حظنا أننا نادرًا ما سنحتاج إلى بدء تعليمة بكائن داخل قوسين، لذا لا تشغل بالك كثيرًا بشأن هذا الغموض والإشكال.

كذلك سيعطيك قراءة خاصية غير موجودة القيمة undefined، ونستطيع استخدام عامل = لإسناد قيمة إلى تعبيرِ خاصية ليغير القيمة الموجودة أصلًا، أو ينشئ خاصيةً جديدةً للكائن إن لم تكن.

بالعودة إلى نموذجنا لمجسات الأخطبوط الذي ذكرناه سابقًا عن الرابطة Binding، فإن رابطات الخصائص متشابهة، فهي تلتقط القيم، لكن قد تكون بعض الرابطات والخصائص الأخرى ممسكة بتلك القيم نفسها، وعليه تستطيع النظر إلى الكائنات على أنها أخطبوطات لها عدد لا نهائي من المجسات، ولكل منها اسم منقوش عليها.

يقطع عامل delete أحد المجسات من الأخطبوط السابق، وهذا العامل هو عاملٌ أحادي، كما يحذف الخاصية المسماة من الكائن حين يُطبَّق على خاصيته، وذلك ممكن رغم عدم شيوعه.

let anObject = {left: 1, right: 2};
console.log(anObject.left);
// → 1
delete anObject.left;
console.log(anObject.left);
// → undefined
console.log("left" in anObject);
// → false
console.log("right" in anObject);
// → true

عند تطبيق العامل الثنائي inعلى سلسلة نصية وكائن، فسيخبرك إذا كان الكائن به خاصية باسم تلك السلسلة النصية، والفرق بين جعل الخاصية undefined وحذفها على الحقيقة، هو أنّ الكائن ما زال يحتفظ بالخاصية في الحالة الأولى مما يعني عدم حمله لقيمة ذات شأن؛ أما في الحالة الثانية فإن الخاصية لم تَعُدْ موجودة، وعليه فستعيد in القيمة false.

تُستخدَم دالة Object.keys لمعرفة الخصائص التي يحتوي عليها الكائن، وذلك بإعطائها كائنًا، فتعيد مصفوفةً من السلاسل النصية التي تمثل أسماء خصائص الكائن. انظر كما يلي:

console.log(Object.keys({x: 0, y: 0, z: 2}));
// → ["x", "y", "z"]

تُستخدَم دالة Object.assign لنسخ جميع الخصائص من كائن إلى آخر، انظر كما يلي:

let objectA = {a: 1, b: 2};
Object.assign(objectA, {b: 3, c: 4});
console.log(objectA);
// → {a: 1, b: 3, c: 4}

وتكون المصفوفات حينئذ نوعًا من الكائنات المتخصصة في تخزين سلاسل من أشياء بعينها، وإذا قيَّمت typeof[]‎، فستُنتج "object"، وسترى هذه المصفوفات كأخطبوطات طويلة بمجساتها في صف أنيق له عناوين من الأعداد. انظر الآن إلى السجل journal الذي يحتفظ به سمير في صورة مصفوفة من الكائنات:

let journal = [
  {events: ["work", "touched tree", "pizza",
            "running", "television"],
   squirrel: false},
  {events: ["work", "ice cream", "cauliflower",
            "lasagna", "touched tree", "brushed teeth"],
   squirrel: false},
  {events: ["weekend", "cycling", "break", "peanuts",
            "juice"],
   squirrel: true},
  /* and so on... */
];

قابلية التغير Mutability

إذا كنت قد قرأت الفصول السابقة، فسترى أنّ أنواع القيم التي تحدثنا عنها من أعداد، وسلاسل نصية، وقيم بوليانية، لا يمكن تغييرها؛ صحيح أنك تستطيع جمعها واستخراج قيم أخرى منها، لكن بمجرد أخذها قيمة لسلسلة نصية فلن تتغير بعدها، وسيبقى النص داخلها كما هو دون تغير، فمثلًا، إن كانت لديك سلسلة نصية تحتوي على "cat"، فلن تستطيع شيفرة أخرى تغيير محرف في هذه السلسلة لتكون "rat".

أما الكائنات فلها شأن آخر، إذ تستطيع تغيير خصائصها، حيث تتخذ قيمة الكائن محتويات مختلفة في كل مرة، كما رأينا قبل قليل أنه يمكن تعديل قيم الكائنات.

حين يكون لدينا عددان 120، و120، فسنقول أنهما نفس العددين سواءً أشارا إلى البتات الحقيقية نفسها أم لا، أما مع الكائنات فهناك فرق بين وجود مرجعين إلى الكائن نفسه، وبين وجود كائنين مختلفين يحتويان نفس الخصائص، انظر الشيفرة التالية:

let object1 = {value: 10};
let object2 = object1;
let object3 = {value: 10};

console.log(object1 == object2);
// → true
console.log(object1 == object3);
// → false

object1.value = 15;
console.log(object2.value);
// → 15
console.log(object3.value);
// → 10

تلتقط رابطتيobject1، وobject2 الكائن نفسه، لهذا ستتغير قيمة object2 إذا تغير object1، فيقال أنّ لهما "الهوية" نفسها إن صح التعبير؛ أما الرابطة object3، فتشير إلى كائن آخر يحتوي على خصائص object1 نفسها، لكنه منفصل ومستقل بذاته.

قد تكون الروابط نفسها متغيرة أو ثابتة، لكن هذا منفصل عن الطريقة التي تتصرف بها قيمها، ورغم أن القيم العددية لا تتغير، إلا أنك تستطيع استخدام الرابطة let لمتابعة عدد متغير من خلال تغيير القيمة التي تشير الرابطة إليها، وبالمثل، فرغم أن تعريف كائن بالرابطة const سيظل يشير إلى الكائن نفسه ولا يمكن تغييرها لاحقًا، إلا أن محتويات هذا الكائن قابلة للتغيير، كما في المثال التالي:

const score = {visitors: 0, home: 0};
// This is okay
score.visitors = 1;
// This isn't allowed
score = {visitors: 1, home: 1};

يوازن العامل == بين الكائنات من منظور هويتها، فلا يعطي true إلا إذا كان لكلا الكائنين القيمة نفسها تمامًا؛ أما عند موازنة كائنات مختلفة، فسيعطي false حتى ولو كان لهذه الكائنات الخصائص نفسها، وعليه فليس هناك عملية موازنة "عميقة" في جافاسكربت توازن بين الكائنات من خلال محتوياتها، لكن من الممكن كتابة ذلك بنفسك.

سجل المستذئب

نعود إلى سمير الذي يظن بأنّه يتحول إلى حيوان في الليل، إذ يبدأ مفسِّر جافاسكربت الخاص به، ويضبط البيئة التي يحتاجها من أجل سجله journal، انظر كما يأتي:

let journal = [];

function addEntry(events, squirrel) {
  journal.push({events, squirrel});
}

لاحظ أنّ الكائن الذي أضيف إلى السجل يبدو غريبًا نوعًا ما، فبدلًا من التصريح عن الخصائص مثل events: events، فهو لا يزيد عن إعطاء اسم الخاصية فقط. ويُعَدّ هذا الأسلوب اختصارًا مشيرًا إلى الشيء نفسه، أي إذا كان اسم الخاصية موضوع بين قوسين وليس متبوعًا بقيمة، فستؤخذ قيمته من الرابطة التي تحمل الاسم نفسه؛ لذا، ففي كل ليلة عند العاشرة مساءً -أو في الصباح التالي أحيانًا-، يسجل سمير يومه كالتالي:

addEntry(["work", "touched tree", "pizza", "running",
          "television"], false);
addEntry(["work", "ice cream", "cauliflower", "lasagna",
          "touched tree", "brushed teeth"], false);
addEntry(["weekend", "cycling", "break", "peanuts",
          "juice"], true);

وهو ينوي اتباع أسلوب إحصائي عند حصوله على نقاط بيانات كافية، وذلك لرؤية أيَّ تلك الأحداث هي التي تحث تحوله إلى حيوان ليلًا.

يختلف المتغير في الإحصاء عن المتغير البرمجي، إذ يكون لدينا مجموعة من المقاييس، بحيث يقاس كل متغير بها جميعًا، وتُمثَّل علاقة الترابط Correlation بين المتغيرات بقيمة بين -1، و1، وعلاقة الترابط هي مقياس اعتمادية المتغير الإحصائي على متغير آخر. فإذا كانت قيمة علاقة الترابط هذه صفرًا، فهذا يعني أنّ المتغيرين غير مرتبطان ببعضهما؛ أما إذا كان 1، فهذا يعني أنّ المتغيرين متطابقان تمامًا. بحيث إذا كنت تعرف أحدهما، فأنت تعرف الأخر يقينًا؛ أما إذا كانت قيمة علاقة الترابط تلك -1، فهذا يعني أنهما متطابقان لكنهما متقابلان، بحيث إن كان الأول true، فالآخر false.

نستخدم معامِل فاي ϕ لحساب مقياس علاقة الترابط بين متغيرين بوليانيين، وهي معادلة يكون دخلها جدول تردد يحتوي على عدد المرات التي لوحظت مجموعات المتغيرات فيها؛ ويصف الخرج علاقة الترابط بينها بحيث يكون عددًا بين -1، و1.

فمثلًا، سنأخذ حدث تناول البيتزا ونضع ذلك في جدول تردد مثل التالي، حيث يشير كل عدد إلى عدد المرات التي وقعت فيها هذه المجموعة في قياساتنا:

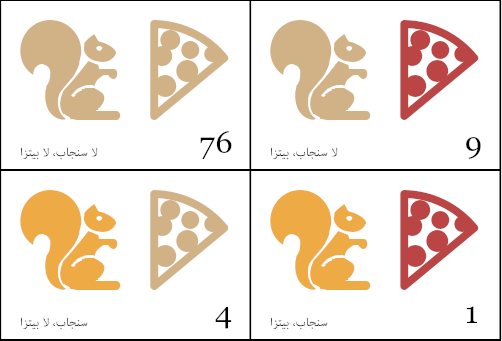
فإذا سمينا هذا الجدول بجدول n مثلًا، فإننا سنستطيع حساب ϕ باستخدام المعادلة التالية:

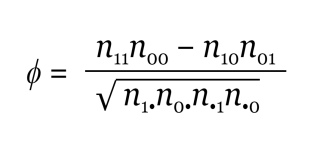
ولا تشغل نفسك بشأن الرياضيات كثيرًا ها هنا، حيث وُضِعت هذه المعادلة لتحويلها إلى جافاسكربت.

تشير الصيغة n₀₁ إلى عدد القياسات التي يكون فيها المتغير الأول squirrel "السنجاب" غير متحقق أو خطأ false، والمتغير الثاني pizza "البيتزا" متحقق أو صحيح true، ففي جدول البيتزا مثلًا، تكون قيمة n₀₁ هي 9.

تشير القيمة n_1•‎ إلى مجموع القياسات التي كان فيها المتغير الأول متحققًا -أي true-، وهي 5 في الجدول المثال. بالمثل، تشير n_•0‎ إلى مجموع القياسات التي كان فيها المتغير الثاني يساوي false.

لذا سيكون الجزء الموجود أعلى خط الفصل في جدول البيتزا 1×76−4×9 = 40، وسيكون الجزء السفلي هو الجذر التربيعي لـ 5×85×10×80، أو 340000√، ونخرج من هذا أن قيمة فاي هي 0.069 تقريبًا، وهي قيمة ضئيلة قطعًا، وعليه فلا يبدو أنّ البيتزا لها تأثير على تحول سمير.

حساب علاقة الترابط

نستطيع تمثيل جدول من صفين وعمودين في جافاسكربت، باستخدام مصفوفة من أربعة عناصر (‎[76, 9, 4, 1]‎)، أو مصفوفة تحتوي على مصفوفتين، بحيث تتكون كل واحدة منهما من عنصرين (‎[[76, 9], [4, 1]]‎)، أو كائن له أسماء خصائص، مثل: "11"، و"01"`.

غير أنّ المصفوفة المسطحة أسهل وتقصِّر طول التعبيرات التي تصل إلى الجدول، وسنفسر فهارس المصفوفة في صورة أعداد ثنائية مكوّنة من بِتَّين، حيث يشير الرقم الأيسر إلى متغير السنجاب، والأيمن إلى متغير الحدث. فمثلًا، يشير العدد الثنائي 10 إلى الحالة التي تحوّل فيها سمير إلى سنجاب، لكن حدث البيتزا مثلًا لم يقع، وقد حدث هذا أربع مرات؛ وبما أن العدد الثنائي 10 ما هو إلا العدد 2 في النظام العشري، فسننخزن هذا الرقم في الفهرس 2 من المصفوفة.

انظر الدالة التي تحسب قيمة معامل ϕ من مثل هذه المصفوفة:

function phi(table) {
  return (table[3] * table[0] - table[2] * table[1]) /
    Math.sqrt((table[2] + table[3]) *
              (table[0] + table[1]) *
              (table[1] + table[3]) *
              (table[0] + table[2]));
}

console.log(phi([76, 9, 4, 1]));
// → 0.068599434

الشيفرة أعلاه هي ترجمة حرفية لمعادلة فاي الرياضية السابقة في جافاسكربت، وتكون فيها Math.sqrt هي دالة الجذر التربيعي التي يوفرها كائن Math في بيئة جافاسكربت القياسية، ويجب إضافة حقلين من الجدول لنحصل على حقول مثل n_1•‎، ذلك أن مجموع الصفوف أو الأعمدة لا يُخزَّن في قاعدة بياناتنا مباشرةً وقد احتفظ سمير بسجله لمدة ثلاثة أشهر، وستجد النتائج لتلك الفترة متاحة في صندوق التجارب لهذا المقال، حيث تُخزَّن في رابطة JOURNAL وهي متاحة للتحميل.

سنكرر الآن على كل الإدخالات، وسنسجّل عدد مرات وقوع حدث التحول إلى سنجاب، وذلك لاستخراج جدول بسطرين وعمودين، وذلك كما يلي:

function tableFor(event, journal) {
  let table = [0, 0, 0, 0];
  for (let i = 0; i < journal.length; i++) {
    let entry = journal[i], index = 0;
    if (entry.events.includes(event)) index += 1;
    if (entry.squirrel) index += 2;
    table[index] += 1;
  }
  return table;
}

console.log(tableFor("pizza", JOURNAL));
// → [76, 9, 4, 1]

يتحقق تابع includes من وجود قيمة ما في المصفوفة، وتَستخدِم الدالة ذلك لتحديد وجود اسم الحدث الذي تريده في قائمة الأحداث في يوم ما.

يبيّن متن الحلقة التكرارية في tableFor أيّ صندوق في الجدول يقع فيه إدخال السجل، من خلال النظر في احتواء الإدخال على حدث بعينه أم لا، والنظر هل وقع الحدث مع وقوع التحول السنجابي أم لا، ثم تزيد الحلقة التكرارية الصندوق الصحيح بمقدار 1 داخل الجدول.

لدينا الآن الأدوات التي نحتاجها في حساب علاقة الترابط الفردية، والخطوة المتبقية هي إيجاد علاقة الترابط لكل نوع من الأحداث تم تسجيله، وننظر هل سنخرج بنتيجة أم لا.

حلقات المصفوفات التكرارية

لدينا حلقة تكرارية في دالة tableFor، وهي:

for (let i = 0; i < JOURNAL.length; i++) {
  let entry = JOURNAL[i];
  // Do something with entry
}

يكثر هذا النوع من الحلقات في جافاسكربت الكلاسيكية، إذ يشيع المرور على المصفوفات عنصرًا عنصرًا، وذلك باستخدام عدّادً على طول المصفوفة واختيار كل عنصر على حِدَة، لكن هناك طريقة أبسط لكتابة مثل تلك الحلقات التكرارية في جافاسكربت الحديثة، وذلك كما يلي:

for (let entry of JOURNAL) {
  console.log(`${entry.events.length} events.`);
}

حين تُكتَب حلقة forمع الكلمة of بعد تعريفِ متغير، ستتكرر على عناصر القيمة المعطاة بعد of، ويصلح هذا في المصفوفات، والسلاسل النصية، وبعض هياكل البيانات الأخرى، كما سيأتي بيانه في المقال السادس.

التحليل النهائي

نحتاج الآن إلى حساب علاقة الترابط لكل نوع من الأحداث التي وقعت في مجموعة البيانات التي جمعها سمير، ويحتاج هذا الحساب أولًا إلى إيجاد كل نوع من أنواع الأحداث. انظر المثال الآتي:

function journalEvents(journal) {
  let events = [];
  for (let entry of journal) {
    for (let event of entry.events) {
      if (!events.includes(event)) {
        events.push(event);
      }
    }
  }
  return events;
}

console.log(journalEvents(JOURNAL));
// → ["carrot", "exercise", "weekend", "bread", …]

تجمع الدالة journalEvents كل أنواع الأحداث من خلال المرور على الأحداث وإضافة الغير موجود منها إلى المصفوفة events، ونستطيع رؤية كل الالتزامات من خلال الحلقة التالية:

for (let event of journalEvents(JOURNAL)) {
  console.log(event + ":", phi(tableFor(event, JOURNAL)));
}
// → carrot:   0.0140970969
// → exercise: 0.0685994341
// → weekend:  0.1371988681
// → bread:   -0.0757554019
// → pudding: -0.0648203724
// and so on...

من هذه النتائج، نستطيع القول أن أغلب علاقات الترابط، مثل: أكل الجزر، والخبز، وغيرها، لا تستفز التحول الحيواني لدى سمير لأنها تقترب من الصفر، لكن من ناحية أخرى، فيبدو أنها تزيد في الإجازات الأسبوعية، وعليه سنرشّح النتائج أكثر لنرى أيَّ علاقات الترابط كانت أكبر من 0.1، أو أقل من -0.1.

for (let event of journalEvents(JOURNAL)) {
  let correlation = phi(tableFor(event, JOURNAL));
  if (correlation > 0.1 || correlation < -0.1) {
    console.log(event + ":", correlation);
  }
}
// → weekend:        0.1371988681
// → brushed teeth: -0.3805211953
// → candy:          0.1296407447
// → work:          -0.1371988681
// → spaghetti:      0.2425356250
// → reading:        0.1106828054
// → peanuts:        0.5902679812

لدينا عاملان بهما علاقة ترابط أقوى مما سواهما، وهما: أكل الفول السوداني الذي له أثر إيجابي قوي على فرصة التحول، وغسل الأسنان الذي له تأثير قوي كذلك لكن في الاتجاه المعاكس.

دعنا نجرب الشيفرة التالية:

for (let entry of JOURNAL) {
  if (entry.events.includes("peanuts") &&
     !entry.events.includes("brushed teeth")) {
    entry.events.push("peanut teeth");
  }
}
console.log(phi(tableFor("peanut teeth", JOURNAL)));
// → 1

هذه نتيجة قوية، إذ تحدث الظاهرة تحديدًا حين يأكل سمير الفول السوداني وينسى غسل أسنانه، وبما أنه عرف هذا، فقد قرر إيقاف أكل الفول السوداني بالكليّة، ووجد ظاهرة تحوله إلى سنجاب لم تتكرر بعدها!

زيادة على المصفوفات

نريد أن نعرّفك على بعض المفاهيم الأخرى المتعلقة بالكائنات قبل إنهاء هذا المقال، فقد رأينا في بداية هذا المقال push، وpop لإضافة العناصر وحذفها من نهاية مصفوفة ما؛ أما التابعان الموافقان لإضافة وحذف العناصر من بداية المصفوفة، فهما: unshift، وshift، وذلك كما يأتي:

let todoList = [];
function remember(task) {
  todoList.push(task);
}
function getTask() {
  return todoList.shift();
}
function rememberUrgently(task) {
  todoList.unshift(task);
}

ينظم البرنامج أعلاه مجموعةً من المهام المرتبة في طابور، حيث تضيف مهامًا إلى نهاية الطابور باستدعاء remember("groceries")‎، وتَستدعِي getTask()‎ إذا أردت فعل شيء ما، وذلك لجلب -وحذف- العنصر الأمامي من الطابور، كما تضيف دالة rememberUrgently مهمةً إلى أول الطابور، وليس إلى آخره.

توفر المصفوفات تابع indexOf الذي يبحث في المصفوفة من بدايتها إلى نهايتها عن قيمة معينة، ويعيد فهرس المكان الذي وجد عنده القيمة المطلوبة، وإذا أردت البحث من نهاية المصفوفة بدلًا من بدايتها، فلدينا تابع مماثل اسمه lastIndexOf، انظر كما يلي:

console.log([1, 2, 3, 2, 1].indexOf(2));
// → 1
console.log([1, 2, 3, 2, 1].lastIndexOf(2));
// → 3

ويأخذ كلا التابعين indexOf، وlastIndexOf وسيطًا ثانيًا اختياريًا يوضح أين يجب أن يبدأ البحث.

يُعَدّ التابع slice من التوابع الأساسية للمصفوفات، إذ يأخذ فهرس البداية والنهاية، ويعيد مصفوفةً تحوي العناصر المحصورة بين هذين الفهرسين، ويكون فهرس البداية موجودًا في هذه المصفوفة الناتجة، أما فهرس النهاية فلا. انظر المثال التالي:

console.log([0, 1, 2, 3, 4].slice(2, 4));
// → [2, 3]
console.log([0, 1, 2, 3, 4].slice(2));
// → [2, 3, 4]

إذا لم يُعط فهرس النهاية لتابع slice، فسيأخذ كل العناصر التي تلي فهرس البداية، وإن لم تذكر فهرس البداية، فسينسخ المصفوفة كلها.

يُستخدَم تابع concat للصق المصفوفات معًا لإنشاء مصفوفة جديدة، وهو في هذا يماثل وظيفة عامل + في السلاسل النصية.

انظر المثال التالي للتابعين السابقين، إذ تأخذ الدالة remove مصفوفةً وفهرسًا، ثم تعيد مصفوفةً جديدةً، بحيث تكون نسخةً من الأصلية بعد حذف العنصر الموجود عند الفهرس المعطى:

function remove(array, index) {
  return array.slice(0, index)
    .concat(array.slice(index + 1));
}
console.log(remove(["a", "b", "c", "d", "e"], 2));
// → ["a", "b", "d", "e"]

إذا مرّرنا وسيطًا ليس بمصفوفة إلى concat، فستضاف تلك القيمة إلى المصفوفة الجديدة كما لو كانت مصفوفة من عنصر واحد.

السلاسل النصية وخصائصها

نستطيع قراءة خصائص من قيم السلاسل النصية، مثل الخاصتين: length، وtoUpperCase، لكن إذا حاولت إضافة خاصية جديدة، فلن تبقى، انظر المثال التالي:

let kim = "Kim";
kim.age = 88;
console.log(kim.age);
// → undefined

ذلك أن قيم السلاسل النصية، والأعداد، والقيم البوليانية، ليست بكائنات. وعليه فلن تمنعك اللغة من وضع خصائص جديدة على هذه القيم، فهي لا تخزن تلك الخصائص على الحقيقة، إذ لا يمكن تغيير تلك القيم كما ذكرنا من قبل؛ غير أنّ هذه الأنواع لها خصائصها المدمجة فيها، فكل قيمة سلسلة نصية لها عدد من التوابع، لعلّ slice، وindexOf أكثرها نفعًا واستخدامًا، واللذين يشبهان في وظائفهما التابعَين المذكورَين قبل قليل، انظر المثال التالي:

console.log("coconuts".slice(4, 7));
// → nut
console.log("coconut".indexOf("u"));
// → 5

الفرق بينهما أنه يستطيع تابع indexOf في السلسلة النصية، البحث عن سلسلة تحتوي على أكثر من محرف واحد؛ بينما تابع المصفوفة الذي يحمل الاسم نفسه لا يبحث إلا عن عنصر واحد، أي كما في المثال التالي:

console.log("one two three".indexOf("ee"));
// → 11

يحذف تابع trim المسافات البيضاء، مثل: المسافات، والأسطر الجديدة، وإزاحات الجداول، وما شابه ذلك، من بداية ونهاية السلسلة النصية، ومثال على ذلك:

console.log("  okay \n ".trim());
// → okay

الدالة zeroPad المستخدَمة في المقال السابق، موجودة هنا على أساس تابع أيضًا، ويسمى padStart، حيث يأخذ الطول المطلوب، ومحرف الحشو على أساس وسائط، كما في المثال التالي:

console.log(String(6).padStart(3, "0"));
// → 006

تستطيع تقسيم سلسلة نصية عند كل ظهور لسلسلة أخرى باستخدام تابع split، ثم دمجها مرةً أخرى باستخدام تابع join، أي كما في المثال التالي:

let sentence = "Secretarybirds specialize in stomping";
let words = sentence.split(" ");
console.log(words);
// → ["Secretarybirds", "specialize", "in", "stomping"]
console.log(words.join(". "));
// → Secretarybirds. specialize. in. stomping

يمكن تكرار السلسلة النصية باستخدام تابع repeat، حيث ينشِئ سلسلةً نصيةً جديدةً تحتوي نسخًا متعددةً من السلسلة الأصلية، وملصقةً معًا. انظر المثال التالي:

console.log("LA".repeat(3));
// → LALALA

وبالنسبة لخاصية length للسلاسل النصية التي رأيناها من قبل، فيحاكي الوصول إلى المحرف داخل سلسلة نصية، الوصول إلى عناصر المصفوفة مع فارق بسيط سنناقشه في المقال الخامس. انظر المثال التالي:

let string = "abc";
console.log(string.length);
// → 3
console.log(string[1]);
// → b

معامل rest

من المفيد لدالة قبول أي عدد من الوسائط، فمثلًا، تحسب الدالة Math.max القيمة العظمى لكل الوسائط المعطاة؛ إذ يمكننا تحقيق ذلك بوضع ثلاث نقاط قبل آخر معامِل للدالة، كما يلي:

function max(...numbers) {
  let result = -Infinity;
  for (let number of numbers) {
    if (number > result) result = number;
  }
  return result;
}
console.log(max(4, 1, 9, -2));
// → 9

وحين تُستدعى هذه الدالة فإن معامل rest يكون ملزَمًا بمصفوفة تحتوي كل الوسائط الأخرى، وإذا كان ثمة معامِلات أخرى قبله، فلا تكون قيمها جزءًا من المصفوفة؛ أما حين يكون هو المعامل الوحيد كما في حالة max، فستحمل المصفوفة كل الوسائط.

تستطيع استخدام صيغة النقاط الثلاثة لاستدعاء دالة مع مصفوفة وسائط، كما في المثال التالي:

let numbers = [5, 1, 7];
console.log(max(...numbers));
// → 7

يوسع هذا المصفوفة إلى استدعاء الدالة ممررًا عناصرها على أساس وسائط منفصلة، ومن الممكن إضافة مصفوفة مثل هذه إلى جانب وسائط أخرى كما في max(9, ...numbers, 2)‎، كذلك تسمح صيغة الأقواس المربعة لمصفوفة، لعامل النقاط الثلاثة، بتوسيع مصفوفة أخرى داخل هذه المصفوفة الجديدة، كما في المثال التالي:

let words = ["never", "fully"];
console.log(["will", ...words, "understand"]);
// → ["will", "never", "fully", "understand"]

الكائن Math

كما رأينا سابقًا، فـ Math ما هو إلا حقيبةٌ من دوال التعامل مع الأعداد، مثل: Math.max للقيمة العظمى، وMath.min للقيمة الصغرى، وMath.sqrt للجذر التربيعي.

يُستخدَم كائن Math على أساس حاوية لمجموعة من الوظائف المرتبطة ببعضها بعضًا، كما أنّه كائن وحيد، إذ لا يوجد كائن آخر يحمل الاسم نفسه، وهو غير مفيد أيضًا إن جاء على أساس قيمة، فهو يوفر فضاء اسم namespace لئلا تضطر الدوال والقيم لتكوّن روابط عامة global bindings، حيث تلوث كثرة هذه الروابط العامة فضاء الاسم، فكلما زاد عدد الأسماء المحجوزة زادت فرصة تغيير قيمة رابطة حالية بالخطأ، ولا بأس مثلًا بتسمية شيء ما باسم max في برنامج تكتبه، إذ أنّ دالة max المدمجة بجافاسكربت محفوظة بأمان داخل كائن Math، لذا فلن تتغير بفعل منك.

لن توقفك أو تحذرك جافاسكربت -على عكس كثير من اللغات الأخرى- من تعريف رابطة باسم مأخوذ من قبل، إلا أن تكون رابطةً صرحْتَ عنها باستخدام let، أو const، أما الروابط القياسية أوالمصرَّح عنها باستخدام var، أو function فلا.

ستحتاج إلى كائن Math إن أردت تنفيذ بعض العمليات المتعلِّقة بحساب المثلثات، وذلك لاحتوائه على دوال الجيب sin، وجيب التمام cos، والظل tan، إضافةً إلى دوالها المعكوسة، وهي: asin، وacos، وatan، كما أن العدد باي π متاح أيضًا في جافاسكربت في صورة Math.PI؛ وكُتِبت بحروف إنجليزية كبيرة تطبيقًا لعادة قديمة في البرمجة، إذ تُكتَب أسماء القيم الثابتة بالحروف الكبيرة.

function randomPointOnCircle(radius) {
  let angle = Math.random() * 2 * Math.PI;
  return {x: radius * Math.cos(angle),
          y: radius * Math.sin(angle)};
}
console.log(randomPointOnCircle(2));
// → {x: 0.3667, y: 1.966}

ولا تقلق إن لم تكن قد تعرضت لهذه الدوال من قبل، حيث ستُشرح حين يأتي ذكرها في المقال الرابع عشر من هذه السلسلة، وقد استخدمنا الدالة Math.random في المثال أعلاه، إذ تعيد عددًا عشوائيًا وهميًا بين الصفر والواحد في كل مرة تستدعيها، مع استثناء الواحد نفسه فلا تعيده. انظر المثال التالي:

console.log(Math.random());
// → 0.36993729369714856
console.log(Math.random());
// → 0.727367032552138
console.log(Math.random());
// → 0.40180766698904335

رغم أنّ الحواسيب آلات تعيينية، أي تتصرف بالطريقة نفسها إن أعطيتها المدخلات ذاتها، إلا أنّه من الممكن جعلها تنتج أعدادًا قد تبدو عشوائية، ولفعل ذلك تحتفظ الآلة بقيمة مخفيّة، وتُجري حسابات معقدة على هذه القيمة المخفيّة لإنشاء واحدة جديدة في كل مرة تسألها فيها إعطاءك عددًا عشوائيًا؛ كما تخزِّن القيمة الجديدة وتعيد عددًا مشتقًا منها، وهكذا تستطيع إنتاج أعداد بطريقة تبدو عشوائية ويصعب التنبؤ بها؛ أما إن أردت أعدادًا صحيحةً وعشوائيةً بدلًا من الأعداد الكسرية، فاستخدام Math.floor على الخرج الذي تحصل عليه من Math.random، حيث تقرِّب العدد إلى أقرب عدد صحيح.

console.log(Math.floor(Math.random() * 10));
// → 2

سيعطيك ضرب العدد العشوائي في 10 عددًا أكبر من أو يساوي الصفر، وأصغر من العشرة؛ وبما أن Math.floor تقرِّبه، فسينتج هذا التعبيرأعدادًا من 0 إلى 9 باحتمالات متساوية.

تقرِّب الدالة Math.ceil إلى عدد صحيح، كما تقرِّب الدالة Math.round إلى أقرب رقم صحيح، وتأخذ الدالة Math.abs القيمة المطلقة لعدد ما، أي تنفي القيمة السالبة وتترك القيمة الموجبة كما هي.

التفكيك

انظر الشيفرة التالية:

function phi(table) {
  return (table[3] * table[0] - table[2] * table[1]) /
    Math.sqrt((table[2] + table[3]) *
              (table[0] + table[1]) *
              (table[1] + table[3]) *
              (table[0] + table[2]));
}

إذا عدنا إلى دالة phi السابقة، فإن أحد الأسباب التي يجعل هذه الدالة صعبةً في قراءتها، هو أنّه لدينا رابطة تشير إلى مصفوفتنا، بينما نريد رابطات لعناصر المصفوفة، أي let n00 = table[0]‎، وهكذا.

لحسن الحظ لدينا طريقة مختصرة في جافاسكربت تفعل ذلك:

function phi([n00, n01, n10, n11]) {
  return (n11 * n00 - n10 * n01) /
    Math.sqrt((n10 + n11) * (n00 + n01) *
              (n01 + n11) * (n00 + n10));
}

هذا يصلح أيضًا للرابطات التي أنشئت باستخدام let، وvar، وconst، فإذا كانت القيمة التي تربطها مصفوفةً تستطيع استخدام الأقواس المربعة لتنظر داخلها لتربط محتوياتها.

كذلك بالنسبة للكائنات إذ نستخدم الأقواس العادية بدلًا من المربعة، انظر المثال التالي:

let {name} = {name: "Faraji", age: 23};
console.log(name);
// → Faraji

لاحظ أنك إذا حاولت تفكيك null، أو undefined، فستحصل على خطأ، وكذلك إن حاولت الوصول مباشرةً إلى إحدى خصائص هاتين القيمتين.

صيغة JSON

بما أن الخصائص تلتقط قيمها ولا تحتويها، فتُخزَّن المصفوفات والكائنات في ذاكرة الحاسوب على أساس سلاسل من البتات حاملةً عناوينًا لمحتوياتها، وهذه العناوين هي أماكن في الذاكرة، لذا فإن احتوت مصفوفة على مصفوفة أخرى داخلها، فستشغل من الذاكرة قطاعًا واحدًا على الأقل للمصفوفة الداخلية، وواحدًا آخرًا للمصفوفة الخارجية، حيث سيحتوي على عدد ثنائي يمثل موضع المصفوفة الداخلية، مع أشياء أخرى قطعًا.

وإن أردت حفظ بيانات في ملف لاستخدامها لاحقًا أو إرسالها إلى حاسوب آخر عبر الشبكة، فعليك تحويل هذه العناوين المتشابكة إلى وصف يمكن تخزينه أو إرساله، وبهذا تستطيع إرسال ذاكرة حاسوبك كلها مع عنوان القيمة التي تريدها، رغم أن هناك طرق أفضل لهذا.

والذي نستطيع فعله هو تحويل سَلسلة البيانات، بمعنى تحويلها إلى وصف بسيط، وثَمَّ استخدام طريقة مشهورة تسمى JSON -تنطق جَيسون- وهي اختصار لصيغة الكائنات في جافاسكربت JavaScipt Object Notation، وتُستخدَم استخدامًا واسعًا على أساس طريقة لتخزين البيانات، وصيغة للتواصل في الإنترنت حتى في اللغات الأخرى غير جافاسكربت.

تحاكي صيغة JSON طريقة جافاسكربت في كتابة المصفوفات والكائنات مع بعض القيود، لذا فيجب إحاطة كل أسماء الخصائص بعلاماتي تنصيص مزدوجة، ولا يُسمح إلا بتعابير البيانات البسيطة، فلا استدعاءات لدوال، ولا روابط، ولا أي شيء فيه حوسبة حقيقية؛ والتعليقات ممنوعة أيضًا.

وإذا عدنا -مرةً أخرى- إلى مثال سمير المتحوِّل، وأردنا تمثيل مدخلًا للسجل الذي يحتفظ به في صورة بيانات JSON، فسيبدو هكذا:

{
  "squirrel": false,
  "events": ["work", "touched tree", "pizza", "running"]
}

تعطينا جافاسكربت دالتي JSON.stringify، وJSON.parse، لتحويل البيانات من وإلى هذه الصيغة، فالأولى تأخذ قيمة من جافاسكربت، وتعيد سلسلةً نصيةً مرمّزةً بصيغة JSON، والثانية تأخذ هذه السلسلة وتحولها إلى القيمة التي ترمِّزها، كما في المثال التالي:

let string = JSON.stringify({squirrel: false,
                             events: ["weekend"]});
console.log(string);
// → {"squirrel":false,"events":["weekend"]}
console.log(JSON.parse(string).events);
// → ["weekend"]

خاتمة

توفر الكائنات والمصفوفات طريقًا لتجميع عدة قيم ووضعها في قيمة واحدة، ويسمح هذا نظريًا لنا بوضع بعض الأشياء المرتبطة ببعضها في حقيبة واحدة، وذلك لنتعامل مع الحقيبة كلها بدلًا من محاولة الإمساك بهذه الأشياء واحدةً واحدةً بأيدينا.

تملك أغلب القيم في جافاسكربت خصائص، باستثناء: null، وundefined، ونستطيع الوصول إلى تلك الخصائص باستخدام value.prop، أو value["prop"]‎.

تميل الكائنات إلى استخدام أسماء خصائصها وتخزين مجموعة منها؛ أما المصفوفات فتحتوي غالبًا على كميات مختلفة من القيم المتطابقة نظريًا وتستخدم الأعداد (بدءًا من الصفر) على أساس أسماء لخصائصها، ولدينا بعض الخصائص المسماة في المصفوفات مثل length، وعددًا من التوابع التي هي دوال تعيش داخل الخصائص وتتحكم عادةً في القيم التي تكون جزءًا منها.

تستطيع تطبيق التكرار على المصفوفات باستخدام نوع خاص من حلقة for التكرارية، أي for(let element of array)‎.

ترجمة -بتصرف- للفصل الرابع من كتاب Elequent Javascript لصاحبه Marijn Haverbeke.

اقرأ أيضًا

• المقال التالي: الدوال العليا في جافاسكريبت
• المقال السابق: هيكل البرنامج في جافاسكريبت
• الدليل الشامل: علم البيانات