هياكل البيانات data structures -أو تدعى بنى المعطيات أحيانًا- مصطلح يتكرر كثيرًا في علوم الحاسوب خصوصًا والبرمجة عمومًا ويعد من المصطلحات المعقدة البسيطة أو السهلة الممتنعة كما أن الكثير يخلط بينه وبين أنواع البيانات أو لا يكاد يميز بينهما، ولابد على أي داخل لمجال علوم الحاسوب ومن يريد تعلم البرمجة أن يفهم هذا المصطلح جيدًا لأنه الأساس الذي سيستند عليه في بناء بقية المفاهيم الأخرى اللاحقة.
بناء على ذلك، جاء هذا المقال ليكون تعريفًا بهياكل البيانات وأنواعها بأسلوب بسيط سهل مدعوم بالصور التوضيحية كل هيكل بيانات بالإضافة إلى ذكر ميزات وعيوب بعض الأنواع، كما يتناول هذا المقال التعريف بأهمية هياكل البيانات وأهم تطبيقاتها والفرق بينها وبين أنواع البيانات، لذا لنبدأ!
ما هي هياكل البيانات؟
تُعَدّ هياكل البيانات data structures من أهم المفاهيم التأسيسية في مجال علوم الحاسوب، فهي ببساطة مجموعة من الوسائل والطرق المستعملة في ترتيب البيانات في ذاكرة الحاسوب بهدف التعامل معها بكفاءة وفعالية وتسهيل إجراء العمليات عليها، وتوجد هناك أنواع أساسية ومتطورة من هياكل البيانات وجميعها مصمَّمة لتنظيم البيانات لاستخدامها في هدف محدَّد.
أهمية هياكل البيانات data structures
أحب بداية ضرب مثال يوضح هياكل البيانات وأهميتها وهو أننا نستعمل هذا المفهوم في حياتنا اليومية بصورة أو بأخرى، لنفترض أن البيانات تمثل ملابسنا، فهل نرمي الملابس في خزانة واحدة كلها؟ لا بالطبع لأن إخراج بنطال معين آنذاك سيستغرق وقتًا من البحث للعثور عليه وإخراج بل نضع الألبسة بطريقة معينة في عدة خزانات وسحابات وبطرق مختلفة بحيث نصل إلى بنطال أو قميص محدد بمجرد طلبه فورًا آنيًا دون تأخير. الأمر نفسه مع ترتيب البهارات وأوعية المطبخ والكتب وكل شيء حولنا تقريبًا.
هذا بالضبط ما يحصل عند كتابة كلمة في محرك البحث لتظهر لك اقتراحات عد قد تطابق تمامًا ما تنوي كتابته في غضون أجزاء من الثانية، فهل تساءلت كيف تمكن محرك البحث من البحث في كم البيانات الضخم الموجودة في الإنترنت ووصل إلى النتيجة؟ لا يمكن ذلك بآلية الرمي العشوائي في مكان واحد التي ذكرناها في ترتيب الملابس تلك بل بتنظيم البيانات ضمن هياكل بيانات تشبه الأوعية والخزانات تسهل الوصول إليها بأسرع ما يمكن.
نظرًا لتطور التطبيقات وازدياد تعقيدها وازدياد كمية البيانات الضخم يومًا بعد يوم والذي تتطلب عملية معالجتها معالجات هائلة السرعة، فكان لا بد من تنظيم البيانات وإدارتها بكفاءة في هياكل البيانات تمثل أوعية تخزين وتنظيم لها، إذ يمكن أن يساعد استخدام هياكل البيانات المناسبة في توفير قدر كبير من الوقت أثناء إجراء عمليات عليها مثل تخزين البيانات أو استرجاعها أو معالجتها، وبالتالي وصول أسرع إلى الذاكرة وتوفير في استهلاك العتاد من عمليات معالجة وطاقة للحاسوب.
من الجدير بالذكر أيضًا أنّ هياكل البيانات ضرورية لتصميم خوارزميات فعالة والتي سنراها في تطبيقات هياكل البيانات ضمن هذا المقال.
الفرق بين أنواع البيانات وهياكل البيانات
يبدو لك أنّ أنواع البيانات Data Types وهياكل البيانات Data Structures وجهان لعملة واحدة لأنّ كلاهما يتعامل مع طبيعة البيانات وتنظيمها، ولكن في الحقيقة الأول يشرح نوع وطبيعة البيانات في حين يمثِّل الآخر التجميعات التي تُخزَّن تلك البيانات فيها، وفيما يلي الفروق الأساسية بين نوع البيانات وهيكل البيانات.
- يمثِّل نوع البيانات ماهية البيانات التي سيجري التعامل معها مثل أن تكون البيانات أعداد أو سلاسل نصية أو رموز …إلخ. في حين يُعَدّ هيكل البيانات تجميعةً collection تحوي تلك البيانات وهناك عدة أنواع من الهياكل تناسب مختلف أنواع البيانات.
- يحدد نوع البيانات ما يترتب عليه من عمليات تطبق على تلك البيانات مثل العمليات الرياضية على الأعداد وعمليات المعالجة على النصوص وهكذا أما هياكل البيانات فتحدد كيفية تخزين البيانات والوصول إليها والبحث فيها وغيرها من العمليات كما تدرس كيفية تحسين الأداء في تلك العمليات.
- يأخذ نوع البيانات شكل التنفيذ المجرد abstract implementation الذي يُعرَّف من خلال لغات البرمجة نفسها، في حين يُنفَّذ هيكل البيانات تنفيذًا حقيقيًا concrete implementation بحيث يُنشأ ليكون متوافقًا مع التصميم الذي يحتاجه المبرمج بالحجم الذي يريده وبنوع البيانات التي سيحتويها ضمن تطبيقه.
- يسمى نوع البيانات بأنه عديم القيمة dataless لأنه لا يخزِّن قيمة البيانات وإنما يمثِّل فقط نوع البيانات التي يمكن تخزينها، في حين يستطيع هيكل البيانات الاحتفاظ بأنواع مختلفة من البيانات مع قيمتها في كائن واحد.
- تحدد أنواع البيانات مع المتغيرات مثلًا في لغات البرمجة عند تعريفها، في حين تحتاج إلى كتابة بعض الخوارزميات لإسناد قيم البيانات إلى المتغيرات عند استخدام هيكل بيانات مثل عمليتَي الإضافة Push والجلب Pop للبيانات.
- لا يُكترث للزمن عند استخدام نوع البيانات، في حين يؤخذ بالحسبان عند استخدام هيكل البيانات (يطلق عليه تعقيد زمني BigO).
تطبيقات هياكل البيانات
يكاد لا يخلو أي تطبيق أو برنامج أو خوارزمية برمجية من وجود هيكل بيانات أو بنية معطيات تساعده في تحقيق الهدف المرجو منه، ومن هذه التطبيقات ما يلي:
- تنظيم البيانات في ذاكرة الحاسوب.
- تمثيل المعلومات في قواعد البيانات.
- خوارزميات معالجة البيانات مثل معالجة النصوص.
- خوارزميات تحليل البيانات مثل data minar.
- خوارزميات البحث في البيانات مثل محرك البحث.
- خورزميات توليد البيانات مثل مولِّد الأعداد العشوائية.
- خوارزميات ضغط البيانات وتفك ضغطها مثل المعتمدَة في برنامج zip.
- خوارزميات تشفير البيانات وتفك تشفيرها مثل المعتمدَة في نظام الأمان.
- البرامج التي تدير الملفات والمجلدات مثل مدير الملفات.
أنواع هياكل البيانات في لغات البرمجة
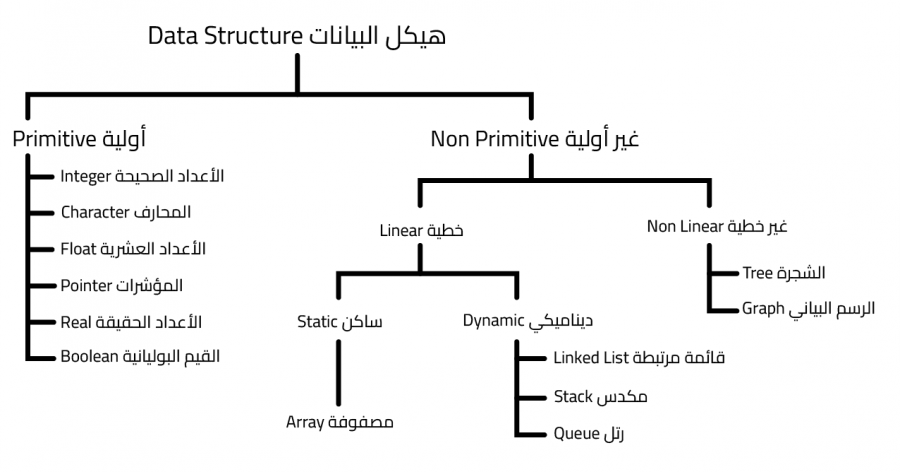
تنقسم هياكل البيانات إلى هياكل بيانات أولية Primitive وهياكل بيانات غير أولية Non Primitive أو هياكل بيانات معقدة وكل منها يضم عدة أقسام سنشرحها تباعًا.
هياكل البيانات الأولية Primitive
هي هياكل البيانات الأساسية والبسيطة والتي تُستخدَم لتخزين قيمة من جزء واحد فقط ذات نوع محدَّد، ويندرج تحت هذا النوع ما يلي:
-
integer: من أجل الأعداد الصحيحة مثل العدد
15. - character: من أجل محرف واحد فقط.
- float: من أجل الأعداد العشرية.
- real: من أجل الأعداد الحقيقية.
- boolean: من أجل القيم البوليانية والذي يأخذ إحدى القيمتين؛ إما محققة true أو غير محققة false.
ملاحظة: قد تتساءل عن هياكل تخزين النصوص، وهي في الحقيقة تدخل ضمن الهياكل الغير أولية أن النصوص مجموعة من الحروف والرموز التي تدعى محارف characters لذا تخزن عادة ضمن مصفوفة وأحيانًا تضيف لغات البرمجة نوعًا خاصًا لها يدعى string سلسلة نصية أو لا يضيف وتكون بالشكل char[] وما تراه [] يدل على هيكل مصفوفة.
يوجد شيء خاص يدعى مؤشر pointer والمشهور في بعض اللغات البرمجية مثل سي C وسي بلس بلس ++C، إذ يُعَدّ مكانًا في الذاكرة ويخزِّن عنوان المتغير الذي يشير إليه والشي الخاص فيه أنه يملك نوع بيانات والذي يجب أن يطابق نوع البيانات الذي يشير إليها.
ملاحظة: ممكن تسمية هياكل البيانات التي تخزن الأعداد العشرية باسم double (عدد عشري مضاعف الدقة) أو float (عدد عشري) عوضًا عن real بصورة عامة ويكمن الاختلاف حسب اللغة البرمجية في عدد الخانات العشرية الممكن تخزينها، أي عدد الخانات بعد الفاصلة العشرية، بالإضافة إلى الحجم في الذاكرة وأخيرًا طريقة التعريف declaration، ففي لغة سي شارب #C يكون تعريف المتغير من نمط float كما يلي:
float x = 1.5f;
أما تعريفه عندما يكون من نمط double، فيكون كما يلي:
double x = 1.5;
ملاحظة: يطلق أحيانًا على هياكل البيانات الأولية أنواع البيانات Data Type.
هياكل البيانات غير الأولية
هي هياكل البيانات التي تُستخدَم من أجل التخزين المعقّد والتي يمكنها أن تحمل أكثر من قيمة في بنيتها، وتنقسم إلى هياكل بيانات خطية Linear وهياكل بيانات غير خطية Non Linear.
هياكل البيانات الخطية
تكون هياكل البيانات خطيّةً إذا كانت عناصرها تشكل تسلسلًا فيما بينها بحيث يرتبط كل عنصر فيها بعنصر سابق وعنصر لاحق ضمن مستوى واحد وفي مسار واحد، ومن هذه الهياكل ما يلي:
- المصفوفة Array
- القائمة المترابطة Linked List
- المكدس Stack
- الرتل Queue
المصفوفة
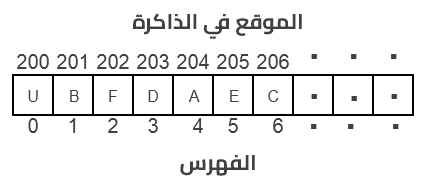
تُعَدّ المصفوفة الخطية array أو المصفوفة ذات البعد الواحد أبسط أنواع الهياكل الخطية، ويمكن تشبيهها بقائمة من عدد محدود من العناصر التي تمتلك النوع ذاته، ويكون بعدها -أو طولها- هو عدد العناصر التي تملكها، كما تُخزّن في الذاكرة بحجم ثابت وبمواقع متجاورة.
كل عنصر من عناصر هذه المصفوفة الخطية يملك فهرسًا للوصول إليه، وعادةً ما يبدأ الفهرس بالعدد 0 أي يكون فهرس العنصر الأخير هو n-1 في مصفوفة بعدها n، وفي بعض لغات البرمجة يكون فهرس البداية هو العدد 1 مثل لغة باسكال، وفيما يلي صورة توضِّح هذه البنية:
ملاحظات:
- يُنظَر إلى السلسلة النصية string على أنها مصفوفة أحادية من المحارف، أي كلمة Hello هي سلسلة نصية وهي مصفوفة طولها 5 مكوّنة من خمسة عناصر بحيث يمثِّل كل عنصر محرفًا من المحارف كما أشرنا سابقًا.
- المصفوفة ثنائية البعد هي أيضًا مجموعة من المتغيرات المفهرسة التي تحتوي على النوع نفسه من البيانات ولكن تخزين البيانات فيها يكون على صورة جدول له أعمدة وأسطر، بحيث يمكن الوصول إلى العنصر في هذه المصفوفة من خلال فهرسين أحدهما يحدِّد السطر والآخر يحدِّد العمود.
من الجدير بالذكر أنّ بُعد المصفوفة ثابت في بعض لغات البرمجة وبالتالي يجب معرفة عدد العناصر قبل تعريفها فإذا أردت تغيير البُعد وإضافة عناصر جديدة، فستحتاج إلى مصفوفة جديدة ببُعد جديد لتنقل إليها العناصر السابقة وبعدها تضيف العناصر الجديدة إليها، كما أنّ إضافة عنصر ما في مكان ما مملوء مسبقًا أي في وسط المصفوفة مثلًا سيستهلك الكثير من العمليات، إذ ستحتاج إلى إزاحة العناصر اللاحقة ليصبح له مكانًا فارغًا، ويُعَدّ ذلك من عيوب استخدام المصفوفات.
هنالك لغات أخرى لا تشترط تحديد عدد عناصر المصفوفة ولكنها تستهلك آنذاك عمليات كثيرة وتكون مكلفة لعمليات المعالجة أما تلك التي تحدد عدد العناصر مسبقًا فذلك عائد إلى توفير عمليات المعالجة. ملاحظة: قد تجد كلمة static ساكن وكلمة dynamic متحرك لتصنيف الأنواع الغير خطية ولكن شرحهما متقدم جدًا يحتاج إلى مقال بأكمله وستحتاج إليه عند التعمق كثيرًا وليس في البداية.
القائمة المترابطة
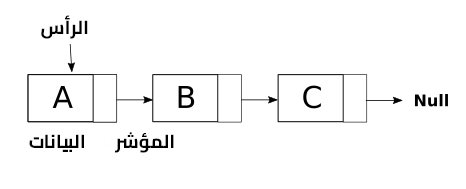
تُعَدّ القائمة المترابطة linked list مجموعةً من العقد التي تخزَّن في الذاكرة بمواقع غير متجاورة، وكل عقدة من عقد القائمة مرتبطة بالعقدة المجاورة لها بمؤشر عدا العقدة الأخيرة التي يكون المؤشر فيها عبارة عن Null.
تسمح هذه البنية بإدراج عناصر جديدة أو حذف عناصر موجودة سابقًا بسهولة وهذا ما يميزها عن المصفوفات؛ أما سرعة الوصول، فتُعَدّ المصفوفات أسرع لأنه يكفي ذكر الفهرس الرابع على عكس القائمة المترابطة التي يجب البدء فيها من الرأس ثم المرور على العناصر بالتتالي إلى حين الوصول إلى العنصر الرابع.
من الجدير بالذكر أنّ القائمة المترابطة تحتاج إلى مساحة إضافية في الذاكرة من أجل المؤشر الذي يرتبط بالعنصر، وهذا عيب آخر من عيوب القوائم المترابطة.
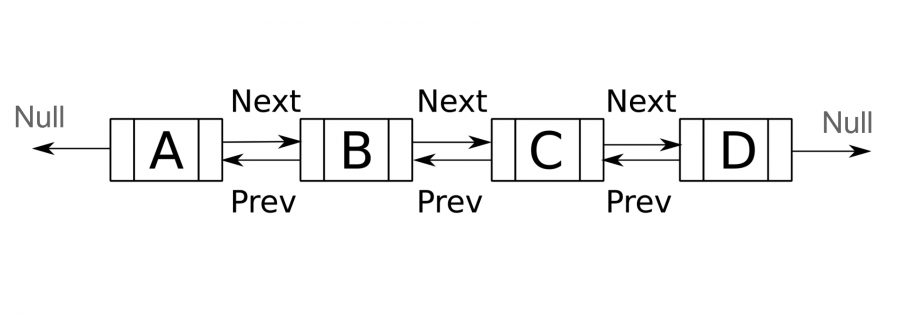
يوجد نوع متطور من القوائم المترابطة وهو القوائم المترابطة المزدوجة Doubly Linked List، إذ ترتبط كل عقدة بمؤشرَين أحدهما يربطها بالعقدة السابقة ويسمى عادةً prev والآخر يربطها بالعقدة التالية ويسمى عادةً next، وبالتالي تحتاج هذه القائمة إلى مساحة إضافية في الذاكرة لامتلاكها على مؤشر إضافي، وبالمثل يكون المؤشر prev في عقدة الرأس Null ومؤشر next في العقدة الأخيرة هو Null.
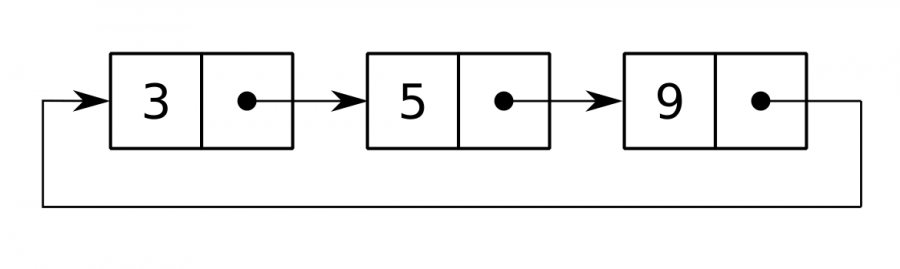
يوجد نوع أخير من القوائم المترابطة وهو القوائم المترابطة الدائرية Circular Linked Lists والتي تُعَدّ تطويرًا عن المفردة بحيث يشير مؤشر next الخاص بعقدة النهاية إلى عقدة الرأس.
كما توجد القوائم الدائرية المزدوجة بحيث يشير مؤشر prev الخاص بعقدة الرأس إلى عقدة النهاية ويشير مؤشر next الخاص بعقدة النهاية إلى عقدة الرأس، وبالتالي لا تحتوي القوائم المترابطة الدائرية على مؤشرات Null.
المكدس
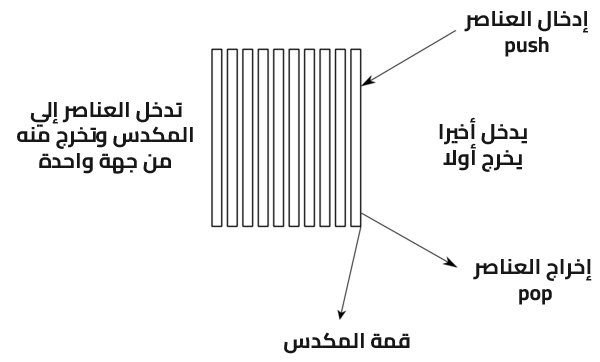
يُعَدّ المكدِّس stack هيكل بيانات خطية يتبع ترتيبًا محددًا في تنفيذ عمليات الحذف والإضافة، والترتيب يكون LIFO أي الذي يدخل آخرًا يخرج أولًا Last In First Out، والذي يميز المكدس هنا هو دخول العناصر وخروجها من قمة المكدِّس أي من جهة واحدة.
تدخل -أو تُضاف- العناصر إلى المكدِّس عن طريق عملية وحيدة وخاصة وهي دفع Push وبالمثل فإنها تخرج منه -أو تُحذَف- عن طريق عملية وحيدة وخاصة أيضًا وتدعى إخراج Pop، وتوجد أيضًا عمليتان خاصتان بالمكدِّس وهما Top -أو Peek- التي تعيد القيمة الموجودة في قمة المكدِّس دون حذفها، والعملية الأخرى هي عملية IsEmpty التي تُعيد القيمة true إذا كان المكدِّس فارغًا.
عند إضافة عنصر إلى مكدِّس ممتلئ لا يستوعب المزيد من العناصر فستحصل حالة طفحان المكدِّس overflow؛ أما عند إجراء عملية الحذف من مكدِّس فارغ، فسنواجه حالة طفحان أو تجاوز الحد الأدنى underflow (قعر المكدس).
الرتل
يُعَدّ الرتل queue أحد هياكل البيانات الخطية شبيه بالمكدس لامتلاكه عمليات خاصة للحذف والإضافة ولكنه يختلف عنه في مكان الحذف والإضافة كما سنرى.
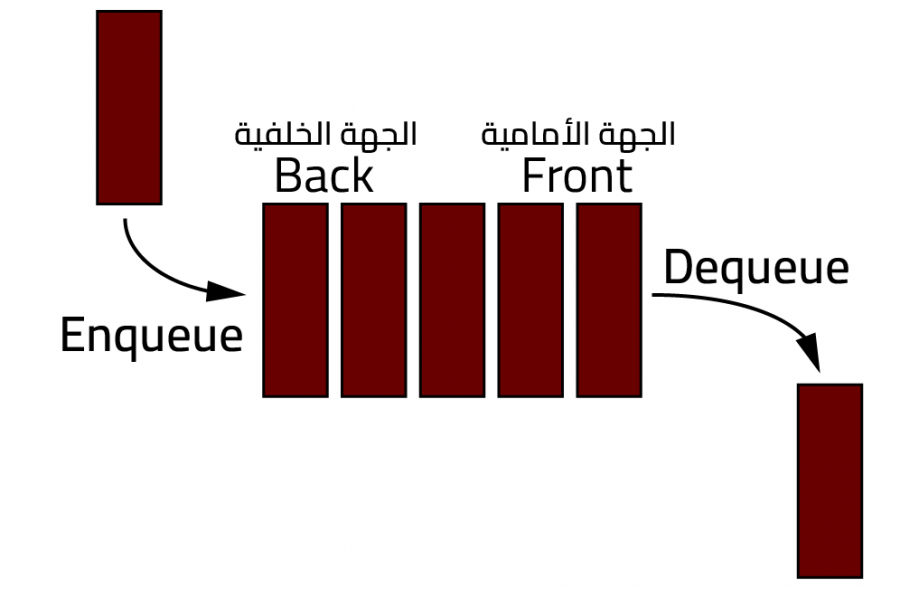
يدعى الرتل أو الطابور بـ FIFO أي الذي يدخل أولًا يخرج أولًا First In First Out بحيث يكون الدخول -أو الإضافة- من الجهة الخلفية rear والخروج -أو الحذف- من الجهة الأخرى أي الأمامية front (كما يحصل عند الوقوف ضمن الطوابير تمامًا لشراء شيء ما)، وتحدث الإضافة عن طريق عملية ENQUEUE أما عملية الحذف فتكون عن طريق عملية DEQUEUE.
يتميز الرتل أيضًا بامتلاكه عمليات خاصة وهي العملية IsFull التي تُعيد true إذا كان الرتل ممتلئًا، والعملية IsEmpty التي تُعيد true إذا كان الرتل فارغًا، والعملية Front التي تُعيد العنصر الأمامي من الرتل، بالإضافة إلى العملية Rear التي تُعيد العنصر الخلفي من الرتل.
هياكل البيانات غير الخطية
لا تحتوي هياكل البيانات غير الخطية -أو المتشعبة- على أيّ تسلسل محدد يربط جميع عناصرها، إذ يمكن أن يكون لكل عنصر أكثر من مسار ليرتبط بالعناصر الأخرى، كما أنّ العناصر الموجودة ضمن هذه الهياكل لا يمكن اجتيازها أو المرور عليها في جولة واحدة أو باستخدام حلقة برمجية واحدة.
وأهم ما يميّز هذا النوع على الرغم من صعوبة التنفيذ موازنةً بالهياكل الخطية التي يزداد فيها تعقيد الوقت مع ازدياد حجم البيانات أنه يُعد أكثر كفاءة في استخدام الذاكرة وأكثر سرعة في تطبيق العمليات مثل عمليات البحث، ومن هذه الهياكل:
- الشجرة
- الرسم البياني
الشجرة
تُعَدّ الشجرة tree هيكل بيانات متعدد المستويات وتُعرَّف على أنها مجموعة من العقد التي تحتوي فيما بينها على علاقة هرمية بحيث تسمى العقدة العليا بالعقدة الجذر، كما تحتوي كل عقدة على أب وحيد، في حين يمكن أن يكون لها أكثر من ابن أو تابع.
تسمى العقد التي تتفرع من عقدة معينة بأبناء children تلك العقدة والتي بدورها تدعى بالعقدة الأب parent، في حين تسمى العقد التي لا تمتلك أبناء بالأوراق leaves.
تمتلك الشجرة عدة أنواع وهي:
- الشجرة الثنائية binary tree
- شجرة البحث الثنائية binary search tree
- شجرة AVL
- شجرة R-B
- شجرة البادئات
الشجرة الثنائية
الشجرة الثنائية binary tree هي شجرة بيانات تمتلك كل عقدة فيها -ما عدا الأوراق- على عقدَتي ابن فقط وهما الابن الأيمن والابن الأيسر.
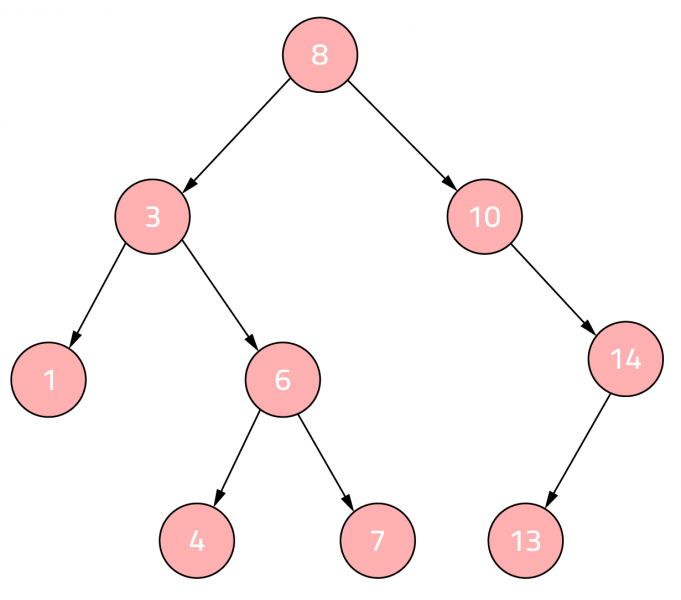
شجرة البحث الثنائية
شجرة البحث الثنائية binary search tree أو BST اختصارًا هي شجرة ثنائية تحقق خاصيتان أساسيتان وهما أنّ العقد الواقعة في الفرع اليميني تكون أكبر من العقدة الأب والعقد الواقعة في الفرع اليساري تكون أصغر من العقدة الأب، مع ضمان وجود ابنَين لكل عقدة وعدم تكرار العقد.
شجرة AVL
تُعَدّ اختصارًا لـ Adelson-Velskii Tree إذ يُعَدّ أديسون Adelson وفيلسكي Velskii مخترعَيها للحفاظ على توازن شجرة البحث الثنائي وذلك لمنع تدهورها إلى قائمة مرتبطة عندما تحتوي الشجرة بأكملها على الشجرة الفرعية اليسرى فقط أو على الشجرة اليمنى فقط مما سينعكس سلبًا على أداء الشجرة، إذ يمكن استخدام سلسلة من عمليات التدوير بحيث تُحدَّد في كل عملية عقدة جذر إلى حين الوصول إلى شجرة بعقدة جذر معينة بحيث تكون متوازنة أي ارتفاع الشجرة اليسرى مساويًا لارتفاع الشجرة اليمنى، ويمكن القول هنا أنّ شجرة AVL هي شجرة BST تحقق شرط التوازن، علمًا أنّ ارتفاع الشجرة هو أكبر عمق موجود لها.
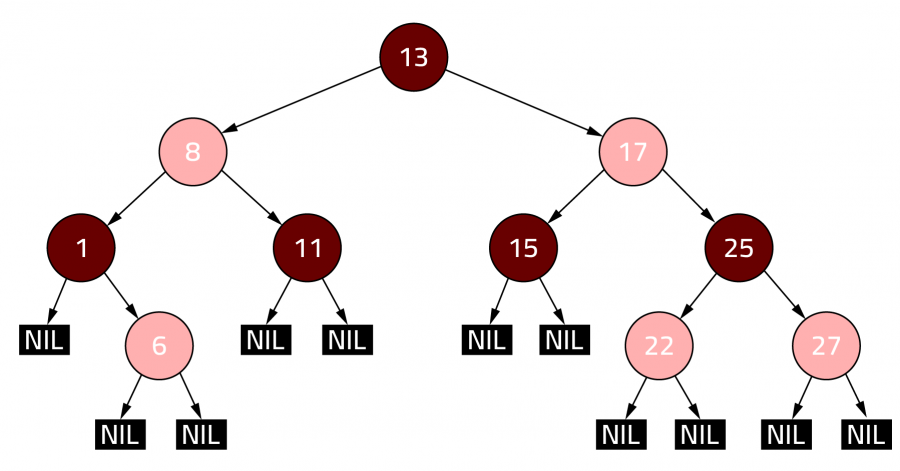
شجرة R-B
تعني الشجرة الحمراء والسوداء Red-Black tree وهي شجرة بحث ثنائية لها خصائص تميزها بحيث تحتوي كل عقدة فيها على بت تخزين يشير إلى لون العقدة والتي يمكن أن تكون حمراء أو سوداء فقط، كما أنّ عقدة الجذر والعقد الأوراق سوداء دائمًا، وإذا كانت العقدة حمراء فيجب أن يكون أبناءها سود، وأخيرًا يجب أن تحتوي جميع المسارات من عقدة إلى أحفادها العدد نفسه من العقد السوداء، فإذا تحقق ما سبق، فستكون الشجرة شجرة بحث ثنائية متوازنة.
شجرة البادئات
تُعَدّ شجرة البادئات Prefix tree نوعًا من أشجار البحث وتعرف أيضًا بالشجرة الرقمية أو tri كما تُعرَف بشجرة القاموس وتُستخدَم في البحث عن الكلمات بصورة عامة بما أنها مكوَّنة من أحرف الهجاء، وأهم ما يميزها أنّ جذرها لا يحتوي على أيّ محرف.
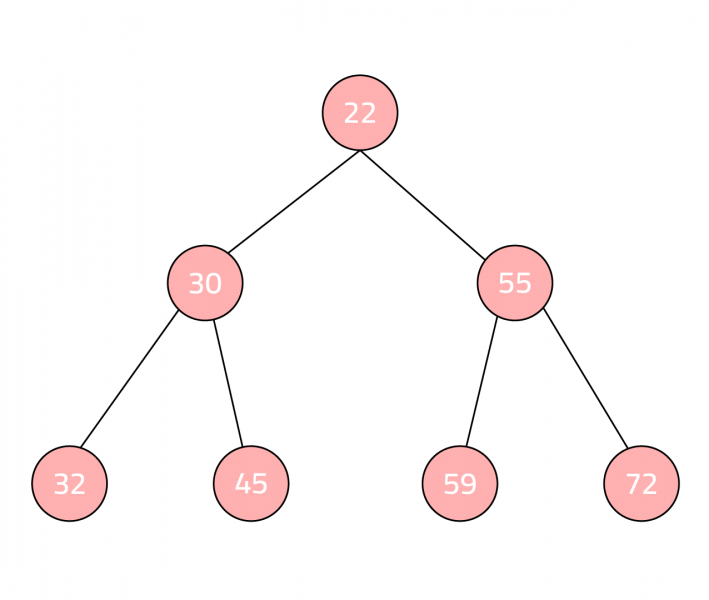
الكومة
تُعَدّ الكومة Heap بنية معطيات شجرية تمتلك خاصة الكومة وهي وجود أسلوب ترتيب متَّبع بين العقد الآباء والعقد الأبناء مثل أن يكون كل أب أكبر من جميع أبنائه وتسمى حينها بالكومة العظمى Max-Heap أو أن يكون كل أب أصغر من جميع أبنائه وتسمى حينها بالكومة الصغرى Min-Heap، وتُستخدَم الكومة بكثرة في خوارزميات الترتيب، كما تتميز الكومة بأنّ جميع مستوياتها ممتلئة بالكامل عدا المستوى الأخير، وفيما يلي صورة توضِّح كومة صغرى.
الرسم البياني
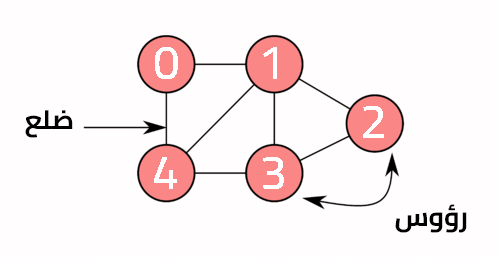
يختلف الرسم البياني graph أو المبيان عن الشجرة في عدم احتوائه على جذر ومن الممكن أن تتصل العقد مع بعضها باتجاه واحد directed graph أو بالاتجاهين معًا Bi-directional أو بدون اتجاه undirected، كما أنّ طبيعة العلاقات بين العقد في هذا النوع ليست ذات طبيعة هرمية، كما تسمى العقد بالرؤوس vertices والروابط التي بينها تسمى بالحواف أو الأضلاع edges ويكون عدد كل من الرؤوس والأضلاع محدودًا.
يكون الزوج (1,2) في الرسم البياني الموجَّه والذي يدل على وجود اتجاه من الرأس 1 إلى الرأس 2 مختلفًا عن الزوج (2,1)، كما تُرمَز مجموعة الرؤوس في هذا النوع بالرمز V ومجموعة الأضلاع بالرمز E ويُستخدَم هذا النوع من البنى في تمثيل الشبكات الواقعية مثل شبكة الهاتف المحمول أو شبكات التواصل الاجتماعي مثل الفيسبوك على سبيل المثال.
التقطيع Hashing
يُعَدّ التقطيع Hashing أو التجزئة تحسينًا لهياكل البيانات السابقة في بعض التطبيقات التي تحتاج إلى ترتيب بياناتها بواسطة أعداد كبيرة وفريدة موجودة ضمن هذه البيانات مثل ترتيب سجلات المرضى ضمن المستشفيات بناءً على أرقام هواتفهم والتي تُعَدّ مفاتيحًا فريدةً unique لهذه السجلات، ويكون ذلك من خلال الاستعانة بدالة تدعى دالة التقطيع hashing function والتي تحوِّل هذا المفتاح الفريد إلى عدد صغير وصحيح بحيث يكون فهرسًا لجدول جديد يدعى جدول التقطيع hashing table.
من الممكن أن يكون فهرس جدول التقطيع هو ذاته رقم هاتف المريض بحيث يكون طوله هو أكبر رقم هاتف موجود ضمن السجلات زائد واحد بما أنّ الفهرسة تبدأ من الصفر، وبالتالي نحصل على سرعة وصول عالية لأيّ سجل من خلال رقم الهاتف الخاص به، ولكن سيتسبب ذلك بتواجد فجوات gaps بين العناصر لعدم الحاجة لوجود جميع أرقام الهواتف المحتملة وبالتالي زيادة حجم التخزين في الذاكرة، لذا تُستخدَم دالة التقطيع لحل هذه المشكلة، وعندها يكون جدول التقطيع مصفوفةً يمثِّل كل عنصر فيها مؤشرًا على السجل الذي يحتوي على رقم الهاتف -في مثالنا- والذي تكون نتيجة تطبيق دالة التقطيع عليه هي فهرس هذا العنصر.
من الضروري التأكد من أنّ دالة التقطيع لا تعطي النتيجة ذاتها لأكثر من مفتاح، فإذا كانت دالة التقطيع مثلًا هي تأخذ فقط الرقم الأخير من رقم الهاتف، فسيكون لرقمَي الهاتف 45451 و 56561 على سبيل المثال النتيجة نفسها أي العدد 1 وبالتالي سيحدث تصادم في جدول التقطيع الذي فهرسه العدد 1، وأحد حلول هذه المشكلة أن يكون كل عنصر من جدول التقطيع مؤشرًا على قائمة مترابطة تحتوي على السجلات التي نتيجة تطبيق دالة التقطيع على أرقام هواتفها هي ذاتها.
ليكن لدينا الأعداد التالية 12 – 17 – 29 – 6 – 30 – 31 – 4 – 8، فإذا كان فهرس جدول التقطيع هو ذاته العدد المعطى، فسنحتاج إلى جدول بحجم 32، ولكن فعليًا نحتاج إلى 8 أماكن للتخزين وبالتالي سنحصل على فجوات وهدر في الذاكرة، لذا سنلجأ إلى دالة التقطيع والتي ستعطي آحاد العدد المُعطى، وبالتالي ستكون نتيجتها 2 – 7 – 9 – 6 – 0 – 1 – 4 – 8 عند تطبيقها على الأعداد السابقة على الترتيب، بحيث يُخزَّن العدد 12 في العنصر الذي فهرسه هو العدد 2 وهكذا، وبالتالي سنحتاج إلى جدول تقطيع بحجم 8 بدلًا من 32 كما يلي:
| 12 | 17 | 29 | 6 | 30 | 31 | 4 | 8 |
|---|---|---|---|---|---|---|---|
| 2 | 7 | 9 | 6 | 0 | 1 | 4 | 8 |
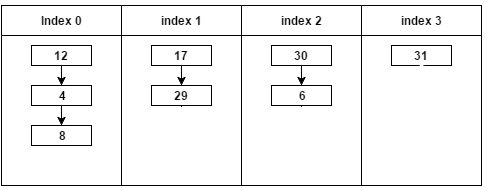
يمكن تقليص حجم هذا الجدول ليصبح 4 بتحسين دالة التقطيع، بحيث يكون الفهرس هو باقي قسمة كل عدد من الأعداد المعطاة على العدد 4، ولكن ستكون نتيجة الأعداد 17 و 19 هي الفهرس 1، أي سيحدث تصادم، ويمكن حل هذه المشكلة بجعل كل عنصر من عناصر جدول التقطيع مؤشرًا على قائمة مترابطة من الأعداد التي باقي قسمتها على العدد 4 هو فهرس هذا العنصر، أي كما في الشكل التالي:
يمكن زيادة حجم جدول التقطيع في المستقبل، كما أنّ هذه التقنية هي الأكثر استخدامًا في جوجل google.
الخاتمة
تعرَّفنا في هذا المقال على هياكل البيانات بكافة أنواعها مع إعطاء أمثلة توضيحية تساعدك على تخيل هذه البنى، بالإضافة إلى التطرق إلى ذكر أهميتها والفرق بينها وبين أنواع البيانات مع ذكر أهم تطبيقاتها.












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.