تُعدّ مسألة استكشاف قواعد الترابط في مبيعات المتاجر من المسائل المهمة جدًا لأصحاب المتاجر الإلكترونية، إذ يسمح إيجاد هذه القواعد بإظهار توصيات recommandations الشراء المناسبة للزبائن مما يساهم في زيادة مبيعات المتجر مثلًا لو عرفنا أن معظم الزبائن تشتري السلعة B مع السلعة A دومًا، فسيكون من المناسب إظهار توصية بشراء السلعة B لكل زبون يطلب شراء السلعة A مما يُحقق، في نهاية المطاف، رضى الزبون وزيادة أرباح المتجر.
نعرض في هذه المقالة استخدام تقنيات تعلم الآلة لإيجاد قواعد الترابط انطلاقًا من حركات الشراء السابقة للمتجر.
بيانات التدريب
نستخدم بيانات عمليات الشراء لأحد متاجر مبيعات التجزئة والمتاحة على الرابط أو يمكنك تنزيلها من الملف data.zip في المقال. تأتي هذه البيانات في الملف Groceries.csv المرفق والذي يحوي حوالي 10000 صف. يحوي كل صف بيانات عربة تسوق واحدة أي مجموعة من السلع التي اشتراها أحد الزبائن معًا كما يُبين الشكل التالي:
أساسيات في التنقيب عن قواعد الترابط
نعرض فيما يلي بعض التعاريف الأساسية في مسألة التنقيب عن قواعد الترابط.
التنقيب عن قواعد الترابط
تُعرّف مسألة التنقيب عن قواعد الترابط كما يلي:
بفرض أن لدينا مجموعة من الإجراءات transactions، يتألف كل إجراء من مجموعة من العناصر items.
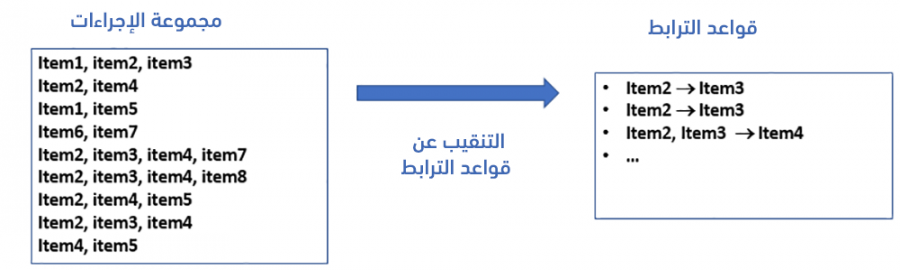
يكون المطلوب إيجاد جميع الترابطات correlations بين ظهور مجموعة جزئية من العناصر مع مجموعة جزئية أخرى. يُبين الشكل التالي مثالًا توضيحيًا:
نستخدم فيما يلي المثال التالي التعليمي والذي يحوي 5 إجراءات:
| الإجراء | Transaction |
|---|---|
| خبز، حليب | Bread,Milk |
| خبز، فوط، عصير، بيض | Bread, Diaper, Juice, Eggs |
| حليب، فوط، عصير، كولا | Milk, Diaper, Juice, Coke |
| خبز، حليب، فوط، عصير | Bread, Milk, Diaper, Juice |
| خبز، حليب، فوط، كولا | Bread, Milk, Diaper, Coke |
نُعطي أولًا أهم التعاريف الأساسية:
مجموعة عناصر itemset
وهي مجموعة من العناصر مثلًا: { Milk , Bread , Diaper} (فوط أطفال، خبز، حليب) كما ندون k-itemset للدلالة على مجموعة عناصر تحوي k عنصر.
عدد الدعم support count لمجموعة من العناصر
وهو عدد مرات تواتر (ظهور) مجموعة من العناصر في الإجراءات مثلًا يكون عدد الدعم في مثالنا التعليمي لمجموعة العناصر السابقة:
sc({Milk, Bread, Diaper}) = 2
الدعم support لمجموعة من العناصر
وهو النسبة المئوية لظهور مجموعة من العناصر في الإجراءات، مثلًا يكون عدد الدعم في مثالنا التعليمي لمجموعة العناصر سابقة الذكر:
s({Milk, Bread, Diaper}) = (2/5)*100 = 40%
الحد الأدنى للدعم minimum support
وهو حد أدنى تجريبي للدعم (يُمكن أن يكون رقم أو نسبة مئوية) نُحدّده لخوارزميات التنقيب عن القواعد.
اقتباسملاحظة: يُمثّل الدعم عمليًا أهمية العناصر، بمعنى أنه كلما كان الدعم مرتفعًا فهذا يحصر اهتمامنا في السلع التي تُباع مرارًا في المتجر.
مجموعة عناصر متواترة frequent itemset
نقول عن مجموعة عناصر أنها متواترة إذا كان دعم المجموعة أكبر أو يساوي الحد الأدنى للدعم.
قاعدة ترابط association rule
وهي اقتضاء من الشكل:
{X} => {Y}
وحيث X و Y هي مجموعات من العناصر (لا تحوي، بالطبع، عناصر مشتركة) مثلاً:
{Milk, Diaper} => {Bread}
الدعم لقاعدة ترابط association rule support
يكون الدعم لقاعدة ترابط X=>Y هو الدعم لاجتماع العناصر X و Y معًا. أي نسبة الإجراءات التي تحوي X و Y معًا من عدد الإجراءات الكلي:
الثقة في قاعدة ترابط association rule confidence
وهو الاحتمال الشرطي لظهور مجموعة العناصر Y في إجراء يحوي X، أي عمليًا احتمال (الثقة) أن تظهر مجموعة العناصر Y في عربة تسوق تحوي العناصر X.
مثلًا يكون الدعم لمجموعة العناصر {Milk, Diaper, Bread} في المثال السابق مساويًا 40% لأن هذه العناصر ظهرت مع بعضها البعض مرتين في الإجراءات الخمسة الكلية.
يُمكن من هذه العناصر الثلاثة {Milk, Diaper, Bread} توليد مجموعة من القواعد المختلفة (يكفي أن نوزع هذه العناصر على الطرف اليساري واليمني بكل الطرق الممكنة لنحصل على جميع القواعد). يُمكن أن يكون لكل قاعدة معامل ثقة مختلف كما تُبين الأمثلة التالية (المحسوبة من مثالنا التعليمي):
{Milk, Diaper} => {Bread} (s=0.4, c=0.67) {Milk, Bread} => {Diaper} (s=0.4, c= 0.67) {Diaper, Bread} => {Milk} (s=0.4, c=0.67) {Bread} => {Milk, Diaper} (s=0.4, c=0.50) {Diaper} => {Milk, Bread} (s=0.4, c=0.5) {Milk} => {Diaper, Bread} (s=0.4, c=0.5)
نعرض في هذه المقالة كيفية استخراج قواعد الترابط التي تحقق دعم وثقة معينين.
إعداد المشروع
يحتاج تنفذ شيفرات هذه المقالة بيئةً برمجيةً للغة بايثون الإصدار 3.8. ويجب أن تتضمن هذه البيئة البرمجية مدير الحِزم pip لتثبيت الحِزم، ومُنشئ البيئات الافتراضية venv لإنشاء بيئاتٍ افتراضيةٍ.
نستخدم محرر الشيفرات البرمجية Jupyter Notebooks، وهو مفيد جدًا لتجربة وتشغيل الأمثلة الخاصة بتَعَلّم الآلة بطريقةٍ تفاعليةٍ، حيث نستطيع من خلاله تشغيل كتلًا صغيرةً من الشيفرات البرمجية ورؤية النتائج بسرعة، مما يُسهّل علينا اختبار الشيفرات البرمجية وتصحيحها.
نحتاج أولًا لتثبيت بعض التبعيات، وذلك لإنشاء مساحة عملٍ للاحتفاظ بملفاتنا قبل أن نتمكن من تطوير برنامجنا.
نُنشئ مجلدًا جديدًا خاصًا بمشروعنا وندخل إليه هكذا:
mkdir asoc
cd asoc
نُنفذّ الأمر التالي لإنشاء البيئة الافتراضية:
python -m venv asoc
ومن ثم الأمر التالي في Linux لتنشيط البيئة الافتراضية:
source asoc/bin/activate
أما في Windows، فيكون أمر التنشيط:
"asoc/Scripts/activate.bat"
نستخدم إصداراتٍ مُحددةٍ من المكتبات اللازمة، من خلال إنشاء ملف requirements.txt في مجلد المشروع، وسيُحدِّد هذا الملف المتطلبات والإصدارات التي سنحتاج إليها.
نفتح الملف requirements.txt في محرر النصوص، ونُضيف الأسطر التالية، وذلك لتحديد المكتبات التي نريدها وإصداراتها:
asttokens==2.0.5 backcall==0.2.0 colorama==0.4.4 cycler==0.11.0 debugpy==1.6.0 decorator==5.1.1 entrypoints==0.4 executing==0.8.3 fonttools==4.33.3 ipykernel==6.13.0 ipython==8.4.0 jedi==0.18.1 joblib==1.1.0 jupyter-client==7.3.1 jupyter-core==4.10.0 kiwisolver==1.4.2 matplotlib==3.5.2 matplotlib-inline==0.1.3 mlxtend==0.20.0 nest-asyncio==1.5.5 numpy==1.22.4 packaging==21.3 pandas==1.4.2 parso==0.8.3 pickleshare==0.7.5 Pillow==9.1.1 prompt-toolkit==3.0.29 psutil==5.9.1 pure-eval==0.2.2 Pygments==2.12.0 pyparsing==3.0.9 python-dateutil==2.8.2 pytz==2022.1 pywin32==304 pyzmq==23.0.0 scikit-learn==1.1.1 scipy==1.8.1 seaborn==0.11.2 six==1.16.0 stack-data==0.2.0 threadpoolctl==3.1.0 tornado==6.1 traitlets==5.2.2.post1 wcwidth==0.2.5
نحفظ التغييرات التي طرأت على الملف ونخرج من محرر النصوص، ثم نُثَبت هذه المكتبات بالأمر التالي:
(asoc) $ pip install -r requirements.txt
بعد تثبيتنا لهذه التبعيات، نُصبح جاهزين لبدء العمل على مشروعنا.
كتابة الشيفرة البرمجية
نُشغّل محرر الشيفرات البرمجية Jupyter Notebook بمجرد اكتمال عملية التثبيت هكذا:
(asoc) $ jupyter notebook
ثم نُنشئ ملفًا جديدًا في داخل المحرر ونُسمّه باسم asc مثلًا.
توليد قواعد الترابط
نعرض في الشيفرة التالية توليد قواعد الترابط للمثال السابق بهدف التعرف على المكتبات اللازمة وآلية استخدامها.
نضع إجراءات المثال السابق أولًا في مصفوفة ثنائية وبحيث يكون كل عنصر منها هو مصفوفة من عناصر إجراء واحد.
نحتاج أولًا إلى توليد إطار بيانات dataframe وبحيث تكون رؤوس الأعمدة هي العناصر وقيم الخلايا هي إما True في حال وجود العنصر في صف row الإجراء الموافق أو False في حال عدم وجوده.
نستخدم الصنف TransactionEncoder من المكتبة mlxtend.preprocessing للوصول إلى ذلك.
# الإجراءات transactions = [['Bread', 'Milk'], ['Bread', 'Diaper', 'Juice', 'Eggs'], ['Milk', 'Diaper', 'Juice', 'Coke' ], ['Bread', 'Milk', 'Diaper', 'Juice'], ['Bread', 'Milk', 'Diaper', 'Coke']] # مكتبة ترميز الإجراءات from mlxtend.preprocessing import TransactionEncoder # إنشاء غرض من الصف te = TransactionEncoder() # ملائمة المرمز مع البيانات te_model = te.fit(transactions) # تحويل الإجراءات rows=te_model.transform(transactions) # استيراد مكتبة إطار البيانات import pandas as pd # بناء إطار بيانات الإجراءات df = pd.DataFrame(rows, columns=te_model.columns_) print(df)
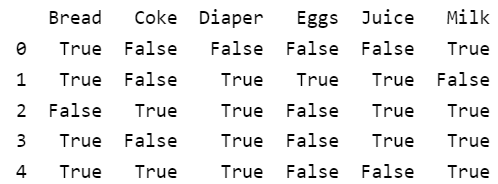
وبالنتيجة يكون لدينا إطار بيانات الإجراءات التالي:
لاحظ مثلًا أن الصف الأول من إطار البيانات يوافق الإجراء الأول: {Bread, Milk}.
نستدعي في الشيفرة التالية الدالة apriori من المكتبة mlxtend.frequent_patterns والتي تحسب العناصر المتواترة في إطار البيانات السابق (df) وفق حد أدنى معين للدعم min_support (يساوي 40% في مثالنا).
يكون ناتج تطبيق هذه الدالة إطار بيانات frequent_itemsets ذي عمودين: مجموعة العناصر المتواترة itemsets والدعم support. نُضيف عمود محسوب جديد لإطار البيانات الناتج يحسب طول كل مجموعة عناصر length.
# مكتبة خوارزمية إيجاد العناصر المتواترة from mlxtend.frequent_patterns import apriori # توليد المجموعات المتواترة مع تحديد الحد الأدنى للدعم frequent_itemsets = apriori(df, min_support=0.4, use_colnames=True) # حساب أطوال مجموعات العناصر frequent_itemsets['length'] = frequent_itemsets['itemsets'].apply(lambda x: len(x)) print(frequent_itemsets)
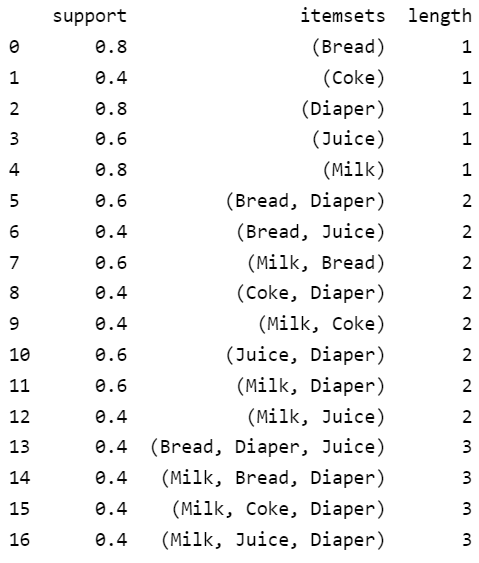
تُظهر الطباعة دعم وطول كل مجموعة من مجموعات العناصر المتواترة:
يُمكن الآن توليد قواعد الترابط باستخدام إطار بيانات العناصر المتواترة frequent_itemsets السابق، كما تُبين الشيفرة التالية.
نستخدم الدالة association_rules من المكتبة mlxtend.frequent_patterns مع تحديد الحد الأدنى للثقة min_threshold (لنأخذ القيمة 60% في مثالنا).
# مكتبة خوارزمية إيجاد قواعد الترابط from mlxtend.frequent_patterns import association_rules # توليد القواعد مع تحديد الحد الأدنى للثقة rules = association_rules(frequent_itemsets,metric="confidence",min_threshold=0.6) # الترتيب التنازلي وفق معامل الثقة rules = rules.sort_values(['confidence'], ascending =[False]) print(rules)
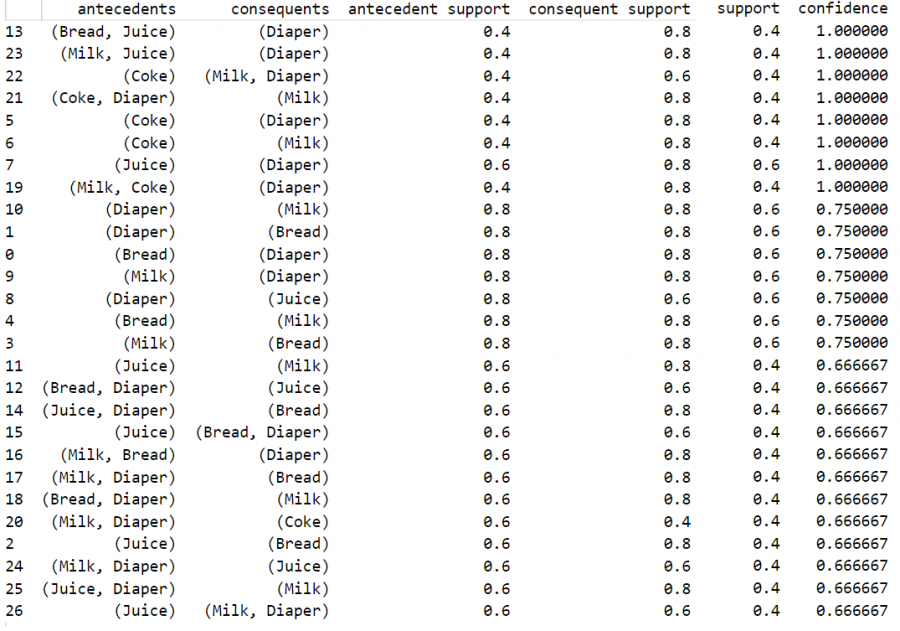
يُبين الشكل التالي قواعد الترابط الناتجة:
يُمكن استخدام رسم الإحداثيات المتوازية parallel_coordinates من المكتبة pandas.plotting لرسم مشاهدة توضيحية للقواعد السابقة.
from matplotlib import pyplot as plt from pandas.plotting import parallel_coordinates # دالة تحويل القواعد إلى إحداثيات def rules_to_coordinates(rules): rules['antecedent'] = rules['antecedents'].apply(lambda antecedent: list(antecedent)[0]) rules['consequent'] = rules['consequents'].apply(lambda consequent: list(consequent)[0]) rules['rule'] = rules.index return rules[['antecedent','consequent','rule']] # توليد الإحداثيات المتوازية coords = rules_to_coordinates(rules) # توليد رسم الإحداثيات المتوازية plt.figure(figsize=(4,8)) parallel_coordinates(coords, 'rule') plt.grid(True) plt.show()
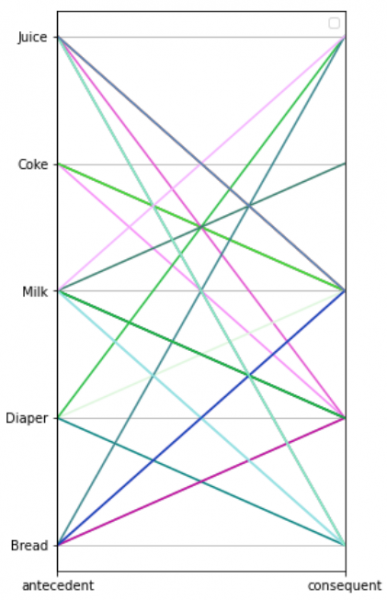
يكون الرسم البياني الناتج:
يُبين الرسم ارتباطات العناصر، وذلك برسم خط بين العنصر من الجهة اليسرى وبين نهاية الخط الأفقي للعنصر الآخر المرتبط معه من الجهة اليمنى، مثلًا يرتبط الحليب Milk مع كل من الخبز Bread و الفوط Diaper.
تحميل بيانات المتجر
نبدأ أولًا بتحميل بيانات المتجر من الملف Groceries.csv ضمن إطار من البيانات DataFrame من مكتبة Pandas ومن ثم عرض بعضها:
# تحميل بيانات المتجر df = pd.read_csv('Groceries.csv',header=None) df.head()
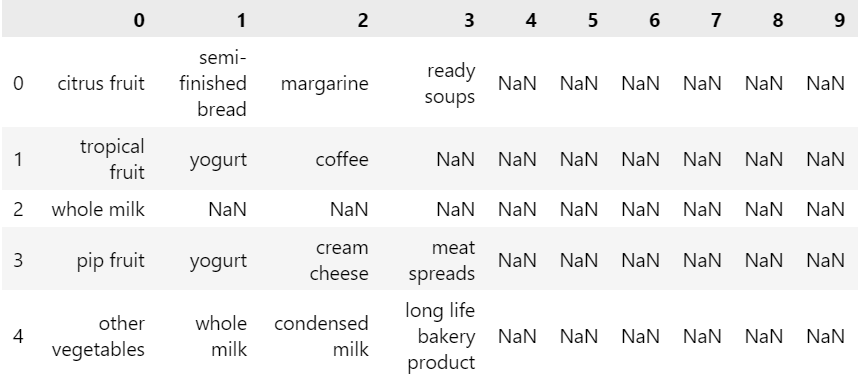
يظهر لنا أوائل صفوف الملف:
نلاحظ وجود قيم كثيرة فارغة NaN وذلك لأن عدد العناصر في كل صف غير متساوي.
نحذف في الشفرة التالية القيم الفارغة، ثم نُنشئ مصفوفة الإجراءات والتي هي مصفوفة يكون كل عنصر منها مصفوفة من عناصر صف واحد من إطار البيانات:
# حذف القيم الفارغة # وإنشاء مصفوفة transactions = df.T.apply(lambda x: x.dropna().tolist()).tolist() print(transactions[1:10]))
يُبين الشكل التالي مثلًا العناصر العشرة الأولى من مصفوفة الإجراءات الناتجة:
نستخدم في الشيفرة التالية مُرمز الإجراءات للحصول على إطار بيانات الإجراءات:
# إنشاء غرض من الصف te = TransactionEncoder() # ملائمة المرمز مع البيانات te_model = te.fit(transactions) # تحويل الإجراءات rows=te_model.transform(transactions) # بناء إطار بيانات الإجراءات df = pd.DataFrame(rows, columns=te_model.columns_) print(df.shape)
مما يُعطي:
(9835, 169)
لاحظ أن عدد أعمدة إطار البيانات الناتج هو 169 عمودًا مما يعني وجود 169 عنصرًا مختلفًا فقط في الإجراءات البالغ عددها 9835 إجراء.
نستدعي في الشيفرة التالية الدالة apriori والتي تحسب العناصر المتواترة في إطار البيانات df وفق حد أدنى معين للدعم min_support يساوي 0.5% (هو رقم تجريبي حصلنا عليه بتكرار توليد العناصر المتواترة وقواعد الترابط حتى الوصول لقواعد ترابط عددها محدود نسبيًا).
يكون ناتج تطبيق هذه الدالة إطار بيانات frequent_itemsets ذي عمودين: مجموعة العناصر المتواترة itemsets والدعم support. نُضيف عمود محسوب جديد لإطار البيانات الناتج يحسب طول length كل مجموعة عناصر.
# توليد المجموعات المتواترة مع تحديد الحد الأدنى للدعم frequent_itemsets = apriori(df, min_support=0.005, use_colnames=True) # حساب أطوال مجموعات العناصر frequent_itemsets['length'] = frequent_itemsets['itemsets'].apply(lambda x: len(x)) print(frequent_itemsets)
تُبين النتائج أن لدينا 1001 مجموعة من العناصر المتواترة المُحققة للحد الأدنى للدعم ويتراوح طولها بين 1 و 4:
يُمكن الآن توليد قواعد الترابط باستخدام إطار بيانات العناصر المتواترة السابق كما تُبين الشيفرة التالية. نستخدم الدالة association_rules مع تحديد الحد الأدنى للثقة 55% (رقم تجريبي حصلنا عليه بعد عدة محاولات لتوليد قواعد الترابط حتى وصلنا لمجموعة معقولة من القواعد).
# توليد القواعد مع تحديد الحد الأدنى للثقة rules = association_rules(frequent_itemsets,metric="confidence",min_threshold=0.55) # الترتيب التنازلي وفق معامل الثقة rules = rules.sort_values(['confidence'], ascending =[False]) print(rules)
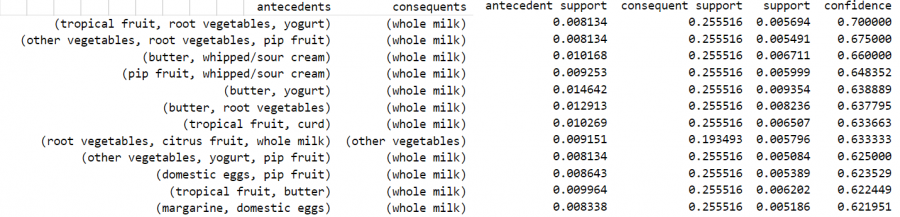
يُبين الشكل التالي قواعد الترابط الناتجة (حوالي 50 قاعدة):
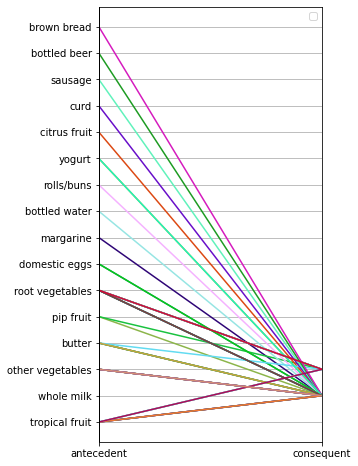
يُمكن استخدام رسم الإحداثيات المتوازية لرسم مشاهدة توضيحية للقواعد السابقة:
from pandas.plotting import parallel_coordinates # دالة تحويل القواعد إلى إحداثيات def rules_to_coordinates(rules): rules['antecedent'] = rules['antecedents'].apply(lambda antecedent: list(antecedent)[0]) rules['consequent'] = rules['consequents'].apply(lambda consequent: list(consequent)[0]) rules['rule'] = rules.index return rules[['antecedent','consequent','rule']] # توليد الإحداثيات المتوازية coords = rules_to_coordinates(rules) # توليد رسم الإحداثيات المتوازية plt.figure(figsize=(4,8)) parallel_coordinates(coords, 'rule') plt.legend([]) plt.grid(True) plt.show()
يكون الرسم البياني الناتج:
الخلاصة
عرضنا في هذه المقالة خطوات بناء إيجاد قواعد الترابط بين مبيعات العناصر في المتاجر.
يُمكن تجربة المثال كاملًا من موقع Google Colab من الرابط أو تنزيله من الملف المرفق.
الملف المرفق: data (1).zip

















أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.