خطوات تنفيذ مشروع عن تعلم الآلة في بايثون: الجزء الثاني

نعرض في هذه السلسلة من المقالات تسلسل خطوات تنفيذ مسألة حقيقية في تعلّم الآلة بهدف تسليط الضوء على أهم الصعوبات التي يُمكنها مواجهة المبرمج وكيفية التغلب عليها.

شرحنا في المقالة السابقة الخطوات الثلاثة الأولى في مسألة تعلّم الآلة، وهي تنظيف البيانات أولًا، ومن ثم إجراء التحليل الاستكشافي لها بهدف اختيار الميزات المناسبة للمسألة، وأخيرًا تحديد خط الأساس الذي سنقيّم أداء نموذج التعلّم وفقه.

نتابع في هذه المقالة عرض إنشاء عدة نماذج تعلّم مختلفة باستخدام بايثون، وذلك بهدف موازنة هذه النماذج لاختيار الأفضل منها، ومن ثم آلية ضبط ومعايرة المعاملات الفائقة للنموذج المختار بشكل أمثلي. وأخيرًا كيفية تقويم النموذج النهائي باستخدام بيانات الاختبار المتوفرة. يُمكن تنزيل واستخدام ومشاركة الشيفرة المتاحة للعموم من مستودع github.

اختيار النموذج وتقييمه

نُذكّر بأننا نريد بناء نموذج يتنبأ بمعامل نجمة الطاقة Energy Star Score لمدينة نيويوركk مع التركيز على دقة النتائج وقابلية تفسيرها وذلك باستخدام بيانات الطاقة المتاحة للعموم. وبهذا تكون المسألة المطروحة مسألة تعلّم آلة من نمط موجه عبر الانحدار كما عرضنا سابقًا.

كي لا نغوص في الموازنات الكثيرة بين نماذج تعلّم الآلة المعروفة ونتمعن في مخططات موازنة النماذج سنجرب العديد منها عمليًا لاختيار الأمثل.

لنتذكر أن تعلّم الآلة مازال حقلًا تجريبيًا، وقد يكون من المستحيل معرفة النموذج الأمثل مسبقًا.

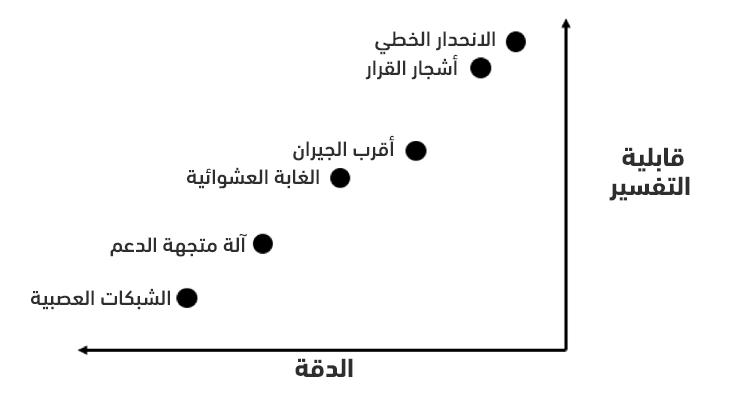
نبدأ عادةً بتجربة نموذج بسيط قابل للتفسير مثل نموذج الانحدار الخطي linear regression، وفي حال كانت دقته غير مقبولة، فسننتقل لنماذج أكثر تعقيدًا. يُبين الشكل التالي (المرسوم بشكل تجريبي) العلاقة بين الدقة accuracy وقابلية التفسير interpretability.

سنجرب النماذج الخمسة التالية:

• الانحدار الخطي Linear Regression.
• انحدار أقرب الجيران K-Nearest Neighbors Regression.
• انحدار الغابة العشوائية Random Forest Regression.
• الانحدار المعزز بالتدرج Gradient Boosted Regression.
• انحدار آلة متجهة الدعم Support Vector Machine Regression.

لن نغوص في الخلفية النظرية لهذه النماذج بل سنُركز على برمجتها وتقويمها. يُمكن العودة للمزيد من التفاصيل للمقال العربي المفاهيم الأساسية لتعلم الآلة، وللمرجع المجاني من Introduction to Statistical Learning، وللكتاب Hands-On Machine Learning with Scikit-Learn and TensorFlow، لأخذ معرفة أكثر حول ذلك.

احتساب القيم الناقصة

حذفنا في مرحلة تنظيف البيانات الأعمدة التي يتجاوز فيها عدد القيم الناقصة 50% من قيم العمود. وسيتعين علينا الآن ملء القيم الناقصة المتبقية لأن جميع خوارزميات التعلّم لا تعمل بوجود قيم ناقصة.

لنبدأ أولًا بعرض كل البيانات باستخدام الشيفرة التالية:

import pandas as pd
import numpy as np

# قراءة البيانات ووضعها في إطار بيانات 
train_features = pd.read_csv('data/training_features.csv')
test_features = pd.read_csv('data/testing_features.csv')
train_labels = pd.read_csv('data/training_labels.csv')
test_labels = pd.read_csv('data/testing_labels.csv')

Training Feature Size:  (6622, 64)
Testing Feature Size:   (2839, 64)
Training Labels Size:   (6622, 1)
Testing Labels Size:    (2839, 1)

والذي يُظهر:

لاحظ أن كل قيمة "ليست رقمًا" NaN تُمثّل قيمةً ناقصة، وهنا سنستبدل ببساطة كل قيمة ناقصة بالقيمة الأوسط median لعمودها. يُمكن العودة للمرجع لمعاينة طرق أخرى لاستبدال القيم الناقصة.

نُنشئ في الشيفرة التالية كائنًا Scikit-Learn من النمط Imputer مع إسناد استراتيجيته إلى القيمة الأوسط، ونُدرّب بعدها هذا الكائن باستخدام بيانات التدريب عن طريق تابع الملاءمة imputer.fit، ومن ثم نستخدمه لملء القيم الناقصة في كل من بيانات التدريب والاختبار باستخدام تابع التحويل imputer.transform. لاحظ أن القيم الناقصة في بيانات الاختبار تُستبدل بالقيمة الأوسط لبيانات التدريب.

نستخدم هذه الطريقة في الحساب لتجنب الوقوع في فخ تسرب بيانات الاختبار test data leakage, وبهذا لا تختلط بيانات الاختبار مع بيانات التدريب أبدًا.

# إنشاء كائن الحساب مع استراتيجية القيمة الأوسط
imputer = Imputer(strategy='median')

# الملاءمة مع ميزات التدريب
imputer.fit(train_features)

# حساب كل من بيانات التدريب والاختبار
X = imputer.transform(train_features)
X_test = imputer.transform(test_features)

Missing values in training features:  0
Missing values in testing features:   0

يؤدي تنفيذ الشيفرة السابقة إلى الحصول على ميزات لها قيم حقيقية منتهية وبدون أي نقص فيها.

تحجيم الميزات

نعني بتحجيم الميزات الإجرائية العامة التي تُغير مجال قيم الميزة، وهي عملية ضرورية لأن الميزات تأتي عادةً بوحدات مختلفة، وبالتالي ستتوزع قيمها على مجالات مختلفة، تتأثر بعض النماذج كثيرًا ولاسيما تلك التي تحسب المسافة بين الأمثلة بمجالات هذه القيم، مثل نموذج آلة متجهة الدعم support vector machine ونموذج أقرب الجيران، بينما لا تتطلب بعض النماذج بالضرورة تحجيم الميزات، مثل نموذج الانحدار الخطي linear regression ونموذج الغابة العشوائية random forest. وتكون هذه الخطوة ضروريةً في جميع الأحوال عند الحاجة لموازنة نماذج التعلّم المختلفة.

نفعّل من أجل إرجاع قيم أي ميزة إلى المجال [0-1] من أجل كل قيمة في ميزة بطرح أصغر قيمة للميزة من هذه القيمة، ومن ثم القسمة على ناتج طرح أعلى قيمة للميزة من أصغر قيمة للميزة (مجال الميزة). تّدعى هذه العملية أحيانًا بالتسوية normalization أو التوحيد standardization.

يُمكن لنا برمجة العملية الحسابية السابقة طبعًا بسهولة، إلا أننا نستخدم الكائن MinMaxScaler في Scikit-Learn والذي ينجزها، وتُطابق شيفرة التحجيم شيفرة الحساب السابق مع استبدال scaler بـ imputer. سنؤكد على أننا نُدرّب باستخدام بيانات التدريب فقط ونحسب لكل البيانات بما فيها بيانات الاختبار كما نوّه سابقًا.

# إنشاء كائن التحجيم مع المجال 0 إلى 1
scaler = MinMaxScaler(feature_range=(0, 1))

# الملاءمة مع بيانات التدريب
scaler.fit(X)

# تحويل كل من بيانات التدريب والاختبار
X = scaler.transform(X)
X_test = scaler.transform(X_test)

تكون لكل ميزة بعد تنفيذ هذه الشيفرة قيمة صغرى هي 0 وقيمة عظمى هي 1.

يُستحسن فهم كل من عملية احتساب القيم الناقصة وعملية تحجيم الميزات جيدًا لأنهما موجودتان عمليًا في أي مشروع تعلّم آلة.

تنفيذ نماذج تعلم الآلة باستخدام Scikit-Learn

يُعدّ إنشاء النماذج وتدريبها ومن ثم استخدامها للتنبؤ أمرًا يسيرًا بعد أن أنهينا مراحل تنظيف البيانات وإعدادها. نستخدم المكتبة Scikit-Learn في بايثون والتي يتوفر لها توثيق ممتاز وطريقة بناء موحدة لكل نماذج التعلّم، مما يسمح بتنفيذ العديد من النماذج بسرعة.

تُبين الشيفرة التالية آلية إنشاء نموذج الانحدار المعزز بالتدرج Gradient Boosted Regression وتدريبه باستخدام تابع الملاءمة fit، ومن ثم اختباره باستخدام تابع التنبؤ predict.

from sklearn.ensemble import GradientBoostingRegressor

# إنشاء النموذج
gradient_boosted = GradientBoostingRegressor()

# ملاءمة النموذج مع بيانات التدريب
gradient_boosted.fit(X, y)

# التنبؤ باستخدام بيانات الاختبار
predictions = gradient_boosted.predict(X_test)

# تقويم النموذج
mae = np.mean(abs(predictions - y_test))

print('Gradient Boosted Performance on the test set: MAE = %0.4f' % mae)

حيث يكون الناتج:

Gradient Boosted Performance on the test set: MAE = 10.0132

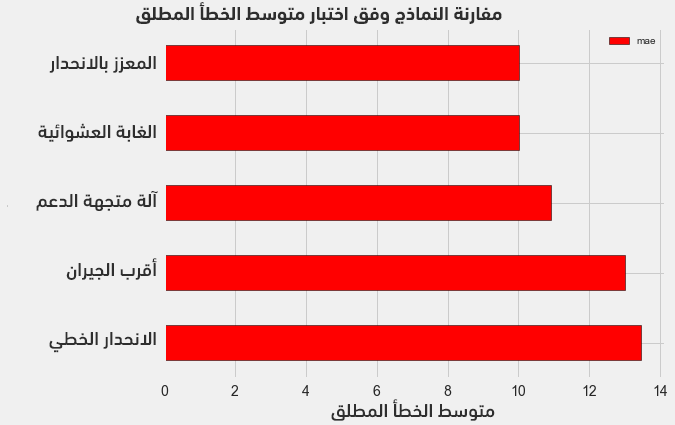
لاحظ أن كل عملية من العمليات الأساسية (إنشاء وتدريب واختبار) تأخذ سطرًا واحدًا فقط، وبالتالي لبناء بقية النماذج يكفي تغيير اسم النموذج المطلوب في الشيفرة. يُبين الشكل التالي نتائج النماذج المختبرة:

تُثبت الأرقام في الشكل أن جميع نماذج تعلّم الآلة قابلة للتطبيق في مسألتنا لأنها جميعها تتميز بمتوسط قيم خطأ مطلق أصغر من خط الأساس المُحدّد لمسألتنا (وهو 24.5) والذي حُسب باستخدام القيمة الأوسط للهدف (معامل نجمة الطاقة).

لاحظ تقارب متوسط الخطأ المطلق لكل من نموذج الانحدار المعزز MAE=10.013 ونموذج الغابة العشوائية MAE=10.014. قد لا تكون الموازنة في هذه المرحلة عادلةً بين النماذج لاسيما بالنسبة لنموذج آلة متجهة الدعم support vector machine لأننا تركنا القيم الافتراضية لمعاملات النماذج دون أي معايرة أو ضبط.

معايرة المعاملات الفائقة وصولا لنموذج أمثلي

يُمكن الوصول لنموذج أمثلي بمعايرة معاملاته الفائقة وفق معطيات المشروع. لنُبين أولًا الفرق بين المعاملات الفائقة لنموذج والمعاملات الأخرى له:

• المعاملات الفائقة hyperparameters: هي إعدادات خوارزمية التعلّم قبل التدريب (والتي وضعها مصممو الخوارزمية) مثل عدد الجيران في نموذج أقرب الجيران أو عدد الأشجار في نموذج الغابة العشوائية.
• المعاملات parameters: هي المعاملات التي يتعلّمها النموذج أثناء التدريب مثل أوزان نموذج الانحدار الخطي.

تؤثر عملية معايرة المعاملات الفائقة على أداء النموذج لاسيما لجهة التوزان المطلوب بين مشكلة قلة التخصيص underfitting ومشكلة فرط التخصيص overfitting، واللتان تؤديان إلى نموذج غير قادر على تعميم أمثلة التدريب، وبالتالي لن يتمكن من التنبؤ مع معطيات جديدة. ويُمكن العودة للرابط من أكاديمية حسوب للمزيد من التفصيل حول هاتين المشكلتين.

تظهر مشكلة قلة التخصيص عندما لا يكون للنموذج درجات حرية كافية ليتعلّم الربط بين الميزات والهدف، وبالتالي يكون له انحياز كبير نحو قيم معينة للهدف. يُمكن تصحيح قلة التخصيص بجعل النموذج أكثر تعقيدًا، بينما تظهر مشكلة فرط التخصيص عندما يخزن النموذج بيانات التدريب، فيكون له بالتالي تباين كبير، والذي يُمكن تصحيحه بالحد من تعقيد النموذج باستخدام التسوية regularization.

تكمن المشكلة في معايرة المعاملات الفائقة بأن قيمها المثلى تختلف من مسألة لأخرى، وبالتالي تُعَد الطريقة الوحيدة للوصول لهذه القيم المثلى هي تجريب قيم مختلفة مع كل مجموعة بيانات تدريب جديدة.

يحاول الكثيرون مثل مخبر Epistasis الوصول للقيم المثلى باستخدام خوارزميات مناسبة مثل الخوارزميات الجينية، إذ يوفر Scikit-Learn لحسن الحظ العديد من الطرق لتقويم المعاملات الفائقة وبالتالي سنعتمد في مشروعنا عليها دون تعقيد الأمور أكثر.

البحث العشوائي مع التقييم المتقاطع

تُدعى الطريقة التي سنستخدمها في إيجاد القيم المثلى بالبحث العشوائي مع التقويم المتقاطع random search with cross validation:

• البحث العشوائي: نُعرّف شبكة grid من قيم المعاملات الفائقة، ومن ثم نختار تركيبات مختلفة منها عشوائيًا، أي أننا لا نختار كل التركيبات الممكنة مثل سلوك البحث الشبكي (يكون أداء البحث العشوائي لحسن الحظ قريب من البحث الشبكي مع تخفيض كبير في الزمن اللازم).
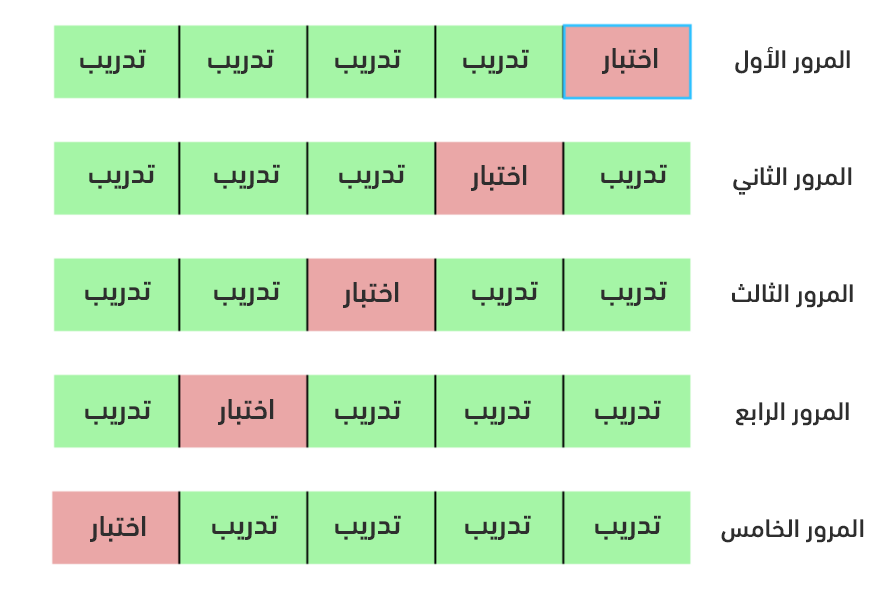
• التقييم المتقاطع: وهو الطريقة المستخدمة لتقويم مجموعة قيم محدّدة للمعاملات الفائقة، عوضًا عن تقسيم البيانات إلى بيانات للتدريب وبيانات للتقويم، مما يُخفّض من البيانات التي يُمكن لنا استخدامها للتدريب، كما نستخدم التقويم المتقاطع مع عدد محدّد من الحاويات K-Fold. إذ تُقسم بيانات التدريب إلى عدد K من الحاويات ومن ثم ننكرر ما يلي K مرة: في كل مرة ندرب النموذج مع بيانات K-1 حاوية، ومن ثم تقويمه مع بيانات الحاوية K. حيث يكون مقياس الأداء النهائي هو متوسط الخطأ لكل التكرارات.

يوضح الشكل التالي فكرة التقويم المتقاطع من أجل K=5:

يُمكن تلخيص خطوات البحث العشوائي مع التقويم المتقاطع كما يلي:

1. إعداد شبكة من المعاملات الفائقة.
2. اختيار مجموعة عشوائية من تركيبات قيم المعاملات الفائقة.
3. إنشاء نموذج مع قيم المعاملات المختارة.
4. تقويم النموذج باستخدام التقويم المتقاطع.
5. اختيار تركيب قيم المعاملات ذو الأداء الأفضل.

لن نبرمج هذه الخطوات طبعًا لأن الكائن RandomizedSearchCV في Scikit-Learn ينجز كل ذلك.

طرق التعزيز المتدرج مرة أخرى

يُعدّ نموذج الانحدار المعزز بالتدرج Gradient Boosted Regression (المستخدم في حالتنا) من طرق المجموعات، بمعنىً أنه يدرب مجموعةً من المتدربين الضعفاء (أشجار قرار) تسلسليًا، وبحيث أن كل متدرب يستفيد من أخطاء المتدرب السابق، بخلاف نموذج الغابة العشوائية والذي يدرب مجموعةً من المتدربين الضعفاء على التوازي ومن ثم يتنبأ عن طريق الانتخاب بينهم.

تصدرت طرقُ التعزيز طرقَ تعلّم الآلة في السنوات الأخيرة لاسيما بعد فوزها في العديد من مسابقات التعلّم، إذ تستخدم طريقة التعزيز المتدرجِ النزولَ المتدرجَ Gradient Descent لتخفيض تابع الكلفة عن طريق تدريب المتدربين واحدًا تلو الآخر، بحيث يستفيد كل متدرب من أخطاء المتدرب السابق.

تسبق بعض المكتبات أداء المكتبة Scikit-Learn المستخدمة في مشروعنا مثل XGBoost، إلا أننا سنحافظ على استخدامها مع بياناتنا الصغيرة نسبيًا نظرًا لدقتها الواضحة.

معايرة المعاملات الفائقة في نموذج الانحدار المعزز بالتدريج

يُمكن العودة لتوثيق Scikit-Learn لتفاصيل المعاملات الفائقة، والتي سنجد القيم الأمثل لها:

• loss تابع الخسارة والذي يجب تخفيضه.
• n_estimators عدد المتدربين الضعفاء (أشجار القرار).
• max_depth العمق الأعظم لشجرة القرار.
• min_samples_leaf العدد الأصغر للأمثلة في ورقة شجرة قرار.
• min_samples_split العدد الأصغر المطلوب لتقسيم عقدة في شجرة قرار.
• max_features العدد الأعظم للميزات المطلوب لتقسيم عقدة في شجرة قرار.

قد لا نجد أحدًا يفهم كيفية تأثير هذه المعاملات على بعضها البعض، ولابدّ من التجريب للوصول إلى القيم المثلى لها.

نبني في الشيفرة التالية شبكةً من قيم المعاملات الفائقة، حيث نُنشئ كائن RandomizedSearchCV ونبحث باستخدام 4 حاويات للتقويم المتقاطع مع 25 تركيبةً مختلفةً لقيم المعاملات الفائقة:

# تابع الخسارة المطلوب تخفيضه
loss = ['ls', 'lad', 'huber']

# عدد أشجار القرار المستخدمة
n_estimators = [100, 500, 900, 1100, 1500]

# العمق الأعظم لكل شجرة
max_depth = [2, 3, 5, 10, 15]

# عدد الأمثلة الأصغر لكل ورقة
min_samples_leaf = [1, 2, 4, 6, 8]

# عدد الأمثلة الأصغر لتقسيم عقدة
min_samples_split = [2, 4, 6, 10]

# العدد الأعظم للميزات المستخدمة لتقسيم عقدة
max_features = ['auto', 'sqrt', 'log2', None]

# تعريف شبكة المعاملات الفائقة للبحث فيها
hyperparameter_grid = {'loss': loss,
                       'n_estimators': n_estimators,
                       'max_depth': max_depth,
                       'min_samples_leaf': min_samples_leaf,
                       'min_samples_split': min_samples_split,
                       'max_features': max_features}

# إنشاء نموذج معايرة المعاملات الفائقة
model = GradientBoostingRegressor(random_state = 42)

# إعداد البحث العشوائي مع 4 حاويات للتقويم المتقاطع
random_cv = RandomizedSearchCV(estimator=model,
                               param_distributions=hyperparameter_grid,
                               cv=4, n_iter=25, 
                               scoring = 'neg_mean_absolute_error',
                               n_jobs = -1, verbose = 1, 
                               return_train_score = True,
                               random_state=42)

# الملاءمة مع بيانات التدريب
random_cv.fit(X, y)

نعاين الكائن RandomizedSearchCV بعد الانتهاء من البحث لنعرف النموذج الأمثل:

# إيجاد أفضل تركيبة ممكنة من القيم 
random_cv.best_estimator_
GradientBoostingRegressor(loss='lad', max_depth=5,
                          max_features=None,
                 min_samples_leaf=6,
                          min_samples_split=6,
                          n_estimators=500)

يُمكن لنا استخدام هذه النتائج لإنجاز البحث الشبكي باستخدام معاملات للشبكة قريبة من هذه المعاملات المثلى. لن يؤدي المزيد من البحث والمعايرة إلى تحسين ملحوظ على الأرجح، وذلك لأن عملية هندسة الميزات التي عملنا عليها في البداية كان لها التأثير الأكبر في تحسين نتائج النموذج، إذ يطبق في الحقيقة أيضًا قانون تناقص العوائد law of diminishing في تعلّم الآلة والذي يقول: لقد أعطت هندسة الميزات الأثر الأكبر في تحسين النموذج ولن تؤدي معايرة المعاملات الفائقة إلا للقليل من التحسن.

يُمكن تجربة تغيير عدد المتدربين مثلًا (أشجار القرار)، مع الحفاظ على بقية قيم المعاملات الفائقة ثابتةً مما يسمح لنا بمعاينة تأثير هذا المعامل. يُمكن الاطلاع على الشيفرة الموافقة والتي تعطي النتائج التالية:

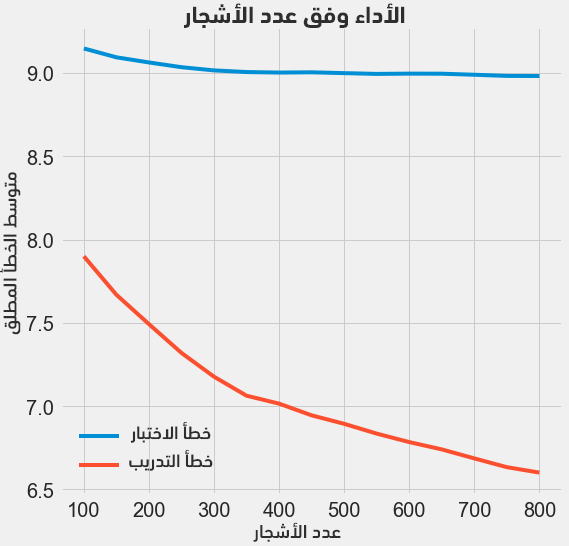
لاحظ أنه كلما ازداد عدد الأشجار يقل الخطأ سواءً في بيانات التدريب أو في بيانات الاختبار، كما يتناقص الخطأ في التدريب بسرعة أكبر من الخطأ في الاختبار. لكن يبدو أن نموذجنا ذو فرط تخصيص overfitting، حيث أن له أداءً ممتازًا مع بيانات التدريب لا يصل له مع بيانات الاختبار.

نتوقع دائمًا بعض الانخفاض في الأداء مع بيانات الاختبار عن بيانات التدريب (لا تنسى أن النموذج يرى كل بيانات التدريب)، لكن وجود فارق كبير في الأداء بين التدريب والاختبار يعني مشكلة فرط التخصيص، والتي يُمكن حلها بزيادة بيانات التدريب أو تخفيض تعقيد النموذج عبر المعاملات الفائقة. نحافظ على قيم المعاملات الفائقة كما هي ونترك للقارئ محاولة البحث عن حل لمشكلة فرط التخصيص.

نعتمد من أجل النموذج النهائي القيمة 800 لمعامل عدد الأشجار لأنها تُعطي أقل خطأ نتيجة التقويم المتقاطع.

التقويم باستخدام بيانات الاختبار

سنستخدم بيانات الاختبار والتي أخفيناها تمامًا عن نموذج التعلّم أثناء مرحلة التدريب، إذ سيُعطي اختبار النموذج طبعًا مع هذه البيانات مؤشرًا لأداء النموذج مع البيانات الحقيقية لاحقًا.

تحسب الشيفرة التالية متوسط الخطأ المطلق (معيار الأداء) لكل من النموذج الأولي والنموذج النهائي الذي حصلنا عليه بعد معايرة المعاملات الفائقة:

# التنبؤ باستخدام النموذج الأولي والنهائي
default_pred = default_model.predict(X_test)
final_pred = final_model.predict(X_test)

Default model performance on the test set: MAE = 10.0118.
Final model performance on the test set:   MAE = 9.0446.

أدت معايرة المعاملات الفائقة إلى تحسين الأداء بنسبة 10% تقريبًا وهي نسبة قد تكون مهمةً في التطبيقات الحقيقية رغم الوقت الذي خصصناه لتنفيذها.

يُمكن معايرة الوقت الذي يستغرقه تدريب النموذج باستخدام التعليمة السحرية ‎%timeit في محيط التطوير المستخدم Jupyter Notebooks:

%%timeit -n 1 -r 5
default_model.fit(X, y)

ويكون ناتج الشيفرة مثلًا:

1.09 s ± 153 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)

تُظهر النتيجة أن تدريب النموذج الأولي يحتاج لحوالي ثانية واحدة فقط وهو زمن معقول جدًا؛ أما النموذج النهائي فهو ليس بهذه السرعة إذ يستغرق حوالي 12 ثانيةً:

%%timeit -n 1 -r 5
final_model.fit(X, y)

حيث يكون ناتج الشيفرة مثلًا:

12.1 s ± 1.33 s per loop (mean ± std. dev. of 5 runs, 1 loop each)

يُعزز ذلك مبدأ المقايضة trade-offs العام في تعلّم الآلة، إذ نسعى دومًا لمقايضة الدقة مع قابلية التفسير وانحراف النتائج مع تباينها، والدقة مع زمن التنفيذ وغيرها. ربما يبدو 12 ضعفًا رقمًا كبيرًا نسبيًا إلا أنه ليس بهذا السوء مطلقًا.

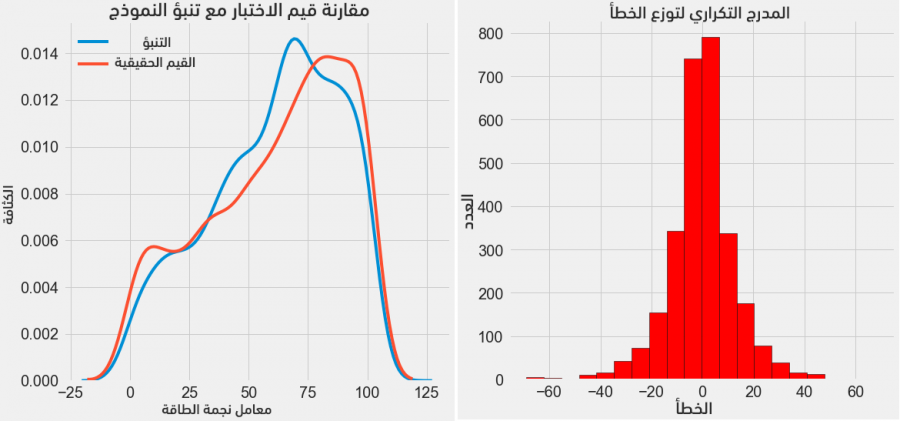
يُمكننا الآن وبعد حصولنا على التنبؤات النهائية فحص فيما إذا يوجد أي انحراف أو مشكلة ما فيها. يُبين الشكل التالي (على اليسار) مخطط الكثافة لتوقعات النموذج (الأزرق) مع القيم الحقيقية (الأحمر)؛ أما على اليمين فيَظهر المدرج التكراري لقيمة الخطأ المرتكب.

يُبين مخطط الكثافة أن توقعات النموذج تتبع تقريبًا توزع القيم الحقيقية على الرغم من أن قمة كثافة التوقعات قريبة من القيمة الأوسط لقيم التدريب (66)، بينما تكون قمة كثافة القيم الحقيقية أقرب للقيمة العظمى (100)؛ أما المدرج التكراري فيُظهر توزعًا طبيعيًا تقريبًا للخطأ المرتكب مع ملاحظة وجود قيم سالبة للخطأ مما يعني توقعات أقل من الحقيقة. كما سنُلقي في المقالة التالية ضوءًا أكبر على النتائج.

دورة الذكاء الاصطناعي

احترف برمجة الذكاء الاصطناعي AI وتحليل البيانات وتعلم كافة المعلومات التي تحتاجها لبناء نماذج ذكاء اصطناعي متخصصة.

اشترك الآن

النتائج

تابعنا في هذه المقالة استعراض العديد من الخطوات في معالجة مسألة تعلّم الآلة:

• احتساب القيم الناقصة وتحجيم الميزات.
• تقويم وموازنة عدة نماذج تعلّم.
• معايرة المعاملات الفائقة باستخدام البحث العشوائي الشبكي والتقويم المتقاطع.
• تقويم النموذج الأفضل مع بيانات الاختبار.

تُبرهن النتائج على إمكانية استخدام البيانات المتوفرة لبناء نموذج تعلّم الآلة بهدف توقع معامل نجمة الطاقة للمباني، إذ يتنبأ نموذج التعلّم من نمط الانحدار المعزز بالتدرج بمعامل نجمة الطاقة مع خطأ من مرتبة 9.1 نقطةً بالنسبة للقيمة الحقيقية في بيانات الاختبار. وقد ساعدت عملية معايرة المعاملات الفائقة رغم الوقت المستغرق لإنجازنا لها لتحسين أداء النموذج، وهي واحدة من المقايضات التي ننجزها في مسائل تعلّم الآلة.

سنحاول في المقالة التالية فهم النموذج المتعلّم الدقيق الذي توصلنا له أكثر لاسيما آلية قيامه بالتنبؤات، كما سنحاول تحديد العوامل المؤثرة في معامل نجمة الطاقة. فمع العلم بأن النموذج المتعلّم الذي توصلنا إليه يبدو دقيقًا، إلا أننا نريد أن نفهم آلية وصوله لنتائجه.

ترجمة -وبتصرف- للمقال A Complete Machine Learning Project Walk-Through in Python: Part Two لكاتبه Will Koehrsen.

اقرأ أيضًا

• دوال الكثافة الاحتمالية في بايثون
• المرجع الشامل إلى تعلم لغة بايثون