تُستخدم الشبكات العصبية كوسيلةٍ للتعلم العميق، فهي واحدةٌ من المجالات الفرعية العديدة لطُرق تطبيق الذكاء الصناعي. وقد اقْتُرحت لأول مرةٍ منذ حوالي 70 عامًا في محاولةٍ لمحاكاة طريقة عمل دماغ الإنسان، إلا أنها أبسط بكثيرٍ من الخلايا العصبية الحقيقة، إذ أن كلّ خليةٍ اصطناعيةٍ مرتبطةٌ بعِدة طبقاتٍ، ولكلّ واحدةٍ منها وزنٌ مُعينٌ يُعبر عن أهمية هذه الطبقة، وذلك لتحديد كيفية استجابة الخلية العصبية عند نشْر البيانات عبرها، وبينما كانت الشبكات العصبية سابقًا محدودةً في عدد الخلايا العصبية التي تستطيع محاكاتها في ذلك الوقت -وهو الأمر الذي انعكس بدوره على تعقيد عملية التعلم التي يمكننا تحقيقها-، إلا أنه في السنوات الأخيرة، ونظرًا للتقدم الكبير في تطوّر الأجهزة، استطعنا أخيرًا بناء شبكاتٍ عصبيةٍ عميقةٍ جدًا، وتدريبها على مجموعات بياناتٍ هائلةٍ وضخمة كذلك، مما أدّى إلى تحقيق قفزاتٍ نوعية في تطور الذكاء الاصطناعي وتحديدًا تعلم الآلة.
سمحت تلك القفزات النوعية للآلات بمُقاربة قدرات البشر، بل وتجاوزتها في أداء بعض المهام المحدودة. ومن بين هذه المهام، قدرتها على التعرف على الكائنات، فعلى الرغم من أن الآلات كانت غير قادرة تاريخيًا على منافسة قوة الرؤية البشرية، إلا أنّ التطورات الحديثة في التعلم العميق جعلت من الممكن بناء شبكاتٍ عصبيةٍ باستطاعتها التعرف على الكائنات والوجوه والنصوص، بل وحتى العواطف!
سنُطبق في هذا المقال قِسمًا فرعيًا صغيرًا من طُرق التعرف على الكائنات، وتحديدًا التعرف على الأرقام المكتوبة بخط اليد، وذلك باستخدام مكتبة TensorFlow، وهي مكتبة بايثون مفتوحة المصدر التي طُوّرت في مختبرات غوغل Google Brain لأبحاث التعلم العميق، كما أنها من أشهر المكتبات الحالية في التعلم العميق، وسنأخذ صورًا مكتوبٌ عليها الأرقام بخط اليد من الرقم 0 وحتى الرقم 9، وسنبني شبكةً عصبيةً وندربها لكي تتعرف على التصنيف المناسب لكل رقمٍ معروضٍ في الصورة وتتنبأ به، ثم تَنسْبه لصنفٍ من أصناف الأرقام الموجودة.
سنفترض إلمامك بمصطلحات ومفاهيم تعلم الآلة، مثل التدريب والاختبار والميزات والأصناف والتحسين والتقييم. لهذا لن تحتاج لخبرةٍ سابقةٍ في مجال التعلم العميق التطبيقي أو بمكتبة TensorFlow، ولمتابعة وفَهم هذا المقال جيدًا ننصحك أولًا بالاطلاع على: المفاهيم الأساسية لتعلم الآلة.
المتطلبات الرئيسية
لإكمال هذا المقال ستحتاج بيئةً برمجيةً للغة بايثون الإصدار 3.8 سواءً كان محليًا أو بعيدًا. ويجب أن تتضمن هذه البيئة البرمجية مدير الحِزم pip لتثبيت الحِزم، ومُنشئ البيئات الافتراضية venv لإنشاء بيئاتٍ افتراضيةٍ.
1. إعداد المشروع
ستحتاج أولًا لتثبيت بعض التبعيات، وذلك لإنشاء مساحة عملٍ للاحتفاظ بملفاتنا قبل أن نتمكن من تطوير برنامج التعرف على الصور، وسنستخدم بيئة بايثون 3.8 الافتراضية لإدارة التبعيات الخاصة بمشروعنا.
سَنُنشئ مجلدًا جديدًا خاصًا بمشروعنا وسندخل إليه هكذا:
mkdir tensorflow-demo cd tensorflow-demo
سننفذّ الأوامر التالية لإنشاء البيئة الافتراضية:
python -m venv tensorflow-demo
ومن ثم الامر التالي في Linux لتنشيط البيئة الافتراضية:
source tensorflow-demo/bin/activate
أما في Windows، فيكون أمر التنشيط:
"tensorflow-demo/Scripts/activate.bat"
بعد ذلك، سنُثبتّ المكتبات التي سنستخدمها.
سنستخدم إصداراتٍ محددةٍ من هذه المكتبات، من خلال إنشاء ملف requirements.txt في مجلد المشروع، وسيُحدِّد هذا الملف المتطلبات والإصدارات التي سنحتاج إليها.
نفتح الملف requirements.txt في محرر النصوص، ونُضيف الأسطر التالية، وذلك لتحديد المكتبات التي نريدها وإصداراتها:
keras==2.6.0 numpy==1.19.5 Pillow==8.4.0 scikit-learn==1.0 scipy==1.7.1 sklearn==0.0 tensorflow==2.6.0
سنحفظ التغييرات التي طرأت على الملف وسنخرج من محرر النصوص، ثم سنُثَبت هذه المكتبات بالأمر التالي:
(tensorflow-demo) $ pip install -r requirements.txt
بعد تثبيتنا لهذه التبعيات، سنُصبح جاهزين لبدء العمل على مشروعنا.
2. استيراد مجموعة بيانات MNIST
تُسمى مجموعة البيانات التي سنستخدمها، بمجموعة بيانات MNIST، وهي مجموعةٌ كلاسيكيةٌ في مجتمع مُطوري تعلم الآلة، وتتكون من صورٍ لأرقامٍ مكتوبةٍ بخط اليد، بحجم 28×28 بكسل. ونستعرض فيما يلي بعض الأمثلة للأرقام المُتضمنة فيها:
لاحظ أنه ينبغي أن نستخدم ملفًا واحدًا لجميع أعمالنا في هذا المقال، ولنُنشئ برنامج بايثون يتعامل مع مجموعة البيانات هذه، سننشئ ملفًا جديدًا باسم main.py، وسنفتح هذا الملف بأي محرر شيفرات لدينا -مثل VS code- وسنُضيف هذه الأسطر البرمجية لاستيراد المكتبات اللازمة:
import tensorflow as tf import numpy as np from sklearn.preprocessing import OneHotEncoder #مكتبة معالجة الصور from PIL import Image #التوافقية مع إصدار سابق tf.compat.v1.disable_v2_behavior()
وسنضيف أيضًا هذه الأسطر من الشيفرات البرمجية لملفك لاستيراد مجموعة بيانات MNIST وذلك باختيار صور التدريب المتاحة من Tensorflow ومن ثم نُنزلها ونقسمها إلى جزئين: الأول للتدريب والثاني للاختبار:
#اختيار بيانات التدريب mnist = tf.keras.datasets.mnist #تنزيل بيانات التدريب والاختبار (x_train, y_train), (x_test, y_test) = mnist.load_data() #طباعة عدد بيانات التدريب والاختبار print (len(x_train)) print (len(x_test)) #تحجيم البيانات بين 0 و 1 x_train, x_test = x_train / 255.0, x_test / 255.0 #الترميز الأحادي النشط y_train = [[i] for i in y_train] y_test = [[i] for i in y_test] enc = OneHotEncoder(sparse=True) enc.fit(y_train) y_train = enc.transform(y_train) y_test = enc.transform(y_test)
تقوم الدالة 'mnist.load_data' بتنزيل البيانات وتقسيمها إلى مجموعتين واحدة للتدريب (60000 صورة) والمجموعة الثانية للاختبار (10000 صورة).
وعند قراءة البيانات سنستخدم الترميز الأحادي النشط One-Hot Encoding لتمثيل التصنيفات للصور. حيث يَستَخدم الترميز الأحادي النشط One-Hot Encoding متجهًا vector مُكونٌ من قيمٍ ثنائيةٍ لتمثيل القيم الرقمية أو الصنفية. ونظرًا لأن أصنافنا مخصصةٌ لتمثيل الأرقام من 0 إلى 9، فإن المتجه سيحتوي على 10 قيمٍ، واحدةٌ لكلّ رقمٍ ممكنٍ. وتُسنَد إحدى هذه القيم بوضع القيمة 1، وذلك لتمثيل الرقم في هذا المؤشر للمتجه، كما ستُسنَد القيم الباقية بالقيمة 0. فمثلًا، سيُمثلُ الرقم 3 من خلال المتجه هكذا: [0 ،0 ،0 ،1 ،0 ،0 ،0 ،0 ،0 ،0]. وسنلاحظ وجود القيمة 1 في الفهرس 3، لذلك فإن المتجه سيُمثِلُ الرقم 3.
ولتمثيل الصور الفعلية والتي تكون بحجم 28x28 بكسل، يتوجب علينا تسويتها في المتجه 1D بحجم 784 بكسل، وهو ناتج ضرب 28×28. وسنخزن هذه البكسلات والتي ستُشكل الصورة لاحقًا، وذلك في قيمٍ تتراوح بين 0 و255، حيث ستحدّد هذه القيم تدرج اللون الرمادي للبكسل، وستُعرَض صورنا باللونين الأبيض والأسود فقط. لذلك سيُمثلُ البكسل الأسود بالقيمة 255، والبكسل الأبيض بالقيمة 0، وذلك مع التدرجات المختلفة للون الرمادي بينهم.
والآن بعد استيرادنا للبيانات، حان الوقت للتفكير في كيفية بناء الشبكة العصبية.
3. تحديد بنية الشبكة العصبية
يُشير مصطلح بنية الشبكة العصبية لعناصرٍ متنوعةٍ، مثل عدد الطبقات في الشبكة وعدد الوِحدات في كلّ طبقةٍ، كما يشير إلى كيفية توصيل هذه الوِحدات بين الطبقات المختلفة. ونظرًا لأن الشبكات العصبية مستوحاةٌ من كيفية عمل الدماغ البشري، فسنستخدم مصطلح الوِحدة ليُمثّل ما يُمكن تسميته بيولوجيًا بالخلايا العصبية.
تأخذ الوِحدات بعض القيم من الوِحدات السابقة مثل مُدخلاتٍ لها، حيث تتشابه مع الخلايا العصبية التي تُمرر إشاراتها حول الدماغ، ثمّ تُجري عمليةً حسابيةً، وتُمرر القيمة الجديدة مثل مُخرجاتٍ إلى وِحداتٍ أخرى، وهكذا. تُوضع هذه الوِحدات على شكل طبقاتٍ متراكبةٍ فوق بعضها البعض مشكّلةً الشبكة العصبية، بحيث يمكن للشبكة أن تتألف كحدٍ أدنى من طبقتين، طبقةٌ لإدخال القيم، وطبقةٌ أخرى لإخراج القيم. يُستخدم مصطلح الطبقة المخفية لجميع الطبقات الموجودة بين طبقات المُدخلات وطبقات المُخرجات الخارجية، أي أن تلك الطبقات تكون مخفيةً عن العالم الحقيقي.
تحقق البُنى المختلفة للشبكة نتائجًا مختلفةً عن بعضها البعض، ويمكن اتخاذ الأداء مثل معيارٍ للحكم على هذه البُنى المختلفة، كما يمكن اتخاذ عناصر أخرى معيارًا للحكم، مثل الوسطاء والبيانات ومدة التدريب.
سنضيف هذه الأسطر البرمجية التالية لملفك، وذلك لتخزين عدد الوِحدات المُخصصة لكلّ طبقةٍ ووضعها في متغيّراتٍ عامةٍ. وهذه الطريقة ستسمح لنا بتغيير بِنية الشبكة بمكانٍ واحدٍ، وفي نهاية هذا المقال يمكنك اختبار مدى تأثير الأعداد المختلفة من الطبقات والوِحدات على نتائج نموذجنا:
n_input = 784 # input layer (28x28 pixels) n_hidden1 = 512 # 1st hidden layer n_hidden2 = 256 # 2nd hidden layer n_hidden3 = 128 # 3rd hidden layer n_output = 10 # output layer (0-9 digits)
يُوضح الرسم البياني التالي تصورًا للبِنية التي صمّمناها، مع توصيل كلّ طبقةٍ بالطبقات المحيطة بها توصيلًا كاملًا:
ويرتبط مصطلح الشبكة العصبية العميقة Deep Neural Network بعدد الطبقات المخفية، وعادةً ما تُشير كلمة السطحية في مصطلح الشبكة العصبية السطحية إلى وجود طبقةٍ مخفيةٍ واحدةٍ، بينما تُشير كلمة العميقة إلى وجود طبقاتٍ مخفيةٍ متعددةٍ. ونظريًا إذا أُعطِيت الشبكة العصبية السطحية ما يكفي من بياناتٍ للتدريب، فيجب أن تَقدِر على تمثيل أي وظيفةٍ يمكن للشبكة العصبية العميقة أن تؤدّيها. ولكن من ناحية الفعالية الحسابية، فغالبًا ما يكون نتائج استخدام شبكةٍ عصبيةٍ عميقةٍ ذات حجمٍ صغيرٍ أفضل من النتائج التي تُعطيها الشبكة العصبية السطحية ذات العدد الكبير من الوِحدات المخفية، وذلك عند تأديتهم لنفس المَهمة.
كما أن الشبكات العصبية السطحية غالبًا ما تواجه مشكلة فَرط التخصيص Overfitting، إذ يكون هدف الشبكة الأساسي هو حفظ بيانات التدريب التي شاهدتها، ولكنها لن تستطيع تعميم المعرفة التي اكتسبتها على البيانات الجديدة، وهذا هو السبب في كون استخدام الشبكات العصبية العميقة أكثر شيوعًا، إذ أنها تسمح للطبقات المتعددة الموجودة بين البيانات المُدخلة الأولية والبيانات المُصنفة الناتجة، بتعلم الميزات على مستوياتٍ متنوعةٍ، مما يُعزز قدرة الشبكة على التعلم وتعميم الفكرة.
ومن العناصر الأخرى للشبكة العصبية التي يجب تعريفها هنا هي الوسطاء الفائقة Hyperparameters، فعلى عكس الوسطاء العادية التي تُحدث قيمها أثناء عملية التدريب، سنُسند قيم الوسطاء الفائقة في البداية وسنثبتها طوال العملية.
أسنِد المتغيّرات بالقيم التالية في ملفك:
learning_rate = 1e-4 n_iterations = 1000 batch_size = 128 dropout = 0.5
يمثل معدل التعلم Learning Rate مدى تعديل الوسطاء في كلّ خطوةٍ من عملية التعلّم، إذ تُعَد هذه التعديلات مكونًا رئيسيًا للتدريب، فبعد كلّ عملية مرور ٍعبر الشبكة، سنضبط أوزان الطبقات قليلًا لأهمية ذلك في محاولةٍ لتقليل الخسارة، حيث يمكن لمعدل التعلم المرتفع أن يتحقق بسرعة، ولكن يمكن كذلك أن تتجاوز القيم المثلى عند تحديثها في كلّ مرة.
يشير مصطلح عدد التكرارات Number Of Iterations إلى عدد مرات مرورنا على خطوة التدريب، ويشير حجم الدفعة Batch Size لعدد أمثلة التدريب التي نستخدمها في كل خطوة، كما ويمثل المتغير dropout الموضع الذي نحذف عنده بعضًا من الوِحدات عشوائيًا. وسنستخدم المتغير dropout في الطبقة النهائية المخفية لإعطاء كلّ وِحدة من الوحدات احتمالًا بنسبة 50٪ للتخلص منها في كلّ خطوة تدريبٍ، وهذا سيساعد على منع ظهور مشكلة فرط التخصيص Overfitting.
حددنا الآن بِنية شبكتنا العصبية والوسطاء الفائقة التي ستُؤثر على عملية التعلّم، والخطوة التالية هي بناء الشبكة مثل مخططٍ بيانيٍ من خلال مكتبة TensorFlow.
4. بناء مخطط بياني من خلال مكتبة TensorFlow
لبناء شبكتنا، لابد لنا من إعداد الشبكة مثل مخططٍ بيانيٍ حسابي من خلال مكتبة TensorFlow لتنفيذه. والمفهوم الأساسي لمكتبة TensorFlow هو tensor، وهو بنية بياناتٍ مشابهةٍ لبِنية المصفوفة Array، أو القائمة List. وهذا المتغير سيهيَأ ويُعالَج عند مروره عبر المخطط البياني للشبكة عبر عملية التعلّم.
وسنبدأ بتحديد ثلاثة متغيراتٍ tensors من نوع placeholders، وهو نوع tensor تُسندُ قيمته لاحقًا. والآن سنضيف الشيفرة البرمجية التالية إلى الملف الذي نعمل عليه:
X = tf.compat.v1.placeholder("float", [None, n_input]) Y = tf.compat.v1.placeholder("float", [None, n_output]) keep_prob = tf.compat.v1.placeholder(tf.float32)
إنّ الوسيط الوحيد الذي يتوجب علينا تحديده عند التعريف هو حجم البيانات التي سنُسندها لاحقًا، وبالنسبة للمتغير X سنستخدم شكل [None، 784]، إذ ستمثل القيمة None كميةً غير محددةٍ، وسنُسند كميةً غير محددةٍ من الصور ذات حجم 784 بكسل. بحيث يصبح شكل المتغير Y هو [None، 10]، وستمثل None عددًا غير محددٍ من التصنيفات الناتجة، مع وجود 10 أصنافٍ محتملةٍ. وسنستخدم في المتغير keep_prob tensor من نوع placeholders للتحكم في معدل dropout، وسنجعله من نوع placeholders وذلك لجعله متغيرًا من نوعٍ قابلٍ للتعديل، بدلًا من كونه متغيرًا من نوعٍ غير قابلٍ للتعديل immutable variable، وذلك لأننا نريد استخدام نفس tensor التدريب عند إسناد dropout بالقيمة 0.5، ونفس tensor الاختبار عند إسناد dropout بالقيمة 1.0.
والوسطاء التي ستُحدث قيمها الشبكة العصبية في عملية التدريب هي القيم الخاصة بوزن كلّ طبقةٍ، والتي تُعبر عن الأهمية وقيم التحيز bias values، لذلك سنحتاج لإسنادهم بقيمٍ إبتدائيةٍ بدلًا من قيمٍ فارغةٍ. وهذه القيم هي الأساس الذي ستبدأ الشبكة رحلة التعلم انطلاقًا منها، إذ ستُستخدم في تفعيل دوال الشبكة العصبية، والتي تُمثِلُ قوة الاتصالات بين الوِحدات.
ونظرًا لاستمرار تحسين القيم أثناء عملية التدريب، يمكننا ضبطها حاليًا بالقيمة 0. لاحظ أن القيمة الأولية في الواقع لها تأثيرٌ كبيرٌ على الدقة النهائية للنموذج. وسنستخدم التوزيع الاحتمالي الطبيعي المنقطع Truncated normal distribution لتوليد قيمٍ عشوائيةٍ لأوزان الطبقات، بحيث يكونون قريبين من الصفر حتى يتمكنوا من التعديل إما باتجاهٍ إيجابيٍ أو سلبيٍ، كما يكونون مختلفين قليلًا، وذلك ليُنتِجوا أخطاءً مختلفةً، وبهذه الطريقة سنضمن بأن يتعلم النموذج شيئًا مفيدًا.
والآن سنضيف هذه الأسطر البرمجية التالية لملفنا الذي نعمل عليه:
weights = { 'w1': tf.Variable(tf.random.truncated_normal([n_input, n_hidden1], stddev=0.1)), 'w2': tf.Variable(tf.random.truncated_normal([n_hidden1, n_hidden2], stddev=0.1)), 'w3': tf.Variable(tf.random.truncated_normal([n_hidden2, n_hidden3], stddev=0.1)), 'out': tf.Variable(tf.random.truncated_normal([n_hidden3, n_output], stddev=0.1)), }
بالنسبة للتحيز Bais، سنستخدم قيمةً ثابتةً صغيرةً لضمان تنشيط جميع tensors المراحل الأولية، وبالتالي المساهمة في الانتشار. وستُخزن الأوزان وجميع tensors التحيزات في objects قواميس Dictionary لسهولة الوصول إليها.
أضف هذه الشيفرة البرمجية للملف الذي نعمل عليه وذلك لتعريف التحيز وقِيَمه:
biases = { 'b1': tf.Variable(tf.constant(0.1, shape=[n_hidden1])), 'b2': tf.Variable(tf.constant(0.1, shape=[n_hidden2])), 'b3': tf.Variable(tf.constant(0.1, shape=[n_hidden3])), 'out': tf.Variable(tf.constant(0.1, shape=[n_output])) }
والآن جهّز طبقات الشبكة العصبية من خلال تعريف العمليات التي ستتعامل مع tensors المرحلة الحالية. وأضف هذه الشيفرة البرمجية للملف الذي نعمل عليه:
layer_1 = tf.add(tf.matmul(X, weights['w1']), biases['b1']) layer_2 = tf.add(tf.matmul(layer_1, weights['w2']), biases['b2']) layer_3 = tf.add(tf.matmul(layer_2, weights['w3']), biases['b3']) layer_drop = tf.nn.dropout(layer_3, keep_prob) output_layer = tf.matmul(layer_3, weights['out']) + biases['out']
ستنفذ كلّ طبقةٍ مخفيةٍ عملية ضربٍ للمصفوفة على نتائج الطبقة التي سبقتها وعلى أوزان الطبقة الحالية، وسيُضاف التحيز لهذه القيم. في الطبقة المخفية الأخيرة، سنُطبِّق عملية التسرب dropout بالقيمة 0.5 للمتغير Keep_prob الخاص بنا.
الخطوة الأخيرة في بناء المخطط البياني، هي تحديد دالة الخسارة التي نريد تحسينها. والاختيار الشائع لدالة الخسارة في المكتبة البرمجية TensorFlow هو الانتروبي المشترك Joint Antropy، والمعروف كذلك باسم فقدان السجل log-loss، وهو الذي يُحدد الفرق بين التوزيعين الاحتماليين لكلً من التنبؤات والتصنيف. ويمكن أن تكون قيمة الانتروبي المشترك 0، وذلك في أفضل الأحوال عند التصنيف المثالي، وذلك مع انعدام الخسارة تمامًا.
سنحتاج كذلك إلى اختيار خوارزمية التحسين المناسبة، والتي سنستخدمها لتقليل الناتج من دالة الخسارة. وتُسمى هذه العملية بعملية تحسين الانحدار التدريجي، وهي طريقةٌ شائعةٌ للعثور على الحد الأدنى للدالة، من خلال اتخاذ خطواتٍ تكراريةٍ على طول التدرج في الاتجاه السلبي التنازلي. وهناك العديد من الخيارات لخوارزميات تحسين الانحدار التدريجي المُطبقة في المكتبة البرمجية TensorFlow، إلا أننا سنستخدم في هذا المقال خوارزمية المُحسِّن أدم Adam optimizer، الذي يعمتد على عملية تحسين الانحدار التدريجي باستخدام الزخم أو كمية الحركة Momentum، وذلك بتسريع عملية التنعيم من خلال حساب متوسط ٍمُرجَّحٍ بكثرة للتدرجات، واستخدام ذلك في التعديلات مما يؤدي لتقاربٍ أسرع. وسنضيف هذه الشيفرة للملف الذي نعمل عليه:
cross_entropy = tf.reduce_mean( tf.nn.softmax_cross_entropy_with_logits( labels=Y, logits=output_layer )) train_step = tf.compat.v1.train.AdamOptimizer(1e-4).minimize(cross_entropy)
عرّفنا حتى الآن الشبكة وبنيناها باستخدام المكتبة البرمجية TensorFlow، والخطوة التالية هي إرسال البيانات عبر المخطط البياني لتدريبها، ومن ثَمّ اختبارها للتحقق فيما إن كانت تعلمت شيئًا بالفعل أم لا.
5. التدريب والاختبار
تتضمن عملية التدريب تغذية المخطط البياني للشبكة بمجموعة بيانات التدريب، وتحسين نتيجة دالة الخسارة، إذ أن في كلّ مرةٍ تمر فيها الشبكة عبر مجموعةٍ إضافيةٍ من صور التدريب، فستُحدثُ الوسطاء لتقليل الخسارة، وذلك بهدف تحسين دقة التنبؤ للأرقامٍ؛ أما عملية الاختبار، فتتضمن تشغيل مجموعة بيانات الاختبار الخاصة بنا عبر المخطط البياني المدرّب، كما ستتتبع عدد الصور التي صح التنبؤ بها، حتى نحسب الدقة جيدًا.
قبل البدء في عملية التدريب، سوف نحدد دالة تقييم الدقة لكي نتمكن من طباعتها على مجموعاتٍ صغيرةٍ من البيانات أثناء التدريب. هذه البيانات المطبوعة ستسمح لنا بالتحقق من انخفاض الخسارة وزيادة الدقة، وذلك بدءًا من المرور الأول عبر المخطط البياني، وحتى المرور الأخير؛ كما ستسمح لنا بتتبّع ما إذا نفذنا عمليات مرور ٍكافيةً عبر المخطط البياني للوصول لنتيجةٍ مناسبةٍ ومثاليةٍ أم لا:
correct_pred = tf.equal(tf.argmax(output_layer, 1), tf.argmax(Y, 1)) accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
سنستخدم الدالة arg_max في المتغيّر right_pred للموازنة بين الصور التي صَحَ توقُّعها، وذلك بالنظر لقيمة التنبؤات output_layer والتصنيفات Y، وسنستخدم الدالة equal لإعادة هذه النتائج مثل قائمةٍ مؤلفةٍ من قيمٍ بوليانيةٍ. ويمكننا بعد ذلك تحويل هذه القائمة للنوع float، وذلك لحساب المتوسط للحصول على درجة الدقة الإجمالية.
الآن نحن جاهزون لتهيئة الجلسة لتشغيل المخطط البياني، إذ سنرسل للشبكة أمثلة التدريب الخاصة بنا، وبمجرد انتهاء التدريب، سنرسل أمثلة اختبارٍ جديدةٍ عبر المخطط البياني نفسه لتحديد دقة النموذج.
أضف هذه الشيفرة للملف الذي نعمل عليه:
init = tf.compat.v1.global_variables_initializer() sess = tf.compat.v1.Session() sess.run(init)
إن جوهر عملية التدريب في التعلم العميق هو تحسين ناتج دالة الخسارة. ونحن هنا سنهدف إلى تقليل الفرق بين التصنيفات المُتوقعة للصور والتصنيفات الحقيقية لها. وستتضمن هذه العملية أربع خطواتٍ تتكرر لعددٍ محددٍ من مرات المرور عبر المخطط البياني، وهي:
- دفع القيم إلى الأمام عبر الشبكة.
- حساب الخسارة.
- دفع القيم للخلف عبر الشبكة.
- تحديث الوسطاء.
ففي كلّ خطوة تدريب، سنعدِّل الوسطاء قليلًا في محاولةٍ لتقليل نتائج دالة الخسارة. وفي الخطوة التالية مع تَقدُّم عملية التعلّم، يجب أن نشاهد انخفاضًا في الخسارة، حيث سنوقِف التدريب في النهاية، وسنستخدم الشبكة مثل نموذجٍ لاختبار بياناتنا الجديدة.
سنضيف هذه الشيفرة البرمجية للملف الذي نعمل عليه:
# التدريب على دفعات صغيرة for i in range(n_iterations): startbatch = (i*batch_size) % len(x_train) endbatch = ((i+1)*batch_size) % len(x_train) batch_x = np.array(x_train[startbatch:endbatch]) batch_x = batch_x.reshape(batch_size, -1) batch_y = y_train[startbatch:endbatch].toarray() if batch_x.shape != (128, 784): continue sess.run(train_step, feed_dict={ X: batch_x, Y: (batch_y), keep_prob: dropout }) # طباعة الخسارة والدقة لكل دفعة صغيرة if i % 100 == 0: minibatch_loss, minibatch_accuracy = sess.run( [cross_entropy, accuracy], feed_dict={X: batch_x, Y: batch_y, keep_prob: 1.0} ) print( "Iteration", str(i), "\t| Loss =", str(minibatch_loss), "\t| Accuracy =", str(minibatch_accuracy) )
بعد 100 عملية مرورٍ لكلّ خطوة تدريبٍ والتي أرسلنا فيها مجموعةً صغيرةً من الصور عبر الشبكة، سنطبع نتائج دالة الخسارة والدقة لتلك الدفعة. وينبغي ألّا نتوقع هنا انخفاض معدل الخسارة وزيادة الدقة، لأن القيم لكل دفعةٍ صغيرةٍ. إذ أن النتائج ليست للنموذج بأكمله. فنحن نستخدم مجموعاتٍ صغيرةٍ من الصور بدلًا من إرسال كلّ صورةٍ بمفردها، وذلك لتسريع عملية التدريب والسماح للشبكة برؤية عددٍ من الأمثلة المختلفة قبل تحديث الوسطاء.
وبمجرد اكتمال التدريب، يمكننا تشغيل الجلسة على الصور المخصصة للاختبار. وهذه المرة سنستخدم القيمة 1.0 مثل مُعدلِ تَسرّب dropout للمتغيّر Keep_prob، وذلك للتأكد من أن جميع الوِحدات نشطةٌ في عملية الاختبار.
أضف هذه الشيفرة البرمجية للملف الذي نعمل عليه:
إعداد صور الاختبار كمتجهات أحادية طول كل منها 28*28 # x_test = x_test.reshape(-1,784) test_accuracy = sess.run(accuracy, feed_dict={X: x_test, Y: y_test.toarray(), keep_prob: 1.0}) print("\nAccuracy on test set:", test_accuracy)
والآن سنشغّل برنامجنا، لنعرف مدى دقة شبكتنا العصبية في التعرف على الأرقام المكتوبة بخط اليد. وسنحفظ التغييرات في الملف main.py الذي نعمل عليه.
نَفِّذ الأمر التالي في الوِحدة الطرفية لتنفيذ الشيفرة البرمجية:
(tensorflow-demo) $ python main.py
سترى نتيجةً مشابهةً لما يلي، ويمكن أن تختلف قليلًا نتائج الخسارة والدقة الفردية:
Iteration 0 | Loss = 3.67079 | Accuracy = 0.140625 Iteration 100 | Loss = 0.492122 | Accuracy = 0.84375 Iteration 200 | Loss = 0.421595 | Accuracy = 0.882812 Iteration 300 | Loss = 0.307726 | Accuracy = 0.921875 Iteration 400 | Loss = 0.392948 | Accuracy = 0.882812 Iteration 500 | Loss = 0.371461 | Accuracy = 0.90625 Iteration 600 | Loss = 0.378425 | Accuracy = 0.882812 Iteration 700 | Loss = 0.338605 | Accuracy = 0.914062 Iteration 800 | Loss = 0.379697 | Accuracy = 0.875 Iteration 900 | Loss = 0.444303 | Accuracy = 0.90625 Accuracy on test set: 0.9206
ولمحاولة تحسين دقة نموذجنا، أو لمعرفة المزيد حول تأثير ضبط الوسطاء الفائقة hyperparameters، يمكننا تغييرها لاختبار تأثيرها المنعكس على معدّل التعلم وعتبة التسرب Dropout Threshold، وكذا حجم الدفعة من الصور في كمية الأمثلة وعدد مرات المرور عبر المخطط، كما يمكننا كذلك تغيير عدد الوِحدات في طبقاتنا المخفية وتغيير عدد الطبقات المخفية نفسها، وذلك لنرى كيف ستؤثر بنية الشبكة العصبية على النموذج سواءً بزيادة دقته أو بتخفيضها.
وللتأكد من أن الشبكة تتعرف جيدًا على الصور المكتوبة بخط اليد، فسنختبرها على صورةٍ خاصةٍ بنا، فإذا كنت تعمل على جهازك المحلي وترغب في استخدام صورٍ من جهازك، يمكنك استخدام أي محرر رسوماتٍ لإنشاء صورة بأبعاد 28x28 بكسل لأي رقمٍ تريده. مثلًا:
نزل الصورة وانقلها إلى مجلد المشروع (تأكد أنها باسم test_image.png أو غير اسمها في الشيفرة) ثم أضف في نهاية الملف main.py هذا السطر البرمجي التالي لتحميل صورة الاختبار للرقم المكتوب بخط اليد:
img = np.array(Image.open("test_image.png").convert('L')).ravel()
إن الدالة open من مكتبة الصور Image تحمّل صورة الاختبار مثل مصفوفةٍ رباعية الأبعاد 4D، حيث تحتوي على قنوات الألوان الثلاث الرئيسية RGB بالإضافة إلى الشفافية، ولكن هذا ليس نفس التمثيل الذي استخدمناه سابقًا عند القراءة من مجموعة البيانات باستخدام المكتبة البرمجية TensorFlow، لذلك سنحتاج للقيام ببعض المهام الإضافية ليتناسب تنسيق هذه الصور مع التنسيق الذي سبق واعتمدناه في الخوارزمية.
سنستخدم الدالة convert مع الوسيط L لتقليل تمثيل 4D RGBA إلى قناة لونٍ رماديةٍ واحدةٍ، وسنُخزنها على هيئة مصفوفة numpy. وسنستدعي ravel لتسوية المصفوفة.
الآن بعد أن صححّنا بنية معلومات الصورة، يمكننا تشغيل الجلسة بنفس الطريقة السابقة، ولكن هذه المرة سنُرسل صورةً واحدةً فقط للاختبار. وسنضيف الشيفرة التالية للملف لاختبار الصورة وطباعة التصنيف الناتج، هكذا:
prediction = sess.run(tf.argmax(output_layer, 1), feed_dict={X: [img]}) print ("Prediction for test image:", np.squeeze(prediction))
وتُستدعى الدالة np.squeeze على المتغير prediction ليُعِيد عددًا صحيحًا وفريدًا إلى المصفوفة. وسيتضح من الناتج أن الشبكة العصبية قد تعرفت على الصورة كرقم 4، هكذا:
Prediction for test image: 4
يمكنك الآن تجربة عملية اختبار الشبكة باستخدام صورٍ أكثر تعقيدًا مثل الأرقام المتشابهة مع الأرقام الأخرى، أو أرقامٍ مكتوبةٍ بخطٍ سيئٍ أو حتى خاطئةٍ، وذلك لمعرفة وقياس مدى نجاحها.
الخلاصة
في هذا المقال، نجحنا في تدريب شبكةٍ عصبيةٍ لتصنيف مجموعة بياناتٍ MNIST بدقةٍ تصل إلى 92٪، واختبارها على صورةٍ خاصةٍ بنا، مع العلم بأنه قد تحققت نسبة أعلى في الأبحاث العلمية الحديثة وكانت حوالي 99٪ لنفس الفكرة، وذلك باستخدام بُنىً مختلفةً لشبكةٍ عصبيةٍ ذات تعقيدٍ أكبر، بحيث تتضمن طبقات تلافيفية. وتستخدم تلك الشبكات بِنيةً ثنائية الأبعاد للصورة لتمثيل المحتويات تمثيلًا أفضل من تمثيل نموذجنا السابق، إذ أن نموذجنا يُسوّي كلّ البكسلات في متجهٍ واحدٍ مكوّنٍ من 784 وِحدة. ويمكنك قراءة المزيد على الموقع الرسمي للمكتبة TensorFlow، والاطلاع على الأوراق البحثية التي تُفصِّل أدق النتائج على موقع MNIST.
والآن بعد أن تعرفنا على كيفية بناء شبكةٍ عصبيةٍ وتدريبها، يمكنك تجربة هذا التطبيق واستخدامه على بياناتك الخاصة، أو اختبارها على مجموعات بياناتٍ شائعةٍ مختلفةٍ عن تلك التي استخدمناها مثل: مجموعة البيانات من غوغل أو مجموعة البيانات من CIFAR-10، وذلك للتعرف على صورٍ أكثر عموميةٍ وشموليةٍ.
ترجمة -وبتصرف- للفصل How To Build a Neural Network to Recognize Handwritten Digits with TensorFlow من كتاب Python Machine Learning Projects لكاتبته Ellie Birbeck
يُمكن تنزيل الكود كاملًا من Recognize-Handwritten-Numbers-MNIST-master.
اقرأ أيضًا
- إعداد شبكة عصبية صنعية وتدريبها للتعرف على الوجوه
- النسخة الكاملة من كتاب مدخل إلى الذكاء الاصطناعي وتعلم الآلة
- النسخة العربية الكاملة من كتاب البرمجة بلغة بايثون


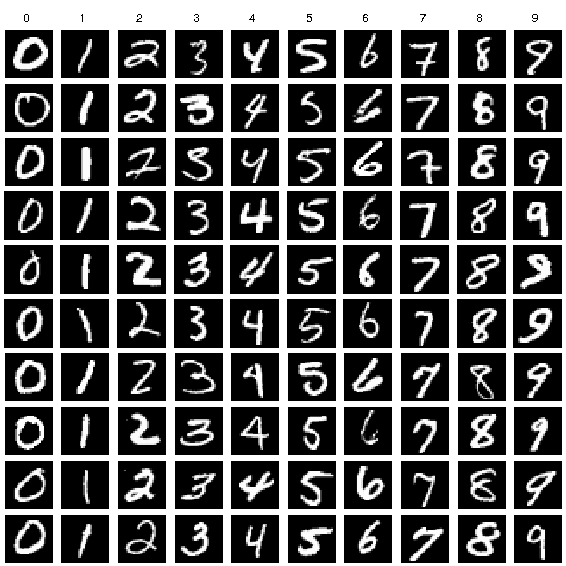












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.