تُعدّ مسألة تصنيف العملاء أي تجزئتهم إلى مجموعات متشابهة في سلوكها (عمليات الشراء والتسوق) من المسائل الهامة في عالم التسويق وذلك بهدف إعداد حملات تسويقية مختلفة مناسبة لكل مجموعة من المجموعات المُستهدفة.
سنعرض في هذه المقالة استخدام خوارزميات العنقدة Clustering لاستكشاف مجموعات العملاء أو الزبائن المختلفة، ويُمكن تنزيل بيانات التدريب والشيفرة البرمجية من الملف المضغوط (والذي تجده أيضًا بنهاية المقال)، لتتمكن من فهم المحتوى أكثر.
نستخدم في هذه المقالة التعليمية مجموعة بيانات حول 200 زبون تتألف من عمودين:
- الدخل السنوي للزبون بآلاف الدولارات Annual Income.
- تقييم الزبون Spending Score وهو رقم يتراوح بين 1 و 100 ويعكس مدى ولاء الزبون للمتجر والمبالغ التي أنفقها في الشراء منه (100 يعني الزبون الأكثر انفاقًا).
يُمكن تنزيل هذه البيانات المتاحة على موقع Kaggle أو من الرابط هنا.
ما هي العنقدة Clustering
العنقدة هي عملية تجزئة (تقسيم) مجموعة من البيانات إلى عناقيد clusters (مجموعات) وبحيث تكون العناصر الموجودة في عنقود واحد متشابهة فيما بينها وأقل تشابهًا مع عناصر العناقيد الأخرى.
تندرج خوارزميات العنقدة ضمن خوارزميات التعلم الآلي المدعوة "ليست تحت الإشراف" unsupervised بمعنى أن البيانات المُقدّمة في البداية لا تحوي أي تسميات labels أو تصنيفات بشكل مُسبق. سنرى مثًلا أن مسألة تحديد عدد العناقيد هو مسألة مهمة يجب الاعتناء بها إذ لا نعرف مُسبقًا ما هو عدد العناقيد الأمثلي.
نعرض في هذه المقالة نوعين أساسيين من خوارزميات العنقدة:
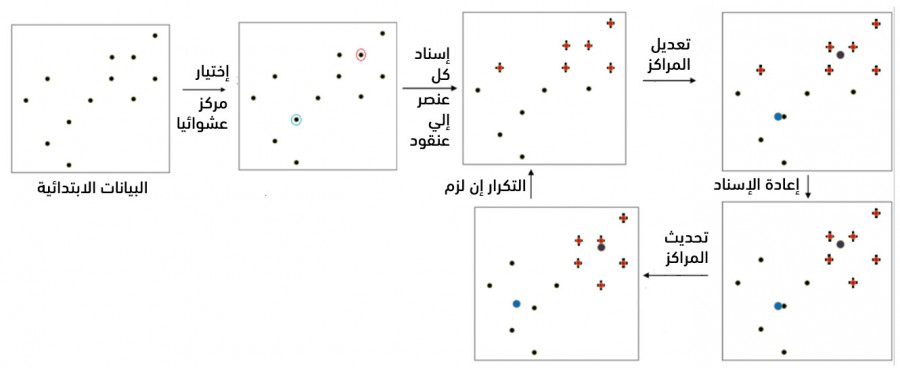
- خوارزميات التجزئة Partitioning: تبدأ هذه الخوارزميات بتجزئة عناصر البيانات إلى k عنقود (مختارة بشكل عشوائي) ومن ثم تُكرر تعديل هذه المجموعات وصولًا إلى حل جيد. من أشهر هذه الخوارزميات الخوارزمية المدعوة k-means (أي k وسطي).
- الخوارزميات التكتلية Agglomerative: تبني هذه الخوارزمية هرمية من العناقيد حيث تبدأ بوضع كل عنصر من عناصر البيانات في عنقود مستقل ثم تكرر دمج العناقيد المتشابهة وصولًا إلى عنقود واحد في نهاية المطاف.
الخوارزمية K-Means
تُعدّ الخوارزمية K-Means من أشهر وأبسط خوارزميات العنقدة بالتجزئة:
دخل الخوارزمية:
- عدد العناقيد المطلوب k
- بيانات التدريب وهي عبارة عن مجموعة من العناصر (أشعة رقمية): {x1, x2, . . . , xN} حيث xi هو شعاع من الأرقام.
خرج الخوارزمية:
- تُسندّ الخوارزمية كل عنصر من عناصر الدخل إلى أحد العناقيد (التي عددها k).
المعالجة:
- تختار الخوارزمية أولًا k شعاع من أشعة الدخل بشكل عشوائي كمراكز العناقيد.
- تُكرر الخوارزمية ما يلي وصولًا إلى التقارب:
- إسناد كل شعاع من أشعة الدخل إلى المركز الأقرب
- حساب المركز الجديد لكل عنقود
يعني التقارب عدم انتقال أي شعاع من عنقوده الحالي الموضوع فيه إلى عنقود آخر.
يُبين الشكل التالي المراحل الأساسية للخوارزمية:
لفهم مراحل الخوارزمية نعرض أولًا خطوات تنفيذها على المثال التعليمي التالي:
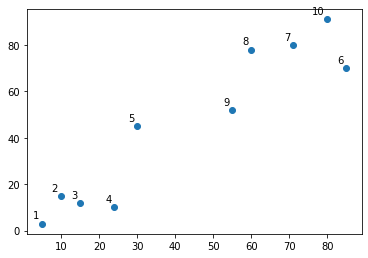
ليكن لدينا مجموعة العناصر العشرة التالية:
D = { (5,3), (10,15), (15,12), (24,10), (30,45), (85,70), (71,80), (60,78), (55,52), (80,91) }
وبفرض أننا نريد تقسيمها إلى عنقودين (k=2).
لنختار مثلًا العنصر الأول كمركز للعنقود الأول والعنصر الثاني مركزًا للعنقود الثاني أي:
c1(x) = 5, c1(y)=3 c2(x) = 10 , c2(y)=15
نحسب الآن بُعد (المسافة الإقليدية euclidean distance) كل عنصر من عناصر البيانات عن كل من المركزين ونُسند العنصر إلى المركز الأقرب. يكون لدينا:
| رقم | العنصر | المسافة الإقليدية عن المركز الأول | المسافة الإقليدية عن المركز الثاني | العنقود المُسند إليه |
|---|---|---|---|---|
| 1 | (5,3) | 0 | 13 | C1 |
| 2 | (10,15) | 13 | 0 | C2 |
| 3 | (15,12) | 13.45 | 5.83 | C2 |
| 4 | (24,10) | 20.24 | 14.86 | C2 |
| 5 | (30,45) | 48.87 | 36 | C2 |
| 6 | (85,70) | 104.35 | 93 | C2 |
| 7 | (71,80) | 101.41 | 89 | C2 |
| 8 | (60,78) | 93 | 80 | C2 |
| 9 | (55,52) | 70 | 58 | C2 |
| 10 | (80,91) | 115.52 | 103.32 | C2 |
نحسب الآن مركزي العنقودين فنحصل على:
c1(x) = 5, c1(y)=3 c2(x) = (10 + 15 + 24 + 30 + 85 + 71 + 60 + 55 + 80) / 9 = 47.77 c2(y) = (15 + 12 + 10 + 45 + 70 + 80 + 78 + 52 + 91) / 9 = 50.33
نُعيد العملية لنحصل على:
| رقم | العنصر | المسافة الإقليدية عن المركز الأول | المسافة الإقليدية عن المركز الثاني | العنقود المُسند إليه |
|---|---|---|---|---|
| 1 | (5,3) | 0 | 63.79 | C1 |
| 2 | (10,15) | 13 | 51.71 | C1 |
| 3 | (15,12) | 13.45 | 50.42 | C1 |
| 4 | (24,10) | 20.24 | 46.81 | C1 |
| 5 | (30,45) | 48.87 | 18.55 | C2 |
| 6 | (85,70) | 104.35 | 42.1 | C2 |
| 7 | (71,80) | 101.41 | 37.68 | C2 |
| 8 | (60,78) | 93 | 30.25 | C2 |
| 9 | (55,52) | 70 | 7.42 | C2 |
| 10 | (80,91) | 115.52 | 51.89 | C2 |
نحسب الآن مركزي العنقودين الجديدين فنحصل على:
c1(x) = (5, 10, 15, 24) / 4 = 13.5 c1(y) = (3, 15, 12, 10) / 4 = 10.0 c2(x) = (30 + 85 + 71 + 60 + 55 + 80) / 6 = 63.5 c2(y) = (45 + 70 + 80 + 78 + 52 +91) / 6 = 69.33
نُعيد العملية مرة أخرى لنحصل على:
| رقم | العنصر | المسافة الإقليدية عن المركز الأول | المسافة الإقليدية عن المركز الثاني | العنقود المُسند إليه |
|---|---|---|---|---|
| 1 | (5,3) | 11.01 | 88.44 | C1 |
| 2 | (10,15) | 6.1 | 76.24 | C1 |
| 3 | (15,12) | 2.5 | 75.09 | C1 |
| 4 | (24,10) | 10.5 | 71.27 | C1 |
| 5 | (30,45) | 38.69 | 41.4 | C1 |
| 6 | (85,70) | 93.33 | 21.51 | C2 |
| 7 | (71,80) | 90.58 | 13.04 | C2 |
| 8 | (60,78) | 82.37 | 9.34 | C2 |
| 9 | (55,52) | 59.04 | 19.3 | C2 |
| 10 | (80,91) | 104.8 | 27.23 | C2 |
نحسب الآن مركزي العنقودين الجديدين فنحصل على:
c1(x) = (5, 10, 15, 24, 30) / 5 = 16.8 c1(y) = (3, 15, 12, 10, 45) / 5 = 17.0 c2(x) = (85 + 71 + 60 + 55 + 80) / 5 = 70.2 c2(y) = (70 + 80 + 78 + 52 + 91) / 5 = 74.2
نُعيد العملية فلا يتغير إسناد أي عنصر مما يعني التقارب وثبات المراكز والعناقيد clusters.
إعداد المشروع
يحتاج تنفذ شيفرات هذه المقالة بيئةً برمجيةً للغة بايثون الإصدار 3.8. ويجب أن تتضمن هذه البيئة البرمجية مدير الحِزم pip لتثبيت الحِزم، ومُنشئ البيئات الافتراضية venv لإنشاء بيئاتٍ افتراضيةٍ.
نستخدم محرر الشيفرات البرمجية Jupyter Notebooks، وهو مفيد جدًا لتجربة وتشغيل الأمثلة البرمجية بطريقةٍ تفاعليةٍ، حيث نستطيع من خلاله تشغيل كتلًا صغيرةً من الشيفرات البرمجية ورؤية النتائج بسرعة، مما يُسهّل علينا اختبار الشيفرات البرمجية وتصحيحها.
نحتاج أولًا لتثبيت بعض التبعيات، وذلك لإنشاء مساحة عملٍ للاحتفاظ بملفاتنا قبل أن نتمكن من تطوير برنامجنا. نُنشئ مجلدًا جديدًا خاصًا بمشروعنا وندخل إليه هكذا:
mkdir clustering
cd clustering
نُنفذّ الأمر التالي لإنشاء البيئة الافتراضية:
python -m venv clustering
ومن ثم الأمر التالي في Linux لتنشيط البيئة الافتراضية:
source clustering/bin/activate
أما في Windows، فيكون أمر التنشيط:
"clustering/Scripts/activate.bat"
نستخدم إصداراتٍ محددةٍ من المكتبات اللازمة، من خلال إنشاء ملف requirements.txt في مجلد المشروع، وسيُحدِّد هذا الملف المتطلبات والإصدارات التي سنحتاج إليها.
نفتح الملف requirements.txt في محرر النصوص، ونُضيف الأسطر التالية، وذلك لتحديد المكتبات التي نريدها وإصداراتها:
jupyter==1.0.0 numpy==1.21.5 scikit-learn==1.0.1 scipy==1.7.3 pandas==1.3.5 matplotlib==3.5.1
نحفظ التغييرات التي طرأت على الملف ونخرج من محرر النصوص، ثم نُثَبت هذه المكتبات بالأمر التالي:
(clustering) $ pip install -r requirements.txt
بعد تثبيتنا لهذه التبعيات، نُصبح جاهزين لبدء العمل على مشروعنا.
كتابة شيفرة تطبيق العنقدة للعملاء
نُشغّل محرر الشيفرات البرمجية Jupyter Notebook بمجرد اكتمال عملية التثبيت. هكذا:
(clustering) $ jupyter notebook
ثم نُنشئ ملفًا جديدًا في داخل المحرر ونُسمّه باسم clust مثلًا.
تنفيذ المثال التعليمي
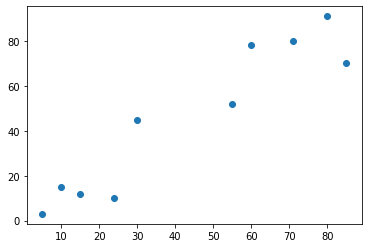
نبدأ أولًا بإنشاء بيانات المثال التعليمي السابق ورسمها باستخدام المكتبة matplotlib:
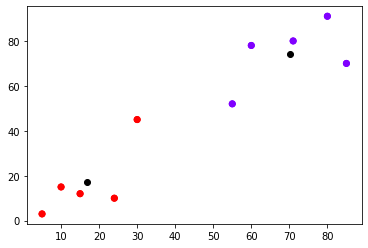
# المكتبة الرقمية import numpy as np # مكتبة الرسم import matplotlib.pyplot as plt # إنشاء البيانات X = np.array([[5,3], [10,15], [15,12], [24,10], [30,45], [85,70], [71,80], [60,78], [55,52], [80,91],]) # الرسم plt.scatter(X[:,0],X[:,1]) plt.show()
مما يُظهر:
تُبين الشيفرة التالية استخدام الصف KMeans من مكتبة العنقدة sklearn.cluster. نُنشئ أولًا غرض (نموذج model) من هذا الصف مع تحديد عدد العناقيد المطلوبة. تُنفذّ الطريقة fit خوارزمية KMeans على بيانات التدريب لإيجاد العناقيد المطلوبة. تُرقّم الخوارزمية العناقيد بدءًا من الصفر (تسميات labels). يُمكن طبعًا طباعة مراكز العناقيد.
# KMeans from sklearn.cluster import KMeans # إنشاء غرض من الصف # تحديد عدد العناقيد المطلوب kmeans = KMeans(n_clusters=2) # الملائمة مع البيانات kmeans.fit(X) # طباعة المراكز print(kmeans.cluster_centers_) # طباعة تسميات العناقيد print(kmeans.labels_)
يكون الخرج:
[[70.2 74.2] [16.8 17. ]] [1 1 1 1 1 0 0 0 0 0]
يُمكن الآن استخدام النموذج المُتعلم السابق للتنبؤ بعنقود أي مثال جديد وذلك باستخدام الطريقة predict كما تُبين الشيفرة التالية:
# التنبؤ print(kmeans.predict([[10,10]]))
حيث يكون الخرج مثلًا:
[1]
يُمكن أيضًا رسم نقاط التدريب مع مراكزها بلون مميز كما تُبين الشيفرة التالية:
# الرسم مع المراكز plt.scatter(X[:,0],X[:,1], c=kmeans.labels_, cmap='rainbow') plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, cmap='rainbow') plt.scatter(kmeans.cluster_centers_[:,0] ,kmeans.cluster_centers_[:,1], color='black')
يكون الخرج:
ننتقل الآن لمعالجة مسألتنا الأساسية وهي عنقدة الزبائن. تعرض الشيفرة التالية تحميل البيانات من الملف shopping-data.csv ووضعها في إطار بيانات من المكتبة pandas.
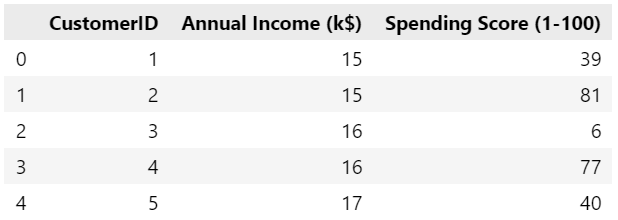
# مكتبة إطار البيانات import pandas as pd # تحميل البيانات customer_data = pd.read_csv('shopping-data.csv') # إظهار ترويسة البيانات customer_data.head()
تظهر أوائل البيانات:
نحذف في الشيفرة التالية رقم الزبون من إطار البيانات كي لا يدخل في عملية حساب العناقيد. ثم نُنشئ نموذجًا متعلمًا من الصف KMeans مع عدد العناقيد مساويًا لخمسه (نعرض لاحقًا كيفية تحديدنا لهذا الرقم):
# حذف رقم الزبون data = customer_data.iloc[:, 1:3].values # إنشاء النموذج المتعلم kmeans = KMeans(n_clusters=5) # الملائمة مع البيانات kmeans.fit(data) # طباعة المراكز print(kmeans.cluster_centers_) # طباعة التسميات print(kmeans.labels_)
يكون الإظهار:
[[88.2 17.11428571] [55.2962963 49.51851852] [25.72727273 79.36363636] [86.53846154 82.12820513] [26.30434783 20.91304348]] [4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 2 4 1 4 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 0 3 1 3 0 3 0 3 1 3 0 3 0 3 0 3 0 3 1 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3 0 3]
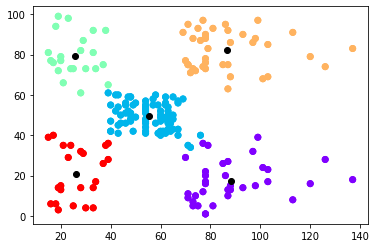
يُمكن الآن أن نرسم النقاط مع المراكز باستخدام الشيفرة التالية:
# الرسم plt.scatter(data[:,0],data[:,1], c=kmeans.labels_, cmap='rainbow') plt.scatter(data[:,0], data[:,1], c=kmeans.labels_, cmap='rainbow') plt.scatter(kmeans.cluster_centers_[:,0] ,kmeans.cluster_centers_[:,1], color='black') plt.show()
مما يُعطي:
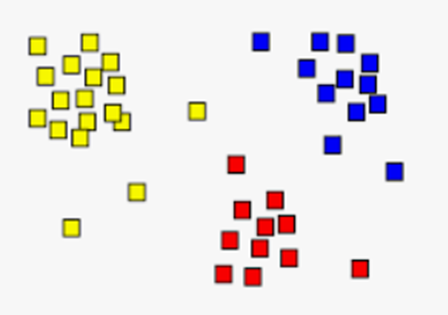
تفسير نتائج العنقدة تقييمها
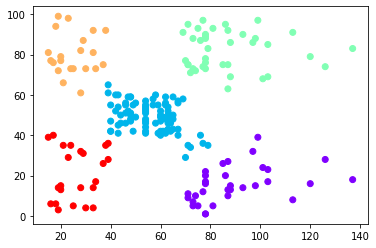
يُمكن لنا بمعاينة الشكل السابق استنتاج ما يلي (وهو الهدف الأساسي من عملية العنقدة):
- الزبائن في أعلى اليمين (نقاط البيانات الصفراء) هم الزبائن ذوو الرواتب المرتفعة والإنفاق المرتفع. هؤلاء هم الزبائن الواجب استهدافهم دومًا والمحافظة عليهم.
- الزبائن في أعلى اليسار (نقاط البيانات الخضراء) هم الزبائن ذوو الرواتب المنخفضة والإنفاق المرتفع. هؤلاء هم الزبائن الواجب العناية بهم واستهدافهم بحملات التخفيضات مثلًا.
- الزبائن في أسفل اليمين (نقاط البيانات البنفسجية) هم الزبائن ذوو الرواتب المرتفعة والإنفاق المنخفض. هؤلاء هم الزبائن الواجب جذبهم بالطرق التسويقية ما أمكن ذلك.
- الزبائن في أسفل اليسار (نقاط البيانات الحمراء) هم الزبائن ذوو الرواتب المنخفضة والإنفاق المنخفض. لا داع لإضاعة الكثير من الوقت والجهد معهم.
- الزبائن في الوسط (نقاط البيانات الزرقاء) هم الزبائن أصحاب الدخل المتوسط والإنفاق المتوسط. يُمكن استهدافهم أيضًا لاسيما أن عددهم كبيرًا كما يُبين الشكل السابق.
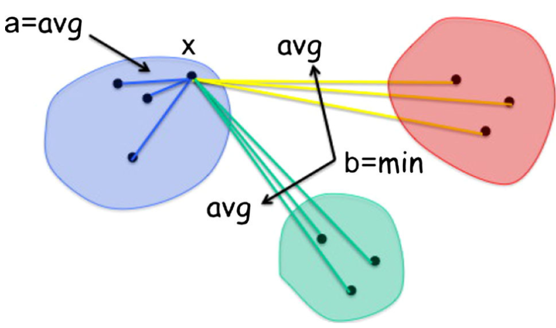
يُمكن تقييم نتائج العنقدة باستخدام المعامل المدعو Silhouette Coefficient، ويُحسب هذا المعامل من أجل عنصر بيانات x كما يلي:
حيث:
- a هي وسطي المسافات بين x وبين العناصر الموجودة في نفس العنقود الموجود فيه العنصر x.
- b هي وسطي المسافات بين x وبين العناصر الموجودة في العناقيد القريبة من عنقود x.
كما يُبين الشكل التالي:
يُمكن ملاحظة ما يلي حول هذا المعامل:
- أفضل قيمة له هي 1 وأسوأ قيمة له هي -1.
- تُشير القيمة 0 إلى وجد تراكب overlapping في العناقيد.
- تدل القيمة السالبة على وجود العنصر x في عنقود خاطئ إذ يوجد عنقود آخر أقرب إلى x.
يكون المعامل silhouette_score لمجموعة من البيانات وسطي قيمة المعامل لكل منها أي:
يُمكن تضمين حساب هذا المعامل من sklearn.metrics كما تُبين الشيفرة التالية:
from sklearn.metrics import silhouette_score cluster_labels = kmeans.fit_predict(data) # حساب المعامل silhouette_avg = silhouette_score(data, cluster_labels) print(silhouette_avg)
يكون لطريقة حساب المعامل silhouette_score معاملي دخل الأول هو البيانات والثاني هو تسميات العناقيد الناتجة عن استدعاء الطريقة fit_predict أولًا.
يكون الناتج في مثالنا:
0.553931997444648
إيجاد عدد العناقيد الأمثلي
يُمكن استخدام المعامل Silhouette Coefficient لإيجاد عدد العناقيد الأمثلي المناسب لبيانات التدريب وذلك بحساب المعامل مع قيم مختلفة لعدد العناقيد ومن ثم اختيار العدد الذي يُعطي قيمة أعظمية للمعامل كما تُبين الشيفرة التالية:
# مجموعة القيم الممكنة range_n_clusters = [2, 3, 4, 5, 6, 7] for n_clusters in range_n_clusters: clusterer = KMeans(n_clusters=n_clusters) cluster_labels = clusterer.fit_predict(data) # حساب المعامل silhouette_avg = silhouette_score(data, cluster_labels) print( "For n =", n_clusters, "silhouette_score is :", silhouette_avg, )
مما يُظهر المعامل من أجل كل قيمة محتملة لعدد العناقيد:
For n = 2 silhouette_score is : 0.2968969162503008 For n = 3 silhouette_score is : 0.46761358158775435 For n = 4 silhouette_score is : 0.4931963109249047 For n = 5 silhouette_score is : 0.553931997444648 For n = 6 silhouette_score is : 0.5376203956398481 For n = 7 silhouette_score is : 0.5270287298101395
وبالتالي نلاحظ أن القيمة الأمثلية هي خمسة عناقيد.
الخوارزميات التكتلية
تمتاز الخوارزميات التكتلية بأنها توفر طريقة معاينة بسيطة لإيجاد عدد العناقيد الأمثلي عن طريق رسم شجرة دمج العناقيد مع بعضها البعض dendrogram:
دخل الخوارزمية:
- بيانات التدريب وهي عبارة عن مجموعة من الأشعة الرقمية: {x1, x2, . . . , xN} حيث xi هو شعاع من الأرقام.
خرج الخوارزمية:
- شجرة دمج العناقيد مع بعضها البعض dendrogram.
المعالجة:
- تبدأ الخوارزمية بوضع كل عنصر من عناصر البيانات في عنقود.
- تُكرر الخوارزمية ما يلي وصولًا إلى عنقود وحيد:
- دمج أقرب عنقودين مع بعضهما البعض
توجد عدة طرق لإيجاد أقرب عنقودين، من أبسطها الطريقة المسماة بالربط البسيط Single Linkage والتي تحسب المسافة بين عنقودين كما يلي: المسافة بين عنقودين هي أصغر مسافة بين عنصرين من هذين العنقودين.
نستخدم فيما يلي الخوارزمية التكتلية مع البيانات التعليمية ومن ثم مع بيانات الزبائن.
تعرض الشيفرة التالية طريقة بسيطة لتسمية نقاط البيانات التعليمية (العشرة) لتسهيل عملية المشاهدة والمتابعة:
# التسميات : 2,1, ..., 10 labels = range(1, 11) plt.subplots_adjust(bottom=0.1) plt.scatter(X[:,0],X[:,1]) # تسمية النقاط for label, x, y in zip(labels, X[:, 0], X[:, 1]): plt.annotate( label, xy=(x, y), xytext=(-3, 3), textcoords='offset points', ha='right', va='bottom') plt.show()
يكون الخرج:
نبدأ أولًا بالشيفرة اللازمة لرسم شجرة الدمج dendrogram من أجل إيجاد عدد العناقيد الأمثل:
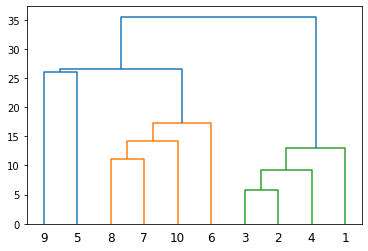
# المكتبات اللازمة from scipy.cluster.hierarchy import dendrogram, linkage # اختيار الربط البسيط linked = linkage(X, 'single') # التسميات: 2,1, .. ,10 labelList = range(1, 11) # dendrogram dendrogram(linked, orientation='top', labels=labelList, distance_sort='descending', show_leaf_counts=True) plt.show()
نُعاين شجرة الدمج الناتجة والتي تُبين أن عدد العناقيد المُمكن هو عنقودين:
نستدعي الآن الدالة AgglomerativeClustering مع طلب عدد العناقيد مساويًا إلى 2:
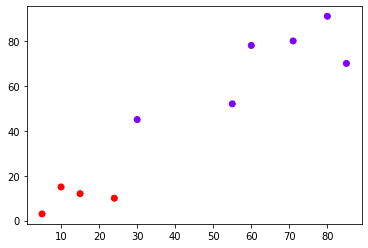
from sklearn.cluster import AgglomerativeClustering # العنقدة التكتلية cluster = AgglomerativeClustering(n_clusters=2) # الملائمة مع البيانات cluster.fit_predict(X)
والتي تُظهر تسميات عنقود كل عنصر:
array([1, 1, 1, 1, 0, 0, 0, 0, 0, 0], dtype=int64)
يُمكن أيضًا رسم العناقيد:
# الرسم plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow') plt.show()
يكون الإظهار:
ننتقل الآن إلى مسألة الزبائن باستخدام شيفرة مماثلة:
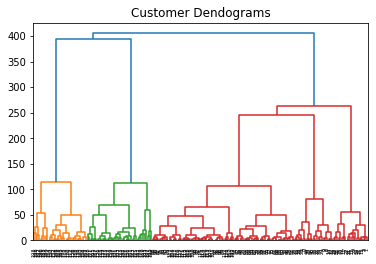
# نوع الربط linked = linkage(data, 'ward') # dendrogram dendrogram(linked, orientation='top', distance_sort='descending', show_leaf_counts=True) # الرسم plt.title("Customer Dendograms") plt.show()
يُمكن معاينة شجرة الدمج الناتجة:
والتي تُبين أن عدد العناقيد المناسب هو 5.
نستدعي الدالة AgglomerativeClustering في الشيفرة التالية:
cluster = AgglomerativeClustering(n_clusters=5, affinity='euclidean', linkage='ward') cluster.fit_predict(data) # الرسم plt.scatter(data[:,0], data[:,1], c=cluster.labels_, cmap='rainbow') plt.show()
ويكون الخرج:
وهو، بالطبع، يُشابه ما حصلنا عليه سابقًا مع الخوارزمية KMeans.
الخلاصة
عرضنا في هذه المقالة خطوات بناء نموذج تعلّم لعنقدة مجموعة من البيانات مع آليات اختيار عدد العناقيد المناسب للمسألة.
يُمكن تجربة المثال كاملًا من موقع Google Colab من الرابط، ولا تنس الاطلاع على ملف بيانات التدريب والشيفرة البرمجية.


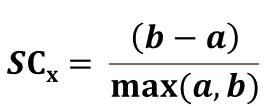
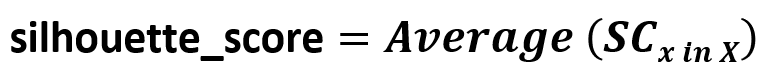












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.