سنناقش في هذا المقال كائنات الرسوميات الحاسوبية التي هي الأشعة والنقاط وكيفية تمثيلها في الحاسوب بوصفها مصفوفات عمودية، فالمصفوفة العمودية
column matrix هي كائن رياضي له العديد من الاستخدامات إلى جانب استخدامه في الرسوميات الحاسوبية، ولكن سنتعرف في هذا المقال على كيفية استخدامها في الرسوميات الحاسوبية فقط.
سنتعرّف في هذا المقال على المواضيع التالية:
- نمذجة وعرض الرسوميات الحاسوبية.
- النقاط والأشعة الهندسية.
- المصفوفات العمودية والسطرية.
- حساب الإزاحات.
- مساواة المصفوفات العمودية.
- أسماء المصفوفات العمودية وعناصرها.
- تمثيل النقاط باستخدام المصفوفات العمودية.
تُعَد النقاط والأشعة الهندسية ضروريةً في الرسوميات الحاسوبية، ويجب تمثيلها بطريقة تسهّل التعامل معها، لذا تُعَد المصفوفة العمودية الخيار المعتاد لذلك.
تستخدم بعض كتب الرسوميات مصطلح الشعاع العمودي Column Vector للتعبير عن الكائن الذي نسميه في مقالنا بالمصفوفة العمودية، إذ يُعَد ذلك مجرد اختلافٍ في المصطلحات ولا يؤثر على المفاهيم أو الصيغ التي سنوضّحها لاحقًا، ولكن المشكلة الأسوأ هي أن بعض الكتب تستخدم المصفوفات السطرية Row Matrices، فالمصفوفات العمودية والمصفوفات السطرية متكافئة، ولكن المعادلات المكتوبة باستخدام المصفوفات السطرية ليست هي نفسها المكتوبة باستخدام المصفوفات العمودية. يمكننا ضبط هذه الاختلافات، ولكنها مزعجة قليلًا.
مثال مشهد السائح الافتراضي
ما هما نوعا الكائنات الهندسية التي يمكن تمثيلها باستخدام المصفوفات العمودية؟ هما النقاط والأشعة.
تتكون الرسوميات الحاسوبية من نشاطين: أولهما إنشاء عالم خيالي ثلاثي الأبعاد في الحاسوب، وثانيهما إنتاج صور ثنائية الأبعاد لذلك العالم من نقاط نظر مختلفة. يشبه برنامج الرسوميات السائحَ الذي يتجول في معالم طبيعية رائعة ويلتقط الصور بالكاميرا، ويُجهَّز السائح الافتراضي بكاميرا سينمائية مع الرسوم المتحركة الحاسوبية.
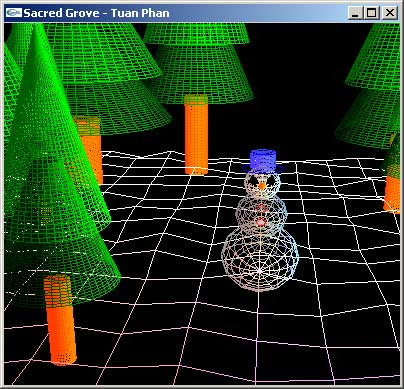
يتكون المشهد الخيالي من كائنات في فضاء ثلاثي الأبعاد، ويُحدَّد كل كائن باستخدام النقاط والخطوط التي تقع على سطحه مثل المشهد الشتوي السابق لصاحبه توان فان Tuan Phan. يتكون هذا النموذج من نقاط وقطع مستقيمة تربط بينها، وهناك حاجة إلى مزيدٍ من العمل لملء المنطقة بين القطع المستقيمة ولتطبيق الإضاءة للحصول على صورة واقعية.
صورة المشهد الكاملة
هل يمكن تمثيل الكرة باستخدام النقاط والخطوط؟ نعم، بالتأكيد. انظر إلى جسد رجل الثلج، إذ يبدو الشكل وكأنه كرة عند ملء المضلعات.
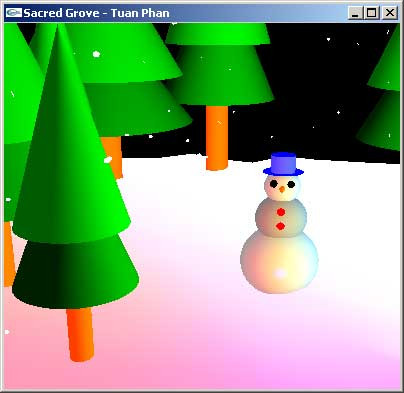
هذه هي الصورة الكاملة، مع ملء المضلعات وتطبيق الإضاءة وإلقاء قليلٍ من ندف الثلج.
يمكنك طلب نماذج من الكرات والأسطوانات والأقماع ووضعها في مشهدك في المكان الذي تريده باستخدام حزم الرسوميات الحاسوبية ثلاثية الأبعاد مثل OpenGL التي تملأ أيضًا المضلعات تلقائيًا وتطبّق نموذج الإضاءة لإنتاج تظليل واقعي.
مشهد افتراضي آخر
هل يمكن لسائحنا الافتراضي أن يتجول في مشهد الثلوج الافتراضي ويلتقط صورة مختلفة؟ نعم، يمكنه ذلك.
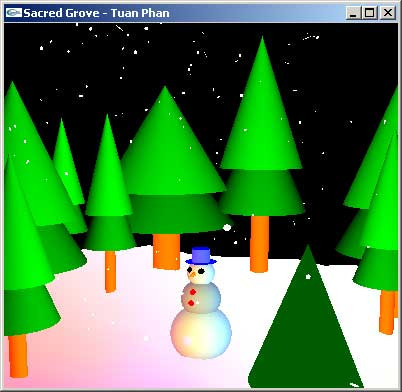
يضع نموذج المشهد الثلجي كائنات مختلفة في فضاء ثلاثي الأبعاد، وبالتالي يمكن لسائحنا الافتراضي أن يتجول على يمين رجل الثلج ويلتقط صورةً أخرى ثنائية الأبعاد باستخدام الكاميرا الافتراضية، إذ أُنتِجت الصورة السابقة باستخدام النموذج والإضاءة نفسها، ولكن مع وضعٍ مختلف للكاميرا.
الشعاع Vector
ما هي النقطة؟ وضحنا في المقال السابق مفهوم النقطة بأنها موقع في الفضاء، حيث تُعَد النقطة في الهندسة موقعًا في الفضاء فليس لها حجم وخاصيتها الوحيدة هي الموقع، بينما تكون النقطة عادةً في الرسوميات الحاسوبية هي رأس الشكل ثلاثي الأبعاد.
أما الشعاع الهندسي فله خاصيتان: الطول والاتجاه، ولكن ليس له موقع ثابت في الفضاء، فإذا كان له موقع ثابت، فسيكون قطعة مستقيمة. قد يكون الحديث عن شيء ليس له موقع أمرًا غريبًا، ولكنه يسهّل تطبيق الرسوميات الحاسوبية ثلاثية الأبعاد.
يسمى هذا المزيج من "المسافة والاتجاه" بالإزاحة Displacement أحيانًا، ويمكن تطبيق الإزاحة نفسها (أي إزاحة واحدة فقط) على كل نقطة من النقاط المختلفة. لنفترض أن لدينا المكعب التالي مثلًا، إذ يحتوي الوجه الأمامي على أربعة رؤوس (أربع نقاط). إذا تحركتَ من كل نقطة من هذه النقاط بمقدار المسافة والاتجاه نفسه، فستصل إلى النقاط الأربعة للوجه الخلفي. تمثل العبارة "المسافة والاتجاه نفسه" الشعاعَ الذي يظهر بوصفه خطًا مع رأس سهم، ويوضح الشكل التالي هذا الشعاع أربع مرات، مرة واحدة لكل نقطة من الوجه.
المصفوفة العمودية
لنفترض أنك قضيت عطلة الربيع على الشاطئ والشمس مشرقة، فهل يسطع ضوء الشمس في الاتجاه نفسه لكل الموجودين على الشاطئ؟ نعم، إذ يكون "الاتجاه نحو الشمس" نفسه لكل الموجودين على الشاطئ، وبالتالي فهو شعاع.
نهتم أحيانًا بالاتجاه فقط دون الاهتمام بالموقع أو بالطول كما في السؤال السابق، لذا نستخدم الشعاع لهذا الغرض، فطوله ليس مهمًا، لأننا نستخدم طولًا واحدًا في كثير من الأحيان. نهتم في أحيانٍ أخرى بكلٍ من الاتجاه والحجم، وعندها يُستخدَم كلٌّ من اتجاه وطول الشعاع.
يمكن تمثيل الشعاع بقائمةٍ من الأعداد تدعى المصفوفة العمودية، والتي هي قائمة مرتبة من الأعداد المكتوبة ضمن عمود. تستخدم بعض الكتب كلمة "شعاع" لتعبّر عن فكرة الشعاع وتمثيله بوصفه ترتيبًا لثلاثة أعداد، ولكن يمكن أن يكون ذلك مربكًا أحيانًا. إليك فيما يلي مثالًا لمصفوفة عمودية:
يسمى كل عددٍ في المصفوفة العمودية عنصرًا Element، وتكون هذه الأعداد حقيقية real، ويسمى عدد العناصر في الشعاع بالبُعد Dimension. المصفوفة السطرية Row Matrix هي قائمة مرتبة من الأعداد المكتوبة في صف واحد مثل المصفوفة السطرية:
(12.5, -9.34).
سنمثّل الأشعة دائمًا باستخدام مصفوفات عمودية بهدف التناسق، وتمثل بعض الكتب الأشعة باستخدام مصفوفات سطرية، إذ لا يحدث ذلك فرقًا جوهريًا، ولكنه يغيّر بعض الصيغ الرياضية قليلًا.
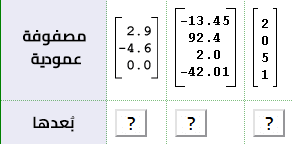
ما هو عدد العناصر الموجودة في كل مصفوفة عمودية؟
الجواب هو:
استخدام المتغيرات بوصفها عناصر مصفوفة
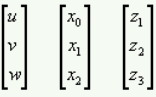
يمكن أن تكون عناصر المصفوفة العمودية متغيرات variables كما يلي:
يُعطَى العنصر الأول في المصفوفة العمودية أحيانًا الفهرس "0" أوالفهرس "1" أحيانًا.
العرض المناسب للمصفوفة العمودية
هل المصفوفة العمودية التالية:
هي المصفوفة العمودية التالية نفسها؟
لا يمكن ذلك، فالمصفوفة العمودية هي قائمة مرتبة من الأعداد، وهذا يعني أن كل موضع في المصفوفة العمودية يحتوي على عدد أو متغير معين.
يُعَد مظهر المصفوفات العمودية غريبًا في النصوص المطبوعة، لذا من الشائع كتابتها كما يلي:
(2.9, -4.6, 0.0) T
يرمز الحرف "T" إلى منقول المصفوفة Transpose الذي يعني تحويل الصفوف إلى أعمدة (سنوضح لاحقًا بالتفصيل معنى المنقول).
المساواة بين المصفوفات
هل المصفوفة (1.2, -3.9, 0.0) تساوي المصفوفة (1.2, -3.9, 0.0)T؟ لا، فالمصفوفة الأولى هي مصفوفة سطرية، والمصفوفة الثانية هي مصفوفة عمودية، أي مكتوبة ضمن صف، ولكن الحرف "T" يعني أنها مصفوفة عمودية، إذ تُعَد المصفوفات السطرية والمصفوفات العمودية أنواعًا مختلفة من الكائنات، ولا يمكن أن تكون متساوية.
ربما لم نميّز سابقًا بين المصفوفات السطرية والمصفوفات العمودية، ولم نوضِّح اختلاف الأشعة الهندسية عن المصفوفات العمودية المستخدمة لتمثيل هذه الأشعة، إذ يمكن أن تبدو هذه الاختلافات صعبة حاليًا، ولكن أبقِها حاضرةً في ذهنك لتجنب الالتباس مستقبلًا.
يمكن أن تكون المصفوفتان العموديتان متساويتين إذا كانت:
- كلتا المصفوفتين مصفوفةً عمودية.
- لكل منهما البعد (عدد العناصر) نفسه.
- العناصر المقابلة لبعضها البعض في المصفوفتين متساوية.
يمكن أن تكون المصفوفتان السطريتان متساويتين إذا كان:
- كلتا المصفوفتين مصفوفات سطرية.
- لكل منهما البعد (عدد العناصر) نفسه.
- العناصر المقابلة لبعضها البعض في المصفوفتين متساوية.
الفروق الدقيقة بين المصفوفات
هل المصفوفتان السطريتان (8.0, -1.63, 7.0, 0.0) و (8.0, -1.63, 7.0, 1.0) متساويتان؟ لا.
يمكن مقارنة المصفوفات من النوع نفسه فقط، إذ يمكنك المقارنة بين مصفوفتين عموديتين ثلاثيتي الأبعاد، أو مصفوفتين سطريتين رباعيتي الأبعاد مثلًا، فليس من المنطقي مقارنة مصفوفة سطرية ثلاثية الأبعاد مع مصفوفة عمودية ثلاثية الأبعاد.
( 6, 8, 12, -3 )T = ( 6, 8, 12, -3)T
( 6, 8, 12, -3 ) = ( 6, 8, 12, -3 )
( 6, 8, 12, -3 ) ≠ ( -2.3, 8, 12, -3 )
( 6, 8, 12, -3 )T ≠ ( 6, 8, 12, -3 )
( 6, 8, 12, -3 )T ≠ ( 6, 8, 12 )T
يمثل المحرف ≠ عدم المساواة (قد يكون من الصعب رؤيته باستخدام متصفح الويب). تكون القواعد أحيانًا مريحة وتؤدي إلى عدم الدقة في التمييز بين المصفوفات السطرية والمصفوفات العمودية، ولكن سيؤدي إبقاء التمييز بينها واضحًا إلى تجنب الارتباك مستقبلًا.
هل تُعَد المصفوفتان العموديتان (1.53, -0.03, 9.03, 0.0, +8.64)T و (1.53, -0.03, 9.03, 1.0, -8.64)T متساويتين؟ لا، ليستا متساويتين.
أسماء المصفوفات
من المفيد أن يكون للمصفوفات أسماء، إذ يُستخدَم عادةً حرف صغير بخط عريض لمصفوفة سطرية أو عمودية كما يلي:
a = ( 1.2, -3.6 )
x = ( x1, x2, x3, x4 )
r = ( r0, r1 )T
من المعتاد استخدام الأسماء من بداية أحرف الأبجدية الإنجليزية للمصفوفات العمودية التي تكون عناصرها معروفة مثل المصفوفة a السابقة، واستخدام الأسماء من نهاية أحرف الأبجدية الإنجليزية للمصفوفات العمودية التي تكون عناصرها متغيرات. تكون أسماء عناصر المصفوفة العمودية غالبًا مؤلفة من اسم المصفوفة العمودية الكاملة مع رمز سفلي مثل المصفوفة العمودية r وعناصرها r0 وr1.
من الصعب كتابة الأحرف ذات الخط العريض بالقلم الرصاص أو بالطباشير، لذا بدلًا من ذلك يُوضَع سهم أو شريط فوق اسم المصفوفة العمودية كما يلي:
_ -> x x
لنفترض أن لدينا ما يلي:
x = ( x1, x2 )
y = ( 3.2, -8.6 )
x = y
ما الذي يجب أن يكون صحيحًا بشأن x1 و x2؟
x1 = 3.2 و x2 = -8.6
تمثيل الأشعة باستخدام المصفوفات العمودية
تُستخدَم المصفوفات العمودية لتمثيل الأشعة وتُستخدَم لتمثيل النقاط أيضًا. يُستخدَم في الفضاء ثنائي الأبعاد نوع البيانات نفسه -وتكون مصفوفات عمودية ثنائية الأبعاد- لتمثيل نوعين مختلفين من الكائنات الهندسية هما النقاط والأشعة، ويُعَد ذلك أمرًا مربكًا، لذا سنصحح هذا الوضع لاحقًا.
يوضح الشكل السابق شعاع الإزاحة الذي يمثل الفرق بين نقطتين في المستوي x-y، إذ نستخدم حاليًا أمثلةً في فضاء ثنائي الأبعاد، وسيأتي الفضاء ثلاثي الأبعاد لاحقًا.
- النقطة A لها الإحداثيات: x=2 و y=1، ويمكن تمثيلها بمصفوفة عمودية: (2, 1)T.
- النقطة B لها الإحداثيات: x=7 و y=3، ويمكن تمثيلها بمصفوفة عمودية: (7, 3)T.
يمكن حساب الإزاحة من النقطة A إلى النقطة B في مسألتين منفصلتين هما:
- الإزاحة x هي الفرق بين قيم X أي: 7-2 = 5.
- الإزاحة y هي الفرق بين قيم Y أي: 3-1 = 2.
وشعاع الإزاحة المُعبَّر عنه بمصفوفة هو: (5, 2)T = d.
تُصوَّر أشعة الإزاحة على شكل سهم يربط بين نقطتين، إذ تكون النقطة A هي ذيل الشعاع، والنقطة B هي رأس الشعاع في الرسم البياني، ولكن تذكّر أن الأشعة ليس لها موضع، لذا يُعَد هذا الرسم مجرد مكان مناسب لرسمها، ولا يعبّر عن موضعها.
الإزاحة Displacement
تمثل المصفوفة العمودية d شعاع الإزاحة من النقطة A إلى النقطة B، فما هي المصفوفة العمودية التي تمثل الإزاحة من النقطة B إلى النقطة A؟
الإزاحة من النقطة B إلى النقطة A هي:
- الإزاحة x هي: 2-7 = -5
- الإزاحة y هي: 1-3 = -2
وبالتالي فإن المصفوفة العمودية التي تمثل الإزاحة هي: (-5, -2)T = e
يؤشر شعاع الإزاحة إلى الاتجاه المعاكس عند زيارة النقاط بالترتيب المعاكس، ويكون كل عنصر ناتجًا عن ضرب القيمة القديمة بالعدد -1 في المصفوفة العمودية.
تختلف الإزاحة من النقطة A إلى النقطة B عن الإزاحة من النقطة B إلى النقطة A، إذ يمكن التفكير في الإزاحة بوصفها "إرشادات حول كيفية المشي من نقطة إلى أخرى"؛ لذا إذا كنت واقفًا عند النقطة A وترغب في الوصول إلى النقطة B، فإن الإزاحة (5, 2)T تقول "امشِ 5 وحدات في الاتجاه الموجب X، ثم امشِ وحدتين في الاتجاه الموجب Y". تحتاج بالطبع إلى اتجاهات مختلفة للانتقال من النقطة B إلى النقطة A، حيث تقول الإزاحة (-5, -2)T "امشِ 5 وحدات في الاتجاه السالب X، ثم امشِ وحدتين في الاتجاه السالب Y"، مما يعيدك إلى النقطة A.
يمكن التعبير عن الإزاحة من نقطة البداية إلى نقطة النهاية كما يلي:
الإزاحة = (x نقطة النهاية - x نقطة البداية, y نقطة النهاية - y نقطة البداية)T
لنفترض أن النقطة C هي: x=4, y=2 وأن النقطة D هي: x=3, y= 5، فما هي المصفوفة العمودية التي تمثل الإزاحة من C إلى D؟
- X لنقطة النهاية - X لنقطة البداية = 3 - 4 = -1
- Y لنقطة النهاية - Y لنقطة البداية = 5 - 2 = 3
إذًا فالمصفوفة العمودية هي: (-1, 3)T
قراءة الإزاحات من الرسوم البيانية الورقية
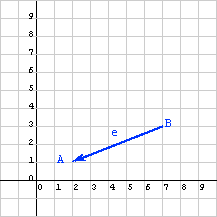
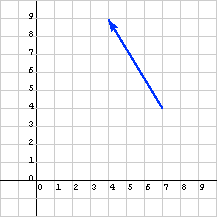
يوضح الرسم البياني التالي شعاعًا بين نقطتين، حيث يمكن قراءة عناصر الإزاحة بين النقطتين من الرسم البياني من خلال حساب عدد المربعات من ذيل الشعاع إلى رأسه: (-3, 5)T.
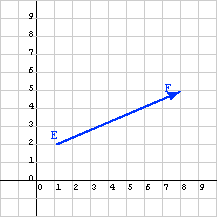
افعل الشيء ذاته الآن مع الرسم البياني التالي:
ما هي الإزاحة من النقطة E إلى النقطة F؟ الإزاحة هي: (7, 3)T
للتحقق من إجابتك، ابدأ من نقطة البداية واتبع التعليمات التالية: امشِ بمقدار 7 وحدات على محور X، ثم امشِ بمقدار 3 وحدات على محور Y. إذا كانت إجابتك صحيحة، فسينتهي بك الأمر عند نقطة النهاية.
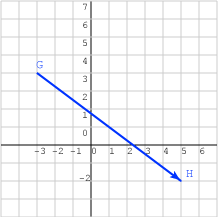
ليس للأشعة موقع محدد
ما هي الإزاحة من النقطة G: (-3, 4)T إلى النقطة H: (5, -2)T؟ يمكن الإجابة على هذا السؤال من خلال طرح قيم نقطة البداية G من القيم المقابلة لنقطة النهاية H ويعطي ذلك: (8, -6)T.
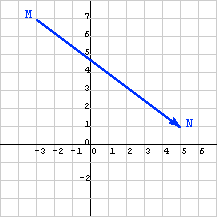
احسب الآن الإزاحة من النقطة M إلى النقطة N في الرسم البياني التالي من خلال طرح قيم نقطة البداية N من القيم المقابلة لنقطة النهاية M، ويعطي ذلك: (8, -6)T، وهي القيمة نفسها للرسم البياني السابق.
يُعَد شعاع الإزاحة هندسيًا من النقطة G إلى النقطة H هو شعاع الإزاحة نفسه من النقطة M إلى النقطة N، وتكون المصفوفتان العموديتان متساويتين باستخدام قاعدة مساواة المصفوفات العمودية. يُعَد ذلك منطقيًا، لأنك تقطع المسافة والاتجاه نفسه للمشي من النقطة M إلى النقطة N عند المشي من النقطة G إلى النقطة H، وبالتالي توضح هذه الرسوم البيانية الإزاحات مع الطول والاتجاه نفسه ولكن مع نقاط بداية مختلفة، فليس للأشعة موقعٌ محدد. من الشائع رسم الشعاع على شكل سهم في الرسوم البيانية، ذيله عند نقطة ورأسه عند نقطة أخرى، ولكن يمكن أن يمثل أيّ سهم له الطول والاتجاه نفسه هذا الشعاع.
طرح النقاط
هل تُعَدّ الإزاحة بين نقطتين فريدة؟ نعم، هذا صحيح.
يمكن كتابة صيغة حساب شعاع الإزاحة على النحو التالي، إذ تساوي الإزاحة من النقطة S (نقطة البداية) إلى النقطة F (نقطة النهاية) ما يلي:
F - S = ( Xf , Yf )T - ( Xs , Ys )T = ( Xf-Xs , Yf-Ys )T
تُستخدَم نقطتان في هذه العملية لإنتاج شعاع واحد، فمن الغريب أن ينتج عن طرح كائنين لهما النوع نفسه كائنٌ من نوع آخر، وهذا يقودنا إلى السؤال التالي: إذا طرحنا نقطةً ثلاثية الأبعاد من نقطة أخرى ثلاثية الأبعاد، فهل ستكون النتيجة شعاعًا؟ نعم، إذ تعمل هذه الطريقة في الفضاء ثلاثي الأبعاد وثنائي الأبعاد.
تدريب عملي لحساب الإزاحة
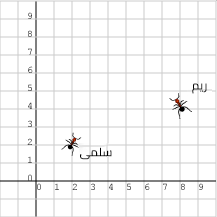
لنفترض أن النملة ريم ضاعت عند النقطة (8, 4)T، فأوجد الإزاحة التي ستوصِلها إلى صديقتها سلمى عند النقطة (2, 2)T، أو ما هي الإزاحة التي يجب أن تتحرك بها ريم للعثور على صديقتها سلمى؟
لنطرح النقاط (سلمى - ريم):
(2, 2)T - (8, 4)T = (-6, -2)T
ستحصل على الإجابة نفسها من خلال عدّ مربعات ورقة الرسم البياني.
استخدام الأعداد الحقيقية
قد نرغب في تجنب الأعداد السالبة وبالتالي سنحسب الإزاحة بصورة غير صحيحة، إذ يُعَد وجود إزاحات سالبة أمرًا طبيعيًا، فالجزء "السلبي" مطلوب لإظهار الاتجاه.
شيء آخر يجب أخذه في الحسبان وهو أن عناصر المصفوفة العمودية هي أعداد حقيقية، ولكن استخدمنا في الأمثلة أعدادًا صحيحة لتسهيل الأمور فقط، فلا يوجد أيّ خطأ في المصفوفة العمودية (-1.2304, 9.3382)T.
لنفترض أن لدينا النقطتان: النقطة B وهي: ( 4.75, 6.23 ) والنقطة A وهي: ( 1.25, 4.03 )، فما هي الإزاحة من النقطة A إلى النقطة B؟
الإزاحة من النقطة A إلى النقطة B هي:
( 4.75, 6.23 ) - ( 1.25, 4.03 ) = ( 3.50, 2.20 )T
وصلنا إلى نهاية هذا المقال، وسنناقش في المقال التالي العمليات على الأشعة والعمليات المكافئة باستخدام المصفوفات العمودية.
ترجمة -وبتصرُّف- للفصل Vectors, Points, and Column Matrices من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.




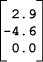

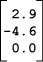














أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.