think stats دوال الكتلة الاحتمالية في بايثون

قبل البدء في ذكر تفاصيل المقال، تجدر الإشارة إلى أنه توجد الشيفرة الخاصة بهذا المقال في ملف probability.py في مستودع ThinkStats2 على GitHub.

دوال الكتلة الاحتمالية

تُعَد دالة الكتلة الاحتمالية probability mass function -أو PMF اختصارًا- طريقةً أخرى لتمثيل التوزيع، وهي دالة تحوّل القيمة إلى احتمالها.

الاحتمال هو تردد يُعبَّر عنه على أساس كسر من حجم العينة n، حيث نقسِّم التردد على n لتحويله إلى احتمال، وهذا ما يُسمى بالتوحيد normalization.

إذا كان لدينا مدرَّج تكراري Hist، فيمكننا إنشاء قاموس dictionary يربط كل قيمة باحتمالها، كما يلي:

n = hist.Total()
d = {}
for x, freq in hist.Items():
    d[x] = freq / n

أو يمكننا استخدام الصنف Pmf الموجود في thinkstats2.

يأخذ باني الصنف Pmf مثل Hist قائمةً أو pandas Series -أي سلسلة بانداز- أو قاموسًا dictionary، أو مدرَّجًا تكراريًا Hist، أو كائن Pmf آخر، وإليك مثالًا عن استخدام قائمة بسيطة:

>>> import thinkstats2
>>> pmf = thinkstats2.Pmf([1, 2, 2, 3, 5])
>>> pmf
Pmf({1: 0.2, 2: 0.4, 3: 0.2, 5: 0.2})

سنلاحظ هنا أنّ صنف Pmf موحّد بحيث يكون الاحتمال الكلي هو 1. يتشابه الكائنان Pmf وHist في الكثير من الأمور، إذ يرثان الكثير من التوابع صنف أب مشترك، حيث يؤدي التابعان Values وitems مثلًا العمل نفسه في كل من Hist وPmf، ويكمن الفرق الأكبر في أنّ Hist يحوّل القيم إلى عدّاد صحيح integer counters؛ أما Pmf فيحوِّل القيم إلى احتمال عشري floating-point probabilities. ويمكن استخدام Prob للبحث عن الاحتمال المرتبط بقيمة معينة كما يلي:

>>> pmf.Prob(2)
0.4

كما يمكننا في هذه الحالة استخدام عامِل القوس المربع [] للحصول على النتيجة نفسها كما يلي:

>>> pmf[2]
0.4

يمكن تعديل Pmf حالي بزيادة الاحتمال المرتبط بقيمة معينة كما يلي:

>>> pmf.Incr(2, 0.2)
>>> pmf.Prob(2)
0.6

أو ضرب الاحتمال بمعامل factor كما يلي:

>>> pmf.Mult(2, 0.5)
>>> pmf.Prob(2)
0.3

إذا عدَّلت Pmf ما، فقد تكون النتيجة غير موحَّدة، أي قد لا يكون مجموع الاحتمالات 1، ويمكننا هنا استدعاء دالة Total التي تُعيد مجموع الاحتمالات للتحقق من هذا:

>>> pmf.Total()
0.9

كما يمكننا استدعاء Normalize لإعادة التوحيد:

>>> pmf.Normalize()
>>> pmf.Total()
1.0

يوفّر كائن Pmf التابع Copy الذي يعمل على إنشاء وتعديل نسخة دون التأثير على النسخة الأصلية. وقد تبدو الصيغة المذكورة في هذه الفقرة غير متّسقة، إلا أنّ كل التسميات السابقة تجري وفق نظام معيَّن كما يلي:

يدلّ Pmf على الصنف class، ويدل pmf على نسخة instance من الصنف؛ أما PMF فهو مصطلح الدالة الكتلة الاحتمالية الرياضي.

رسم دوال الكتلة الاحتمالية

يوفِّر thinkplot طريقتَين لرسم دوال الكتلة الاحتمالية:

• يمكن استخدام thinkplot.Hist لرسم دالة الكتلة الاحتمالية على أساس رسم بياني شريطي، حيث يكون الرسم البياني الشريطي مفيدًا جدًا إذا كان عدد القيم في Pmf صغيرًا.
• يمكن استخدام thinkplot.Pmf لرسم دالة الكتلة الاحتمالية على أساس دالة خطوة step function، كما يُعدّ هذا الخيار مفيدًا جدًا في حال وجود عدد كبير من القيم وفي حال كانت دالة الكتلة الاحتمالية منتظمة، في حين تعمل هذه الدالة مع كائنات Hist أيضًا.

يزودنا pyplot أيضًا بدالة تُدعى hist؛ حيث تأخذ متسلسلةً من القيم ثم تحسب المدرَّج التكراري وترسمه، كما لا نستخدِم pyplot.hist عادةً لأننا نستخدِم كائنات Hist.

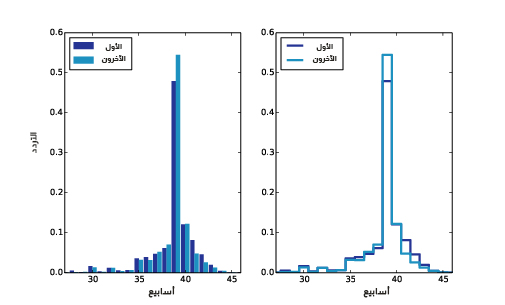
يُظهِر الشكل السابق دالة الكتلة الاحتمالية لمدة الحمل بالأطفال الأوائل وبقية الأطفال، وذلك باستخدام الرسم البياني الشريطي الموجود على يسار الشكل ودالة الخطوة الموجودة على يمين الشكل.

يمكننا موازنة التوزيعين من دون أن يضللنا الفرق في حجم العيّنة بين التوزيعين، وذلك برسم دالة الكتلة الاحتمالية PMF بدلًا من رسم المدرَّج التكراري histogram.

بناءً على هذا الشكل يكون احتمال ولادة الطفل الأول في الوقت المحدد -أي في الأسبوع التاسع والثلاثين 39- أقل من البقية، ومن المحتمل أكثر أن يتأخر في الولادة أي حتى الأسبوع 41 والأسبوع 42.

تكون الشيفرة التي تولِّد الشكل السابق كما يلي:

    thinkplot.PrePlot(2, cols=2)
    thinkplot.Hist(first_pmf, align='right', width=width)
    thinkplot.Hist(other_pmf, align='left', width=width)
    thinkplot.Config(xlabel='weeks',
                     ylabel='probability',
                     axis=[27, 46, 0, 0.6])

    thinkplot.PrePlot(2)
    thinkplot.SubPlot(2)
    thinkplot.Pmfs([first_pmf, other_pmf])
    thinkplot.Show(xlabel='weeks',
                   axis=[27, 46, 0, 0.6])

تأخذ PrePlot معاملَين اختياريّين هما rows وcols لتصنع شبكةً من الأشكال، وفي حالتنا هذه سيتوضَّع شكلان في سطر واحد، حيث يُظهر الشكل الأول الموجود في الجهة اليسرى الـ Pmfs باستخدام thinkplot.Hist كما رأينا سابقًا؛ أمّا الاستدعاء الثاني لـ PrePlot فهو يضبط مولّد اللون، ومن ثمّ ينتقل SubPlot إلى الشكل الثاني الموجود في الجهة اليمنى ويعرض الـ Pmfs باستخدام thinkplot.Pmfs، كما استخدِم خيار axis لضمان توضُّع الشكلين على المحاور ذاتها، وهذه فكرة جيّدة إذا كان الهدف هو الموازنة بين شكلين اثنين.

رسوم بيانية أخرى

تفيد كل من دوال الكتلة الاحتمالية والمدرَّجات التكرارية في اسكتشاف البيانات ومحاولة تحديد الأنماط patterns والعلاقات relationships، لكن حالما نعلم بما يحصل، فستصبح الخطوة التالية الجيدة هي تصميم رسم بياني يجعل الأنماط التي حدَّدتها واضحةً قدر الإمكان.

تكون الفوارق الكبرى في التوزيعات في بيانات المسح الوطني لنمو الأسرة NSFG قريبةً من المنوال mode، لذا فمن المنطقي تكبير الصورة على هذا الجزء من الرسم البياني وتحويل البيانات للتأكد من الاختلافات:

    weeks = range(35, 46)
    diffs = []
    for week in weeks:
        p1 = first_pmf.Prob(week)
        p2 = other_pmf.Prob(week)
        diff = 100 * (p1 - p2)
        diffs.append(diff)

    thinkplot.Bar(weeks, diffs)

يدل المتغير weeks في الشيفرة السابقة على مجال الأسابيع؛ أما diffs فهو الفارق بين دالتي كتلة احتمالية بالنقاط المئوية.

يُظهِر الشكل التالي النتيجة على أساس مخطط شريطي bar chart، كما يُظهِر هذا الشكل النمط بوضوح أكبر، إذ يشير إلى قلة احتمال ولادة الأطفال الأوائل في الأسبوع 39، ويزداد احتمال الولادة في الأسبوعين 41 و42.

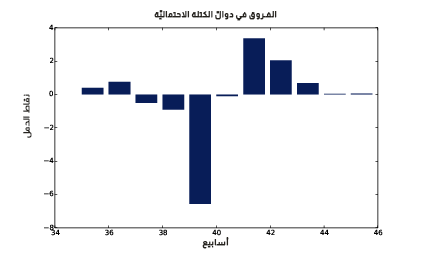
كما يُظهِر الشكل السابق الفرق بالنقاط المئوية أسبوعيًا.

لنضع هذه النتيجة نصب أعيننا مبدئيًا ومؤقتًا فحسب، حيث استخدمنا مجموعة البيانات نفسها لتحديد الفرق الواضح ومن ثم اخترنا تصورًا يجعل هذا الفرق واضحًا، إلا أنه لا يمكننا التأكد من أنّ هذا التأثير حقيقي، إذ يُمكن أن يكون بسبب التباين العشوائي، لكننا سنعالِج هذا لاحقًا.

مفارقة حجم الصفوف الدراسية

سنوضِّح قبل المتابعة أحد أنواع الحسابات التي يمكننا إجراؤها باستخدام كائنات Pmf، وسنسمّي هذا المثال: "مفارقة حجم الصف الدراسي"

تكون نسبة الطلاب إلى أعضاء الهيئة التدريسية في الكثير من الجامعات والكليّات الأمريكية هي حوالي 10:1، ولكن غالبًا ما يفاجَأ الطلاب أن المتوسط الحسابي لحجم الصف الدراسي الذي يدرسون فيه أكبر من 10. ولهذا التناقض سببين اثنين هما:

• يدرس الطلاب عادةً حوالي 4 - 5 صفوف دراسية في الفصل الدراسي الواحد، لكن غالبًا ما يدرِّس الأستاذ حوالي صفًا أو صفَين دراسيَين.
• يفضل عدد قليل من الطلاب التواجد في صف دراسي صغير، إلا أنّ عدد الطلاب كبير في صف دراسي ضخم.

بالطبع فإنّ التاثير الأول واضح، كما يصبح واضحًا حالما يُشار إليه على الأقل، كما أنّ التأثير الثاني أقل وضوحًا، وسنأخذ مثالًا على هذا كما يلي:

لنفترض أنّ الكليّة توفِّر 65 صفًا دراسيًا في الفصل الدراسيّ الواحد مع التوزيع التالي للأحجام:

 size      count
 5- 9          8
10-14          8
15-19         14
20-24          4
25-29          6
30-34         12
35-39          8
40-44          3
45-49          2

إذا سألت عميد الكليّة عن المتوسط الحسابي لحجم الصف الدراسي، فسيبني دالة كتلة احتمالية ويحسب المتوسط mean، ويبلغك بأنّ المتوسط الحسابي لحجم الصف الدراسي هو 23.7، وستكون الشيفرة الموافقة لهذا كما يلي:

    d = { 7: 8, 12: 8, 17: 14, 22: 4, 
          27: 6, 32: 12, 37: 8, 42: 3, 47: 2 }

    pmf = thinkstats2.Pmf(d, label='actual')
    print('mean', pmf.Mean())

لكن إذا أجريت مسحًا لمجموعة من الطلاب وسألتهم عن عدد الطلاب في صفهم وحسبت المتوسط، فسنعتقِد أنّ المتوسط الحسابي للصف الدراسي أكبر، لكن دعنا نرى كم سيكون أكبر.

سنحسب في البداية التوزيع حسب ملاحظة الطلاب، حيث يكون الاحتمال المرتبط بحجم الصف الدراسي "منحازًا biased" إلى عدد الطلاب في الصف الدراسي.

def BiasPmf(pmf, label):
    new_pmf = pmf.Copy(label=label)

    for x, p in pmf.Items():
        new_pmf.Mult(x, x)

    new_pmf.Normalize()
    return new_pmf

لكل صف دراسي حجم هو x، وسنضرب الاحتمال بـ x وهو عدد الطلاب الذين يلاحظون حجم الصف الدراسي، حيث ستكون النتيجة هي Pmf جديد يمثِّل التوزيع المتحيِّز، ويمكننا رسم التوزيع الحقيقي والمُلاحظ كما يلي:

    biased_pmf = BiasPmf(pmf, label='observed')
    thinkplot.PrePlot(2)
    thinkplot.Pmfs([pmf, biased_pmf])
    thinkplot.Show(xlabel='class size', ylabel='PMF')

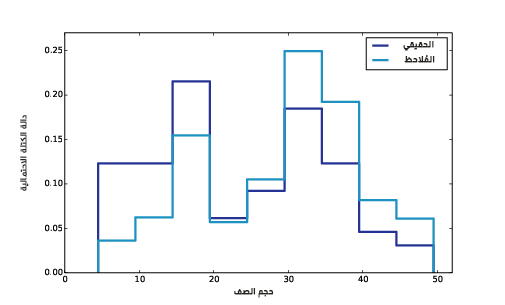
يُظهر الشكل السابق توزيع أحجام الصفوف الدراسية الفعلية والملاحظة من قِبَل الطلاب، كما يُظهِر النتيجة، حيث نرى أنه في التوزيع المتحيِّز هناك عدد أقل من الصفوف الدراسية ذات العدد الطلابي القليل، وعدد أكبر من الصفوف الدراسية ذات العدد الطلابي الكبير، كما يكون متوسط التوزيع المتحِيّز هو 29.1، أي أعلى بحوالي 25% من المتوسط الفعلي.

من الممكن عكس هذه العملية أيضًا، حيث ستفترض أنك تريد إيجاد توزيع أحجام الصفوف الدراسية في الكليّة، ولكن لم يتسنّ لك الحصول على بيانات موثوقة من العميد، لذا سيكون البديل هو اختيار عيّنة عشوائية من الطلّاب وسؤالهم عن عدد الطلاب في صفوفهم الدراسية.

ستكون النتيجة متحيِّزةً للأسباب التي ناقشناها للتو، ولكن يمكنك استخدامها لتقدير التوزيع الفعلي. وستجعل الدالة التالية الـ Pmf غير متحيِّزة:

def UnbiasPmf(pmf, label):
    new_pmf = pmf.Copy(label=label)

    for x, p in pmf.Items():
        new_pmf.Mult(x, 1.0/x)

    new_pmf.Normalize()
    return new_pmf

تشبه الدالة السابقة دالة BiasPmf، إلا أنّ الفارق الوحيد هو تقسيم BiasPmf كل احتمال على x بدلًا من إجراء عملية الجداء.

فهرسة إطار البيانات

سنلقي الآن نظرةً على تحديد الأسطر، حيث سننشئ بدايةً مصفوفة نمباي NumPy تحوي أعدادًا عشوائيةً سنستخدمها لتهيئة إطار بيانات كما يلي:

>>> import numpy as np
>>> import pandas
>>> array = np.random.randn(4, 2)
>>> df = pandas.DataFrame(array)
>>> df
          0         1
0 -0.143510  0.616050
1 -1.489647  0.300774
2 -0.074350  0.039621
3 -1.369968  0.545897

تُرَقَّم الأسطر والأعمدة بدءًا من الصفر في الحالة الافتراضية، لكن يمكنك تزويد الأعمدة بأسماء كما يلي:

>>> columns = ['A', 'B']
>>> df = pandas.DataFrame(array, columns=columns)
>>> df
          A         B
0 -0.143510  0.616050
1 -1.489647  0.300774
2 -0.074350  0.039621
3 -1.369968  0.545897 

كما يمكنك إعطاء أسماء للأسطر، حيث تُدعى مجموعة أسماء الأسطر بالفهرس index، وتدعى أسماء الأسطر نفسها بالعناوين labels.

>>> index = ['a', 'b', 'c', 'd']
>>> df = pandas.DataFrame(array, columns=columns, index=index)
>>> df
          A         B
a -0.143510  0.616050
b -1.489647  0.300774
c -0.074350  0.039621
d -1.369968  0.545897

وكما رأينا في المقال السابق، تُحدِّد الفهرسة البسيطة عمودًا وتُعيد سلسلةً Series كما يلي:

>>> df['A']
a   -0.143510
b   -1.489647
c   -0.074350
d   -1.369968
Name: A, dtype: float64

يمكننا استخدام سمة loc لتحديد سطر عن طريق عنوانه، والتي تُعيد سلسلةً Series كما يلي:

>>> df.loc['a']
A   -0.14351
B    0.61605
Name: a, dtype: float64

إذا علِمت موقع السطر الذي من نمط integer، فيمكنك استخدام سمة iloc بدلًا من عنوانه، والتي تُعيد سلسلةً Series أيضًا، أي كما يلي:

>>> df.iloc[0]
A   -0.14351
B    0.61605
Name: a, dtype: float64

يمكن أن تأخذ السمة loc قائمةً من العناوين وتكون النتيجة في هذه الحالة إطار بيانات DataFrame، أي كما يلي:

>>> indices = ['a', 'c']
>>> df.loc[indices]
         A         B    
a -0.14351  0.616050
c -0.07435  0.039621 

كما يمكنك في النهاية استخدام شريحة slice لتحديد مجالًا من الأسطر عن طريق عنوان العنوان بالصورة التالي:

>>> df['a':'c']
                                               A         B      
a -0.143510  0.616050
b -1.489647  0.300774
c -0.074350  0.039621

أو عن طريق الموقع الذي من نمط integer:

>>> df[0:2]
          A         B         
a -0.143510  0.616050
b -1.489647  0.300774

ستكون النتيجة في كلتا الحالتين إطار بيانات، لكن نلاحظ أنّ النتيجة الأولى تتضمّن نهاية الشريحة على عكس الثانية التي لا تحوي النهاية.

اقتباس

نصيحة: إذا حوَت الأسطر على عناوين ليست من نمط صحيح وبسيط simple integers، فيُفضَّل استخدام العناوين دائمًا وتجنُّب المواقع التي نمطها integer.

تمارين

حلُّ هذه التمارين موجود في: chap03soln.ipynb و chap03soln.py في مستودع ThinkStats2 على GitHub حيث ستجد كل الملفات والشيفرات. 

التمرين الأول

إذا سألنا الأطفال عن عدد الأطفال الموجودين في عائلتهم كما في مفارقة حجم الصف الدراسي، حيث من المحتمل أكثر أن يظهر في عيّنتك عدد كبير من العائلات التي لديها العديد من الأطفال، ولا يوجد احتمال ظهور عائلة لا تحتوي على أيّ أولاد في العيّنة؛ فاستخدم متغيِّر المستجيب NUMKDHH الموجود في المسح الوطني لنموّ الأسرة NSFG لبناء التوزيع الفعلي لعدد الأطفال تحت عمر 18 سنة في المنزل.

احسب الآن التوزيع المتحيِّز الذي نراه إن سألنا الأطفال عن عدد الأطفال تحت عمر الثمانية عشر، مع حساب الأطفال أنفسهم الموجودين في منازلهم.

ارسم التوزيع الحقيقي والمتحيِّز واحسب متوسطهم، مع العلم أنه يمكنك استخدام chap03ex.ipynb على أساس نقطة انطلاق من المستودع السابق.

التمرين الثاني

حسبنا في المقال السابق متوسط عيّنة عن طريق جمع العناصر وتقسيمها على n.

إذا كانت لديك دالة كتلة احتمالية، فيمكنك حساب المتوسط لكن مع اختلاف طفيف في العملية:

حيث تكون x_i هي القيم الفريدة في دالة الكتلة الاحتمالية وفي p_i =PMF(x_i)، وبالمثل يمكننا حساب التباين بالصورة التالية:

اكتب دالتَين بحيث تكون الأولى باسم PmfVar والثانية باسم PmfMean تأخذان كائن Pmf وتحسبان المتوسط mean والتباين variance، ولاختبار هذه التوابع، تأكّد من أنها متوافقة مع التّوابع Mean وVar التي يزودنا بها Pmf.

التمرين الثالث

لقد كانت بدايتنا هي طرح السؤال "هل من المرجَّح أن تتأخر ولادة الأطفال الأوائل؟"، ولتناول هذا السؤال، حسبنا الفرق في المتوسطات بين مجموعات الأطفال babies، لكننا تجاهلنا احتمال أن يكون هناك فرق في موعد الولادة بين الأطفال الأوائل وبقية الأطفال للأم ذاتها. ولتناول هذه النسخة من السؤال، حدِّد المستجيبات اللواتي لديهن طفلين على الأقل واحسب الاختلافات الزوجية. فهل تؤدي هذه الصيغة من السؤال إلى ظهور نتيجة مختلفة؟

اقتباس

تلميح: استخدِم nsfg.MakePregMap.

التمرين الرابع

يبدأ جميع العدائين في الوقت ذاته في معظم سباقات الجري، فإذا كنت عدّاءً سريعًا، فستتخطى غالبًا الكثير من الأشخاص في بداية السباق، ولكن بعد عدّة أميال سيصبح جميع من حولك يركض بالسرعة نفسها.

لاحظنا ظاهرةً غريبةً عندما ركضنا في سباق التتابع لمسافات طويلة -209 ميل- للمرة الأولى، فعندما تجاوزنا عدّاءً آخرًا، كنا أسرع منه بكثير في أغلب الأحيان، وعندما كان تجاوزنا عدّاء آخر، كان أسرع منا بكثير في أغلب الأحيان.

اعتقدنا في البداية أنّ توزيع السرعات هو ثنائي النسق bimodal، وهذا يعني أنه كان هناك العديد من العدائين البطيئين والعديد من العدائين السريعين، وقلّة قليلة منهم يركضون سرعتنا ذاتها، ومن ثم أدركنا أننا كنا ضحية تحيُّز مشابه لأثر حجم الصف الدراسي.

كان السباق غريبًا من ناحيتين هما: أنه قد كانت بداية السباق متداخلة، حيث بدأت الفِرق بأوقات مختلفة، كما تضمنت العديد من الفِرق متسابقِين بقدرات متنوعة.

انتشر العدّاؤون نتيجةً لذلك على طول المضمار مع وجود علاقة طفيفة بين السرعة والموقع، وعندما انضممنا إلى السباق كان العدّاؤون بقربنا يشكِّلون -إلى حد كبير- عيّنةً عشوائيّةً من العدّائين في السباق.

إذًا من أين أتى التحيُّز؟ كان احتمال تجاوزنا لعدّاءً أو تجاوز عدّاء لنا خلال الوقت الذي أمضيناه في المضمار؛ يتناسب مع الاختلاف في سرعاتنا، حيث أنّه من المرجَّح تجاوز عدّاء بطيء، ومن المرجَّح أن يتجاوزنا عدّاء سريع، ولكن من غير المرجَّح أن يرى العدّاؤون الذين يركضون بالسرعة ذاتها بعضهم البعض.

اكتب دالّة باسم ObservedPmf تأخذ Pmf الذي يمثِّل التوزيع الفعلي لسرعات العدّائِين وسرعة العداء المراقِب، وتُعيد صنف Pmf جديد يمثل توزيع سرعات العدّائين تبعًا للمراقِب.

يمكنك استخدام relay.py لاختبار دالتك، حيث يقرأ النتائج من سباق جيمس جويس رامبل James Joyce Ramble بطول مسار 10 كيلو متر في ديدهام في ماساتشوستس، ويحوِّل سرعة العدّاء إلى ميل في الساعة mph.

احسب توزيع السرعات التي ستلاحظها أنت إذا ركضت بسباق تتابعي relay race بسرعة 7.5 ميل في الساعة مع مجموعة العدّائِين هذه.

اقتباس

ملاحظة: حل هذا التمرين موجود في relay_soln.py.

المصطلحات الأساسية

• دالة الكتلة الاحتمالية Probability mass function- أو PMF اختصارًا-: تمثِّل التوزيع على أساس دالة تحوِّل القيم إلى احتمالاتها.
• الاحتمال probability: هو تردد يُعبَّر عنه على أساس كسر fraction من حجم العيّنة.
• التوحيد normalization: هو عملية تقسيم التردد على حجم العيّنة بهدف الحصول على احتمال.
• الفهرس index: هو عمود خاص في إطار بيانات البانداز pandas، بحيث يحتوي على تسميات الأسطر.

ترجمة -وبتصرف- للفصل Chapter 3 Probability mass functions analysis من كتاب Think Stats: Exploratory Data Analysis in Python.

اقرأ أيضًا

• المقال السابق: التوزيعات الإحصائية في بايثون
• تحليل البيانات الاستكشافية لإثبات النظريات الإحصائية