تُعد مكتبة NumPy إحدى مكتبات لغة بايثون Python وتُستخدم للتعامل مع المصفوفات، وتهدف إلى توفير كائن مصفوفة أسرع بما يصل إلى 50 مرة من قوائم بايثون التقليدية.
يطلق على كائن المصفوفة في مكتبة NumPy اسم ndarray، ويوفر العديد من الوظائف الداعمة التي تجعل التعامل مع المصفوفات أمرًا سهلًا جدًا.
تعتمد مكتبة NumPy على العمليات على المتجهات vectorization، فإذا كنت معتادًا على التعامل مع لغة بايثون، فهذه هي الصعوبة الرئيسية التي ستواجهها لأنك ستحتاج إلى تغيير طريقة تفكيرك، كما ستتغير نوع العناصر التي ستستخدمها.
أكثر العناصر شيوعًا في مكتبة NumPy هي المتجهات vectors والمصفوفات arrays والعروض views والدوال العمومية ufuns.
هذا المقال جزء من سلسلة متقدمة حول NumPy وإليك كامل روابط السلسلة:
- مفاهيم متقدمة حول مكتبة NumPy في بايثون
- استخدام المتجهات vectorization في لغة بايثون مع مكتبة NumPy
- الاعتماد على المتجهات في حل المشاكل باستعمال مكتبة NumPy في بايثون
- تخصيص أسلوب المتجهات Custom vectorization عبر استعمال مكتبة NumPy
- ما بعد مكتبة NumPy في بايثون
مثال بسيط
سنأخذ مثالًا بسيطًا وهو المشي العشوائي random walk، إذ يتوجب علينا في الطريقة التقليدية المعتمدة على البرمجة كائنية التوجه OOP تعريف صنف class يأخذ الاسم RandomWalker، ثم إنشاء التابع walk لإرجاع الموقع الحالي بعد كل خطوة عشوائية. يمكن تنفيذ هذا المثال باستخدام التعليمات البرمجية التالية:
class RandomWalker: def __init__(self): self.position = 0 def walk(self, n): self.position = 0 for i in range(n): yield self.position self.position += 2*random.randint(0, 1) - 1 walker = RandomWalker() walk = [position for position in walker.walk(1000)]
وتعطي تجربة قياس السرعة النتيجة التالية:
>>> from tools import timeit >>> walker = RandomWalker() >>> timeit("[position for position in walker.walk(n=10000)]", globals()) 10 loops, best of 3: 15.7 msec per loop
النهج الإجرائي Procedural approach
يمكننا لحل مثل هذه المشكلة البسيطة حفظ تعريف الصنف والتركيز على دالة المشي walk التي تحسب المواقع المتتالية بعد كل خطوة عشوائية.
def random_walk(n): position = 0 walk = [position] for i in range(n): position += 2*random.randint(0, 1)-1 walk.append(position) return walk walk = random_walk(1000)
توفر هذه الطريقة من استهلاك وحدة المعالجة المركزية CPU ولكن ليس لحدٍ كبير لأنها تشبه الطريقة السابقة المعتمدة على البرمجة كائنية التوجه.
>>> from tools import timeit >>> timeit("random_walk(n=10000)", globals()) 10 loops, best of 3: 15.6 msec per loop
النهج المعتمد على المتجهات Vectorized approach
يمكننا باستخدام وحدة itertools تحسين الأداء بطريقة أفضل، إذ تقدم هذه الوحدة مجموعةً من الدوال لإنشاء تكرارات لحلقات فعالة. نلاحظ أن مثال المشي العشوائي ما هو إلا تراكم خطوات، لذلك سنعيد كتابة الدالة بإنشاء جميع الخطوات أولًا، ثم تجميعها بدون استخدام أي حلقة، كما توضح التعليمات التالية:
def random_walk_faster(n=1000): from itertools import accumulate # Only available from Python 3.6 steps = random.choices([-1,+1], k=n) return [0]+list(accumulate(steps)) walk = random_walk_faster(1000)
اعتمدنا في هذا المثال على المتجهات في الدالة، فبدلًا من استخدام التكرار لاختيار الخطوات وإضافتها إلى الموضع الحالي، أنشأنا أولًا جميع الخطوات دفعةً واحدةً، ثم استخدمنا دالة التجميع accumulate لحساب جميع المواضع. تخلصنا من الحلقة وبالتالي أصبح تنفيذ التعليمات أسرع:
>>> from tools import timeit >>> timeit("random_walk_faster(n=10000)", globals()) 10 loops, best of 3: 2.21 msec per loop
لاحظ أننا وفرنا 85% من وقت الحساب مقارنةً بالإصدار السابق، لكن الإيجابية التي تميز الإصدار الجديد هي تبسيط العمليات المعقدة على المتجهات. سنحتاج إلى استبدال أدوات itertools بأدوات numpy:
def random_walk_fastest(n=1000): # No 's' in numpy choice (Python offers choice & choices) steps = np.random.choice([-1,+1], n) return np.cumsum(steps) walk = random_walk_fastest(1000)
هذه الطريقة سهلة وتوفر الكثير من الوقت كما توضح النتائج التالية:
>>> from tools import timeit >>> timeit("random_walk_fastest(n=10000)", globals()) 1000 loops, best of 3: 14 usec per loop
يركز هذا الدليل يركز على الاعتماد على المتجهات سواءٌ كان ذلك على مستوى المشكلة أو الشيفرات البرمجية، وسنوضح أهمية هذا الاختلاف قبل الانتقال إلى دراسة المتجهات المخصصة.
سهولة القراءة مقابل السرعة
قبل الانتقال إلى القسم التالي، سنلقي نظرةً على مشكلة محتملة قد تواجهها بعد أن تصبح على دراية بمكتبة NumPy؛ فمكتبة NumPy مكتبة قوية جدًا ويمكنك أن تصنع العجائب بها، ولكن هذا على حساب سهولة القراءة، لذلك إذا أهملت إضافة التعليقات أثناء كتابة التعليمات البرمجية، فلن تتمكن من معرفة وظيفة بعض التعليمات بعد بضع أسابيع أو ربما أيام.
على سبيل المثال هل يمكنك معرفة ما هي نتيجة تنفيذ الدالتين التاليتين؟ ربما ستتمكن من فهم الدالة الأولى ولكن من غير المرجح أن تفهم الثانية:
def function_1(seq, sub): return [i for i in range(len(seq) - len(sub)) if seq[i:i+len(sub)] == sub] def function_2(seq, sub): target = np.dot(sub, sub) candidates = np.where(np.correlate(seq, sub, mode='valid') == target)[0] check = candidates[:, np.newaxis] + np.arange(len(sub)) mask = np.all((np.take(seq, check) == sub), axis=-1) return candidates[mask]
استخدمت الدالة الثانية مكتبة NumPy وهي أسرع بعشر مرات، ولكن المشكلة هي بصعوبة قراءة وفهم التعليمات البرمجية التي تستخدمها.
تشريح المصفوفة
كما أوضحنا سابقًا ينبغي أن تكون لديك خبرةً أساسيةً في التعامل مع مكتبة NumPy قبل المتابعة في هذا الدليل، وإذا لم يكن لديك هذه الخبرة فمن الأفضل أن تتعلم عنها قبل العودة إلى هنا، وبناءً على ذلك سنبدأ هذا الدليل بتذكير سريع على الهيكلية الأساسية للمصفوفات المعقدة، خاصةً بما يتعلق بتخطيط الذاكرة وعرضها ونسخ البيانات وتحديد نوعها، وهذه مفاهيم أساسية يجب أن تفهمها إذا كنت تريد أن تستفيد من فلسفة مكتبة numpy.
لنفكر في مثال بسيط نريد من خلاله مسح جميع القيم في مصفوفة من النوع np.float32. كيف يمكن كتابة تعليمات تنفذ المثال السابق بسرعة؟ الصيغة أدناه واضحة إلى حد ما (على الأقل لأولئك الذين هم على دراية بمكتبة NumPy) ولكن السؤال أعلاه يطلب العثور على أسرع عملية.
>>> Z = np.ones(4*1000000, np.float32) >>> Z[...] = 0
إذا دققت بنوع عناصر المصفوفة dtype وحجمها، يمكنك ملاحظة أنه يمكن تحويل هذه المصفوفة إلى العديد من أنواع البيانات "المتوافقة" الأخرى. نقصد هنا أنه يمكن تقسيم Z.size * Z.itemsize إلى أنواع عناصر dtype جديدة.
>>> timeit("Z.view(np.float16)[...] = 0", globals()) 100 loops, best of 3: 2.72 msec per loop >>> timeit("Z.view(np.int16)[...] = 0", globals()) 100 loops, best of 3: 2.77 msec per loop >>> timeit("Z.view(np.int32)[...] = 0", globals()) 100 loops, best of 3: 1.29 msec per loop >>> timeit("Z.view(np.float32)[...] = 0", globals()) 100 loops, best of 3: 1.33 msec per loop >>> timeit("Z.view(np.int64)[...] = 0", globals()) 100 loops, best of 3: 874 usec per loop >>> timeit("Z.view(np.float64)[...] = 0", globals()) 100 loops, best of 3: 865 usec per loop >>> timeit("Z.view(np.complex128)[...] = 0", globals()) 100 loops, best of 3: 841 usec per loop >>> timeit("Z.view(np.int8)[...] = 0", globals()) 100 loops, best of 3: 630 usec per loop
ولكن في الواقع فإن طريقة تصفية جميع القيم ليست هي الأسرع، فقد زاد معدل السرعة بنسبة 25% من خلال تحويل بعض عناصر المصفوفة إلى نوع البيانات np.float64، بينما زاد معدل السرعة بنسبة 50% من خلال عرض المصفوفة واستخدام نوع البيانات np.int8. تتعلق أسباب التسريع بهيكلية عمل مكتبة numpy.
تخطيط الذاكرة Memory layout
يُعرّف الصنف ndarray وفقًا لتوثيق Numpy كما يلي:
اقتباستتكون نسخة صنف ndarray من جزء أحادي البعد قريب من ذاكرة الحاسب (يملكه كائن معين أو مصفوفة) إلى جانب مخطط الفهرسة الذي يعين أعداد صحيحة N في موقع العنصر من الكتلة.
المصفوفة هي كتلة مجاورة من الذاكرة يمكن الوصول إلى عناصرها باستخدام مخطط الفهرسة indexing scheme، الذي يحدد شكل ونوع البيانات، وهذا هو المطلوب لتعريف مصفوفة جديدة.
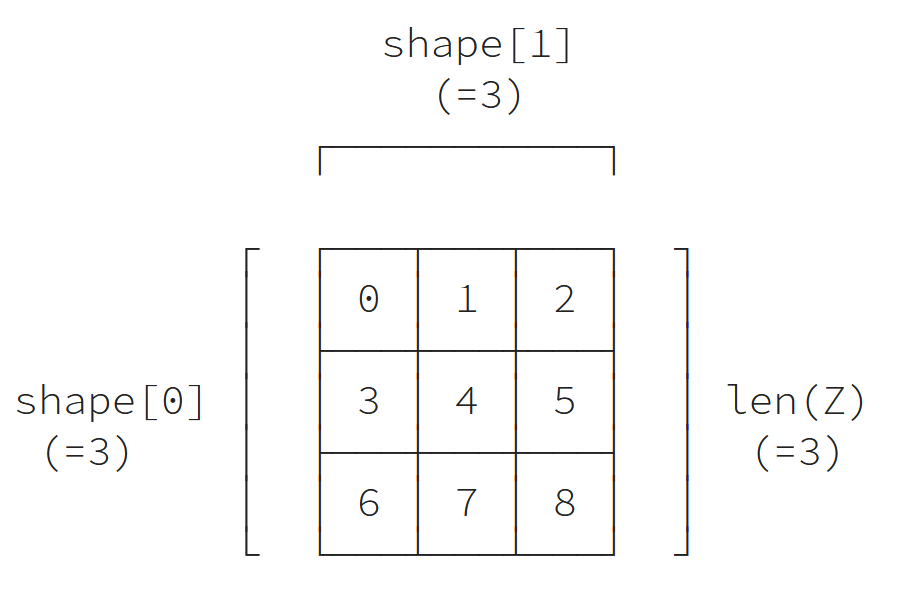
Z = np.arange(9).reshape(3,3).astype(np.int16)
حجم عناصر المصفوفة Z في التعليمة السابقة هو 2 بايت (int16)، وعدد أبعاد (len(Z.shape هو 2.
>>> print(Z.itemsize) 2 >>> print(Z.shape) (3, 3) >>> print(Z.ndim) 2
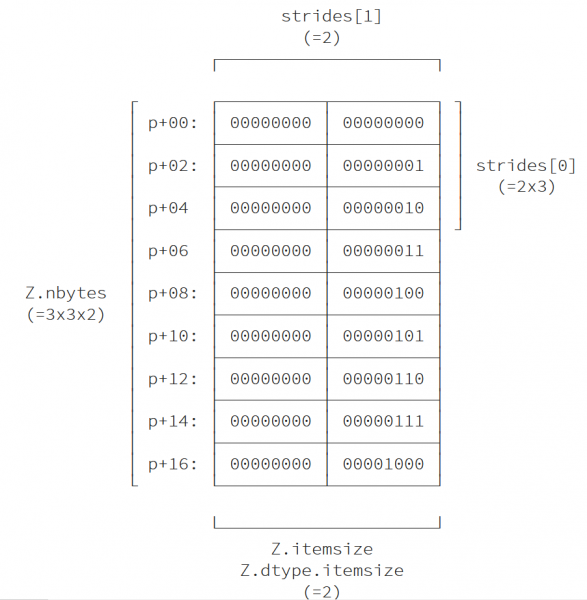
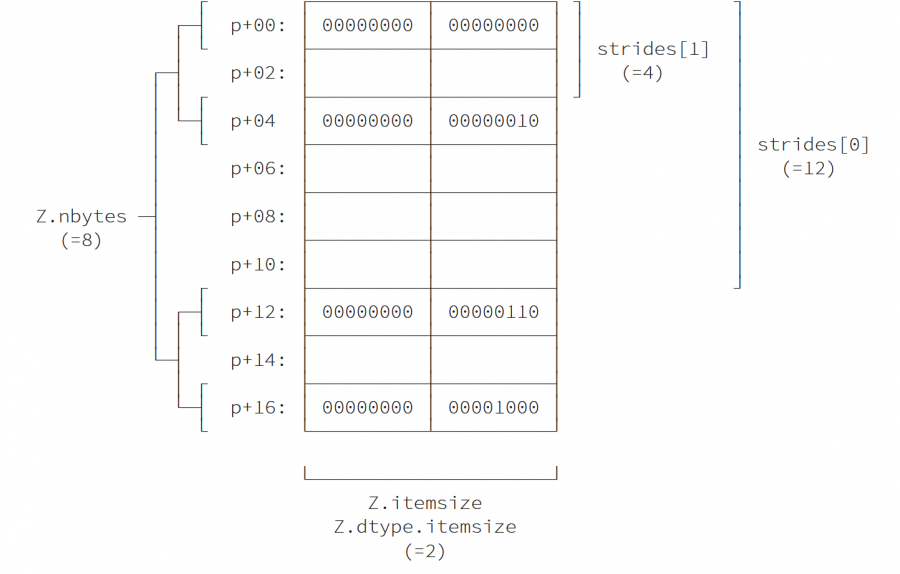
نظرًا لأن Z ليست طريقة عرض، يمكننا استنتاج خطوات المصفوفة التي تحدد عدد البايتات التي يجب أن تخطوها لاجتياز كل بعد من أبعاد المصفوفة.
>>> strides = Z.shape[1]*Z.itemsize, Z.itemsize >>> print(strides) (6, 2) >>> print(Z.strides) (6, 2)
لنتمكن من الوصول إلى عنصر معين (مصمم بواسطة فهرس index tuple)، أي كيفية حساب إزاحة البداية والنهاية:
offset_start = 0 for i in range(ndim): offset_start += strides[i]*index[i] offset_end = offset_start + Z.itemsize
سنستخدم الآن طريقة التحويل tobytes للتأكد من المعلومة السابقة:
>>> Z = np.arange(9).reshape(3,3).astype(np.int16) >>> index = 1,1 >>> print(Z[index].tobytes()) b'\x04\x00' >>> offset = 0 >>> for i in range(Z.ndim): ... offset + = Z.strides[i]*index[i] >>> print(Z.tobytes()[offset_start:offset_end] b'\x04\x00'
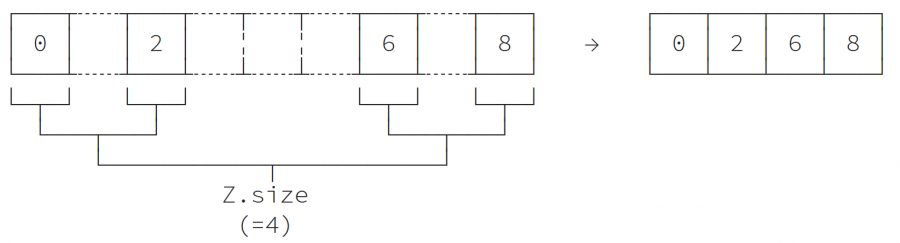
يمكن تمثيل هذه المصفوفة بطرق (تخطيطات) مختلفة:
- تخطيط العنصر item layout
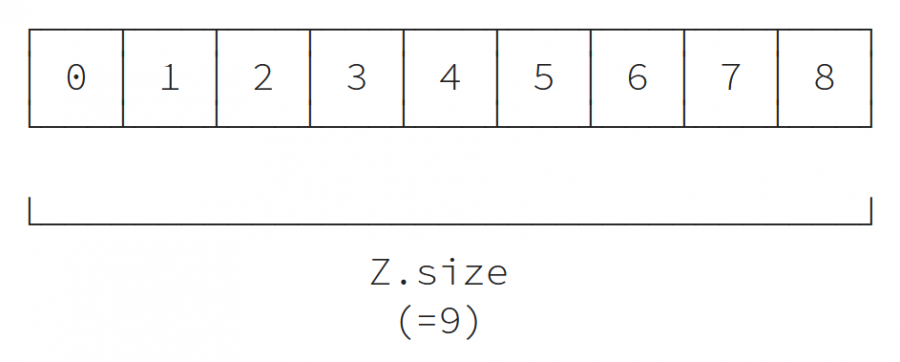
- تخطيط العنصر المسطّح Flattened item layout
- تخطيط الذاكرة Memory layout (C order, big endian)
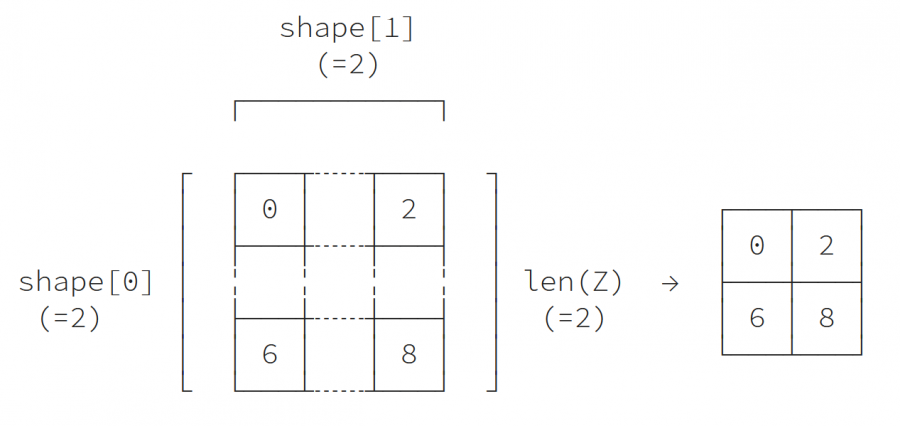
إذا أخذنا الآن شريحة من Z، فإن النتيجة هي عرض المصفوفة الأساسية Z:
V = Z[::2,::2]
يُحدّد هذا العرض باستخدام نوع dtype وشكل وخطوات، إذ أصبح من غير الممكن استنتاج الخطوات strides من النوع والشكل فقط:
- تخطيط العنصر item layout
- تخطيط العنصر المسطّح Flattened item layout
- تخطيط الذاكرة Memory layout (C order, big endian)
العروض والنسخ
تُعد العروض Views والنسخ copies مفاهيمًا مهمة لتحسين حساباتك الرقمية. بالرغم من تعاملنا مع هذه المفاهيم في الفقرات السابقة إلا أن الموضوع أكثر تعقيدًا.
الوصول المباشر وغير المباشر
أولًا علينا التمييز بين نوعي الفهرسة indexing و fancy indexing؛ إذ يعيد النوع الأول عرضًا view دائمًا، بينما يعيد النوع الثاني نسخةً copy. يؤدي تعديل العرض في الحالة الأولى إلى تعديل المصفوفة الأساسية، بينما لن يحدث ذلك في الحالة الثانية:
>>> Z = np.zeros(9) >>> Z_view = Z[:3] >>> Z_view[...] = 1 >>> print(Z) [ 1. 1. 1. 0. 0. 0. 0. 0. 0.] >>> Z = np.zeros(9) >>> Z_copy = Z[[0,1,2]] >>> Z_copy[...] = 1 >>> print(Z) [ 0. 0. 0. 0. 0. 0. 0. 0. 0.]
إذا كنت تريد استخدام نوع الفهرسة fancy indexing فمن الأفضل الاحتفاظ بنسخة الفهرس fancy index ثم التعامل معه:
>>> Z = np.zeros(9) >>> index = [0,1,2] >>> Z[index] = 1 >>> print(Z) [ 1. 1. 1. 0. 0. 0. 0. 0. 0.]
إذا لم تكن متأكدًا مما إذا كانت نتيجة الفهرسة هي عرض أو نسخة، فيمكنك التحقق باستخدام الأداة base؛ فإذا كانت النتيجة "None"، فسيكون النوع هو نسخة:
>>> Z = np.random.uniform(0,1,(5,5)) >>> Z1 = Z[:3,:] >>> Z2 = Z[[0,1,2], :] >>> print(np.allclose(Z1,Z2)) True >>> print(Z1.base is Z) True >>> print(Z2.base is Z) False >>> print(Z2.base is None) True
لاحظ أن بعض وظائف numpy تُعيد عرضًا view، مثل ravel عندما يكون ذلك ممكنًا، بينما يعيد البعض الآخر نسخةً copy، مثل flatten:
>>> Z = np.zeros((5,5)) >>> Z.ravel().base is Z True >>> Z[::2,::2].ravel().base is Z False >>> Z.flatten().base is Z False
نسخة مؤقتة Temporary copy
يمكن إنشاء النسخ بطريقة صريحة كما في الأمثلة السابقة، ولكن الطريقة الأكثر استخدمًا هي الإنشاء الضمني للنسخ الوسيطة. يوضح المثال التالي إجراء العمليات الحسابية باستخدام المصفوفات:
>>> X = np.ones(10, dtype=np.int) >>> Y = np.ones(10, dtype=np.int) >>> A = 2*X + 2*Y
أنشأنا في هذا المثال ثلاث مصفوفات وسيطة: مصفوفة للاحتفاظ بنتيجة X*2 والثانية للاحتفاظ بنتيجة Y*2، والأخيرة لإيجاد نتيجة Y*2 + X*2، وتكون المصفوفات في هذه الحالة صغيرة الحجم ولا تحدث هذه الطريقة أي فرق واضح؛ ولكن في حال كانت المصفوفات كبيرة الحجم فعليك أن تكون حذرًا مع هذه التعبيرات وتفكر بطريقة مختلفة لإيجاد الحل، فعلى سبيل المثال إذا كانت النتيجة النهائية هي فقط المهمة ولم تكن بحاجة إلى X أو Y، فسيكون الحل البديل:
>>> X = np.ones(10, dtype=np.int) >>> Y = np.ones(10, dtype=np.int) >>> np.multiply(X, 2, out=X) >>> np.multiply(Y, 2, out=Y) >>> np.add(X, Y, out=X)
استغنينا باستخدام هذا الحل البديل عن فكرة إنشاء مصفوفات مؤقتة، لكن المشكلة أن هناك بعض الحالات التي تتطلب إنشاء هذه النسخ المؤقتة وهذا يؤثر على الأداء كما هو موضح في المثال التالي:
>>> X = np.ones(1000000000, dtype=np.int) >>> Y = np.ones(1000000000, dtype=np.int) >>> timeit("X = X + 2.0*Y", globals()) 100 loops, best of 3: 3.61 ms per loop >>> timeit("X = X + 2*Y", globals()) 100 loops, best of 3: 3.47 ms per loop >>> timeit("X += 2*Y", globals()) 100 loops, best of 3: 2.79 ms per loop >>> timeit("np.add(X, Y, out=X); np.add(X, Y, out=X)", globals()) 1000 loops, best of 3: 1.57 ms per loop
الخلاصة
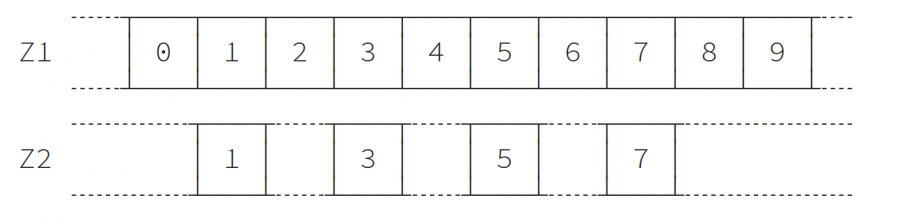
في الختام سندرس المثال التالي: لنفرض لدينا متجهين Z1 و Z2، ونرغب في معرفة ما إذا كان Z2 هو عرض view للمتجه Z1، وإذا كانت الإجابة نعم فما هو هذا العرض view؟
>>> Z1 = np.arange(10) >>> Z2 = Z1[1:-1:2]
أولاً سنحدد نوع الفهرسة وهل Z1 هي أساس Z2:
>>> print(Z2.base is Z1) True
حتى الآن تأكدنا أن Z2 هي عرض view للمتغير Z1، مما يعني أنه يمكن التعبير عن Z2على النحو التالي: [Z1[start:stop:step.
وتكمن الصعوبة في التعرف على البداية والتوقف والخطوة؛ إذ يمكننا بالنسبة للخطوة استخدام خاصية strides لأي مصفوفة تعطي عدد البايتات للانتقال من عنصر إلى آخر في كل بُعد. في حالتنا ولأن كلا المصفوفتين أحادي البعد، يمكننا مقارنة الخطوة الأولى فقط.
>>> step = Z2.strides[0] // Z1.strides[0] >>> print(step) 2
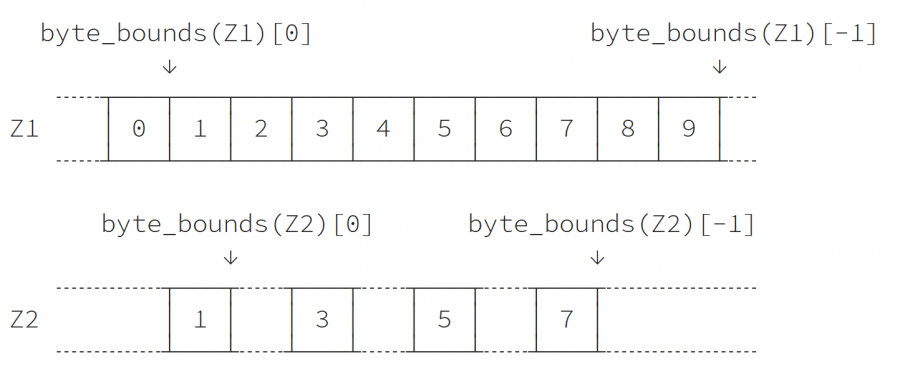
الصعوبة التالية هي العثور على مؤشرات البداية والتوقف، إذ يمكننا فعل ذلك بالاستفادة من طريقة byte_bounds التي تُرجع مؤشرًا إلى نقاط نهاية المصفوفة.
>>> offset_start = np.byte_bounds(Z2)[0] - np.byte_bounds(Z1)[0] >>> print(offset_start) # bytes 8 >>> offset_stop = np.byte_bounds(Z2)[-1] - np.byte_bounds(Z1)[-1] >>> print(offset_stop) # bytes -16
يعد تحويل هذه الإزاحات offset إلى مؤشرات أمرًا سهلاً باستخدام حجم العناصر مع الأخذ بالحسبان أن offset_stop سلبي (حد نهاية Z2 أصغر منطقيًا من حد النهاية لمصفوفة Z1)، لذلك نحتاج إلى إضافة حجم عناصر Z1 للحصول على فهرس النهاية الصحيحة:
>>> start = offset_start // Z1.itemsize >>> stop = Z1.size + offset_stop // Z1.itemsize >>> print(start, stop, step) 1, 8, 2
وعند اختبار النتائج نحصل على ما يلي:
>>> print(np.allclose(Z1[start:stop:step], Z2)) True
يمكنك التمرين من خلال تحسين هذا التنفيذ الأول والبسيط جدًا من خلال مراعاة:
- خطوات سلبية.
- مصفوفة متعددة الأبعاد.
ترجمة -وبتصرف- للفصلين Introduction و Anatomy of an array من كتاب From Python to Numpy لصاحبه Nicolas P. Rougier.











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.