يعد الاعتماد على المتجهات في المشاكل أصعب بكثير من متجهات الشيفرات لأنه يعني أنه يتعين عليك إعادة التفكير في مشكلتك من أجل جعلها معتمدة على المتجهات vectorizable، وهذا يعني غالبًا أن عليك استخدام خوارزمية مختلفة لحل مشكلتك، أو حتى الأسوأ من ذلك، فقد تحتاج إلى ابتكار خوارزمية جديدة. وبالتالي تكمن الصعوبة في التفكير خارج الصندوق.
لتوضيح ذلك دعنا نفكر في مشكلة بسيطة، ولنفرض لدينا متجهين X و Y، ونريد حساب مجموع [X * Y [j لجميع أزواج المؤشرات i و j. أحد الحلول البسيطة والواضحة هو كتابة:
def compute_python(X, Y): result = 0 for i in range(len(X)): for j in range(len(Y)): result += X[i] * Y[j] return result
ولكن تتضمن الشيفرات السابقة حلقتين وبالتالي فإن التنفيذ سيكون بطيئًا:
>>> X = np.arange(1000) >>> timeit("compute_python(X,X)") 1 loops, best of 3: 0.274481 sec per loop
كيف يمكن جعل المشكلة معتمدة على المتجهات إذًا؟ إذا كنت تتذكر مقرر الجبر الخطي، فربما تكون قد حددت التعبير [X * Y [j ليكون مشابهًا جدًا لتعبير المصفوفة، لذلك ربما يمكننا الاستفادة من سرعة NumPy. أحد الحلول الخاطئة هو بكتابة:
def compute_numpy_wrong(X, Y):
return (X*Y).sum()
هذا الحل خاطئ لأن التعبير X * Y يحسب في الواقع متجهًا جديدًا Z وفقًا لما يلي: [Z = X * Y [i، وليس هذا ما نريده، لذلك سنجرب استغلال ميزة البث broadcasting لمكتبة NumPy وإعادة تشكيل المتجهين أولًا ثم ضربهما:
def compute_numpy(X, Y): Z = X.reshape(len(X),1) * Y.reshape(1,len(Y)) return Z.sum()
أصبح لدينا [Z[i,j] == X[i,0]*Y[0,j، وإذا حسبنا مجموع كل عناصر Z، سنحصل على النتيجة المتوقعة. سنتأكد الآن من مقدار التحسن في السرعة الذي اكتسبناه في هذه الطريقة:
>>> X = np.arange(1000) >>> timeit("compute_numpy(X,X)") 10 loops, best of 3: 0.00157926 sec per loop
هذا أفضل، فقد حصلنا على عامل سرعة أكبر بحوالي 150 مرة، ولكن لا يزال بإمكاننا تحسين هذا العامل.
بالعودة إلى الطريقة الأولى، يمكنك أن تلاحظ أن الحلقة الداخلية تستخدم [X [i الذي لا يعتمد على المؤشر j، مما يعني أنه يمكن إزالته من الحلقة الداخلية. يمكن إعادة كتابة الشيفرة على النحو التالي:
def compute_numpy_better_1(X, Y): result = 0 for i in range(len(X)): Ysum = 0 for j in range(len(Y)): Ysum += Y[j] result += X[i]*Ysum return result
ونظرًا لأن الحلقة الداخلية لا تعتمد على المؤشر i، فيمكننا أن نحسبها مرةً واحدةً فقط:
def compute_numpy_better_2(X, Y): result = 0 Ysum = 0 for j in range(len(Y)): Ysum += Y[j] for i in range(len(X)): result += X[i]*Ysum return result
خفضنا التعقيد بفضل إزالة الحلقة الداخلية من "(O(n2" إلى "(O(n". وبنفس الطريقة يمكننا كتابة:
def compute_numpy_better_3(x, y): Ysum = 0 for j in range(len(Y)): Ysum += Y[j] Xsum = 0 for i in range(len(X)): Xsum += X[i] return Xsum*Ysum
أخيرًا، بعد أن أدركنا أننا نحتاج فقط إلى حاصل ضرب المجموع لكلٍ من X و Y على التوالي، يمكننا الاستفادة من دالة np.sum وكتابة:
def compute_numpy_better(x, y): return np.sum(y) * np.sum(x)
وبالتالي حصلنا على شيفرات برمجية أقصر وأرتب وأسرع:
>>> X = np.arange(1000)
>>> timeit("compute_numpy_better(X,X)")
1000 loops, best of 3: 3.97208e-06 sec per loop
بهذه الطريقة نكون قد أعدنا صياغة المشكلة، مستغلين حقيقة أن: "∑ij XiYj = ∑iXi∑jYj".
وتعلمنا الآن أن هناك نوعين من التحويل المعتمد على المتجهات، وهما: متجهات الشيفرات ومتجهات المشكلة. يُعد النوع الثاني من المتجهات هو الأصعب والأكثر أهمية لأنك من خلاله يمكنك توقع مكاسب هائلة في تحسين السرعة. اكتسبنا في هذا المثال البسيط عامل سرعة أكبر بمقدار 150 مرة عند استخدام متجهات الشيفرة، واكتسبنا عامل قدره 70000 باستخدام متجهات المشكلة، أي من خلال كتابة مشكلتنا بطريقة مختلفة فقط.
إذا أعدنا كتابة الحل الأخير بطريقة بايثون فإن التحسين سيكون جيدًا ولكن ليس مثل استخدام numpy:
def compute_python_better(x, y): return sum(x)*sum(y)
هذا الإصدار الجديد من بايثون أسرع بكثير من إصدار بايثون السابق، لكنه لا يزال أبطأ 50 مرةً من الإصدار numpy:
>>> X = np.arange(1000) >>> timeit("compute_python_better(X,X)") 1000 loops, best of 3: 0.000155677 sec per loop
إيجاد المسار
يتعلق اكتشاف المسار بإيجاد أقصر مسار في الرسم البياني. يمكن تقسيم هذا إلى مشكلتين مختلفتين: العثور على مسار بين كل عقدتين في الرسم البياني والعثور على أقصر مسار، وسنوضح ذلك من خلال اكتشاف المسار في متاهة، لذلك ستكون المهمة الأولى هي بناء المتاهة.
متاهة سياج أخضر تحيط بمنزل Longleat الفخم في إنجلترا. صورة Prince Rurik، 2005.
بناء متاهة
توجد عدة خوارزميات لإنشاء متاهة، لكننا سنستخدم هنا خوارزمية معينة تعمل عن طريق إنشاء "n" (الكثافة) جزيرة بطول "p" (التعقيد). تنشأ الجزيرة من خلال اختيار نقطة بداية عشوائية بإحداثيات فردية، ثم نختار اتجاهًا عشوائيًا.
إذا كانت الخلية التي تملك خطوتين في اتجاه معين حرة سيُضاف جدار في أول وثاني خطوة في هذا الاتجاه، وتُكرر العملية n خطوة لهذه الجزيرة، وبالتالي ننشيء p جزيرة. يكون كل من n و p أعداد عشرية float لتتكيف مع حجم المتاهة. تكون الجزر صغيرة جدًا مع هذا التعقيد المنخفض ويكون حل المتاهة سهلًا، وتحتوي المتاهة على مزيدٍ من "الغرف الفارغة الكبيرة" مع الكثافة المنخفضة.
def build_maze(shape=(65, 65), complexity=0.75, density=0.50): # Only odd shapes shape = ((shape[0]//2)*2+1, (shape[1]//2)*2+1) # ضبط التعقيد والكثافة نسبةً إلى حجم المتاهة n_complexity = int(complexity*(shape[0]+shape[1])) n_density = int(density*(shape[0]*shape[1])) # بناء المتاهة الفعلية Z = np.zeros(shape, dtype=bool) # ملء الحدود Z[0, :] = Z[-1, :] = Z[:, 0] = Z[:, -1] = 1 # تبدأ الجزر بنقطة مع انحياز من طرف الحدود P = np.random.normal(0, 0.5, (n_density, 2)) P = 0.5 - np.maximum(-0.5, np.minimum(P, +0.5)) P = (P*[shape[1], shape[0]]).astype(int) P = 2*(P//2) # إنشاء الجزر for i in range(n_density): # Test for early stop: if all starting point are busy, this means we # won't be able to connect any island, so we stop. T = Z[2:-2:2, 2:-2:2] if T.sum() == T.size: break x, y = P[i] Z[y, x] = 1 for j in range(n_complexity): neighbours = [] if x > 1: neighbours.append([(y, x-1), (y, x-2)]) if x < shape[1]-2: neighbours.append([(y, x+1), (y, x+2)]) if y > 1: neighbours.append([(y-1, x), (y-2, x)]) if y < shape[0]-2: neighbours.append([(y+1, x), (y+2, x)]) if len(neighbours): choice = np.random.randint(len(neighbours)) next_1, next_2 = neighbours[choice] if Z[next_2] == 0: Z[next_1] = 1 Z[next_2] = 1 y, x = next_2 else: break return Z
هنا رسم متحرك يوضح عملية التوليد.
بناء متاهة متدرجة مع التحكم في التعقيد والكثافة.
خوارزمية الاتساع أولا Breadth-first
تعالج خوارزمية البحث ذات الاتساع أولًا Breadth-first (وكذلك خوارزمية العمق أولًا depth-first) مشكلة إيجاد مسار بين عقدتين من خلال فحص جميع الاحتمالات بدءًا من عقدة الجذر والتوقف بمجرد العثور على حل (الوصول إلى العقدة الوجهة). تعمل هذه الخوارزمية في الوقت الخطي بالتعقيد (|O(|V| + |E، إذ يمثل V عدد الرؤوس vertices و E هو عدد الحواف. كتابة مثل هذه الخوارزمية ليس صعبًا بشرط أن يكون لديك بنية البيانات الصحيحة. في حالتنا فإن تمثيل المتاهة على شكل مصفوفة ليس هو الحل الأنسب، ونحتاج إلى تحويله إلى رسم بياني حقيقي وفق اقتراح فالنتين بريوخانوف Valentin Bryukhanov.
def build_graph(maze): height, width = maze.shape graph = {(i, j): [] for j in range(width) for i in range(height) if not maze[i][j]} for row, col in graph.keys(): if row < height - 1 and not maze[row + 1][col]: graph[(row, col)].append(("S", (row + 1, col))) graph[(row + 1, col)].append(("N", (row, col))) if col < width - 1 and not maze[row][col + 1]: graph[(row, col)].append(("E", (row, col + 1))) graph[(row, col + 1)].append(("W", (row, col))) return graph
ملاحظة: إذا استخدمنا خوارزمية العمق أولاً فلا يوجد ضمان للعثور على أقصر مسار، ويمكننا فقط للعثور على مسار إذا كان موجودًا.
بعد الانتهاء من ذلك، تكون كتابة خوارزمية الاتساع أولًا أمرًا سهلًا. نبدأ من عقدة البداية ونزور العقد في العمق الحالي ونكرر العملية حتى الوصول إلى العقدة النهائية إن أمكن. والسؤال هنا: هل نحصل بهذه الطريقة على أقصر طريق لاستكشاف الرسم البياني؟ في هذه الحالة المحددة "نعم"، لأننا لا نملك رسمًا بيانيًا مرجحًا للحافة، أي أن جميع الحواف لها نفس الوزن (أو التكلفة).
def breadth_first(maze, start, goal): queue = deque([([start], start)]) visited = set() graph = build_graph(maze) while queue: path, current = queue.popleft() if current == goal: return np.array(path) if current in visited: continue visited.add(current) for direction, neighbour in graph[current]: p = list(path) p.append(neighbour) queue.append((p, neighbour)) return None
طريقة بيلمان فورد Bellman-Ford
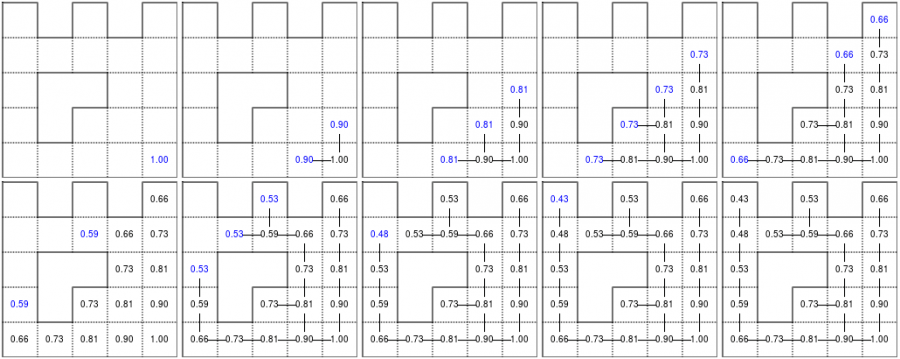
خوارزمية بيلمان فورد Bellman-Ford قادرة على إيجاد المسار الأمثل في الرسم البياني باستخدام عملية الانتشار، إذ تعثر على المسار الأفضل عن طريق تصاعد التدرج الناتج. تعمل هذه الخوارزمية في الوقت التربيعي (|O(|V||E، إذ يمثّل V عدد الرؤوس و E عدد الحواف. في حالتنا البسيطة لن نواجه الكثير من المشاكل. الخوارزمية موضحة أدناه في الشكل (القراءة من اليسار إلى اليمين ومن أعلى إلى أسفل). بعد فهم الخوارزمية يمكننا صعود التدرج اللوني من عقدة البداية، ويمكنك التحقق من الشكل الذي يؤدي إلى أقصر طريق.
قيم خوارزمية التكرار في متاهة بسيطة. بمجرد الوصول إلى المدخل، يكون من السهل العثور على أقصر طريق عن طريق صعود تدرج القيمة.
نبدأ بتعيين عقدة الخروج على القيمة 1، بينما تُعيّن كل عقدة أخرى بالقيمة 0 باستثناء الجدران، ثم نكرر العملية بحيث تحسب القيمة الجديدة لكل خلية على أنها القيمة القصوى بين قيمة الخلية الحالية وقيم الخلايا الأربعة المُخفّضة المتجاورة (gamma=0.9 في الحالة أدناه). تبدأ العملية بمجرد أن تصبح قيمة عقدة البداية موجبة تمامًا.
يُعد التنفيذ باستخدام NumPy أبسط إذا استفدنا من ميزات عامل الترشيح العام generic_filter (من scipy.ndimage) لعملية الانتشار:
def diffuse(Z): # North, West, Center, East, South return max(gamma*Z[0], gamma*Z[1], Z[2], gamma*Z[3], gamma*Z[4]) # Build gradient array G = np.zeros(Z.shape) # Initialize gradient at the entrance with value 1 G[start] = 1 # Discount factor gamma = 0.99 # We iterate until value at exit is > 0. This requires the maze # to have a solution or it will be stuck in the loop. while G[goal] == 0.0: G = Z * generic_filter(G, diffuse, footprint=[[0, 1, 0], [1, 1, 1], [0, 1, 0]])
لكن في هذه الحالة بالتحديد يكون الأمر بطيئًا إلى حد ما، ومن الأفضل إعداد حلنا الخاص، وإعادة استخدام جزء من تشفير لعبة الحياة:
# Build gradient array G = np.zeros(Z.shape) # Initialize gradient at the entrance with value 1 G[start] = 1 # Discount factor gamma = 0.99 # We iterate until value at exit is > 0. This requires the maze # to have a solution or it will be stuck in the loop. G_gamma = np.empty_like(G) while G[goal] == 0.0: np.multiply(G, gamma, out=G_gamma) N = G_gamma[0:-2,1:-1] W = G_gamma[1:-1,0:-2] C = G[1:-1,1:-1] E = G_gamma[1:-1,2:] S = G_gamma[2:,1:-1] G[1:-1,1:-1] = Z[1:-1,1:-1]*np.maximum(N,np.maximum(W, np.maximum(C,np.maximum(E,S))))
بمجرد الانتهاء من ذلك، يمكننا صعود التدرج للعثور على أقصر طريق كما هو موضح في الشكل أدناه:
إيجاد المسار باستخدام خوارزمية بيلمان-فورد. تشير الألوان المتدرجة إلى القيم المنتشرة من نقطة نهاية المتاهة (أسفل اليمين). عُثر على المسار من خلال التدرج التصاعدي من الهدف.
خوارزمية تدفقات السوائل Fluid Dynamics
فيما يلي سنوضح طريقة عمل خوارزمية تدفقات السوائل، وكيفية تنفيذها برمجيًا.
التدفق الهيدروديناميكي بمستويين مختلفين من التقريب، نهر نيكار، هايدلبرغ، ألمانيا. صورة Steven Mathey، 2012.
طريقة لاغرانج Lagrangian مقابل أويلريان Eulerian
في نظرية الحقل الكلاسيكية، فإن مواصفات لاغرانج للحقل هي طريقة للنظر إلى حركة السوائل، إذ يتبّع المراقب حركة السائل عبر المكان والزمان، ويعطينا رسم موقع كل جزء عبر الزمن مسار ذلك الجزء، ويمكن تخيل هذا على أنه الجلوس في قارب والانجراف في النهر.
تعد مواصفات أويلريان لحقل التدفق طريقةً للنظر إلى حركة السوائل التي تركز على مواقع محددة في الفضاء الذي يتدفق من خلاله السائل مع مرور الوقت. يمكن تصور ذلك من خلال الجلوس على ضفة النهر ومشاهدة الماء يمر من الموقع الثابت. أي بعبارة أخرى، في حالة أويلريان يُقسم جزءٌ من الفضاء إلى خلايا وتحتوي كل خلية على متجه السرعة ومعلومات أخرى، مثل الكثافة ودرجة الحرارة. نحتاج في حالة لاغرانج إلى فيزياء تعتمد على الجسيمات مع تفاعلات ديناميكية وعمومًا نحتاج إلى عدد كبير من الجسيمات.
لكلتا الطريقتين مزايا وعيوب ويعتمد الاختيار بين الطريقتين على طبيعة مشكلتك، ويمكنك أيضًا مزج الطريقتين في طريقة هجينة. مع ذلك، فإن أكبر مشكلة في المحاكاة القائمة على الجسيمات هي أن تفاعل الجسيمات يتطلب إيجاد الجسيمات المجاورة وهذا له تكلفة كما رأينا في حالة أسراب الطيور Boids في المقال السابق. إذا استهدفنا بايثونو NumPy فقط، فمن الأفضل اختيار طريقة أويلريان لأن الاعتماد على المتجهات سيكون عديم الأهمية تقريبًا مقارنةً بطريقة لاغرانج.
كتابة الشيفرة باستخدام مكتبة NumPy
لن نشرح كل النظرية الكامنة وراء ديناميك السوائل الحسابية لوجود العديد من الموارد عبر الإنترنت التي تشرح هذا بطريقة جيدة. لماذا نختار حسابات السائل إذًا؟ لأن النتائج تكون غالبًا جيدة ورائعة. سنعمل على تبسيط المشكلة أكثر من خلال تنفيذ طريقة من رسوميات الحاسوب بحيث يكون الهدف هو السلوك المقنع.
سنعمل على تبسيط المشكلة أكثر من خلال تنفيذ طريقة من رسوميات الحاسوب، إذ لا يكون الهدف هو التصحيح ولكن السلوك المقنع. كتب جو ستام Jos Stam مقالًا لطيفًا جدًا لصالح SIGGRAPH عام 1999 يصف تقنية الحصول على سوائل مستقرة بمرور الوقت (أي لا يتباعد حلها على المدى الطويل). وكتب ألبيرتو سانتينيAlberto Santini تعليمات باستخدام لغة البرمجة بايثون (استخدم حينها numarray). الآن، علينا فقط تكييفها مع مكتبة NumPy الحديثة وتسريعها قليلًا باستخدام الحيل المعقدة. لن نشرح الشيفرات لأنها طويلة جدًا.
محاكاة الدخان باستخدام خوارزمية السوائل المستقرة بواسطة جو ستام. تأتي معظم مقاطع الفيديو الصحيحة من حزمة Glumpy وتستخدم GPU (عمليات الإطارات الاحتياطية، أي عدم وجود OpenCL أو CUDA) لإجراء عمليات حسابية أسرع.
أخذ عينات الضجيج الأزرق
يشير الضجيج الأزرق blue noise إلى مجموعات العينات التي لها توزيعات عشوائية وموحدة مع عدم وجود أي انحياز طيفي. هذا الضجيج مفيد جدًا في مجموعة متنوعة من تطبيقات الرسوم، مثل التصيير rendering والتردد dithering وما إلى ذلك، وقد اقترحت عدة طرق لتحقيق مثل هذا الضجيج، ولكن الطريقة الأكثر بساطة هي بالتأكيد طريقة دارت DART.
طريقة دارت DART
تُعد طريقة دارت DART واحدةً من أقدم وأبسط الطرق، وهي تعمل عن طريق الرسم المتسلسل لنقاط عشوائية موحدة وقبول فقط تلك التي تقع على مسافة لا تقل عن كل عينة مقبولة سابقة، ولذلك فهي طريقة بطيئة جدًا لأن كل مرشح جديد يحتاج إلى اختباره مقابل المرشحين المقبولين السابقين؛ وكلما زادت النقاط التي تقبلها كانت الطريقة أبطأ. لنفكر في وحدة السطح والحد الأدنى لنصف القطر r لفرضه في كل نقطة.
التعبئة الأكثر كثافة للدوائر في المستوى هي الشبكة السداسية لشكل خلية النحل، وتحسب الكثافة بالصيغة:
بالنظر إلى الدوائر ذات نصف القطر r، يمكننا أن نكتب:
نحن نعلم الحد الأعلى النظري لعدد الأقراص الممكن وضعها على السطح ولكن من المحتمل ألا نصل إلى هذا الحد الأقصى بسبب المواضع العشوائية. علاوةً على ذلك، نظرًا لرفض الكثير من النقاط بعد قبول القليل منها، سنحتاج إلى وضع حد لعدد المحاكمات الفاشلة المتتالية قبل أن نوقف العملية كاملةً.
import math import random def DART_sampling(width=1.0, height=1.0, r = 0.025, k=100): def distance(p0, p1): dx, dy = p0[0]-p1[0], p0[1]-p1[1] return math.hypot(dx, dy) points = [] i = 0 last_success = 0 while True: x = random.uniform(0, width) y = random.uniform(0, height) accept = True for p in points: if distance(p, (x, y)) < r: accept = False break if accept is True: points.append((x, y)) if i-last_success > k: break last_success = i i += 1 return points
تركنا لك تمرين إيجاد اتجاه توجيه لطريقة دارت DART. إذ تكمن الفكرة في إجراء حساب مسبق لعدد منتظم كافٍ من العينات العشوائية، إضافةً إلى المسافات المقترنة واختبار تضمينها التسلسلي.
طريقة بريدسون Bridson
إذا لم تسبب متجهات الطريقة السابقة أي صعوبة حقيقية، فإن تحسين السرعة ليس جيدًا وتظل الجودة منخفضة وتعتمد على المعامل k؛ فكلما كان هذا المعامل أعلى، كان ذلك أفضل لأنه يتحكم بصورةٍ أساسية في مدى صعوبة محاولة إدخال عينة جديدة، ولكن عندما يكون هناك عدد كبير فعلًا من العينات المقبولة، فإن فرصة واحد فقط ستسمح لنا بالعثور على موقع لإدخال عينة جديدة. يمكننا زيادة قيمة k ولكن هذا سيجعل الطريقة أبطأ دون أي ضمان في الجودة. حان الوقت للتفكير خارج الصندوق ولحسن الحظ، فعل روبرت بريدسون ذلك لنا واقترح طريقة بسيطة لكنها فعالة:
-
الخطوة 0: تهيئة شبكة خلفية ذات
nبُعد لتخزين العينات وتسريع البحث المكاني. نختار حجم الخلية المراد تقييدها من خلال
بحيث تحتوي كل خلية شبكية على عينة واحدة على الأكثر، وبالتالي يمكن تنفيذ الشبكة مثل مصفوفة بسيطة من الأعداد الصحيحة ذات البعد n: يشير الرقم الافتراضي "1-" إلى عدم وجود عينة، بينما يعطي العدد الصحيح غير السالب مؤشر العينة الموجود في الخلية.
-
الخطوة 1. حدد العينة الأولية x0، التي تُختار عشوائيًا من المجال، وأدخلها في شبكة الخلفية وهيّئ "القائمة النشطة" (مجموعة من مؤشرات العينة) باستخدام هذا المؤشر (صفر).
-
الخطوة 2: عندما لا تكون القائمة النشطة فارغة، اختر منها مؤشرًا عشوائيًا وليكن
i. عليك توليد ما يصل إلى "k" من النقاط المختارة بطريقة موحدة من الحلقة الكروية بين نصف القطر "r" و "2r" وحول xi. تحقق من أجل كل نقطة مما إذا كانت على مسافة "r" من العينات الموجودة (باستخدام شبكة الخلفية لاختبار العينات القريبة فقط). إذا كانت نقطة ما بعيدة بحد كافٍ عن العينات الموجودة فأرسلها على أنها عينة تالية وأضفها إلى القائمة النشطة. إذا لم يعثر على مثل هذه النقط بعد "k" محاولة، عليك إزالةiمن القائمة النشطة.
لا يطرح التنفيذ مشكلة حقيقية ويُترك بمثابة تمرين للقارئ. لاحظ أن هذه الطريقة ليست سريعة فحسب ولكنها تقدم أيضًا جودة أفضل (المزيد من العينات) من طريقة دارت DART ومع وجود عدد كبير من المحاولات.
الخلاصة
يعد المثال الأخير الذي كنا ندرسه هو مثال جيد، لأن متجهات المشكلة أكثر أهمية من متجهات الشيفرات، وقد كنا محظوظين في هذه الحالة المحددة بما يكفي لإنجاز العمل ولكن لن يكون الأمر كذلك دائمًا. نأمل أن تكون الآن مقتنعًا أنه من الجيد البحث عن حلول بديلة بمجرد العثور على حل. ستعمل دائمًا على تحسين السرعة من خلال متجهات الشيفرات والتعليمات البرمجية ولكن في هذه العملية فقد تفوتك تحسينات كبيرة.
ترجمة -وبتصرّف- للفصل Problem vectorization من كتاب From Python to Numpy لصاحبه Nicolas P. Rougier.






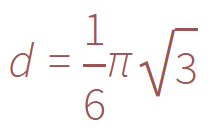
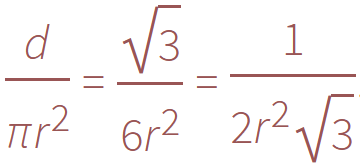
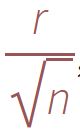











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.