ركَّزت هذه السلسلة على الأساليب الحسابية مثل المحاكاة وإعادة أخذ العينات، لكن قد يكون من الأسرع حل بعض المسائل بالاستعانة بالأساليب التحليلية، حيث سنتناول في هذا المقال بعضًا من هذه الطرق وسنشرح كيفية عملها، كما سنقدِّم اقتراحات في نهاية المقال لدمج الأساليب الحسابية والتحليلية لتحليل البيانات الاستكشافية.
توجد الشيفرة الخاصة بهذا المقال في الملف normal.py، في مستودع الشيفرات ThinkStats2 على GitHub.
التوزيع الطبيعي
دعنا نتحدث عن المسألة الموجودة في مقال التقدير Estimation الإحصائي في بايثون:
اقتباسلنفترض أنك عالم تهتم بدراسة الغوريلات في محمية للحياة البرية، وقد تجد عند وزن 9 إناث أنّ x̄=90 kg والانحراف المعياري للعينة هو S = 7.5 kg؛ فإذا استخدمت x̄ لتقدير متوسط جميع الأفراد، فما هو الخطأ المعياري للمقدار؟
يجب أن يكون توزيع أخذ عينات x̄ معروفًا إذا أردنا الإجابة على هذا السؤال، وكما رأينا في قسم توزيع أخذ العينات في مقال التقدير Estimation الإحصائي في بايثون المشار إليه بالأعلى، فإننا قرّبنا التوزيع عن طريق إجراء محاكاة للتجربة -أي تجربة وزن 9 إناث غوريلا- ثم حساب x̄ لكل تجربة محاكاة وتجميع توزيع التقديرات، وتكون النتيجة هنا هي تقريب لتوزيع أخذ العينات، ثم نستخدِم توزيع أخذ العينات لحساب الأخطاء المعيارية وفواصل الثقة:
- يُعَدّ الانحراف المعياري لتوزيع أخذ العينات هو الخطأ المعياري للتقدير، ويكون في هذا المثال حوالي 2.5 كيلوغرامًا.
- الفاصل بين المئين 5 والمئين 95 لتوزيع أخذ العينات هو فاصل ثقة 90% تقريبًا، وإذا أجرينا التجربة عدة مرات، فسنتوقع أن يكون التقدير في هذا الفاصل 90% من المرات، حيث تكون قيمة فاصل الثقة 90% في هذا المثال هي (94, 86) كيلوغرامًا.
سنجري الآن الحسابات ذاتها بأسلوب تحليلي، وسنستفيد من حقيقة أنّ أوزان إناث الغوريلا البالغات هي توزيع طبيعي تقريبًا، إذ تملك التوزيعات الطبيعية خاصتين اثنتين تجعلها قابلةً للتحليل، فهي مغلقة في التحويل الخطي والإضافة، لكنا نحتاج إلى بعض الرموز لشرح معنى هذا الكلام، فإذا كان توزيع كمية X طبيعيًا وكان يحوي وسيطَين هما µ وσ، فيمكننا القول:
| X ∼ N (µ, σ2) |
حيث يشير الرمز ∼ إلى أن الكمية موزعة ويشير الرمز N إلى طبيعي normal؛ أما التحويل الخطي لـ X فهو X′ = a X + b، حيث أنّ a وb هما عددان حقيقيان، وتكون عائلة من التوزيعات مغلقةً في التحويل الخطي إذا كانت X′ في عائلة X نفسها، ويكون للتوزيع الطبيعي هذه الخاصية إذا كان X ∼ N (µ, σ2).
| X′ ∼ N (a µ + b, a2 σ2) |
تُعَدّ التوزيعات الطبيعية مغلقةً في الإضافة، فإذا كانت Z = X + Y و X ∼ N (µX, σX2) وY ∼ N (µY, σY2) فيكون:
| Z ∼ N (µX + µY, σX2 + σY2) |
تكون المعادلة التالية محققة في الحالة الخاصة عندما Z = X + X
| Z ∼ N (n µX, n σX2) |
إذا سحبنا n قيمة من X وجمعناها يكون عمومًا:
| X ∼ N (µ, σ2) |
توزيعات أخذ العينات
لدينا كل ما نحتاجه لحساب توزيع أخذ عينات x̄، وتذكَّر أنه سنحسب x̄ عن طريق وزن n إناث غوريلا ونجمع القيم لنحسب الوزن الكلي ثم نقسم المجموع على n، فبفرض أنّ X توزيع أوزان الغوريلا هو توزيع طبيعي تقريبًا:
| X ∼ N (µ, σ2) |
يكون الوزن الكلي Y موزعًا إذا وزَنّا n غوريلا.
| Y ∼ N (n µ, n σ2) |
يكون Z متوسط العينة موزعًا إذا قسمنا على n وبالاستعانة بالمعادلة الثالثة.
Z ∼ N(, 2ln)
بالاستعانة بالمعادلة الأولى بافتراض a = 1/n.
يكون توزيع Z هو توزيع أخذ عينات x̄، ومتوسط Z هو µ الذي يظهر أن x̄ هو تقدير غير متحيز للمقدار µ، في حين يكون تباين توزيع أخذ العينات هو σ2/n، لذا فإن الانحراف المعياري لتوزيع أخذ العينات الذي يمثل الخطأ المعياري للتقدير هو σ / √n، ويكون σ في هذا المثال هو 7.5 كيلوغرامًا وn هو 9، لذا يكون الخطأ المعياري هو 2.5 كيلوغرامًا، ونلاحظ أنّ النتيجة متسقة مع التقدير الذي نتج عن المحاكاة لكن أسرع في الحساب.
يمكننا أيضًا استخدام توزيع أخذ العينات لحساب فواصل الثقة، حيث أنّ فاصل الثقة 90% لـ x̄ هو الفاصل بين المئين 9 والمئين 95 لـ Z، وبما أنّ توزيع Z توزيع طبيعي، فيمكننا حساب قيم المئين عن طريق تقييم دالة التوزيع التراكمي العكسية، كما لا يوجد شكل مغلق من دالة التوزيع التراكمي للتوزيع الطبيعي أو دالة التوزيع التراكمي العكسية، لكن توجد أساليب عددية سريعة وهي موجود على أساس تنفيذ برمجي في حزمة ساي باي SciPy كما رأينا في قسم التوزيع الطبيعي في مقال نمذجة التوزيعات Modelling distributions في بايثون، كما تزودنا مكتبة thinkstats2 بدالة مغلفة تجعل دالة ساي باي SciPy سهلة الاستخدام:
def EvalNormalCdfInverse(p, mu=0, sigma=1): return scipy.stats.norm.ppf(p, loc=mu, scale=sigma)
يعيد المئين الموافق من توزيع طبيعي له الوسيطين mu وsigma إذا كان لدينا احتمال p، كما حسبنا من أجل فاصل الثقة 90% للمقدار x̄ المئين 5 والمئين 95 كما يلي:
>>> thinkstats2.EvalNormalCdfInverse(0.05, mu=90, sigma=2.5) 85.888 >>> thinkstats2.EvalNormalCdfInverse(0.95, mu=90, sigma=2.5) 94.112
لذا إذا أجرينا التجربة عدة مرات، فسنتوقع أن يكون التقدير في المدى (94.1, 85.9) حوالي 90% من المرات، وهذا متسق مع النتائج التي حصلنا عليها عندما أجرينا محاكاة.
تمثيل التوزيعات الطبيعية
عرّفنا صنفًا يدعى Normal يمثِّل التوزيع الطبيعي ويرمز المعادلات الموجودة في الأقسام السابقة بهدف توضيح هذه الحسابات، أي كما يلي:
class Normal(object): def __init__(self, mu, sigma2): self.mu = mu self.sigma2 = sigma2 def __str__(self): return 'N(%g, %g)' % (self.mu, self.sigma2)
يمكننا استنساخ الصنف Normal لتمثيل توزيع أوزان الغوريلا:
>>> dist = Normal(90, 7.5**2) >>> dist N(90, 56.25)
يزودنا الصنف Normal بالدالة Sum التي تأخذ حجم العينة n وتعيد توزيع مجموع n قيمة باستخدام المعادلة الثالثة:
def Sum(self, n): return Normal(n * self.mu, n * self.sigma2)
يمكن تطبيق عمليات القسمة والضرب باستخدام المعادلة الأولى:
def __mul__(self, factor): return Normal(factor * self.mu, factor**2 * self.sigma2) def __div__(self, divisor): return 1 / divisor * self
يمكننا الآن حساب توزيع أخذ عينات المتوسط مع حجم عينة قدره 9:
>>> dist_xbar = dist.Sum(9) / 9 >>> dist_xbar.sigma 2.5
يكون الانحراف المعياري لتوزيع أخذ العينات هو 2.5 كيلوغرامًا كما رأينا في القسم السابق، وأخيرًا يزودنا الصنف Normal بالدالة Percentile التي تحسب فاصل الثقة كما يلي:
>>> dist_xbar.Percentile(5), dist_xbar.Percentile(95) 85.888 94.113
هذه هي الإجابة ذاتها التي حصلنا عليها سابقًا، حيث سنستخدم الصنف Normal مرةً أخرى لاحقًا، لكن علينا استكشاف بعض أساليب التحليل الأخرى أولًا قبل ذلك.
مبرهنة النهاية المركزية
رأينا في الأقسام السابقة أنه إذا جمعنا القيم المأخوذة من توزيع طبيعي، فسيكون توزيع المجموع طبيعيًا، ولكن لا تتميز معظم التوزيعات الأخرى بهذه الخاصية، أي إذا جمعنا القيم المأخوذة من توزيعات أخرى، فلن يكون المجموع توزيعًا تحليليًا عادةً، لكن إذا جمعنا n قيمة من معظم التوزيعات، فسيتقارب توزيع المجموع إلى التوزيع الطبيعي مع زيادة n.
وبتحديد أكبر، إذا كان لتوزيع القيم متوسطًا µ وانحرافًا معياريًا σ، فسيكون توزيع المجموع N(n µ, nσ 2) تقريبًا، وتكون هذه النتيجة هي مبرهنة النهاية المركزية -أو CLT اختصارًا-، إذ تُعَدّ من أفضل الأدوات للتحليل الإحصائي، لكن مع بعض التحذيرات وهي:
- يجب أخذ القيم بصورة مستقلة، إذ لا يمكن تطبيق مبرهنة النهاية المركزية إذا كانت القيم مترابطة على الرغم من أنه نادرًا ما يمثِّل مشكلةً أثناء التطبيق العملي.
- يجب انتماء القيم إلى التوزيع نفسه على الرغم أنه يمكن التغاضي عن هذا الشرط إلى حد ما.
- يجب أخذ القيم من توزيع له متوسط وتباين محدودَين، لذا لا تنطبق معظم توزيعات باريتو Pareto على هذا الشرط.
-
يعتمد معدل التقارب على تجانف التوزيع، إذ تتلاقى المجاميع من التوزيع الأسي إذا كانت
nصغيرةً، في حين تتطلب مجاميع القيم المأخوذة من التوزيع اللوغاريتمي الطبيعي أحجامًا أكبر.
تشرح مبرهنة النهاية المركزية انتشار التوزيعات الطبيعية في العالم الطبيعي، وتتأثر العديد من خصائص الكائنات الحية بالعوامل الوراثية والبيئية التي يكون تأثيرها مضافًا، كما تكون الخصائص التي نقيسها هي مجموع عدد كبير من التأثيرات الصغيرة، لذا يميل توزيعها إلى أن يكون طبيعيًا.
اختبار مبرهنة النهاية المركزية
سنجري بعض التجارب لنرى متى وكيف تنطبق مبرهنة النهاية المركزية، وسنجرب في البداية توزيعًا أسيًا:
def MakeExpoSamples(beta=2.0, iters=1000): samples = [] for n in [1, 10, 100]: sample = [np.sum(np.random.exponential(beta, n)) for _ in range(iters)] samples.append((n, sample)) return samples
تولِّد الدالة MakeExpoExamples عينات من مجاميع القيم الأسية، حيث استخدمنا مصطلح القيم الأسية على أساس اختصار لجملة القيم المأخوذة من توزيع أسي، ويكون beta هو وسيط التوزيع؛ أما iters هو عدد المجاميع التي يجب توليدها، ولتفسير هذه الدالة سنبدأ من الداخل أولًا، حيث نحصل على تسلسل من n قيمة أسية في كل استدعاء للدالة np.normal.exponential ونحسب مجموعها.
يُعَدّ sample قائمةً لهذه المجاميع وبطول iters، ومن الصعب التمييز بين n وiters، لكن n هو عدد التعبيرات في كل مجموع، وiters هو عدد المجاميع التي نحسبها لوصف توزيع المجاميع، حيث أنّ القيمة المعادة هي قائمة من أزواج (n, sample)، ثم ننشئ رسمًا احتماليًا طبيعيًا لكل زوج:
def NormalPlotSamples(samples, plot=1, ylabel=''): for n, sample in samples: thinkplot.SubPlot(plot) thinkstats2.NormalProbabilityPlot(sample) thinkplot.Config(title='n=%d' % n, ylabel=ylabel) plot += 1
تأخذ NormalPlotSamples قائمة الأزواج من MakeExpoSamples وتولِّد سطرًا من رسوم الاحتمالات الطبيعية.
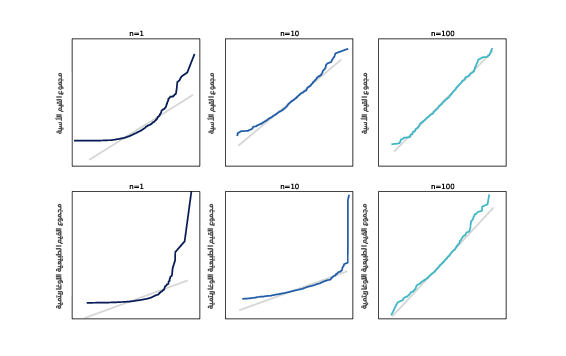
يوضِّح الشكل السابق توزيع مجاميع القيم الأسية في السطر العلوي والقيم اللوغاريتمية الطبيعية في السطر السفلي، كما يُظهر الشكل السابق الموجود في الأعلى النتائج، إذ يكون توزيع المجموع أسيًا من أجل n=1، لذا فإن رسم الاحتمال الطبيعي ليس مستقيمًا، لكن إذا كان n=10، فيكون توزيع المجموع طبيعيًا تقريبًا، وإذا كان n=100، فلا يمكن تمييز التوزيع عندها عن الطبيعي.
يُظهر الشكل السابق في السطر السفلي نتائجًا مشابهةً للتوزيع اللوغاريتمي الطبيعي، إذ عادةً ما تكون التوزيعات اللوغاريتمية الطبيعية أكثر تجانفًا من التوزيعات الأسية، لذا يأخذ توزيع المجاميع وقتًا أطول لكي يتقارب، وإذا كان n=10، يكون الرسم الاحتمالي الطبيعي أبعد ما يكون عن المستقيم، لكن إذا كان n=100 فيكون التوزيع طبيعيًا تقربيًا.
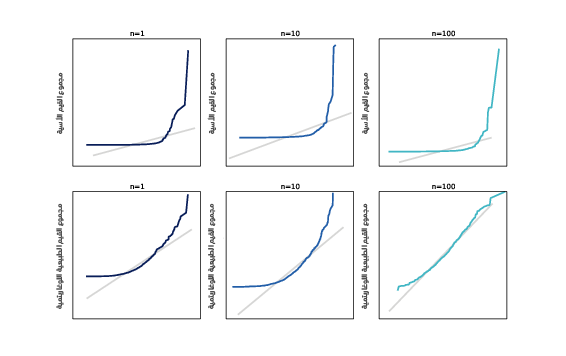
يُظهر الشكل السابق توزيعات مجاميع قيم باريتو Pareto في السطر العلوي والقيم الأسية المترابطة في السطر السفلي، حيث تُعَدّ توزيعات باريتو Pareto أكثر تجانفًا من التوزيعات اللوغاريتمية الطبيعية، وغالبًا لا يكون للعديد من توزيعات باريتو Pareto متوسطًا وتباينًا محدودَين اعتمادًا على المعامِلات، وبالتالي لا تنطبق مبرهنة النهاية المركزية على توزيع باريتو Pareto، كما يُظهر الشكل السابق في السطر العلوي توزيعات مجاميع قيم باريتو Pareto، فحتى إذا كان n=100، فسيكون الرسم الاحتمالي الطبيعي أبعد ما يكون عن المستقيم.
ذكرنا أيضًا أنه لا يمكن تطبيق مبرهنة النهاية المركزية إذا كانت القيم مترابطةً، ولاختبار ذلك سنولِّد قيمًا مترابطةً من التوزيع الأسي، علمًا أنّ خطوات الخوارزمية لتوليد القيم المترابطة هي:
- توليد القيم العادية المترابطة.
- استخدام دالة التوزيع التراكمي الطبيعي لجعل القيم موحدةً. 3.استخدام دالة التوزيع التراكمي العكسية الأسية لتحويل القيم الموحَّدة إلى أسية.
تعيد الدالة GenerateCorrelated مكررًا لـ n قيمة طبيعية من الارتباط التسلسلي rho :
def GenerateCorrelated(rho, n): x = random.gauss(0, 1) yield x sigma = math.sqrt(1 - rho**2) for _ in range(n-1): x = random.gauss(x*rho, sigma) yield x
تكون القيمة الأولى قيمةً طبيعيةً معياريةً، وتعتمد كل قيمة لاحقة على سابقتها، أي إذا كانت القيمة السابقة هي x، فيكون متوسط القيمة التالية هوx * rho ويكون التباين هو 1-rho**2، علمًا أنّ random.gauss تأخذ الانحراف المعياري على أساس وسيط ثان وليس التباين، كما تأخذ الدالة GenerateExpoCorrelated التسلسل الناتج وتجعله أسيًا:
def GenerateExpoCorrelated(rho, n): normal = list(GenerateCorrelated(rho, n)) uniform = scipy.stats.norm.cdf(normal) expo = scipy.stats.expon.ppf(uniform) return expo
حيث يكون normal قائمةً من القيم الطبيعية المترابطة، وuniform تسلسلًا من القيم الموحَّدة التي تقع بين 0 و1، وexpo تسلسلًا مترابطًا من القيم الأسية، في حين ترمز ppf إلى دالة نقطة النسبة المئوية percent point function التي هي اسم آخر لدالة التوزيع التراكمي المعكوسة.
يُظهر الشكل السابق في السطر السفلي توزيعات مجاميع القيم الأسية المترابطة إذا كان rho=0.9، ويبطئ الترابط من معدل التقارب، لكن إذا كان n=100، فيكون الرسم الاحتمالي الطبيعي مستقيمًا تقريبًا، لذا على الرغم من أنّ مبرهنة النهاية المركزية لا تطبق تمامًا عندما تكون القيم مترابطة، إلا أنه نادرًا ما تشكِّل الترابطات المتوسطة مشكلةً أثناء التطبيق العملي، كما تهدف هذه التجارب إلى إظهار الطريقة التي تعمل بها مبرهنة النهاية المركزية بالإضافة إلى إظهار ماذا يحدث عندما لا تعمل، ودعونا الآن نرى كيف يمكننا استخدامها.
تطبيق مبرهنة النهاية المركزية
علينا العودة إلى المثال الموجود في قسم اختبار الفرق في المتوسطات في مقال اختبار الفرضيات الإحصائية، وهو اختيار الفرق الواضح في متوسط مدة الحمل للأطفال الأوائل والأطفال الآخرين، وكما رأينا فإن الفرق الواضح هو حوالي 0.078 أسبوع:
>>> live, firsts, others = first.MakeFrames() >>> delta = firsts.prglngth.mean() - others.prglngth.mean() 0.078
تذكَّر منطق اختبار الفرضيات: نحسب القيمة الاحتمالية p-value وهي احتمال الفرق المرصود في ظل فرضية العدم، فإذا كان الاحتمال صغيرًا، فنستنتج أنه من غير المرجح أن يكون الفرق المرصود ناجمًا عن الصدفة فحسب، وتكون فرضية العدم في هذا المثال هي أنّ توزيع مدة الحمل هي نفسها للأطفال الأوائل ولبقية الأطفال، لذا يمكننا حساب توزيع أخذ عينات المتوسط كما يلي:
dist1 = SamplingDistMean(live.prglngth, len(firsts)) dist2 = SamplingDistMean(live.prglngth, len(others))
علمًا أنّ توزيعي أخذ العينات مبنيان على البيانات نفسها وهي مجموعة الولادات الحية كلها، حيث تأخذ SamplingDistMeans تسلسلًا من القيم وحجم العينة، وتعيد كائنًا طبيعيًا يمثِّل توزيع أخذ العينات:
def SamplingDistMean(data, n): mean, var = data.mean(), data.var() dist = Normal(mean, var) return dist.Sum(n) / n
يمثِّل mean متوسط البيانات؛ أما var فهو التباين، وسننشئ تقريبًا لتوزيع البيانات بالاستعانة بتوزيع طبيعي dist، إذ يُعَدّ توزيع البيانات في هذا المثال لاطبيعيًا، لذا فإنّ هذا التقريب غير جيد، لكن علينا الآن حساب dis.Sum(n)/n وهو توزيع أخذ عينات متوسط n قيمة، ويكون حسب مبرهنة النهاية المركزية أنّ توزيع أخذ عينات المتوسط هو توزيع طبيعي حتى لو لم يكن توزيع البيانات طبيعيًا، ثم نحسب توزيع أخذ عينات الفرق في المتوسطات، حيث يعلم الصنف Normal كيفية تطبيق الطرح باستخدام المعادلة الثانية:
def __sub__(self, other): return Normal(self.mu - other.mu, self.sigma2 + other.sigma2)
لذا يمكننا حساب توزيع أخذ عينات الفرق كما يلي:
>>> dist = dist1 - dist2 N(0, 0.0032)
يكون المتوسط هو 0، وهذا منطقي لأننا نتوقع أن يكون للعينتين من التوزيع نفسه المتوسط نفسه وسطيًا، ويكون تباين توزيع أخذ العينات هو 0.0032، كما يزودنا الصنف Normal بالدالة Prob التي تقيّم دالة التوزيع التراكمي الطبيعية، ويمكننا استخدام Prob لحساب احتمالية وجود فرق بحجم delta في ظل فرضية العدم:
>>> 1 - dist.Prob(delta) 0.084
يعني هذا أنّ القيمة الاحتمالية للاختبار أحادي الجانب هو 0.84؛ أما بالنسبة للاختبار ثنائي الجانب فسنحسب كما يلي:
>>> dist.Prob(-delta) 0.084
ظهر لدينا النتيجة نفسها لأن التوزيع الطبيعي متناظر، ويكون مجموع الذيول هو 0.168، وهو متسق مع التقدير في قسم اختبار الفرق في المتوسطات في مقال اختبار الفرضيات الإحصائية الذي كانت قيمته 0.17.
اختبار الارتباط
استخدمنا في قسم اختبار الارتباط في مقال اختبار الفرضيات الإحصائية من هذه السلسلة والمشار إليه بالأعلى، اختبار التبديل permutation test لاختبار الارتباط بين وزن الطفل عند الولادة وعمر الأم، ووجدنا أنه ذو دلالة إحصائية والقيمة الاحتمالية هي أقل من 0.001، حيث يمكننا فعل الشيء ذاته لكن بأسلوب تحليلي مبني على نتيجة رياضية: إذا كان لدينا متغيرين موزعَين طبيعيًا وغير مترابطَين، فإذا ولدنا عينةً حجمها n وحسبنا ارتباط بيرسون r ثم حسبنا الارتباط بعد التحويل، يكون:
| t = r |
|
|
يُعَدّ توزيع t هو توزيع ستيودنت الاحتمالي Student’s t-distribution مع معامِل n-2، حيث يُعَدّ التوزيع t توزيعًا تحليليًا، ويمكن حساب دالة التوزيع التراكمي بفعالية باستخدام دوال غاما gamma، حيث يمكننا استخدام النتيجة لحساب توزيع أخذ عينات الارتباط في ظل فرضية العدم، أي إذا ولَّدنا التسلسلات غير المترابطة للقيم الطبيعية، فما هو توزيع الارتباط؟ تأخذ الدالة StudentCdf حجم العينة n ويُعيد توزيع أخذ عينات الارتباط:
def StudentCdf(n): ts = np.linspace(-3, 3, 101) ps = scipy.stats.t.cdf(ts, df=n-2) rs = ts / np.sqrt(n - 2 + ts**2) return thinkstats2.Cdf(rs, ps
حيث أنّ ts هي مصفوفة نمباي NumPy لتوزيع t وهو الارتباط بعد التحويل، كما تحتوي ps على الاحتمالات الموافقة المحسوبة باستخدام دالة التوزيع التراكمي لتوزيع ستيودنت الاحتمالي وهي منفَّذة برمجيًا في حزمة ساي باي SciPy، ويمثِّل معامِل توزيع t (أي t-distribution) الذي يدعى df درجات الحرية degrees of freedom، ولن نشرح هذا المصطلح لكن يمكنك القراءة عنه في صفحة الويكيبيديا.
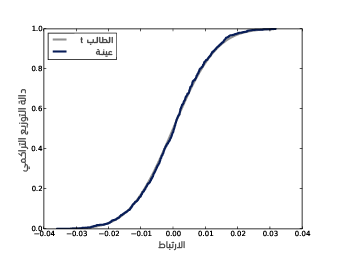
يوضِّح الشكل السابق توزيع أخذ عينات ارتباط القيم الطبيعية غير المرتبطة، ويتوجب علينا تطبيق التحويل العكسي إذا أردنا تحويل ts إلى معاملات الترابط rs:
| r = t / | √ |
|
تكون النتيجة هي توزيع أخذ عينات r في ظل فرضية العدم، كما يُظهر الشكل السابق هذا التوزيع إلى جانب التوزيع الذي ولَّدناه في قسم اختبار الارتباط في مقال اختبار الفرضيات الإحصائية، وذلك عن طريق تطبيق إعادة أخذ العينات، فالتوزيعان متطابقان تقريبًا، فعلى الرغم من أنّ التوزيعين الفعليين ليسا طبيعيين، إلا أنّ معامِل ارتباط بيرسون مبني على متوسطي وتبايني العينة، وبحسب مبرهنة النهاية المركزية فإنّ الإحصائيات المبنية على العزوم موزعة توزيعًا طبيعيًا حتى لو لم تكن البيانات كذلك.
نستنتج من الشكل السابق أنّ قيمة الارتباط المرصود هو 0.07، ومن غير المرجح أن تظهر لنا هذه القيمة إذا لم تكن المتغيرات مرتبطةً، كما يمكننا حساب مدى احتمال حدوث ذلك باستخدام التوزيع التحليلي:
t = r * math.sqrt((n-2) / (1-r**2)) p_value = 1 - scipy.stats.t.cdf(t, df=n-2)
نحسب قيمة t الموافقة لـ r=0.07 ثم نقيِّم توزيع t عند t، ونلاحظ أنّ النتيجة هي 2.9e-11، إذ يُظهر هذا المثال إحدى ميزات الأسلوب التحليلي، حيث يمكننا حساب قيم احتمالية صغيرة جدًا لكن لا يهمنا هذا الأمر في الحالات الواقعية عادةً.
اختبار مربع كاي
استخدمنا في قسم اختبارات مربع كاي الموجود في مقال اختبار الفرضيات الإحصائية إحصائيات مربع كاي لنختبر فيما إن كان حجر النرد ملتويًا، حيث تقيس إحصائية مربع كاي الانحراف الكلي الموحَّد عن القيم المتوقعة في جدول:
| χ2 = |
|
|
يُعَدّ توزيع أخذ العينات فيها تحليليًا في ظل فرضية العدم، وهو من أسباب شيوع استخدام إحصائية مربع كاي، وبصدفة رائعة فإنه يدعى توزيع مربع كاي، ويمكن حساب دالة التوزيع التراكمي لمربع كاي بكفاءة باستخدام دوال غاما تمامًا مثل توزيع t.
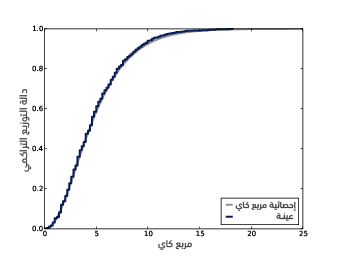
يوضِّح الشكل السابق توزيع أخذ عينات إحصائية مربع كاي للنرد العادل ذي الوجوه الستة، حيث تزودنا مكتبة ساي باي SciPy بتنفيذ برمجي لتوزيع مربع كاي الذي يمكننا استخدامه لحساب توزيع أخذ عينات إحصائية مربع كاي كما يلي:
def ChiSquaredCdf(n): xs = np.linspace(0, 25, 101) ps = scipy.stats.chi2.cdf(xs, df=n-1) return thinkstats2.Cdf(xs, ps)
يُظهر الشكل السابق النتيجة التحليلية إلى جانب التوزيع الذي حصلنا عليه عن طريق تطبيق إعادة أخذ العينات، وهما متماثلان جدًا خاصةً من حيث شكل الذيل وهو الجزء الذي يهمنا، كما يمكننا استخدام هذا التوزيع لحساب القيمة الاحتمالية لإحصائية الاختبار chi2:
p_value = 1 - scipy.stats.chi2.cdf(chi2, df=n-1)
نرى أن النتيجة هي 0.041 وهي متسقة مع النتيجة التي رأيناها في قسم اختبارات مربع كاي الموجود في مقال اختبار الفرضيات الإحصائية، حيث أن معامِل توزيع مربع كاي هو درجة الحرية أيضًا، ويكون المعامِل الصحيح في هذه الحالة هو n-1 حيث أنّ n هو حجم الجدول 6، وقد يكون اختيار هذا المعامِل أمرًا صعبًا، وفي الواقع لا نستطيع التأكد من أننا أصبنا حتى نولِّد شكلًا مثل الشكل السابق لنقارن النتائج التحليلية مع نتائج إعادة أخذ العينات.
نقاش
تركِّز هذه السلسلة على الأساليب الحسابية مثل إعادة أخذ العينات والتبديل، وتملك هذه الأساليب ميزات لا تمتلكها الأساليب التحليلية مثل:
- سهلة الفهم والشرح، إذ يُعَدّ اختبار الفرضيات على سبيل المثال من أصعب المواضيع في مجال لإحصاء، ولا يستطيع العديد من الطلاب فهم ماهية القيم الاحتمالية، لكن الطريقة التي شرحناها في مقال اختبار الفرضيات الإحصائية جعلت المفهوم أوضح والتي هي حساب إحصائية الاختبار ومحاكاة فرضية العدم.
- متينة ومتعددة الاستعمالات، إذ غالبًا ما تكون الأساليب التحليلية مبنيةً على افتراضات لا تنطبق على الواقع؛ أما الأساليب الحسابية فهي تتطلب افتراضات أقل ويمكن تعديلها وتوسيعها بصورة أسهل.
- يمكن تصحيحها، لكن غالبًا ما تكون الأساليب التحليلية أشبه بالصندوق الأسود، حيث تدخل الأعداد وتخرج الأساليب النتائج، لذا من السهل ارتكاب أخطاء خفية ومن الصعب التأكد من صحة النتائج ومن الصعب إيجاد المشكلة إذا كانت خاطئة؛ أما الأساليب الحسابية فهي قابلة للتطوير والاختبار التدريجي مما يعزِّز الثقة في النتائج.
لكن هناك سلبية واحدة وهي أنّ الأساليب الحسابية بطيئة، لكن إذا أخذنا السلبيات والإيجابيات بالحسبان، فنعتقد أنّ العملية التالية هي الأفضل:
- استخدم الأساليب الحسابية أثناء الاستكشاف، وإذا وجدت إجابةً مرضيةً وزمنًا مقبولًا للتنفيذ، يمكنك التوقف.
- إذا لم يكن زمن التنفيذ مقبولًا، فابحث عن حلول للتحسين.
- إذا كان استخدام الأسلوب التحليلي أنسب من الأسلوب الحسابي، فاستخدم الأسلوب الحسابي ليكون أساسًا للمقارنة، إذ سيوفِّر لك هذا الأمر إمكانية التحقق المتبادل في النتائج الحسابية والتحليلية.
لم تتطلب معظم المسائل التي عملت عليها تجاوز الخطوة الأولى من العملية السابقة.
تمارين
يوجد حل هذه التمارين في الملف chap14soln.py في مستودع الشيفرات ThinkStats2 على GitHub..
تمرين 1
رأينا في قسم التوزيع اللوغاريتمي الطبيعي الموجود في مقال نمذجة التوزيعات Modelling distributions في بايثون، أنّ توزيع أوزان البالغين لوغاريتمي طبيعي تقريبًا، وتتمثَّل إحدى التفسيرات في أنّ الوزن الذي يكتسبه الشخص في كل عام يتناسب مع وزنه الحالي، ويكون وزن البالغين في هذه الحالة ناتجًا عن عدد كبير من العوامل التي نطبق بينها عملية جداء:
| w = w0 f1 f2 … fn |
حيث أنّ w هو وزن البالغ، وw<sub>0</sub> هو وزن الطفل عند الولادة، وf<sub>i</sub> هو عامل الوزن المكتسب في العام i، علمًا أنّ لوغاريتم الجداء هو جمع لوغاريتمات العوامل:
| logw = logw0 + logf1 + logf2 + ⋯ + logfn |
يكون توزيع logw حسب مبرهنة النهاية المركزية طبيعيًا تقريبًا إذا كانت n كبيرةً، مما يعني أنّ توزيع w لوغاريتمي طبيعي، ويمكنك من أجل نمذجة هذه الظاهرة اختيار توزيع منطقي لـ f ثم توليد عينة من أوزان البالغين عن طريق اختيار قيمة عشوائية من توزيع أوزان المواليد ثم اختيار تسلسل عوامل من توزيع f وحساب الجداء؛ ما هي قيمة n التي نحتاجها للتقارب من توزيع لوغاريتمي طبيعي؟
تمرين 2
استخدمنا في هذا المقال مبرهنة النهاية المركزية لإيجاد توزيع أخذ عينات الفرق في المتوسطات δ في ظل فرضية العدم التي تقول أنّ العينتين مأخوذتان من البيانات نفسها، يمكننا أيضًا استخدام هذا التوزيع لإيجاد الخطأ المعياري للتقدير ولفواصل الثقة لكن لن تكون النتيجة صحيحة تمامًا، وبصورة أدق، يجب حساب توزيع أخذ العينات الخاص بـ δ بموجب الفرضية البديلة التي مفادها أنّ العينات مأخوذة من مجموعات مختلفة.
أوجد هذا التوزيع واستخدمه لحساب الخطأ المعياري وفاصل الثقة 90% للفرق في المتوسطات.
تمرين 3
بحث القائمون على ورقة بحثية حديثة في تأثيرات التدخل الهادف إلى تخفيف النمطية بين الجنسَين فيما يخص توزيع المهام داخل المجموعات في الكليات الهندسية، حيث أجاب الطلاب والطالبات على استطلاع قبل وبعد التدخل، وكان مفاد الاستطلاع الطلب من المشاركين تقييم مساهمتهم في كل جانب من جوانب المشاريع الصفيّة على مقياس مكوَّن من 7 نقاط.
سجّل الطلاب الذكور قبل التدخل درجات أعلى فيما يخص البرمجة في المشروع مقارنةً بالطالبات، وسجّل الرجال في المتوسط درجة 3.57 مع خطأ معياري قدره 0.28، بينما سجّلت النساء في المتوسط 1.91 مع خطأ معياري قدره 0.32.
احسب توزيع أخذ العينات للفجوة بين الجنسين -أي الفرق في المتوسطات-، واختبر ما إذا كان التوزيع ذا دلالة إحصائية، ولا تحتاج إلى معرفة حجم العينة لتحسب توزيعات أخذ العينات لأنك تعلم الأخطاء المعيارية للمتوسطات المقدَّرة.
أصبحت الفجوة بعد التدخل أصغر، حيث أصبح المتوسط الحسابي للرجال هو 3.44 وبخطأ معياري قدره 0.16؛ أما المتوسط الحسابي للنساء فهو 3.18 وبخطأ معياري قدره 0.16؛ احسب توزيع العينات للفجوة بين الجنسين مرةً أخرى واختبرها.
اختبر أخيرًا التغيير في الفجوة بين الجنسين، وما هو توزيع أخذ عينات هذا التغيير؟ وهل له دلالة إحصائية؟
ترجمة -وبتصرف- للفصل Chapter 14 Analytics methods analysis من كتاب Think Stats: Exploratory Data Analysis in Python.












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.