يُقصد باستخدام المتجهات vectorization في الشيفرة أن المشكلة التي تحاول حلها قابلةٌ للتحليل بطبيعتها ولا تتطلب سوى استخدام بعض الحيل لجعلها أسرع، وهذا لا يعني أن الأمر سهل أو مباشر، ولكنه على الأقل لا يستلزم إعادة التفكير في كامل مشكلتك. يتطلب الأمر بعض الخبرة لمعرفة أين يمكن استخدام المتجهات في الشيفرة. سنوضح ذلك من خلال مثال بسيط، إذ نريد تلخيص قائمتين من الأعداد الصحيحة.
سنستخدم الدالة البسيطة التالية:
def add_python(Z1,Z2): return [z1+z2 for (z1,z2) in zip(Z1,Z2)]
إعادة كتابة الشيفرة السابقة عبر المتجهات من مكتبة NumPy بسهولة كبيرة بالشكل التالي:
def add_numpy(Z1,Z2): return np.add(Z1,Z2)
وكما هو متوقع تظهر المقارنة أن الطريقة الثانية هي الأسرع:
>>> Z1 = random.sample(range(1000), 100) >>> Z2 = random.sample(range(1000), 100) >>> timeit("add_python(Z1, Z2)", globals()) 1000 loops, best of 3: 68 usec per loop >>> timeit("add_numpy(Z1, Z2)", globals()) 10000 loops, best of 3: 1.14 usec per loop
كما أنها تتكيف أيضًا مع شكل Z1 و Z2، وهذا هو سبب عدم كتابة Z1 + Z2 لأن هذه الطريقة لن تعمل إذا كان كل من Z1 و Z2 قائمتين. تُفسّر عملية الجمع الداخلية في الطريقة الأولى المعتمدة على تابع لغة بايثون بطريقة مختلفة اعتمادًا على طبيعة الكائنين؛ وإذا أخذنا في الحسبان قائمتين متداخلتين، نحصل على المخرجات التالية:
>>> Z1 = [[1, 2], [3, 4]] >>> Z2 = [[5, 6], [7, 8]] >>> Z1 + Z2 [[1, 2], [3, 4], [5, 6], [7, 8]] >>> add_python(Z1, Z2) [[1, 2, 5, 6], [3, 4, 7, 8]] >>> add_numpy(Z1, Z2) [[ 6 8] [10 12]]
تربط الطريقة الأولى القائمتين معًا، بينما تربط الطريقة الثانية القوائم الداخلية معًا، وتحسب الطريقة الأخيرة ما هو متوقع. يمكنك إعادة كتابة تعليمات بايثون بحيث تضم قوائم متداخلة مختلفة الحجم.
المتجه الموحد Uniform vectorization
يُعد المتجه الموحد أبسط شكل من أشكال المتجهات، إذ تشترك جميع العناصر في نفس العملية الحسابية في كل خطوة زمنية مع عدم وجود معالجة محددة لأي عنصر. لعبة الحياة هي إحدى الحالات النمطية التي اخترعها جون كونواي John Conway وهي إحدى أقدم الأمثلة على المشغلات الآلية الخلوية cellular automata، التي تمثّل مجموعةً من الخلايا التي ترتبط معًا بمفهوم الجيران وتكون متجّهاتها بسيطة.
اقتباستُعرف المشغلات الآلية الخلوية بالإنكليزية باسم "cellular automata"، تدل على مصفوفة من الخلايا يمكن أن تأخذ عددًا منته من الحالات حيث كل حالة مستقبلية للخلية تتعلق بحالتها الحاضرة وبحالة الخلايا المجاورة لها. إن التحول من حالة إلى أخرى يحكم بقواعد معرفة مسبقًا.
سنحدّد بدايةً قواعد اللعبة ثم سندرس كيفية جعلها معتمدة على المتجهات:
يظهر نسيج صدفة الحلزون نمط مشغل آلي خلوي على غلافها الخارجي. الصورة لريتشارد لينج 2005.
لعبة الحياة
يمكنك الحصول على فكرة حول لعبة الحياة في موقع ويكيبيديا؛ وهي لعبة معتمدة على المشغلات الآلية الخلوية، وابتكرها عالم الرياضيات البريطاني جون هورتون كونواي John Horton Conway في عام 1970. اللعبة هي لعبة بدون لاعب، مما يعني أن تطورها يُحدّد من خلال حالتها الأولية، ولا تحتاج اللعبة إلى مدخلات من اللاعبين، ويتفاعل المراقب مع لعبة الحياة من خلال إنشاء تكوين أولي ومراقبة كيفية تطور اللعبة.
عالم لعبة الحياة هي شبكة متعامدة ثنائية الأبعاد لا نهائية من الخلايا المربعة، لكل منها حالتين محتملتين (حياة أو موت)، وترتبط حالة كل خلية بجاراتها الثمانية، وهي الخلايا المتجاورة أفقيًا، أو رأسيًا، أو قطريًا، وتحدث في كل خطوة في الوقت المناسب التحولات التالية:
- تموت أي خلية حية لها أقل من اثنين من الجيران الأحياء (كما لو كانت بسبب الاحتياجات الناجمة عن نقص السكان).
- تموت أي خلية لها أكثر من ثلاثة جيران أحياء (كما لو كان السبب هو الاكتظاظ).
- تعيش أي خلية حية لها اثنان أو ثلاثة من الجيران الأحياء للجيل القادم.
- تصبح أي خلية ميتة مع ثلاثة جيران أحياء بالضبط خليةً حية.
يشكل النمط الأولي "أصل seed" النظام. يُنشأ الجيل الأول من خلال القواعد السابقة في وقت واحد على كل خلية (تحدث الولادات والوفيات في وقت واحد)، أي كل جيل هو نتيجة خالصة للجيل السابق، ويستمر تطبيق القواعد بطريقة مستمرة لخلق أجيال أخرى.
كتابة شيفرة بلغة بايثون
يمكننا كتابة شيفرة لعبة Game of Life في لغة بايثون باستخدام قائمة list تمثّل اللوحة، إذ من المفترض أن تتطور الخلايا. تُجهز هذه اللوحة بحدود صفرية "0" مما يسمح بتسريع الأمور قليلًا عن طريق تجنب إجراء اختبارات محددة للحدود عند حساب الجيران.
Z = [[0,0,0,0,0,0], [0,0,0,1,0,0], [0,1,0,1,0,0], [0,0,1,1,0,0], [0,0,0,0,0,0], [0,0,0,0,0,0]]
يكون عدد الجيران واضحًا عند أخذ الحدود بالحسبان:
def compute_neighbours(Z): shape = len(Z), len(Z[0]) N = [[0,]*(shape[0]) for i in range(shape[1])] for x in range(1,shape[0]-1): for y in range(1,shape[1]-1): N[x][y] = Z[x-1][y-1]+Z[x][y-1]+Z[x+1][y-1] \ + Z[x-1][y] +Z[x+1][y] \ + Z[x-1][y+1]+Z[x][y+1]+Z[x+1][y+1] return N
نكرر الخطوة في الوقت المناسب، ولذلك نحسب عدد الجيران لكل خلية داخلية ثم نحدث كامل اللوحة وفقًا للقواعد الأربعة المذكورة أعلاه:
def iterate(Z): N = compute_neighbours(Z) for x in range(1,shape[0]-1): for y in range(1,shape[1]-1): if Z[x][y] == 1 and (N[x][y] < 2 or N[x][y] > 3): Z[x][y] = 0 elif Z[x][y] == 0 and N[x][y] == 3: Z[x][y] = 1 return Z
يوضح الشكل أدناه أربعة تكرارات على منطقة 4×4، إذ أن الحالة الأولية هي طائرة شراعية glider، وهي بنية اكتُشفت عام 1970.
من المعروف أن نمط الطائرة الشراعية يكرر نفسه خطوةً واحدةً قطريًا خلال أربعة تكرارات.
كتابة شيفرة Numpy
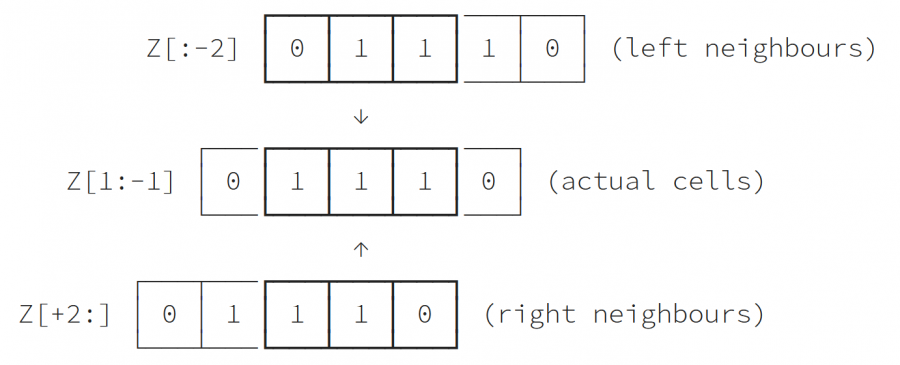
بناءً على التعليمات السابقة المكتوبة بلغة بايثون، نلاحظ أن شيفرة لعبة الحياة ينقسم إلى قسمين، أحدهما مسؤول عن حساب عدد الجيران والآخر مسؤول عن تطبيق القواعد. يُعد حساب عدد الجيران أمرًا سهلًا نسبيًا، لأننا حرصنا على إضافة حد فارغ حول النطاق arena. ومن خلال النظر في العروض الجزئية للنطاق يمكننا الوصول إلى الجيران بطريقة حدسية كما توضح هذه الحالة أحادية البعد:
يتطلب الانتقال إلى الحالة ثنائية البعد حسابات إضافية للتأكد من مراعاة جميع الجيران الثمانية.
N = np.zeros(Z.shape, dtype=int) N[1:-1,1:-1] += (Z[ :-2, :-2] + Z[ :-2,1:-1] + Z[ :-2,2:] + Z[1:-1, :-2] + Z[1:-1,2:] + Z[2: , :-2] + Z[2: ,1:-1] + Z[2: ,2:])
يمكننا لتطبيق القاعدة كتابة التعليمات البرمجية باستخدام تابع argwhere الذي سينتج عنه رقم المؤشر عندما يكون الشرط المحدد صحيحًا:
# المصفوفات المسطحة N_ = N.ravel() Z_ = Z.ravel() # تطبيق القواعد R1 = np.argwhere( (Z_==1) & (N_ < 2) ) R2 = np.argwhere( (Z_==1) & (N_ > 3) ) R3 = np.argwhere( (Z_==1) & ((N_==2) | (N_==3)) ) R4 = np.argwhere( (Z_==0) & (N_==3) ) # ضبط قيم جديدة Z_[R1] = 0 Z_[R2] = 0 Z_[R3] = Z_[R3] Z_[R4] = 1 # كن متأكدًا من بقاء الحدود فارغة Z[0,:] = Z[-1,:] = Z[:,0] = Z[:,-1] = 0
رغم عدم استخدام الإصدار الأول للحلقات المتداخلة لكنه يبقى بعيدًا على أن يكون أمثليًا بسبب استخدام استدعاءات argwhere التي قد تكون بطيئة جدًا، ويمكننا بدلًا من ذلك تحليل القواعد إلى الخلايا التي ستبقى على قيد الحياة (أي التي ستبقى عند قيمة 1) والخلايا التي ستلد وذلك بالاستفادة من القدرة المنطقية لمكتبة Numpy:
اقتباسلم نكتب
Z = 0لأن هذا سيعين ببساطة القيمة "0" إلىZالتي ستصبح بعد ذلك قيمةً مفردة.
birth = (N==3)[1:-1,1:-1] & (Z[1:-1,1:-1]==0) survive = ((N==2) | (N==3))[1:-1,1:-1] & (Z[1:-1,1:-1]==1) Z[...] = 0 Z[1:-1,1:-1][birth | survive] = 1
إذا دققت في أول سطرين ستلاحظ أن المتغيرين birth و survive مصفوفتان يمكن استخدامهما لتعيين قسم المصفوفة Z إلى القيمة "1" بعد محوها.
تمرين
يمكن أن ينتج عن تفاعل الأصناف الكيميائية وانتشارها مجموعةً متنوعةً من الأنماط، تذكرنا غالبًا بتلك التي نراها في الطبيعة، ومن أمثلة هذا التفاعل نموذج معادلات جراي سكوت Gray-Scott، ولمزيد من المعلومات حول هذا النظام الكيميائي راجع مقالة الأنماط المعقدة في نظام بسيط.
لنفكر في نوعين كيميائيين U و V، ولكل منهما تركيز u و v ومعدل انتشاء Du و Dv. يُحوّل V إلى P بمعدل تحويل k. يمثل f معدل العملية التي تشبع U وتجعل كل من U و V و P يتلاشى. ويمكن كتابة ذلك على النحو التالي:
استنادًا إلى مثال لعبة الحياة سنجرب تنفيذ نظام نشر التفاعل. فيما يلي مجموعة من المعاملات التي سنحتاج إلى اختبارها:
| الاسم | Du | Dv | f | k |
|---|---|---|---|---|
| Bacteria 1 | 0.16 | 0.08 | 0.035 | 0.065 |
| Bacteria 2 | 0.14 | 0.06 | 0.035 | 0.065 |
| Coral | 0.16 | 0.08 | 0.060 | 0.062 |
| Fingerprint | 0.19 | 0.05 | 0.060 | 0.062 |
| Spirals | 0.10 | 0.10 | 0.018 | 0.050 |
| Spirals Dense | 0.12 | 0.08 | 0.020 | 0.050 |
| Spirals Fast | 0.10 | 0.16 | 0.020 | 0.050 |
| Unstable | 0.16 | 0.08 | 0.020 | 0.055 |
| Worms 1 | 0.16 | 0.08 | 0.050 | 0.065 |
| Worms 2 | 0.16 | 0.08 | 0.054 | 0.063 |
| Zebrafish | 0.16 | 0.08 | 0.035 | 0.060 |
والنتائج هي كالآتي:
والآتي:
إضافةً إلى ما يلي:
المتجهات الزمنية Temporal vectorization
مجموعة Mandelbrot هي مجموعةٌ من الأعداد العقدية c التي لا تتباعد diverge فيها الدالة "fc(z) = z2 + c" عند تكرارها بدءًا من z = 0، أي من أجل التسلسل "… ,((fc(0), fc(fc(0" وتظل محدودة بالقيمة المطلقة. من السهل حسابها ولكنها قد تستغرق وقتًا طويلَا جدًا لأنك تحتاج إلى التأكد من أن رقمًا معينًا لا يتباعد، ويُنفّذ ذلك من خلال تكرار الحساب حتى أقصى عدد من التكرارات، وبعد ذلك إذا كان الرقم لا يزال ضمن الحدود يكون غير متباعد، وبالتأكيد كلما زاد عدد مرات التكرار زادت الدقة التي تحصل عليها.
بروكلي رومانسكو، يُظهر شكلًا قريبًا من كسورية fractal طبيعية. صورة جون سوليفان، 2004.
كتابة شيفرة بايثون
تكتب التعليمات البرمجية على النحو التالي:
def mandelbrot_python(xmin, xmax, ymin, ymax, xn, yn, maxiter, horizon=2.0): def mandelbrot(z, maxiter): c = z for n in range(maxiter): if abs(z) > horizon: return n z = z*z + c return maxiter r1 = [xmin+i*(xmax-xmin)/xn for i in range(xn)] r2 = [ymin+i*(ymax-ymin)/yn for i in range(yn)] return [mandelbrot(complex(r, i),maxiter) for r in r1 for i in r2]
الجزء المثير للاهتمام والبطيء في الشيفرات السابقة هو دالة mandelbrot التي تحسب التسلسل "(((…fc(fc(fc". جعل هذه الشيفرات معتمدة على المتجهات ليس أمرًا واضحًا تمامًا بسبب تعليمة return الداخلية التي توحي بعملية فاضلية للعنصر. بمجرد أن يتباعد لا نحتاج إلى التكرار مرةً أخرى ويمكننا إرجاع عدد التكرارات في حال عدم التباعد، ولكن كيف يمكن أن تفعل Numpy الشيء نفسه؟
كتابة الشيفرة باستخدام مكتبة Numpy
الحيلة هي البحث في كل قيم التكرار التي لم تتباعد بعد وتحديث المعلومات المتعلقة بهذه القيم فقط. نظرًا لأننا نبدأ من "Z = 0"، فإننا نعلم أن كل قيمة ستُحدث مرةً واحدةً على الأقل (عندما تكون مساويةً للصفر فإنها لم تتباعد بعد)، وستتوقف عن التحديث بمجرد تباعدها. ولفعل ذلك سنستخدم فهرسة fancy indexing مع الدالة (less(x1,x2 التي ترجع القيمة الحقيقية للعنصر المحقق (x1<x2).
def mandelbrot_numpy(xmin, xmax, ymin, ymax, xn, yn, maxiter, horizon=2.0): X = np.linspace(xmin, xmax, xn, dtype=np.float32) Y = np.linspace(ymin, ymax, yn, dtype=np.float32) C = X + Y[:,None]*1j N = np.zeros(C.shape, dtype=int) Z = np.zeros(C.shape, np.complex64) for n in range(maxiter): I = np.less(abs(Z), horizon) N[I] = n Z[I] = Z[I]**2 + C[I] N[N == maxiter-1] = 0 return Z, N
وإليك النتيجة:
>>> xmin, xmax, xn = -2.25, +0.75, int(3000/3) >>> ymin, ymax, yn = -1.25, +1.25, int(2500/3) >>> maxiter = 200 >>> timeit("mandelbrot_python(xmin, xmax, ymin, ymax, xn, yn, maxiter)", globals()) 1 loops, best of 3: 6.1 sec per loop >>> timeit("mandelbrot_numpy(xmin, xmax, ymin, ymax, xn, yn, maxiter)", globals()) 1 loops, best of 3: 1.15 sec per loop
كتابة الشيفرة الأسرع باستخدام Numpy
سيكون الربح بزيادة السرعة خمسة أضعاف تقريبًا وليس بالقدر الذي نتوقعه، ومن أسباب هذه المشكلة هو أن الدالة np.less تشير إلى اختبارات xn × yn في كل تكرار، بينما نعلم أن بعض القيم قد تباعدت فعلًا، وحتى إذا أجريت هذه الاختبارات على المستوى C (من خلال numpy)، ستبقى التكلفة كبيرة. توجد طريقةٌ أخرى اقترحها دان جودمان Dan Goodman وذلك بالعمل على مصفوفة ديناميكية في كل تكرار بحيث تخزن فقط النقاط التي لم تتباعد بعد، وهذا يتطلب إضافة أسطر برمجية إضافية ولكن ستكون النتيجة أسرع وتؤدي إلى تحسين عامل السرعة عشر مرات مقارنةً بالطريقة الأولى.
def mandelbrot_numpy_2(xmin, xmax, ymin, ymax, xn, yn, itermax, horizon=2.0): Xi, Yi = np.mgrid[0:xn, 0:yn] Xi, Yi = Xi.astype(np.uint32), Yi.astype(np.uint32) X = np.linspace(xmin, xmax, xn, dtype=np.float32)[Xi] Y = np.linspace(ymin, ymax, yn, dtype=np.float32)[Yi] C = X + Y*1j N_ = np.zeros(C.shape, dtype=np.uint32) Z_ = np.zeros(C.shape, dtype=np.complex64) Xi.shape = Yi.shape = C.shape = xn*yn Z = np.zeros(C.shape, np.complex64) for i in range(itermax): if not len(Z): break # Compute for relevant points only np.multiply(Z, Z, Z) np.add(Z, C, Z) # Failed convergence I = abs(Z) > horizon N_[Xi[I], Yi[I]] = i+1 Z_[Xi[I], Yi[I]] = Z[I] # Keep going with those who have not diverged yet np.negative(I,I) Z = Z[I] Xi, Yi = Xi[I], Yi[I] C = C[I] return Z_.T, N_.T
وتصبح النتيجة كما يلي:
>>> timeit("mandelbrot_numpy_2(xmin, xmax, ymin, ymax, xn, yn, maxiter)", globals()) 1 loops, best of 3: 510 msec per loop
إظهار النتائج
من أجل تصور نتائجنا يمكننا عرض المصفوفة N مباشرةً باستخدام الأمر imshow من مكتبة matplotlib ولكن هذا سينتج صورة مخططة banded وهي نتيجة معروفة لخوارزمية عد الهروب escape count المستخدمة. يمكن التخلص من هذا الربط من خلال حساب الهروب الجزئي وذلك عن طريق قياس مدى هبوط النقطة المتكررة خارج حدود قطع الهروب. فيما يلي صورة للنتيجة، إذ استخدمنا التسوية الطبيعية recount normalization، وأضفنا خريطة ألوان طبيعية (gamma=0.3) إضافةً إلى تظليل فاتح.
تمرين
نريد الآن قياس البعد الكسري لمجموعة ماندلبورت Mandelbrot باستخدام بُعد Minkowski–Bouligand dimension، ولفعل ذلك نحتاج إلى حسابات لمربع بأبعاد متناقص، كما هو موضح في لقطة الشاشة التالية، وكما تتوقع لا يمكننا استخدام تعليمات بايثون العادية لأنها ستكون بطيئة جدًا. الهدف من التمرين هو كتابة دالة باستخدام NumPy تأخذ مصفوفة عشرية ثنائية الأبعاد وتُرجع البعد. ينبغي توحيد القيم الموجودة في المصفوفة بين 0 و1.
المتجهات المكانية
تشير المتجهات المكانية إلى الحالة التي تشارك فيها العناصر نفس الحساب ولكنها تتفاعل مع مجموعة فرعية فقط من العناصر الأخرى، وكانت هذه الحالة موجودةٌ فعلًا في لعبة الحياة، ولكن في بعض المواقف هناك صعوبة إضافية لأن المجموعة الفرعية ديناميكية وتحتاج إلى التحديث في كل تكرار؛ فمثلًا في أنظمة الجسيمات تتفاعل الجسيمات غالبًا مع الجيران المحليين، وينطبق هذا أيضًا على حالة "boids" التي تحاكي سلوكيات السرب flocking.
برنامج Boids
الطيور المتدفقة هي مثال على التنظيم الذاتي في علم الأحياء. صورة Christoffer A Rasmussen، 2012.
يُعد Boids برنامج حياة اصطناعية طُور بواسطة كريج رينولدز Craig Reynolds في عام 1986 وهو يحاكي سلوك سرب الطيور. اسم Boid هو اختصار إلى " bird-oid object" والذي يشير إلى كائن يمثل الطيور.
كما هو الحال مع معظم برامج محاكاة الحياة الاصطناعية، فإن Boids هو مثال على السلوك الناشئ، أي أن تعقيد Boids ينشأ من تفاعل العوامل الفردية والالتزام بمجموعة من القواعد البسيطة. القواعد المطبقة في عالم Boids هي كما يلي:
- الانفصال separation: إرشاد لتجنب ازدحام رفاق السرب المحليين.
- المحاذاة alignment: إرشاد نحو متوسط اتجاه رفاق السرب المحليين.
- التماسك cohesion: الإرشاد للتحرك نحو متوسط الموضع (مركز الكتلة) للرفاق الحاليين.
تنفيذ الشيفرة باستخدام تعليمات بايثون العادية
نظرًا لأن كل boid هو كيان مستقل له العديد من الخاصيات، مثل الموضع والسرعة فمن الطبيعي أن نبدأ بكتابة الصنف Boid:
import math import random from vec2 import vec2 class Boid: def __init__(self, x=0, y=0): self.position = vec2(x, y) angle = random.uniform(0, 2*math.pi) self.velocity = vec2(math.cos(angle), math.sin(angle)) self.acceleration = vec2(0, 0)
الكائن vec2 هو صنف بسيط جدًا يتعامل مع جميع عمليات المتجه الشائعة بمكونين، وهذا سيوفر علينا بعض الكتابة في صنف Boid الرئيسي. يوجد بعض حزم المتجهات في فهرس حزمة Python، ولكن استخدامها سيكون مبالغة في مثل هذا المثال البسيط.
يُعد السرب حالةً صعبة لبايثون العادية لأنه يتفاعل مع الجيران المحليين، ومع ذلك ونظرًا لأن أسراب الطيور تتحرك فإن العثور على مثل هؤلاء الجيران المحليين يتطلب حسابات في كل مرة تقطع المسافة إلى سرب طيور آخر لفرز تلك الطيور الموجودة في نصف قطر تفاعل معين، وبالتالي تكون الطريقة النموذجية لكتابة القواعد الثلاثة:
def separation(self, boids): count = 0 for other in boids: d = (self.position - other.position).length() if 0 < d < desired_separation: count += 1 ... if count > 0: ... def alignment(self, boids): ... def cohesion(self, boids): …
لإكمال الصورة، يمكننا أيضًا إنشاء كائن Flock:
class Flock: def __init__(self, count=150): self.boids = [] for i in range(count): boid = Boid() self.boids.append(boid) def run(self): for boid in self.boids: boid.run(self.boids)
يمكن أن نحصل باستخدام هذا النهج على ما يصل إلى 50 سربًا حتى يصبح وقت الحساب بطيئًا جدًا للحصول على رسم متحرك سلس. سنحصل بالاعتماد على مكتبة Numpy على أداء أفضل بكثير، ولكن قبل الانتقال إلى استخدام هذه المكتبة سنشير إلى المشكلة الرئيسية الموجودة في شيفرات بايثون السابقة؛ فكما تلاحظ يوجد في الشيفرات الكثير من التكرار، أي بتعبير أدق نحن لا نستغل حقيقة أن المسافة الإقليدية انعكاسية أي: |x − y| = |y − x|.
والحقيقة أن كل دالة تحسب "n2" مسافة بينما حساب مسافة "n2/2" كافي، إذا خُزّنت تخزينًا مؤقتًا بطريقة صحيحة. وأيضًا تعيد كل قاعدة حساب كل مسافة دون تخزين نتيجة الدوال الأخرى تخزينًا مؤقتًا، وفي النهاية، نكون قد حسبنا "3n2" مسافة بدلًا من "n2/2".
كتابة الشيفرة باستخدام مكتبة NumPy
تتخذ كتابة الشيفرة باستخدام مكتبة Numpy نهجًا مختلفًا، سنجمع كل كائنات أسراب الطيور boids في مصفوفة الموضع ومصفوفة السرعة:
n = 500 velocity = np.zeros((n, 2), dtype=np.float32) position = np.zeros((n, 2), dtype=np.float32)
الخطوة الأولى هي حساب الجيران لكل كائنات boids، ولذلك نحتاج إلى حساب المسافات المزدوجة:
dx = np.subtract.outer(position[:, 0], position[:, 0]) dy = np.subtract.outer(position[:, 1], position[:, 1]) distance = np.hypot(dx, dy)
كان بإمكاننا استخدام دالة scipy cdist لكننا سنحتاج إلى المصفوفتين dx و dy لاحقًا، وبمجرد حسابها سيكون من الأسرع استخدام تابع hypot. لاحظ شكل المسافة (n,n) وكل خط يرتبط بكائن boid واحد، أي أن كل سطر يعطي المسافة إلى جميع كائنات boids الأخرى.
يمكننا الآن حساب الجيران من هذه المسافات وفقًا للقواعد الثلاثة، مستفيدين من إمكانية دمجها معًا. يمكننا حساب قناع للمسافة والذي يكون موجبًا تمامًا (أي ليس له ارتباط ذاتي)، ثم جداء هذا القناع مع أقنعة المسافات الأخرى.
mask_0 = (distance > 0) mask_1 = (distance < 25) mask_2 = (distance < 50) mask_1 *= mask_0 mask_2 *= mask_0 mask_3 = mask_2
ملاحظة: إذا افترضنا أن أسراب الطيور boids لا يمكن أن تحتل نفس الموضع، فكيف يمكن حساب mask_0 بفعالية أكثر؟
ثم نحسب عدد الجيران داخل نصف القطر المحدد ونتأكد من أنه 1 على الأقل لتجنب القسمة على الصفر.
mask_1_count = np.maximum(mask_1.sum(axis=1), 1) mask_2_count = np.maximum(mask_2.sum(axis=1), 1) mask_3_count = mask_2_count
الآن، سنكتب القواعد الثلاث:
المحاذاة
# حساب متوسط السرعة للجيران المحليين target = np.dot(mask, velocity)/count.reshape(n, 1) # توحيد النتيجة norm = np.sqrt((target*target).sum(axis=1)).reshape(n, 1) target *= np.divide(target, norm, out=target, where=norm != 0) # المحاذاة بسرعة ثابتة target *= max_velocity # الناتج steering حساب مسار الإرشاد alignment = target - velocity
التماسك
# حساب مركز الجاذبية للجيران المحليين center = np.dot(mask, position)/count.reshape(n, 1) # حساب الاتجاه إلى المركز target = center - position # توحيد النتيجة norm = np.sqrt((target*target).sum(axis=1)).reshape(n, 1) target *= np.divide(target, norm, out=target, where=norm != 0) # (max_velocity) التماسك بسرعة ثابتة target *= max_velocity # الناتج steering حساب مسار الإرشاد cohesion = target - velocity
الانفصال
# حساب قوة التنافر من الجيران المحليين repulsion = np.dstack((dx, dy)) # تتناسب القوة عكسيًا مع المسافة repulsion = np.divide(repulsion, distance.reshape(n, n, 1)**2, out=repulsion, where=distance.reshape(n, n, 1) != 0) # حساب الاتجاه بعيدًا عن الآخرين target = (repulsion*mask.reshape(n, n, 1)).sum(axis=1)/count.reshape(n, 1) # توحيد النتيجة norm = np.sqrt((target*target).sum(axis=1)).reshape(n, 1) target *= np.divide(target, norm, out=target, where=norm != 0) # (max_velocity) الانفصال بسرعة ثابتة target *= max_velocity # الناتج steering حساب مسار الإرشاد separation = target - velocity
يجب أن تكون مسارات الإرشاد الثلاث الناتجة (الانفصال والمحاذاة والتماسك) محدودةً من حيث الحجم. وسنترك لك الدمج بين هذه القواعد.
التحديث الناتج للسرعة والموضع:
acceleration = 1.5 * separation + alignment + cohesion velocity += acceleration position += velocity
أخيرًا نتخيل النتيجة باستخدام مخطط مبعثر scatter موجه مخصص.
Boids هو برنامج حياة اصطناعية، طُوِّر بواسطة Craig Reynolds في عام 1986، والذي يحاكي سلوك الطيور المتدفقة.
تمرين
نحن الآن جاهزون لعرض أسراب الطيور boids، وأسهل طريقة لذلك هي استخدام دالة الرسوم المتحركة matplotlib ومخطط مبعثر. لسوء الحظ لا يمكننا توجيه التبعثر بطريقة فردية ونحتاج إلى صنع كائنات خاصة باستخدام توابع PathCollection العائد للدالة matplotlib. يمكن تعريف مسار المثلث البسيط كما يلي:
v= np.array([(-0.25, -0.25), ( 0.00, 0.50), ( 0.25, -0.25), ( 0.00, 0.00)]) c = np.array([Path.MOVETO, Path.LINETO, Path.LINETO, Path.CLOSEPOLY])
يمكن تكرار هذا المسار عدة مرات داخل المصفوفة ويمكن جعل كل مثلث مستقلاً.
n = 500 vertices = np.tile(v.reshape(-1), n).reshape(n, len(v), 2) codes = np.tile(c.reshape(-1), n)
لدينا الآن مصفوفة (n, 4, 2) ومجموعة (n, 4) للشيفرات التي تمثل عدد n من boids. نحن مهتمون بمعالجة مصفوفة vertices لتعكس الترجمة والقياس والدوران لكل كائنات boids.
كيف يمكن أن تكتب وظائف الترجمة والقياس والتدوير؟
الخلاصة
درسنا من خلال هذه الأمثلة الثلاثة ثلاثة أشكال لاستخدام المتجهات في الشيفرات:
- المتجهات الموحدة، إذ تشترك العناصر في نفس الحساب دون قيد أو شرط وللمدة نفسها.
- المتجهات الزمانية، إذ تشترك العناصر في نفس الحساب ولكنها تتطلب عددًا مختلفًا من التكرارات.
- المتجهات المكانية، إذ تشترك العناصر في نفس الحساب ولكن على الوسطاء المكانية الديناميكية.
ومن المحتمل أن يكون هناك العديد من أشكال متجهات الشيفرات. كما أوضحنا سابقًا يعد هذا النوع من المتجهات من أبسط الأنواع على الرغم من أننا رأينا أنه من الصعب حقًا تنفيذه ويتطلب بعض الخبرة أو بعض المساعدة أو كليهما.
ترجمة -وبتصرف- للفصل Code vectorization من كتاب From Python to Numpy لصاحبه Nicolas P. Rougier.

















أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.