توابع التعامل مع المجموعات في جافا سكريبت

نشرح في هذه المقالة التوابع الجديدة للتعامل مع المجموعة set في لغة جافا سكريبت JavaScript، والتي أصبحت متوفرة ومتاحة على جميع متصفحات الويب منذ النسخة Firefox 127. فمن المفيد الاطلاع على توابع المجموعات لاسيما للمطورين الجدد الذين يتعاملون مع بنية المجموعة set لأول مرة ويتطلعون لاستخدامها في بناء تطبيقاتهم، حيث سنسلط الضوء على المزايا الرئيسية لهذه التوابع ونوضح سبب الحاجة لاستخدامها في بناء التطبيقات من خلال الأمثلة العملية.

ما هي التوابع الجديدة للتعامل مع المجموعات

نستعرض فيما يلي أهم التوابع الجديدة للمجموعة set المدعومة من أغلب المتصفحات الحديثة وهي كالتالي:

• التابع ()intersection : يعيد مجموعة جديدة تحتوي على العناصر الموجودة في كلا المجموعتين أي تقاطع المجموعتين
• التابع ()union: يعيد مجموعة جديدة تضم جميع العناصر الموجودة في المجموعتين أي اجتماع المجموعتين
• التابع ()difference: يعيد مجموعة جديدة تحتوي على العناصر غير المتشابهة في المجموعتين أي فرق المجموعتين
• التابع ()symetricDifference: يعيد مجموعة جديدة تحتوي على العناصر الموجودة في أحد المجموعتين وغير الموجودة في المجموعة الثانية
• التابع ()isSubsetOf: يعيد قيمة منطقية تشير فيما إذا كانت جميع عناصر المجموعة الأولى مجموعة فرعية محتواة ضمن المجموعة الثانية أي هل المجموعة الأولى مجموعة جزئية من المجموعة الثانية.
• التابع ()isSupersetOf: يعيد قيمة منطقية تشير إلى ما إذا كانت المجموعة الأولى مجموعة شاملة للمجموعة الثانية، أي هل جميع العناصر في المجموعة الثانية موجودة في المجموعة الأولى.
• التابع ()isDisjointFrom: يرجع قيمة منطقية تشير فيما إذا كانت المجموعتان مستقلتين أي المجموعة الأولى لا تحتوي على عناصر مشتركة مع المجموعة الثانية.

سنوضح لك في الفقرات القادمة معنى واستخدام هذه التوابع باستخدام الأمثلة العملية.

ما هي المجموعة في لغة جافا سكريبت JavaScript

المجموعة Set هي بنية بيانات مشابهة للمصفوفة Array، ولكنها تختلف عنها في أنها لا تسمح بتخزين القيم المكررة. بمعنى آخر، يمكن تخزين كل قيمة في Set لمرة واحدة فقط، حتى إذا كانت القيمة مكررة عند إضافتها.

على سبيل المثال، إذا أخذنا قائمة من العناصر وأضفناها إلى مجموعة Set، ثم فحصنا عناصر المجموعة، سنلاحظ أن العناصر المكررة في القائمة قد حذفت تلقائيًا. إليك مثال توضيحي:

قد يبدو هذا المثال بسيطًا ولا يعكس بالكامل أهمية استخدام المجموعات، ولكن من المفيد للغاية أن توفر لغة البرمجة طريقة لإنشاء مجموعات فريدة ومميزة من العناصر، خاصة عندما تتعامل مع أنواع أو كائنات أكبر وأكثر تعقيدًا. على سبيل المثال، يمكنك إضافة العناصر إلى مجموعة set بالطريقة التالية:

const dogs = new Set();
const yoshi = { name: "Yoshi", personality: "Friendly" };
dogs.add(yoshi);

هناك ميزة أخرى لاستخدام المجموعات sets وهي أن التحقق من وجود عنصر في المجموعة أسرع من التحقق من وجوده في مصفوفة، مما يجعلها مثالية في الحالات التي تتطلب مراقبة الأداء عند التعامل مع البيانات الضخمة. كما يمكنك إنشاء مجموعات جديدة ذات خصائص منطقية محددة بناء على مجموعات موجودة، وهو ما سنناقشه في الفقرات القادمة.

اجتماع مجموعتين

يمكننا باستخدام دمج المجموعات التحقق من العناصر الموجودة في إحدى المجموعتين أو كليهما.

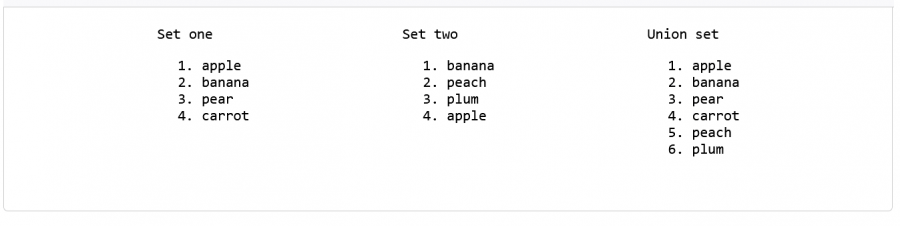
لدينا في المثال التالي مجموعتان ونريد الحصول على مجموعة ثالثة تضم جميع عناصر المجموعتين ولكن بدون تكرار، سنكتب كالتالي:

// إنشاء اجتماع المجموعتين
const unionSet = set1.union(set2);

// عرض العناصر في الاجتماع
unionSet.forEach((item) => {
  const li = document.createElement("li");
  li.textContent = item;
  unionList.appendChild(li);
});

نستخدم عناصر المحتوى النصي textContent في لغة HTML لكل عنصر من عناصر القائمة، مما يشكل لدينا مجموعات من السلاسل النصية sets of strings. وتكمن أهمية استخدام المجموعات عندما نخزن أنواع متعددة من البيانات داخلها، مثل المصفوفات والكائنات.

إن استخدام المجموعات sets مفيد للغاية لأننا لا نحتاج إلى إجراءات إضافية لإزالة التكرار أو التحقق من المساواة أو أي مقارنات أخرى، فكما شرحنا سابقًا عند استخدام المجموعة، ستكون جميع عناصر المجموعة قيم فريدة وغير مكررة. وبالتالي، فإن التابع union سينتج لنا مجموعة ثالثة تحتوي على العناصر الفريدة الموجودة في إما المجموعة الأولى أو الثانية أو كليهما.

تقاطع مجموعتين

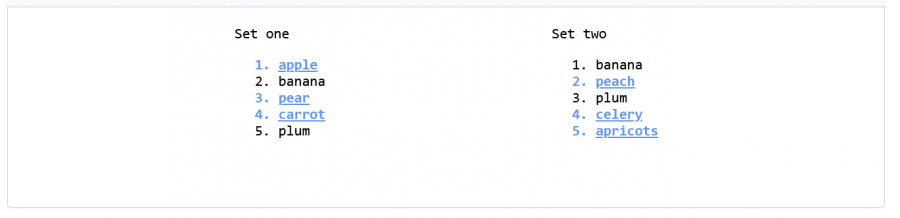
يمكننا باستخدام تقاطع المجموعات معرفة العناصر الموجودة في كلتا المجموعتين وتحديد العناصر المشتركة بينهما. في المثال التالي، سنستخدم تقاطع المجموعات لاستخراج العناصر المشتركة بين المجموعتين وعرضها بدلاً من دمجها في مجموعة ثالثة كما فعلنا باستخدام التابع union في الفقرة السابقة:

// إنشاء مجموعة تقاطع المجموعتين
const intersectionSet = set1.intersection(set2);

// المرور على العناصر في القوائم وتحديد العناصر المشتركة
allListItems.forEach((item) => {
  if (intersectionSet.has(item.textContent)) {
    item.className = "match";
  }
});

الفرق التناظري لمجموعة

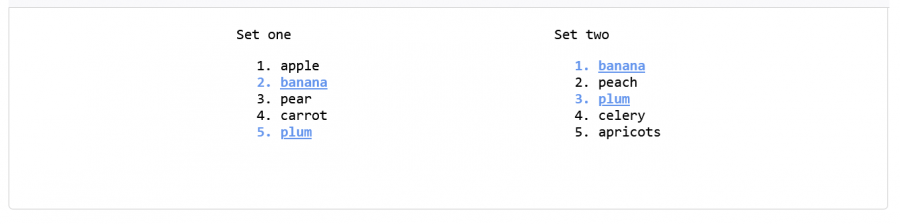
سنستعرض في ما يلي مفهوم الفرق التناظري أو المتماثل الذي يسمح لنا بالتحقق من العناصر الموجودة في إحدى المجموعتين فقط وليس كليهما، قد يبدو المفهوم للوهلة الأولى معقدًا بعض الشي .لكنه سيتضح من خلال المثال التالي:

const setNotBoth = set1.symmetricDifference(set2);

allListItems.forEach((item) => {
  if (setNotBoth.has(item.textContent)) {
    item.className = "match";
  }
});

استخدامنا في هذا الكود التابع symmetricDifference لحساب الاختلاف التناظري بين المجموعتين set1 و set2. والنتيجة مجموعة تحتوي على العناصر التي توجد في إحدى المجموعتين ولكن ليس في كليهما. قد يكون ما سبق جديد وغير مفهوم بالنسبة لك، لفهم الموضوع قارن الفرق التناظري للمجوعات مع تقاطع المجموعات، وعندها ستجد فالتابع symmetricDifference يعمل بطريقة منطقية معاكسة للتابع intersection، وهنا سينتهي هذا الالتباس بالنسبة لك.

فرق المجموعات

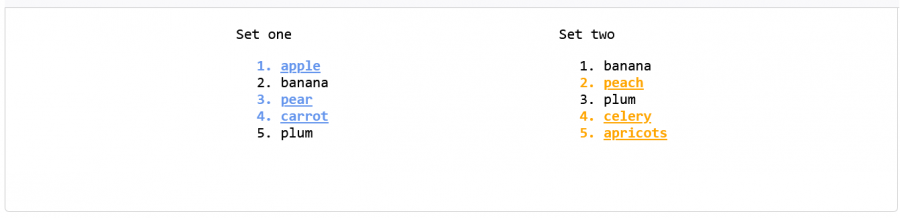
يمكننا استخدام تابع الفرق للتحقق من العناصر الموجودة في إحدى المجموعات وغير الموجودة في المجموعة الأخرى. في المثال التالي، سننشئ مجموعتين بدلاً من مجموعة واحدة. بداية ننشئ المجموعة الأولى set1only باستخدام التابع set1.difference(set2)‎، مما يعطينا العناصر الموجودة في المجموعة الأولى فقط.

بعد ذلك، سنقوم بنفس العملية مع المجموعة الثانية set2only لمعرفة العناصر الموجودة في المجموعة الثانية وغير الموجودة في المجموعة الأولى. ويمكننا باستخدام التابع difference لكل مجموعة تحديد العناصر التي لا تظهر في المجموعة الأخرى.

const set1only = set1.difference(set2);
const set2only = set2.difference(set1);

allListItems.forEach((item) => {
  if (set1only.has(item.textContent)) {
    item.className = "setOneMatch";
  } else if (set2only.has(item.textContent)) {
    item.className = "setTwoMatch";
  }
});

المجموعة الفرعية والمجموعة الشاملة والمجموعة المنفصلة

آخر التوابع والمفاهيم الجديدة الخاصة بالمجموعات التي سنتظرق إليها في هذا المقال هي توابع المجموعة الفرعية Subset والمجموعة الشاملة Superset والمجموعة المنفصلة Disjoint from Set.

فالنتيجة في جميع توابع المجموعات التي تعرفنا عليها سابقًا كانت عبارة عن مجموعة جديدة، أما النتيجة في التوابع الحالية فهي عبارة عن قيمة منطقية تشير إلى حالة منطقية معينة.

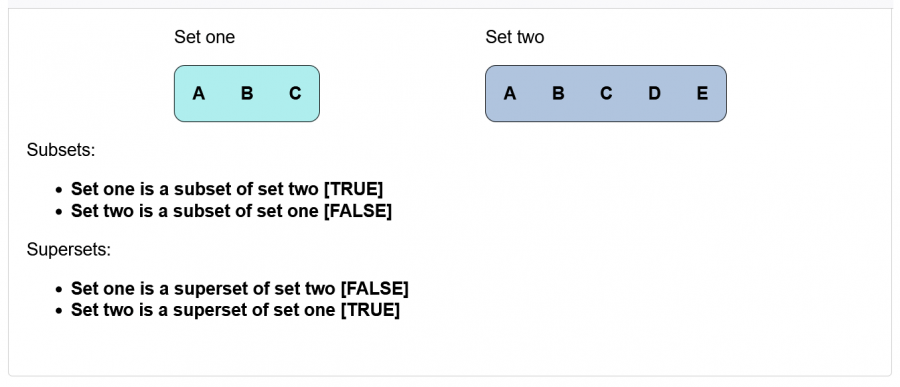
سنتعرف في البداية على التابعين subset و superset، حيث نحصل على النتيجة من خلال بعض عبارات التحقق المنطقية. على سبيل المثال، يمكننا التحقق مما إذا كانت المجموعة الأولى مجموعة جزئية من المجموعة الثانية، ومن ثم إضافة نص منطقي True أو False للعنصر بناءً على نتيجة التحقق.

if (set1.isSubsetOf(set2)) {
  oneSubTwo.textContent += " [TRUE]";
} else {
  oneSubTwo.textContent += " [FALSE]";
}

يمكننا باستخدام التابع isSubsetOf()‎ التحقق مما إذا كانت جميع عناصر المجموعة الأولى تظهر بالكامل في المجموعة الثانية. بينما يمكننا باستخدام التابع isSupersetOf()‎ التحقق من العكس أي معرفة إذا كانت المجموعة الأولى تحتوي على جميع عناصر المجموعة الثانية بالإضافة إلى عناصر أخرى.

أما التابع الأخير الذي سنتعرف عليه فهو isDisjointFrom()‎‎، حيث يمكننا من خلاله معرفة ما إذا كانت المجموعتان لا تملكان أي عناصر مشتركة بينهما.

لاحظ في المثال أدناه أن المجموعتين الأولى والثانية لا تحققان شروط التابع isDisjointFrom()‎‎، لأن هناك عنصر مشترك بينهما وهو العنصر C، أما المجموعة الثالثة فهي منفصلة عن المجموعتين الأولى والثانية لأنها لا تحتوي على أي عناصر مشتركة مع أي منهما.

الخلاصة

إن مفهوم المجموعات sets في لغة جافا سكريبت هو مفهوم مهم ويفترض أنه قد أصبح مفهومًا بالنسبة لك، حيث ستحتاجه في تطبيقات عديدة مثل إزالة التكرار من قائمة تحتوي على بعض القيم المكررة أو التحقق بسرعة مما إذا كان عنصر موجودًا في مجموعة أو إجراء العمليات الرياضية والمنطقية بين المجموعات. نتمنى لكم الاستفادة الجيدة من هذا المقال، وفي حال كان لديكم أي تساؤل يمكن تركه في قسم التعليقات أسفل المقال أو كتابته في قسم الأسئلة والأجوبة في الأكاديمية.

ترجمة وبتصرف للمقال New JavaScript Set methods لكاتبه Brian Smith.

اقرأ أيضًا

• القوائم lists والمجموعات sets في جافا
• مدخل إلى البيانات وأنواعها: التجميعات Collections
• هياكل البيانات: الكائنات والمصفوفات في جافاسكريبت
• التعامل مع الصفوف والمجموعات والقواميس في بايثون