تُتيح لك الكائنات تخزين القيم في مجموعات ذات مفاتيح، وهذا أمر طيّب. ولكنّك دومًا ما ستحتاج في عملك إلى مجموعة مرتّبة، أي أنّ العناصر مرتّبة: عنصر أوّل، عنصر ثانٍ، عنصر ثالث، وهكذا دواليك. تُفيدنا هذه الطريقة في تخزين أمور مثل: المستخدمين والبضائع وعناصر HTML وغيرها.
هنا يكون استعمال الكائنات غير موفّق، إذ أنّها لا تقدّم لنا أيّ تابِع يتيح تحديد ترتيب العناصر، فلا يمكننا إضافة خاصيةً جديدةً تحلّ بين الخاصيات الموجودة. لم تُصنع الكائنات لهذا الغرض بتاتًا.
توجد بنية بيانات أخرى باسم Array (ندعو هذا النوع بالمصفوفة) وهي تتيح لنا تخزين مجموعات العناصر مرتّبةً.
التصريح
توجد صياغتان اثنتان لإنشاء مصفوفة فارغة:
let arr = new Array(); let arr = [];
تحتاج في عملك أغلب الوقت (ونقول أغلب الوقت) الصياغةَ الثانية. يمكننا أيضًا تقديم عناصر أوليّة للمصفوفة نكتبها في أقواس:
let fruits = ["Apple", "Orange", "Plum"];
لاحظ أنّ عناصر المصفوفات مرقّمة (مُفهرسة) بدءًا من الرقم صفر. ويمكننا أن نأخذ عنصرًا منها بكتابة ترتيبه في أقواس معقوفة:
let fruits = ["Apple", "Orange", "Plum"]; alert( fruits[0] ); // Apple/تفاحة alert( fruits[1] ); // Orange/برتقالة alert( fruits[2] ); // Plum/برقوق
يمكن أيضًا تعويض أحد العناصر بأخرى:
fruits[2] = 'Pear'; // ["Apple", "Orange", "Pear"]
…أو إضافة أخرى جديدة إلى المصفوفة:
fruits[3] = 'Lemon'; // ["Apple", "Orange", "Pear", "Lemon"]
نعرف باستعمال التابع length إجمالي العناصر في المصفوفة:
let fruits = ["Apple", "Orange", "Plum"]; alert( fruits.length ); // 3
يمكننا أيضًا استعمال alert لعرض المصفوفة كاملةً.
let fruits = ["Apple", "Orange", "Plum"]; alert( fruits ); // Apple,Orange,Plum
كما يمكن للمصفوفات تخزين أيّ نوع من البيانات. مثلًا:
// قيم مختلفة الأنواع let arr = [ 'Apple', { name: 'John' }, true, function() { alert('hello'); } ]; // خُذ الكائن ذا الفهرس 1 ثمّ اعرض اسمه alert( arr[1].name ); // John // خُذ الدالة في الفهرس 3 ثمّ شغّلها arr[3](); // hello
الفاصلة نهاية الجملة كما الكائنات، يمكن أن نُنهي عناصر المصفوفات بفاصلة ,:
let fruits = [ "Apple", "Orange", "Plum", ];
يُسهّل أسلوب الكتابة «بالفاصلة نهاية الجملة» إضافة العناصر وإزالتها، إذ أن الأسطر البرمجية كلها تصير متشابهة.
توابِع الدفع والجلب
من بين أنواع المصفوفات، تُعدّ الطوابير أكثرها استعمالًا. تعني الصفوف (في علوم الحاسوب) تجميعات العناصر المرتّبة والتي تدعم العمليتين هاتين:
-
الدفع
push: يُضيف عنصرًا نهاية الصفّ -
الأخذ
shift: يأخذ عنصرًا من بداية الصفّ، فيتحرّك الصفّ ويصير العنصر الثاني هو الأول فيه.
تدعم المصفوفات كلتا العمليتين هاتين. وفي الحياة العملية، استعمال هاتين العمليتين ضروري دومًا. نأخذ مثلًا مجموعة رسائل مرتّبة يجب عرضها على الشاشة، أو «صف رسائل».
هناك طريقة أخرى لاستعمال المصفوفات، وهي بنية البيانات بالاسم «كومة».
تدعم الأكوام عمليتين أيضًا:
-
الدفع
push: يُضيف عنصرًا نهاية الكومة. -
السحب
pop: يأخذ عنصرًا من نهاية الكومة.
أي أنّ العناصر الجديدة تُضاف دومًا إلى آخر الكومة، وتُزال أيضًا من نهايتها. عادةً ما نرسم هذه الأكوام مثل أكوام بطاقات اللعب: البطاقات الجديدة تُضاف أعلى الكومة، وتُأخذ من أعلاها أيضًا:
في الأكوام، آخر عنصر ندفعه إليها يكون أوّل من يُأخذ، ويسمّى هذا بمبدأ «آخر من يدخل أول من يخرج» (Last-In-First-Out). أمّا في الطوابير، فهي «أول من يدخل أول من يخرج» (First-In-First-Out).
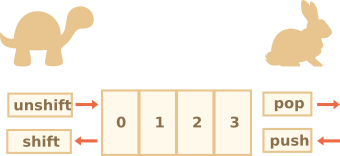
تعمل المصفوفات في جافاسكربت بالطريقتين، صفوف أو أكوام. يمكنك استعمالها لإضافة العناصر وإزالتها من/إلى بداية المصفوفة ونهايتها.
تُسمّى بنية البيانات هذه (في علم الحاسوب) باسم «الطوابير ذات الطرفين».
التوابع التي تؤثّر على نهاية المصفوفة:
-
pop: يستخرج آخر عنصر من المصفوفة ويُعيده:let fruits = ["Apple", "Orange", "Pear"]; alert( fruits.pop() ); // أزِل «Pear» بتنبيه عبر الدالة alert alert( fruits ); // Apple, Orange
-
push: يُضيف العنصر إلى آخر المصفوفة:let fruits = ["Apple", "Orange"]; fruits.push("Pear"); alert( fruits ); // Apple, Orange, Pear
باستدعاء fruits.push(...) كأنّما استدعيت fruits[fruits.length] = ....
التوابِع التي تؤثّر على بداية المصفوفة:
-
shift: يستخرج أوّل عنصر من المصفوفة وتُعيده:let fruits = ["Apple", "Orange", "Pear"]; alert( fruits.shift() ); // أزِل التفاحة واعرضها بِ alert alert( fruits ); // Orange, Pear
-
unshift: يُضيف العنصر إلى أوّل المصفوفة:let fruits = ["Orange", "Pear"]; fruits.unshift('Apple'); alert( fruits ); // Apple, Orange, Pear
يمكنك أيضًا إضافة أكثر من عنصر في استدعاء واحد من push وunshift:
let fruits = ["Apple"]; fruits.push("Orange", "Peach"); fruits.unshift("Pineapple", "Lemon"); // ["Pineapple", "Lemon", "Apple", "Orange", "Peach"] alert( fruits );
داخليًا وخلف الكواليس
المصفوفات هي كائنات، كائنات من نوع خاص. القوسان المعقوفان المستعملان للدخول إلى الخاصيات arr[0] هما فعليًا جزء من صياغة الكائنات. داخليًا، لا يفرق ذاك عن obj[key] (إذ arr هو الكائن والأرقام تلك مفاتيح).
ما تفعله المصفوفات هو «توسعة» الكائنات بتقديم توابِع خاصّة تعمل مع البيانات والمجموعات المرتّبة، إضافةً إلى تقديم خاصية length، ولكنّ أساسها ما زال الكائنات.
تذكّر أنّ هناك 7 أنواع أساسية في جافاسكربت، فقط. المصفوفة هي كائن، وتتصرّف بناءً على ذلك، ككائن.
فمثلًا، عند نسخها تُنسخ بالمرجع (By reference):
let fruits = ["Banana"] let arr = fruits; // انسخها بالمرجع (متغيران اثنان يُشيران إلى نفس المصفوفة) alert( arr === fruits ); // true arr.push("Pear"); // عدّل المصفوفة «بالمرجع» alert( fruits ); // صاروا الآن عنصرين: Banana, Pear
…إلا أنّ المميز حقًا في المصفوفات هي آلية تمثيلها داخليًا، إذ يحاول المحرّك تخزين عناصرها متتابعةً في مساحة الذاكرة، أي واحدة بعد الأخرى، تمامًا مثلما وضّحت الرسوم في هذا الفصل. هناك أيضًا طُرق أخرى لتحسين (optimization) المصفوفات فتعمل بسرعة كبيرة حقًا.
ولكن، لو لم نعمل مع المصفوفة على أنّها «تجميعة مرتّبة» بل وكأنّها كائن مثل غيرها، فسينهار هذا كله.
يمكننا (تقنيًا) كتابة هذا:
// نصنع مصفوفة let fruits = []; // نُسند خاصيةً لها فهرس أكبر من طول المصفوفة بكثير fruits[99999] = 5; // نُنشئ خاصيةً لها أيّ اسم fruits.age = 25;
أجل، يمكننا فعل هذا، فالمصفوفات في أساسها كائنات، ويمكننا إضافة ما نريد من خاصيات لها.
ولكن المحرّك هنا سيرى بأنّا نُعامل المصفوفة معاملة الكائن العادي. وبهذا -في هذه الحالة- لا تنفع أنواع التحسين المخصّصة للكائنات، وسيُعطّلها المحرّك، وتضيع كل فوائد المصفوفات.
هذه طرائق يمكنك فيها إساءة استعمال المصفوفات:
-
إضافة خاصيات ليست عددية مثل
arr.test = 5. -
الفراغات، أي تُضيف
arr[0]وبعدهاarr[1000](دون عناصر بينها). -
ملء المصفوفة بالعكس، أي
arr[1000]ثمarr[999]وهكذا.
نرجوك هنا أن تعتبر المصفوفات بنًى خاصّة تتعامل مع البيانات المرتّبة، فهي تقدّم لك توابِع خاصّة لهذا بالذات. يتغيّر تعامل محرّكات جافاسكربت حين تتعامل مع المصفوفات، فتعمل مع البيانات المرتّبة المتتابعة، فمن فضلك استعمِلها بهذه الطريقة. لو أردت مفاتيح لا عددية، أو مثلما في الحالات الثلاث أعلاه، فغالبًا لا تكون المصفوفة ما تبحث عنه، بل الكائنات العادية {}.
الأداء
يعمل التابِعان push/pop بسرعة، بينما shift/unshift بطيئان.
لماذا يكون التعامل مع نهاية المصفوفة أسرع من التعامل مع بدايتها؟ لنأخذ نظرة عمًا يحدث أثناء تنفيذ الشيفرة:
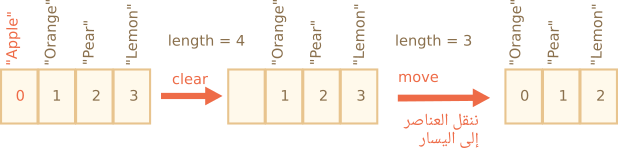
// خُذ عنصرًا واحدًا من الأوّل fruits.shift();
لا يكفي أن تأخذ العنصر ذا الفهرس 0 وتُزيله، بل عليك أيضًا إعادة ترقيم بقية العناصر وفقًا لذلك.
ما تفعله عملية shift هي ثلاث أمور:
-
إزالة العنصر ذا الفهرس
0. -
تحريك كل العناصر الأخرى إلى يسار المصفوفة، وإعادة ترقيمها من الفهرس رقم
1إلى0، ومن2إلى1، وهكذا. -
تحديث خاصية الطول
length.
زِد العناصر في المصفوفات، تزيد الوقت اللازم لتحريكها، وتزيد عدد العمليات داخل الذاكرة.
مثل shift، تفعل unshift نفس الأمور: فلنُضيف عنصرًا إلى بداية المصفوفة، علينا أولًا تحريك كل العناصر إلى اليمين، أي نزيد فهارسها كلها.
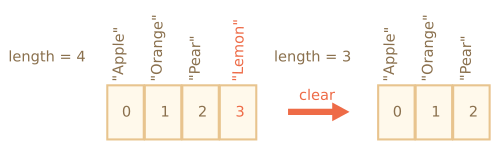
وماذا عن push/pop؟ ليس عليها تحريك أيّ عنصر. فلاستخراج عنصر من النهاية، يمحي التابِع pop الفهرس ويعدّل الطول length فيقصّره.
إجراءات عملية pop:
// خُذ عنصرًا واحدًا من الآخر fruits.pop();
لا تحتاج عملية pop إلى تحريك ولا مقدار ذرة، لأنّ العناصر تبقى كما هي مع فهارسها. لهذا السبب سرعتها تفوق سرعة البرق، أي أقصى سرعة ممكنة.
ذات الأمر للتابِع push.
الحلقات
هذه إحدى أقدم الطرق للمرور على عناصر المصفوفات، استعمال حلقة for بالمرور على فهارس المصفوفة:
let arr = ["Apple", "Orange", "Pear"]; for (let i = 0; i < arr.length; i++) { alert( arr[i] ); }
ولكن المصفوفات تسمح بطريقة أخرى للمرور عليها، for..of:
let fruits = ["Apple", "Orange", "Plum"]; // المرور على عناصر المصفوفة for (let fruit of fruits) { alert( fruit ); }
لا تتيح لك حلقة for..of الوصول إلى فهرس العنصر الحالي في الحلقة، بل قيمة العنصر فقط، وفي أغلب الأحيان هذا ما تحتاج، كما وأنّ الشيفرة أقصر.
طالما المصفوفات كائنات، فيمكننا (نظريًا) استعمال for..in:
let arr = ["Apple", "Orange", "Pear"]; for (let key in arr) { alert( arr[key] ); // Apple, Orange, Pear }
ولكن الواقع أنّ الطريقة هذه سيئة، ففيها عدد من المشاكل:
-
تمرّ الحلقة
for..inعلى كل الخاصيات مجتمعةً، وليس العددية منها فقط. توجد في المتصفّح وغيرها من بيئات كائنات «شبيهة بالمصفوفات». أي أن لها خاصية الطولlengthوخاصيات الفهارس، ولكن لها أيضًا توابِع وخاصيات لا عددية أخرى لا نحتاجها أغلب الأحيان، إلّا أنّ حلقةfor..inستمرّ عليها هي أيضًا. لذا لو اضطررت للعمل مع الكائنات الشبيهة بالمصفوفات، فهذه الخاصيات «الأخرى» ستتسبّب بالمتاعب بلا شك. -
أداء حلقة
for..inيكون بالنحو الأمثل على الكائنات العامة لا المصفوفات، ولهذا سيكون أبطأ 10 أو 100 مرة. طبعًا فالأداء سريع جدًا مع ذلك. هذه السرعة الإضافية ستنفع غالبًا في الحالات الحرجة (أي حين يجب أن يكون تنفيذ الحلقة بأسرع وقت ممكن). مع ذلك، الحرس واجب والاهتمام بهذا الاختلاف مهم.
لكن في أغلب الأحيان، استعمال for..in للمصفوفات فكرة سيئة.
كلمتان حول «الطول»
تتحدّث خاصية الطول length تلقائيًا متى ما عدّلنا المصفوفة. وللدّقة، فهي ليست عدد القيم في المصفوفة، بل أكبر فهرس موجود زائدًا واحد.
فمثلًا، لو كان لعنصر واحد فهرس كبير، فسيكون الطول كبيرًا أيضًا:
let fruits = []; fruits[123] = "Apple"; alert( fruits.length ); // 124
لكنّنا لا نستعمل المصفوفات هكذا. سجّلها عندك.
هناك ما هو عجيب حول خاصية length، ألا وهي أنّها تقبل الكتابة. لو زِدنا قيمتها يدويًا، لا نرى شيئًا تغيّر، ولكن لو أنقصناها، تُبتر المصفوفة حسب الطول، ولا يمكن العودة عن هذه العملية. طالِع هذا المثال:
let arr = [1, 2, 3, 4, 5]; // نبتر المصفوفة ونُبقي عنصرين فقط arr.length = 2; alert( arr ); // [1, 2] // نُعيد الطول الذي كان في الأوّل arr.length = 5; // undefined القيم المبتورة لا تعود، وإنما تصبح alert( arr[3] );
إذًا، فالطريقة الأسهل والأبسط لمسح المصفوفة هي: arr.length = 0;.
new Array()
هناك صياغة أخرى يمكن استعمالها لإنشاء المصفوفات:
let arr = new Array("Apple", "Pear", "etc");
ولكنّها نادرًا ما تُستعمل، فالأقواس المعقوفة [] أقصر. كما وأنّ هذه الطريقة تقدّم ميزة… مخادعة، إن صحّ التعبير.
إن استدعيت new Array وفيها مُعامل واحد فقط (عددي)، فستُنشأ مصفوفة لا عناصر فيها، ولكن بالطول المحدّد.
هاك طريقة يمكنك بها تخريب حياتك، لو أردت:
let arr = new Array(2); // هل ستكون المصفوفة [2]؟ alert( arr[0] ); //غير معرّفة! ليس فيها عناصر. alert( arr.length ); // طولها 2
في هذا الشيفرة، كل عناصر new Array(number) لها القيمة undefined. ولهذا نستعمل الأقواس المعقوفة غالبًا، لنتجنّب هذه المفاجئات السارّة، إلّا لو كنت تعي حقًا ما تفعله.
المصفوفات متعدّدة الأبعاد
يمكن أن تكون عناصر المصفوفات مصفوفات أخرى أيضًا. نستغلّ هذه الميزة فنعمل مصفوفات متعدّدة الأبعاد لتخزين المصفوفات الرياضية مثلًا:
let matrix = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]; alert( matrix[1][1] ); // 5، العنصر في الوسط
تحويل المصفوفات إلى سلاسل نصية
تُنفّذ المصفوفات تابِع toString خاصّ بها، فيُعيد قائمة من العناصر مفصولة بفواصل. خُذ هذا المثال:
let arr = [1, 2, 3]; alert( arr ); // 1,2,3 alert( String(arr) === '1,2,3' ); // true
جرّب هذه، أيضًا:
alert( [] + 1 ); // "1" alert( [1] + 1 ); // "11" alert( [1,2] + 1 ); // "1,21"
ليس للمصفوفات Symbol.toPrimitive ولا دالة valueOf، بل تُنفّذ التحويل toString فقط لا غير. هكذا تصير [] سلسلة نصية فارغة، و[1] تصير "1" و[1,2] تصير "1,2".
متى ما أضاف مُعامل الجمع الثنائي "+" شيئًا إلى السلسلة النصية، حوّله إلى سلسلة نصية هو الآخر. هكذا هي الخطوة التالية:
alert( "" + 1 ); // "1" alert( "1" + 1 ); // "11" alert( "1,2" + 1 ); // "1,21"
ملخص
المصفوفات نوع خاصّ من الكائنات، وهي مخصّصة لتخزين البيانات عناصر مرتّبة، كما وإدارتها أيضًا.
-
التصريح
// الأقواس المعقوفة (طبيعية) let arr = [item1, item2...]; // new Array (نادرة جدًا) let arr = new Array(item1, item2...);
باستدعاء new Array(number) تُنشئ مصفوفة بالطول المحدّد، ولكن بلا أيّ عنصر.
-
خاصية الطول
lengthهي طول المصفوفة، أو للدّقة، آخر فهرس عددي زائدًا واحد. التوابِع المختلفة على المصفوفات تعدّل هذه الخاصية تلقائيًا. -
إن قصّرنا خاصية
lengthيدويًا، فنحن نبتر المصفوفة حسب القيمة الجديدة.
يمكننا استعمال المصفوفة كما الصفوف ذات الطرفين، بالعمليات الآتية:
-
push(...items): تُضيفitemsإلى النهاية. -
pop(): تُزيل العنصر من النهاية وتُعيده. -
shift(): تُزيل العنصر من البداية وتُعيده. -
unshift(...items): تُضيفitemsإلى البداية.
لتمرّ على عناصر المصفوفة:
-
for (let i=0; i<arr.length; i++)-- تتنفّذ بسرعة، ومتوافقة مع المتصفحات القديمة. -
for (let item of arr)-- الصياغة الحديثة للعناصر فقط. -
for (let i in arr)-- إيّاك واستعمالها.
سنرجع إلى المصفوفات لاحقًا ونتعلّم توابِع أخرى لإضافة العناصر وإزالتها واستخراجها، كما وترتيب المصفوفات. هذا كله في الفصل التالي، توابع المصفوفات.
تمارين
هل تُنسخ المصفوفات؟
الأهمية: 3
ما ناتج هذه الشيفرة؟
let fruits = ["Apples", "Pear", "Orange"]; // ادفع عنصرًا جديدًا داخل «النسخة» let shoppingCart = fruits; shoppingCart.push("Banana"); // ماذا في fruits؟ alert( fruits.length ); // ?
الحل
الناتج هو 4:
let fruits = ["Apples", "Pear", "Orange"]; let shoppingCart = fruits; shoppingCart.push("Banana"); alert( fruits.length ); // 4
هذا لأنّ المصفوفات كائنات. فكِلا shoppingCart وfruits يُشيران إلى نفس المصفوفة ذاتها.
العمليات على المصفوفات
الأهمية: 5
فلنجرّب خمس عمليات على المصفوفات.
-
أنشِئ مصفوفة باسم
stylesتحوي العنصرين «Jazz» و«Blues». - أضِف «Rock-n-Roll» إلى نهايتها.
- استبدِل القيمة في الوسط بالقيمة «Classics». يجب أن تعمل الشيفرة الذي ستكتبه ليجد القيمة في الوسط مع أيّ مصفوفة كانت لو كان طولها عدد فردي.
- أزِل القيمة الأولى من المصفوفة واعرضها.
- أضِف «Rap» و«Reggae» إلى بداية المصفوفة.
المصفوفة خلال العمليات هذه:
Jazz, Blues Jazz, Blues, Rock-n-Roll Jazz, Classics, Rock-n-Roll Classics, Rock-n-Roll Rap, Reggae, Classics, Rock-n-Roll
الحل
let styles = ["Jazz", "Blues"]; styles.push("Rock-n-Roll"); styles[Math.floor((styles.length - 1) / 2)] = "Classics"; alert( styles.shift() ); styles.unshift("Rap", "Reggae");
النداء داخل سياق المصفوفة
الأهمية: 5
ما الناتج؟ لماذا؟
let arr = ["a", "b"]; arr.push(function() { alert( this ); }) arr[2](); // ?
الحل
من ناحية الصياغة، فالاستدعاء arr[2]() هو نفسه النداء القديم obj[method]()، فبدل obj هناك arr، وبدل method هناك 2.
إذًا فما أمامنا هو نداء الدالة arr[2] وكأنّها تابِع لكائن. وبالطبيعة، فهي تستلم this الذي يُشير إلى الكائن arrوتكتب المصفوفة ناتجًا:
let arr = ["a", "b"]; arr.push(function() { alert( this ); }) arr[2](); // "a","b",function
للمصفوفة ثلاث قيم: الاثنتين من البداية، مع الدالة.
جمع الأعداد المُدخلة
الأهمية: 4
اكتب دالة sumInput() تؤدّي الآتي:
-
طلب القيم من المستخدم باستعمال
promptوتخزينها في مصفوفة. - أن ينتهي الطلب لو أدخل المستخدم قيمة غير عددية، أو سلسلة نصية فارغة، أو ضغطَ «ألغِ».
- حساب مجموع عناصر المصفوفة وإعادتها.
ملاحظة: الصفر 0 عدد مسموح، لذا لا تُوقف الطلب لو رأيته.
الحل
انتبه هنا على التفصيل الصغير في الحل، صغير ولكن مهمّ: لا يمكننا تحويل قيمة المتغير value إلى عدد مباشرةً بعد prompt، لأنّه بعدما نُجري value = +value، لن نفرّق بين السلسلة النصية الفارغة (أي علينا إيقاف الطلب) من الصفر (قيمة صالحة). عوض ذلك نؤجّل ذلك لما بعد.
function sumInput() { let numbers = []; while (true) { let value = prompt("A number please?", 0); // هل نلغي الطلب؟ if (value === "" || value === null || !isFinite(value)) break; numbers.push(+value); } let sum = 0; for (let number of numbers) { sum += number; } return sum; } alert( sumInput() );
أكبر مصفوفة فرعية
الأهمية: 2
البيانات المُدخلة هي مصفوفة من الأعداد، مثل arr = [1, -2, 3, 4, -9, 6]. والمهمة هي: البحث عن مصفوفة فرعية متتابعة في arr لها أكبر ناتج جمع.
اكتب دالة getMaxSubSum(arr) لتُعيد ذلك الناتج.
مثال:
getMaxSubSum([-1, 2, 3, -9]) = 5 (مجموع 2+3) getMaxSubSum([2, -1, 2, 3, -9]) = 6 (مجموع 2+(-1)+2+3) getMaxSubSum([-1, 2, 3, -9, 11]) = 11 (وهكذا...) getMaxSubSum([-2, -1, 1, 2]) = 3 getMaxSubSum([100, -9, 2, -3, 5]) = 100 getMaxSubSum([1, 2, 3]) = 6 (نأخذها كلها)
إن كانت القيم كلها سالبة فيعني هذا ألا نأخذ شيئا (المصفوفة الفرعية فارغة)، وبهذا يكون الناتج صفرًا:
getMaxSubSum([-1, -2, -3]) = 0
يُحبّذ لو تفكّر -رجاءً- بحلّ سريع: O(n2) أو حتّى O(n) لو أمكنك.
الحل
- النسخة البطيئة
يمكننا حساب كلّ ناتج جمع فرعي ممكن.
أبسط طريقة هي أخذ كلّ عنصر وحساب مجموع المصفوفات الفرعية بدءًا من مكان العنصر.
فمثلًا إن كان لدينا [-1, 2, 3, -9, 11]:
// نبدأ بِ -1: -1 -1 + 2 -1 + 2 + 3 -1 + 2 + 3 + (-9) -1 + 2 + 3 + (-9) + 11 // نبدأ بِ 2: 2 2 + 3 2 + 3 + (-9) 2 + 3 + (-9) + 11 // نبدأ بِ 3: 3 3 + (-9) 3 + (-9) + 11 // نبدأ بِ -9: -9 -9 + 11 // نبدأ بِ 11: 11
في الواقع فالشيفرة هي حلقات متداخلة، تمرّ الحلقة العلوية على عناصر المصفوفة، والسفلية تعدّ النواتج الفرعية بدءًا من العنصر الحالي.
function getMaxSubSum(arr) { let maxSum = 0; // إن لم نأخذ أيّ عنصر، فسنُرجع الصفر 0 for (let i = 0; i < arr.length; i++) { let sumFixedStart = 0; for (let j = i; j < arr.length; j++) { sumFixedStart += arr[j]; maxSum = Math.max(maxSum, sumFixedStart); } } return maxSum; } alert( getMaxSubSum([-1, 2, 3, -9]) ); // 5 alert( getMaxSubSum([-1, 2, 3, -9, 11]) ); // 11 alert( getMaxSubSum([-2, -1, 1, 2]) ); // 3 alert( getMaxSubSum([1, 2, 3]) ); // 6 alert( getMaxSubSum([100, -9, 2, -3, 5]) ); // 100
مدى التعقيد الحسابي لهذا الحل هو O(n2). أي بعبارة أخرى، لو زِدت حجم المصفوفة مرتين اثنتين، فسيزيد وقت عمل الخوارزمية أربع مرات أكثر.
يمكن أن تؤدّي هذه الخوازرميات للمصفوفات الكبيرة (نتحدّث عن 1000 و10000 وأكثر) إلى بطء شديد في التنفيذ.
- النسخة السريعة
لنمرّ على عناصر المصفوفة ونحفظ ناتج جمع العناصر الحالي في المتغير s. متى ما صار s سالبًا، نعيّنه صفرًا s=0. إجابتنا على هذا هي أكبر قيمة من هذا المتغير s.
لو لم يكن هذا الوصف منطقيًا، فيمكنك مطالعة الشيفرة، قصيرة للغاية:
function getMaxSubSum(arr) { let maxSum = 0; let partialSum = 0; for (let item of arr) { // لكلّ item في arr partialSum += item; // نُضيفه إلى partialSum maxSum = Math.max(maxSum, partialSum); // نتذكّر أكبر قيمة if (partialSum < 0) partialSum = 0; // لو كانت سالبة فالصفر } return maxSum; } alert( getMaxSubSum([-1, 2, 3, -9]) ); // 5 alert( getMaxSubSum([-1, 2, 3, -9, 11]) ); // 11 alert( getMaxSubSum([-2, -1, 1, 2]) ); // 3 alert( getMaxSubSum([100, -9, 2, -3, 5]) ); // 100 alert( getMaxSubSum([1, 2, 3]) ); // 6 alert( getMaxSubSum([-1, -2, -3]) ); // 0
على الخوارزمية هنا أن تمرّ مرورًا واحدًا فقط على المصفوفة، أي أن التعقيد الحسابي هو O(n).
يمكنك أن تجد معلومات مفصّلة أكثر عن الخوارزمية هنا: Maximum subarray problem. لو لم يكن هذا واضحًا بعد، فالأفضل لو تتعقّب ما تفعل الخوارزمية في الأمثلة أعلاه، وترى ما تفعله من حسابات. «التعقّب يغني عن ألف كلمة»… ربّما.
ترجمة -وبتصرف- للفصل Arrays من كتاب The JavaScript language
اقرأ أيضًا
- المقال التالي: توابع المصفوفات (Array methods)
- المقال السابق: السلاسل النصية (strings)











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.