اقتباسالرسم خدعة.
إم سي إسكر M.C. Escher، مقتبس بواسطة برونو إرنست Bruno Ernst في المرآة السحرية لإم سي إسكر.
تعطينا المتصفحات طرقًا عدة لعرض الرسوميات على الشاشة، وأبسط تلك الطرق هي استخدام التنسيقات لموضعة وتلوين عناصر شجرة DOM العادية، ويمكن فعل الكثير بهذا كما رأينا في اللعبة التي في المقال السابق، كما يمكننا جعل العقد كما نريد بالضبط من خلال إضافة صور خلفية شبه شفافة إليها، أو أن نديرها أو نزخرفها باستخدام التنسيق transform، لكننا سنستخدِم عناصر DOM هكذا لغير الغرض الذي صُممت له، كما ستكون بعض المهام مثل رسم سطر بين نقطتين عشوائيتين غريبةً إذا نفذناها باستخدام عناصر HTML عادية.
لدينا بديلين هنا، حيث أن البديل الأول مبني على DOM ويستخدِم الرسوميات المتجهية القابلة للتحجيم Scalable Vector Graphics -أو SVG اختصارًا- بدلًا من HTML، كما يمكن النظر إلى SVG على أنها صيغة توصيف مستندات تركِّز على الأشكال بدلًا من النصوص، ويمكن تضمين مستند SVG مباشرةً في مستند HTML أو إدراجه باستخدام الوسم <img>؛ أما البديل الثاني فيدعى اللوحة Canvas، وهو عنصر DOM واحد يغلف صورةً ما، ويوفر واجهةً برمجيةً لرسم الأشكال على مساحة تشغلها عقدة ما.
الفرق الأساسي بين اللوحة وصورة SVG هو أن الوصف الأصلي للشكل في الأخيرة محفوظ بحيث يمكن نقله أو إعادة تحجيمه في أيّ وقت؛ أما اللوحة فتحوِّل الأشكال إلى بكسلات -وهي النقاط الملونة على الشاشة- بمجرد رسمها، كما لا تتذكر ما تمثله تلك البكسلات، والطريقة الوحيدة لنقل شكل على لوحة هي بمسح اللوحة أو الجزء الذي يحيط بالشكل، ثم إعادة رسمه بالشكل في موضع جديد.
الرسوميات المتجهية القابلة للتحجيم SVG
لن تخوض هذه السلسلة في تفاصيل SVG وإنما سنشرح كيفية عملها باختصار، كما سنعود إلى عيوبها في نهاية المقال، والتي يجب وضعها في حسبانك حين تريد اتخاذ قرار بشأن آلية الرسم المناسبة لتطبيق ما.
فيما يلي مستند HTML مع صورة SVG بسيطة:
<p>Normal HTML here.</p> <svg xmlns="http://www.w3.org/2000/svg"> <circle r="50" cx="50" cy="50" fill="red"/> <rect x="120" y="5" width="90" height="90" stroke="blue" fill="none"/> </svg>
تغيِّر السمة xmlns عنصرًا ما -وعناصره الفرعية- إلى فضاء اسم XML مختلف، حيث يحدِّد ذلك الفضاء المعرَّف بواسطة رابط تشعبي URL الصيغة التي نستخدِمها الآن، وعلى ذلك يكون للوسمين <circle> و<rect> معنىً هنا في SVG، رغم أنهما لا يمثِّلان شيئًا في لغة HTML، كما يرسمان هنا الأشكال باستخدام التنسيق والموضع اللذين يحدَّدان بواسطة سماتهما.
تنشئ هذه الوسوم عناصر DOM وتستطيع السكربتات أن تتفاعل معها كما تفعل وسوم HTML تمامًا، إذ تغيِّر الشيفرة التالية مثلًا عنصر <circle> ليُلوَّن باللون السماوي Cyan:
let circle = document.querySelector("circle"); circle.setAttribute("fill", "cyan");
عنصر اللوحة
يمكن رسم رسوميات اللوحة على عنصر <canvas>، كما تستطيع إعطاء مثل هذا العنصر سمات عرض width وطول height لتحديد حجمها بالبكسلات، وتكون اللوحة الجديدة فارغةً تمامًا، مما يعني أنها شفافة وتظهر مثل مساحة فارغة في المستند، كما يسمح الوسم <canvas> بتنسيقات مختلفة من الرسم، ونحتاج إلى إنشاء سياق context أولًا للوصول إلى واجهة الرسم الحقيقية، وهو كائن توفر توابعه واجهة الرسم.
لدينا حاليًا تنسيقَين من أنماط الرسم المدعومَين دعمًا واسعًا هما "2d" للرسم ثنائي الأبعاد و"webgl" للرسم ثلاثي الأبعاد من خلال واجهة OpenGL، كما أننا لن نناقش واجهة OpenGL هنا، وإنما سنقتصر على الرسم ثنائي الأبعاد، لكن إذا أردت النظر في الرسم ثلاثي الأبعاد فاقرأ في WebGL، إذ توفر واجهةً مباشرةً لعتاد الرسوميات، وتسمح لك بإخراج مشاهد معقدة بكفاءة عالية باستخدَام جافاسكربت.
نستطيع إنشاء سياق بواسطة التابع getContext على <canvas> لعنصر DOM كما يلي:
<p>Before canvas.</p> <canvas width="120" height="60"></canvas> <p>After canvas.</p> <script> let canvas = document.querySelector("canvas"); let context = canvas.getContext("2d"); context.fillStyle = "red"; context.fillRect(10, 10, 100, 50); </script>
يرسم المثال مستطيلًا أحمرًا بعرض 100 بكسل وارتفاع 50 بكسل بعد إنشاء كائن السياق، ويكون الركن الأيسر العلوي في الإحداثيات هو (10,10)، كما يضع نظام الإحداثيات في عنصر اللوحة الإحداثيات الصفرية (0,0) في الركن الأيسر العلوي كما في HTML وSVG، بحيث يتجه محور الإحداثي y لأسفل من هناك، وبالتالي يكون (10,10) مزاحًا عشرة بكسلات إلى الأسفل وإلى يمين الركن الأيسر العلوي.
الأسطر والأسطح
نستطيع ملء الشكل في واجهة اللوحة، مما يعني أننا سنعطي مساحته لونًا أو نقشًا بعينه، أو يمكن تحديده stroked بأن يُرسَم خطًا حول حوافه، وما قيل هنا سيقال في شأن SVG أيضًا، كما يملأ التابع fillRect مستطيلًا ويأخذ إحداثيات x وy للركن العلوي الأيسر للمستطيل ثم عرضه ثم ارتفاعه، ويرسم التابع strokeRect بالمثل الخطوط الخارجية للمستطيل، لكن لا يأخذ هذان التابعان معاملات أخرى، فلا يحدَّد وسيط ما لون الملء ولا سماكة التحديد ولا غيرها، كما قد يُتوقَّع في مثل هذه الحالة، والذي يحدِّد تلك العناصر هي خصائص سياق الكائن، حيث تتحكم الخاصية fillStyle بطريقة ملء الأشكال، ويمكن تعيينها لتكون سلسلةً نصيةً تحدِّد لونًا ما باستخدام ترميز الألوان في CSS؛ أما الخاصية strokeStyle فهي شبيهة بأختها السابقة، لكن تحدد اللون المستخدَم في التحديد، كما يُحدَّد عرض الخط بواسطة الخاصية lineWidth التي قد تحتوي أي عدد موجب.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.strokeStyle = "blue"; cx.strokeRect(5, 5, 50, 50); cx.lineWidth = 5; cx.strokeRect(135, 5, 50, 50); </script>
إذا لم تُحدَّد سمة عرض width أو طول height كما في المثال، فسيحصل عنصر اللوحة على عرض افتراضي مقداره 300 بكسل وطول مقداره 150 بكسل.
المسارات
المسار هو متسلسلة من الأسطر، ويأخذ عنصر اللوحة ثنائي الأبعاد منظورًا استثنائيًا لوصف مثل تلك المسارات من خلال التأثيرات الجانبية بالكامل، كما لا تُعَدّ المسارات قيمًا يمكن تخزينها وتمريرها من مكان إلى آخر، بل إذا أردنا فعل شيء بمسار ما، فيمكن إنشاء متسلسلة من استدعاءات التوابع لوصف شكله.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.beginPath(); for (let y = 10; y < 100; y += 10) { cx.moveTo(10, y); cx.lineTo(90, y); } cx.stroke(); </script>
ينشئ هذا المثال مسارًا فيه عدد من أجزاء أسطر أفقية ثم يحدِّدها باستخدام التابع stroke، ويبدأ كل جزء أُنشئ بواسطة lineTo عند الموضع الحالي للمسار، كما يكون ذلك الموضع عادةً في نهاية الجزء الأخير، إلا إذا استدعيت moveTo، حيث سيبدأ الجزء التالي في تلك الحالة عند الموضع الممرَّر إلى moveTo.
يُملأ كل شكل لوحده عند ملء المسار باستخدام التابع fill، وقد يحتوي المسار على عدة أشكال، بحيث تبدأ كل حركة moveTo شكلًا جديدًا، ولكن سيحتاج المسار إلى أن يغلَق قبل إمكانية ملئه، بحيث تكون بدايته ونهايته في الموضع نفسه، فإذا لم يكن المسار مغلقًا، فسيضاف السطر من نهايته إلى بدايته، ويُملأ الشكل المغلَّف بالمسار المكتمِل.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.beginPath(); cx.moveTo(50, 10); cx.lineTo(10, 70); cx.lineTo(90, 70); cx.fill(); </script>
يرسم هذا المثال مثلثًا مملوءًا. لاحظ أنّ ضلعيَن فقط من أضلاع المثلث هما اللذان رُسما صراحةً؛ أما الثالث الذي يبدأ من الركن السفلي الأيمن إلى القمة فيُضمَّن ولن يكون موجودًا عند تحديد المسار، كما يُستخدَم التابع closePath لغلق المسار صراحةً من خلال إضافة جزء سطر حقيقي إلى بداية المسار، وسيُرسم هذا الجزء عند تحديد المسار.
المنحنيات
قد يحتوي المسار على خطوط منحنية، وتكون هذه الخطوط أعقد في رسمها من الخطوط المستقيمة، حيث يرسم التابع quadraticCurveTo منحني إلى نقطة ما، كما يُعطى التابع نقطة تحكم ونقطة وجهة لتحديد انحناء الخط، ويمكن تخيل نقطة التحكم على أنها تسحب الخط لتعطيه انحناءه؛ أما الخط نفسه فلن يمر عليها وإنما سيكون اتجاهه عند نقطتي البدء والنهاية، بحيث إذا رُسم خط مستقيم في ذلك الاتجاه فسيشير إلى نقطة التحكم، ويوضِّح المثال التالي ذلك:
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.beginPath(); cx.moveTo(10, 90); // control=(60,10) goal=(90,90) cx.quadraticCurveTo(60, 10, 90, 90); cx.lineTo(60, 10); cx.closePath(); cx.stroke(); </script>
سنرسم المنحنى التربيعي من اليسار إلى اليمين، وتكون نقطة التحكم هي (60,10)، ثم نرسم خطين يمران بنقطة التحكم تلك ويعودان إلى بداية الخط. سيكون الشكل الناتج أشبه بشعار أفلام ستار تريك Star Trek، كما تستطيع رؤية تأثير نقطة التحكم، بحيث تبدأ الخطوط تاركة الأركان السفلى في اتجاه نقطة التحكم ثم تنحني مرةً أخرى إلى هدفها.
يرسم التابع bezierCurveTo انحناءً قريبًا من ذلك، لكن يكون له نقطتي تحكم أي واحدة عند كل نهاية خط بدلًا من نقطة تحكم واحدة، ويوضِّح المثال التالي سلوك هذا المنحنى:
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.beginPath(); cx.moveTo(10, 90); // control1=(10,10) control2=(90,10) goal=(50,90) cx.bezierCurveTo(10, 10, 90, 10, 50, 90); cx.lineTo(90, 10); cx.lineTo(10, 10); cx.closePath(); cx.stroke(); </script>
تحدد نقطتا التحكم الاتجاه عند كلا النهايتين للمنحنى، وكلما ابتعدنا عن النقطة الموافقة لهما زاد انتفاخ المنحنى في ذلك الاتجاه، كما ستكون تلك المنحنيات أصعب من حيث العمل عليها، فليس من السهل معرفة كيفية إيجاد نقاط التحكم التي توفر الشكل الذي تبحث عنه، حيث نستطيع حسابها أحيانًا، لكن سيكون علينا إيجاد قيمة مناسبة من خلال التجربة والخطأ أحيانًا أخرى.
يُستخدَم التابع arc على أساس طريقة لرسم خط ينحني على حواف دائرة، كما يأخذ زوجًا من الإحداثيات من أجل مركز القوس، ونصف قطر، ثم زاوية بداية وزاوية نهاية.
نستطيع من خلال هذين المعاملَين الأخيرين رسم جزء من الدائرة فقط دون رسمها كلها، كما تقاس الزوايا بالراديان radian وليس بالدرجات، ويعني هذا أن الدائرة الكاملة لها زاوية مقدارها 2π أو 2 * Math.PI، وهي تساوي 6.28 تقريبًا، كما تبدأ الزاوية العد عند النقطة التي على يمين مركز الدائرة وتدور باتجاه عقارب الساعة من هناك، وهنا تستطيع استخدام 0 للبداية ونهاية تكون أكبر من 2π -لتكن 7 مثلًا- من أجل رسم الدائرة كلها.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.beginPath(); // center=(50,50) radius=40 angle=0 to 7 cx.arc(50, 50, 40, 0, 7); // center=(150,50) radius=40 angle=0 to ½π cx.arc(150, 50, 40, 0, 0.5 * Math.PI); cx.stroke(); </script>
رسم المخطط الدائري
لنقل أننا نريد رسم مخطط دائري لنتائج استبيان رضا العملاء عن شركة ما ولتكن EconomiCorp مثلًا، بحيث تحتوي رابطة results على مصفوفة من الكائنات التي تمثل نتائج الاستبيان.
const results = [ {name: "Satisfied", count: 1043, color: "lightblue"}, {name: "Neutral", count: 563, color: "lightgreen"}, {name: "Unsatisfied", count: 510, color: "pink"}, {name: "No comment", count: 175, color: "silver"} ];
سنرسم عددًا من الشرائح الدائرية يتكون كل منها من قوس وزوج من الخطوط ينتهيان إلى مركز ذلك القوس، كما نستطيع حساب الزاوية التي يأخذها كل قوس من خلال قسمة الدائرة الكلية 2π على العدد الكلي للاستجابات، ومن ثم ضرب ذلك العدد -زاوية الاستجابة- في عدد الأشخاص الذين اختاروا عنصرًا ما.
<canvas width="200" height="200"></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); let total = results .reduce((sum, {count}) => sum + count, 0); // ابدأ من القمة let currentAngle = -0.5 * Math.PI; for (let result of results) { let sliceAngle = (result.count / total) * 2 * Math.PI; cx.beginPath(); // center=100,100, radius=100 // من الزاوية الحالية، باتجاه عقارب الساعة بحذاء زاوية الشريحة cx.arc(100, 100, 100, currentAngle, currentAngle + sliceAngle); currentAngle += sliceAngle; cx.lineTo(100, 100); cx.fillStyle = result.color; cx.fill(); } </script>
لا يخبرنا المخطط ماذا تعني تلك الشرائح، لذا سنحتاج إلى طريقة نرسم بها نصوصًا على اللوحة.
النصوص
يوفر سياق رسم اللوحة ثنائي الأبعاد التابعَين fillText وstrokeText، حيث يُستخدَم الأخير في تحديد الأحرف، لكن الذي نحتاج إليه هو fillText عادةً، إذ سيملأ حد النص المعطى بتنسيق fillStyle الحالي.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.font = "28px Georgia"; cx.fillStyle = "fuchsia"; cx.fillText("I can draw text, too!", 10, 50); </script>
تستطيع تحديد حجم النص وتنسيقه ونوع خطه أيضًا باستخدام الخاصية font، ولا يعطينا هذا المثال إلا حجم الخط واسم عائلته، كما من الممكن إضافة ميل الخط italic أو سماكته bold إلى بداية السلسلة النصية لاختيار تنسيق ما، في حين يوفر آخر وسيطين لكل من fillText وstrokeText الموضع الذي سيُرسم فيه الخط، كما يشيران افتراضيًا إلى موضع بداية قاعدة النص الأبجدية التي تكوِّن السطر الذي تقف الحروف عليه، لكن لا تحسب الأجزاء المتدلية من الأحرف مثل حرف j أو p، ونستطيع تغيير الموضع الأفقي ذاك بضبط الخاصية textAlign لتكون "end" أو "center"، وتغيير الموضع الرأسي كذلك من خلال ضبط textBaseline لتكون "top" أو "middle" أو "bottom".
الصور
يُفرَّق عادةً في رسوميات الحواسيب بين الرسوميات المتجهية vector graphics والرسوميات النقطية bitmap graphics، فالأولى هي التي شرحناها في بداية هذا المقال والتي تصف الصورة وصفًا منطقيًا لشكلها؛ أما الرسوميات النقطية فلا تصف الأشكال الحقيقية، بل تعمل مع بيانات البكسلات الخاصة بالصورةk والتي هي مربعات من النقاط الملونة على الشاشة.
يسمح لنا التابع drawImage برسم بيانات البكسلات على اللوحة، ويمكن استخراج تلك البيانات من عنصر <img> أو من لوحة أخرى، كما ينشئ المثال التالي عنصر <img> منفصل ويحمِّل ملف الصورة إليه، لكنه لا يستطيع البدء بالرسم مباشرةً من تلك الصورة بما أنّ المتصفح قد لا يكون حمَّلها بعد، ولحل هذا فإننا نسجل معالج الحدث "load" لتنفيذ الرسم بعد تحميل الصورة.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); let img = document.createElement("img"); img.src = "img/hat.png"; img.addEventListener("load", () => { for (let x = 10; x < 200; x += 30) { cx.drawImage(img, x, 10); } }); </script>
سيرسم التابع drawImage الصورة بحجمها الحقيقي افتراضيًا، لكن يمكن إعطاؤه وسيطَين إضافيين لتحديد عرض وطول مختلفَين، فإذا أعطي drawImage تسعة وسائط، فيمكن استخدامه لرسم جزء من الصورة، ويوضِّح الوسيط الثاني حتى الخامس -أي x وy والعرض والطول- المستطيل الذي في الصورة المصدرية والتي يجب نسخها؛ أما الوسيط السادس حتى التاسع فتعطينا المستطيل على اللوحة الذي سيُنسخ، كما يمكن استخدام هذا لتحزيم عدة شرائح أو عناصر من صورة (تسمى sprites أي عفاريت) في ملف صورة واحد، ثم رسم الجزء الذي نحتاج إليه فقط، فلدينا مثلًا هذه الصورة التي تحتوي على شخصية لعبة في عدة وضعيات:
إذا غيرنا الوضع الذي نرسمه فسنستطيع عرض تحريك يبدو مثل شخصية تمشي، في حين نستخدِم التابع clearRect لتحريك صورة على اللوحة، وهو يمثِّل fillRect، لكنه يجعل المستطيل شفافًا بدلًا من تلوينه حاذفًا البكسلات المرسومة سابقًا، ونحن نعرف أنّ كل عفريت وكل صورة فرعية يكون عرضها 24 بكسل وارتفاعها 30 بكسل، وعلى ذلك تحمِّل الشيفرة التالية الصورة ثم تضبط فترةً زمنيةً متكررةً لرسم الإطار التالي:
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); let img = document.createElement("img"); img.src = "img/player.png"; let spriteW = 24, spriteH = 30; img.addEventListener("load", () => { let cycle = 0; setInterval(() => { cx.clearRect(0, 0, spriteW, spriteH); cx.drawImage(img, // المستطيل المصدر cycle * spriteW, 0, spriteW, spriteH, // مستطيل الوجهة 0, 0, spriteW, spriteH); cycle = (cycle + 1) % 8; }, 120); }); </script>
تتعقب رابطة cycle موضعنا في هذا التحريك وتتزايد مرةً لكل إطار، ثم تقفز عائدةً إلى المجال 0 إلى 7 باستخدام عامِل الباقي، بعدها تُستخدَم هذه الرابطة بعد ذلك لحساب الإحداثي x الذي يحتوي عليه العفريت الذي في الوضع الحالي في الصورة.
التحول
ماذا لو أردنا جعل الشخصية تمشي إلى اليسار بدلًا من اليمين؟ لا شك أننا نستطيع رسم مجموعة أخرى من عناصر العفاريت، لكننا نستطيع توجيه اللوحة أيضًا لترسم الصورة بعكس الطريقة التي ترسمها بها، كما سيزيد استدعاء التابع scale حجم أيّ شيء يُرسم بعده، وهو يأخذ معاملَين أحدهما لضبط المقياس الأفقي والآخر للعمودي.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); cx.scale(3, .5); cx.beginPath(); cx.arc(50, 50, 40, 0, 7); cx.lineWidth = 3; cx.stroke(); </script>
سيتسبب تغيير حجم الصورة في تمديد كل شيء فيها أو ضغطه بما فيها عرض الخط، وإذا غيّرنا المقياس ليكون بقيمة سالبة، فستنقلب الصورة معكوسة، حيث يحدث الانعكاس حول النقطة (0,0) التي تعني أننا سنقلب أيضًا اتجاه نظام الإحداثيات، فحين نطبِّق مقياسًا أفقيًا مقداره -1، فسيكون الشكل المرسوم عند الموضع 100 على إحداثي x في الموضع الذي كان -100 من قبل، لذا لا نستطيع إضافة cx.scale(-1, 1) من أجل عكس الصورة وحسب قبل استدعاء drawImage، لأنه سيجعل الصورة تتحرك خارج اللوحة بحيث تكون غير مرئية، ونعدّل الإحداثيات المعطاة إلى drawImage من أجل ضبط هذا برسم الصورة في الموضع -50 على الإحداثي x بدلًا من 0.
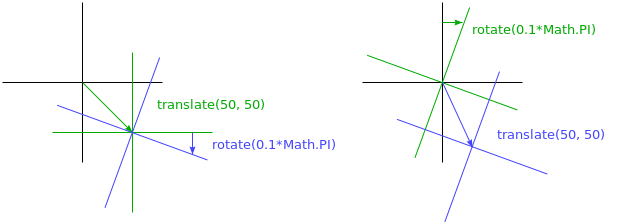
هناك حل آخر لا يحتاج إلى الشيفرة التي تنفذ الرسم كي يدرك تغير المقياس، وهو تعديل المحور الذي يحدث تغيير الحجم حوله، كما يمكن استخدام عدة توابع أخرى غير scale للتأثير في نظام إحداثيات اللوحة، حيث تستطيع تدوير الأشكال المرسومة تاليًا باستخدام التابع rotate ونقلها باستخدام translate، لكن المثير في الأمر والمحير أيضًا هو أنّ تلك التحويلات تُكدَّس، بمعنى أنّ كل واحد يُحدِث نسبةً إلى ما قبله من تحولات، وبناءً عليه فإذا استخدمنا translate لتحريك 10 بكسلات مرتين أفقيًأ، فسيُرسم كل شيء مزاحًا إلى اليمين بمقدار 20 بكسل؛ أما إذا أزحنا مركز نظام الإحداثيات أولًا إلى (50,50) ثم دوّرنا بزاوية 20 درجة -أي 0.1π راديان-، فسيَحدث التدوير حول النقطة (50,50).
لكن إذا نفذّنا التدوير بمقدار عشرين درجة أولًا ثم أزحنا بمقدار (50,50)، فسيحدث الإزاحة عند نظام الإحداثيات المدوَّر، وعليه سيعطينا اتجاهًا مختلفًا، ونستنتج من هذا أنّ ترتيب تطبيق التحويلات مهم. وتعكس الشيفرة التالية الصورة حول الخط العمودي عند الموضع x:
function flipHorizontally(context, around) { context.translate(around, 0); context.scale(-1, 1); context.translate(-around, 0); }
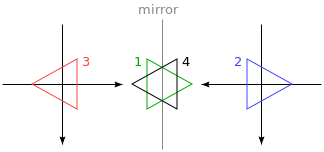
ننقل المحور y إلى حيث نريد لمرآتنا أن تكون ونطبِّق المرآة، ثم نعيد المحور مرةً أخرى إلى موضعه المناسب في العالم المعكوس، وتوضِّح الصورة التالية ذلك:
توضِّح الصورة نظام الإحداثيات قبل وبعد الانعكاس على طول الخط المركزي وتُرقَّم المثلثات لتوضيح كل خطوة، فإذا رسمنا مثلثًا عند الموضع x الموجب، فسيكون حيث يكون المثلث 1، إذ نستدعي flipHorizontally لينفِّذ الإزاحة إلى اليمين أولًا لنصل إلى المثلث 2، ثم يغيِّر الحجم ويعكس المثلث إلى الموضع 3، غير أنه لا يُفترض أن يكون هناك إذا عُكِس في الخط المعطى، فيأتي استدعاء translate الثاني ليصلح ذلك، بحيث يلغي الإزاحة الأولى ويُظهِر المثلث 4 في الموضع الذي يُفترض أن يكون فيه تمامًا، ونستطيع الآن رسم الشخصية المعكوسة في الموضع (100,0) من خلال عكس العالم حول المركز العمودي للشخصية.
<canvas></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); let img = document.createElement("img"); img.src = "img/player.png"; let spriteW = 24, spriteH = 30; img.addEventListener("load", () => { flipHorizontally(cx, 100 + spriteW / 2); cx.drawImage(img, 0, 0, spriteW, spriteH, 100, 0, spriteW, spriteH); }); </script>
تخزين التحويلات ومحوها
تظل التحويلات قائمةً حتى بعد رسمنا لتلك الشخصية المعكوسة، إذ سيكون كل شيء نرسمه بعد ذلك معكوسًا أيضًا وقد لا نريد هذا، حيث من الممكن هنا حفظ التحويل الحالي ثم إجراء بعض الرسم والتحويل، وبعدها استعادة التحويل القديم مرةً أخرى، فغالبًا يُعَدّ ما سبق الإجراء الأفضل لإجراء وظيفة دالة ما تحتاج إلى تحويل نظام الإحداثيات لفترة مؤقتة، حيث سنحفظ أيّ تحويل استخدمته الشيفرة التي استدعت الدالة، ثم تضيف الدالة ما تشاء من التحويلات فوق التحويل الحالي، وبعد ذلك نرجع إلى التحول الذي بدأنا به مرةً أخرى.
يدير عملية التحول تلك التابعَين save وrestore على سياق اللوحة ثنائية الأبعاد لأنهما يحتفظان بمكدس من حالات التحول، وحين نستدعي save، فستُدفَع الحالة الراهنة إلى المكدس، ثم تؤخَذ الحالة التي على قمة المكدس مرةً أخرى عند استدعاء restore وتُستخدم على أنها التحول الحالي للسياق، كما نستطيع كذلك استدعاء resetTransform من أجل إعادة ضبط التحول بالكامل.
توضِّح الدالة branch في المثال التالي ما يمكن فعله بدالة تغير التحول، ثم تستدعي دالةً -هي نفسها في هذه الحالة- تتابع الرسم بالتحول المعطى، حيث ترسم تلك الدالة شكلًا يشبه الشجرة من خلال رسم خط ثم نقل مركز نظام الإحداثيات إلى نهاية ذلك الخط، ثم استدعاء نفسها مرتين، مرةً مدارةً إلى اليسار، ثم مرةً أخرى مدارة إلى اليمين، إذ يقلل كل استدعاء من طول الفرع المرسوم ثم يتوقف التعاود حين يقل الطول عن 8.
<canvas width="600" height="300"></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); function branch(length, angle, scale) { cx.fillRect(0, 0, 1, length); if (length < 8) return; cx.save(); cx.translate(0, length); cx.rotate(-angle); branch(length * scale, angle, scale); cx.rotate(2 * angle); branch(length * scale, angle, scale); cx.restore(); } cx.translate(300, 0); branch(60, 0.5, 0.8); </script>
إذا لم توجد استدعاءات إلى save وrestore فسيكون موضع ودران الاستدعاء الذاتي للمرة الثانية للدالة branch هما اللذان أُنشئا بالاستدعاء الأول، إذ لن تتصل بالفرع الحالي وإنما بالفرع الداخلي الأقصى إلى اليمين والمرسوم بالاستدعاء الأول، وعلى ذلك يكون الشكل الناتج ليس شجرةً أبدًا.
عودة إلى اللعبة
عرفنا الآن ما يكفي عن الرسم على اللوحة وسنعمل الآن على نظام عرض مبني على لوحة من أجل اللعبة التي من المقال السابق، إذ لم تعُد الشاشة الجديدة تعرض صناديق ملونة فحسب، وإنما سنستخدِم drawImage من أجل رسم صور تمثِّل عناصر اللعبة، كما سنعرِّف كائن عرض جديد يدعى CanvasDisplay ويدعم الواجهة نفسها مثل DOMDisplay من المقال السابق خاصةً التابعَين syncState وclear، حيث سيحتفظ هذا الكائن بمعلومات أكثر قليلًا من DOMDisplay، فبدلًا من استخدام موضع التمرير لعنصر DOM الخاص به، فهو يتتبع نافذة رؤيته التي تخبرنا بالجزء الذي ننظر إليه في المستوى، ثم يحتفظ بالخاصية flipPlayer التي تمكّن اللاعب من مواجهة الاتجاه الذي كان يتحرك فيه حتى لو كان واقفًا لا يتحرك.
class CanvasDisplay { constructor(parent, level) { this.canvas = document.createElement("canvas"); this.canvas.width = Math.min(600, level.width * scale); this.canvas.height = Math.min(450, level.height * scale); parent.appendChild(this.canvas); this.cx = this.canvas.getContext("2d"); this.flipPlayer = false; this.viewport = { left: 0, top: 0, width: this.canvas.width / scale, height: this.canvas.height / scale }; } clear() { this.canvas.remove(); } }
يحسب التابع syncState أولًا نافذة رؤية جديدة ثم يرسم مشهد اللعبة عند الموضع المناسب.
CanvasDisplay.prototype.syncState = function(state) { this.updateViewport(state); this.clearDisplay(state.status); this.drawBackground(state.level); this.drawActors(state.actors); };
سيكون على هذا التنسيق من العرض إعادة رسم الخلفية عند كل تحديث على عكس DOMDisplay، ولأن الأشكال التي على اللوحة ما هي إلا بكسلات، فليس لدينا طريقةً لتحريكها أو حتى حذفها بعد رسمها، والطريقة الوحيدة لدينا لتحديث شاشة اللوحة هي مسحها ثم إعادة رسم المشهد.، وقد يحدث أن نكون قد مرّرنا نافذة الرؤية من الشاشة، وهذا يتطلب أن تكون الخلفية في موضع مختلف.
يتحقق التابع updateViewport إذا كان اللاعب قريبًا للغاية من حافة الشاشة أم لا، وإذا كان كذلك فسينقل نافذة الرؤية، وهو في هذا يشبه التابع scrollPlayerIntoView الخاص بـ DOMDisplay.
CanvasDisplay.prototype.updateViewport = function(state) { let view = this.viewport, margin = view.width / 3; let player = state.player; let center = player.pos.plus(player.size.times(0.5)); if (center.x < view.left + margin) { view.left = Math.max(center.x - margin, 0); } else if (center.x > view.left + view.width - margin) { view.left = Math.min(center.x + margin - view.width, state.level.width - view.width); } if (center.y < view.top + margin) { view.top = Math.max(center.y - margin, 0); } else if (center.y > view.top + view.height - margin) { view.top = Math.min(center.y + margin - view.height, state.level.height - view.height); } };
تتأكد الاستدعاءات إلى Math.max وMath.min من أنّ نافذة الرؤية لا تعرض مساحةً خارج المستوى، حيث تضمن Math.max(x, 0) أنّ العدد الناتج ليس أقل من صفر، كما تضمن Math.min بقاء القيمة تحت الحد المعطى، وسنستخدم عند مسح الشاشة لونًا مختلفًا وفقًا لحالة اللعب إذا فازت أو خسرت، بحيث يكون لونًا فاتحًا في حالة الفوز، وداكنًا في الخسارة.
CanvasDisplay.prototype.clearDisplay = function(status) { if (status == "won") { this.cx.fillStyle = "rgb(68, 191, 255)"; } else if (status == "lost") { this.cx.fillStyle = "rgb(44, 136, 214)"; } else { this.cx.fillStyle = "rgb(52, 166, 251)"; } this.cx.fillRect(0, 0, this.canvas.width, this.canvas.height); };
نمر على المربعات المرئية في نافذة الرؤية الحالية من أجل رسم الخلفية باستخدام الطريقة نفسها التي اتبعناها في التابع touches في المقال السابق.
let otherSprites = document.createElement("img"); otherSprites.src = "img/sprites.png"; CanvasDisplay.prototype.drawBackground = function(level) { let {left, top, width, height} = this.viewport; let xStart = Math.floor(left); let xEnd = Math.ceil(left + width); let yStart = Math.floor(top); let yEnd = Math.ceil(top + height); for (let y = yStart; y < yEnd; y++) { for (let x = xStart; x < xEnd; x++) { let tile = level.rows[y][x]; if (tile == "empty") continue; let screenX = (x - left) * scale; let screenY = (y - top) * scale; let tileX = tile == "lava" ? scale : 0; this.cx.drawImage(otherSprites, tileX, 0, scale, scale, screenX, screenY, scale, scale); } } };
ستُرسم المربعات غير الفارغة باستخدام drawImage، وتحتوي الصورة otherSprites على الصور المستخدَمة للعناصر سوى اللاعب، فهي تحتوي من اليسار إلى اليمين على مربع الحائط ومربع الحمم البركانية وعفريت للعملة.
تكون مربعات الخلفية بقياس 20*20 بكسل بما أننا سنستخدم نفس المقياس الذي استخدمناه في DOMDisplay، وعلى ذلك ستكون إزاحة مربعات الحمم البركانية هي 20 -وهي قيمة رابطة scale-؛ أما إزاحة الجدران فستكون صفرًا، كما لن ننتظر تحميل عفريت الصورة لأنّ استدعاء drawImage بصورة لم تحمَّل بعد فلن يُحدث شيئًا، وبالتالي فقد نفشل في رسم اللعبة في أول بضعة إطارات أثناء تحميل تلك الصورة لكنها ليست تلك بالمشكلة الكبيرة، وسيظهر المشهد الصحيح بمجرد انتهاء التحميل بما أننا نظل نحدث الشاشة.
ستُستخدم الشخصية الماشية التي رأيناها سابقًا لتمثل اللاعب، ويجب على الشيفرة التي ترسمها اختيار العفريت الصحيح والاتجاه الصحيح كذلك لحركة اللاعب الآنية، إذ تحتوي أول ثمانية عفاريت على تأثير المشي، كما نكرر تلك العناصر عند مشي اللاعب على الأرضية وفقًا للزمن الحالي، وبما أننا نبدِّل الإطارات كل 60 ميلي ثانية، فسنقسم الوقت على 60 أولًا؛ أما حين يقف اللاعب ساكنًا فسنرسم العفريت التاسع، ونستخدِم العنصر العاشر من أقصى اليمين من أجل رسم تأثير القفز الذي نعرفه من خلال كون السرعة العمودية لا تساوي صفرًا.
يجب على التابع تعديل إحداثيات x والعرض بمقدار معطى (playerXOverlap) لمعادلة عرض العفاريت بما أنها أعرض من كائن اللاعب -24 بكسل بدلًا من 16- لتسمح ببعض المساحة للأذرع والأقدام.
let playerSprites = document.createElement("img"); playerSprites.src = "img/player.png"; const playerXOverlap = 4; CanvasDisplay.prototype.drawPlayer = function(player, x, y, width, height){ width += playerXOverlap * 2; x -= playerXOverlap; if (player.speed.x != 0) { this.flipPlayer = player.speed.x < 0; } let tile = 8; if (player.speed.y != 0) { tile = 9; } else if (player.speed.x != 0) { tile = Math.floor(Date.now() / 60) % 8; } this.cx.save(); if (this.flipPlayer) { flipHorizontally(this.cx, x + width / 2); } let tileX = tile * width; this.cx.drawImage(playerSprites, tileX, 0, width, height, x, y, width, height); this.cx.restore(); };
يُستدعى التابع drawPlayer بواسطة drawActors التي تكون مسؤولةً عن رسم جميع الكائنات الفاعلة في اللعبة.
CanvasDisplay.prototype.drawActors = function(actors) { for (let actor of actors) { let width = actor.size.x * scale; let height = actor.size.y * scale; let x = (actor.pos.x - this.viewport.left) * scale; let y = (actor.pos.y - this.viewport.top) * scale; if (actor.type == "player") { this.drawPlayer(actor, x, y, width, height); } else { let tileX = (actor.type == "coin" ? 2 : 1) * scale; this.cx.drawImage(otherSprites, tileX, 0, width, height, x, y, width, height); } } };
عند رسم أيّ شيء غير اللاعب فإننا ننظر أولًا في نوعه لنعرف إزاحة العفريت الصحيح، فمربع الحمم إزاحته 20، اما عفريت العملة فإزاحته 40، أي أنه ضعف مقدار scale، كما يجب طرح موضع نافذة الرؤية على لوحتنا لتتوافق مع أعلى يسار نافذة الرؤية وليس أعلى يسار المستوى، كما يمكن استخدام translate كذلك، فكلاهما يصلح.
يركِّب المستند التالي الشاشة الجديدة بـ runGame:
<body> <script> runGame(GAME_LEVELS, CanvasDisplay); </script> </body>
اختيار واجهة الرسوميات
لدينا عدة خيارات يمكن استخدامها لتوليد الرسوميات في المتصفح من HTML إلى SVG إلى اللوحة، وليس هناك واحد يفضُلها جميعًا في كل حالة، فكل واحد له نقاط قوته وضعفه، فلغة HTML مثلًا تمتاز بالبساطة، كما تتكامل جيدًا مع النصوص، بينما تسمح لك كل من SVG واللوحة برسم النصوص، لكنها لن تمكّنك من موضعة تلك النصوص أو تغليفها إذا أخذت أكثر من سطر واحد؛ أما في الصور المبنية على HTML فسيكون من السهل إدراج كتل نصية فيها.
يمكن استخدام SVG من ناحية أخرى لإنتاج رسوميات واضحة مهما كان مستوى التكبير، فهي مصممة للرسم على عكس HTML، وعليه فهي ملائمة أكثر لهذا الغرض، كذلك تستطيع كل من SVG وHTML بناء هيكل بيانات مثل شجرة DOM تمثل صورتنا، وهذا يمكِّننا من تعديل العناصر بعد رسمها، لذا سيكون من الصعب استخدام اللوحة من أجل تغيير جزء صغير في صورة كبيرة كل حين للاستجابة لأفعال المستخدِم أو بسبب تحريك ما، كما يسمح DOM لنا بتسجيل معالجات أحداث الفأرة على كل عنصر في الصورة حتى الأشكال المرسومة باستخدام SVG؛ أما اللوحة فلا يمكن فعل ذلك فيها.
غير أنه يمكن استخدام نهج المنظور البكسلي pixel-oriented للوحة عند رسم أعداد كبيرة جدًا من عناصر صغيرة، إذ تكون تكلفة الشكل الواحد فيها تافهةً بما أنها لا تبني هياكل بيانات وإنما تكرِّر الرسم على مساحة البكسل نفسها، كما يمكن تنفيذ تأثيرات مثل إخراج مشهد بسرعة بكسل واحد في كل مرة -باستخدام متعقب أشعة ray tracer مثلًا-، أو معالجة لاحقة لصورة باستخدام جافاسكربت مثل تأثير الضباب أو التشويش، وذلك لا يمكن معالجته بواقعية إلا من المنظور البكسلي.
قد نرغب أحيانًا في جمع بعض تلك التقنيات معًا، فقد نرسم مخططًا باستخدام SVG أو اللوحة، لكن نُظهر المعلومات النصية عن طريق وضع عنصر HTML فوق الصورة؛ أما بالنسبة للتطبيقات التي لا تتطلب موارد كثيرة، فليس من المهم أيّ واجهة نختارها، إذ يمكن استخدام العرض الذي بنيناه في هذا المقال من أجل لعبتنا، كان يمكن تنفيذه باستخدام أي من التقنيات الرسومية الثلاثة بما أنه لا يحتاج إلى رسم نصوص أو معالجة تفاعلات للفأرة أو التعامل مع عدد ضخم من العناصر.
خاتمة
لقد ناقشنا في هذا المقال تقنيات رسم التصاميم المرئية والرسوميات في المتصفح مع تناول عنصر <canvas> بالتفصيل، كما عرفنا أنّ عقدة اللوحة تمثِّل مساحةً في مستند قد يرسم برنامجنا عليها، وينفَّذ هذا الرسم من خلال رسم كائن سياقي ينشئه التابع getContext، كما تسمح لنا واجهة الرسم ثنائية الأبعاد بملء وتخطيط أشكال كثيرة، وتحدد خاصية السياق fillStyle كيفية ملء الأشكال، في حين تتحكم الخاصيتان strokeStyle وlineWidth في طريقة رسم الخطوط.
تُرسم المستطيلات وأجزاء النصوص باستدعاء تابع واحد، حيث يرسم التابعان fillRect وstrokeRect مستطيلات، بينما يرسم كل من fillText وstrokeText نصوصًا؛ أما إذا أردنا إنشاء أشكال فيجب علينا بناء مسار أولًا، كما ينشئ استدعاء beginPath مسارًا جديدًا، كما يمكن إضافة خطوط ومنحنيات إلى المسار الحالي باستخدام عدة توابع أخرى، حيث يضيف التابع lineTo مثلًا خطًا مستقيمًا، وإذا انتهى المسار، فيمكن استخدام التابع fill لملئه أو التابع stroke لتحديده.
تُنقل البكسلات من صورة أو لوحة أخرى إلى لوحتنا باستخدام التابع drawImage، حيث يرسم هذا التابع الصورة المصدرية كلها افتراضيًا، لكن يمكن إعطاؤه معاملات إضافية من أجل نَسخ جزء محدد من الصورة، وقد استخدَمنا ذلك في لعبتنا بنسخ أوضاع شخصية اللاعب المختلفة من صورة تحتوي على عدة أوضاع.
تسمح لنا التحولات برسم شكل في اتجاهات مختلفة، فسياق الرسم ثنائي الأبعاد به تحول راهن يمكن تغييره باستخدام التوابع translate وscale وrotate، إذ ستؤثِّر على جميع عمليات الرسم اللاحقة، كما يمكن حفظ حالة التحول باستخدام التابع save واستعادتها باستخدام التابع restore، وأخيرًا يُستخدَم التابع clearRect عند عرض تحريك على اللوحة من أجل مسح جزء من اللوحة قبل إعادة رسمه.
تدريبات
الأشكال
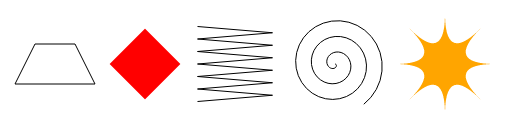
اكتب برنامجًا يرسم الأشكال التالية على لوحة:
- شبه منحرف وهو مستطيل أحد جوانبه المتوازية أطول من الآخر.
-
ماسة حمراء وهي مستطيل مُدار بزاوية 45 درجة مئوية، أو
¼πراديان. - خط متعرِّج Zigzag.
- شكل حلزوني من 100 جزء من خطوط مستقيمة.
- نجمة صفراء.
ربما تود الرجوع إلى شرح كل من Math.cos وMath.sin في مقال نموذج كائن المستند في جافاسكريبت عند رسم آخر شكلين لتعرف كيف تحصل على إحداثيات على دائرة باستخدام هاتين الدالتين، كما ننصحك بإنشاء دالة لكل شكل وتمرير الموضع إليها و-إذا أردت- مرر إليها الخصائص الأخرى مثل الحجم وعدد النقاط على أساس معاملات، كما يوجد حل بديل بأن تكتب أرقامًا ثابتةً في شيفرتك مما سيجعل الشيفرة أصعب في القراءة والتعديل.
تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen.
<canvas width="600" height="200"></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); // شيفرتك هنا. </script>
إرشادات الحل
يمكن رسم شبه المنحرف ببساطة باستخدام مسار، لذا اختر إحداثيات مركزية مناسبة وأضف كل ركن من الأركان الأربعة حول المركز؛ أما الماسة فيمكن رسمها بطريقة بسيطة باستخدام مسار أو باستخدام تحول rotate، وإذا أردت تجربة التحول فسيكون عليك تطبيق طريقة تشبه ما فعلنا في دالة flipHorizontally، كما يجب أن تنتقل translate إلى مركز المستطيل بدلًا من الإحداثي الصفري بما أنك ستدور حول مركزه، ثم تدور ثم تُعاد إلى مكانها مرةً أخرى، وتأكد من إعادة ضبط التحول بعد رسم أيّ شكل ينشئ تحولًا.
أما بالنسبة للخط المتعرِّج فليس من المنطقي كتابة استدعاء جديد إلى lineTo في كل جزء من أجزاء الخط، وإنما يجب استخدام حلقة تكرارية، بحيث تجعل كل تكرار فيها يرسم جزأين -اليمين ثم اليسار مرةً أخرى- أو جزءًا واحدًا من أجل تحديد اتجاه الذهاب إلى اليمين أم اليسار والذي يكون بالاعتماد على عامل حالة من فهرس الحلقة i (مثل إذا كان i % 2 == 0 اذهب لليسار وإلا، لليمين)، كما ستحتاج إلى حلقة تكرارية من أجل الشكل الحلزوني، فإذا رسمت سلسلةً من النقاط تتحرك فيها كل نقطة إلى الخارج على دائرة حول مركز الشكل فستحصل على دائرة؛ أما إذا استخدمت الحلقة التكرارية وغيرت نصف قطر الدائرة التي تضع النقطة الحالية عليها ونفّذت عدة حركات فستحصل على شكل حلزوني.
تُبنى النجمة المصورة من خطوط quadraticCurveTo، لكن يمكن رسمها باستخدام الخطوط المستقيمة أيضًا من خلال تقسيم دائرة إلى ثمانية أجزاء إذا أردت رسم نجمة بثمانية نقاط، أو إلى أي عدد من الأجزاء تريد، ثم ارسم خطوطًا بين تلك النقاط لتجعلها تنحني نحو مركز النجمة؛ أما إذا استخدمت quadraticCurveTo، فستستطيع جعل المركز على أساس نقطة تحكم.
المخطط الدائري
رأينا في هذا المقال مثالًا لبرنامج يرسم مخططًا دائريًا، عدِّل هذا البرنامج ليظهر اسم كل تصنيف بجانب الشريحة التي تمثله، وحاول إيجاد طريقة مناسبة مرئيًا لموضعة ذلك النص تلقائيًا بحيث تصلح لأنواع البيانات الأخرى أيضًا، كما تستطيع الافتراض أنّ التصانيف كبيرة بحيث تترك مساحةً كافيةً لعناوينها، وقد تحتاج إلى دالتي Math.sin وMath.cos مرةً أخرى من مقال نموذج كائن المستند في جافاسكريبت.
تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen.
<canvas width="600" height="300"></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); let total = results .reduce((sum, {count}) => sum + count, 0); let currentAngle = -0.5 * Math.PI; let centerX = 300, centerY = 150; // Add code to draw the slice labels in this loop. for (let result of results) { let sliceAngle = (result.count / total) * 2 * Math.PI; cx.beginPath(); cx.arc(centerX, centerY, 100, currentAngle, currentAngle + sliceAngle); currentAngle += sliceAngle; cx.lineTo(centerX, centerY); cx.fillStyle = result.color; cx.fill(); } </script>
إرشادات الحل
ستحتاج إلى استدعاء fillText وضبط خصائص السياق textAlign وtextBaseline بطريقة تجعل النص يكون حيث تريد، وستكون الطريقة المناسبة لموضعة العناوين هي وضع النصوص على الخطوط الذاهبة من مركز المخطط إلى منتصف الشريحة، كما لا تريد وضع النصوص مباشرةً على جانب المخطط على بعد مقدار ما من البكسلات، وتكون زاوية هذا الخط هي currentAngle + 0.5 * sliceAngle، كما تبحث الشيفرة التالية عن موضع عليه بحيث يكون على بعد 120 بكسل من المركز:
let middleAngle = currentAngle + 0.5 * sliceAngle; let textX = Math.cos(middleAngle) * 120 + centerX; let textY = Math.sin(middleAngle) * 120 + centerY;
أما بالنسبة لـ textBaseline، فإنّ القيمة "middle" مناسبة عند استخدام ذلك المنظور، إذ يعتمد ما تستخدِمه لـ textAlign على الجانب الذي تكون فيه من الدائرة، فإذا كنت على اليسار، فيجب أن تكون "right" والعكس بالعكس، وذلك كي يكون موضع النص بعيدًا عن الدائرة.
إذا لم تعرف كيف تجد الجانب الذي عليه زاوية ما من الدائرة، فانظر في شرح Math.cos في نموذج كائن المستند في جافاسكريبت، إذ يخبرك جيب التمام cosine لتلك الدالة بالإحداثي x الموافق لها، والذي يخبرنا بدوره على أي جانب من الدائرة نحن.
الكرة المرتدة
استخدام تقنية requestAnimationFrame التي رأيناها في مقال نموذج كائن المستند في جافاسكريبت والمقال السابق من أجل رسم صندوق فيه كرة مرتدة تتحرك بسرعة ثابتة وترتد عن جوانب الصندوق عندما تصطدم بها.
تستطيع تعديل شيفرة التدريب لكتابة الحل وتشغيلها في طرفية المتصفح إن كنت تقرأ من متصفح، أو بنسخها إلى codepen.
<canvas width="400" height="400"></canvas> <script> let cx = document.querySelector("canvas").getContext("2d"); let lastTime = null; function frame(time) { if (lastTime != null) { updateAnimation(Math.min(100, time - lastTime) / 1000); } lastTime = time; requestAnimationFrame(frame); } requestAnimationFrame(frame); function updateAnimation(step) { // شيفرتك هنا. } </script>
إرشادات الحل
يسهل رسم الصندوق باستخدام strokeRect، لذا عرِّف رابطةً تحمل حجمه أو عرِّف رابطتَين إذا كان عرض الصندوق يختلف عن طوله؛ أما لإنشاء كرة مستديرة، فابدأ مسارًا واستدعي arc(x, y, radius, 0, 7) الذي ينشئ قوسًا من الصفر إلى أكثر من دائرة كاملة ثم املأ المسار.
استخدِم الصنف Vec من المقال السابق ليصف نموذج سرعة الكرة وموضعها، وأعطه سرعةً ابتدائيةً يفضَّل أن تكون عموديةً فقط أو أفقيةً فقط، ثم اضرب تلك السرعة بمقدار الوقت المنقضي لكل إطار، وحين تقترب الكرة جدًا من حائط عمودي، اعكس المكوِّن x في سرعتها، وبالمثل اعكس المكوِّن y إذا اصطدمت بحائط أفقي، وبعد إيجاد موضع الكرة وسرعتها الجديدين، استخدم clearRect لحذف المشهد وإعادة رسمه باستخدام الموضع الجديد.
الانعكاس المحسوب مسبقا
إنّ أحد عيوب التحولات أنها تبطئ عملية الرسومات النقطية bitmaps، إذ يجب تحويل موضع وحجم كل بكسل، ويتسبب ذلك في زيادة كبيرة في وقت الرسم في المتصفحات، كما لا تمثِّل تلك مشكلةً في لعبتنا التي نرسم فيها عفريتًا واحدًا؛ أما رسم مئات الشخصيات أو آلاف الجزيئات التي تدور في الهواء نتيجة انفجار مثلًا، فستكون تلك معضلةً حقيقيةً.
فكِّر في طريقة تسمح برسم شخصية معكوسة دون تحميل ملفات صور إضافية، ودون الحاجة إلى إنشاء استدعاءات drawImage متحولة لكل إطار.
إرشادات الحل
تستطيع استخدام عنصر اللوحة على أساس صورة مصدرية عند استخدام drawImage، حيث يمكن إنشاء عنصر <canvas> آخر دون إضافته إلى المستند وسحب عناصر العفاريت المعكوسة إليه مرةً واحدةً، وعند رسم إطار حقيقي ننسخ تلك المعكوسة إلى اللوحة الأساسية، لكن يجب توخي الحذر لأن الصور لا تحمَّل فورًا، فنحن ننفِّذ الرسم المعكوس مرةً واحدةً فقط، وإذا نفَّذناه قبل تحميل الصورة، فلن ترسم أي شيء، كما يمكن استخدام معالج "load" الذي على الصورة على أساس مصدر رسم مباشرةً، وسيكون فارغًا إلى أن نرسم الشخصية عليه.
ترجمة -بتصرف- للفصل السابع عشر من كتاب Elequent Javascript لصاحبه Marijn Haverbeke.












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.