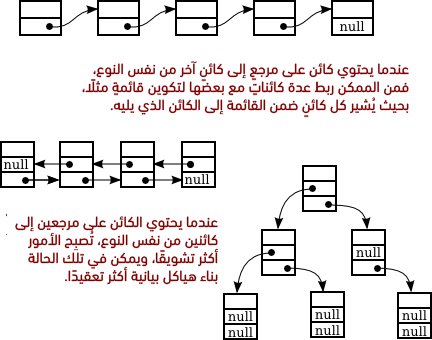
يتضمَّن أي كائنٍ object صالحٍ للاستعمال عددًا من متغيِّرات النسخ instance variables. عندما يُعطى نوع متغير نسخةٍ معين من قِبل اسم صنف class أو واجهة interface، فسيحمل هذا المتغير مرجًعا reference إلى كائنٍ آخر، ويُطلَق على المرجع اسم مؤشر pointer، ويُقال أن المُتغيِّر يُشير إلى كائنٍ ما. ومع ذلك، قد يحتوي المتغيِّر على القيمة الخاصة null؛ وفي تلك الحالة، لا يُشير المُتغير فعليًا إلى أي شيء. في المقابل، عندما يحتوي كائنٌ على متغير نسخة instance variable يُشير فعليًا إلى كائنٍ آخر، يُقال أن الكائنين مربوطين من خلال المؤشر. إن غالبية بنى البيانية data structures المعقدة مبنيّةٌ على تلك الفكرة؛ أي ربط عدة كائناتٍ ببعضها بعضًا.
الترابط التعاودي Recursive Linking
عندما يتضمَّن كائنٌ معينٌ مُتغيِّر نسخة instance variable يُشير إلى كائنٍ آخر من نفس نوع الكائن الأصلي، يُقال أن تعريف الصنف تعاودي recursive. يحدث هذا النوع من التعاود في كثير من الحالات، فإذا كان لدينا مثلًا صنفٌ مُصمَّمٌ لتمثيل الموظفين العاملين ضمن شركةٍ معينة، بحيث يُشرف على كل موظف باستنثاء رئيس الشركة موظفٌ آخر ضمن نفس الشركة. في تلك الحالة، ينبغي أن يتضمَّن الصنف Employee مُتغيّر نسخة من النوع Employee لتمثيل المشرف. يمكننا تعريف الصنف على النحو التالي:
public class Employee { String name; // اسم الموظف Employee supervisor; // مشرف الموظف . . // متغيرات وتوابع نسخ أخرى . } // نهاية صنف الموظف
إذا كان emp متغيرًا من النوع Employee، فإن emp.supervisor هو بالضرورة متغيرٌ آخر من النوع Employee؛ فإذا كان emp يُشير إلى رئيس الشركة، فينبغي أن تكون قيمة emp.supervisor فارغة أي تُساوِي null للدلالة على أن رئيس الشركة ليس لديه أي مشرف. إذا أردنا طباعة اسم المشرف الخاص بموظف معين، يُمكِننا استخدام الشيفرة التالية على سبيل المثال:
if ( emp.supervisor == null) { System.out.println( emp.name + " is the boss and has no supervisor!" ); } else { System.out.print( "The supervisor of " + emp.name + " is " ); System.out.println( emp.supervisor.name ); }
لنفترض الآن أننا نريد معرفة عدد المشرفين الواقعين بين موظفٍ معين وبين رئيس الشركة. كل ما علينا فعله هو تتبُّع متتاليةٍ من المشرفين، وعَدّ عدد الخطوات المطلوبة حتى نصل إلى رئيس الشركة. ألقِ نظرةً على الشيفرة التالية.
if ( emp.supervisor == null ) { System.out.println( emp.name + " is the boss!" ); } else { Employee runner; // For "running" up the chain of command. runner = emp.supervisor; if ( runner.supervisor == null) { System.out.println( emp.name + " reports directly to the boss." ); } else { int count = 0; while ( runner.supervisor != null ) { count++; // Count the supervisor on this level. runner = runner.supervisor; // Move up to the next level. } System.out.println( "There are " + count + " supervisors between " + emp.name + " and the boss." ); } }
بينما يُنفِّذ الحاسوب حلقة التكرار while بالأعلى، سيشير runner مبدئيًا إلى الموظف الأصلي أي emp، ثم إلى مشرف الموظف emp، ثم إلى مشرف مشرف الموظف emp، وهكذا. ستزداد قيمة المُتغيّر count بمقدار الواحد بكل مرةٍ يزور خلالها المُتغيّر runner موظفًا جديدًا، وتنتهي حلقة التكرار عندما يُصبِح runner.supervisor فارغًا، وهو ما يُشير إلى وصولنا إلى رئيس الشركة. سيحتوِي المتغير count في تلك النقطة من البرنامج على عدد الخطوات بين emp ورئيس الشركة.
يُعدّ المتغير supervisor في هذا المثال مفيدًا وبديهيًا نوعًا ما، حيث تُعدّ بنى البيانات data structures المعتمدة على ربط عدة كائناتٍ ببعضها بعضًا مفيدةً جدًا لدرجة أنها تُمثِل موضوعًا رئيسيًا للدراسة بعلوم الحاسوب computer science. سنناقش عدة أمثلةٍ نموذجيةٍ متعلّقةٍ بهذا النوع من بنى البيانات، وسنتناول بالتحديد القوائم المترابطة linked lists ضمن هذا المقال وما يليه.
تتكوَّن أي قائمةٍ مترابطة linked list من سلسلةٍ من الكائنات من نفس النوع، حيث يَربُط مؤشرٌ pointer كائنًا معينًا بالكائن الذي يليه. يشبه ذلك كثيرًا سلسلة المشرفين الواقعة بين الموظف emp ورئيس الشركة بالمثال السابق. من الممكن أيضًا أن نتعرَّض لمواقف ٍأكثر تعقيدًا، وعندها قد يَتضمَّن كائنٌ واحدٌ روابطًا إلى كائناتٍ أخرى عديدة، وهو ما سنناقشه بمقال قادم.
القوائم المترابطة Linked Lists
ستُبنَى القوائم المترابطة linked lists في غالبية الأمثلة المتبقية ضمن هذا المقال من كائناتٍ objects تنتمي إلى الصنف Node المُعرَّف على النحو التالي:
class Node { String item; Node next; }
يُستخدم عادةً مصطلح العقدة node للإشارة إلى أحد الكائنات الموجودة ببنيةٍ بيانيةٍ مترابطة linked data structure، حيث يُمكِننا ربط كائناتٍ من النوع Node ببعضها بعضًا كما هو مُوضَّح بالجزء العلوي من الصورة السابقة. تحتوي كل عقدةٍ على سلسلةٍ نصيةٍ من النوع String بالإضافة إلى مؤشرٍ للعقدة التالية ضمن القائمة إن وُجدت. يُمكِننا دائمًا تمييز العقدة الأخيرة بمثل تلك القائمة؛ حيث سيحمل متغير النسخة next ضمن تلك العقدة القيمة الفارغة null، وليس مؤشرًا إلى عقدةٍ أخرى.
الهدف من ربط العقد بتلك الطريقة هو تمثيل قائمةٍ من السلاسل النصية strings؛ حيث تكون السلسلة النصية الأولى ضمن تلك القائمة مُخزَّنةً بالعقدة الأولى؛ بينما تكون السلسلة النصية الثانية مُخزَّنةً بالعقدة الثانية، وهكذا. في حين اِستخدَمنا مؤشراتٍ وكائناتٍ من النوع Node لبناء البنية البيانية data structure، ستكون البيانات التي نريد تمثيلها بالأساس هي قائمة السلاسل النصية. ونستطيع كذلك تمثيل قائمةٍ من الأعداد الصحيحة، أو قائمةٍ من الأزرار من النوع Button، أو قائمةٍ من أي نوعٍ آخر من البيانات فقط بتغيير نوع متغير النسخة item المُخزَّن بكل عقدة.
على الرغم من تعريف الصنف Nodes بهذا المثال تعريفًا بسيطًا، فما يزال بإمكاننا استخدامه لتوضيح العمليات الشائعة على القوائم المترابطة linked lists، حيث تتضمَّن تلك العمليات ما يلي: حذف عقدةٍ من القائمة، أو إضافة عقدةٍ جديدة إلى القائمة، أو البحث عن سلسلةٍ نصية معينةٍ من النوع String ضمن عناصر القائمةitems. سنناقش مجموعةً من البرامج الفرعية subroutines المسؤولة عن تنفيذ جميع تلك العمليات.
لاستخدام قائمةٍ مترابطةٍ ضمن برنامج، فإنه يحتاج إلى تعريف مُتغيّرٍ يشير إلى العقدة الأولى من تلك القائمة. في الواقع، كل ما يحتاجه البرنامج هو مؤشرٌ واحدٌ فقط إلى العقدة الأولى؛ بينما يمكن الوصول لجميع العقد الأخرى ضمن القائمة من خلال البدء من العقدة الأولى ثم التنقُّل من عقدةٍ لأخرى باتباع الروابط عبر القائمة. سنستخدم دائمًا بالأمثلة التالية متغيرًا اسمه head من النوع Node للإشارة إلى العقدة الأولى بالقائمة المترابطة، وعندما تَكون القائمة فارغةً، ستكون قيمة المتغير head هي القيمة الفارغة null.

إجراء المعالجات الأساسية على قائمة مترابطة
نحتاج عادةً إلى إجراء معالجةٍ معينةٍ على جميع العناصر الموجودة ضمن قائمةٍ مترابطة linked list، حيث لا بُدّ من البدء من رأس head القائمة، ثم التحرُّك من كل عقدةٍ للعقدة التي تليها باتباع المؤشر المُعرَّف ضمن كل عقدة، والتوقُّف أخيرًا عند الوصول إلى نهاية القائمة، وهو ما سندركه عند الوصول إلى القيمة الفارغة null. فإذا كان head متغيرًا من النوع Node، وكان يُشير إلى العقدة الأولى ضِمْن قائمةٍ مترابطة، فستكون الصياغة العامة المُستخدمة لمعالجة جميع عناصر تلك القائمة على النحو التالي:
Node runner; // المؤشر المستخدم لاجتياز القائمة runner = head; // سيُشير runner إلى رأس القائمة مبدئيًا while ( runner != null ) { // استمر إلى أن تصل إلى القيمة الفارغة process( runner.item ); // عالج العنصر الموجود بالعقدة الحالية runner = runner.next; // تحرك إلى العقدة التالية }
يُعدّ المتغير head الطريقة الوحيدة المُتاحة للوصول إلى عناصر القائمة. ونظرًا لأننا بحاجةٍ إلى تعديل قيمة المُتغيِّر runner، فلا بُدّ من إنشاء نسخةٍ من المتغير head، وإلا سنخسر الطريقة الوحيدة المتاحة للوصول إلى القائمة. بناءً على ذلك، سنستخدم تعليمة الإسناد assignment statement التالية runner = head لإنشاء نسخةٍ من المتغير head، حيث سيُشير المتغير runner إلى كل عقدةٍ ضمن القائمة تباعًا، وسيحمل runner.next مؤشرًا إلى العقدة التالية ضمن القائمة. وبالتالي، ستُحرِك تعليمة الإسناد runner = runner.next المؤشر على طول القائمة من عقدةٍ إلى أخرى، وعندما تُصبِح قيمة runner مساويةً للقيمة الفارغة null، نكون قد وصلنا إلى نهاية القائمة.
لاحظ أن شيفرة المعالجة بالأعلى ستعمل بنجاح حتى لو كانت القائمة فارغة؛ لأن قيمة head لقائمةٍ فارغة هي القيمة الفارغة null، وعندها لن يُنفَّذ متن body حلقة التكرار while نهائيًا. يُمكِننا مثلًا طباعة جميع السلاسل النصية strings ضمن قائمةٍ من النوع String بكتابة ما يلي:
Node runner = head; while ( runner != null ) { System.out.println( runner.item ); runner = runner.next; }
يمكننا إعادة كتابة حلقة التكرار while باستخدام حلقة التكرار for، فعلى الرغم من أن المتغير المُتحكِّم بحلقة التكرار for عادةً ما يكون من النوع العددي، فإن ذلك ليس أمرًا ضروريًا. تعرض الشيفرة التالية حلقة تكرار for مُكافِئة لحلقة while بالأعلى:
for ( Node runner = head; runner != null; runner = runner.next ) { System.out.println( runner.item ); }
بالمثل، يُمكِننا أن نجتاز traverse قائمة أعدادٍ صحيحة لحساب حاصل مجموع الأعداد ضمن تلك القائمة، ويُمكننا بناء قائمةٍ مترابطة من الأعداد الصحيحة باستخدام الصنف التالي:
public class IntNode { int item; // أحد الأعداد الصحيحة ضمن القائمة IntNode next; // مؤشر إلى العقدة التالية }
إذا كان head متغيرًا من النوع IntNode، وكان يشير إلى قائمةٍ مترابطة من الأعداد الصحيحة، فإن الشيفرة التالية تحسب حاصل مجموع الأعداد الصحيحة ضمن تلك القائمة.
int sum = 0; IntNode runner = head; while ( runner != null ) { sum = sum + runner.item; // أضف العنصر الحالي إلى المجموع runner = runner.next; } System.out.println("The sum of the list of items is " + sum);
يُمكِننا أيضًا استخدام التعاود recursion لمعالجة قائمة مترابطة، ولكن من النادر استخدامه لمعالجة قائمة؛ لأنه من السهل دومًا استخدام حلقة loop لاجتيازها. ومع ذلك، قد يُساعد فهم طريقة تطبيق التعاود على القوائم على استيعاب كيفية تطبيق المعالجة التعاودية على بنى البيانات الأكثر تعقيدًا.
يُمكِننا النظر لأي قائمةٍ مترابطة غير فارغة على أنها مُكوَّنة من جزئين:
- رأس القائمة head المُكوَّن من العقدة الأولى بالقائمة.
- ذيل القائمة tail المُكوَّن من جميع ما هو متبقي من القائمة.
يُعدّ ذيل القائمة ذاته بمثابة قائمةٍ مترابطةٍ أخرى، والتي هي أقصر من القائمة الأصلية بفارق عقدةٍ واحدة. يُمثِل ذلك أرضيةً مناسبةً نوعًا ما لتطبيق التعاود، حيث يمكن تقسيم معالجة القائمة إلى معالجة رأس القائمة ومعالجةٍ تعاوديةٍ لذيل القائمة، ويُمثِّل العثور على قائمةٍ فارغة الحالة الأساسية base case. تعرض الشيفرة التالية مثلًا خوارزميةً تعاوديةً recursive algorithm لحساب حاصل مجموع الأعداد الصحيحة ضمن قائمة مترابطة.
// إذا كانت القائمة فارغة if the list is empty then // أعد صفر لأنه ليس هناك أي أعداد لجمعها return 0 (since there are no numbers to be added up) otherwise // اضبط listsum إلى العدد الموجود بعقدة الرأس let listsum = the number in the head node // اضبط tailsum إلى حاصل مجموع الأعداد الموجودة بقائمة الذيل تعاوديًا let tailsum be the sum of the numbers in the tail list (recursively) // أضف tailsum إلى listsum add tailsum to listsum return listsum
يتبقى الآن الإجابة على السؤال التالي: كيف نحصل على ذيل قائمة مترابطة غير فارغة؟ إذا كان head متغيرًا يُشير إلى عقدة الرأس لقائمةٍ معينة، فسيشير متغير head.next إلى العقدة الثانية ضمن تلك القائمة، والتي تُمثِل في الوقت نفسه العقدة الأولى بذيل القائمة. لذلك، يُمكِننا النظر إلى head.next على أنه مؤشرٌ إلى ذيل القائمة.
لاحِظ أنه في حالة كانت القائمة الأصلية مُكوَّنةً من عقدةٍ واحدةٍ فقط، فسيكون ذيل القائمة فارغًا، وعليه ستكون قيمة head.next مُساويةً للقيمة الفارغة null. نظرًا لاستخدام مؤشرٍ فارغٍ null pointer عمومًا لتمثيل القوائم الفارغة، فسيظل head.next مُمثِلًا مناسبًا لذيل القائمة حتى في تلك الحالة الخاصة. يمكننا إذًا تعريف الدالة التعاودية التالية بلغة جافا لحساب حاصل مجموع الأعداد ضمن قائمة.
public static int addItemsInList( IntNode head ) { if ( head == null ) { // تُمثِل القائمة الفارغة أحد الحالات الأساسية return 0; } else { // 1 int listsum = head.item; int tailsum = addItemsInList( head.next ); listsum = listsum + tailsum; return listsum; } }
تشير [1] إلى الحالة التعاودية وذلك عندما لا تكون القائمة فارغةً، احسب حاصل مجموع قائمة الذيل، ثم أضفه إلى العنصر الموجود بعقدة الرأس. لاحِظ أنه من الممكن كتابة ذلك في خطوةٍ واحدة على النحو التالي return head.item + addItemsInList( head.next );.
سنناقش الآن مشكلةً أخرى يَسهُل حلها باستخدام التعاود بينما يَصعُب قليلًا بدونه، حيث تتمثل المشكلة بطباعة جميع السلاسل النصية الموجودة ضمن قائمةٍ مترابطةٍ من السلاسل النصية بترتيبٍ معاكسٍ لترتيب حدوثها ضمن القائمة؛ يعني ذلك أن نطبع العنصر الموجود برأس القائمة head بعد طباعة جميع عناصر ذيل القائمة. يقودنا ذلك إلى البرنامج التعاودي recursive routine التالي:
public static void printReversed( Node head ) { if ( head == null ) { // الحالة الأساسية: أن تكون القائمة فارغة // ليس هناك أي شيءٍ لطباعته return; } else { // الحالة التعاودية: القائمة غير فارغة printReversed( head.next ); // اطبع السلاسل النصية بالذيل بترتيب معكوس System.out.println( head.item ); // اطبع السلسلة النصية بعقدة الرأس } }
لا بُدّ من الاقتناع بأن هذا البرنامج يعمل، مع التفكير بإمكانية تنفيذه دون استخدام التعاود recursion.
سنناقش خلال بقية هذا المقال عددًا من العمليات الأكثر تعقيدًا على قائمةٍ مترابطةٍ من السلاسل النصية، حيث ستكون جميع البرامج الفرعية subroutines التي سنتناولها توابع نُسخ instance methods مُعرَّفةً ضمن الصنف StringList الذي نفذَّه الكاتب. يُمثِل أي كائنٍ من النوع StringList قائمةً مترابطةً من السلاسل النصية، حيث يَملُك الصنف متغير نسخة خاص private اسمه head من النوع Node، ويشير إلى العقدة الأولى ضمن القائمة أو يحتوي على القيمة null إذا كانت القائمة فارغة.
تستطيع توابع النسخ instance methods المُعرَّفة بالصنف StringList الوصول إلى head مثل متغير عام global. يُمكِنك العثور على الشيفرة المصدرية للصنف StringList بالملف StringList.java، كما أنه مُستخدمٌ بالبرنامج التوضيحي ListDemo.java، الذي يُمكِّنك من رؤية طريقة استخدامه بوضوح.
سنُلقِي نظرةً على إحدى التوابع المُعرَّفة بالصنف StringList للإطلاع على مثالٍ عن المعالجة البسيطة للقوائم واجتيازها، حيث يبحث التابع ذو النوع StringList عن سلسلةٍ نصيةٍ معينة ضمن قائمة؛ إذا كان searchItem مُمثِلًا للسلسلة النصية التي نبحث عنها، فعلينا موازنة searchItem مع كل عنصرٍ ضمن تلك القائمة، بحيث نتوقف عن المعالجة عند العثور على العنصر الذي نبحث عنه. انظر الشيفرة التالية:
public boolean find(String searchItem) { Node runner; // مؤشر لاجتياز القائمة // ابدأ بفحص رأس القائمة runner = head; while ( runner != null ) { // 1 if ( runner.item.equals(searchItem) ) return true; runner = runner.next; // تحرك إلى العقدة التالية } // 2 return false; } // end find()
حيث تشير كل من [1] و[2] إلى الآتي:
-
[1] افحص السلاسل النصية الموجودة بكل عقدة. إذا كانت السلسلة النصية هي نفسها التي نبحث عنها، أعد القيمة المنطقية
true؛ لأننا ببساطة قد وجدناها بالقائمة. -
[2] عند وصولنا إلى تلك النقطة من البرنامج، نكون قد فحصنا جميع العناصر الموجودة بالقائمة دون العثور على
searchItem، ولذلك سنعيد القيمة المنطقيةfalseللإشارة إلى حقيقة عدم وجود العنصر بالقائمة.
لاحِظ أنه من الممكن أن تكون القائمة فارغةً أي تكون قيمة head مساويةً للقيمة الفارغة null، لذلك ينبغي معالجة تلك الحالة معالجةً سليمةً؛ فإذا احتوى head المُعرَّف بالشيفرة بالأعلى على القيمة null، فلن يُنفَّذ متن حلقة التكرار while نهائيًا، أي لن يعالج التابع أي عقد nodes، وستكون القيمة المعادة هي القيمة false. هذا هو ما نريد فعله تمامًا عندما تكون القائمة فارغة؛ نظرًا لعدم امكانية حدوث searchItem ضمن قائمةٍ فارغة.
الإضافة إلى قائمة مترابطة
قد تكون مشكلة إضافة عنصرٍ جديدٍ إلى قائمةٍ مترابطة أكثر صعوبةً نوعًا ما، بالأخص عندما يكون من الضروري إضافة العنصر إلى منتصف القائمة، وتُعد هذه المشكلة أعقد معالجةٍ سنُجرِيها على بنى البيانات المترابطة linked data structures خلال هذا المقال بالكامل. تُحفَظ العناصر الموجودة بعُقد القائمة المترابطة في الصنف StringList مُرتَّبةً تصاعديًا، لذلك عند إضافة عنصرٍ جديدٍ إلى القائمة، لابُدّ من إضافته إلى الموضع الصحيح وفقًا لذلك الترتيب؛ وهذا يعني أننا سنضطَّر في أغلب الحالات إلى إضافة العنصر الجديد إلى مكانٍ ما بمنتصف القائمة أي بين عقدتين موجودتين بالفعل.
لكي نتمكَّن من فعل ذلك، سيكون من الضروري تعريف متغيرين من النوع Node للإشارة إلى العقدتين اللتين ينبغي أن تقعا على جانبي العقدة الجديدة، حيث يُمثّل previous وrunner بالصورة التالية المتغيرين المذكورين. إلى جانب ذلك، سنحتاج إلى متغيرٍ آخر newNode للإشارة إلى العقدة الجديدة. لتمكين عملية الإضافة insertion، لا بُدّ من إلغاء الرابط الموجود من previous إلى runner، وإضافة رابطين جديدين من previous إلى newNode، ومن newNode إلى runner.
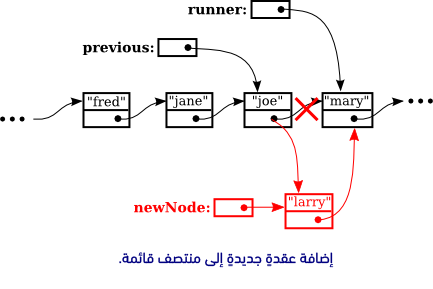
بمجرد ضبط قيمة المتغيرين previous وrunner بحيث يُشيرا إلى العقد الصحيحة، يُمكِننا استخدام الأمر previous.next = newNode; لضبط previous.next لكي يشير إلى العقدة الجديدة، والأمر newNode.next = runner لضبط newNode.next لكي يُشير إلى المكان الصحيح. ولكن قبل أن نستطيع تنفيذ أي من تلك الأوامر، سنحتاج أولًا لضبط كلٍ من runner وprevious كما هو موضحٌ بالصورة السابقة.
الفكرة ببساطة هي أن نبدأ من العقدة الأولى بالقائمة، ثم نتحرك على طول القائمة مرورًا بجميع العناصر الأقل من العنصر الجديد، ويجب علينا الانتباه جيدًا أثناء ذلك حتى لا نقع بمشكلة السقوط خارج نهاية القائمة؛ أي أننا لن نستطيع الاستمرار إذا وصل runner إلى نهاية القائمة وأصبحت قيمته تساوي null. لنفترض أن insertItem هو العنصر المطلوب إضافته إلى القائمة، ولنفترض أيضًا أنه ينتمي إلى مكانٍ ما بمنتصف القائمة، ستَتَمكَّن الشيفرة التالية من ضبط قيمة المتغيرين previous وrunner على نحوٍ صحيح.
Node runner, previous; previous = head; // ابدأ من مقدمة القائمة runner = head.next; while ( runner != null && runner.item.compareTo(insertItem) < 0 ) { previous = runner; // "previous = previous.next" would also work runner = runner.next; }
يستخدم المثال الموضح أعلاه تابع النسخة compareTo() -انظر إلى مقال السلاسل النصية String والأصناف Class والكائنات Object والبرامج الفرعية Subroutine في جافا- المُعرَّف بالصنف String لاختبار ما إذا كان العنصر الموجود بالعقدة node أقل من العنصر المطلوب إضافته.
ليس هناك أي مشكلةٍ فيما سبق باستثناء افتراضنا الدائم بانتماء العقدة الجديدة إلى مكانٍ ما بمنتصف القائمة، وهو أمرٌ غير صحيح؛ فقد تكون قيمة العقدة المطلوب إضافتها insertItem أحيانًا أقل من قيمة العنصر الأول ضمن القائمة، وهنا لا بُدّ من إضافة العقدة الجديدة إلى رأس القائمة، وهو ما تفعله الشيفرة التالية.
newNode.next = head; // Make newNode.next point to the old head. head = newNode; // Make newNode the new head of the list.
من الممكن أيضًا أن تكون القائمة فارغة، وينبغي في هذه الحالة أن تكون newNode هي العقدة الأولى والوحيدة ضمن القائمة. يمكننا إنجاز ذلك ببساطةٍ من خلال تنفيذ تعليمة الإسناد التالية head = newNode، ويعالِج التعريف التالي للتابع insert()، المُعرَّف بالصنف StringList جميع تلك الاحتمالات.
public void insert(String insertItem) { Node newNode; // عقدة تحتوي على العنصر الجديد newNode = new Node(); newNode.item = insertItem; // (N.B. newNode.next == null.) if ( head == null ) { // العنصر الجديد هو العنصر الأول والوحيد ضمن القائمة // اضبط head بحيث تشير إليه head = newNode; } else if ( head.item.compareTo(insertItem) >= 0 ) { // العنصر الجديد أقل من أول عنصر ضمن القائمة // لذلك ينبغي أن يُضبَط بحيث يكون رأسًا للقائمة newNode.next = head; head = newNode; } else { // ينتمي العنصر الجديد إلى مكان ما بعد العنصر الأول ضمن القائمة // ابحث عن موضعه المناسب وأضِفه إليه Node runner; // العقدة المستخدمة لاجتيار القائمة Node previous; // تُشير دائمًا إلى العقدة السابقة لـ runner runner = head.next; // ابدأ بفحص الموضع الثاني ضمن القائمة previous = head; while ( runner != null && runner.item.compareTo(insertItem) < 0 ) { // 1 previous = runner; runner = runner.next; } newNode.next = runner; // أضف newNode بعد previous previous.next = newNode; } } // end insert()
يعني [1] حرّك previous وrunner على طول القائمة إلى أن يقع runner خارج القائمة، أو إلى أن يصل إلى عنصرٍ أكبر من أو يساوي insertItem. بانتهاء تلك الحلقة، سيشير previous إلى الموضع الذي ينبغي إضافة insertItem إليه.
إذا كنت منتبهًا للمناقشة الموضحة أعلاه، فقد تكون لاحظت أن هناك حالةً خاصةً أخرى لم نذكرها، فما الذي سيحدث إذا كان علينا إضافة العقدة الجديدة إلى نهاية القائمة؟ وهذا يحدث إذا كانت جميع عناصر القائمة أقل من العنصر الجديد. في الواقع، يُعالِج البرنامج الفرعي subroutine المُعرَّف بالأعلى تلك الحالة أيضًا ضمن الجزء الأخير من تعليمة if؛ فإذا كان insertItem أكبر من جميع عناصر القائمة، فستنتهي حلقة while بعدما يجتاز runner القائمة بالكامل، وستُصبِح قيمته عندها مساويةً للقيمة الفارغة null.
ولكن عند الوصول إلى تلك النقطة، سيكون previous ما يزال يشير إلى العقدة الأخيرة بالقائمة؛ ولهذا سنُنفِّذ التعليمة previous.next = newNode لإضافة newNode إلى نهاية القائمة. ونظرًا لأن runner يُساوِي القيمة الفارغة null، فسيَضبُط الأمر newNode.next = runner قيمة newNode.next إلى القيمة الفارغة null، وهو ما نحتاج إليه تمامًا لنتمكَّن من الإشارة إلى أن القائمة قد انتهت.
الحذف من قائمة مترابطة
تشبه عملية الحذف عملية الإدخال على الرغم من أنها أبسط نوعًا ما، حيث توجد حالاتٌ خاصة ينبغي أخذها بالحسبان؛ فإذا أردنا حذف العقدة الأولى بقائمة، فينبغي علينا ضبط المُتغيِّر head، وجعله يُشيِر إلى العقدة التي كانت تُعدّ مُسبقًا العقدة الثانية بتلك القائمة.
بما أن المتغير head.next يشير بالأساس إلى العقدة الثانية بالقائمة، يُمكِننا إجراء التعديل المطلوب بتنفيذ التعليمة head = head.next، وعلينا أيضًا التأكُّد من أن البرنامج يعمل على نحوٍ سليم حتى وإن كانت قيمة head.next تُساوِي null. عندما لا يكون هناك سوى عقدةٍ واحدةٍ ضمن قائمةٍ معينة، فستصبح القائمة فارغةً.
أما إذا كنا نريد حذف عقدةٍ بمنتصف قائمةٍ معينة، فعلينا ضبط قيمة المتغيرين previous وrunner كما فعلنا سابقًا؛ حيث يُشير runner إلى العقدة المطلوب حذفها، بينما يُشيِر previous إلى العقدة التي تسبق العقدة المطلوب حذفها ضمن تلك القائمة. بمجرد انتهائنا من ضبط قيمة المتغيرين، سيحذف الأمر previous.next = runner.next; العقدة المعنية، وسيتولى كانس المهملات garbage collector مسؤولية تحريرها. حاول رسم صورةٍ توضيحيةٍ لعملية الحذف. يُمكِننا الآن تعريف التابع delete() على النحو التالي:
public boolean delete(String deleteItem) { if ( head == null ) { // القائمة فارغة، وبالتالي هي بالتأكيد لا تحتوي على deleteString return false; } else if ( head.item.equals(deleteItem) ) { // عثرنا على السلسلة النصية بأول عنصر بالقائمة. احذفه head = head.next; return true; } else { // إذا كانت السلسلة النصية موجودةً بالقائمة، فإنها موجودة بمكانٍ ما بعد // العنصر الأول، وعليه سنبحث عنه بتلك القائمة Node runner; // العقدة المستخدمة لاجتياز القائمة Node previous; // تُشير دائمًا إلى العقدة السابقة للعقدة runner runner = head.next; // ابدأ بفحص الموضع الثاني ضمن القائمة previous = head; while ( runner != null && runner.item.compareTo(deleteItem) < 0 ) { // 1 previous = runner; runner = runner.next; } if ( runner != null && runner.item.equals(deleteItem) ) { // يشير runner إلى العقدة المطلوب حذفها // احذف تلك العقدة بتعديل المؤشر بالعقدة السابقة previous.next = runner.next; return true; } else { // العنصر غير موجود بالقائمة return false; } } } // end delete()
وتعني [1] حَرِك previous وrunner على طول القائمة إلى أن يقع runner خارج القائمة أو إلى أن يَصِل إلى عنصرٍ أكبر من أو يساوي deleteItem. بانتهاء تلك الحلقة، سيُشير runner إلى موضع العنصر المطلوب حذفه، إذا كان موجودًا بالقائمة.
ترجمة -بتصرّف- للقسم Section 2: Linked Data Structures من فصل Chapter 9: Linked Data Structures and Recursion من كتاب Introduction to Programming Using Java.










أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.