مدخل إلى جافا المكدس Stack والرتل Queue وأنواع البيانات المجردة ADT

تُعدّ القائمة المترابطة linked list نوعًا خاصًا من بنى البيانات data structure، حيث تتكوَّن من مجموعة كائناتٍ مربوطةٍ مع بعضها بعضًا باستخدام مؤشرات pointers. استخدمنا في المقال السابق قائمةً مترابطةً لتخزين قائمةٍ مرتّبةٍ من السلاسل النصية من النوع String، كما نفَّذنا عمليات الإضافة والحذف والبحث على تلك القائمة. ومع ذلك، كان بإمكاننا بسهولة تخزين قائمة السلاسل النصية بمصفوفةٍ أو كائنٍ من النوع ArrayList بدلًا من استخدام قائمةٍ مترابطة، وكنا سنتمكَّن من إجراء نفس العمليات على القائمة. على الرغم من أن تنفيذ تلك العمليات سيكون مختلفًا بالتأكيد، إلا أن الواجهات interfaces المُستخدمة والسلوك المنطقي لتلك العمليات سيكون نفسه.

يُشير مصطلح نوع بيانات مجرد abstract data type -أو اختصارًا ADT- إلى مجموعة قيمٍ محتملة ومجموعة من العمليات المسموح بتطبيقها على تلك القيم دون أي تخصيصٍ لطريقة تمثيل تلك القيم أو طريقة تنفيذ تلك العمليات، حيث يُمكِننا مثلًا تعريف قائمةٍ مُرتَّبةٍ من السلاسل النصية باستخدام نوع بياناتٍ مجرد، على أنها أي متتاليةٍ من السلاسل النصية من النوع String شرط أن تكون مُرتَّبةً ترتيبًا تصاعديًا، وبحيث يُمكِننا إجراء عملياتٍ عليها، مثل إضافة سلسلةٍ نصيةٍ جديدة، أو حذف سلسلةٍ نصية، أو البحث عن سلسلةٍ نصيةٍ ضمن القائمة.

يُمكِنك بالتأكيد تنفيذ نفس نوع البيانات المُجرَّد ADT باستخدام طرقٍ مختلفة، فمثلًا قد تُنفِّذ قائمة السلاسل النصية المُرتَّبة باستخدام قائمة مترابطة أو مصفوفة array. في الواقع، تعتمد البرامج المُستخدِمة لهذا النوع من البيانات على التعريف المجرد للنوع، وبالتالي يُمكِنها استخدام أيٍ من تنفيذاتها implementation المُتوفِّرة، كما يُمكِنها التبديل بينها بسهولة؛ وهذا يعني أنه من الممكن تبديل التنفيذ الخاص بنوع بياناتٍ مجردٍ معين دون التأثير على البرنامج، ويُسهِّل ذلك من عملية تنقيح أخطاء debug البرامج. تُعدّ أنواع البيانات المجردة ADTs عمومًا واحدةً من الأدوات الهامة بهندسة البرمجيات software engineering.

سنناقش في هذا المقال نوعين من أنواع البيانات المجردة، هما المكدس stack والرتل queue، حيث تُستخدَم عادةً القوائم المترابطة لتنفيذ كليهما، ولكنها بالتأكيد ليست التنفيذ الأوحد. يُمكِنك النظر للجزء المتبقي من هذا القسم على أساس كونه مناقشةً عن الأكداس والأرتال من ناحية؛ وعلى أساس كونه دراسة حالة case study لأنواع البيانات المجردة من الناحية الأخرى.

9.3.1: المكدسات Stacks

يتكوَّن المكدس stack من متتاليةٍ من العناصر التي يُمكِننا النظر إليها على أنها مجموعةٌ من العناصر المتراكمة فوق بعضها بعضًا، حيث يُمكننا الوصول مباشرةً وفي أي لحظة إلى العنصر الموجود بالأعلى، كما يُمكِننا حذفه من المكدس باستخدام عمليةٍ تُعرَف باسم السحب pop، ويُمكِننا في المقابل حذف عنصرٍ آخر أسفل المكدس فقط بعد سحب pop جميع العناصر الواقعة أعلى ذلك العنصر من المكدس. من الممكن أيضًا إضافة عنصرٍ جديدٍ أعلى المكدس باستخدام عمليةٍ تُعرَف باسم الدفع push. يُمكِن لعناصر المكدس أن تكون من أي نوع، فإذا كانت العناصر قيمٌ من النوع int مثلًا، فيمكن تنفيذ عمليتي السحب pop والدفع push كما في توابع النسخ instance methods التالية:

• void push(int newItem)‎: لإضافة عنصرٍ جديد newItem أعلى المكدس.
• int pop()‎: لحذف العنصر الموجود أعلى المكدس وإعادته.

لاحِظ أنه من الخطأ أن تحاول سحب pop عنصرٍ من مكدسٍ فارغ، ولذلك عليك أن تختبر أولًَا فيما إذا كان المكدس فارغًا أم لا، وسنحتاج بالتالي إلى عمليةٍ أخرى لإجراء ذلك الاختبار، والتي يُمكِننا تنفيذها باستخدام تابع النسخة التالي:

• boolean isEmpty()‎: يعيد القيمة true إذا كان المكدس فارغًا.

نكون الآن قد عرَّفنا مكدسًا من الأعداد الصحيحة على أنه نوع بيانات مجرد abstract data type - ADT، ويُمكِننا تنفيذه بعدة طرقٍ شرط أن يَكُون سلوكه العام مكافئًا للتصور المُجرَّد للمكدس.

لدى تنفيذ المكدس باستخدام القوائم المترابطة linked list، ستكون عقدة رأس القائمة head أعلى المكدس. تُعدّ إضافة العقد إلى مقدمة قائمةٍ مترابطة أو حذفها من المقدمة أسهل بكثير بالموازنة مع الإضافة أو الحذف من منتصف قائمة مترابطة. يَستخدِم الصنف بالشيفرة التالية قائمةً مترابطةً لتنفيذ النوع المجرد ADT مكدس أعداد صحيحة. لاحِظ تعريف الصنف المُوضّح بالأسفل لصنفٍ متداخلٍ nested ساكن static لتمثيل عقد القائمة المترابطة، وهو ما يُعدّ جزءًا من التنفيذ الخاص private implementation للنوع المجرد.

public class StackOfInts {

   private static class Node {
      int item;
      Node next;
   }

    // مؤشر إلى العقدة الموجودة أعلى المكدس
    // ‫إذا كان top يُساوِي القيمة الفارغة، فإن المكدس يكون فارغًا
   private Node top;  

    // ‫أضف N إلى أعلى المكدس
   public void push( int N ) {
      Node newTop;         // العقدة التي ستحمل العنصر الجديد
      newTop = new Node();
      newTop.item = N;     // ‫خزِّن N بالعقدة الجديدة
      newTop.next = top;   // تشير العقدة الجديدة إلى العقدة التي كانت تحتل موضع أعلى المكدس مسبقًا
      top = newTop;        // تُصبح العقدة الجديدة أعلى المكدس
   }

    // 1
   public int pop() {
      if ( top == null )
         throw new IllegalStateException("Can't pop from an empty stack.");
      int topItem = top.item;  // العنصر المسحوب من المكدس
      top = top.next;          // العنصر الموجود أعلى المكدس حاليًا
      return topItem;
   }

   // 2
   public boolean isEmpty() {
      return (top == null);
   }

} // end class StackOfInts

[1] احذف العنصر الموجود في أعلى المكدس، ثم أعده. إذا كان المكدس فارغًا، بلِّغ عن حدوث اعتراض من النوع IllegalStateException.

[2] أعد القيمة المنطقية true إذا كان المكدس فارغًا؛ أما إذا كان يحتوي على عنصرٍ واحد أو أكثر، أعد القيمة المنطقية false.

عليك التأكُّد من فهم طريقة عمل عمليتي السحب pop والدفع push بالقائمة المترابطة، وقد يُساعدك رسم بعض الصور على ذلك. تُمثّل القائمة المترابطة بالأعلى جزءًا من التنفيذ الخاص للصنف StackOfInts، أي لا يحتاج البرنامج الذي يَستخدِم ذلك الصنف إلى معرفة حقيقة كونه يستخدم قائمةً مترابطة.

يُمكننا الآن أيضًا تنفيذ المكدس باستخدام مصفوفةٍ بدلًا من قائمةٍ مترابطة، حيث سنحتاج إلى عدّاد counter لمعرفة عدد الخانات المُستخدَمة فعليًا بالمصفوفة، لأن عدد عناصر المكدس يختلف من وقتٍ لآخر. بفرض أن اسم العداد هو top، فستكون عناصر المكدس مُخزَّنةً بمواضع المصفوفة 0، و1، … حتى top-1، ويتواجد العنصر بالموضِع 0 أسفل المكدس بينما يتواجد العنصر بالموضِع top-1 أعلى المكدس.

من السهل دفع push عنصرٍ إلى المكدس على النحو التالي: ضع العنصر بالموضِع top وزِد قيمة top بمقدار الواحد. وإذا لم نكن نريد وضع حدٍ أقصى لعدد العناصر التي يستطيع المكدس أن يحملها، يُمكِننا استخدام مصفوفةٍ ديناميكية dynamic array، التي كنا قد تعرَّضنا لها بالقسم الفرعي 7.2.4. يعرض التصور النموذجي للمصفوفة المكدس مقلوبًا رأسًا على عقب؛ أي سيظهر أسفل المكدس بأعلى المصفوفة، وهذا في الواقع غير مهم؛ فالمصفوفة هي مجردُ تنفيذٍ للفكرة المجرَّدة للمكدس، وطالما تجري العمليات على المكدس كما ينبغي لها، فليس هناك أي داعٍ للقلق. تعرض الشيفرة التالية تنفيذًا آخرًا للصنف StackOfInts باستخدام مصفوفةٍ ديناميكية.

import java.util.Arrays;  // Arrays.copyOf() من أجل تابع

public class StackOfInts {  // (إصدار بديل، استعمال مصفوفة)

   private int[] items = new int[10];  // مصفوفة لحمل عناصر المكدس

   private int top = 0;  // عدد العناصر الموجودة بالمكدس حاليًا

    // ‫أضف N إلى أعلى المكدس
   public void push( int N ) {
       if (top == items.length) {
           // إذا كانت المصفوفة ممتلئة، أنشِئ واحدة جديدة أكبر حجمًا
           // وانسخ العناصر الموجودة بالمكدس حاليًا إليها
           items = Arrays.copyOf( items, 2*items.length );
       }
       items[top] = N;  // ‫ضع N بالموضِع المتاح التالي
       top++;           // أزد عدد العناصر بمقدار الواحد
   }

   // 1
   public int pop() {
       if ( top == 0 )
          throw new IllegalStateException("Can't pop from an empty stack.");
       int topItem = items[top - 1];  // العنصر الموجود أعلى المكدس
       top--;    // انقص عدد العناصر الموجودة بالمكدس بمقدار الواحد
       return topItem;
   }

   // 2
   public boolean isEmpty() {
      return (top == 0);
   }

} // end class StackOfInts

• [1] احذف العنصر الموجود أعلى المكدس، ثم أعده مثل قيمةٍ للدالة، وإذا كان المكدس فارغًا، بلِّغ عن حدوث اعتراض من النوع IllegalStateException.
• [2] أعد القيمة المنطقية true إذا كان المكدس فارغًا؛ أما إذا كان يحتوي على عنصرٍ واحدٍ أو أكثر، أعد القيمة المنطقية false.

نُعيد التأكيد على أن تنفيذ المكدس على هيئة مصفوفة شأنٌ خاصٌ بالصنف؛ وهذا يعني أنه من الممكن استبدال نسختي الصنف StackOfInts المُعرفتين بالأعلى بعضهما ببعض دون أي مشكلة، لأن واجهتهما العامة public interface متطابقة.

يُمكِننا الآن تحليل زمن تشغيل run time العمليات على المكدس (ألقِ نظرةً على القسم 8.5)، حيث يمكننا قياس حجم المشكلة من خلال عدد العناصر الموجودة بالمكدس؛ فبالنسبة للتنفيذ الذي يَستخدِم قائمةً مترابطة، فإن زمن تشغيل الحالة الأسوأ worst case لعمليتي الدفع push والسحب pop يُساوِي Θ(1)‎، وهذا يعني أن زمن التشغيل أقل من قيمةٍ ثابتةٍ معينة لا تعتمد على عدد عناصر المكدس. يُمكِنك رؤية ذلك بوضوحٍ من خلال الشيفرة ذاتها؛ فتنفيذ العمليتين مُكوَّنٌ من عدة تعليمات إسناد assignment قليلة وبسيطة، وعدد عناصر المكدس ليس له أي دور.

أما بالنسبة للتنفيذ المُعتمِد على مصفوفة، فهناك حالةٌ خاصة تَحدُث أحيانًا أثناء عملية الدفع push، تحديدًا عندما تكون المصفوفة ممتلئة، حيث يُنشِئ الصنف في تلك الحالة مصفوفةً جديدةً ويَنسَخ جميع عناصر المكدس إلى تلك المصفوفة الجديدة. يستغرق ذلك وقتًا يتناسب طرديًا مع عدد عناصر المكدس. لذلك، على الرغم من أن زمن تشغيل عملية الدفع push يُساوِي عادةً Θ(1)‎، فإنه في الحالة الأسوأ worst case يُساوِي Θ(n)‎، حيث تمثّل n عدد العناصر الموجودة بالمكدس. نظرًا لندرة حدوث الحالة الأسوأ، يُمكِننا أن نقول أن زمن تشغيل الحالة المتوسطة average case هو Θ(1)‎.

9.3.2: الأرتال Queues

على نحوٍ مشابه من المكدس، يتكوَّن الرتل queue من متتاليةٍ من العناصر كما يوجد عددٌ من القيود بخصوص الكيفية التي نُضيف بها العناصر إلى الرتل أو نحذفها منه؛ وبخلاف المكدس، فإن الرتل لديه طرفين هما الطرف الأمامي والخلفي، حيث تُضاف العناصر دائمًا إلى الطرف الخلفي من الرتل، بينما تُحذَف من طرفه الأمامي. سنُطلِق على عملية إضافة العناصر إلى الرتل اسم إدراج enqueue، بينما سنُطلِق على عملية حذف العناصر منه اسم "سحب dequeue*، مع الملاحظة بأن هذه التسميات ليست قياسيةً بخلاف عمليتي *الدفع push* والسحب pop.

عند إضافة عنصر إلى الطرف الخلفي من الرتل، فإنه يبقى بالرتل إلى أن تُحذَف جميع العناصر التي تسبقه، ويُعدّ ذلك أمرًا بديهيًا؛ فالرتل queue بالنهاية يُشبه خطًا أو صفًا من العملاء المنتظرين لخدمةٍ معينة، حيث تُقدَم الخدمة للعملاء بنفس ترتيب وصولهم إلى الصف.

يُمكِن لعناصر الرتل أن تكون من أي نوع، فمثلًا قد يكون لدينا رتلًا من النوع العددي الصحيح int، كما يُمكِن تنفيذ عمليتي الإدراج enqueue والسحب dequeue كأنها توابع نسخ instance methods داخل تعريف الصنف QueueOfInts. علاوةً على ذلك، سنحتاج أيضًا إلى تابع نسخة آخر لاختبار فيما إذا كان الرتل queue فارغًا أم لا:

• void enqueue(int N)‎: يضيف عنصرًا جديدًا N إلى الطرف الخلفي من الرتل.
• int dequeue()‎: يَحذِف عنصرًا من الطرف الأمامي من الرتل ويعيده.
• boolean isEmpty()‎: يُعيد القيمة true إذا كان الرتل فارغًا.

يمكننا تنفيذ الرتل باستخدام قائمةٍ مترابطة أو مصفوفة، ومن الممكن أن يكون استخدام مصفوفةٍ لتنفيذ الرتل أعقد قليلًا من استخدامها لتنفيذ المكدس stack، ولهذا لن نتناوله هنا، وسنكتفي بالتنفيذ المبني على قائمةٍ مترابطة.

يُمثِل العنصر الأول بقائمةٍ مترابطة الطرف الأمامي من الرتل، بينما يُمثِل العنصر الأخير بالقائمة الطرف الخلفي من الرتل، وتشبه عملية سحب dequeue عنصرٍ من الطرف الأمامي للرتل عملية سحب pop عنصرٍ من المكدس.

في المقابل، تتضمَّن عملية إدراج enqueue عنصرٍ جديدٍ إلى الرتل ضبط المؤشر pointer الموجود بآخر عقدةٍ ضمن القائمة؛ لكي يُشير إلى عقدةٍ جديدةٍ تحتوي على العنصر المطلوب إضافته. يُمكِننا إجراء ذلك بتنفيذ الأمر tail.next = newNode;‎، حيث تمثّل tail مؤشرًا لآخر عقدةٍ ضمن القائمة المترابطة. بفرض أن head مؤشرٌ لأول عقدةٍ ضمن قائمةٍ مترابطة، يُمكننا استخدام الشيفرة التالية للحصول على مؤشرٍ لآخر عقدةٍ ضمن تلك القائمة:

Node tail;    // سيشير إلى العنصر الأخير ضمن القائمة
tail = head;  // ابدأ من العقدة الأولى
while (tail.next != null) {
   tail = tail.next;  // تحرَك إلى العقدة التالية
}
// 1

[1] بوصولنا إلى تلك النقطة من البرنامج، فإن tail.next يكون فارغًا مما يَعنِي أن tail يُشير إلى آخر عقدةٍ بالقائمة.

ومع ذلك، سيكون من غير المناسب فعل ذلك في كل مرةٍ نرغب فيها بإضافة عنصرٍ جديدٍ إلى الرتل. لزيادة كفاءة الشيفرة بالأعلى، سنُعرِّف متغير نسخة instance variable يحتوي على مؤشرٍ لآخر عقدةٍ ضمن القائمة المترابطة، وهذا سيُعقِّد الصنف QueueOfInts بعض الشيء؛ وبالتالي علينا الانتباه إلى ضرورة تحديث قيمة ذلك المتغير أينما أضفنا عقدةً جديدةً إلى نهاية القائمة. يُمكِننا إذًا إعادة كتابة الصنف QueueOfInts على النحو التالي:

public class QueueOfInts {

   /**
    * ‫كائنٌ من النوع Node
    * يحمل أحد العناصر الموجودة ضمن القائمة المترابطة الممثلة للرتل
    */
   private static class Node {
      int item;
      Node next;
   }

   private Node head = null;  // يشير إلى العنصر الأول ضمن القائمة
   private Node tail = null;  // يُشير إلى العنصر الأخير ضمن القائمة

   // أضف‫ N إلى الطرف الخلفي من الرتل
   public void enqueue( int N ) {
      Node newTail = new Node();  // العقدة التي تحمل العنصر الجديد
      newTail.item = N;
      if (head == null) {
            // 1
         head = newTail;
         tail = newTail;
      }
      else {
          // تُصبِح العقدة الجديدة هي ذيل القائمة بينما لا يتأثر رأسها
         tail.next = newTail;
         tail = newTail;
      }
   }

   // 2
   public int dequeue() {
      if ( head == null)
          throw new IllegalStateException("Can't dequeue from an empty queue.");
      int firstItem = head.item;
      head = head.next;  // أصبح العنصر الثاني مسبقًا العنصر الأول بالرتل

       if (head == null) {
            // 3
         tail = null;
      } 
      return firstItem;
   }

   // ‫أعد القيمة المنطقية `true` إذا كان الرتل فارغًا
   boolean isEmpty() {
      return (head == null);
   }

} // end class QueueOfInts

• [1] بما أن الرتل كان فارغًا، ستصبح العقدة الجديدة العقدة الوحيدة الموجودة بالقائمة؛ ونظرًا لكونها العقدة الأولى والأخيرة، سيشير head وtail إليها.
• [2] احذِف العنصر الموجود بمقدمة الرتل وأعده مثل قيمةٍ للتابع. في حال كان الرتل فارغًا، بلِّغ عن اعتراضٍ من النوع IllegalStateException.
• [3] أصبح الرتل فارغًا، وبما أن العقدة التي حذفناها كانت بمثابة عقدة الرأس head والذيل tail، فلم يَعُدّ هناك ذيلٌ للقائمة في الوقت الحالي.

لفهم الدور الذي يلعبه المؤشر tail بالأعلى، يمكنك التفكير وفقًا لقاعدة الأصناف اللامتغايرة class invariant (أو الصنف اللامتغاير)، التي تعرَّضنا لها بالقسم الفرعي 8.2.3 والتي تنص على: "إذا لم يكن الرتل queue فارغًا، فإن tail يُشير إلى آخر عقدةٍ بالرتل". لا بُدّ أن يكون اللامتغاير صحيحًا ببداية ونهاية كل عملية استدعاءٍ للتابع. إذا طبَقنا تلك القاعدة على التابع enqueue في حالة القوائم غير الفارغة، يُخبرنا اللامتغاير بأننا نستطيع إضافة عقدةٍ جديدةٍ إلى نهاية القائمة بتنفيذ تعليمة مثل tail.next = newNode، كما يُخبرنا بكيفية ضبط قيمة tail قبل العودة من التابع، وجعله يُشير إلى العقدة الجديدة التي أُضيفَت للتو إلى الرتل.

يستخدم الحاسوب الأرتال queues عندما يرغب بمعالجة عنصرٍ واحدٍ فقط بكل مرة في حين تنتظر عناصرٌ أخرى دورها للمعالجة. نستعرض فيما يلي بعض الأمثلة على ذلك:

• برامج جافا المُستخدِمة لعدِّة خيوط threads، حيث يحتفظ الحاسوب بالخيوط التي تطمع بزمنٍ للمعالجة من قِبَل وحدة المعالجة المركزية CPU داخل رتل. عند إنشاء خيطٍ جديد، سيُضيفه الحاسوب إلى الطرف الخلفي من ذلك الرتل. تسير الأمور على النحو التالي: يَحذِف الحاسوب خيطًا من الطرف الأمامي للرتل ثم يُعطِيه بعضًا من زمن المعالجة، وإذا لم ينتهي بعدها، يُرسِله الحاسوب مُجددًا إلى الطرف الخلفي من الرتل لينتظر دوره مرةً أخرى.

• تُخزَّن الأحداث events، مثل نقرات الفأرة وضغطات لوحة المفاتيح داخل رتلٍ اسمه "رتل الأحداث event queue"، ويَحذِف برنامجٌ معينٌ الأحداث الموجودة بذلك الرتل ويُعالِجها واحدًا تلو الآخر. يُمكِن وقوع أحداثٍ كثيرة أخرى بينما يُعالِج البرنامج حدثًا معينًا، ولكن نظرًا لأنها تُخزَّن تلقائيًا داخل ذلك الرتل، فإن البرنامج يُعالِجها دائمًا بنفس ترتيب حدوثها.

• يستقبل خادم الويب web server طلباتٍ من المتصفحات للوصول إلى بعض الصفحات. بطبيعة الحال، تَصِل طلبات جديدة بينما يُعالِج خادم الويب طلبًا سابقًا؛ لذلك تُوضَع الطلبات الجديدة برتلٍ وتنتظر إلى أن يحين دورها للمعالجة، حيث يَضمَن الرتل معالجة الطلبات بنفس ترتيب وصولها.

تُنفِّذ الأرتال سياسة الداخل أولًا، يخرج أولًا FIFO؛ بينما تُنفِّذ الأكداس stacks سياسة الداخل آخرًا، يخرج أولًا LIFO. على نحوٍ مشابهٍ من الأرتال، يُمكِن اِستخدَام الأكداس لحمل العناصر التي تنتظر أن يحين دورها للمعالجة، على الرغم من أنها قد لا تكون عادلة ببعض الأحيان.

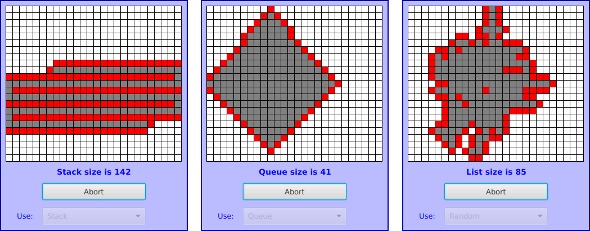
لتوضيح الفرق بين المكدس stack والرتل queue، سنناقش البرنامج التوضيحي DepthBreadth.java. حاول تشغيل البرنامج، فهو يَعرِض شبكة مربعاتٍ مُلوَّنةٍ جميعها باللون الأبيض على نحوٍ مبدئي، وعندما يَنقُر المُستخدِم على مربعٍ أبيض، سيَضِع البرنامج علامةً على ذلك المربع، ثم يُحوِّله إلى اللون الأحمر. بعد ذلك، سيبدأ البرنامج بوضع علاماتٍ على أي مربعٍ مُتصِلٍ أفقيًا أو رأسيًا مع أيٍ من المربعات التي سَبَقَ للبرنامج وضع علامةٍ عليها. بالنهاية، ستُطبَق تلك العملية على جميع مربعات الشبكة.

لنتمكَّن من فهم طريقة عمل البرنامج، سنحاول أن نضع أنفسنا مكان البرنامج: عندما يَنقُر المستخدم على مربع، لنتخيل أننا سنحصل على بطاقةٍ مكتوب عليها موضع ذلك المربع أي رقمي الصف والعمود. سنَضَع بعدها تلك البطاقة في كومة pile، والتي ستَتَضمَّن الآن بطاقةً واحدةً فقط. سنُكرِّر بعد ذلك ما يلي: إذا كانت الكومة فارغةً، نكون قد انتهينا؛ أما إذا لم تكن فارغة، فسنسحب إحدى البطاقات التي تُقابِل إحدى مربعات الشبكة. سنَفْحَص جميع المربعات المجاورة أفقيًا ورأسيًا لذلك المربع؛ فإذا لم نَكن قد مررنا بأيٍ من المربعات المجاورة من قبل، سنُدوِن موضعه على بطاقةٍ جديدة ونضعها بالكومة، ونكون قد انتهينا عندما لا يكون هناك أي بطاقات أخرى بالكومة تنتظر المعالجة.

بهذا البرنامج: عندما يكون هناك مربعٌ بالكومة بانتظار المعالجة، يكون ملوَّنًا باللون الأحمر؛ وبالتالي تُمثِل المربعات الملونة بالأحمر تلك المربعات التي مررنا عبرها ولم نعالجها بعد. يتبدل لونه إلى اللون الرمادي بعد أن نأخذ المربع من الكومة ونعالجه، وبمجرد حدوث ذلك، فإن البرنامج يتخطاه دائمًا ولن يحاول معالجته مرة أخرى؛ لأن جميع المربعات المجاورة له أخذت بالحسبان بالفعل. بالنهاية، سيُعالِج البرنامج جميع المربعات، أي سيتحول لونها جميعًا إلى اللون الرمادي، وسينتهي البرنامج.

يمكنك تشغيل البرنامج باستخدام إحدى الخيارات الثلاثة التالية: المكدس stack أو الرتل queue أو عشوائيًا، وسيتبّع البرنامج نفس النهج العام أيًا كان الخيار، حيث أن الفرق الوحيد بينها هو أسلوب إدارة كومة البطاقات؛ فبالنسبة للمكدس، ستُضاف البطاقات وتُحذَف بأعلى الكومة؛ أما بالنسبة للرتل، ستُضاف البطاقات إلى أسفل الكومة وتُحذَف من أعلى الكومة؛ وبالنسبة للحالة العشوائية، سيختار البرنامج إحدى البطاقات الموجودة بالكومة عشوائيًا.

سيختلف بالتأكيد ترتيب معالجة مربعات الشبكة تمامًا باختلاف نوع الكومة، وهو ما يظهر بوضوحٍ من خلال الصور الثلاثة التالية المأخوذة من البرنامج، حيث سيبدأ البرنامج باختيار مربعٍ بالقرب من منتصف الشبكة مهما كان نوع الكومة المُستخدَمة. يَستخدِم البرنامج على اليسار مكدسًا، أما البرنامج بالمنتصف فيَستخدِم رتلًا، أما البرنامج على اليمين فيَستخدِم الاختيار العشوائي random selection.

تختلف الأنماط الناتجة اختلافًا كبيرً، فعندما يَستخدِم البرنامج مكدسًا stack، فإنه يُحاوِل أن يستكشف أقصى قدرٍ ممكنٍ قبل البدء بإجراء تتبعٍ خلفي backtracking لفحص المربعات التي واجهها مُسبقًا؛ وعندما يستخدم البرنامج رتلًا queue، فإنه يعالج المربعات بنفس ترتيب بُعدها عن النقطة المبدئية تقريبًا؛ أما عندما يستخدم البرنامج الاختيار العشوائي random selection، فإننا نحصل على كائنٍ blob غير منتظم، ولكنه يَكون متصلًا بالتأكيد؛ حيث يمكن للبرنامج أن يواجه مربعًا معينًا فقط في حالة كان ذلك المربع مجاورًا لمربعٍ سَبَقَ أن واجهه البرنامج.

يُمكنك تجريب البرنامج لترى طريقة عمله، وحاول أيضًا فهم طريقة استخدام المكدس والرتل ضمن ذلك البرنامج،وابدأ بمربعٍ واقعٍ بإحدى الزوايا المربعة. بينما ما يزال البرنامج قيد المعالجة، تستطيع أن تنقر على مربعاتٍ بيضاء أخرى، وستُضاف عندها إلى قائمة المربعات التي واجهها البرنامج. في تلك الحالة، إذا كان البرنامج يَستخدِم مكدسًا، ستلاحظِ أن البرنامج يُعالِج المربع الذي نقرت عليه فورًا بينما ستضطّر بقية المربعات الحمراء التي كانت بالفعل تنتظر دورها إلى الانتظار أكثر؛ وإذا كان البرنامج يستخدم رتلًا، فإنه لن يُعالِج المربع الذي نقرت عليه إلا بعد الانتهاء من معالجة جميع المربعات التي كانت موجودة بالفعل ضمن الكومة. يُمكِنك الإطلاع على الشيفرة المصدرية للبرنامج من الملف DepthBreadth.java.

يبدو الرتل أكثر بداهةً لأنه يحدث بصورةٍ أكبر بالحياة الواقعية؛ ولكن في بعض الأحيان، يكون المكدس مناسبًا أكثر أو حتى أساسيًا. فماذا سيحدث مثلًا عندما يستدعي برنامج routine برنامجًا فرعيًا subroutine؟ يُعلَّق البرنامج الأول أثناء تنفيذ البرنامج الفرعي، ولا يكتمل تنفيذه إلى بعد انتهاء البرنامج الفرعي. لنفترض الآن أن ذلك البرنامج الفرعي استدعى بدوره برنامجًا فرعيًا ثانيًا، وأن ذلك البرنامج الفرعي الثاني قد استدعى بدوره برنامجًا ثالثًا، وهكذا، لذلك لا بُدّ من تعليق تنفيذ كل برنامجٍ فرعي بينما تُنفَّذ البرامج الفرعية اللاحقة؛ وهذا يعني أن الحاسوب لا بُدّ أن يحتفظ بحالة جميع البرامج الفرعية المُعلَّقة، وهو ما يفعله باستخدام مكدس.

عند استدعاء برنامجٍ فرعي، يُنشَأ سجلٌ نشطٌ activation record له؛ حيث يحتوي على المعلومات المُتعلِّقة بتنفيذ البرنامج الفرعي، مثل متغيراته المحلية local variables ومعاملاته parameters، ويُوضَع ذلك السجل بالمكدس، ويُحذَف فقط عندما ينتهي البرنامج الفرعي من عمله ويعيد قيمة. إذا استدعى البرنامج الفرعي برنامجًا فرعيًا آخرًا، يُنشَئ سجلًا نشطًا جديدًا للبرنامج الفرعي الآخر ويُدفَع push إلى المكدس أعلى السجل الخاص بالبرنامج الفرعي الأول. يستمر المكدس بالنمو مع كل استدعاءٍ لبرنامجٍ فرعي، ويتقلص حجمه عند انتهاء تلك البرامج الفرعية من عملها.

قد يحتوي المكدس على عدة سجلات لنفس البرنامج الفرعي في حالة البرامج الفرعية التعاودية recursive subroutine؛ أي تلك التي تعاود استدعاء ذاتها تعاوديًا. في الواقع، هذه هي ببساطة الطريقة التي يتمكَّن بها الحاسوب من تذكُّر مجموعة من الاستدعاءات التعاودية بنفس الوقت.

9.3.3: تعبيرات الإلحاق Postfix Expressions

يمكن استخدام المكدس لتحصيل قيم تعبيرات الإلحاق postfix expressions. يُطلَق اسم "تعبير تدوين داخلي infix expression" على أي تعبيرٍ حسابيٍ عادي، مثل "‎2+(15-12)17‎"، حيث يُوضَع العامل operator في هذا النوع من التعبيرات بين معاملين operands، مثل "2 + 2"؛ أما بالنسبة لتعبيرات الإلحاق، يأتي العامل بعد معامليه مثل "‎2 2 ‎+‎". يُمكِن كتابة التعبير "‎2+(15-12)17" بصياغة تعبيرات الإلحاق على النحو التالي "‎2 15 12 - 17 * +‎"، حيث يُطبَق العامل "-" بهذا التعبير على المعاملين اللذين يَسبِقانه أي "15" و"12". يُطبّق العامل "*" بالمثل على المعاملين اللذين يسبقانه أي "‎15 12 -‎" و"17". أخيرًا، يُطبّق "+" على "2" و"‎15 12 - 17 *‎". في الواقع، هذه هي نفس العمليات الحسابية التي يُنفِّذها تعبير التدوين الداخلي الأصلي.

لنفترض الآن أننا نريد معالجة التعبير "‎2 15 12 - 17 * +‎" من اليسار إلى اليمين، وحساب قيمته. سيكون العنصر الأول الذي نواجهه هو 2، ولكن ما الذي يُمكِننا أن نفعله به؟ لا نعرف بهذه النقطة من البرنامج أي عاملٍ ينبغي تطبيقه على العدد 2، كما أننا لا نعرف قيمة المعامل الآخر. ينبغي إذًا أن نتذكر العدد 2 حيث سنحتاج إلى مُعالِجته لاحقًا بدفعه push إلى المكدس.

سننتقل بعدها إلى العنصر التالي، أي 15، والذي سندفعه أيضًا إلى المكدس أعلى العدد 2، ثم ندفع العدد 12. الآن، سنواجه العامل "-"، والذي ينبغي أن نطبّقه على المعاملين اللذين يسبقانه بالتعبير، وبما أننا خزَّنا قيمة هذين المعاملين بالمكدس، يُمكِننا معالجة العامل "-" بسحب pull عددين من المكدس أي 12 و15، ثم نحسب قيمة التعبير "‎15 - 12" لنحصل على الإجابة 3. لا بُدّ من أن نتذكر تلك الإجابة لأننا سنحتاج إلى مُعالِجتها لاحقًا، ولهذا سندفعها إلى المكدس أعلى العدد 2 الذي ما يزال منتظرًا.

سنفحص الآن العنصر التالي بالتعبير، أي العدد 17، والذي سندفعه إلى المكدس أعلى العدد 3. ولنتمكَّن من معالجة العنصر التالي أي "*"، يجب أن نسحب pop عددين من المكدس أي 17 و3، حيث يُمثّل العدد 3 قيمة "‎15 12 -‎". سنحسب الآن حاصل ضرب العددين، وسنحصل على الناتج 51، الذي سندفعه إلى المكدس.

سنجد بعد ذلك أن العنصر التالي بالتعبير هو العامل "+"، والذي يُمكِننا مُعالجته بسحب pop العددين 51 و2 من المكدس، ثم حساب مجموعهما، ودفع الناتج 53 إلى المكدس. أخيرًا، وصلنا إلى نهاية التعبير، ويكون العدد الموجود بالمكدس هو القيمة الإجمالية للتعبير؛ أي أن كل ما علينا فعله هو أن نسحبه من المكدس، ونكون قد انتهينا.

على الرغم من أنك قد ترى أن تعبيرات التدوين الداخلي infix expressions أكثر سهولةً، لكن تتمتع تعبيرات الإلحاق postfix expression ببعض المميزات؛ فهي لا تتطلَّب أي أقواسٍ أو قواعد أولوية precedence rules، حيث يعتمد الترتيب الذي تُطبّق على أساسه العوامل operators على ترتيب حدوثها ضمن التعبير، ويسمح ذلك بكتابة خوارزمياتٍ algorithms بسيطةٍ ومباشرة لتحصيل قيم تعبيرات الإلحاق. ألقِ نظرةً على ما يلي:

// ابدأ بمكدس فارغ
Start with an empty stack
// لكل عنصر ضمن التعبير، نفذ ما يلي
for each item in the expression:
    // إذا كان العنصر عددًا
    if the item is a number:
        // ادفع العدد إلى داخل المكدس
       Push the number onto the stack
    // إذا كان العنصر عاملًا
    else if the item is an operator:
        // اسحب معاملين من المكدس
       Pop the operands from the stack  // Can generate an error
       // طبّق العامل على المعاملين
       Apply the operator to the operands
       // ادفع الناتج إلى المكدس
       Push the result onto the stack
    else
        // هناك خطأ بالتعبير
       There is an error in the expression
// اسحب عددًا من المكدس
Pop a number from the stack  // Can generate an error
// إذا كان المكدس فارغًا
if the stack is not empty:
   // هناك خطأ بالتعبير
   There is an error in the expression
else:
    // القيمة الأخيرة المسحوبة من المكدس هي قيمة التعبير
   The last number that was popped is the value of the expression

علاوةً على ذلك، يمكن الكشف عن الأخطاء الموجودة ضمن أي تعبيرٍ بسهولة. لنفترض مثلًا أنه لدينا التعبير التالي "‎2 3 + ‎"، حيث يُمكِننا بسهولة أن نرى أنه لا توجد معاملاٌت operands كافيةٌ للعامل ""، وستكشف الخوارزمية الموضحة أعلاه عن ذلك الخطأ عندما تحاول سحب pop معاملٍ ثانٍ للعامل "*" من المكدس الذي سيكون فارغًا. قد تحدث مشكلةٌ أخرى عندما لا يكون هناك عددٌ كافٍ من العوامل operators لجميع الأعداد ضمن التعبير مثل "‎2 3 4 +‎". ستكشف الخوارزمية عن ذلك الخطأ عندما يبقى العدد 2 بالمكدس بعد انتهاء الخوارزمية.

يستخدم البرنامج التوضيحي PostfixEval.java تلك الخوارزمية، حيث يسمح للمُستخدم بكتابة تعبيرات إلحاقٍ posftix expression مكوّنةٍ من أعدادٍ حقيقيةٍ موجبة إلى جانب العوامل التالية "+" و"-" و"*" و"/" و"^"، حيث يُمثِل العامل "^" الأس؛ أي يُقيّّم التعبير "‎2 3 ^‎" على النحو التالي 2³؛ كما يطبع البرنامج رسالةً نصيةً أثناء معالجته لكل عنصرٍ ضمن التعبير، ويستخدِم الصنف StackOfDouble المُعرَّف بالملف StackOfDouble.java، والذي يتطابق مع الصنف الأول StackOfInts المُبيَّن أعلاه باستثناء أنه يُخزِّن قيمًا من النوع double بدلًا من النوع int.

الجانب الوحيد الشيّق في هذا البرنامج هو التابع method المُنفِّذ لخوارزمية تحصيل قيمة تعبيرات الإلحاق postfix evaluation. تعرض الشيفرة التالية تنفيذًا لتلك الخوارزمية، والذي هو في الواقع مجرد تحويلٍ مباشرٍ للشيفرة الوهمية المُوضحة بالأعلى إلى لغة جافا.

private static void readAndEvaluate() {

   StackOfDouble stack;  // المكدس المستخدم لتحصيل قيمة التعبير

   stack = new StackOfDouble();  // أنشِئ مكدسًا فارغًا

   System.out.println();

   while (TextIO.peek() != '\n') {

      if ( Character.isDigit(TextIO.peek()) ) {
          // العنصر التالي المُدْخَل عبارة عن عدد
          // اِقرأه وخزنه بالمكدس
         double num = TextIO.getDouble();
         stack.push(num);
         System.out.println("   Pushed constant " + num);
      }
      else {
          // نظرًا لأن العنصر التالي ليس عددًا، فإنه ينبغي أن يكون عاملًا
          // اقرأ العامل ونفذ العملية
         char op;  // ‫العامل الذي ينبغي أن تكون قيمته + أو - أو / أو *
         double x,y;     // المعاملين اللذين سنسحبهما من المكدس
         double answer;  // ناتج العملية
         op = TextIO.getChar();
         if (op != '+' && op != '-' && op != '*' && op != '/' && op != '^') {
             // لا يُمثِل المحرف أي من العمليات المتاحة
            System.out.println("\nIllegal operator found in input: " + op);
            return;
         }
         if (stack.isEmpty()) {
            System.out.println("   Stack is empty while trying to evaluate " + op);
            System.out.println("\nNot enough numbers in expression!");
            return;
         }
         y = stack.pop();
         if (stack.isEmpty()) {
            System.out.println("   Stack is empty while trying to evaluate " + op);
            System.out.println("\nNot enough numbers in expression!");
            return;
         }
         x = stack.pop();
         switch (op) {
         case '+':  
            answer = x + y; 
            break;
         case '-':  
            answer = x - y;  
            break;
         case '*':  
            answer = x * y;  
            break;
         case '/':  
            answer = x / y;  
            break;
         default:   
            answer = Math.pow(x,y);  // (op must be '^'.)
         }
         stack.push(answer);
         System.out.println("   Evaluated " + op + " and pushed " + answer);
      }

      TextIO.skipBlanks();

   }  // end while

    // 1
   if (stack.isEmpty()) {  // يستحيل إذا كان المدخل غير فارغ فعليًا
      System.out.println("No expression provided.");
      return;
   }

   double value = stack.pop();  // قيمة التعبير
   System.out.println("   Popped " + value + " at end of expression.");

   if (stack.isEmpty() == false) {
      System.out.println("   Stack is not empty.");
      System.out.println("\nNot enough operators for all the numbers!");
      return;
   }

   System.out.println("\nValue = " + value);


} // end readAndEvaluate()

[1] إذا وصلنا إلى تلك النقطة من البرنامج، سنكون قد قرأنا المُدْخلات بصورة سليمة. إذا كان التعبير صالحًا، فإن قيمة التعبير ستكون الشيء الوحيد الموجود بالمكدس.

يلجأ الحاسوب عادةً إلى الاعتماد على تعبيرات الإلحاق postfix expressions. في الواقع، تُعدّ آلة جافا الافتراضية Java virtual machine آلة مكدس stack machine، بمعنى أنها تَستخدِم أسلوبًا يعتمد على المكدس لتحصيل قيم التعبيرات expressions. يُمكِن تمديد الخوارزمية بسهولةٍ بحيث تتمكَّن من معالجة المتغيرات variables والثوابت constants.

عندما تواجه الخوارزمية متغيرًا ضمن تعبير، فإن قيمة ذلك المتغير ينبغي أن تُدفَع إلى المكدس، ويُمكن أيضًا تطبيقها على العوامل operators التي تَملُك أكثر أو أقل من مجرد معاملين اثنين operands، حيث يُمكِننا ببساطةٍ سحب pop العدد المطلوب من المعاملات من المكدس، ثم دفع الناتج إليه؛ فيُستخدَم على سبيل المثال عامل الطرح الأحادي "-" ضمن تعبيرٍ مثل "‎-x" له معاملٌ واحد. سنستمر بمناقشة التعبيرات وتحصيل قيمة التعبيرات expression evaluation بالقسمين التاليين.

ترجمة -بتصرّف- للقسم Section 3: Stacks, Queues, and ADTs من فصل Chapter 9: Linked Data Structures and Recursion من كتاب Introduction to Programming Using Java.

اقرأ أيضًا

• مقدمة إلى الاستثناءت exceptions ومعالجتها في جافا
• التوكيد assertion والتوصيف annotation في لغة جافا
• مقدمة إلى صحة البرامج ومتانتها في جافا
• التعاود recursion والمكدس stack في جافاسكربت