مدخل إلى جافا التعاود recursion في جافا

ربما أخبرك أحدهم من قبل بأنك لا تستطيع أن تُعرِّف الشيء بالإشارة إلى ذاته، ولكن هذا ليس صحيحًا عمومًا؛ فإذا أُنجز هذا التعريف بالصورة الصحيحة، فسيُصبِح مُمكِنًا ويتحول إلى تقنيةٍ فعالةٍ للغاية. التعريف التعاودي recursive لشيءٍ أو لمفهومٍ هو ذلك التعريف الذي يُشير إلى نفسه ضِمْن تعريفه، حيث يُمكِننا مثلًا تعريف السلف ancestor بأن يكون إما أبًا أو سلفًا للأب؛ وفي مثال آخر، تعريف الجملة sentence على أنها مكوَّنة -من بين أشياءٍ أخرى كثيرة- من جملتين مرتبطتين بحرف عطفٍ مثل "و".

مثالٌ ثالث هو تعريف المُجلد directory على أنه جزءٌ من قرصٍ صلب disk drive، والذي بدوره قد يحتوي على ملفاتٍ ومجلدات. يُمكِننا أيضًا تعريف المجموعة set بسياق علم الرياضيات على أنها مجموعةٌ من العناصر التي يُمكِنها أن تكون مجموعةً بحد ذاتها. في مثال أخير، يمكن الإشارة إلى إمكانية تعريف التعليمة statement بلغة جافا، على أنها قد تَكُون تَعليمَة while المُكوَّنة بدورها من كلمة while وشرط منطقي وتعليمة.

تستطيع التعريفات التعاودية recursive وصف أكثر المواقف تعقيدًا بعدة كلماتٍ قليلة، فإذا أردنا مثلًا تعريف السلف دون استخدام التعاود، فإننا قد نقول أنه "أبٌ، أو جدٌ، أو جدٌ أكبر،… وهكذا". في الحقيقة، ليس واضحًا ما هو المقصود وراء كلمة "إلخ"، حيث قد تقع بنفس المشكلة إذا حاولت تعريف مجلد على أنه ملفٌ مُكوَّنٌ من قائمةٍ من الملفات التي قد يكون بعضها بدوره قائمةً أخرى من الملفات، والتي قد يكون بعضها أيضًا قائمةً من الملفات، وهكذا". حاول وصف مصطلح تعليمة جافا statement دون استخدام التعاود، وسترى أنه أمرٌ غايةٌ في الصعوبة.

يُمكِننا في الواقع استخدام التعاود مثل تقنيةٍ برمجية، فعلى سبيل المثال البرنامج الفرعي التعاودي recursive subroutine، أو التابع التعاودي recursive method هو ذلك البرنامج أو التابع الذي يُعاود استدعاء ذاته استدعاءً مباشرًا أو غير مباشر. ويعني الاستدعاء المباشر احتواء تعريف البرنامج الفرعي على تعليمة استدعاء برنامجٍ فرعي للبرنامج ذاته قيد التعريف؛ أما الاستدعاء غير المباشر فيعني استدعاء البرنامج الفرعي لبرنامجٍ فرعيٍ ثانٍ، والذي بدوره يستدعي البرنامج الفرعي الأول استدعاءً مباشرًا أو غير مباشر.

تستطيع البرامج الفرعية التعاودية التي تتمكن من معاودة استدعاء ذاتها، أن تُعرِّف بعض المهمات المعقدة بعدة أسطر من الشيفرة. سنناقش بالجزء المتبقي من هذا المقال عدة أمثلة على ذلك، كما سنتعرَّض لأمثلةٍ أخرى خلال المقالات المتبقية من هذه السلسلة.

بحث ثنائي تعاودي Recursive Binary Search

لنبدأ بمثال خوارزمية البحث الثنائي binary search الذي تَعرَّضنا له بمقال البحث والترتيب في المصفوفات Array في جافا، حيث يُستخدم البحث الثنائي للعثور على قيمةٍ مُحدَّدةٍ ضِمْن قائمةٍ مُرتَّبةٍ من العناصر في حالة وجودها ضِمْن تلك القائمة. وتتمحور فكرة الخوارزمية حول فحص عنصر منتصف القائمة، فإذا كان ذلك العنصر يُساوِي القيمة المطلوبة، فإننا نَكُون قد انتهينا بالفعل؛ أما إذا كانت القيمة المطلوبة أقل من قيمة عنصر منتصف القائمة، فإننا نبحث عن تلك القيمة بالنصف الأول من القائمة؛ أما إن لم تَكْن كذلك، فإننا نبحث عنها بالنصف الثاني من القائمة.

يُطلق اسم البحث الثنائي binary search على الأسلوب المُتبَّع للبحث عن قيمةٍ ضِمْن النصف الأول أو الثاني من قائمة؛ أي أن نَفْحَص عنصر منتصف القائمة الذي ما يزال قيد البحث، وبناءً على ذلك إما نَجِد القيمة التي نبحث عنها أو أن نضطَّر إلى إعادة تطبيق البحث الثنائي على النصف المُتبقي من عناصر القائمة. يُعدّ هذا توصيفًا تعاوديًا، ولهذا يُمكِننا تنفيذه بكتابة برنامجٍ فرعيٍ تعاودي recursive subroutine.

قبل كتابة ذلك البرنامج، يجب علينا أخذ نقطتين مهمتين بالحسبان تُمثِلان حقائقًا عامةً عن البرامج الفرعية التعاودية.

• النقطة الأولى: تبدأ خوارزمية البحث الثنائي بفحص عنصر منتصف القائمة، ولكن ما الذي سيحدُث إذا كانت تلك القائمة فارغة؟ ببساطة، إذا لم jكْن هناك أي عناصر ضمن القائمة، فسيستحيل بالتأكيد فحص عنصر منتصف تلك القائمة. كنا قد أضفنا شرطًا مُسبقًا precondition بمقال كيفية كتابة برامج صحيحة باستخدام لغة جافا ينص على ضرورة أن تَكُون القائمة غير فارغة. وبناءً على ذلك، علينا تعديل الخوارزمية، بحيث تأخذ هذا الشرط المُسبَّق بالحسبان. وينقلنا هذا إلى السؤال التالي.
• النقطة الثانية: ما الذي ينبغي أن نفعله في تلك الحالة؟ الإجابة بسيطة، فإذا كانت القائمة فارغة، فيُمكِننا ببساطة استنتاج أن القيمة التي نبحث عنها غير موجودةٍ بالقائمة، أي أنه يُمكِننا إعادة الإجابة دون الحاجة لإجراء أي عملٍ آخر.

يُعدّ وصولنا لقائمةٍ فارغة وفقًا لخوارزمية البحث الثنائي حالةً أساسيةً base case؛ حيث أن الحالة الأساسية لخوارزمية تعاودية، هي تلك الحالة المُمكن مُعالجتها مباشرةً دون الحاجة لإعادة تطبيق الخوارزمية تطبيقًا تعاوديًا. بالإضافة إلى ذلك، يُعدّ العثور على القيمة المطلوبة بعنصر منتصف القائمة وفقًا لخوارزمية البحث الثنائي حالةً أساسيةً أخرى، حيث نكون قد انتهينا دون الحاجة لأي إجراءٍ تعاوديٍ آخر.

تتعلَّق النقطة الثانية بمعاملات parameters البرنامج الفرعي، حيث تُصاغ المشكلة عادةً بكوننا نبحث عن قيمةٍ معينة ضمن قائمة، وتستقبل النسخة الأصلية غير التعاودية non-recursive من برنامج البحث الثنائي تلك القائمة على أنها مصفوفة. في المقابل، لابُدّ أن تُمكِّننا النسخة التعاودية من تطبيق البرنامج الفرعي تطبيقًا تعاوديًا على جزءٍ معينٍ من القائمة الأصلية. بصياغةٍ أخرى، إذا كان البرنامج الفرعي الأصلي مُصمَّمًا للبحث ضمن كامل المصفوفة، فلا بُدّ للبرنامج الفرعي التعاودي أن يَكُون قادرًا على البحث ضِمْن جزءٍ معينٍ من المصفوفة، وبناءً على ذلك لا بُدّ أن يستقبل البرنامج الفرعي معاملاتٍ تُحدِّد ذلك الجزء من المصفوفة الذي ينبغي البحث ضمنه. ولكي تَكُون قادرًا على حل مشكلةٍ معينة حلًا تعاوديًا، فعادةً ما يَكُون من الضروري تَعمِيم المشكلة بعض الشيء.

يوضح المثال التالي خوارزمية البحث الثنائي التعاودي التي تبحث عن قيمة مُحدٍَّدة ضمن جزءٍ من مصفوفة أعداد صحيحة.

static int binarySearch(int[] A, int loIndex, int hiIndex, int value) {

   if (loIndex > hiIndex) {
      // 1
      return -1;
   }

   else {
       // 2
      int middle = (loIndex + hiIndex) / 2;
      if (value == A[middle])
         return middle;
      else if (value < A[middle])
         return binarySearch(A, loIndex, middle - 1, value);
      else   // ‫لابُدّ أن تكون القيمة أكبر من [A[middle
         return binarySearch(A, middle + 1, hiIndex, value);
   }

} // end binarySearch()

• [1] جاء موضع البداية لنطاق البحث قبل موضع نهايته؛ أي ليس هناك أي عناصرٍ فعليةٍ ضمن ذلك النطاق، مما يعني أن القيمة غير موجودةٍ بالقائمة الفارغة.
• [2] انظر للموضع بمنتصف القائمة، فإذا كانت القيمة بذلك الموضع، أعِد هذا الموضع؛ أما إذا لم تكن، فابحث بالنصف الأول أو الثاني من القائمة بحثًا تعاوديًا.

يُحدِّد المعاملان loIndex وhiIndex بالبرنامج الفرعي السابق جزء المصفوفة المطلوب البحث فيه. لاحظ أنه ما يزال بإمكاننا استدعاء binarySearch(A, 0, A.length - 1, value)‎ للبحث ضمن المصفوفة بأكملها. في حال وقوع أي من الحالتين الأساسيتين base cases، أي عند عدم وجود أي عناصرٍ أخرى ضمن النطاق المخصص من فهارس المصفوفة، أو عندما تكون القيمة بمنتصف النطاق المُخصَّص هي نفسها القيمة المطلوب العثور عليها؛ فيمكن عندها للبرنامج الفرعي إعادة الإجابة تلقائيًا دون اللجوء إلى التعاود؛ بينما يضطر في الحالات الأخرى إلى الاستدعاء التعاودي recursive call لحساب الإجابة ثم يعيدها.

يواجه الكثير من المبرمجين في البداية صعوبةً ليدركوا أن التعاود يعمل بنجاح فعليًا، حيث تَكمُن الفكرة في تَحقُّق أمرين لضمان عمل التعاود بالشكل السليم، أولهما أنه لا بُدّ من تخصيص واحدةٍ أو أكثر من الحالات الأساسية base cases المُمكِن معالجتها تلقائيًا دون اللجوء إلى التعاود. ثانيًا، عند تطبيق التعاود أثناء حل المشكلة، فلا بُدّ أن تكون المشكلة أصغر بطريقةٍ ما بكل مرة؛ وبتعبيرٍ آخر، لابُدّ أن تكون المشكلة بكل مرةٍ أقرب إلى واحدةٍ من الحالات الأساسية بالموازنة مع المشكلة الأصلية.

يَعنِي ما سبق أنه إذا كنا نستطيع حلّ نُسخٍ أصغر من مشكلةٍ معينة، وكذلك تَقسِيم النسخ الكبيرة من تلك المشكلة إلى نسخٍ أصغر، فيمكننا حل تلك المشكلة مهما بلغ حجمها. وفي النهاية، سنتمكَّن من تقسيم النسخة الكبيرة من المشكلة عبر عدة خطوات إلى النسخة الأصغر من المشكلة؛ أي إلى واحدةٍ من الحالات الأساسية. في الواقع، يتطلّب ذلك الاحتفاظ بقدرٍ هائلٍ من التفاصيل، ولكن لحسن الحظ لست مطالبًا بإجراء أي من ذلك يدويًا، حيث يُجرِيه الحاسوب بدلًا منك. في المقابل، عليك فقط تحديد الخطوط العريضة أي الحالات الأساسية وكيفية تقسيم المشكلة الكبيرة إلى مشكلاتٍ صغيرة.

يُجري الحاسوب كل ما هو مطلوب لتقسيم المشكلة الكبيرة إلى مشكلاتٍ أصغر عبر كثيرٍ من الخطوات، حتى يَصِل إلى أيٍ من الحالات الأساسية. ستدفعك محاولة التفكير بكيفية إجراء عملية التقسيم تفصيليًا إلى الجنون، وستشعر أن التعاود عمليةً معقدةً وصعبة، لكنه في الحقيقة أسلوبٌ رائعٌ وفعال، وعادةً ما يُعدّ الطريقة الأبسط لحل المشكلات المُعقدة.

تذكَّر دومًا القاعدتين الأساسيتين:

• لا بُدّ من تخصيص واحدة أو أكثر من الحالات الأساسية base cases.
• لا بُدّ من تطبيق البرنامج الفرعي تطبيقًا تعاوديًا recursively على مشكلاتٍ أصغر من المشكلة الأصلية.

يُعدّ انتهاك أي من هاتين القاعدتين أخطاءً شائعةً أثناء كتابة البرامج الفرعية التعاودية، وينتج عن انتهاك أي من القاعدتين عادةً حدوث تعاودٍ لا نهائي infinite recursion؛ أي يستمر البرنامج الفرعي باستدعاء نفسه مرةً بعد أخرى بصورةٍ لانهائية دون الوصول أبدًا إلى حالة أساسية.

يتشابه التعاود اللانهائي نوعًا ما مع التكرار اللانهائي infinite loop، ولكنه يستهلك أيضًا من ذاكرة الحاسوب؛ حيث تتطلَّب كل عملية استدعاء تعاودي recursive call جزءًا من الذاكرة، وبالتالي ستَنفُد الذاكرة لدى الوقوع بتعاودٍ لا نهائي، ثم ينهار crash البرنامج، حيث ينهار البرنامج نتيجةً لحدوث اعتراض exception من النوع StackOverflowError بلغة جافا تحديدًا.

مشكلة أبراج هانوي Hanoi

درسنا حتى الآن خوارزمية البحث الثنائي، والتي يُمكِن تنفيذها بسهولة باستخدام حلقة while بدلًا من التعاود. سنتناول الآن مشكلةً يسهُل حلّها بالتعاود ويَصعُب بدونه، وهي مثالٌ نموذجيٌ يُعرَف باسم مشكلة أبراج هانوي The Towers of Hanoi، حيث تتكوَّن المشكلة من مجموعة أقراصٍ مختلفة الحجم موضوعةٍ على قاعدة بترتيبٍ تنازلي، والمطلوب هو تحريك مجموعة الأقراص من مكدسٍ Stack إلى آخر وفقًا لشرطين، هما:

1. يُمكِن تحريك قرصٍ واحدٍ فقط بكل مرة.
2. لا يُمكِن أبدًا وضع قرصٍ معينٍ فوق آخر أصغر منه.

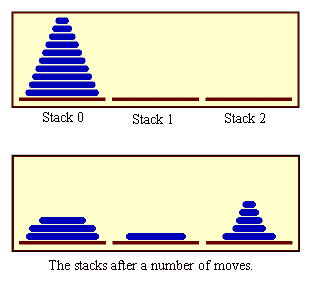
هناك أيضًا قرصٌ إضافيٌ ثالث يُمكِنك استخدامه، حيث يُظهِر النصف الأعلى من الصورة التالية الحالة المبدئية لعشرة أقراص، بينما يُوضِح النصف السفلي حالة الأقراص بعد إجراء عدة حركات. الصورة التالية مأخوذة من البرنامج التوضيحي TowersOfHanoiGUI.java الذي سنتعرض له جزئية لاحقة من هذه السلسلة، حيث سننشئ خلال ذلك البرنامج صورةً متحركةً animation لحل هذه المشكلة خطوةً بخطوة.

تكمن المشكلة ببساطة في تحريك عشرة أقراصٍ من المكدس 0 إلى المكدس 1 وفقًا للشروط المذكورة أعلاه، ويُمكِن أيضًا استخدام المكدس 2 بمثابة موضعٍ مؤقت. يقودنا ذلك إلى السؤال التالي: هل يُمكننا تقسيم هذه المشكلة إلى مشكلاتٍ أصغر من نفس النوع أي تعميم المشكلة قليلًا؟ من البديهي أن يكون حجم المشكلة هو عدد الأقراص المطلوب تحريكها، فإذا كان هناك عدد N من الأقراص بالمكدس 0، فإننا نعرف أنه سيكون علينا بالنهاية تحريك القرص السفلي من المكدس 0 إلى المكدس 1.

مع ذلك وفقًا للشروط، فلا بُدّ أن يكون أول عددٍ N-1 من الأقراص في المكدس 2، وبمجرد أن نُحرِّك القرص N إلى المكدس 1، فسيكون علينا تحريك عدد N-1 من الأقراص من المكدس 2 إلى المكدس 1 لإكمال الحل. لاحِظ أن مشكلة تحريك عدد N-1 من الأقراص هي من نفس نوع المشكلة الأصلية أي تحريك عدد Nمن الأقراص، باستثناء أنها نسخةٌ أصغر من المشكلة، حيث يُمثل ذلك بالضبط ما نريده لإجراء التعاود.

علينا تعميم المشكلة قليلًا، حيث تتطلب المشكلات الأصغر تحريك الأقراص من المكدس 0 إلى المكدس 2، أو من المكدس 2 إلى المكدس 1، بدلًا من مجرد تحريكها من المكدس 0 إلى المكدس 1، وذلك يعني وجوب تمرير كلٍ من مكدس المصدر والوجهة إلى البرنامج الفرعي التعاودي المسؤول عن حل المشكلة.

على الرغم من أن ذلك سيُمكِّننا من تحديد المكدس الاحتياطي ضمنيًا، إلا أنه سيبقى من المريح تمرير المكدس الاحتياطي صراحةً للبرنامج. ويُمثِل وجود قرص واحد فقط الحالة الأساسية، كم سيكون الحل ببساطة في هذه الحالة هو تحريك القرص ضمن خطوةٍ واحدة.

تطبع شيفرة البرنامج الفرعي التالي تعليمات حل المشكلة تفصيليًا خطوةً بخطوة.

static void towersOfHanoi(int disks, int from, int to, int spare) {
    if (disks == 1) {
        // هناك قرصٌ واحدٌ فقط للتحريك. عليك فقط أن تُحرِكه
        System.out.printf("Move disk 1 from stack %d to stack %d%n", 
                               from, to);
    }
    else {
        // 1
        towersOfHanoi(disks-1, from, spare, to);
        System.out.printf("Move disk %d from stack %d to stack %d%n",
                              disks, from, to);
        towersOfHanoi(disks-1, spare, to, from);
    }
}

• [1] حَرِّك جميع الأقراص باستثناء قرصٍ واحدٍ فقط إلى المكدس الاحتياطي، ثم حرِّك القرص السفلي وضَع بقية الأقراص الأخرى فوقه.

يعبِّر هذا البرنامج الفرعي عن الحل التعاودي البديهي، حيث يشتمل الاستدعاء التعاودي بكل مرةٍ على عددٍ أقل من الأقراص، كما أنه يُمكِن حل المشكلة بسهولةٍ في حالتها الأساسية base case؛ أي عند وجود قرصٍ واحدٍ فقط. لحل مشكلة تحريك عدد N من الأقراص من المكدس 0 إلى المكدس 1، ينبغي استدعاء البرنامج الفرعي على النحو التالي TowersOfHanoi(N,0,1,2)‎، ويُبيِّن لنا ما يلي خَرْج البرنامج الفرعي عند ضَبْط عدد الأقراص ليُساوِي 4.

Move disk 1 from stack 0 to stack 2
Move disk 2 from stack 0 to stack 1
Move disk 1 from stack 2 to stack 1
Move disk 3 from stack 0 to stack 2
Move disk 1 from stack 1 to stack 0
Move disk 2 from stack 1 to stack 2
Move disk 1 from stack 0 to stack 2
Move disk 4 from stack 0 to stack 1
Move disk 1 from stack 2 to stack 1
Move disk 2 from stack 2 to stack 0
Move disk 1 from stack 1 to stack 0
Move disk 3 from stack 2 to stack 1
Move disk 1 from stack 0 to stack 2
Move disk 2 from stack 0 to stack 1
Move disk 1 from stack 2 to stack 1

يُبيِّن خَرْج البرنامج بالأعلى تفاصيل حل المشكلة، ولست بحاجةٍ إلى التفكير بطريقة الحل تفصيليًا، حيث من الصعب جدًا تتبُّع تفاصيل عمل الخوارزميات التعاودية بدقة على الرغم من سهولتها وأناقتها، وسيتولى الحاسوب عمومًا مهمة تنفيذ كل تلك التفاصيل. قد تفكر بما سيحدث في حال عدم تحقُّق الشرط المُسبَق precondition، الذي ينص على أن يكون عدد الأقراص موجبًا، حيث سيؤدي ذلك ببساطة إلى حدوث تعاودٍ لا نهائي infinite recursion.

هناك قصةٌ متداولةٌ تشرح السبب وراء تسمية مشكلة أبراج هانوي بذلك الاسم. وفقًا لتلك القصة أُعطيَ مجموعةٌ من الرهبان المتواجدون ببرجٍ معزول قرب هانوي عدد 64 من الأقراص، وطُلِبَ منهم تحريك قرصٍ واحدٍ يوميًا وفقًا لنفس شروط المشكلة بالأعلى؛ وفي اليوم الذي سيكملون فيه تحريك جميع الأقراص من مكدسٍ إلى آخر، سينتهي الكون، لكن لا داعي للقلق، حيث ما يزال أمامنا الكثير من الوقت؛ فعدد الخطوات المطلوبة لحل مشكلة أبراج هانوي لعدد N من الأقراص هو 2^N-1 أي ‎2⁶⁴-1‎ أي ما يَقرُب من 50,000,000,000,000 سنة.

وفقًا لما تطرقنا له في المقال السابق، فإن زمن تشغيل run time خوارزمية أبراج هانوي هو Θ(2ⁿ)‎، حيث تُمثِل n عدد الأقراص المطلوب تحريكها، ونظرًا لنمو الدالة الأسية 2ⁿ بسرعةٍ كبيرة، فإنه من الممكن عمليًا حل مشكلة أبراج هانوي لعددٍ صغيرٍ من الأقراص فقط.

بالإضافة إلى برنامج حل مشكلة أبراج هانوي بالأعلى، هناك أيضًا برنامجين توضيحين آخرين قد ترغب بإلقاء نظرةٍ عليهما، حيث يوفر كل برنامجٍ منهما توضيحًا مرئيًا لخوارزمية تعاودية. البرنامج الأول هو برنامج Maze.java، والذي يَستخدِم التعاود لحل متاهة؛ أما البرنامج الآخر فهو برنامج LittlePentominos.java، الذي يَستخدِم التعاود لحل نوعٍ معروفٍ من الألغاز. في الحقيقة، تستخدم الشيفرة المصدرية لتلك البرامج بعض التقنيات التي لن نتعرَّض الآن، ومع ذلك سيكون من المفيد أن تُشغِّلها وتشاهدها قليلًا.

يُنشِئ البرنامج الأول متاهةً عشوائيةً، ثم يُحاول أن يحل تلك المتاهة بالعثور على مسارٍ عبر المتاهة من ركنها الأيسر العلوي إلى ركنها الأيمن السفلي. في الواقع، تتشابه مشكلة المتاهة كثيرًا مع مشكلة عدّ الكائنات blob-counting، التي سنتعرَّض لها لاحقًا ضمن هذا المقال، حيث يبدأ برنامج حل مشكلة المتاهة التعاودي من مربعٍ معين، ويَفْحَص جميع المربعات المجاورة من خلال إجراء استدعاءٍ تعاودي، وينتهي التعاود إذا تَمكَّن البرنامج من الوصول إلى الركن الأيمن السفلي للمتاهة. في حال لم يتمكَّن البرنامج من العثور على حلٍ من مربعٍ معين، فإنه سيَخرُج من ذلك المربع ويحاول بمكانٍ آخر. يشيع استخدام ذلك الأسلوب ويُعرَف باسم التتبع الخلفي التعاودي recursive backtracking.

يُعدّ البرنامج الآخر LittlePentominos تنفيذًا للغزٍ تقليدي، حيث أن pentomino هو شكلٌ متصلٌ مُكوَّنٌ من خمسة مربعات متساوية الحجم. هناك بالتحديد 12 شكلًا محتملًا يُمكن تكوينه بتلك الطريقة بدون عدّ الانعكاسات أو الدورانات المحتملة للأشكال، والمطلوب هو وضع الأشكال الاثنى عشر داخل لوحة 8x8 مملوءة مبدئيًا بأربعة من تلك الأشكال.

يفحص الحل التعاودي اللوحة المملوءة جزئيًا، كما يفحص جميع الأشكال المتبقية واحدةً تلو الأخرى، ويُحاول أن يضعها بالموضِع المتاح التالي من اللوحة؛ فإذا كان الموضع مناسبًا، فإنه يعاود استدعاء ذاته استدعاءً تعاوديًا لإكمال الحل؛ أما إذا فشل أثناء ذلك، فإنه سينتقل إلى الشكل التالي. لاحِظ أن ذلك يُعدّ مثالًا آخر على أسلوب التتبع الخلفي التعاودي، وستجد في بنتومينوس نسخةً أعم من البرنامج بميزاتٍ أخرى متعددة.

خوارزمية ترتيب تعاودي

سنناقش الآن كيفية كتابة خوارزميةٍ تعاوديةٍ لترتيب مصفوفة، وربما يُعَد هذا البرنامج الأكثر عمليًا حتى الآن. لقد تعرَّضنا لخوارزميتي الترتيب بالإدراج insertion sort والترتيب الانتقائي selection sort بمقال البحث والترتيب في المصفوفات Array في جافا، وعلى الرغم من سهولة هاتين الخوارزميتين وبساطتهما، إلا أنهما بطيئتان عند تطبيقهما على المصفوفات الكبيرة. في الواقع، تتوفَّر خوارزمياتٌ أخرى أسرع لترتيب المصفوفات، مثل الترتيب السريع Quicksort؛ التي أثبتت كونها واحدةً من أسرع خوارزميات الترتيب بغالبية الحالات، وهي في الواقع خوارزميةٌ تعاودية recursive algorithm.

تعتمد خوارزمية الترتيب السريع Quicksort على فكرةٍ بسيطةٍ وذكية، فإذا كانت لدينا قائمةٌ من العناصر، فسنختار أي عنصر منها وسنُطلِق عليه اسم المحور pivot، حيث يُستخدم العنصر الأول مثل محور، وبعد ذلك سنُحرِك جميع العناصر التي قيمتها أصغر من قيمة المحور إلى بداية القائمة، كما سنُحرِك جميع العناصر التي قيمتها أكبر من قيمة المحور إلى نهاية القائمة. في الأخير، سنضع المحور بين مجموعتي العناصر، وبذلك نكون قد وضعنا المحور بموضعه الصحيح الذي ينبغي أن يحتله بالمصفوفة النهائية المُرتَّبة بالكامل؛ أي أننا لن نحتاج إلى تحريكه مجددًا، وسنُشير إلى تلك العملية باسم QuicksortStep.

يُمكنك بسهولة أن ترى أن العملية السابقة QuicksortStep ليست تعاودية، وإنما تُستخدم فقط من قِبل خوارزمية الترتيب السريع Quicksort. تعتمد سرعة الخوارزمية الأساسية على كتابة تنفيذ سريع لعملية QuicksortStep، ونظرًا لأن تلك العملية ليست محور المناقشة، فإننا سنكتفي بعرض تنفيذٍ لها دون مناقشتها تفصيليًا. انظر الشيفرة التالية:

 static int quicksortStep(int[] A, int lo, int hi) {

    int pivot = A[lo];  // Get the pivot value.

    // 0    
    while (hi > lo) {

       // Loop invariant (See Subsection Subsection 8.2.3):  A[i] <= pivot
       // for i < lo, and A[i] >= pivot for i > hi.

       while (hi > lo && A[hi] >= pivot) {
           // 1
          hi--;
       }

       if (hi == lo)
          break;

        // 2
       A[lo] = A[hi];
       lo++;

       while (hi > lo && A[lo] <= pivot) {
           // 3
          lo++;
       }

       if (hi == lo)
          break;

        // 4
       A[hi] = A[lo];
       hi--;

    } // end while

     // 5
    A[lo] = pivot;
    return lo;

 }  // end QuicksortStep

• [0] تُحدِّد الأعداد hi وlo نطاق الأعداد المطلوب فحصها. اُنقُص العدد hi وزِد العدد lo حتى يُصبحِا متساويين، وحرِّك الأعداد التي قيمتها أكبر من قيمة المحور بحيث تقع قبل hi، وحرِّك أيضًا الأعداد التي قيمتها أقل من قيمة المحور، بحيث تقع بعد lo. بالبداية، سيكون الموضع A[lo]‎ متاحًا لأن قيمته قد نُسخَت إلى المتغير المحلي pivot.
• [1] حرِك hi للأسفل بعد الأعداد الأكبر من قيمة المحور، ولاحِظ أنه ليست هناك حاجةً لتحريك أيٍ من تلك الأعداد.
• [2] العدد A[hi]‎ أقل من قيمة المحور، ولذلك يُمكِنك تحريكه إلى المساحة المتاحة A[lo]‎، وبالتالي سيُصبِح الموضع A[hi]‎ مُتاحًا.
• [3] حرِك lo للأعلى قبل الأعداد الأقل من قيمة المحور. لاحِظ أنه ليس هناك حاجةً لتحريك أيٍ من تلك الأعداد.
• [4] العدد A[lo]‎ أكبر من قيمة المحور، لذلك حرِكه إلى المساحة المتاحة A[hi]‎ وبالتالي سيُصبِح الموضع A[lo]‎ متاحًا.
• [5] ستُصبِح قيمة lo مساويةً لقيمة hi بهذه النقطة من البرنامج، كما ستتبقَّى مساحةٌ متاحةٌ لذلك الموضع بين الأعداد الأقل من قيمة المحور والأعداد الأكبر منه. ضع المحور بذلك المكان ثم أعِد موضعه.

بمجرد حصولنا على التنفيذ السابق لعملية QuicksortStep، ستُصبِح خوارزمية الترتيب السريع Quicksort لترتيب قائمة من العناصر بسيطةً جدًا؛ فهي تتكوَّن من مجرد تطبيق عملية QuicksortStep على تلك القائمة، ثم تطبيق الخوارزمية تطبيقًا تعاوديًا على العناصر الواقعة على كلٍ من يسار الموضع الجديد للمحور ويمينه. سنحتاج أيضًا إلى تخصيص الحالات الأساسية base cases، وفي حال احتواء القائمة على عنصرٍ واحدٍ فقط أو عدم احتوائها على أية عناصر، فذلك يعني أنها مُرتَّبة فعلًا، أي لا حاجة لأي إجراءٍ تعاوديٍ آخر.

static void quicksort(int[] A, int lo, int hi) {
   if (hi <= lo) {
         // 1
      return;
   }
   else {
         // 2
      int pivotPosition = quicksortStep(A, lo, hi);
      quicksort(A, lo, pivotPosition - 1);
      quicksort(A, pivotPosition + 1, hi);
   }
}

• [1] طول القائمة يُساوي 0 أو 1، لذلك لسنا بحاجةٍ إلى أي إجراءاتٍ أخرى.
• [2] سنُطبِّق عملية quicksortStep للحصول على موضع المحور الجديد، ثم سنُطبِّق عملية quicksort تعاوديًا لترتيب تلك العناصر التي تسبق المحور، وتلك التي تليه.

كان تعميم المشكلة ضروريًا، حيث كانت المشكلة الأصلية هي ترتيب كامل المصفوفة، بينما ضُبطَت الخوارزمية التعاودية recursive algorithm، بحيث تُصبِح قادرةً على ترتيب جزءٍ معينٍ من المصفوفة. يُمكنك استخدام البرنامج الفرعي quickSort()‎ لترتيب مصفوفةٍ بأكملها من خلال استدعاء quicksort(A, 0, A.length - 1)‎.

تُعدّ خوارزمية الترتيب السريع Quicksort مثالًا شيقًا على تحليل الخوارزميات analysis of algorithms؛ لأن زمن تنفيذ الحالة الوسطى average case يختلف تمامًا عن زمن تنفيذ الحالة الأسوأ worst case.

سنتناول هنا تحليلًا عاميًا informal للخوارزمية، فبالنسبة للحالة الوسطى، ستُقسِّم عملية quicksortStep المشكلة إلى مشكلتين فرعيتين ويكون حجمهما في المتوسط متساويًا؛ وذلك يعني أننا نُقسِّم مشكلةً بحجم 'n' إلى مشكلتين بحجم 'n/2' تقريبًا، ثم نُقسِّمهما إلى أربع مشكلات بحجم 'n/4' تقريبًا، وهكذا.

نظرًا لأن حجم المشكلة يقل إلى النصف في كل مرحلة، فسيكون لدينا عدد log(n)‎ من المراحل. يتناسب القدر المطلوب من المعالجة بكل مرحلةٍ من تلك المراحل مع 'n'؛ أي تُفحَص بالمرحلة الأولى جميع عناصر المصفوفة ويُحتمَل تحريكها.

ستكون لدينا بالمرحلة الثانية مشكلتين فرعيتين، حيث تقع جميع عناصر المصفوفة عدا واحدٍ ضمن واحدةٍ من المشكلتين، وبالتالي ستُفحَص جميع تلك العناصر ويُحتمَل تحريكها، وبذلك يكون لدينا إجماليًا عدد n من الخطوات في كلتا المشكلتين الفرعيتين.

بالمرحلة الثالثة، ستكون لدينا أربعة مشكلات فرعية وعدد n من الخطوات، وهذا يعني أن لدينا عدد log(n)‎ من المراحل تقريبًا؛ حيث تشتمل كل مرحلةٍ على عدد n من الخطوات، ولهذا يكون زمن تشغيل الحالة الوسطى average case لخوارزمية الترتيب السريع هو Θ(n*log(n))‎.

يَفترِض هذا التحليل تقسيم عملية quicksortStep المشكلة إلى أجزاءٍ متساويةٍ تقريبيًا. وفي الحالة الأسوأ worst case، سيُقسِّم كل تطبيق لعملية quicksortStep مشكلةً بحجم n إلى مشكلتين، حيث تكون الأولى بحجم 0 والأخرى بحجم n-1. يحدث ذلك عندما يكون موضع عنصر المحور ببداية أو نهاية المصفوفة بعد الترتيب، وفي هذه الحالة سيكون لدينا عدد n من المراحل، ويكون زمن تشغيل الحالة الأسوأ هو Θ(n<sup>2</sup>)‎.

يندر وقوع الحالة الأسوأ؛ حيث تعتمد على أن تَكون عناصر المصفوفة مُرتَّبةً بطريقةٍ خاصةٍ جدًا، لذلك يُعدّ متوسط أداء خوارزمية الترتيب السريع Quicksort في العموم جيدًا جدًا، باستثناء بعض الحالات النادرة. يُعدّ كَوْن المصفوفة مُرتَّبة بالكامل أو تقريبًا، واحدةً من تلك الحالات النادرة، وإذا أردنا توخّي الدقة، فهي ليست بتلك الحالة النادرة عمليًا. سيستغرق تطبيق خوارزمية الترتيب السريع المُوضَّحة أعلاه على مصفوفةٍ كبيرةٍ مُرتَّبة وقتًا طويلًا، ويُمكِننا في الغالب تَجنُّب حدوث ذلك باختيار موضع المحور عشوائيًا بدلًا من استخدام العنصر الأول دائمًا.

تتوفَّر خوازرميات ترتيبٍ أخرى بزمن تشغيلٍ يُساوِي Θ(n*log(n))‎ بالحالتين الأسوأ والوسطى؛ واحدةٌ منها هي خوارزمية الترتيب بالدمج MergeSort، والتي تُعدّ من الخوارزميات سهلة الفهم، ويُمكِنك البحث عنها إذا كنت مهتمًا.

عد الكائنات Blob

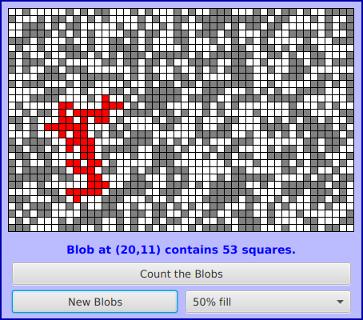
سنفحص الآن مثالًا آخرًا، حيث سنَعُدّ خلاله عدد المربعات الموجودة ضمن تكتلٍ من المربعات المتصلة، وسنُطلِق على ذلك التكتل اسم كائن blob. يعرض البرنامج التوضيحي Blobs.java شبكةً grid من المربعات الصغيرة مُلوّنةً بالأبيض والرمادي والأحمر. وتُظهِر الصورة التالية لقطة شاشةٍ من البرنامج، والتي يُمكِنك أن ترى خلالها شبكة المربعات مع بعض أزرار التحكم.

تُعدّ المربعات الحمراء والرمادية مملوءةً أما المربعات البيضاء فهي فارغة. سنُعرِّف الكائن blob لهذا المثال على النحو التالي: يتكوَّن أي كائنٍ من مربعٍ معين مملوءٍ، بالإضافة إلى جميع المربعات المملوءة التي يُمكِن الوصول إليها من خلال ذلك المربع الأصلي، وذلك عن طريق خلال التحرك لأعلى، أو لأسفل، أو لليمين، أو لليسار عبر مربعاتٍ مملوءةٍ أخرى. إذا نقر المُستخدِم على أي مربعٍ مملوءٍ بالبرنامج، فسيَعُدّ الحاسوب عدد المربعات التي يشتملها الكائن المُتضمِّن للمربع المنقور عليه، وسيُبدِّل لون تلك المربعات إلى الأحمر، حيث أظهرت الصورة السابقة إحدى الكائنات باللون الأحمر.

يُوفِّر البرنامج أيضًا أزرار تحكم أخرى مثل زر كائنات جديدة New Blobs، الذي يؤدي النقر عليه إلى إنشاء نمطٍ عشوائي جديدٍ بالشبكة، كما تتوفَّر أيضًا قائمةٌ لتخصيص النسبة التقريبية للمربعات التي ينبغي ملؤها بالنمط الجديد، حيث ستؤدي زيادة تلك النسبة إلى الحصول على كائناتٍ بأحجام أكبر. إلى جانب ما سبق، يتوفَّر أيضًا زر عدّ الكائنات Count the Blobs، الذي سيحسُب بطبيعة الحال عدد الكائناتٍ المختلفة الموجودة بالنمط.

يعتمد البرنامج على التعاود recursion لحساب عدد المربعات التي يحتويها كائنٌ blob معين؛ فإذا لم يستخدم البرنامج التعاود، فستكون المهمة صعبة التنفيذ. على الرغم من تسهيل التعاود لحل تلك المشكلة نسبيًا، فما يزال من الضروري استخدام تقنيةٍ أخرى جديدة يشيع استخدامها بعددٍ من التطبيقات الأخرى.

سنُخزِّن بيانات شبكة المربعات بمصفوفةٍ ثنائية الأبعاد من القيم المنطقية boolean

boolean[][]  filled;

تكون قيمة filled[r][c]‎ مساويةً للقيمة المنطقية true إذا كان المربع بالصف r والعمود c مملوءًا. وسنُخزِّن عدد صفوف الشبكة بمتغير نسخة instance variable اسمه rows، بينما سنُخزِّن عدد الأعمدة بمتغير النسخة columns. يستخدم البرنامج تابع نسخةٍ تعاودي recursive instance method اسمه getBlobSize(r,c)‎ لعدّ عدد المربعات بكائن، حيث يستطيع التابع الاستدلال على الكائن المطلوب الذي عدّ عدد مربعاته من خلال المعاملين r وc؛ أي عليه أن يَعُدّ عدد مربعات الكائن المُتضمِن للمربع الواقع بالصف r والعمود c، وإذا كان المربع بالموضِع (r,c) فارغًا، فستكون الإجابة ببساطة صفرًا؛ أما إذا لم يَكْن كذلك، فينبغي للتابع getBlobSize()‎ أن يَعُدّ جميع المربعات المملوءة المُمكن الوصول إليها من المربع الموجود بالموضِع (r,c).

تتلخَّص الفكرة باستدعاء getBlobSize()‎ استدعاءً تعاوديًا لحساب عدد المربعات المملوءة المُمكن الوصول إليها من المواضع المجاورة، أي (r+1,c) و(r-1,c) و(r,c+1) و(r,c-1). بحساب حاصل مجموع تلك الأعداد، ثم زيادتها بمقدار الواحد لعدّ المربع بالموضِع (r,c) نفسه، نكون قد حصلنا على العدد الكلي للمربعات المملوءة المُمكِن الوصول إليها من الموضع (r,c). تعرض الشيفرة التالية تنفيذًا لتلك الخوارزمية، ولكنها تعاني من عيبٍ خطر؛ فهي ببساطة تؤدي إلى حدوث تعاودٍ لا نهائي infinite recursion.

int getBlobSize(int r, int c) {  // BUGGY, INCORRECT VERSION!!
      // 1
   if (r < 0 || r >= rows || c < 0 || c >= columns) {
       // هذا الموضع غير موجودٍ بالشبكة، أي ليس هنالك أي كائنٍ بذلك الموضع
       // أعد كائنًا حجمه يساوي صفر
      return 0;
   }
   if (filled[r][c] == false) {
       // المربع ليس جزءًا من الكائن، لذلك أعد القيمة صفر
      return 0;
   }
    // 2
   int size = 1;  

   size += getBlobSize(r-1,c);
   size += getBlobSize(r+1,c);
   size += getBlobSize(r,c-1);
   size += getBlobSize(r,c+1);
   return size;
}  // end INCORRECT getBlobSize()

• [1] لاحِظ أن هذه الطريقة غير صحيحة، حيث تحاول عَدّ كل المربعات المملوءة التي يُمكِن الوصول إليها من الموضع (r,c).
• [2] عَدّ المربع بذلك الموضع، ثم عَدّ عدد الكائنات المتصلة بذلك المربع ارتباطًا أفقيًا أو رأسيًا

لسوء الحظ، سيَعُدّ البرنامج بالأعلى نفس المربع أكثر من مرة، فإذا تضمّن الكائن مربعين على الأقل، فسيحاول البرنامج عدّ كل مربعٍ منهما بصورةٍ لانهائية. لنتخيل أننا نقف بالموِضِع (r,c) ونحاول أن نتبّع التعليمات، حيث تخبرنا التعليمة الأولى بأنه علينا التحرك للأعلى بمقدار صفٍ واحدٍ، ثم نُطبِق نفس الإجراء على ذلك المربع. بينما نُنفِّذ ذلك الإجراء، سيتعيّن علينا أن نتحرك لأسفل بمقدار صفٍ واحد، ونُطبِق نفس الإجراء مرةً أخرى، ولكن سيُعيدنا ذلك إلى الموضع (r,c) مجددًا، حيث سيتعين علينا التحرك لأعلى مجددًا، وهكذا.

يُمكِننا أن نرى بوضوحٍ أننا سنستمر بذلك إلى الأبد، لذلك علينا أن نتأكَّد من أننا نُعالِج كل مربعٍ ونَعُدّه مرةً واحدةً فقط حتى لا ينتهي بنا الحال جيئةً وذهابًا. يَكْمُن الحل بأن نترك أثرًا من القيم المنطقية boolean مثل علامةٍ لتمييز المربعات التي زرناها فعليًا. بمجرد وضع تلك العلامة على مربعٍ معين، فلن نُعالجه مرةً أخرى، وسيقل بذلك عدد المربعات المتبقية غير المُعالَجة ونكون قد أحرزنا تقدمًا بتقليل حجم المشكلة، وعليه نتجنَّب حدوث تعاودٍ لا نهائي.

سنُعرِّف مصفوفةً أخرى من القيم المنطقية visited[r][c]‎ لتمييز المربعات التي زارها البرنامج وعالجها بالفعل، حيث أنه من الضروري بالطبع ضَبْط قيم جميع عناصر تلك المصفوفة إلى القيمة المنطقية false قبل استدعاء getBlobSize()‎. عندما يواجه التابع getBlobSize()‎ مربعًا لم يزره من قبل، فسيَضبُط القيمة المقابلة لذلك المربع بالمصفوفة visited إلى القيمة المنطقية true؛ وفي المقابل، عندما يواجه التابع getBlobSize()‎ مربعًا زاره من قبل، فعليه ببساطةٍ تخطيه دون إجراء أي معالجةٍ أخرى. في الحقيقة، يَكثُر استخدام ذلك الأسلوب من تمييز العناصر المُعالَجَة من غير المُعالجة بالخوارزميات التعاودية recursive algorithms. اُنظُر النسخة المُعدَّلة من التابع getBlobSize()‎.

int getBlobSize(int r, int c) {
   if (r < 0 || r >= rows || c < 0 || c >= columns) {
       // هذا الموضع غير موجود بالشبكة، أي ليس هنالك أي كائنٍ بذلك الموضع
       // أعد كائنًا حجمه يساوي صفر
      return 0;
   }
   if (filled[r][c] == false || visited[r][c] == true) {
       // المربع ليس جزءًا من الكائن أو عُدّ من قبل، لذلك أعِد صفرًا
      return 0;
   }
   visited[r][c] = true;   // 1
   int size = 1;  // 2
   size += getBlobSize(r-1,c);
   size += getBlobSize(r+1,c);
   size += getBlobSize(r,c-1);
   size += getBlobSize(r,c+1);
   return size;
}  // end getBlobSize()

• [1] ضع علامةً تُبيِّن أن البرنامج زار هذا الموضع حتى لا نَعُدّه مرةً أخرى أثناء الاستدعاءات التعاودية.
• [2] عدّ المربع بذلك الموضع، ثم عدّ عدد الكائنات المتصلة بذلك المربع ارتباطًا أفقيًا أو رأسيًا.

يَستخدِم البرنامج التابع المُعرَّف أعلاه لتحديد حجم كائنٍ معين عندما ينقُر المُستخدِم على مربعٍ ينتمي لذلك الكائن. بعد انتهاء التابع getBlobSize()‎ من مهمته، ستكون المصفوفة visited مضبوطةً بحيث تُشير إلى جميع مربعات الكائن. بناءً على ذلك، سيُظهِر التابع المسؤول عن رسم الشبكة المربعات التي قد زارها باللون الأحمر، وعليه سيُصبِح الكائن مرئيًا. يُستخدَم التابع getBlobSize()‎ أيضًا لعدّ عدد الكائنات، كما هو موضحٌ في الشيفرة التالية.

void countBlobs() {

   int count = 0; // عدد الكائنات

   // 1
   for (int r = 0; r < rows; r++)
      for (int c = 0; c < columns; c++)
         visited[r][c] = false;

   // 2
   for (int r = 0; r < rows; r++)
      for (int c = 0; c < columns; c++) {
         if (getBlobSize(r,c) > 0)
            count++;
      }

   draw();  // 3

   message.setText("The number of blobs is " + count);

} // end countBlobs()

• [1] أولًا، امسح المصفوفة visited. سيحدِّد التابع getBlobSize()‎ كل مربعٍ مملوءٍ مر عليه من خلال ضبط عنصر المصفوفة المقابل إلى القيمة المنطقية true. وبمجرد زيارة مربعٍ معين ووضع علامةٍ عليه، فسيبقى كذلك إلى أن ينتهي التابع من عدّ كل الكائنات، وسيمنع هذا عدّ نفس الكائن أكثر من مرة.
• [2] استدعِ التابع getBlobSize()‎ لكل موضعٍ في الشبكة من أجل حساب حجم الكائن الموجود بذلك الموضع؛ فإذا كان حجمه لا يُساوي الصفر، فزِد قيمة العداد بمقدار الواحد. لاحِظ أنه في حالة عُدنا إلى موضعٍ ينتمي لكائنٍ زرناه من قبل، فسيعيد التابع getBlobSize()‎ القيمة صفر، وبذلك لن نَعُدّ ذلك الكائن مرةً أخرى.
• [3] أعِد رسم شبكة المربعات. لاحِظ أن كل المربعات المملوءة ستكون باللون الأحمر.

ترجمة -بتصرّف- للقسم Section 1: Recursion من فصل Chapter 9: Linked Data Structures and Recursion من كتاب Introduction to Programming Using Java.

اقرأ أيضًا

• كيفية كتابة برامج صحيحة باستخدام لغة جافا
• تطبيق عملي: بناء لعبة ورق في جافا
• التعاود recursion والمكدس stack في جافاسكربت