الأشجار الثنائية Binary Trees في جافا

ناقشنا في المقالين السابقين كيفية ارتباط الكائنات مع بعضها لتكوين قوائم. لنتخيل الآن أنه لدينا كائنٌ يحتوي على مؤشرين pointers إلى كائنين من نفس النوع. ستُصبح في هذه الحالة بنى البيانات data structures الناتجة أكثر تعقيدًا من القوائم المترابطة linked list. سنناقش في هذا المقال أحد أبسط البنى البيانية التابعة لذلك النوع، وتحديدًا ما يُعرَف باسم "الأشجار الثنائية binary trees"؛ حيث يحتوي أي كائنٍ ضمن شجرةٍ ثنائيةٍ على مؤشرين، يُطلَق عليهما عادةً left وright. بالإضافة إلى تلك المؤشرات، يمكن للعقد أن تحتوي بالطبع على أي نوعٍ آخر من البيانات، فقد تتكوَّن مثلًا شجرةٌ ثنائيةٌ binary tree من الأعداد الصحيحة من كائناتٍ من النوع التالي:

class TreeNode {
   int item;        // بيانات العقدة
   TreeNode left;   // مؤشر إلى الشجرة الفرعية اليسرى
   TreeNode right;  // مؤشر إلى الشجرة الفرعية اليمنى
}

يُمكِن للمؤشرين left وright أن يكونا فارغين في كائنٍ من النوع TreeNode، أو أن يُشيرا إلى كائناتٍ أخرى من النوع TreeNode. عندما تُشير عقدةٌ node معينةٌ إلى عقدةٍ أخرى، تُعدّ الأولى أبًا parent للثانية التي تُعدّ "عُقدة ابن child". يُمكِن للابن في الأشجار الثنائية binary tree أن يكون "ابنًا أيسر left child"، أو "ابنًا أيمن right child"، وقد يكون لعقدةٍ معينة "ابنٌ أيمن" حتى لو لم يكن لديها "ابنٌ أيسر". تُعدّ العقدة 3 أبًا للعقدة 6 في الصورة التالية على سبيل المثال، كما تُعدّ العقد 4 و5 أبناءً للعقدة 2.

لا تُعدّ أي بنيةٍ structure مُكوَّنةٍ من هذا النوع من العقد شجرةً ثنائية binary tree؛ ولكن لا بُدّ أن تتوفَّر بها بعض الخاصيات، وهي:

وجود عقدةٍ واحدةٍ فقط بدون أب ضمن الشجرة، ويُطلَق على تلك العقدة اسم "جذر الشجرة root".
تملُك كل العقد الأخرى ضمن الشجرة أبًا واحدًا فقط.
عدم وجود أي حلقاتٍ loops بالشجرة، أي لا يُمكِن بأي حالٍ من الأحوال البدء بعقدةٍ معينة ثم التحرك منها لعقدٍ أخرى عبر سلسلةٍ من المؤشرات ثم الانتهاء بنفس العقدة التي بدأت منها.

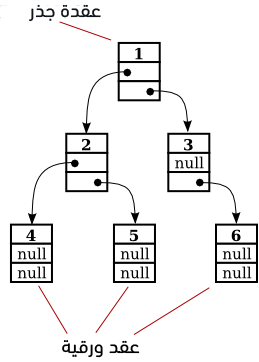
يُطلَق على العقد التي ليس لديها أي أبناءٍ اسم العقد الورقية leaves، ويُمكِنك تمييز هذا النوع من العقد بسهولة؛ نظرًا لاحتواء مؤشريها الأيمن والأيسر على القيمة الفارغة null. وفقًا للتصور العام للشجرة الثنائية binary tree، فإن عقدة الجذر root node تُعرَض بالأعلى بينما تُعرَض العقد الورقية بالأسفل، وهو ما يُخالف واقع الأشجار الحقيقية تمامًا. ولكن على الأقل، ما يزال بإمكاننا رؤية بنيةٍ تفريعيةٍ شبيهةٍ بالأشجار وهو السبب وراء تسميتها بذلك الاسم.

اجتياز الشجرة Tree Traversal

لنفكر بعقدةٍ node ما ضمن شجرةٍ ثنائية binary tree، فإذا نظرنا إلى تلك العقدة مصحوبةً بجميع العقد المُشتقَة منها، أي أبنائها وأبناء أبنائها …إلخ، فستشكّل تلك المجموعة من العقد شجرةً ثنائيةً binary tree يُطلَق عليها اسم شجرة فرعية subtree من الشجرة الأصلية. تُشكِّل العقد 2 و4 و5 في الصورة السابقة على سبيل المثال شجرةً فرعية، ويُطلَق عليها اسم شجرةٍ فرعيةٍ يُسرى مُشتقّةٍ من الجذر root؛ وبالمثل، تُشكِّل العقد 3 و6 شجرةً فرعيةً يُمنى مُشتقةً من الجذر.

تتكوَّن أي شجرةٍ ثنائية binary tree غير فارغة من عقدة جذر root node، وشجرةٍ فرعيةٍ يسرى، وشجرةٍ فرعيةٍ يُمنى، وقد تكون أي شجرةٍ فرعيةٍ منهما فارغةً أو حتى كلتيهما. يُعدّ ما سبق تعريفًا تعاوديًا recursive يتماشى مع التعريف التعاودي للصنف TreeNode، وبالتالي لا ينبغي أن تكون حقيقة شيوع استخدام البرامج الفرعية التعاودية recursive subroutines لمعالجة الأشجار أمرًا مفاجئًا.

لنفكر الآن بمشكلة عدّ العقد الموجودة في شجرة ثنائية، حيث من الممكن تصميم خوارزميةٍ غير تعاوديةٍ لحل تلك المشكلة، ولكن لا تتوقَّع أن تَصِل إليها بسهولة. تَكْمُن المشكلة في تذكُّر العقد التي ما تزال بحاجة للعدّ، وهو في الواقع ليس بالأمر السهل، بل إنه مستحيلٌ في حالة عدم استخدام بنيةٍ بيانيةٍ إضافية، مثل المكدس stack أو الرتل queue على الأقل.

في المقابل، ستصبح الخوارزمية في غاية السهولة لدى استخدام التعاود recursion، حيث إما أن تكون الشجرة فارغةً، أو مُكوَّنةً من جذرٍ وشجرتين فرعيتين subtrees؛ فإذا كانت الشجرة فارغةً، فإن عدد العقد ببساطة يُساوِي صفر، وتمثّل الحالة الأساسية base case للتعاود؛ أما إذا لم تكن فارغة، فينبغي تطبيق التعاود لحساب عدد العقد بالشجرتين الفرعيتين، ثم حساب مجموعهما، وزيادة الناتج بمقدار الواحد لعدّ الجذر، وهو ما يُعطينا العدد الكلي للعقد الموجودة بالشجرة. ألقِ نظرةً على شيفرة جافا التالية:

static int countNodes( TreeNode root ) {
   if ( root == null )
      return 0;  // الشجرة فارغة ولا تحتوي على أي عقد
   else {
      int count = 1;   // ابدأ بعدّ الجذر
       // أضف عدد العقد بالشجرة الفرعية اليسرى
      count += countNodes(root.left);  
       // أضف عدد العقد بالشجرة الفرعية اليمنى
      count += countNodes(root.right); 

       return count;  // أعد العدد الإجمالي
   }
} // end countNodes()

سنناقش مثالًا آخر وهو مشكلة طباعة العناصر الموجودة في شجرة ثنائية binary tree،فإذا كانت الشجرة فارغةً، فليس هناك شيءٌ ينبغي فعله؛ أما إذا كانت الشجرة غير فارغةٍ، فهذا يعني أنها تتكوَّن من جذرٍ بالإضافة إلى شجرتين فرعيتين subtrees، وينبغي في هذه الحالة طباعة العنصر الموجود بعقدة الجذر ثم استخدام التعاود recursion لطباعة عناصر الشجرتين الفرعيتين. تعرض الشيفرة التالية برنامجًا فرعيًا subroutine يطبع جميع العناصر الموجودة بالشجرة ضمن سطر خرجٍ وحيد.

static void preorderPrint( TreeNode root ) {
   if ( root != null ) {  // (Otherwise, there's nothing to print.)
      System.out.print( root.item + " " );  // اطبع عنصر الجذر
      preorderPrint( root.left );   // اطبع العناصر بالشجرة الفرعية اليسرى
      preorderPrint( root.right );  // اطبع العناصر بالشجرة الفرعية اليمنى
   }
} // end preorderPrint()

يُطلق على التابع المُعرَّف بالأعلى اسمpreorderPrint؛ لأنه يستخدم اجتيازًا ذا ترتيبٍ سابق preorder traversal، وعند استخدام هذا النوع من الاجتياز، سيعالج البرنامج عقدة الجذر root node أولًا، ثم يجتاز الشجرة الفرعية اليسرى left subtree، وبعدها يجتاز الشجرة الفرعية اليمنى right subtree.

في المقابل، إذا استخدم البرنامج اجتيازًا ذا ترتيبٍ لاحق، فإنه يجتاز الشجرة الفرعية اليسرى أولًا، ثم الشجرة الفرعية اليمنى، وأخيرًا يُعالِج عقدة الجذر؛ أما إذا كان البرنامج يستخدم اجتيازًا مُرتّبًا inorder traversal، فإنه يجتاز الشجرة الفرعية اليسرى أولًا، ثم يُعالِج عقدة الجذر root node، ويجتاز أخيرًا الشجرة الفرعية اليمنى. تختلف البرامج الفرعية المعتمدة على اجتيازٍ ذي ترتيبٍ لاحق أو اجتيازٍ مُرتّبٍ أثناء طباعة محتويات الشجرة عن التابع preorderPrint()‎ فقط بمَوضِع تعليمة طباعة عنصر عقدة الجذر.

static void postorderPrint( TreeNode root ) {
   if ( root != null ) {  // (Otherwise, there's nothing to print.)
       // اطبع العناصر بالشجرة الفرعية اليسرى
      postorderPrint( root.left );   
       // اطبع العناصر بالشجرة الفرعية اليمنى
      postorderPrint( root.right );  
      System.out.print( root.item + " " );  // اطبع عنصر الجذر
   }
} // end postorderPrint()


static void inorderPrint( TreeNode root ) {
   if ( root != null ) {  // (Otherwise, there's nothing to print.)
       // اطبع العناصر بالشجرة الفرعية اليسرى
      inorderPrint( root.left );   
      System.out.print( root.item + " " );  // اطبع عنصر الجذر
       // اطبع العناصر بالشجرة الفرعية اليمنى
      inorderPrint( root.right );  
   }
} // end inorderPrint()

يُمكِننا تطبيق البرامج الفرعية المبينة أعلاه على الشجرة الثنائية المُوضحة بالصورة المعروضة ببداية هذا المقال، حيث سنجد اختلاف ترتيب طباعة العناصر بكل حالةٍ كما هو مُبيَّن على النحو التالي:

preorderPrint outputs:   1  2  4  5  3  6

postorderPrint outputs:  4  5  2  6  3  1

inorderPrint outputs:    4  2  5  1  3  6

بالنسبة للتابع preorderPrint: يُطبَع عنصر الجذر وهو العدد 1 أولًا قبل أي عناصر أخرى. لاحِظ أن الأمر نفسه يَنطبِق على الأشجار الفرعية المُشتقَة من الجذر؛ أي نظرًا لأن عنصر الجذر للشجرة الفرعية اليسرى left subtree يُساوي 2، فيُطبَع العدد 2 قبل العناصر الأخرى الواقعة ضمن تلك الشجرة الفرعية أي 4 و5، يُطبَع بالمثل عنصر الجذر 3 قبل العدد 6. يعني ذلك أنه عند استخدام اجتيازٍ ذي ترتيبٍ سابق preorder traversal، فإنه يُطبَّق على جميع مستويات الشجرة دون استثناء، ويُمكنك بالمثل تحليل الترتيب الناتج عن استخدام الطريقتين الأخريين من الاجتياز traversal.

أشجار الترتيب الثنائية Binary Sort Trees

تعرَّضنا بمقال بنى البيانات المترابطة Linked Data Structures لمثالٍ عن قائمةٍ مترابطة likned list من السلاسل النصية strings تحتفظ بها بحيث تكون مُرتّبةً ترتيبًا تصاعديًا. تعمل القوائم المترابطة جيدًا عند استخدامها مع عددٍ قليلٍ من السلاسل النصية، ولكنها تُصبِح غير فعالةٍ في حالة وجود عددٍ كبيرٍ من العناصر. عند إضافة عنصرٍ إلى القائمة، يتطلَّب تحديد موضع ذلك العنصر في المتوسط فحص نصف العناصر الموجودة بالقائمة، كما يتطلَّب العثور على عنصر ضمن القائمة نفس الوقت تقريبًا.

في المقابل، إذا كانت السلاسل النصية مُخزّنةً بمصفوفةٍ مرتّبةٍ وليس بقائمةٍ مترابطة، يُصبِح البحث أكثر فعاليةً، حيث من الممكن عندها تطبيق البحث الثنائي binary search. ولكن، عند إضافة عنصرٍ جديد، فإن المصفوفة لا تكون فعالة؛ لأننا سنضطّر إلى تحريك نصف عناصر المصفوفة تقريبًا لتوفير مساحةٍ للعنصر المطلوب إضافته. في الحقيقة، تُخزِّن الشجرة الثنائية binary tree قائمةً مُرتبةً بطريقةٍ تجعل كُلًا من عمليتي البحث والإدخال أكثر فعالية، وعند استخدام شجرةٍ ثنائيةٍ بتلك الطريقة، يُطلَق عليها اسم شجرة الترتيب الثنائية binary sort trees -أو اختصارًا BST.

تتمتع شجرة الترتيب الثنائية هي بالنهاية شجرة ثنائية binary tree بخاصيتين إضافيتين؛ فلأجل كل عقدةٍ node ضمن الشجرة، فإن العنصر الموجود بتلك العقدة أكبر من أو يُساوِي جميع العناصر الموجودة بالشجرة الفرعية subtree اليسرى المشتقة من تلك العقدة، كما أنه أقل من أو يساوي جميع العناصر الموجودة بالشجرة الفرعية اليمنى المشتقة من نفس العقدة. تَعرِض الصورة التالية مثالًا لشجرة ترتيب ثنائية binary sort tree مكوَّنةٍ من عناصرٍ من النوع String.

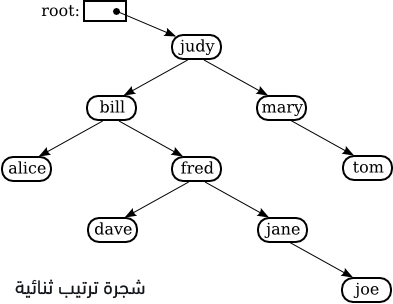
تتميز أشجار الترتيب الثنائية بخاصيةٍ أخرى، حيث يؤدي تطبيق اجتياز مُرتبٍ inorder traversal على تلك الشجرة إلى معالجة عناصرها بترتيبٍ تصاعدي، وتُعدّ تلك الخاصية بمثابة طريقةٍ أخرى لتعريفها؛ فإذا استخدمنا مثلًا اجتيازًا مُرتبًا من أجل طباعة عناصر الشجرة المعروضة بالصورة، فستُطبَع بترتيبٍ أبجدي. يَضمَن تعريف هذا النوع من الاجتياز طباعة جميع العناصر الموجودة بالشجرة الفرعية اليسرى المشتقة من العنصر "judy" قبل طباعة ذلك العنصر ذاته.

نظرًا لاستخدامنا شجرة ترتيبٍ ثنائية، فهذا يعني أنه لا بُدّ وأن تَسبِق عناصر الشجرة الفرعية اليسرى المُشتقَّة من العنصر "judy" العنصر "judy" وفقًا للترتيب الأبجدي، كما لا بُدّ أن تلحق عناصر الشجرة الفرعية اليمنى العنصر "judy" وفقًا للترتيب الأبجدي؛ يعني ذلك أننا نطبع "judy" بموضعها الأبجدي الصحيح. يُمكِن تطبيق نفس المنطق على الأشجار الفرعية subtrees؛ أي أننا سنطبع "Bill" بعد "alice" وقبل "fred" وأحفاده، وسنطبع "Fred" بعد "dave" وقبل "jane" و"joe"، وهكذا.

لنفترض أننا نريد أن نبحث عن عنصرٍ معينٍ داخل شجرة بحثٍ ثنائية binary search tree. سنوازن ذلك العنصر مع عنصر جذر الشجرة؛ فإذا كانا متساويين، فإننا نكون قد انتهينا؛ أما إذا كان العنصر الذي نبحث عنه أقل من عنصر الجذر، فعلينا أن نُضيِّق نطاق البحث إلى عناصر الشجرة الفرعية اليسرى المشتقة من الجذر، أما الشجرة الفرعية اليمنى فيُمكِن إلغاؤها لأنها تحتوي على عناصرٍ أكبر من أو تساوي الجذر. وبالمثل، إذا كان العنصر الذي نبحث عنه أكبر من عنصر الجذر، يُمكِننا تضييق نطاق البحث إلى عناصر الشجرة الفرعية اليمنى.

يُمكِننا بكلتا الحالتين إعادة تطبيق نفس عملية البحث على واحدةٍ من الشجرتين الفرعيتين. علاوةً على ذلك، إذا أردنا إضافة عنصرٍ جديد، فسيكون الأمر مشابهًا، حيث سنبدأ بالبحث عن الموضع الذي ينبغي أن ينتمي إليه العنصر الجديد، وبعد العثور عليه، يُمكِننا بسهولة أن إنشاء عقدةٍ جديدة، وربطها بذلك الموضع من الشجرة.

تمتاز عمليتا البحث searching والإضافة insertion إلى شجرة بحثٍ ثنائية binary search tree بالكفاءة، بالأخص عندما تكون الشجرة متزنةٌ تقريبًا؛ حيث تُعدّ الشجرة الثنائية مُتزِنةً balanced، إذا كانت الشجرة الفرعية اليسرى المُشتقَّة من كل عقدةٍ بالشجرة تحتوي تقريبًا على نفس عدد العقد الذي تحتويه الشجرة الفرعية اليمنى المُشتقَّة من نفس العقدة، وعندما يكون الفرق بين العددين مساويًا للواحد على الأكثر، تُعدّ الشجرة الثنائية متزنةً تمامًا.

في الحقيقة، ليست كل الأشجار الثنائية متزنةً، ولكن إذا أنشأنا الشجرة بحيث تُضَاف العناصر إليها بترتيبٍ عشوائي، ستزداد احتمالية أن تكون الشجرة متزنةً تقريبًا؛ أما إذا كان ترتيب الإدخال غير عشوائي، فستكون الشجرة غير متزنة. أثناء البحث بشجرة ترتيبٍ ثنائية binary sort tree، تلغي كل عملية موازنة comparison إحدى الشجرتين الفرعيتين؛ وهذا يعني أنه إذا كانت الشجرة متزنةً، فإن عدد العناصر قيد البحث يقل إلى النصف في كل مرة، ويُشبه ذلك خوارزمية البحث الثنائي binary search algorithm تمامًا، أي أننا نحصل على خوارزمية بنفس الفاعلية عند استخدام شجرة الترتيب الثنائية.

وفقًا لمصطلحات التحليل المقارب asymptotic analysis المُوضحة في مقال تحليل الخوارزميات في جافا، فإن زمن تشغيل الحالة الوسطى average case لعمليات البحث والإضافة والحذف على شجرة بحثٍ ثنائية يُساوِي Θ(log(n))‎، حيث تُمثّل n عدد عناصر الشجرة، ويأخذ المتوسط بالحسبان جميع احتمالات الترتيب المختلفة التي يُمكِن أن نُدْخِل بها العناصر إلى الشجرة.

طالما كان ترتيب الإدخال المُستخدَم فعليًا عشوائيًا، فغالبًا ما سيكون زمن التشغيل الفعلي قريبًا جدًا من القيمة المتوسطة. ومع ذلك، فإن زمن تشغيل الحالة الأسوأ worst case لنفس العمليات يُساوِي Θ(n)‎، ,هو أسوأ بكثيرٍ من Θ(log(n))‎. تحدث الحالة الأسوأ عند إدخال العناصر بترتيبٍ معين، فإذا أدخلنا مثلًا العناصر مرتبةً ترتيبًا تصاعديًا، فستتحرك العناصر دائمًا إلى اليمين أثناء تحركها لأسفل الشجرة، وسنَحصُل في النهاية على شجرةٍ أقرب ما تكون لقائمةٍ مترابطة linked list مُكوّنةٍ من سلسلةٍ خطيةٍ من العقد مربوطةٍ معًا عبر مؤشرات أبنائها اليُمنى.

تستغرق العمليات على مثل تلك الشجرة نفس الزمن الذي تستغرقه عند تطبيقها على قائمةٍ مترابطة. تتوفَّر بنى بيانية data structures أخرى تشبه أشجار الترتيب الثنائية باستثناء تنفيذ عمليتي إدخال العقد وحذفها بطريقةٍ تَضمَن دومًا بقاء الشجرة متزنةً تقريبًا. بالنسبة لهذا النوع من بنى البيانات، فإن زمن تشغيل الحالة الوسطى والحالة الأسوأ لعمليات البحث والإضافة والحذف تُساوِي Θ(log(n))‎. سنناقش فيما يلي نسخًا بسيطةً من عمليتي الإدخال والبحث.

يستخدم البرنامج التوضيحي SortTreeDemo.java أشجار الترتيب الثنائية، حيث يتضمن برامجًا فرعيةً تُنفِّذ كُلًا من عمليات البحث والإدخال وكذلك اجتيازً مُرتبًا inorder traversal. سنَفْحَصفيما يلي برنامجي البحث والإدخال فقط. يَسمَح برنامج main()‎ التالي للمُستخدِم بكتابة سلاسلٍ نصيةٍ ثم إدخالها إلى الشجرة.

تُمثَل العقد ضمن الشجرة الثنائية بالبرنامج SortTreeDemo باستخدام الصنف المتداخل الساكن static nested التالي، حيث يُعرِّف الصنف باني كائن constructor بسيطٍ لتسهيل إنشاء العقد.

private static class TreeNode {
   String item;      // بيانات العقدة
   TreeNode left;    // مؤشر إلى الشجرة الفرعية اليسرى
   TreeNode right;   // مؤشر إلى الشجرة الفرعية اليمنى
   TreeNode(String str) {
       // يُنشِيء الباني عقدةً تحتوي على سلسلة نصية
       // لاحِظ أن المؤشرين الأيمن والأيسر فارغان في تلك الحالة
      item = str;
   }
}  // end class TreeNode

يُشير متغير عضوٍ ساكنٍ static member variable اسمه root من النوع TreeNode إلى شجرة الترتيب الثنائية binary sort tree التي يستخدمها البرنامج.

// مؤشر إلى عقدة جذر الشجرة 
// ‫عندما تكون الشجرة فارغة، فإن root يُساوي null
private static TreeNode root;

يستخدم البرنامج برنامجًا فرعيًا تعاوديًا recursive subroutine اسمه treeContains للبحث عن عنصرٍ معينٍ ضمن الشجرة، حيث يُنفِّذ ذلك البرنامج خوارزمية البحث للأشجار الثنائية التي تعرَّضنا لها بالأعلى.

static boolean treeContains( TreeNode root, String item ) {
   if ( root == null ) {
       // الشجرة فارغةٌ، أي أن العنصر غير موجود بالتأكيد
      return false;
   }
   else if ( item.equals(root.item) ) {
       // عثرنا على العنصر المطلوب بعقدة الجذر
      return true;
   }
   else if ( item.compareTo(root.item) < 0 ) {
       // إذا كان العنصر موجودًا، فلا بُدّ أن يقع بالشجرة الفرعية اليسرى
      return treeContains( root.left, item );
   }
   else {
       // إذا كان العنصر موجودًا، فلا بُدّ أن يقع بالشجرة الفرعية اليمنى
      return treeContains( root.right, item );
   }
}  // end treeContains()

عندما يَستدعِي برنامج main البرنامج المُعرَّف بالأعلى، فإنه يُمرِّر المتغير العضو الساكن root مثل قيمةٍ للمعامل الأول؛ حيث يُشير root إلى جذر شجرة الترتيب الثنائية بالكامل.

لا يُعدّ استخدام التعاود recursion في تلك الحالة ضروريًا، حيث يُمكِننا استخدام خوارزميةٍ غير تعاودية non-recursive بسيطةٍ للبحث ضمن شجرة الترتيب الثنائية binary sort tree على النحو التالي: ابدأ من الجذر، وتحرَّك لأسفل الشجرة إلى أن تَعثُر على العنصر المطلوب أو أن تصل إلى مؤشرٍ فارغ null pointer. نظرًا لاتّباع البحث مسارًا واحدًا على طول الشجرة، يُمكِننا استخدام حلقة while لتنفيذه. تَعرِض الشيفرة التالية نسخةً غير تعاودية من برنامج البحث.

private static boolean treeContainsNR( TreeNode root, String item ) {
   TreeNode runner;  // المؤشر المستخدم لاجتياز الشجرة
   runner = root;    // ابدأ بعقدة الجذر
   while (true) {
      if (runner == null) {
            // وقعنا إلى خارج الشجرة دون العثور على العنصر
         return false;  
      }
      else if ( item.equals(runner.item) ) {
            // لقد عثرنا على العنصر المطلوب
         return true;
      }
      else if ( item.compareTo(runner.item) < 0 ) {
          // إذا كان العنصر موجودًا، فلا بُدّ أن يكون بالشجرة الفرعية اليسرى
          // ولذلك، حرك المؤشر إلى يسار المستوى التالي
         runner = runner.left;
      }
      else {
          // إذا كان العنصر موجودًا، فلا بُدّ أن يكون بالشجرة الفرعية اليمنى
          // ولذلك، حرك المؤشر إلى يمين المستوى التالي
         runner = runner.right;
      }
   }  // end while
} // end treeContainsNR();

يشبه البرنامج الفرعي المسؤول عن إضافة عنصرٍ جديدٍ إلى الشجرة كثيرًا النسخة غير التعاودية من برنامج البحث. وينبغي لبرنامج الإدخال معالجة حالة كون الشجرة فارغة؛ ففي تلك الحالة، لا بُدّ من تعديل قيمة root، وضَبْطها لتُشير إلى عقدةٍ تحتوي على العنصر الجديد.

root = new TreeNode( newItem );

ولكن هذا يعني أنه ليس بإمكاننا تمرير الجذر مثل معامل parameter إلى البرنامج الفرعي subroutine؛ حيث من المستحيل لأي برنامجٍ فرعيٍ تعديل القيمة المُخزَّنة فعليًا بالمعامل (تستطيع بعض لغات البرمجة الأخرى فعل ذلك).

هناك عدة طرقٍ لحل تلك المعضلة، ولكن الطريقة الأسهل هي استخدام برنامج إدخالٍ غير تعاودي non-recursive يُمكنه الوصول إلى قيمة المتغير العضو الساكن root مباشرةً. إحدى الاختلافات بين عملية إضافة عنصرٍ وعملية البحث عن عنصرٍ، هي أنه علينا الانتباه حتى لا نقع بمشكلة "السقوط خارج الشجرة"؛ أي علينا التوقُّف عن البحث قبل أن تُصبِح قيمة runner مساويةً للقيمة الفارغة null، وعند الوصول إلى موضعٍ فارغٍ بالشجرة، يُمكِننا إضافة العنصر الجديد إليه.

// 0
private static void treeInsert(String newItem) {
   if ( root == null ) {
       // ‫الشجرة فارغة. سنَضبُط root لكي يُشير إلى العقدة الجديدة التي 
       // تحتوي على العنصر الجديد. ستُصبِح تلك العقدة هي العقدة الوحيدة 
       // بالشجرة
      root = new TreeNode( newItem );
      return;
   }
   TreeNode runner;  // المؤشر المستخدم لاجتياز الشجرة للعثور على موضع العقدة الجديدة
   runner = root;   // سنبدأ من جذر الشجرة
   while (true) {
      if ( newItem.compareTo(runner.item) < 0 ) {
        // 1
         if ( runner.left == null ) {
            runner.left = new TreeNode( newItem );
            return;  // أضفنا العنصر الجديد إلى الشجرة
         }
         else
            runner = runner.left;
      }
      else {
            // 2
         if ( runner.right == null ) {
            runner.right = new TreeNode( newItem );
            return;  // أضفنا العنصر الجديد إلى الشجرة
         }
         else
            runner = runner.right;
      }
   } // end while
}  // end treeInsert()

حيث تعني كل من:

[0]: أضف العنصر إلى شجرة الترتيب الثنائية، التي يُشير إليها المُتغيِّر العام root. لاحِظ أنه من غير الممكن تمرير root مثل مُعاملٍ للبرنامج؛ لأنه قد يُعدِّل قيمة root في حين لا تؤثر التعديلات الواقعة على قيم المعاملات الصورية formal parameters بالقيمة الفعلية للمعامل.
[1]: نظرًا لأن العنصر الجديد أقل من العنصر الموجود بالعقدة التي يشير إليها runner، فينتمي العنصر إذًا إلى الشجرة الفرعية اليسرى المشتقة من runner. إذا كان runner.left فارغًا، أضف العقدة الجديدة هناك؛ أما إذا لم تكن فارغة، فحرِك المؤشر runner إلى يسار المستوى التالي.
[2]: نظرًا لأن العنصر الجديد أكبر من العنصر الموجود بالعقدة التي يُشير إليها runner، فإن العنصر إذًا ينتمي إلى الشجرة الفرعية اليمنى المُشتقَّة من runner. إذا كان runner.right فارغًا، أضف العقدة الجديدة هناك؛ أما إذا لم تكن فارغة، فحرِك المؤشر runner إلى يمين المستوى التالي.

أشجار التعبير Expression Trees

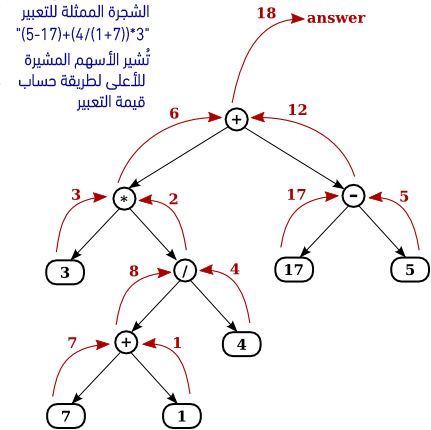
يُعدّ تخزين التعابير الحسابية mathematical expression مثل "‎15*(x+y)‎" أو "‎sqrt(42)+7" تطبيقًا آخرًا على استخدام الأشجار trees، حيث سنكتفي الآن بالتعبيرات المكوَّنة من أعدادٍ وعواملٍ بسيطة مثل "+" و"-" و"" و"/". لنفترض مثلًا أنه لدينا التعبير التالي "‎3*((7+1)/4)+(17-5)‎"، الذي يتكوَّن من تعبيرين فرعيين subexpressions، هما "‎3*((7+1)/4)‎" و"‎(17-5)‎" بالإضافة إلى العامل "+"؛ فإذا مَثَّلنا التعبير مثل شجرةٍ ثنائية binary tree، فستَحمِل عقدة الجذر root node العامل "+"، بينما ستُمثِل الأشجار الفرعية subtrees المُشتقَّة من عقدة الجذر التعابير الفرعية "‎3*((7+1)/4)‎" و"‎(17-5)‎".

تحمل كل عقدةٍ بالشجرة عددًا أو عاملًا operator؛ حيث تُعدّ العقدة التي تحمل عددًا عقدةً ورقيةً leaf node؛ أما العقدة التي تحمل عاملًا operator، فإنها تملُك شجرتين فرعيتين تُمثلان المعاملين operands اللذين ينبغي أن يُطبَق عليهما ذلك العامل. تُبين الصورة بالأسفل رسمًا توضيحيًا لتلك الشجرة، والتي سنُشير إليها باسم "شجرة تعبير expression tree".

إذا كان لدينا شجرة تعبير، فسيكون من السهل حساب قيمة التعبير الذي تمثله تلك الشجرة. تملك كل عقدةٍ ضمن الشجرة قيمةً معينة؛ فإذا كانت العقدة عقدةً ورقيةً، فإن قيمتها ببساطة هي نفس قيمة العدد الذي تحمله؛ أما إذا احتوت العقدة على عامل operator، ستُحسب قيمتها عن طريق حساب قيم عقدها الأبناء child nodes، ثم تطبيق العامل على تلك القيم.

تُبيِّن الأسهم الصاعدة بالصورة التالية طريقة المعالجة، حيث نلاحِظ أن قيمة عقدة الجذر root node هي قيمة كل التعبير. تتوفَّر استخداماتٌ أخرى لأشجار التعبير expression trees. على سبيل المثال، إذا طبقّنا اجتيازًا ذا ترتيبٍ لاحق postorder traversal على الشجرة، فإننا سنَحصُل على تعبير الإلحاق المكافئ postfix expression.

تتكوَّن أي شجرة تعبير من نوعين من العقد: العقد التي تحتوي على أعداد، والعقد التي تحتوي على عوامل operators. علاوةً على ذلك، قد نرغب بإضافة أنواعٍ أخرى من العقد لاستغلال الأشجار بصورةٍ أفضل، مثل استخدام عقدٍ تحتوي على متغيرات. الآن، إذا أردنا العمل مع أشجار التعبير expression trees بلغة جافا، كيف يُمكننا التعامل مع أنواع العقد المختلفة؟ أحد الطرائق التي ستُغضِب المتعصبين للبرمجة كائنية التوجه object-oriented، هو تضمين متغير نسخة instance variable بكل كائن عقدة node object لتحديد نوع العقدة. اُنظر الشيفرة التالية:

enum NodeType { NUMBER, OPERATOR }   // Possible kinds of node.

class ExpNode {  // A node in an expression tree.

    NodeType kind;  // نوع العقدة
    double number;  // قيمة عُقدة ممثلة لعدد
    char op;        // قيمة العامل بعقدة ممثلة لعامل
    // مؤشرات إلى الشجرتين الفرعيتين المشتقتين من عقدة العامل
    ExpNode left;   
    ExpNode right;  

    ExpNode( double val ) {
        // يُنشِئ هذا الباني عقدة ممثلة لعدد
       kind = NodeType.NUMBER;
       number = val;
    }

    ExpNode( char op, ExpNode left, ExpNode right ) {
        // يُنشِئ هذا الباني عقدة ممثلة لعامل
       kind = NodeType.OPERATOR;
       this.op = op;
       this.left = left;
       this.right = right;
    }

 } // end class ExpNode

يُعطي البرنامج الفرعي التعاودي التالي قيمة شجرة التعبير expression tree:

static double getValue( ExpNode node ) {
    // أعد قيمة التعبير الذي تُمثِله الشجرة التي تُشير إليها العقدة‫ node
    if ( node.kind == NodeType.NUMBER ) {
        // قيمة العقد العددية هي ببساطة العدد الذي تحمله
       return node.number;
    }
    else {  // لابُدّ أن يكون عاملًا
            // احسب قيمة المعاملين ثم ادمجهما معًا باستخدام العامل
       double leftVal = getValue( node.left );
       double rightVal = getValue( node.right );
       switch ( node.op ) {
          case '+':  return leftVal + rightVal;
          case '-':  return leftVal - rightVal;
          case '*':  return leftVal * rightVal;
          case '/':  return leftVal / rightVal;
          default:   return Double.NaN;  // Bad operator.
       }
    }
 } // end getValue()

يتوفَّر حل آخر يميل إلى البرمجة كائنية التوجه object-oriented، على الرغم من أن الطريقة السابقة ستعمل بنجاح. نظرًا لوجود نوعين فقط من العقد، فمن البديهي أن يكون لدينا صنفين classes لتمثيل كل نوعٍ منهما، هما ConstNode وBinOpNode. لتمثيل الفكرة العامة لعقدةٍ ضمن شجرة تعبير، سنحتاج إلى صنفٍ آخر، وليكن اسمه ExpNode.

سنُعرِّف الصنفين ConstNode وBinOpNode بحيث يكونا أصنافًا فرعيةً subclasses مُشتقّةً من الصنف ExpNode، ونظرًا لأن أي عقدةٍ فعليةٍ ستكون من الصنف ConstNode أو الصنف BinOpNode، فسينبغي أن يكون الصنف ExpNode صنفًا مجردًا abstract class (ألقِ نظرةً على مقال الوراثة والتعددية الشكلية Polymorphism والأصناف المجردة Abstract Classes في جافا). لأننا نريد بالأساس تحصيل قيمة العقد، فإننا سنُعرِّف تابع نسخة instance method في كل صنف عقدة لتحصيل قيمتها. انظر الشيفرة التالية:

abstract class ExpNode {
       // يُمثل عقدة من أي نوع بشجرة تعبير

    abstract double value();  // يُعيد قيمة العقدة

} // end class ExpNode


class ConstNode extends ExpNode {
       // يُمثِل عقدى تحمل عددًا

    double number;  // العدد الموجود بالعقدة

    ConstNode( double val ) {
          // ‫يُنشِئ الباني عقدة تحتوي على قيمة val
       number = val;
    }

    double value() {
        // القيمة هي العدد الذي تحمله العقدة
        return number;
    }

 } // end class ConstNode


 class BinOpNode extends ExpNode {
       // تُمثِل عقدة تحمل عاملًا

    char op;        // العامل
    ExpNode left;   // المعامل الأيسر
    ExpNode right;  // المعامل الأيمن

    BinOpNode( char op, ExpNode left, ExpNode right ) {
          // يُنشِئ الباني عقدة تحمل البيانات المخصصَّة
       this.op = op;
       this.left = left;
       this.right = right;
    }

    double value() {
        // احسب قيمة المعاملين الأيمن والأيسر ثم اِدْمجهما معًا باستخدام العامل
        double leftVal = left.value();
        double rightVal = right.value();
        switch ( op ) {
            case '+':  return leftVal + rightVal;
            case '-':  return leftVal - rightVal;
            case '*':  return leftVal * rightVal;
            case '/':  return leftVal / rightVal;
            default:   return Double.NaN;  // Bad operator.
         }
    }

 } // end class BinOpNode

ينتمي المعاملان الأيمن والأيسر بعقد الصَنْف BinOpNode إلى النوع ExpNode وليس BinOpNode، ويسمح ذلك للمعاملات بأن تكون من النوع ConstNode، أو النوع BinOpNode، أو حتى أي نوعٍ آخر مُشتقٍّ من النوع ExpNode. بما أن كل عقدةٍ من النوع ExpNode تُعرِّف تابع النسخة value()‎، يُمكِننا إذًا استدعاء left.value()‎ لحساب قيمة المعامل الأيسر؛ فإذا كان left من النوع ConstNode، سيؤدي استدعاء left.value()‎ إلى استدعاء التابع value()‎ المُعرَّف بالصنف ConstNode؛ أما إذا كان left من النوع BinOpNode، فسيؤدي استدعاء التابع value()‎ إلى استدعاء التابع value()‎ المُعرَّف بالصنف BinOpNode، وبذلك تَعرِف كل عقدةٍ الطريقة المناسبة لحساب قيمتها.

قد يبدو الأسلوب كائني التوجه أعقد قليلًا بالبداية، ولكنه يتمتع بعدة مميزات، منها عدم هدره للذاكرة. كان الاستخدام الفعلي بالصنف ExpNode الأصلي مقتصرًا على بعض متغيرات النسخ instance variables بكل عقدة، كما أننا أضفنا متغير نسخةٍ إضافي لتمكيننا من معرفة نوع العقدة. الأهم من ذلك هو امكانية إضافة أنواعٍ جديدةٍ من العقد بطريقةٍ أبسط، فكل ما علينا فعله هو إنشاء صنفٍ فرعي subclass جديدٍ مُشتقٍّ من الصنف ExpNode بدلًا من تعديل صنفٍ موجود بالفعل.

سنعود مجددًا للحديث عن موضوع أشجار التعبير في المقال التالي، حيث سنناقش خلاله طريقة إنشاء شجرة تعبير تُمثّل تعبيرًا معينًا.

ترجمة -بتصرّف- للقسم Section 4: Binary Trees من فصل Chapter 9: Linked Data Structures and Recursion من كتاب Introduction to Programming Using Java.