الأشعة خاصية الاتجاه Direction للأشعة الهندسية في التصاميم ثلاثية الأبعاد

يناقش هذا المقال خاصيةً مهمةً أخرى للشعاع وهي خاصية الاتجاه، إذ ناقشنا في المقال السابق خاصية الطول، حيث تعرّف هاتان الخاصيتان الشعاع.

سنوضّح في هذا المقال المواضيع التالية:

• المنحى Orientation أو اتجاه الحركة للأشعة ثنائية الأبعاد (مُمثَّلة في إطار إحداثي معين).
• الغموض عند استخدام قوس الظل arc tan لحساب الزاوية.
• تحويل الطول والمنحى إلى مكونات مصفوفة عمودية.
• قياس الزوايا بوحدتي الراديان Radian والدرجة المئوية.
• استخدام لغتي البرمجة سي C وجافا Java مع قوس الظل.

الأشعة المحاذية للمحورين X-Y

ما هو اتجاه الشعاع الذي تمثله المصفوفة العمودية ‎(4, 0)^T‎؟ يوازي هذا الشعاع المحور X لإطار الإحداثيات الذي نستخدمه، وسيكون هذا الشعاع غالبًا أفقيًا ويؤشّر إلى اليمين (أو يمكن القول أن الشعاع له منحى مقداره 0 درجة).

للشعاع ثنائي الأبعاد الذي يحاذي محور الإحداثيات -كما هو الحال مع ‎(4, 0)^T‎- منحًى يسهل رؤيته، ويكون عند 0 درجة أو 90 درجة أو 180 درجة أو 270 درجة.

يُعبَّر عن منحى الشعاع عادةً من خلال زاوية مع المحور x الموجب لإطار الإحداثيات، وهناك طريقتان لذلك:

• تُقاس الزاوية من 0 إلى 360 درجة بعكس اتجاه دوران عقارب الساعة ابتداءً من المحور x الموجب.
• تُقاس الزاوية من 0 إلى ‎+180 درجة بعكس اتجاه دوران عقارب الساعة, ابتداءً من المحور x الموجب، أو تُقاس من 0 إلى ‎-180 درجة مع اتجاه دوران عقارب الساعة ابتداءً من المحور x الموجب.

حساب زاوية الشعاع عن المحور X

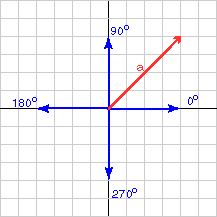
ما هو اتجاه الشعاع a في المخطط البياني السابق؟ يكون منحى الشعاع a = (4, 4)^T‎ بزاوية مقدارها 45 درجة.

يجب أن تعطي الرياضيات الإجابة نفسها، إذ يُقدَّر ميل Slope الشعاع a بما يلي:

(التغير في قيمة x)/(التغير في قيمة y)‫ = 4.0/4.0 = 1.0

بالتالي تكون الزاوية باستخدام قوس الظل هي: 45‎ = arc tan( 1.0 )‎ درجة.

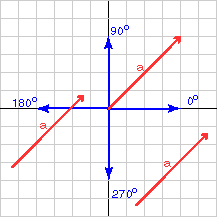
ليس للأشعة موقع، لذا لا يعتمد الطول ولا الاتجاه على المكان الذي ترسم فيه الشعاع، وتكون صيغة اتجاه الشعاع ثنائي الأبعاد هي:

angle of (x, y)^T = arc tan( y/x )

وللتأكيد يعني استخدام قوس الظل لقيمةٍ ما arc tan( z )‎ أنه تم العثور على الزاوية التي لها ظل tangent مقداره z، وتذكّر -عند حسابها باستخدام الآلة الحاسبة- أن الإجابة يمكن أن تكون بالراديان أو بالدرجات، إذ تمنحك معظم الآلات الحاسبة خيار استخدام أيّ من هذين التنسيقين. وبما أن الآلات الحاسبة تعطي عادةً الإجابة محصورةً بين ‎-90.0 و ‎+90.0 درجة (أو بين ‎-pi و ‎+pi راديان)، فقد تضطر إلى تعديل الإجابة (سنوضح ذلك لاحقًا).

يمكنك أيضًا استخدام الآلة الحاسبة على حاسوبك، فإذا كنت تستخدم نظام التشغيل ويندوز، فانقر على الخيار "علمي Scientific" في قائمة "العرض View" للآلة الحاسبة التي تحتوي على قوس الظل arc tan الذي يمكن أن يكون له تسمية هي tan^-1‎.

ما هو منحى الشعاع الذي تمثله المصفوفة العمودية: ‎k = (3,4)^T‎ (باستخدام الآلة الحاسبة)؟

‪arc tan( y/x ) = arc tan( 4/3 ) = arc tan( 1.333333333333 ) = 53.13 درجة

التعامل مع القيم السالبة

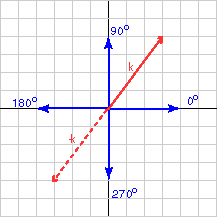
يوضح المخطط البياني السابق الشعاع الذي تمثله المصفوفة العمودية: ‎k = (3,4)^T‎، والذي حسبنا منحاه ليكون 53.13 درجةً عن محور x الموجب، وبالتالي يبدو كل شيء صحيحًا.

لنحسب الآن منحى الشعاع ‎-k = (-3,-4)^T‎ من خلال استخدام الصيغة التالية:

‪arc tan( y/x ) = arc tan( -4/-3 ) = arc tan( 4/3 ) = arc tan( 1.333333333333 ) = 53.13 درجة

لاحظ وجود خطأ، إذ أعطتنا هذه الصيغة الزاوية نفسها للشعاع الذي يؤشّر إلى الاتجاه المعاكس لاتجاه الشعاع الأول. تكمن المشكلة في فقدان المعلومات عند قسمة ‎-4 على ‎-3، إذ لا يمكننا تفريق هذه النتيجة عن نتيجة قسمة ‎+4 على ‎+3، وبالتالي هذه الصيغة ليست كافيةً لتعطيك الإجابة الصحيحة، ويجب عليك رسم الشعاع ثم تعديل الإجابة.

لاحظ من المخطط البياني أن منحى الشعاع ‎-k الذي يُعبَّر عنه بالدرجات من 0 إلى 360 بعكس اتجاه عقارب الساعة عن المحور x هو (180 + 53.13) = 233.13 درجة.

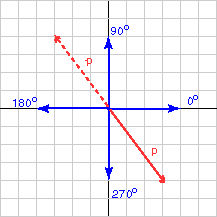
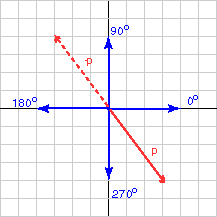
ما هو منحى الشعاع الذي تمثله المصفوفة العمودية: ‎ p = (3,-4)^T‎(استخدم تطبيق الآلة الحاسبة الموجود على حاسوبك)؟

ضع الأعداد في حاسبة ويندوز كما يلي:

‪arc tan( y/x ) = arc tan( -4/3 ) = arc tan( -1.333333333333 ) = -53.13 درجة

يبدو الحساب صحيحًا في المخطط البياني السابق، وإذا أردتَ التعبير عن الزاوية بعكس اتجاه دوران عقارب الساعة، فهي 360 - 53.130 = 306.870 درجة، ولكن سيعطيك الشعاع ‎-p النتيجة نفسها للأسف، لذا ارسم دائمًا الشعاع عندما تحسب منحاه، بعدها يمكنك أن ترى أن الزاوية التي تريدها للشعاع ‎-p هي 180 - 53.130 = 126.87 درجة.

تتوفر الدالة atan2(y, x)‎ في معظم لغات البرمجة، إذ تحسب هذه الدالة الزاوية بالراديان بين المحور x الموجب والنقطة المعطاة بالإحداثيات (x, y)، وتستخدِم إشارتَي x و y لتحديد الربع الصحيح للزاوية.

ما هو منحى الشعاع ‎u = (-4,-2)^T‎ ؟ (ارسم الشعاع أولًا، ثم استخدم الآلة الحاسبة)؟

عوّض القيم في الصيغة واستخدم الآلة الحاسبة لإيجاد الناتج:

‪arc tan( y/x ) = arc tan( -2/-4 ) = arc tan( 0.5 ) = 26.565 درجة

ولكن سترى عند رسم الشعاع أنه يقع في الربع الخطأ، لذا يجب أن تكون الإجابة 180 + 26.565 = 206.565 درجة.

حساب السمتين (x, y) الخاصتين بالشعاع

لنفترض أنك تعلم أن الشعاع يمكن تمثيله بمصفوفة عمودية ‎(x, y)^T‎ باستخدام إطار إحداثي معين، ويمكن حساب هاتين السمتين x و y كما يلي:

‪orientation of (x, y)^T = arc tan( y/x )

‪|(x, y)^T| = √( x² + y² )

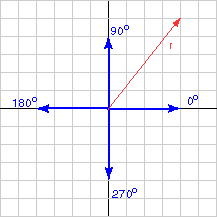
ارسم الشعاع r الذي تمثله المصفوفة العمودية ‎(4, 5)^T‎، ثم قدّر طوله واتجاهه، وأجرِ العمليات الحسابية للحصول على الإجابة الدقيقة كما يلي:

• الطول:

‪| r | = | (4,5)^T | = √(16+25) = 6.40

• الاتجاه:

‪direction = arc tan{ 5/4 } = 51.34 درجة

تحويل الطول والاتجاه إلى السمتين (x, y)

لنفترض أن لديك طول واتجاه وتريد التعبير عنهما بشعاع عمودي ثنائي الأبعاد، يمكنك فعل ذلك باتباع الخطوات التالية:

• أنشئ مخططًا بيانيًا.
• احسب قيمة x من خلال إسقاط الطول على المحور x باستخدام length*cos( θ )‎.
• احسب قيمة y من خلال إسقاط الطول على المحور y باستخدام length*sin( θ )‎.
• تحقق من الإجابات وفق المخطط البياني.

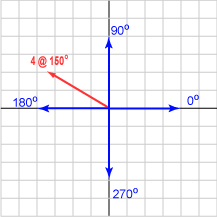
لنفترض أن لدينا شعاعًا طوله 4 ومنحاه بزاويةٍ مقدارها 150 درجة. إذًا ما هي المصفوفة العمودية التي تمثّل هذا الشعاع؟ سنمثّل هذا الشعاع بالمصفوفة العمودية ثنائية الأبعاد ‎( -3.464, 2.0 )^T‎ .

حساب الزوايا بالراديان

اتبع الخطوات التالية في هذا الحساب:

• أنشئ مخططًا بيانيًا كما يلي:

• احسب قيمة x من خلال إسقاط الطول على المحور x كما يلي:

‪4 * cos( 150 ) = -3.464

• احسب قيمة y من خلال إسقاط الطول على المحور y كما يلي:

‪4 * sin( 150 ) = 2.0

• تحقق من الإجابات وفق المخطط البياني (تبدو جيدة).

كن حذرًا بشأن استخدام هذه الصيغ وتوقّع الإجابات الصحيحة، خاصةً عند البرمجة بلغة سي أو جافا، إذ يمكن للمكتبات الرياضية الخاصة بلغة البرمجة أن تعطي أشياءً غير متوقعة إن لم تكن حذرًا، ولكن توجد ثلاثة أماكن يجب توخي الحذر فيها بصورة خاصة وهي:

1. من المتوقع أن يكون وسيط sin()‎ و cos()‎ و tan()‎ بالراديان، والقيمة التي تعيدها atan()‎ بالراديان.
2. من المتوقع أن يكون وسيط معظم الدوال الرياضية من النوع double، ولكن إذا استخدمتَ عددًا عشريًا float أو عددًا صحيحًا int، فلن تحصل على رسالة خطأ، بل مجرد إجابة غريبة غير صحيحة.
3. توجد عدة إصدارات من دالة "arc tan" في معظم مكتبات لغة سي، وكلٌ منها مخصَّص لمجال مختلف من قيم الخرج.

يُعبَّر عن الزوايا عادةً بالراديان، وتُقاس الزوايا بعكس اتجاه عقارب الساعة ابتداءً من المحور x الموجب (أو تُقاس الزاوية السالبة باتجاه عقارب الساعة ابتداءً من المحور x الموجب أحيانًا)، إذ يوجد ما مقداره 2‎ pi راديان في الدائرة الكاملة، أي أن:

(‎(2 pi راديان = 360 درجة

لنفترض أن لدينا شعاعًا له طول length وزاوية angle! أوجد في هذه الحالة قيمة vector[0]‎ التي تمثل المركّبة x، وأوجد قيمة vector[1]‎ التي تمثّل المركّبة y الخاصة بهذا الشعاع.

#include <math.h>

double length, angle;  /* طول وزاوية الشعاع */
double vector[2];      /* عناصر الشعاع */

 . . .

length = قيمةٌ ما
angle  = عددٌ ما بالدرجات

vector[0] = ????

vector[1] = ????

لنفترض أن رمز pi هو M_PI، ولكن لسوء الحظ تستخدم المصرّفات Compilers المختلفة رموز PI مختلفة وتعرّفها في ترويسات ملفات مختلفة، لذا يجب أن تستخدم الرمز المناسب لنظام تشغيلك بدلًا من تعريف PI بنفسك.

ملاحظة: إذا لم تكن على دراية بلغة سي، فيمكنك عَدّ هذه الشيفرة بأنها مكتوبة بلغة جافا.

#include <math.h>

double length, angle;
double vector[2];

 . . .

length = قيمةٌ ما
angle = عددٌ ما بالدرجات

vector[0] =  length * cos( angle*M_PI/180.0 )

vector[1] =  length * sin( angle*M_PI/180.0 )

تدريب عملي

تذكّر أولًا الخطوات التي يجب اتخاذها لتحويل الشعاع المعلوم طوله واتجاهه إلى (x,y):

1. أنشئ مخططًا بيانيًا.
2. احسب قيمة x من خلال إسقاط الطول على المحور x باستخدام length*cos( θ )‎.
3. احسب قيمة y من خلال إسقاط الطول على المحور y باستخدام length*sin( θ )‎. 4: تحقق من الإجابات وفق المخطط البياني.

وتبقى الخطوات نفسها إذا كانت الزاوية مُعطاةً بالراديان.

تدريب 1:

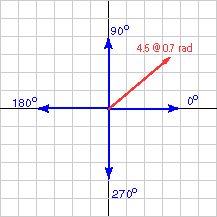
ليكن لدينا شعاع طوله 4.5 (بأيّ وحدة طول) وزاوية منحاه 0.70 راديان، ولنعبّر عن هذا الشعاع بالصيغة ‎( x, y )^T‎ كما يلي:

1. أنشئ مخططًا بيانيًا كما يلي:

2. احسب قيمة x من خلال إسقاط الطول على المحور x كما يلي:

‪4.5*cos( 0.70 ) = 3.442

3. احسب قيمة y بإسقاط الطول على المحور y كما يلي:

‪4.5*sin( 0.70 ) = 2.899

4. تحقق من الإجابات وفق المخطط البياني.

تدريب 2:

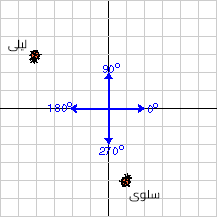
لنفترض أن الدعسوقة ليلى أضاعت صديقتها سلوى، ولكن كان مع ليلى هاتف محمول لحسن الحظ وكان:

• موقع ليلى عند النقطة ‎(1, -4)‎.
• موقع سلوى عند النقطة ‎( -4, 3)‎.

اتصل بليلى وأخبرها في أيّ اتجاه وإلى أيّ مسافة يجب أن تمشي للوصول إلى صديقتها سلوى.

الحل:

الاتجاه = 125.54 درجة، والمسافة = 8.60.

كان عليك أن تتذكر كيفية حساب الإزاحة للحصول على الإجابة، إذ يمكنك حساب شعاع الإزاحة بين نقطتين (أو بين الدعسوقتين) كما يلي:

(المكان الذي تريد أن تكون فيه) - (مكانك الحالي) = (الإزاحة التي تحتاجها)

إذًا الإزاحة التي يجب أن تمشيها ليلى هي:

‪( -4, 3) - (1, -4) = (-5, 7)

ولكن تحتاج ليلى إلى مسافة وجهة هما:

• المسافة: ‎√(25 + 49) = 8.60

• الاتجاه: ‪arc tan( 7/-5 ) = arc tan( -1.4 ) = -54.46 درجة

• نعدّل الاتجاه بالنظر إلى المخطط البياني ويصبح الاتجاه هو: 180 - 54.46 = 125.54 درجة

هل يمكن تطبيق الأفكار المتعلقة بمنحى الشعاع ثنائي الأبعاد الواردة في هذا المقال في الفضاء ثلاثي الأبعاد؟ نعم، ولكن ليس بهذه السهولة، إذ سيتطلب منحى الأشعة ثلاثية الأبعاد مزيدًا من العمل.

وصلنا إلى نهاية هذا المقال الذي تعرّفنا فيه على خاصية الاتجاه الخاصة بالشعاع، وسنناقش في المقال التالي حاصل ضرب شعاع وقيمة عددية.

ترجمة -وبتصرُّف- للفصل Vector Direction من كتاب Vector Math for 3D Computer Graphics لصاحبه Bradley Kjell.

اقرأ أيضًا

• المقال السابق تعرف على خاصية الطول Length للأشعة الهندسية وكيفية حسابه.
• المعاملات (parameters) في جافا.
• الأنواع الحقيقية والصحيحة في لغة سي C.