سنتحدث في هذه المقالة عن بعض المفاهيم العامة المتعلقة بخوارزميات الترتيب، ثم نستعرض 10 من أشهر خوارزميات ترتيب المصفوفات.
قبل أن نواصل، سنعطي بعض التعاريف العامة.
- خوارزميات الترتيب المستقرة: تكون خوارزمية ترتيب ما مستقرةً stable إذا كانت تحافظ على الترتيب النسبي للعناصر التي لها نفس قيمة المفتاح الذي يُجرى الترتيب وفقًا له.
-
خوارزميات الترتيب الموضعية In place algorithms: نقول أنّ خوارزمية ترتيب ما هي خوارزمية موضعية In place إذا كانت الذاكرة الإضافية التي تستخدمها أثناء الترتيب تساوي
O(1)(دون احتساب المصفوفة المراد ترتيبها). -
أسوء حالة تعقيدية Worst case complexity: نقول أنّ أسوء حالة تعقيدية Worst case complexity لخوارزمية تساوي
O(T(n))إذا كان وقت تشغيلها لا يزيد عنT(n)مهما كانت المدخلات. -
أفضل حالة تعقيدية Best case complexity: نقول أنّ أفضل حالة تعقيدية Best case complexity لخوارزمية ما تساوي
O(T(n))إذا كان وقت تشغيلها لا يقل عنT(n)مهما كانت المدخلات. -
أوسط حالة تعقيدية Average case complexity: نقول أنّ أوسط حالة تعقيدية Average case complexity لخوارزمية ترتيب ما تساوي
O(T(n))إذا كان متوسط أوقات تشغيلها بالنسبة لجميع المدخلات الممكنة يساويT(n).
استقرار الترتيب Stability in Sorting
تكون خوارزمية الترتيب مستقرةً إذا كانت تحافظ على الترتيب النسبي للقيم ذات المفاتيح المتساوية في المصفوفة المُدخلة الأصلية بعد ترتيبها. أي إن كانت خوارزمية الترتيب مستقرةً وكان هناك كائنَان لهما مفاتيح متساوية، فسيكون ترتيبُهما في الخرج المُرتّب مماثلًا لتَرتيبهما في المصفوفة المدخلة غير المرتبة. انظر مصفوفة الأزواج التالية:
(1, 2) (9, 7) (3, 4) (8, 6) (9, 3)
سنحاول ترتيب المصفوفة حسب العنصر الأول في كل زوج. سيخرج الترتيب المستقر لهذه القائمة ما يلي:
(1, 2) (3, 4) (8, 6) (9, 7) (9, 3)
وهو ترتيبٌ مستقر لأنّ (9, 3) تظهر بعد (9, 7) في المصفوفة الأصلية أيضًا. أما الترتيب غير مستقر فيكون كما يلي:
(1, 2) (3, 4) (8, 6) (9, 3) (9, 7)
قد ينتج عن الترتيب غير المستقر الخرج نفسه الذي يٌنتجه الترتيب المستقر أحيانًا، لكن ليس دائمًا.
هذه بعض أشهر أنواع التراتيب المستقرة:
- الترتيب بالدمج Merge sort.
- الترتيب بالإدراج Insertion sort.
- ترتيب بالجذر Radix sort .
- ترتيب Tim.
- الترتيب بالفقاعات Bubble Sort.
هذه بعض أنواع التراتيب غير المستقرة:
- الترتيب بالكومة Heap sort.
- الترتيب السريع Quick sort.
سوف نستعرض في بقية هذه المقالة 10 خوارزميات ترتيب شهيرة.
الترتيب بالفقاعات Bubble Sort
| المعامِل | الوصف |
|---|---|
| ترتيب مستقر | نعم |
| ترتيب موضعي | نعم |
| أفضل حالة تعقيد |
(O(n
|
| أسوء حالة تعقيد |
(O(n^2
|
| أوسط حالة تعقيد |
(O(n^2
|
| تعقيد المساحة |
(O(1
|
توازن خوارزمية الفقاعات BubbleSort كل زوج متتالي من العناصر في المصفوفة غير المرتبة، ثمّ تبدل مواضعهما إن كان تَرتيبهما خاطئًا. ويوضّح المثال التالي كيفية عمل خوارزمية الفقاعات على المصفوفة {6,5,3,1,8,7,2,4} (تُحاط الأزواج قيد المقارنة في كل خطوة بالرمز "**"):
{6,5,3,1,8,7,2,4} {**5,6**,3,1,8,7,2,4} -- 5 < 6 -> تبديل {5,**3,6**,1,8,7,2,4} -- 3 < 6 -> تبديل {5,3,**1,6**,8,7,2,4} -- 1 < 6 -> تبديل {5,3,1,**6,8**,7,2,4} -- 8 > 6 -> لا تبديل {5,3,1,6,**7,8**,2,4} -- 7 < 8 -> تبديل {5,3,1,6,7,**2,8**,4} -- 2 < 8 -> تبديل {5,3,1,6,7,2,**4,8**} -- 4 < 8 -> تبديل
نحصل بعد الدورة الأولى على المصفوفة {5,3,1,6,7,2,4,8}، لاحظ أنّ أكبر قيمة غير مرتبة في المصفوفة (8 في هذه الحالة) ستصل دائمًا إلى موضعها النهائي. للتأكد من أنّ المصفوفة مرتّبة ترتيبًا صحيحًا وأنّ كل عناصرها في المواضع الصحيحة، سيكون علينا تكرار هذه العملية n-1 مرّة، حيث يمثّل n طول المصفوفة المراد ترتيبها.
خوارزمية الترتيب بالفقاعات التي تُعرف أيضًا باسم الترتيب المتدرّج Sinking Sort، هي خوارزمية ترتيب بسيطة تمرّ مرارًا وتكرارًا على المصفوفة حتى ترتّبها، وتوازن كل زوج متتال من العناصر، ثمّ تبدّلهما إن كان ترتيبهما خاطئًا.
الرسم البياني التالي يمثّل آلية عمل خوارزمية الترتيب بالفقاعات:
هذه تطبيقات لخوارزمية الترتيب بالفقاعات بعدة لغات برمجة.
void bubbleSort(vector<int>numbers) { for(int i = numbers.size() - 1; i >= 0; i--) { for(int j = 1; j <= i; j++) { if(numbers[j-1] > numbers[j]) { swap(numbers[j-1],numbers(j)); } } } }
void bubble_sort(long list[], long n) { long c, d, t; for (c = 0 ; c < ( n - 1 ); c++) { for (d = 0 ; d < n - c - 1; d++) { if (list[d] > list[d+1]) { /* تبديل */ t = list[d]; list[d] = list[d+1]; list[d+1] = t; } } } }
- هذا تطبيق يستخدم المؤشرات:
void pointer_bubble_sort(long * list, long n) { long c, d, t; for (c = 0 ; c < ( n - 1 ); c++) { for (d = 0 ; d < n - c - 1; d++) { if ( * (list + d ) > *(list+d+1)) { /* تبديل */ t = * (list + d ); * (list + d ) = * (list + d + 1 ); * (list + d + 1) = t; } } } }
public class BubbleSort { public static void SortBubble(int[] input) { for (var i = input.Length - 1; i >= 0; i--) { for (var j = input.Length - 1 - 1; j >= 0; j--) { if (input[j] <= input[j + 1]) continue; var temp = input[j + 1]; input[j + 1] = input[j]; input[j] = temp; } } } public static int[] Main(int[] input) { SortBubble(input); return input; } }
#!/usr/bin/python input_list = [10,1,2,11] for i in range(len(input_list)): for j in range(i): if int(input_list[j]) > int(input_list[j+1]): input_list[j],input_list[j+1] = input_list[j+1],input_list[j] print input_list
- جافا:
public class MyBubbleSort { public static void bubble_srt(int array[]) {//main logic int n = array.length; int k; for (int m = n; m >= 0; m--) { for (int i = 0; i < n - 1; i++) { k = i + 1; if (array[i] > array[k]) { swapNumbers(i, k, array); } } printNumbers(array); } } private static void swapNumbers(int i, int j, int[] array) { int temp; temp = array[i]; array[i] = array[j]; array[j] = temp; } private static void printNumbers(int[] input) { for (int i = 0; i < input.length; i++) { System.out.print(input[i] + ", "); } System.out.println("\n"); } public static void main(String[] args) { int[] input = { 4, 2, 9, 6, 23, 12, 34, 0, 1 }; bubble_srt(input); } }
function bubbleSort(a) { var swapped; do { swapped = false; for (var i=0; i < a.length-1; i++) { if (a[i] > a[i+1]) { var temp = a[i]; a[i] = a[i+1]; a[i+1] = temp; swapped = true; } } } while (swapped); } var a = [3, 203, 34, 746, 200, 984, 198, 764, 9]; bubbleSort(a); console.log(a); // [ 3, 9, 34, 198, 200, 203, 746, 764, 984 ]
الترتيب بالدمج Merge Sort
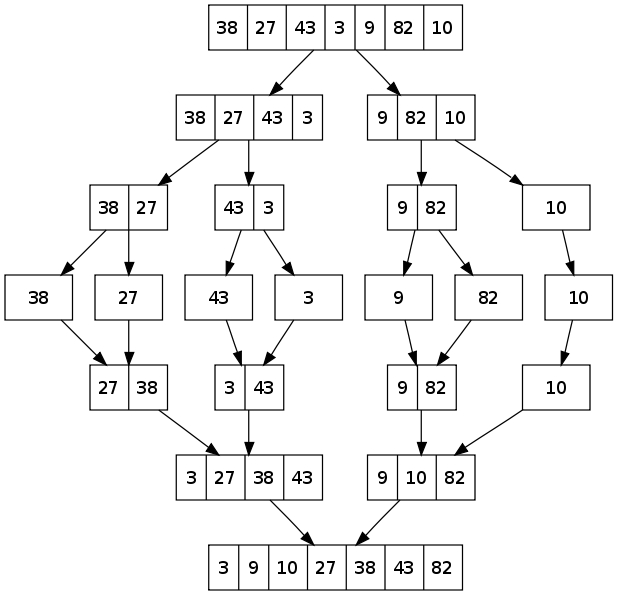
الترتيب بالدمج هي خوارزمية تعتمد مبدأ فرّق تسد، إذ تقسم المصفوفةَ المدخلةَ إلى نصفين بشكل متتابع إلى أن تصبح لدينا n مصفوفة أحادية، حيث n يمثل حجم المصفوفة المُدخلة.
بعد ذلك، تُدمج المصفوفات الجزئية المرتبة مثنى مثنى، إذ يُضاف أصغر العنصرين المتقابلين في المصفوفتين المراد دمجهما في كل خطوة. تستمر هذه العملية إلى حين الانتهاء من بناء المصفوفة المُرتّبة. يوضح المثال التالي آلية عمل خوارزمية الترتيب بالدمج:
التعقيد الزمني للخوارزمية: T(n) = 2T(n/2) + Θ(n).
يمكن تطبيق التكرارية أعلاه إما باستخدام طريقة الشجرة التكرارية Recurrence Tree method أو الطريقة الرئيسية (Master method)، يمكنك معرفة تفاصيل هاتين الطريقتين من هنا.
تعقيد الطريقة الرئيسية يساوي Θ(nLogn) في جميع الحالات الثلاث (الأسوأ والمتوسطة والفضلى)، ذلك أنّ الترتيب بالدمج يقسّم المصفوفة تعاوديًا إلى أنصاف، ويستغرق وقتًا خطيًا لدمج نصفين، حيث لدينا:
-
المساحة الإضافية:
O(n). - نموذج الخوارزمية: فرّق تسد.
- الموضعيّة: على العموم، التطبيقات الشائعة للخوارزمية لا تكون موضعية.
- مستقرة: نعم.
هذه بعض تطبيقات خوارزمية الدمج في بعض لغات البرمجة:
package main import "fmt" func mergeSort(a []int) []int { if len(a) < 2 { return a } m := (len(a)) / 2 f := mergeSort(a[:m]) s := mergeSort(a[m:]) return merge(f, s) } func merge(f []int, s []int) []int { var i, j int size := len(f) + len(s) a := make([]int, size, size) for z := 0; z < size; z++ { lenF := len(f) lenS := len(s) if i > lenF-1 && j <= lenS-1 { a[z] = s[j] j++ } else if j > lenS-1 && i <= lenF-1 { a[z] = f[i] i++ } else if f[i] < s[j] { a[z] = f[i] i++ } else { a[z] = s[j] j++ } } return a } func main() { a := []int{75, 12, 34, 45, 0, 123, 32, 56, 32, 99, 123, 11, 86, 33} fmt.Println(a) fmt.Println(mergeSort(a)) }
- لغة C
int merge(int arr[],int l,int m,int h) { int arr1[10],arr2[10]; // مصفوفتان مؤقتتان hold the two arrays to be merged int n1,n2,i,j,k; n1=m-l+1; n2=h-m; for(i=0; i<n1; i++) arr1[i]=arr[l+i]; for(j=0; j<n2; j++) arr2[j]=arr[m+j+1]; arr1[i]=9999; // لتحديد نهاية كل مصفوفة مؤقتة arr2[j]=9999; i=0; j=0; for(k=l; k<=h; k++) { // دمج مصفوفتين مرتبتين if(arr1[i]<=arr2[j]) arr[k]=arr1[i++]; else arr[k]=arr2[j++]; } return 0; } int merge_sort(int arr[],int low,int high) { int mid; if(low<high) { mid=(low+high)/2; // فرق تسد merge_sort(arr,low,mid); merge_sort(arr,mid+1,high); // Combine merge(arr,low,mid,high); } return 0; }
- لغةC#
public class MergeSort { static void Merge(int[] input, int l, int m, int r) { int i, j; var n1 = m - l + 1; var n2 = r - m; var left = new int[n1]; var right = new int[n2]; for (i = 0; i < n1; i++) { left[i] = input[l + i]; } for (j = 0; j < n2; j++) { right[j] = input[m + j + 1]; } i = 0; j = 0; var k = l; while (i < n1 && j < n2) { if (left[i] <= right[j]) { input[k] = left[i]; i++; } else { input[k] = right[j]; j++; } k++; } while (i < n1) { input[k] = left[i]; i++; k++; } while (j < n2) { input[k] = right[j]; j++; k++; } } static void SortMerge(int[] input, int l, int r) { if (l < r) { int m = l + (r - l) / 2; SortMerge(input, l, m); SortMerge(input, m + 1, r); Merge(input, l, m, r); } } public static int[] Main(int[] input) { SortMerge(input, 0, input.Length - 1); return input; } }
- جافا: هذا تطبيق بلغة جافا يستخدم المقاربة العامة.
public interface InPlaceSort<T extends Comparable<T>> { void sort(final T[] elements); } public class MergeSort < T extends Comparable < T >> implements InPlaceSort < T > { @Override public void sort(T[] elements) { T[] arr = (T[]) new Comparable[elements.length]; sort(elements, arr, 0, elements.length - 1); } // نتحقق من كلا الجانبين، ثم ندمجهما private void sort(T[] elements, T[] arr, int low, int high) { if (low >= high) return; int mid = low + (high - low) / 2; sort(elements, arr, low, mid); sort(elements, arr, mid + 1, high); merge(elements, arr, low, high, mid); } private void merge(T[] a, T[] b, int low, int high, int mid) { int i = low; int j = mid + 1; // b نختار أصغر عنصر منهما، ثم نضعه في for (int k = low; k <= high; k++) { if (i <= mid && j <= high) { if (a[i].compareTo(a[j]) >= 0) { b[k] = a[j++]; } else { b[k] = a[i++]; } } else if (j > high && i <= mid) { b[k] = a[i++]; } else if (i > mid && j <= high) { b[k] = a[j++]; } } for (int n = low; n <= high; n++) { a[n] = b[n]; }}}
- Java: هذا تطبيق آخر للخوارزمية بلغة Java، ولكن وفق منظور تصاعدي (من الأسفل إلى الأعلى)
public class MergeSortBU { private static Integer[] array = { 4, 3, 1, 8, 9, 15, 20, 2, 5, 6, 30, 70, 60,80,0,9,67,54,51,52,24,54,7 }; public MergeSortBU() { } private static void merge(Comparable[] arrayToSort, Comparable[] aux, int lo,int mid, int hi) { for (int index = 0; index < arrayToSort.length; index++) { aux[index] = arrayToSort[index]; } int i = lo; int j = mid + 1; for (int k = lo; k <= hi; k++) { if (i > mid) arrayToSort[k] = aux[j++]; else if (j > hi) arrayToSort[k] = aux[i++]; else if (isLess(aux[i], aux[j])) { arrayToSort[k] = aux[i++]; } else { arrayToSort[k] = aux[j++]; } } } public static void sort(Comparable[] arrayToSort, Comparable[] aux, int lo, int hi) { int N = arrayToSort.length; for (int sz = 1; sz < N; sz = sz + sz) { for (int low = 0; low < N; low = low + sz + sz) { System.out.println("Size:"+ sz); merge(arrayToSort, aux, low, low + sz -1 ,Math.min(low + sz + sz - 1, N - 1)); print(arrayToSort); } } } public static boolean isLess(Comparable a, Comparable b) { return a.compareTo(b) <= 0; } private static void print(Comparable[] array) {http://stackoverflow.com/documentation/algorithm/5732/merge-sort# StringBuffer buffer = new StringBuffer();http://stackoverflow.com/documentation/algorithm/5732/merge-sort# for (Comparable value : array) { buffer.append(value); buffer.append(' '); } System.out.println(buffer); } public static void main(String[] args) { Comparable[] aux = new Comparable[array.length]; print(array); MergeSortBU.sort(array, aux, 0, array.length - 1); } }
def merge(X, Y): " دمج مصفوفتين مرتبتين " p1 = p2 = 0 out = [] while p1 < len(X) and p2 < len(Y): if X[p1] < Y[p2]: out.append(X[p1]) p1 += 1 else: out.append(Y[p2]) p2 += 1 out += X[p1:] + Y[p2:] return out def mergeSort(A): if len(A) <= 1: return A if len(A) == 2: return sorted(A) mid = len(A) / 2 return merge(mergeSort(A[:mid]), mergeSort(A[mid:])) if __name__ == "__main__": # Generate 20 random numbers and sort them A = [randint(1, 100) for i in xrange(20)] print mergeSort(A)
الترتيب بالإدراج
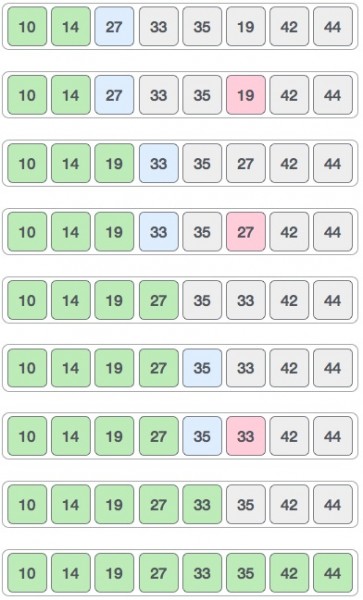
الترتيب بالإدراج هي إحدى خوارزميات الترتيب البسيطة، إذ ترتّب العناصر واحدًا تلو الآخر بنفس الطريقة التي ترتّب فيها أوراق اللعب يدويًّا.
الرسم البياني التالي يوضّح آلية عمل خوارزمية الترتيب بالإدراج:
المصدر: ويكيبديا
يمكنك معرفة المزيد من التفاصيل حول آلية عمل الخوارزمية من ويكي حسوب.
هذا تطبيق لخوارزمية الترتيب بالإدراج بلغة هاسكل Haskell:
insertSort :: Ord a => [a] -> [a] insertSort [] = [] insertSort (x:xs) = insert x (insertSort xs) insert :: Ord a => a-> [a] -> [a] insert n [] = [n] insert n (x:xs) | n <= x = (n:x:xs) | otherwise = x:insert n xs
الترتيب بالدلو Bucket Sort
الترتيب بالدلو هي خوارزمية ترتيب توزّع عناصر المصفوفة المراد ترتيبها على عدد من الدلاء (مصفوفات)، ثمّ تُرتّب عناصر كل دلو على حدة باستخدام خوارزمية ترتيب مختلفة، أو بتطبيق خوارزمية الترتيب بالدلو تكراريًا، يمكنك معرفة المزيد من التفاصيل عن هذه الخوارزمية من موسوعة حسوب.
هذا تطبيق لخوارزمية الترتيب بالدلو بلغة C#
public class BucketSort { public static void SortBucket(ref int[] input) { int minValue = input[0]; int maxValue = input[0]; int k = 0; for (int i = input.Length - 1; i >= 1; i--) { if (input[i] > maxValue) maxValue = input[i]; if (input[i] < minValue) minValue = input[i]; } List<int>[] bucket = new List<int>[maxValue - minValue + 1]; for (int i = bucket.Length - 1; i >= 0; i--) { bucket[i] = new List<int>(); } foreach (int i in input) { bucket[i - minValue].Add(i); } foreach (List<int> b in bucket) { if (b.Count > 0) { foreach (int t in b) { input[k] = t; k++; } } } } public static int[] Main(int[] input) { SortBucket(ref input); return input; } }
الترتيب السريع Quicksort
خوارزمية الترتيب السريع هي خوارزمية ترتيب تنتقي عنصرًا من عناصر المصفوفة وتجعله محورًا، ثمّ تقسّم المصفوفة المعطاة حول ذلك العنصر، بحيث تأتي جميع العناصر الأصغر من المحور قبله، وجميع العناصر الأكبر منه تأتي بعده. تُطبّق الخوارزمية تكراريًا على الأقسام حتى تُرتّب المصفوفة بالكامل، وهناك طريقتان لتقديم هذه الخوارزمية.
طريقة لوموتو Lomuto
في هذه الطريقة يُنتقى أحد العناصر ليكون محور الترتيب، وغالبًا ما يكون العنصر الأخير من المصفوفة، ويُحفظ فهرس المحور ثم تُتعقّب المواقع التي تحتوي على العناصر التي تساوي قيمة المحور أو تصغُره، ويُجرى التبديل بين موقعي العنصرين إن عُثِر على عنصر أصغر من المحور، ويُزاد فهرس المحور بواحد. فيما يلي شيفرة عامة للخوارزمية:
partition(A, low, high) is pivot := A[high] i := low for j := low to high – 1 do if A[j] ≤ pivot then swap A[i] with A[j] i := i + 1 swap A[i] with A[high] return i
آلية الترتيب السريع:
quicksort(A, low, high) is if low < high then p := partition(A, low, high) quicksort(A, low, p – 1) quicksort(A, p + 1, high)
يوضّح المثال التالي آلية عمل خوارزمية الترتيب السريع:
طريقة هور Hoare
تستخدم طريقة هور مؤشرين يبدآن بالإشارة إلى طرفي المصفوفة المُقسّمة، ثم يتحركان نحو بعضهمًا إلى أن يحصل انقلاب، أي تصبح القيمة الصغرى في الجانب الأيسر من المحور، والكبرى في الجانب الأيمن منه؛ وعند حصول الانقلاب تبدّل الخوارزمية بين موقعي القيمتين وتعاد العملية مرةً أخرى.
عندما تلتقي الفهارس، تتوقف الخوارزمية ويُعاد الفهرس النهائي. تُعد طريقة هور أكثر فعاليةً من طريقة Lomuto، لأنّ عدد التبديلات التي تجريها أقل بثلاث مرات في المتوسط من طريقة Lomuto، كما أنّها أكثر فعاليةً في إنشاء الأقسام حتى عندما تكون جميع القيم متساوية.
quicksort(A, lo, hi) is if lo < hi then p := partition(A, lo, hi) quicksort(A, lo, p) quicksort(A, p + 1, hi)
شيفرة عامة لتقسيم المصفوفة:
partition(A, lo, hi) is pivot := A[lo] i := lo - 1 j := hi + 1 loop forever do: i := i + 1 while A[i] < pivot do do: j := j - 1 while A[j] > pivot do if i >= j then return j swap A[i] with A[j]
هذا تطبيق لخوارزمية الترتيب السريع بلغة بايثون:
def quicksort(arr): if len(arr) <= 1: return arr pivot = arr[len(arr) / 2] left = [x for x in arr if x < pivot] middle = [x for x in arr if x == pivot] right = [x for x in arr if x > pivot] return quicksort(left) + middle + quicksort(right) print quicksort([3,6,8,10,1,2,1])
الخرج الناتج:
[1 ، 1 ، 2 ، 3 ، 6 ، 8 ، 10]
وهذا تطبيق لطريقة Lomuto بلغة جافا:
public class Solution { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int[] ar = new int[n]; for(int i=0; i<n; i++) ar[i] = sc.nextInt(); quickSort(ar, 0, ar.length-1); } public static void quickSort(int[] ar, int low, int high) { if(low<high) { int p = partition(ar, low, high); quickSort(ar, 0 , p-1); quickSort(ar, p+1, high); } } public static int partition(int[] ar, int l, int r) { int pivot = ar[r]; int i =l; for(int j=l; j<r; j++) { if(ar[j] <= pivot) { int t = ar[j]; ar[j] = ar[i]; ar[i] = t; i++; } } int t = ar[i]; ar[i] = ar[r]; ar[r] = t; return i; }
الترتيب بالعد Counting Sort
-
المساحة الإضافية:
O(n+k) - التعقيد الزمني:
-
الحالة الأسوأ:
O(n+k). -
الحالة الأفضل:
O(n). -
الحالة المتوسطة
O(n+k).
الترتيب بالعد Counting sort هي خوارزمية لترتيب الكائنات وفقًا لمفاتيحها.
خطوات الخوارزمية:
- أنشئ مصفوفة C حجمها يساوي عدد العناصر الفريدة في المصفوفة المُدخلة A.
- املأ المصفوفة ? لكل x عنصر فريد من المصفوفة المُدخلة، تحتوي C[x] تردّد ذلك العنصر في المصفوفة المُدخلة A.
- حوّل C إلى مصفوفة بحيث يشير C[x] إلى عدد القيم التي تصغُر x عبر التكرار في المصفوفة، وعيّن مجموع القيمة السابقة لكل C [x]، وكذلك جميع القيم في C التي تظهر قبله.
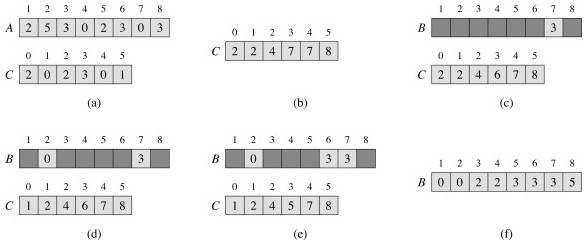
- كرِّر خلفيًا على المصفوفة A مع وضع كل قيمة في مصفوفة B جديدة مرتبة في الفهرس المسجّل في C. ولكل A [x]، نعيّن قيمة B [C [A [x]]] إلى A [x]، مع إنقاص قيمة C [A [x]] بمقدار واحد في حال وجود قيم مكرّرة في المصفوفة الأصلية غير المرتبة.
يوضّح المثال التالي آلية عمل خوارزمية الترتيب بالعد:
وفي ما يلي مثال توضيحي للخوارزمية:
for x in input: count[key(x)] += 1 total = 0 for i in range(k): oldCount = count[i] count[i] = total total += oldCount for x in input: output[count[key(x)]] = x count[key(x)] += 1 return output
يمكنك الاطلاع على المزيد من التفاصيل والأمثلة التوضيحية عن خوارزمية الترتيب بالعدّ من موسوعة حسوب
الترتيب بالكومة Heap Sort
-
المساحة الإضافية:
O(1). -
التعقيد الزمني
:O(nlogn).
الترتيب بالكومة هي خوارزمية تستند على الكومة الثنائية Binary Heap، وهي مشابهة لخوارزمية الترتيب بالتحديد Selection Sort التي تعتمد على اختيار العنصر الأكبر في المصفوفة في البداية، ثمّ تضعه في نهاية المصفوفة، ثمّ تعيد العملية على بقية العناصر.
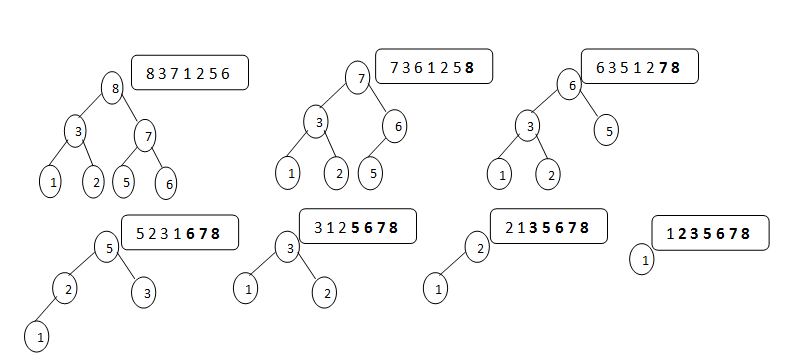
هذا مثال توضيحي لخوارزمية الترتيب بالكومة:
function heapsort(input, count) heapify(a,count) end <- count - 1 while end -> 0 do swap(a[end],a[0]) end<-end-1 restore(a, 0, end) function heapify(a, count) start <- parent(count - 1) while start >= 0 do restore(a, start, count - 1) start <- start - 1
وهذا مثال على آلية عمل خوارزمية الترتيب بالكومة على المصفوفة [2,3,7,1,8,5,6]:
هذا تطبيق لخوارزمية الترتيب بالكومة بلغة C#:
public class HeapSort { public static void Heapify(int[] input, int n, int i) { int largest = i; int l = i + 1; int r = i + 2; if (l < n && input[l] > input[largest]) largest = l; if (r < n && input[r] > input[largest]) largest = r; if (largest != i) { var temp = input[i]; input[i] = input[largest]; input[largest] = temp; Heapify(input, n, largest); } } public static void SortHeap(int[] input, int n) { for (var i = n - 1; i >= 0; i--) { Heapify(input, n, i); } for (int j = n - 1; j >= 0; j--) { var temp = input[0]; input[0] = input[j]; input[j] = temp; Heapify(input, j, 0); } } public static int[] Main(int[] input) { SortHeap(input, input.Length); return input; } }
الترتيب بالتدوير Cycle Sort
الترتيب بالتدوير هي خوارزمية موضعية غير مستقرة، وتُعدّ مثاليةً من حيث عدد مرات الكتابة في المصفوفة الأصلية وعدد مرات الكتابة في الذاكرة، فكل عنصر يُكتب إمّا مرةً واحدةً إن لم يكن في موضعه الصحيح، أو لا يُكتب على الإطلاق.
يمكنك معرفة المزيد من التفاصيل والأمثلة التوضيحية عن خوارزمية الترتيب بالتدوير من موسوعة حسوب
هذا مثال توضيحي عن تطبيق على الخوارزمية:
(input) output = 0 for cycleStart from 0 to length(array) - 2 item = array[cycleStart] pos = cycleStart for i from cycleStart + 1 to length(array) - 1 if array[i] < item: pos += 1 if pos == cycleStart: continue while item == array[pos]: pos += 1 array[pos], item = item, array[pos] writes += 1 while pos != cycleStart: pos = cycleStart for i from cycleStart + 1 to length(array) - 1 if array[i] < item: pos += 1 while item == array[pos]: pos += 1 array[pos], item = item, array[pos] writes += 1 return outout
ترتيب الفردي-الزوجي Odd-Even Sort
-
المساحة الإضافية:
O(n) -
التعقيد الزمني:
O(n)
خوارزمية ترتيب الفردي-الزوجي Odd-Even Sort (أو الترتيب بالطوب Brick sort هي خوارزمية ترتيب بسيطة طُوِّرت لتُستخدم مع المعالجات المتوازية ذات التقاطعات المحلية parallel processors with local interconnection.
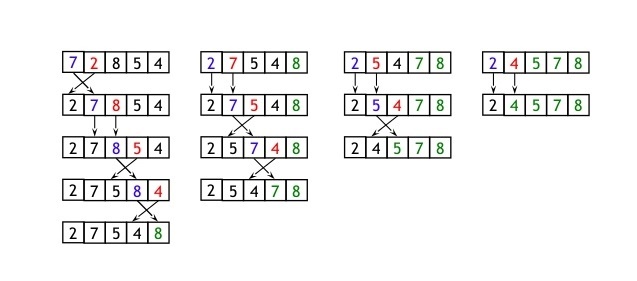
توازن هذه الخوارزمية بين جميع أزواج العناصر المتجاورة ذات الفهارس الفردية / الزوجية في المصفوفة، وتبدل العناصر إذا وجدت أنّ الزوج مرتّب ترتيبًا خاطئًا. تكرر الخوارزمية الخطوة نفسها، لكن هذه المرة على الأزواج ذات الفهارس الزوجية / الفردية، وتستمر في المناوبة بين النمط زوجي / فردي وفردي / زوجي إلى أن تُرتّب المصفوفة.
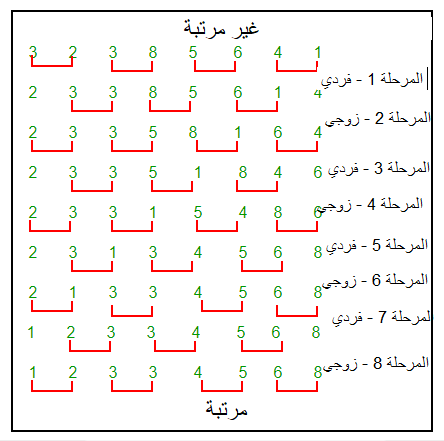
هذا مثال توضيحي لخوارزمية الطوب Brick:
if n>2 then 1. apply odd-even merge(n/2) recursively to the even subsequence a0, a2, ..., an-2 and to the odd subsequence a1, a3, , ..., an-1 2. comparison [i : i+1] for all i element {1, 3, 5, 7, ..., n-3} else comparison [0 : 1]
هذا رسم توضيحي لآلية عمل خوارزمية الترتيب فردي/زوجي على مجموعة عشوائية:
المصدر: ويكيبيديا
وهذا مثال توضيحي على الخوارزمية:
وفيما يلي تطبيق بلغة C# لخوارزمية الترتيب بقوالب الطوب:
public class OddEvenSort { private static void SortOddEven(int[] input, int n) { var sort = false; while (!sort) { sort = true; for (var i = 1; i < n - 1; i += 2) { if (input[i] <= input[i + 1]) continue; var temp = input[i]; input[i] = input[i + 1]; input[i + 1] = temp; sort = false; } for (var i = 0; i < n - 1; i += 2) { if (input[i] <= input[i + 1]) continue; var temp = input[i]; input[i] = input[i + 1]; input[i + 1] = temp; sort = false; } } } public static int[] Main(int[] input) { SortOddEven(input, input.Length); return input; } }
الترتيب بالتحديد Selection Sort
-
المساحة الإضافية:
O(n) -
التعقيد الزمني:
O(n^2)
الترتيب بالتحديد هي خوارزمية موضعية لترتيب المصفوفات، تعقيدها الزمني يساوي O (n2)، ما يجعلها غير فعالة مع المصفوفات الكبيرة، وعادةً ما يكون أداؤها أسوأ من خوارزميات الإدراج المماثلة. بالمقابل، تتميّز خوارزمية الترتيب بالتحديد بالبساطة وقد تتفوّق أداءً على بعض الخوارزميات الأعقد في بعض الحالات، خاصّةً عندما تكون الذاكرة الإضافية محدودة.
تقسّم الخوارزمية المصفوفة إلى قسمين هما مصفوفة تضم العناصر المرتبة فعليًا، والتي تُبنى من اليسار إلى اليمين من مقدمة المصفوفة (اليسرى)؛ فيما تضم المصفوفة الأخرى العناصر المتبقية التي تنتظر أن تُرتّب، والتي تشغل بقية المصفوفة.
وتكون المصفوفة المرتّبة فارغةً في البداية، بينما تحتوى المصفوفة غير المرتّبة كل عناصر المصفوفة المُدخلة. تبحث الخوارزمية عن أصغر عنصر (أو أكبر عنصر، بحسب غرض الترتيب) في المصفوفة غير المرتّبة وتبدّله بالعنصر غير المرتّب الموجود في أقصى اليسار (أي تضعه في المكان الصحيح)، ثمّ تنقل حدود المصفوفة الفرعية عنصرًا واحدًا إلى اليمين .
هذا مثال توضيحي للخوارزمية:
function select(list[1..n], k) for i from 1 to k minIndex = i minValue = list[i] for j from i+1 to n if list[j] < minValue minIndex = j minValue = list[j] swap list[i] and list[minIndex] return list[k]
وهذا تمثيل بصري للخوارزمية:
وهذا مثال على خوارزمية الترتيب بالتحديد:
فيما يلي تطبيق على لخوارزمية بلغة C #:
public class SelectionSort { private static void SortSelection(int[] input, int n) { for (int i = 0; i < n - 1; i++) { var minId = i; int j; for (j = i + 1; j < n; j++) { if (input[j] < input[minId]) minId = j; } var temp = input[minId]; input[minId] = input[i]; input[i] = temp; } } public static int[] Main(int[] input) { SortSelection(input, input.Length); return input; } }
وهذا تطبيق على الخوارزمية بلغة إكسير Elixir:
defmodule Selection do def sort(list) when is_list(list) do do_selection(list, []) end def do_selection([head|[]], acc) do acc ++ [head] end def do_selection(list, acc) do min = min(list) do_selection(:lists.delete(min, list), acc ++ [min]) end defp min([first|[second|[]]]) do smaller(first, second) end defp min([first|[second|tail]]) do min([smaller(first, second)|tail]) end defp smaller(e1, e2) do if e1 <= e2 do e1 else e2 end end end Selection.sort([100,4,10,6,9,3]) |> IO.inspect
ترجمة -بتصرّف- للفصول من 28 إلى 38 من الكتاب Algorithms Notes for Professionals.

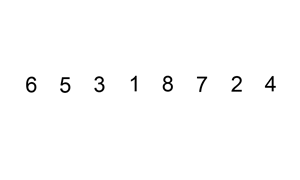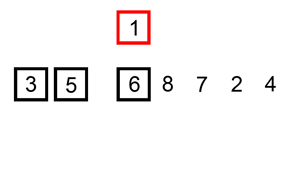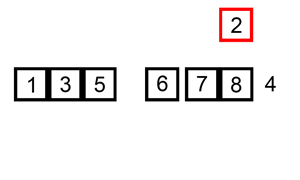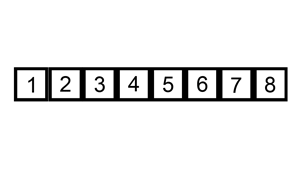















أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.