البرمجة الديناميكية هي مفهوم يُستخدم على نطاق واسع، وغالبًا ما تستخدم لأجل التحسين optimization، ومبدأ عملها هو تبسيط المشكلة المعقدة عبر تقسيمها إلى مشاكل تكرارية recursive فرعية وأبسط من المشكلة الأصلية.
هناك صفتان رئيسيتان لا بد من وجودهما في المشكلة حتى يمكن تطبيق البرمجة الديناميكية عليها، وهما: البنية المثلى Optimal substructure، والتداخل بين المشاكل الفرعية Overlapping sub-problems. تستخدم البرمجة الديناميكية مفهومًا يسمى التذكير memoization من أجل العثور على الحل المثالي.
مسافة التحرير
إذا أُعطِيت سلسلتين نصيتين str1 وstr2، فما هو العدد الأدنى للعمليات التي يمكن إجراؤها على str1 لتحويلها إلى str2؟ في تلك الحالة يكون إجراء هاتين الوظيفتين معًا؛ أما خلاف ذلك فسنتحقّق مما إذا كان؟ انظر تنفيذ الحل أدناه في لغة جافا لهذه المشكلة:
public class EditDistance { public static void main(String[] args) { // TODO Auto-generated method stub String str1 = "march"; String str2 = "cart"; EditDistance ed = new EditDistance(); System.out.println(ed.getMinConversions(str1, str2)); } public int getMinConversions(String str1, String str2){ int dp[][] = new int[str1.length()+1][str2.length()+1]; for(int i=0;i<=str1.length();i++){ for(int j=0;j<=str2.length();j++){ if(i==0) dp[i][j] = j; else if(j==0) dp[i][j] = i; else if(str1.charAt(i-1) == str2.charAt(j-1)) dp[i][j] = dp[i-1][j-1]; else{ dp[i][j] = 1 + Math.min(dp[i-1][j], Math.min(dp[i][j-1], dp[i-1][j-1])); } } } return dp[str1.length()][str2.length()]; } }
سيكون الخرج الناتج:
3
خوارزمية جدولة المهام الموزونة Weighted Job Scheduling Algorithm
يُطلق أحيانًا على خوارزمية جدولة المهام الموزونة اسم خوارزمية اختيار الأنشطة الموزونة Weighted Activity Selection Algorithm، حيث تحاول هذه الخوارزمية حل المشكلة التالية: إذا كانت لديك قائمة من الوظائف وكان لكل وظيفة وقت بدء ووقت انتهاء والربح الذي تحقّقه عند الانتهاء منها، فما هو أقصى ربح يمكن أن تحقّقه؟ علمًا بأنّه لا يمكنك تنفيذ وظيفتين في الوقت نفسه؟
تشبه هذه المشكلة مشكلة "اختيار النشاط باستخدام الخوارزمية الجشعة Greedy Algorithm"، لكن هناك جانبًا آخر ينبغي أن يُؤخذ بالحسبان، إذ يجب نركّز على تحقيق أقصى قدر من الأرباح بدلًا من زيادة عدد الوظائف المطلوبة إلى أقصى حد، ولا يهم هنا عدد الوظائف المنجزة.
لنأخذ مثالا عمليًا:
+---------------------------------+---------+---------+---------+---------+---------+--------+ | Name | A | B | C | D | E | F | +---------------------------------+---------+---------+---------+---------+---------+--------+ |(Start Time, Finish Time) | (2,5) | (6,7) | (7,9) | (1,3) | (5,8) | (4,6) | +---------------------------------+---------+---------+---------+---------+---------+--------+ | Profit | 6 | 4 | 2 | 5 | 11 | 5 | +---------------------------------+---------+---------+---------+---------+---------+--------+
يحتوي الجدول أعلاه على أسماء الوظائف ووقت بدايتها ونهايتها وأجرها. وتستطيع ملاحظة أنك إذا قمت بالعملين A وE، فستحصل على أقصى ربح ممكن (وهو 17)، لكن السؤال الآن هو: كيف يمكن العثور على ذلك باستخدام خوارزمية؟
أول شيء سنفعله هو ترتيب الوظائف حسب أوقات انتهائها ترتيبًا غير متناقص non-decreasing order، وذلك لأنّه عند اختيار وظيفة تستغرق وقتًا قليلًا لتنفيذها، سيتبّقى وقت أطول ينقضي في اختيار الوظائف الأخرى. انظر أدناه حيث الوظائف مرتبةً:
+--------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +--------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+
ستصبح لدينا المصفوفة المؤقّتة الإضافية Acc_Prof التي يساوي حجمها n (إجمالي عدد الوظائف)، وتحتوي أقصى قدر من الأرباح المتراكمة جرّاء أداء الوظائف.
لتوضيح الفكرة، سنهيّئ initializing قيم المصفوفة بأرباح كل وظيفة، وهذا يعني أنّ العنصر Acc_Prof سيخزّن في البداية أرباح إنجاز الوظيفة رقم i.
+-------------------------+---------+---------+---------+---------+---------+---------+ | Acc_Prof | 5 | 6 | 5 | 4 | 11 | 2 | +-------------------------+---------+---------+---------+---------+---------+---------+
سنشير الآن إلى الموضع 2 بالرمز i، وإلى الموضع 1 بالرمز j. تُبنى استراتيجيتنا هنا على تكرار j من 1 إلى i-1، ونزيد i بمقدار 1 عقب كلّ تكرار إلى أن تساوي i قيمة n +1:
j i +----------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +----------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +----------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +----------------------------------+---------+---------+---------+---------+---------+-------+ | Acc_Prof | 5 | 6 | 5 | 4 | 11 | 2 | +----------------------------------+---------+---------+---------+---------+---------+-------+
سنتحقق الآن ممّا إذا كان هناك تداخل بين الوظيفتين و[j]، أي إذا كان وقت إنتهاء الوظيفة [j] أكبر من وقت بدء الوظيفة ، إذ لا يمكن في تلك الحالة إجراء هاتين الوظيفتين معًا؛ أما خلاف ذلك فسنتحقّق مما إذا كان Acc_Prof[j] + Profit > Acc_Prof، وإذا كان كذلك، فسنجري التحديث الآتي:
Acc_Prof = Acc_Prof[j] + Profit
if Job[j].finish_time <= Job[i].start_time if Acc_Prof[j] + Profit[i] > Acc_Prof[i] Acc_Prof[i] = Acc_Prof[j] + Profit[i] endif endif
تمثّل Acc_Prof[j] + Profit هنا الربح المتراكم الناتج عن القيام بهاتين الوظيفتين، وتتداخل الوظيفة [j] مع ، لذا لا يمكن القيام بهما معًا. وبما أن j يساوي i-1، فسنزيد قيمة i إلى i +1، أي 3، ثمّ نجعل j = 1.
j i +---------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +---------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +---------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +---------------------------------+---------+---------+---------+---------+---------+-------+ | Acc_Prof | 5 | 6 | 5 | 4 | 11 | 2 | +---------------------------------+---------+---------+---------+---------+---------+-------+
لا تتداخل الوظيفتان [j] و الآن، أمّا الربح الإجمالي الذي يمكن تحصيله بتنفيذهما، فهو Acc_Prof[j] + Profit = 5 + 5 = 10، وهو أكبر من Acc_Prof ، لذا نجري التحديث Acc_Prof = 10، كما نزيد أيضًا قيمة j بـ 1 لنحصل على ما يلي:
j i +--------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +--------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Acc_Prof | 5 | 6 | 10 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+
تتداخل هنا [j] مع ، بينما تساوي j قيمة i-1، لذا نزيد i بمقدار 1، ونجعل j = 1 لنحصل على التالي:
j i +--------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +--------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Acc_Prof | 5 | 6 | 10 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+
الآن، لا تتداخل الوظيفتان [j] و، بينما يساوي الربح المتراكم القيمة 5 + 4 = 9، وهو أكبر من Acc_Prof، لذا نجري التحديث Acc_Prof = 9، ونزيد j بمقدار 1.
j i +--------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +--------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Acc_Prof | 5 | 6 | 10 | 9 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+
كذلك، لا تتداخل [j] و الآن، أمّا الربح المتراكم فيساوي: 6 + 4 = 10، وهو أكبر من Acc_Prof . سنجري التحديث Acc_Prof = 10 مرّةً أخرى ، ونزيد j بـ 1 لنحصل على:
j i +--------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +--------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Acc_Prof | 5 | 6 | 10 | 10 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+
إذا واصلنا هذه العملية وكررنا الجدول بأكمله، فسيبدو جدولنا كما يلي:
+--------------------------------+---------+---------+---------+---------+---------+-------+ | Name | D | A | F | B | E | C | +--------------------------------+---------+---------+---------+---------+---------+-------+ |(Start Time, Finish Time) | (1,3) | (2,5) | (4,6) | (6,7) | (5,8) | (7,9) | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Profit | 5 | 6 | 5 | 4 | 11 | 2 | +--------------------------------+---------+---------+---------+---------+---------+-------+ | Acc_Prof | 5 | 6 | 10 | 14 | 17 | 8 | +--------------------------------+---------+---------+---------+---------+---------+-------+
اقتباستجاوزنا بعض الخطوات للإيجاز.
إذا كررنا عبر المصفوفة Acc_Prof، فسنجد أنّ الربح الأقصى الممكن هو 17.
انظر إلى الشيفرة التوضيحية التالية:
Procedure WeightedJobScheduling(Job) sort Job according to finish time in non-decreasing order for i -> 2 to n for j -> 1 to i-1 if Job[j].finish_time <= Job[i].start_time if Acc_Prof[j] + Profit[i] > Acc_Prof[i] Acc_Prof[i] = Acc_Prof[j] + Profit[i] endif endif endfor endfor maxProfit = 0 for i -> 1 to n if maxProfit < Acc_Prof[i] maxProfit = Acc_Prof[i] return maxProfit
تعقيد تعبئة المصفوفة Acc_Prof هو O(n2)، بينما يستغرق اجتياز المصفوفة O(n)، لذا فإنّ التعقيد الكلي لهذه الخوارزمية هو O (n2).
والآن، إذا أردنا العثور على الوظائف التي تحقّق أقصى قدر من الربح، فسنحتاج إلى عبور المصفوفة أو اجتيازها بترتيب عكسي، وإذا تطابق Acc_Prof مع الربح الأقصى maxPro، فسندفع push اسم الوظيفة إلى مكدّس stack، ونطرح أرباح تلك الوظيفة من قيمة maxPro. سنستمرّ في فعل هذا حتى يصير maxProT t> 0، أو نصل إلى نقطة البداية في المصفوفة Acc_Prof. وستبدو الشيفرة التوضيحية كالتالي:
Procedure FindingPerformedJobs(Job, Acc_Prof, maxProfit): S = stack() for i -> n down to 0 and maxProfit > 0 if maxProfit is equal to Acc_Prof[i] S.push(Job[i].name maxProfit = maxProfit - Job[i].profit endif endfor
تعقيد هذا الإجراء هو O (n).
اقتباستنبيه: إذا كان هناك أكثر من جدول أعمال واحد يمكن أن يحقق لنا أقصى قدر من الأرباح، فلن تعطينا هذه الخوارزمية إلا واحدًا منها فقط.
أطول تسلسل مشترك Longest Common Subsequence
لتكن str1 وstr2 سلسلتان نصيّتان، حيث سنحاول العثور على أطول تتابع sub-sequence مشترك بينهما من الحروف.
انظر إلى الأمثلة التوضيحية التالية:
- أكبر تتابع مشترك للسلسلتين النصيتين “ABCDGH” و“AEDFHR” هو “ADH”، وطوله 3.
- أطول تتابع مشترك بين “AGGTAB” و“GXTXAYB” هو “GTAB”، وطوله 4.
فيما يلي تطبيق للحلّ في لغة جافا:
public class LCS { public static void main(String[] args) { // TODO Auto-generated method stub String str1 = "AGGTAB"; String str2 = "GXTXAYB"; LCS obj = new LCS(); System.out.println(obj.lcs(str1, str2, str1.length(), str2.length())); System.out.println(obj.lcs2(str1, str2)); } //Recursive function public int lcs(String str1, String str2, int m, int n){ if(m==0 || n==0) return 0; if(str1.charAt(m-1) == str2.charAt(n-1)) return 1 + lcs(str1, str2, m-1, n-1); else return Math.max(lcs(str1, str2, m-1, n), lcs(str1, str2, m, n-1)); } //دالة تكرارية public int lcs2(String str1, String str2){ int lcs[][] = new int[str1.length()+1][str2.length()+1]; for(int i=0;i<=str1.length();i++){ for(int j=0;j<=str2.length();j++){ if(i==0 || j== 0){ lcs[i][j] = 0; } else if(str1.charAt(i-1) == str2.charAt(j-1)){ lcs[i][j] = 1 + lcs[i-1][j-1]; }else{ lcs[i][j] = Math.max(lcs[i-1][j], lcs[i][j-1]); } } } return lcs[str1.length()][str2.length()]; } }
سيكون الخرج الناتج كالآتي:
4
أعداد فيبوناتشي
هذا منظور تصاعدي لطباعة عدد فيبوناتشي التاسع باستخدام البرمجة الديناميكية:
انظر إلى الشجرة التكرارية التالية:
fib(5) / \ fib(4) fib(3) / \ / \ fib(3) fib(2) fib(2) fib(1) / \ / \ / \ fib(2) fib(1) fib(1) fib(0) fib(1) fib(0) / \ fib(1) fib(0)
في هذا المثال، تكون كل من fib(0) وfib(1) وfib(3) هي المشاكل المتداخلة الفرعية overlapping sub-problems، إذ أنّ b(0) تكرّرت 3 مرات، في حين تكرّرت fib(1) خمس مرات، وتكرّرت fib(3) مرّتين. انظر الشيفرة التالية:
public int fib(int n){ int f[] = new int[n+1]; f[0]=0;f[1]=1; for(int i=2;i<=n;i++){ f[i]=f[i-1]+f[i-2]; } return f[n]; }
تعقيد الشيفرة أعلاه يساويO(n) .
أطول سلسلة نصية فرعية مشتركة Longest Common Substring
إذا كان لدينا السلسلتان النصيتان str1 وstr2، فيجب أن نبحث عن أطول سلسلة نصية فرعية مشتركة longest common substring بينهما. انظر الأمثلة التوضيحية التالية:
-
الدخل: x = abcdxyz وy = xyzabcd والخرج: 4 -، لأنّ أطول سلسلة نصية فرعية مشتركة هي
abcd، ويبلغ طولها 4. -
الدخل: x = zxabcdezy وy = yzabcdezx والخرج: 6 -، لأنّ أطول سلسلة نصية فرعية مشتركة هي
abcdez، وطولها هو 6.
هذا تطبيق في لغة جافا لخوارزمية تحلّ هذه المشكلة:
public int getLongestCommonSubstring(String str1,String str2){ int arr[][] = new int[str2.length()+1][str1.length()+1]; int max = Integer.MIN_VALUE; for(int i=1;i<=str2.length();i++){ for(int j=1;j<=str1.length();j++){ if(str1.charAt(j-1) == str2.charAt(i-1)){ arr[i][j] = arr[i-1][j-1]+1; if(arr[i][j]>max) max = arr[i][j]; } else arr[i][j] = 0; } } return max; }
التعقيد الزمني للخوارزمية أعلاه يساوي O(m*n).
تطبيقات البرمجة الديناميكية
تقوم البرمجة الديناميكية على فكرة تقسيم مشكلة معقدة إلى مشاكل أصغر وأبسط متكرّرة كما ذكرنا أول حديثنا، وسنركّز في هذه الفقرة على التطبيقات، وليس على إنشاء خوارزميات البرمجة الديناميكية.
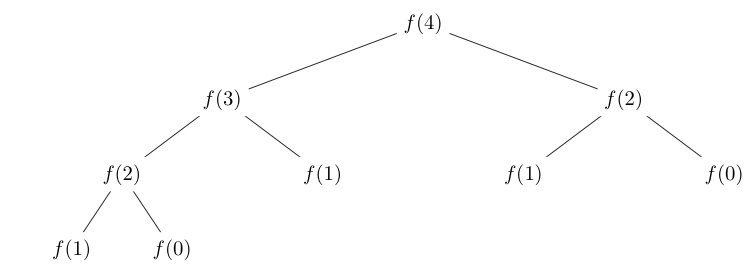
تعرضنا لأعداد فيبوناتشي كذلك قبل قليل، وتعَد هذه الأعداد من المواضيع الرئيسية للبرمجة الديناميكية، إذ أنّ المنظور التكراري التقليدي يتطلّب الكثير من الحسابات المكرّرة. سنستخدم في هذه الأمثلة الحالة الأساسية f( 0) = f (1) =1. فيما يلي مثال على شجرة تكرارية لـ fibonacci(4)، لاحظ أنّ هناك حسابات مكرّرة:
في البرمجة غير الديناميكية، يساوي التعقيد الزمني O(2^n)، فيما يساوي تعقيد المكدّس Stack complexity القيمة O(n).
def fibonacci(n): if n < 2: return 1 return fibonacci(n-1) + fibonacci(n-2)
هذه هي الطريقة البديهية لحلّ المشكلة، حيث لن تتجاوز مساحة المكدّس stack space القيمة O(n) عندما تنزل إلى الفرع الأول التكراري recursive branch مجريًا استدعاءات لـ fibonacci(n-1) تباعًا إلى أن تصل إلى الحالة الأساسية (أي n < 2).
النقطة الرئيسية هنا هي أنّ وقت التشغيل أسّي exponential، ما يعني أنّه سيتضاعف في كل خطوة، حيث سيستغرق fibonacci(15) مثلًا ضعف المدة التي يستغرقها fibonacci(14)
-
الخوارزمية التذكيرية Memoized: التعقيد الزمني يساوي
O(n)، ويساوي تعقيد المساحة Space complexity القيمة O(n)، فيما يساوي تعقيد المكدّسO(n).
memo = [] memo.append(1) # f(1) = 1 memo.append(1) # f(2) = 1 def fibonacci(n): if len(memo) > n: return memo[n] result = fibonacci(n-1) + fibonacci(n-2) memo.append(result) # f(n) = f(n-1) + f(n-2) return result
نقدّم باستخدام المنظور التذكيري memoized approach مصفوفةً تمثّل جميع استدعاءات الدوال السابقة ، ويكون الموقع memo[n] نتيجةً لاستدعاء الدالة fibonacci(n). يتيح لنا هذا مقايضة تعقيد مساحة O(n) بوقت تشغيل O(n)، إذ ستنتفي الحاجة إلى إعادة حساب استدعاءات الدوالّ المكررة.
-
البرمجة الديناميكية التكرارية وقت التشغيل يساوي
O(n)، وتعقيد المساحة هوO(n)بدون مكدّس تكراري recursive stack.
def fibonacci(n): memo = [1,1] # f(0) = 1, f(1) = 1 for i in range(2, n+1): memo.append(memo[i-1] + memo[i-2]) return memo[n]
إذا قسّمت المشكلة إلى عناصرها الأساسية فستلاحظ أنّه لحساب fibonacci(n). تحتاج إلى حساب fibonacci(n-1) وfibonacci(n-2)، كما يمكن ملاحظة أنّ الحالة الأساسية ستظهر في نهاية تلك الشجرة التكرارية كما هو موضّح أعلاه.
صار من المنطقي الآن باستخدام هذه المعلومات أن نحسب الحل من الخلف، أي بدءًا من الحالات الأساسية، ثمّ الصعود إلى الأعلى. ولكي نحسب الآن fibonacci(n)، sنحتاج إلى حساب جميع أعداد فيبوناتشي الخاصة بكل الأعداد الأصغر من n.
الفائدة الرئيسية لهذا المنظور هي أنّنا لم نَعُد نحتاج إلى مكدّس تكراري، مع الحفاظ على وقت التشغيل O(n) في نفس الوقت. لا يزال تعقيد المساحة هو O(n)، لكن يمكن تغيير ذلك أيضًا.
-
البرمجة الديناميكية التكرارية المتقدمة Advanced Iterative Dynamic Programming: يساوي وقت التشغيل
O(n)، أما تعقيد المساحة فهوO(1)، وبدون مكدّس تكراري recursive stack.
def fibonacci(n): memo = [1,1] # f(1) = 1, f(2) = 1 for i in range (2, n): memo[i%2] = memo[0] + memo[1] return memo[n%2]
يبدأ منظور البرمجة الديناميكية التكرارية من الحالات الأساسية كما لوحظ أعلاه، وتصعد انطلاقًا منها إلى النتيجة النهائية. تنطبق نفس الملاحظة التي أشرنا لها سابقًا بخصوص المكدّس التكراري هنا، فلأجل تحويل تعقيد المساحة إلى O(1) (أي تعقيد ثابت)، لن نحتاج إلّا إلى fibonacci(n-1) وfibonacci(n-2) لبناء قيمة فيبوناتشي fibonacci(n)، وهذا يعني أننا سنكتفي بحفظ نتيجتي (n-1) و(n-2) وحسب في كلّ مرة.
لتخزين آخر نتيجتين، نستخدم مصفوفة ثنائية مع تغيير قيمة الفهرس الذي سنعيّنه باستخدام الصيغة i % 2، والتي تتراوح قيمتها بين 0 و1 كما يلي: 0، 1، 0، 1، 0، 1، ...، i % 2.
وقد أضفنا فهرسي المصفوفة معًا لعلمنا أنّ الإضافة تبادلية (5 + 6 = 11 و 6 + 5 =11)، ثم عيّنّا النتيجة إلى أقدم النقطتين (المُشار إليها بواسطة i % 2)، وخزّنّا النتيجة النهائية بعد ذلك في الموضع n%2.
اقتباسملاحظة: قد يكون من الأفضل في بعض الأحيان استخدام التذكير التكراري iterative memoized لأجل الدوال التي تجري الكثير من الحسابات المتكرّرة، إذ تُخزَّن النتائج السابقة في ذاكرة تخزين مؤقت، مما قد يجعل تعقيد الاستدعاءات اللاحقة المكرّرة ثابتًا ( يساوي
O(1).
ترجمة -بتصرّف- للفصلين 14 و 15 من كتاب Algorithms Notes for Professionals.
اقرأ أيضًا
- المقالة السابقة: خوارزمية تحديد المسار النجمية A* Pathfinding
- كيف تتعلم البرمجة
- تعلم البرمجة












أفضل التعليقات
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.