تندرج جميع التوزيعات التي استخدمناها حتى الآن تحت اسم التوزيعات التجريبية empirical distributions لأنها مبنية على ملاحظات تجريبية وهي بالضرورة عيّنات محدودة.
يأتي التوزيع التحليلي analytic distribution بديلًا عنها، وهو يتميز بدالة توزيع تراكمي -cumulative distribution function أو CDF اختصارًا-، والتي تتصف بأنها دالة رياضية، حيث يمكننا استخدام التوزيعات التحليلية لنمذجة التوزيعات التجريبية. ويكون النموذج model في هذا السياق مبسَّطًا ولا يتعمق في التفاصيل الغير ضرورية.
يناقش هذا المقال التوزيعات التحليلية الشائعة وطريقة استخدامها لنمذجة البيانات من مصادر متنوعة، وتوجد الشيفرة الخاصة بهذا المقال في analytic.py في مستودع ThinkStats2 على GitHub.
التوزيع الأسي
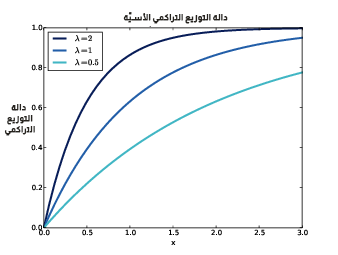
يوضِّح الشكل السابق دوال التوزيع التراكمي للتوزيعات الأسية مع معامِلات متنوعة.
ستكون البداية مع التوزيع الأسي exponential distribution لأنه سهل نسبيًا، وتكون الصيغة الرياضية لدالة التوزيع التراكمي للتوزيع الأسي هي:
CDF(x) = 1- e-λx
يحدِّد المعامِل λ شكل التوزيع، ويُظهر الشكل السابق شكل دالة التوزيع التراكمي عندما تكون λ=0.5 وλ=1 وλ=2.
تظهر التوزيعات الأسيّة في العالم الحقيقي عندما ندرس سلسلة من الأحداث ونقيس الأزمنة الفاصلة بينها، وتُدعى أوقات الوصول البينية interarrival times، حيث إذا كان احتمال حصول الأحداث متساو في أيّ وقت كان فسيبدو توزيع أوقات الوصول البينية أنه التوزيع الأسي، كما يمكنك الاطلاع على هذه الورقة للاستئناس.
سنلقي نظرةً على أوقات الوصول البينية الخاصة بالولادات على أساس مثال عن الفكرة السابقة، ففي يوم 18 من شهر 12 عام 1997، ولِد 44 طفلًا في مستشفى في مدينة بريسبان في أستراليا1، حيث وُثِّق وقت ولادة جميع هؤلاء الأطفال في صحيفة محلية، كما توجد مجموعة البيانات كاملةً في ملف babyboom.dat في مستودع ThinkStats2.
df = ReadBabyBoom() diffs = df.minutes.diff() cdf = thinkstats2.Cdf(diffs, label='actual') thinkplot.Cdf(cdf) thinkplot.Show(xlabel='minutes', ylabel='CDF')
تقرأ الدالة ReadBabyBoom ملف البيانات وتُعيد إطار بيانات DataFrame مع الأعمدة التالية: time يدل على وقت الولادة وsex يدل على جنس المولود، وweight_g يدل على الوزن عند الولادة، وminutes يدل على وقت الولادة بعد تحويله إلى الدقائق منذ منتصف الليل.
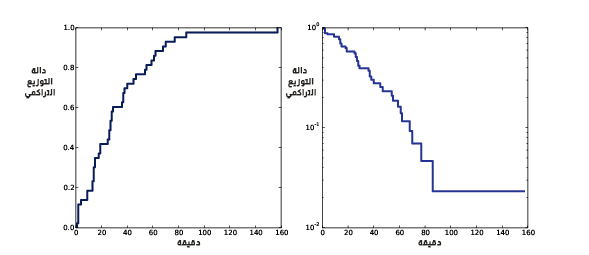
يوضِّح الشكل السابق دالة التوزيع التراكمي لأوقات الوصول البينية في الجهة اليمنى، ودالة التوزيع التراكمي المتمِّمة complementary cumulative distribution function -أو CCDF اختصارًا- على مقياس لوغاريتمي على محور y في الجهة اليسرى، كما أنّ diffs هو الفارق بين أزمنة الولادة المتتالية، وcdf هو توزيع أوقات الوصول البينية هذه، كما يُظهر الشكل السابق دالة التوزيع التراكمي، إذ يبدو أن للدالة الشكل العام للتوزيع الأسي، لكن كيف يمكننا التيقن من هذا؟
تتمثل إحدى الطرق في رسم دالة التوزيع التراكمي المتمِّمة complementary CDF ومعادلتها 1-CDF(x) على مقياس لوغاريتمي على محور y -أي المحور العمودي-، كما تكون النتيجة هي عبارة عن خط مستقيم في حال كانت البيانات من توزيع أسّي، وسنرى تطبيقًا عمليًا لهذا.
إذا رسمت دالة التوزيع التراكمي المتمِّمة لمجموعة بيانات معيّنة تعتقد أنها أسيّة، فستتوقع رؤية دالة مثل التي يُعبّر عنها بالصيغة الرياضية التالية:
y ≈ e-λx
بتطبيق اللوغاريتم على الطرفين:
logy ≈ -λx
أي أنّ دالة التوزيع التراكمي المتمِّمة على مقياس لوغاريتمي على المحور العمودي هي عبارة عن خط مستقيم بميل قدره λ-، وفيما يلي الشيفرة التي تولِّد الرسم:
thinkplot.Cdf(cdf, complement=True) thinkplot.Show(xlabel='minutes', ylabel='CCDF', yscale='log')
يمكن لدالة thinkplot.Cdf حساب دالة التوزيع التراكمي المتمِّمة قبل الرسم وذلك بفضل الوسيط complement=True، كما يمكن للدالة thinkplot.Show ضبط مقياس محور x -أي المحور الأفقي- ليصبح لوغاريتميًا بفضل الوسيط yscale='log'.
يُظهِر الشكل اليميني السابق النتيجة، وفي الواقع فإنّ الخرج ليس خطًا مستقيمًا مما يعني أنّ التوزيع الأسي ليس نموذجًا مثاليًا لهذه البيانات، ومن المرجَّح أنّ الافتراض الأساسي -الذي يقول أنّ احتمال الولادة نفسه لأيّ وقت من اليوم- ليس صحيحًا تمامًا، ومع ذلك قد يكون من المنطقي نمذجة مجموعة البيانات هذه بتوزيع أسي، حيث يمكننا تلخيص التوزيع بمعامِل واحد إذا استخدمنا هذا التبسيط في عملية النمذجة.
يمكن تفسير المعامِل λ على أنّه معدّل rate أي عدد الأحداث التي تحدث وسطيًا في وحدة الزمن، أي في هذا المثال وُلِد 44 طفلًا في 24 ساعة، لذا فإن المعدل هو λ=0.306 ولادة في الدقيقة الواحدة، كما يكون متوسط mean التوزيع الأسي هو 1/λ، لذا فإنّ متوسط الزمن بين الولادات هو 32.7 دقيقة.
التوزيع الطبيعي normal distribution
يُستخدَم التوزيع الطبيعي normal distribution والذي يُدعى أيضًا "التوزيع الغاوسي" استخدامًا كبيرًا لأنه يصف العديد من الظواهر -يصفها بصورة تقريبية على الأقل-، ولم يأتِ هذا الانتشار الواسع للتوزيع الطبيعي من عبث، بل يوجد سبب مقنع سنناقشه في مقال لاحق، في القسم الرابع تحت عنوان "نظرية الحد المركزيّ".
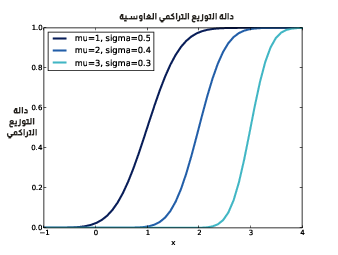
يوضِّح الشكل السابق دالة التوزيع التراكمي لتوزيعات طبيعية مع مجال وسائط parameters ما. ويتميّز التوزيع الطبيعي بمعامِلَين اثنين هما μ المتوسط mean، وσ الانحراف المعياري standard deviation.
يُعَدّ التوزيع الطبيعي القياسي standard normal distribution حالةً خاصةً من التوزيع الطبيعي يكون فيها المتوسط مساويًا للصفرμ = 0 وقيمة الانحراف المعياري مساويةً للواحد σ = 1، حيث يمكن تعريف دالة التوزيع التراكمي الخاصة بهذا التوزيع على أنّه تكامل لا يحوي على حلّ منغلق الشكل إلا أنه هناك خوارزميات تستطيع تقييمه بكفاءة.
تزوِّدنا مكتبة ساي باي SciPy بإحدى هذه الخوارزميات، حيث أنّ scipy.stats.norm هو كائن يمثِّل توزيعًا طبيعيًا، ويزوِّدنا بتابع cdf يقيّم دالة التوزيع التراكمي القياسية الطبيعية:
>>> import scipy.stats >>> scipy.stats.norm.cdf(0) 0.5
هذه النتيجة صحيحة، حيث يكون وسيط median التوزيع الطبيعي هو 0 -كما هو الحال في المتوسط mean-، ونصف القيم أقلّ من الوسيط، وبالتالي CDF(0)=0.5.
تأخذ الدالة norm.cdf معامِلَين اختياريين هما loc الذي يحدِّد المتوسط mean، وscale الذي يحدِّد الانحراف المعياري، ويسّهِل مستودع thinkstats2 علينا هذه الدالة عن طريق تزويدنا بالدالة EvalNormalCdf التي تأخذ معامِلَين اختياريين هما mu وsigma وتقيِّم دالة التوزيع التراكمي عند x:
def EvalNormalCdf(x, mu=0, sigma=1): return scipy.stats.norm.cdf(x, loc=mu, scale=sigma)
يُظهِر الشكل السابق دوال التوزيع التراكمي للتوزيعات الطبيعية مع مجال من المعامِلات، كما يُعَدّ هذا الشكل السّيني sigmoid للمنحنيات صفة مميّزة للتوزيع الطبيعي.
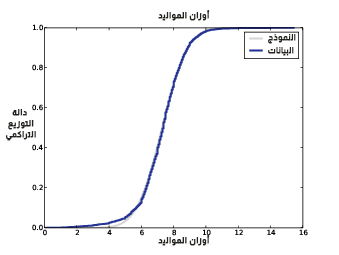
ألقينا في المقال السابق نظرةً على توزيع أوزان الولادات في المسح الوطني لنمو الأسرة، ويُظهِر الشكل التالي دوال التوزيع التراكمي التجريبي لأوزان جميع الولادات الحية، كما يُظهِر التوزيع الطبيعي مع مراعاة أن قيمة التباين variance وقيمة المتوسط mean هي ذاتها في الحالتين.
يوضِّح الشكل السابق دالة التوزيع التراكمي لأوزان الولادات مع نموذج طبيعي، حيث يُعَدّ التوزيع الطبيعي نموذجًا جيّدًا لمجموعة البيانات هذا، لذا فإن لخصّنا هذا التوزيع بالمعامِلات التالية: μ=7.28 وσ=1.24، فسيكون الخطأ الناتج صغير، مع العلم أنّ الخطأ هنا يشير إلى الفرق بين النموذج والبيانات.
هناك تناقض discrepancy بين البيانات وبين النموذج تحت المئين العاشر، حيث أنه يوجد في التوزيع عدد أطفال خفيفي الوزن أكثر من المتوقع في التوزيع الطبيعي، لكن إذا كنا مهتمين بدراسة الأطفال الخدّج، فسيكون الحصول على نتيجة دقيقة لهذا الجزء من التوزيع أمرًا هامًّا، لذلك قد لا يكون النموذج الطبيعي مناسبًا لهذا الغرض.
رسم الاحتمال الطبيعي normal probability plot
هناك تحويلات بسيطة يمكن استخدامها لاختبار فيما إذا كان التوزيع التحليلي يُعَدّ نموذجًا جيدًا لمجموعة بيانات معينة أم لا، ويمكن تطبيق ذلك على التوزيعات الأسية بالإضافة إلى بعض الأنواع الأخرى. وعلى الرغم من استحالة تطبيق هذه التحويلات على التوزيع الطبيعي، إلا أنه يوجد حل بديل يدعى رسم الاحتمال الطبيعي normal probability plot، كما يمكن توليده بطريقتين إحداهما صعبة والأخرى سهلة، ويمكنك الاطلاع على الطريقة الصعبة من هنا.
أما بالنسبة للطريقة السهلة، فإليك الخطوات التالية:
- رتّب القيم في العيّنة.
-
بدءًا من توزيع طبيعي قياسي -أي
μ=0وσ=1-، وولِّد عيّنة عشوائية لها حجم العيّنة نفسه ثم رتّبها. - ارسم القيم المرتّبة من العيّنة والقيم العشوائية.
تكون النتيجة خطًا مستقيمًا مع نقطة تقاطع ميو mu أي μ وميل قدره سيمغا sigma أيσ إذا كان توزيع العيّنة طبيعيًا تقريبًا.
يزوّدنا مستودع thinkstats2 بالدالة NormalProbability التي تأخذ عيّنةً وتُعيد مصفوفتَي نمباي NumPy، أي كما يلي:
xs, ys = thinkstats2.NormalProbability(sample)
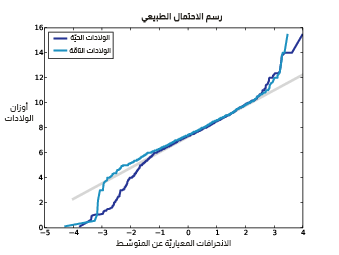
يوضِّح الشكل السابق رسم الاحتمال الطبيعي لعيّنات عشوائية من توزيع طبيعي، حيث تحتوي المصفوفة ys على القيم المرتّبة من العيّنة؛ أما المصفوفة xs فتحتوي على القيم العشوائية من التوزيع الطبيعي القياسي. وقد وَلّدنا بعض العيّنات المزيفة التي استقيناها من توزيعات طبيعية ذات معامِلات متنوعة وذلك بهدف اختبار الدالة NormalProbability، حيث يُظهِر الشكل السابق النتائج.
نلاحظ أنّ الخطوط مستقيمة تقريبًا مع وجود انحراف في القيم الموجودة في الذيول أكثر من القيم القريبة من المتوسط.
دعنا نجري التجربة على البيانات الحقيقية الآن. تولِّد هذه الشيفرة رسمًا احتماليًا طبيعيًا لبيانات أوزان الولادات الموجودة في القسم السابق، حيث ترسم هذه الشيفرة خطًا رماديًا يمثِّل النموذج، وخطًا أزرقًا يمثِّل البيانات.
def MakeNormalPlot(weights): mean = weights.mean() std = weights.std() xs = [-4, 4] fxs, fys = thinkstats2.FitLine(xs, inter=mean, slope=std) thinkplot.Plot(fxs, fys, color='gray', label='model') xs, ys = thinkstats2.NormalProbability(weights) thinkplot.Plot(xs, ys, label='birth weights')
تمثِّل weights سلسلة بانداز pandas Series لأوزان الولادات، كما يمثِّل mean المتوسط، في حين يمثِّل std الانحراف المعياري. وتأخذ الدالة FitLine تسلسلًا sequence من xs ونقطة تقاطع ومَيل، كما تُعيد xs وys اللتين تمثِّلان خطًا مع المعامِلات المُعطاة مقيّمًا عند القيم في xs.
تُعيد الدالة NormalProbability مصفوفتَين xs وys تحتويان على قيم من التوزيع الطبيعي القياسي وقيمًا من weights، حيث يجب أن تكون البيانات مطابقةً للنموذج في حال كان توزيع الأوزان طبيعيًا.
يوضِّح الشكل السابق رسم الاحتمال الطبيعي لأوزان الولادات.
يُظهر الشكل السابق نتائج جميع الولادات الحيّة وجميع الولادات التامة -التي كانت مدة الحمل فيها أكثر من 36 أسبوعًا-، حيث يُطابق المنحينان النموذج قرب المتوسط وينحرفان عند الذيول. كما أنّ وزن الأطفال الأكثر وزنًا أكثر مما يتوقّعه النموذج، ووزن الأطفال الأخف وزنًا أقل مما يتوقّعه النموذج.
عندما نحدِّد الولادات التامة فقط سنستبعد بعض الأطفال خفيفي الوزن مما يقلّل من التناقض في الذيل المنخفض من التوزيع. وبحسب هذا الرسم فإنّ النموذج الطبيعي يصف التوزيع وصفًا جيدًا مع بعض الانحرافات المعيارية ضمن المتوسط، لكن لا توجد في الذيول، لكن كَون النموذج مناسبًا بما فيه الكفاية للتطبيقات العملية أم لا، فهو أمر يعود إلى الغرض من النمذجة.
التوزيع اللوغاريتمي الطبيعي The lognormal distribution
إذا كان للوغاريتمات مجموعة من القيم توزيعًا طبيعيًا، فستمتلك القيم توزيعًا لوغاريتميًا طبيعيًا lognormal distribution، كما أنّ دالة التوزيع التراكمي للتوزيع اللوغاريتمي الطبيعي هي ذاتها بالنسبة للتوزيع الطبيعي لكن مع استبدال logx بـ x.
CDFlognormal(x) = CDFnormal(logx)
عادةً ما تتم الإشارة إلى معامِلات التوزيع اللوغاريتمي الطبيعي بـ μ وσ، لكنها لا تشير هنا إلى المتوسط والانحراف المعياري كما هو الحال سابقًا، إذ يكون المتوسط للتوزيع اللوغاريتمي الطبيعي هو exp(μ + σ2/2)؛ أما الانحراف المعياري فهو معقد، ويمكنك الاطلاع عليه من هنا.
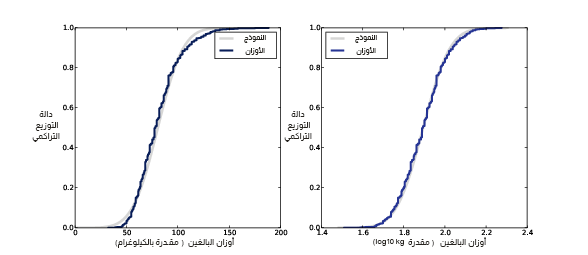
يوضِّح الشكل السابق دالة التوزيع التراكمي لأوزان البالغين على مقياس خطي في الجهة اليسرى، ومقياس لوغاريتمي في الجهة اليمنى.
إذا كانت العيّنة تمثِّل توزيعًا لوغاريتميًا طبيعيًا تقريبًا ورسمتَ دالة التوزيع التراكمي الخاصة بها على مقياس لوغاريتمي على المحور الأفقي -أي محور x-، فستكون له خصائص شكل التوزيع الطبيعي.
يمكنك إنشاء رسم احتمالي طبيعي باستخدام لوغاريتم القيم في العيّنة لاختبار ما إذا كان النموذج اللوغاريتمي الطبيعي يناسب العيّنة، كما سنلقي نظرةً على توزيع أوزان البالغين على سبيل المثال والذي يُعَدّ توزيعًا لوغاريتميًا طبيعيًا تقريبًا.2
يُجري المركز الوطني للوقاية من الأمراض المزمنة وتعزيز الصحة مسحًا سنويًا على أساس جزء من نظام مراقبة عوامل المخاطر السلوكية Behavioral Risk Factor Surveillance System -أو BRFSS3 اختصارًا-، حيث قابل المسؤولون عن المسح 414509 مستجيبًا عام 2008 وسألوهم عن معلوماتهم الديموغرافية وصحتهم والمخاطر الصحية التي تحيط بهم، ومن بين المعلومات التي جمعوها هي أوزان 398484 مستجيب مقدرةً بالكيلوغرام.
يحوي المستودع repository الخاص بهذا الكتاب ملفًا باسم CDBRFS08.ASC.gz وهو ملف أسكي ASCII -أي الشيفرة القياسية الأمريكية لتبادل المعلومات- ذو عرض ثابت يحتوي على بيانات نظام مراقبة عوامل المخاطر السلوكية، وكذلك يحوي ملفًا باسم brfss.py الذي يقرأ الملف ويحلِّل البيانات.
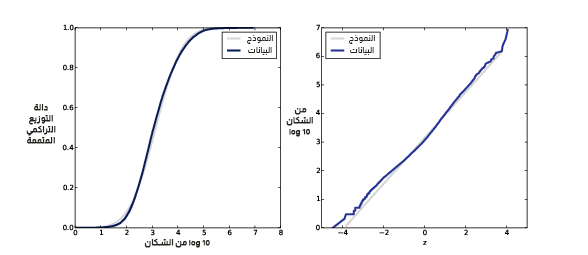
يُظهر الشكل السابق اليساري توزيع أوزان البالغين على مقياس خطي وباستخدام نموذج طبيعي؛ أما الشكل اليميني فيُظهر التوزيع نفسه على مقياس لوغاريتمي وباستخدام نموذج لوغاريتمي طبيعي، كما نلاحظ أنّ النموذج اللوغاريتمي الطبيعي أكثر ملاءمةً للعيّنة، إلا أن هذا التمثيل للبيانات لا يجعل الفرق واضحًا بصورة كبيرة.
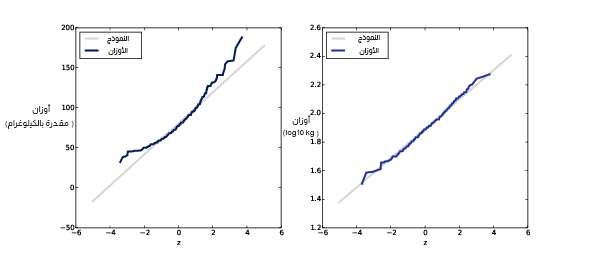
رسم الاحتمال الطبيعي لأوزان البالغين على مقياس خطي في الجهة اليسرى ومقياسًا لوغاريتميًا في الجهة اليمنى.
يُظهر الشكل السابق الرسوم الاحتمالية الطبيعية لأوزان البالغين w ويُظهر الرسوم الاحتمالية الطبيعية للوغاريتماتها log10w. وبهذا فقد أصبح من الواضح الآن أنّ البيانات تنحرف انحرافًا كبيرًا عن النموذج الطبيعي، لكن من ناحية أخرى نرى أنّ النموذج اللوغاريتمي الطبيعي يلائم البيانات جيدًا.
توزيع باريتو The Pareto distribution
سُمي توزيع باريتو Pareto distribution بهذا الاسم نسبةً إلى الاقتصادي فيلفريدو باريتو Vilfredo Pareto الذي استخدَم هذا التوزيع في وصف توزيع الثروات، ولمزيد من التفاصيل يمكنك الاطلاع على توزيع باريتو بويكيبيديا.
لقد اعتُمِد هذا التوزيع من ذلك الوقت لوصف الظواهر الطبيعية والاجتماعية بما في ذلك أحجام المدن والبلدات وذرات الرمل والنيازك وحرائق الغابات والزلازل.
الصيغة الرياضيّة لدالة التوزيع التراكمي لتوزيع باريتو Pareto distribution هي:
CDF(x) =1- xxm-
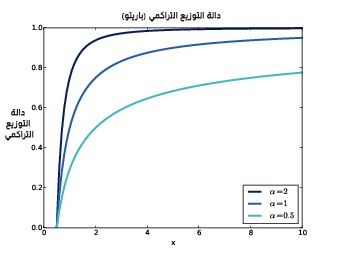
يحدِّد المعامِلَين xm وα الموقع وشكل التوزيع، حيث xm هي أصغر قيمة ممكنة، ويُظهر الشكل التالي دوال التوزيع التراكمي لتوزيعات باريتو Pareto distributions مع افتراض أنّ xm = 0.5 وتجريب عدة قيم مختلفة لـ α.
يوضِّح الشكل السابق دوال التوزيع التراكمي لتوزيعات باريتو Pareto distributions بمعامِلات مختلفة.
هناك اختبار مرئي بسيط يخبرنا عما إن كان التوزيع التجريبي يلائم توزيع باريتو Pareto distribution أم لا، ويبدو لنا على مقياس لوغاريتمي-لوغاريتمي أنّ دوال التوزيع التراكمي المتمِّمة هي خط مستقيم، وسنرى التطبيق العملي لهذا.
y = xxm -
بتطبيق اللوغاريتم على الطرفين يكون لدينا:
logy ≈ -α(logx - logxm)
لذا فإن رسمت logy مقابل logx، فيجب أن يبدو الشكل مستقيمًا مع ميل قدره -α ونقطة تقاطع هي α logxm .
سنأخذ أحجام المدن والبلدات على أساس مثال عن هذا، حيث ينشر مكتب الإحصاء الأمريكي The U.S. Census Bureau عدد السكان في كل مدينة وبلدة في الولايات المتحدة.
يوضِّح الشكل السابق دوال التوزيع التراكمي المتمِّمة لسكان المدينة والبلدة على مقياس لوغاريتمي-لوغاريتمي أي أنّ المقياس المستخدَم للمحورين الأفقي والعمودي هو لوغاريتمي.
يمكن تنزيل بيانات هذا المركز من هنا، كما توجد هذه البيانات في مستودع الكتاب تحت اسم PEP_2012_PEPANNRES_with_ann.csv، ويحتوي هذا المستودع على ملف populations.py الذي يقرأ الملف ويرسم توزيع السكان.
يُظهر الشكل السابق وقوع أكبر 1% من البلدات والمدن التي تقل عن 10-2 على طول خط مستقيم، لذا يمكننا استنتاج أنّ ذيل هذا التوزيع يناسب نموذج باريتو Pareto model وهذا يطابق قول بعض الباحثِين.
ينمذِج التوزيع اللوغاريتمي الطبيعي من ناحية أخرى البيانات جيدًا، ويوضِّح الشكل التالي دالة التوزيع التراكمي للسكان ونموذجًا لوغاريتميًا طبيعيًا في الجهة اليسرى، وفي الجهة اليمنى رسمًا احتماليًا طبيعيًا، كما نستنتج أنّ الرسمَين يُظهران ملاءمةً جيدةً بين البيانات والنموذج.
لا يُعَدّ كل نموذج لوحده هنا مثاليًا في الواقع، حيث ينطبق نموذج باريتو Pareto model على أكبر 1% من المدن فقط، لكنه أكثر ملاءمةً لهذا الجزء من التوزيع، كما يناسب النموذج اللوغاريتمي الطبيعي بقية البيانات أي ما يقارب 99% من البيانات، أي يعتمد مدى ملاءمة نموذج معيّن للبيانات على جزء التوزيع الذي نهتم بدراسته.
يُظهر الشكل السابق دالة التوزيع التراكمي لسكان المدينة والبلدة على مقياس لوغاريتمي على المحور الأفقي x في الجهة اليسرى، ورسم الاحتمال الطبيعي للسكان بعد تطبيق تحويل لوغاريتمي log-transformation على السكان في الجهة اليمنى.
اقتباستوضيح: في التحويل اللوغاريتمي تُحوَّل كل x في البيانات إلى log(x).
توليد أعداد عشوائية
يمكن استخدام دوال التوزيع التراكمي التحليلية لتوليد أعداد عشوائية إذا كان لدينا دالة توزيع مُعطاة مسبقًا، حيث أنّ p=CDF(x)، وإذا كانت هناك طريقة فعالة لحساب دالة التوزيع التراكمي العكسية، فسيمكننا توليد قيم عشوائية مع التوزيع المناسب وذلك عن طريق اختيار p من توزيع موحَّد بين 0 و1، ومن ثم اختيار x=ICDF(p).
الصيغة الرياضية على سبيل المثال لدالة التوزيع التراكمي للتوزيع الأسي هي:
p = 1- e-λx
بحل المعادلة بالنسبة لـ x ينتج:
x = -log(1-p) / λ
كما تكون الشيفرة الموافقة بلغة بايثون:
def expovariate(lam): p = random.random() x = -math.log(1-p) / lam return x
تأخذ الدالة expovariate معامِلًا هو lam وتُعيد قيمةً عشوائيةً مختارة من التوزيع الأسي مع المعامِل lam.
إليك ملاحظتين اثنتين حول هذا التنفيذ: استدعينا المعامِل lam لأن lambda هي كلمة مفتاحية في لغة بايثون، وبما أن log0 هي قيمة غير معرَّفة undefined، فيجب أن نكون حذرين قليلًا.
اقتباستوضيح: لامدا أو lambda تقابل الحرف الإغريقي المذكور آنفًا .
يمكن أن تُعيد الدالة random.random القيمة 0 لكن لا يمكنها إعادة 1، لذا يمكن أن تكون قيمة 1-pهي 1، لكن لا يمكن أن تكون 0، وبالتالي تكون قيمة log(1-p) هي دائمًا معرَّفة.
بم تفيدنا النمذجة؟
ذكرنا في بداية المقال أنه يمكن نمذجة العديد من الظواهر التي تحصل في الحياة الواقعية باستخدام النماذج التحليلية، لذا قد تقول: "ماذا إذًا؟"
تُعَدّ التوزيعات التحليلية تجريدات مثل حال النماذج الأخرى، أي أنّها تُهمل التفاصيل التي لا علاقة لها بموضوع الدراسة. فمثلًا، قد يكون في التوزيع الملحوظ أخطاء في القياس أو عيوب متعلقة بالعيّنة، فتأتي النماذج التحليلية لتخفيف هذه المشاكل.
كما تُعَدّ النماذج التحليلية شكلًا form من ضغط البيانات، حيث أنه عندما يناسب نموذج معيّن لمجموعة بيانات، فسيمكن عندها تلخيص كمية كبيرة من البيانات باستخدام مجموعة صغيرة من المعامِلات.
قد نتفاجأ في حال وجدنا أنّ بيانات إحدى الظواهر الطبيعية قد لاءمت توزيعًا تحليليًا، لكن يمكن أن توفِّر لنا هذه الملاحظات معلومات أكثر عن النظم الفيزيائية.
يمكننا في بعض الأحيان وصف السبب الذي يجعل توزيعًا ملحوظًا يظهر بشكل معيّن، فغالبًا ما تكون توزيعات باريتو Pareto distributions على سبيل المثال، نتيجةً لعمليات توليدية ذات رد فعل إيجابي أو ما يُعرَف باسم عمليات الإلحاق التفضيلية preferential attachment processes.
تصلح التوزيعات التحليلية للتحليل الرياضي كما سنرى في مقال لاحق، لكن من المهم أن نتذكّر أن جميع النماذج غير مثالية، ولا يمكن للبيانات الصادرة من العالم الحقيقي أن تناسب التوزيع التحليلي بصورة مثالية.
يتحدث الأفراد في بعض الأحيان كما لو كانت البيانات تُولَّد من نماذج، فقد يسأل البعض مثلًا فيما إذا كان توزيع أطوال البشر طبيعيًا، أو قد يسألون فيما إن كان توزيع الدخل لوغاريتميًا طبيعيًا، وإذا أخذنا الأمور بحَرفيّة فستكون هذه الأقوال غير صحيحة بسبب وجود فروق بين النماذج الرياضية والعالم الحقيقي.
تفيد هذه النماذج إذا استطاعت التقاط الجوانب التي تهمنا من العالم الحقيقي وإهمال التفاصيل غير المهمة في آن واحد، لكن "الجوانب التي تهمنا" و"التفاصيل غير المهمة" هي أمور معتمدة على الغرض من استخدام النموذج.
تمارين
يمكنك الانطلاق من chap05ex.ipynb لحل هذه التمارين، مع العلم أن الحل الخاص بنا موجود في ملف chap05soln.ipynb في مستودع ThinkStats2 على GitHub حيث ستجد كل الشيفرات والملفات المطلوبة.
التمرين الأول
يُعَدّ توزيع الأطوال في نظام مراقبة عوامل المخاطر السلوكية BRFSS طبيعيًا تقربيًا مع العلم أنّ المعامِلات بالنسبة للرجال هي μ=178 cm وσ = 7.7، وبالنسبة للنساء هي μ=163 cm وσ = 7.3.
هناك شرط للانتساب لمجموعة بلو مان وهو أن يكون الفرد ذكرًا طوله بين ''10'5 قدمًا -أي حوالي 177.8 سنتي مترًا- و''1'6 قدمًا -أي حوالي 185.42 سنتي مترًا-. فما هي نسبة الرجال الأمريكيين الذي ينطبق عليهم هذا الشرط؟
اقتباستلميح: استخدم
scipy.stats.norm.cdf.
التمرين الثاني
للتعرف على توزيع باريتو Pareto distribution، سنرى كيف سيكون العالم مختلفًا فيما لو كان توزيع أطوال البشر هو عن باريتو Pareto.
يمكننا الحصول على توزيع ذي قيمة صغرى منطقية 1m أي مترًا واحدًا، ووسيط median هو 1.5 m أي متر ونصف، أي في حال كانت المعامِلات هي xm = 1 وα=1.7.
ارسم هذا التوزيع وأجب عن الأسئلة التالية:
- ما هو متوسط mean أطوال البشر في عالم باريتو؟
- ما هي نسبة fraction الأشخاص الذين يقل طولهم عن المتوسط؟
- إذا كان هناك 7 مليار فرد في عالم باريتو، فكم هو عدد الأفراد الذي من المتوقع أن يزيد طولهم عن كيلومتر واحد؟
- كم طول أطول شخص ممكن توقّعه؟
التمرين الثالث
يُعَدّ توزيع وايبول Weibull distribution تعميمًا للتوزيع الأسي الذي يظهر في تحليل الفشل، حيث يمكنك الاطلاع على ذلك في ويكيبيديا للمزيد من المعلومات، وتكون الصيغة الرياضية لدالة التوزيع التراكمي لهذا التوزيع بالصورة التالية:
CDF(x) = 1 - e-(x/λ)k
لكن هل يمكننا إيجاد تحويل ليبدو توزيع وايبول خطًا مستقيمًا؟ علامَ يدل كل من الميل ونقطة التقاطع؟ استخدِم هنا random.weibullvariate لتوليد عيّنة من توزيع وايبول واستخدِمه في اختبار تحويلك.
التمرين الرابع
لا نتوقع أن يكون التوزيع التجريبي مناسبًا للتوزيع التحليلي بدقة من أجل القيم الصغيرة من n، حيث تتمثل إحدى طرق تقييم جودة الملاءمة في توليد عيّنة من توزيع تحليلي ومن ثم التحقق من مدى ملاءمتها للبيانات.
رسمنا مثلًا في القسم الأول -التوزيع الأسي- توزيع الوقت بين الولادات، ورأينا أنه أسي تقريبًا، لكن التوزيع مبني على 44 نقطة بيانات فقط.
لنرى ما إذا كانت البيانات قد أتت من توزيع أسي، يجب عليك توليد 44 قيمة من توزيع أسي له متوسط البيانات هذه نفسها، أي بوجود 33 دقيقة بين الولادة والأخرى. وارسم توزيع القيم العشوائية ووازنه مع التوزيع الفعلي، كما يمكنك استخدام random.expovariate لتوليد القيم.
التمرين الخامس
ستجد في مستودع هذا الكتاب مجموعةً من ملفات البيانات تُدعى mystery0.dat و mystery1.dat وهكذا، حيث يحتوي كل ملف على تسلسل من الأعداد العشوائية المولَّدة من توزيع تحليلي.
كما ستجد ملفًا يدعى test_models.py وهو عبارة عن سكربت يقرأ البيانات من ملف ويرسم دالة التوزيع التراكمي مع مجموعة متنوعة من التحويلات، إذ يمكنك تشغيل الملف عن طريق استخدام مثل التعليمة التالية:
$ python test_models.py mystery0.dat
يمكنك استنتاج نوع التوزيع المولَّد في كل ملف بناءً على الرسوم هذه، لكن إذا كنت في حيرة من أمرك، فيمكنك البحث في ملف mystery.py الذي يحتوي على الشيفرة التي ولَّدت الملفات.
التمرين السادس
تكون توزيعات الدخل والثروة في بعض الأحيان منمذجةً باستخدام توزيعات باريتو Pareto distributions وتوزيعات لوغاريتمية طبيعية lognormal، ولكي نرى أيّ منها أفضل سنلقي نظرةً على مجموعة من البيانات.
يُعَدّ المسح السكاني الحالي Current Population Survey -أو CPS اختصارًا- جهدًا مشتركًا بين مكتب إحصاءات العمل ومكتب التعداد لدراسة الدخل والمتغيرات ذات الصلة.
حمّلنا الملف hinc06.xls وهو عبارة عن جدول بيانات spreadsheet إكسل يحوي معلومات عن دخل الأسرة المعيشية household income، وحوَّلناه إلى hinc06.csv وهو ملف ستجده في المستودع الخاص بهذا الكتاب، كما ستجد hinc.py الذي يقرأ الملف السابق.
استخرج توزيع مجموعة المداخيل من مجموعة البيانات هذه، وهل يُعَد أيّ توزيع من التوزيعات التحليلية الواردة في هذا المقال نموذجًا جيدًا للبيانات؟
يوجد حل هذا التمرين في الملف hinc_soln.py فستجد كل الشيفرات والملفات في مستودع ThinkStats2.
مفاهيم أساسية
- التوزيع التجريبي exponential distribution: هو توزيع القيم في عيّنة ما.
- التوزيع الأسي analytic distribution: هو التوزيع الذي تتصف دالة التوزيع التراكمي الخاصة به بأنّها دالة تحليلية.
- النموذج model: هو تبسيط يقدِّم معلومات مفيدة، حيث غالبًا ما تُعَدّ التوزيعات التحليلية أنها نماذجَ جيدة لتوزيعات تجريبية empirical distributions أكثر تعقيدًا.
- فاصل الوصول interarrival time: هو الزمن الفاصل بين حدثين اثنين.
- دالة التوزيع التراكمي المتمِّمة complementary CDF: هي دالة تحوِّل القيمة x إلى كسر من القيم التي تتجاوز x، وتكون صيغتها الرياضية 1-CDF(x).
- التوزيع الطبيعي القياسي standard normal distribution: هو حالة خاصة من التوزيع الطبيعي تكون قيمة الانحراف المعياري standard deviation فيه هي 1، وقيمة المتوسط mean هي 0.
- رسم الاحتمال الطبيعي normal probability plot: هو رسم للقيم الموجودة في عيّنة ما مقابل قيم عشوائية من توزيع طبيعي قياسي.
ترجمة -وبتصرف- للفصل Chapter 5 Modelling distributions analysis من كتاب Think Stats: Exploratory Data Analysis in Python














أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.