دوال الكثافة الاحتمالية في بايثون

توجد الشيفرة الخاصة بهذا الفصل في ملف density.py في مستودع ThinkStats2 على GitHub.

دوال الكثافة الاحتمالية probability density functions

يمكن تعريف دالة الكثافة الاحتمالية probability density function -أو PDF اختصارًا- على أنها مشتق دالة التوزيع التراكمي cumulative distribution function -أو CDF اختصارًا-، وتكون الصيغة الرياضية على سبيل المثال لدالة الكثافة الاحتمالية الخاصة بالتوزيع الأسي exponential distribution هي:

PDF_expo(x) = λ e^−λ x

كما تكون الصيغة الرياضية لدالة الكثافة الاحتمالية الخاصة بالتوزيع الطبيعي normal distribution هي:

PDF_normal(x) =

√

2 π

exp

⎡
⎢
⎢
⎢
⎢
⎢
⎣

−

⎛
⎜
⎜
⎝

x − µ

⎞
⎟
⎟
⎠

⎤
⎥
⎥
⎥
⎥
⎥
⎦

وبطبيعة الحال، لا يفيدنا في أغلب الأحيان تقييم دالة الكثافة الاحتمالية لقيمة معيّنة مثل x، كما لا تكون النتيجة احتمالًا بل كثافة احتمالية.

تُعرّف الكثافة في الفيزياء على أنها كتلة المادة لكل وحدة حجم، ومن أجل الحصول على الكتلة يجب أن نضرب بالحجم أو علينا إجراء تكامل مع الحجم في حال لم تكن الكثافة ثابتة، وكذلك فإنّ الكثافة الاحتمالية تقيس الاحتمال لكل وحدة x، لذا فمن أجل الحصول على كتلة احتمالية يجب إجراء تكامل مع x.

يزوّدنا مستودع thinkstats2 بصنف class يسمى Pdf يمثِّل دالة الكثافة الاحتمالية، كما يزوِّدنا كل كائن من Pdf بالتوابع التالية:

Density يأخذ هذا التابع قيمة x ويُعيد كثافة التوزيع عند x.
Render يقيِّم هذا التابع الكثافة عند مجموعة متقطِّعة من القيم ويعيد زوجًا من التسلسلات sequences والتي هي xs أي القيم التي رُتّبت وdf أي الكثافة الاحتمالية الخاصة بهذه القيم.
MakePmf يقيِّم هذا التابع الكثافة عند مجموعة متقطّعة من القيم ويعيد صنف Pmf بعد توحيده بحيث يكون مقاربًا للصنف Pdf.
GetLinspace يُعيد هذا التابع المجموعة الافتراضية من النقاط التي يستخدِمها كل من التابعَين Render وMakePmf

يُعَدّ Pdf صنف أب مجرَّد abstract parent class أو صنفًا مورِّثًا -أي أن صنف ترثه عدة أصناف أخرى-، وتدلّ كلمة مجرَّد على عدم إمكانية استنساخه أي لا يمكن إنشاء كائن Pdf، وبالتالي علينا بدلًا عن ذلك تعريف صنف ابن يرث من الصنف Pdf ويعرِّف التابعَين Density وGetLinspace؛ أما التابعين Render وMakePmf فسيتكفّل الصنف Pdf بتعريفهما.

يزوّدنا مستودع thinkstats2 على سبيل المثال بصنف يُدعى NormalPdf يقيِّم دالة الكثافة الطبيعية، وتكون الشيفرة الموافقة له كما يلي:

class NormalPdf(Pdf):

    def __init__(self, mu=0, sigma=1, label=''):
        self.mu = mu
        self.sigma = sigma
        self.label = label

    def Density(self, xs):
        return scipy.stats.norm.pdf(xs, self.mu, self.sigma)

    def GetLinspace(self):
        low, high = self.mu-3*self.sigma, self.mu+3*self.sigma
        return np.linspace(low, high, 101)

يحتوي كائن الصنف NormalPdf على المعامِلَين mu وsigma، كما يستخدِم التابع Density الكائن scipy.stats.norm الذي يمثِّل توزيعًا طبيعيًا ويزوِّدنا بالتابعَين cdf وpdf، بالإضافة إلى العديد من التوابع الأخرى -ويمكنك الاطلاع على نمذجة التوزيعات Modelling distributions-.

تُنشِئ الشيفرة الموجودة في المثال التالي الصنف NormalPdf مع المتوسط mean والتباين variance الخاصَّين بأطوال الإناث البالغات مقدَّرةً بالسنتيمتر ومأخوذةً من نظام مراقبة عوامل المخاطر السلوكية BRFSS، ومن ثم تحسب هي كثافة التوزيع في موقع يبعد انحرافًا معياريًا واحدًا عن المتوسط كما يلي:

>>> mean, var = 163, 52.8
>>> std = math.sqrt(var)
>>> pdf = thinkstats2.NormalPdf(mean, std)
>>> pdf.Density(mean + std)
0.0333001

تكون النتيجة حوالي 0.03 مقدَّرةً بواحدة كتلة احتمالية لكل سنتيمتر، كما نشدِّد على فكرة أنّ الكثافة الاحتمالية لا تعنينا لوحدها لكن إذا رسمنا الصنف Pdf كما يلي، فيمكننا رؤية شكل التوزيع:

>>> thinkplot.Pdf(pdf, label='normal')
>>> thinkplot.Show()

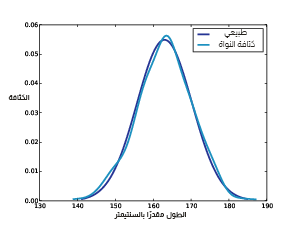
يرسم التابع thinkplot.Pdf الصنف Pdf على أساس دالة منتظمة smooth على عكس التابع thinkplot.Pmf الذي يرسم الصنف Pmf على أساس دالة خطوة، ويُظهِر الشكل التالي النتيجة بالإضافة إلى دالة الكثافة الاحتمالية المقدَّرة من عيّنة، والتي سنحسبها في القسم التالي.

يمكننا استخدام التابع MakePmf من أجل إنشاء نسخة تقريبية من الصنف Pdf كما يلي:

>>> pmf = pdf.MakePmf()

يحتوي الصنف Pmf الناتج على 101 نقطة افتراضيًا تبتعد عن بعضها بمسافات متساوية من mu-3sigma إلى mu+3sigma، ويمكن للتابعَين MakePmf وRender أخذ الوسطاء المفتاحية التالية: low وhigh وn بصورة اختيارية.

يوضِّح الشكل السابق دالة كثافة احتمالية طبيعية لنمذجة أطوال الإناث البالغات في الولايات المتحدة الأمريكية، وتقدير كثافة نواة العيّنة في حال كانت n=500.

تقدير كثافة النواة

يُعَد تقدير كثافة النواة Kernel density estimation -أو KDE اختصارًا- خوارزميةً تأخذ عيّنة، وتوجِد دالة كثافة احتمالية منتظمة تناسب البيانات، ويمكنك قراءة تفاصيل على ويكيبيديا.

تزوّدنا scipy بتنفيذ لتقدير كثافة النواة، كما يزوّدنا مستودع thinkstats2 بصنف يُدعى EstimatedPdf يستخدِم ذلك التنفيذ كما يلي:

class EstimatedPdf(Pdf):

    def __init__(self, sample):
        self.kde = scipy.stats.gaussian_kde(sample)

    def Density(self, xs):
        return self.kde.evaluate(xs)

يأخذ التابع __init__ عيّنةً ويحسب تقدير كثافة النواة، حيث يكون الناتج كائن gaussian_kde الذي يزوِّدنا بتابع evaluate؛ أما التابع Density فيأخذ قيمةً أو تسلسلًا يُدعى gaussian_kde.evaluate ويُعيد الكثافة الناتجة، كما تَظهر الكلمة Gaussian في الاسم لأنها تستخدم مرشِّحًا يعتمد على التوزيع الغاوسي لجعل تقدير كثافة النواة منتظمًا smooth.

إليك شيفرةً تولِّد عيّنةً من توزيع طبيعي ومن ثم تنشِئ صنف EstimatedPdf يناسبها:

>>> sample = [random.gauss(mean, std) for i in range(500)]
>>> sample_pdf = thinkstats2.EstimatedPdf(sample)
>>> thinkplot.Pdf(sample_pdf, label='sample KDE')

تمثِّل sample قائمةً تحوي أطوال عشوائية عددها 500؛ أما sample_pdf فهو كائن Pdf يحتوي على تقدير كثافة النواة المقدَّر من العيّنة.

يُظهر الشكل السابق دالة الكثافة الطبيعية وتقدير كثافة النواة بناءً على العيّنة التي تحتوي على أطوال عشوائية عددها 500، بحيث يكون التقدير مناسبًا للتوزيع الأصلي.

يُعَدّ تقدير دالة الكثافة عن طريق تقدير كثافة النواة مفيدًا لعدة أغراض منها:

التصوّر/التوضيح المرئي Visualization: فغالبًا ما تُعَدّ دوال الكثافة التراكمية أفضل توضيح مرئي للتوزيع خلال مرحلة استكشاف المشروع، حيث أنه بإمكانك بعد النظر إلى دالة التوزيع التراكمي تحديد فيما إذا كانت دالة الكثافة الاحتمالية المقدَّرة تُعَدّ نموذجًا مناسبًا للتوزيع أم لا، فإذا كانت كذلك فستكون خيارًا أفضل لتمثيل التوزيع في حال لم يكن الجمهور المستهدف على اطلاع على دوال التوزيع التراكمي.
الاستيفاء Interpolation: تفيد دالة الكثافة الاحتمالية المقدَّرة في الانتقال من عيّنة إلى نموذج للسكان، حيث يمكنك استخدَام تقدير كثافة النواة لاستيفاء كثافة القيم التي لا تظهر في العيّنة إذا كنت تعتقد أنّ توزيع السكان منتظمًا smooth.
المحاكاة Simulation: غالبًا ما تكون المحاكاة مبنيّة على توزيع العيّنة، فإذا كان حجم العيّنة صغيرًا قد يكون من المناسب استخدام تقدير كثافة النواة KDE من أجل جعل توزيع العيّنة منتظمًا، مما يسمح للمحاكاة باستكشاف المزيد من النتائج المحتملة بدلًا من تكرار البيانات الملحوظة.

إطار التوزيع The distribution framework

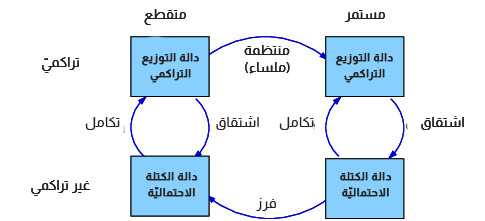
يوضِّح الشكل السابق إطارًا يربط بين تمثيلات دوال التوزيع.

الآن بعد مرورنا على دوال الكتلة الاحتمالية PMFs ودوال التوزيع التراكمي CDFs ودوال الكثافة الاحتمالية PDFs، سنتوقف قليلًا لنراجع هذه المفاهيم، حيث يُظهر الشكل السابق كيفية ارتباط هذه الدوال ببعضها البعض.

بدأنا بدراسة دوال الكتلة الاحتمالية التي تمثِّل احتمالات مجموعة متقطِّعة من القيم، حيث يمكننا الانتقال من دالة كتلة احتمالية PMF إلى دالة توزيع تراكمي CDF عن طريق جمع الكتل الاحتمالية للحصول على الاحتمالات التراكمية، وللانتقال من دالة توزيع تراكمي إلى دالة كتلة احتمالية يمكننا حساب الفروق في الاحتمالات التراكمية، كما سنرى تنفيذ هذه العمليات في الأقسام القليلة القادمة.

يمكن تعريف دالة الكثافة الاحتمالية على أنها مشتق من دالة التوزيع التراكمي المستمرة، أو على نحو مكافئ بأنها تكامل لدالة الكثافة الاحتمالية -أي نحصل على دالة توزيع تراكمي عن طريق تطبيق تكامل على دالة الكثافة الاحتمالية-، حيث تحوِّل دالة الكثافة الاحتمالية القيم إلى كثافات احتمالية، ويجب تطبيق التكامل للحصول على احتمال.

يمكننا جعل التوزيع منتظمًا بعدة طرق من أجل الانتقال من توزيع متقطِّع إلى توزيع مستمر، وإحدى أشكال التنظيم أو التنعيم smoothing هي افتراض أنّ مصدر البيانات هو توزيع تحليلي مستمر -مثل التوزيع الأسي أو الطبيعي-، ومن ثم تقدير معامِلات التوزيع، كما يمكننا جعل التوزيع منتظمًا عن طريق تقدير كثافة النواة KDE على أساس خيار آخر.

يُعَدّ التكميم quantizing -أو التقطيع discretizing- عمليةً معاكسةً لعملية التنظيم smoothing، كما يمكننا توليد دالة الكتلة الاحتمالية التي تُعدّ تقريبًا لدالة الكثافة الاحتمالية وذلك عن طريق تقييم دالة الكثافة الاحتمالية عند نقاط متقطِّعة، كما يمكننا الحصول على تقريب أفضل باستخدام التكامل العددي.

سنستخدم مصطلح دالة الكثافة التراكمية للدلالة على دالة التوزيع التراكمي المتقطعة، وذلك بهدف التمييز بين دوال التوزيع التراكمي المستمرة ودوال التوزيع التراكمي المتقطِّعة، لكننا نعتقد أن هذا المصطلح غير مستخدَم من قِبَل أيّ شخص آخر.

تنفيذ Hist

لا بدّ أنك الآن تجيد استخدام الأنواع الأساسية التي يزوّدنا بها مستودع thinkstats2 وهي: Hist وPmf وCdf وPdf، كما ستزوِّدنا الأقسام القليلة القادمة بتفاصيل حول تنفيذها، وقد تساعدك هذه المعلومات على استخدام هذه الأصناف استخدامًا فعّالًا لكنها ليست ضروريةً تمامًا.

يرث الصنفان Hist وPmf توابعهما من صنف أب يُدعى ‎_DictWrapper‎ حيث تشير الشَرطة السفلية underscore إلى أن الصنف "داخلي"، أي لا يمكن استخدامه من قِبَل شيفرات موجودة في وحدات modules أخرى؛ أمّا اسم الصنف فيشير إلى قاموس مغلّف Dictionary Wrapper، والسمة الأساسية فيه هي d أي القاموس dictionary الذي يحوِّل القيم إلى تردداتها.

يمكن أن تنتمي القيم إلى أيّ نوع قابل للتجزئة hashable، وعلى الرغم أنه يجب أن تكون الترددات قيمًا صحيحةً إلا أنها يمكن أن تنتمي إلى أي نوع عددي.

يحتوي ‎_DictWrapper على توابع ملائمة لكلًا من الصنف Hist والصنف Pmf بما فيها __init__ و Values و Items و Render بالإضافة إلى توفير توابع محوِّلة هي Set و Incr و Mult و Remove فكل هذه التوابع مُنفَّذة مع عمليات القاموس، انظر مثلًا:

# class _DictWrapper

    def Incr(self, x, term=1):
        self.d[x] = self.d.get(x, 0) + term

    def Mult(self, x, factor):
        self.d[x] = self.d.get(x, 0) * factor

    def Remove(self, x):
        del self.d[x]

يزوّدنا الصنف Hist بالتابع Freq الذي يوجِد تردد قيمة معطاة.

هذه التوابع تعمل عوامِل وتوابع Hist بزمن ثابت لأنها مبنية على قواميس، أي أنّ زمن تنفيذها لا يزداد مع ازدياد حجم الصنف Hist.

تنفيذ Pmf

يتشابه الصنفان Pmf وHist إلى حد التطابق تقريبًا إلا أنّ Pmf يحوِّل القيم إلى احتمالات عشرية؛ أما Hist فيحول القيم إلى ترددات نوعها صحيح integer، بحيث إذا كان مجموع الاحتمالات مساويًا للواحد فسيكون Pmf موحَّدًا.

اقتباس

توضيح: تنظيم أو توحيد للواحد أو توحيد أحادي هي عملية حسابية بسيطة لتبسيط النسب وهي على نمط النظام المئوي المعروف، مع اختلاف أنّ النسبة طبقًا للنظام المئوي تقع بين 0 % و100% بينما في التوحيد للواحد فستقع النسبة بين 0 و1، كما يمكنك الاطلاع على المصدر.

يزوِّدنا الصنف Pmf بالتابع Normalize الذي يحسب مجموع الاحتمالات ويقسمها على معامِل factor كما يلي:

# class Pmf

    def Normalize(self, fraction=1.0):
        total = self.Total()
        if total == 0.0:
            raise ValueError('Total probability is zero.')

        factor = float(fraction) / total
        for x in self.d:
            self.d[x] *= factor

        return total

يحدِّد المتغير fraction مجموع الاحتمالات بعد توحيدها للواحد، حيث أنّ القيمة الاقتراضية هي الواحد، وإذا كان مجموع الاحتمالات 0 فلا يمكن توحيد الصنف Pmf، لذا سترمي دالة Normalize خطأً من النوع ValueError. يملك الصنفان Hist وPmf الباني نفسه، حيث يأخذ هذا الباني وسيطًا ليكون dict أو Hist أو Pmf أو Cdf، أو سلسلة بانداز pandas Series أو قائمةً من أزواج (قيمة وتردد) أو تسلسلًا من القيم.

إذا أنشأت نسخةً من الصنف Pmf، فستكون النتيجة موحَّدة إلى الواحد (normalized)؛ أما إذا أنشأت نسخةً من الصنف Hist، فلن تكون النتيجة موحَّدة إلى الواحد، حيث يمكنك إنشاء صنف Pmf فارغ وتعديله لبناء صنف Pmf غير موحَّد، إذ أنّ معدلات Pmf لا لا تعيد توحيد الصنف Pmf.

تنفيذ Cdf

تحوّل دالة التوزيع التراكمي القيم إلى احتمالاتها التراكمية، لذا كان من الممكن تنفيذ Hist على أساس ‎_‎DictWrapper إلا أنّ القيم في الصنف Hist مرتبّة على عكس ‎_DictWrapper.

يُعَد حساب دالة التوزيع التراكمي العكسية inverse CDF مفيدًا في البعض الأحيان، بحيث تكون دالة التوزيع التراكمي العكسية هي تحويل الاحتمال التراكمي إلى قيمته، لذا اخترنا التنفيذ الذي يحوي قائمتَين مرتبتَين وذلك لكي نستطيع إجراء بحث lookup أمامي أو عكسي في زمن تنفيذ لوغاريتمي عن طريق استخدام البحث الثنائي binary search.

اقتباس

توضيح: قد لا يكون الفرق بين search وlookup واضحًا أو معروفًا لدى الكثيرين، إلا أنه موجود، حيث أنه في عملية lookup نفترض أن القيمة التي نبحث عنها موجودة، وتكون لدينا طريقةً واضحةً لاستخراجها؛ أمّا في عملية search فلسنا واثقين من وجود القيمة التي نبحث عنها وقد لا يكون لدينا طريقةً واضحة لاستخراجها.

يمكن لباني Cdf أن يأخذ تسلسلًا من القيم على أساس معامِل له أو قد يأخذ سلسلة بانداز pandas Series أو قاموسًا dictionary يحوِّل القيم إلى احتمالاتها، أو تسلسلًا من أزواج (القيمة والاحتمال) أو Hist، أو Pmf، أو Cdf، أو إذا أُعطي الباني معامِلان فسيعاملهما على أساس تسلسل مرتّب من القيم، وتسلسل من الاحتمالات التراكمية الموافقة.

يمكن للباني إنشاء Hist بإعطاء تسلسل أو سلسلة بانداز pandas Series، أو قاموس، ومن ثم يستخدِم Hist من أجل تهيئة السمات:

        self.xs, freqs = zip(*sorted(dw.Items()))
        self.ps = np.cumsum(freqs, dtype=np.float)
        self.ps /= self.ps[-1]

تمثِّل xs قائمةً مرتّبةً من القيم وتمثِّل freqs قائمة الترددات الموافقة للقيم الموجودة في xs.

يحسب التابع np.cumsum المجموع التراكمي للترددات علمًا أنّ التقسيم على التردد الكلي يُنتِج الاحتمالات التراكمية، كما يتناسب وقت بناء الصنف Cdf مع n logn في حال كان عدد القيم يساوي n.

إليك تنفيذ التابع Prob الذي يأخذ قيمةً ويُعيد الاحتمال التراكمي:

# class Cdf
    def Prob(self, x):
        if x < self.xs[0]:
            return 0.0
        index = bisect.bisect(self.xs, x)
        p = self.ps[index - 1]
        return p

تزوّدنا الوحدة bisect بتنفيذ البحث الثنائي، وإليك تنفيذ التابع Value الذي يأخذ الاحتمال التراكمي ويُعيد القيمة الموافقة:

# class Cdf
    def Value(self, p):
        if p < 0 or p > 1:
            raise ValueError('p must be in range [0, 1]')

        index = bisect.bisect_left(self.ps, p)
        return self.xs[index]

يمكننا حساب Pmf في حال كان لدينا Cdf عن طريق حساب الفروقات بين احتمالين تراكميَّين متتاليين، وإذا استدعينا باني Cdf ومررنا له Pmf، فسيحسب الفروقات عن طريق استدعاء Cdf.Items كما يلي:

# class Cdf
    def Items(self):
        a = self.ps
        b = np.roll(a, 1)
        b[0] = 0
        return zip(self.xs, a-b)

يُزيح التابع np.roll قيمًا من a إلى اليمين ويُدحرج القيمة الأخيرة إلى البداية، كما نستبدل القيمة 0 بالعنصر الأول من b ثم نحسب الفرق a-b، وتكون النتيجة هي مصفوفة نمباي NumPy من الاحتمالات.

يزوِّدنا Cdf بالتابعَين Shift وScale الذين يعدِّلان القيم الموجودة في Cdf إلا أنه يجب التعامل مع الاحتمالات على أنها قيم ثابتة غير قابلة للتبديل أو التعديل.

العزوم moments

عندما نأخذ عيّنةً ونحولّها إلى عدد منفرد أي نقلّصها، سينتج لدينا ما يُعرف بالإحصائية، وقد رأينا عدة إحصائيات حتى الآن، منها المتوسط mean والتباين variance والوسيط median والانحراف الربيعي interquartile range.

يُعِدّ العزم الخام raw moment نوعًا من أنواع الإحصائيات، فإذا كانت لديك إحصائية تحوي قيمًا عددها x_i‎ فستكون الصيغة الرياضية للعزم الخام رقم k أي kth raw moment كما يلي:

m′_k =

∑

x_i^k

أو إذا كنت تفضِّل صيغة بايثون، فهذه هي الشيفرة الموافقة:

def RawMoment(xs, k):
    return sum(x**k for x in xs) / len(xs)

وفي حال كنا نريد إيجاد العزم الأول أي k=1 ستكون النتيجة هي متوسط العيّنة x̄، وفي الواقع لا تفيدنا العزوم الخام لوحدها إلّا أنها تُستخدَم في بعض أنواع الحسابات.

تُعَدّ العزوم المركزية أكثر فائدةً من العزوم الخام، وتكون الصيغة الرياضية للعزم المركزي ذو الرقم k كما يلي:

m_k =

∑

(x_i − x)^k

أمّا الشيفرة الموافقة في بايثون فتكون كما يلي:

def CentralMoment(xs, k):
    mean = RawMoment(xs, 1)
    return sum((x - mean)**k for x in xs) / len(xs)

إذا كانت k=2 فستكون النتيجة هي العزم المركزي الثاني، أي ما يُعرَف بالتباين variance، وقد يفيدنا التعريف الخاص بالتباين في معرفة السبب وراء تسمية هذه الإحصائيات بالعزوم، حيث إذا ثبّتنا ثقلًا على طول مسطرة في كل موقع x_i‎ ومن ثم دوّرنا المسطرة حول المتوسط mean، فسيكون عزم العطالة -أو عزم القصور الذاتي- مساويًا لتباين القيم، وإذا لم تكن لديك فكرةً مسبقةً عن عزم العطالة، فيمكنك الاطلاع على معنى عزم القصور الذاتي.

من المهم وضع واحدات القياس في الحسبان عند التعامل مع الإحصائيات المبنية على العزوم، فإذا كانت القيم x_i‎ مقدَّرةً بالسنتيمتر، فسيكون العزم الخام الأول مقدَّرًا بالسنتيمتر أيضًا، لكن يكون العزم الثاني مقدَّرًا بالسنتيمتر مربّع أي cm²‎، ويكون العزم الثالث مقدَّرًا بالسنتيمتر مكعَّب أي cm³‎ وهكذا.

وبسبب هذه الواحدات فإنه من الصعب تفسير وفهم العزوم لوحدها، لذا عادةً ما يُحسب الانحراف المعياري عند ذكر العزم الثاني، حيث يمكن حساب الانحراف المعياري عن طريق تطبيق الجذر التربيعي على التباين، لذا فهو يُقدَّر واحدات قياس x_i‎ نفسها. 8

معامل التجانف Skewness

التجانف skewness هو خاصية تصف شكل التوزيع، فإذا كان التوزيع متناظرًا حول النزعة المركزية central tendency سنقول أنّه غير متجانف unskewed، وإذا كانت القيم ممتدة إلى أقصى اليمين فسيكون متجانفًا إلى اليمين؛ أما إن كانت ممتدة إلى أقصى اليسار فسيكون متجانفًا إلى اليسار.

لا يدل في الواقع استخدام كلمة متجانف skewed على المعنى المعتاد منحازة biased، حيث يصف التجانف شكل التوزيع فقط ولا يذكر أيّ معلومات حول ما إن كانت عملية أخذ العيّنات منحازةً أم لا.

عادةً ما يتم حساب كمية تجانف -أو انحراف- توزيع معيّن عن طريق استخدام عدة أنواع من الإحصائيات، فإذا كان لدينا تسلسل من القيم x_i‎، فيمكننا حساب تجانف العيّنة sample skewness التي يرمز لها g₁ بالصورة التالية:

def StandardizedMoment(xs, k):
    var = CentralMoment(xs, 2)
    std = math.sqrt(var)
    return CentralMoment(xs, k) / std**k

def Skewness(xs):
    return StandardizedMoment(xs, 3)

يكون g₁ هو العزم القياسي standardized moment الثالث، أي أنه وُحِّد normalized ولذلك ليس له واحدات قياس.

يدل التجانف السالب على أنّ التوزيع متجانف إلى اليسار -أي منحرف نحو اليسار-؛ أمّا التجانف الموجب فيدل على أنّ التوزيع متجانف إلى اليمين -أي منحرف نحو اليمين-، كما يدل مقدار g_{1‎ على قوة التجانف إلا أنه ليس من السهل تفسيره لوحده.}

بالنظر إلى الجانب العملي يمكننا القول إن حساب عيّنة التجانف sample skewness ليست فكرةً سديدةً في أغلب الأحيان، إذ يخلق وجود القيم الشاذة outliers تأثيرًا غير متناسب على g_1‎.

توجد طريقة أخرى لتقييم لاتناظر توزيع معيّن من خلال دراسة العلاقة بين المتوسط والوسيط، حيث تؤثِّر القيم المتطرِّفة على المتوسط أكثر مما تؤثره على الوسيط، لذا يكون المتوسط أقل من الوسيط في التوزيعات التي تتجانف إلى اليسار، ويكون المتوسط أكبر من الوسيط في التوزيعات التي تتجانف إلى اليمين.

يُعدّ معامل التجانف المتوسط لبيرسون Pearson’s median skewness coefficient مقياسًا للتجانف يعتمد على الفرق بين متوسط العيّنة والوسيط، وتكون الصيغة الرياضية له كما يلي:

g_p = 3 (x − m) / S

حيث يكون x̄ متوسط العيّنة وm هي الوسيط وS هي الانحراف المعياري، وتكون شيفرة بايثون كما يلي:

def Median(xs):
    cdf = thinkstats2.Cdf(xs)
    return cdf.Value(0.5)

def PearsonMedianSkewness(xs):
    median = Median(xs)
    mean = RawMoment(xs, 1)
    var = CentralMoment(xs, 2)
    std = math.sqrt(var)
    gp = 3 * (mean - median) / std
    return gp

تُعَدّ الإحصائية متينةً robust أي أنها أقل عرضة لتأثير القيم الشاذة outliers.

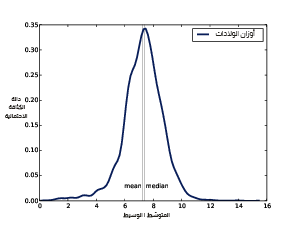
يوضِّح الشكل السابق دالة الكثافة الاحتمالية PDF المقدَّرة لبيانات أوزان المواليد من المسح الوطني لنمو الأسرة NSFG.

سنرى مثالًا عن هذا وهو تجانف أوزان المواليد في بيانات حالات الحمل الموجودة في المسح الوطني لنموّ الأسرة NSFG، وفيما يلي الشيفرة التي ترسم دالة الكتلة الاحتمالية وتقدِّرها:

    live, firsts, others = first.MakeFrames()
    data = live.totalwgt_lb.dropna()
    pdf = thinkstats2.EstimatedPdf(data)
    thinkplot.Pdf(pdf, label='birth weight')

يُظهِر الشكل السابق النتيجة، حيث يبدو الذيل الأيسر أطول من الذيل الأيمن لذا قد نعتقد أنّ التوزيع متجانفًا إلى اليسار، كما نجد أنّ المتوسط الذي يقدَّر بحوالي 3.29 كيلوغرامًا أي 7.27 رطلًا هو أقل من الوسيط الذي يقدَّر بحوالي 3.34 كيلوغرامًا أي 7.38 رطلًا، لذلك يتناسب هذا مع التجانف إلى اليسار، كما نجد أنّ معاملَي التجانف سالبان، حيث تكون قيمة عيّنة التجانف-0.59، وقيمة معامل التجانف المتوسط لبيرسون هو -0.23.

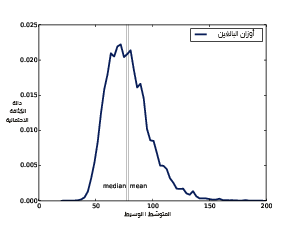
يوضِّح الشكل السابق دالة الكثافة الاحتمالية المقدَّرة لبيانات أوزان البالغين من نظام مراقبة عوامل المخاطر السلوكية BRFSS؛ أما الآن فسنوازن بين هذا التوزيع وبين توزيع أوزان البالغين في نظام مراقبة عوامل المخاطر السلوكية BRFSS، وفيما يلي الشيفرة الموافقة لذلك:

    df = brfss.ReadBrfss(nrows=None)
    data = df.wtkg2.dropna()
    pdf = thinkstats2.EstimatedPdf(data)
    thinkplot.Pdf(pdf, label='adult weight')

يُظهر الشكل السابق النتيجة، حيث يبدو التوزيع متجانفًا إلى اليمين، وبالطبع يكون المتوسط الذي يقدَّر بحوالي 35.8338 كيلوغرامًا أي 79.0 رطلًا أكبر من الوسيط الذي يقدَّر بحوالي 35.06269 كيلوغرامًا أي 77.3 رطلًا، كما تكون عيّنة التجانف هي 1.1، ومعامل التجانف المتوسط لبيرسون هو 0.26.

يمكننا الاستنتاج من إشارة مُعامِل التجانف ما إذا كان التوزيع متجانفًا إلى اليمين أو إلى اليسار، لكن من الصعب تفسيرها بخلاف ذلك.

تُعَد عيّنة التجانف أقل متانةً أي أنها أكثر عرضةً لتأثير القيم الشاذة، ونتيجةً لذلك فإنّ العيّنة أقل موثوقيةً عند تطبيقها على التوزيعات المتجانفة، أي هي غير موثوقة كثيرًا في أكثر وقت نحتاجها فيه بأن تكون موثوقة.

يعتمد معامِل التجانف المتوسط لبيرسون على المتوسط والتباين المحسوبَين، لذا فهو أكثر عرضةً لتأثير القيم الشاذة، لكن بما أنه لا يعتمد على عزم ثالث فهو أكثر متانةً إلى حد ما.

تمارين

يوجد حل هذا التمرين في chap06soln.py في مستودع ThinkStats2 على GitHub.

تمرين 1

من المعروف أن توزيع الدخل يتجانف إلى اليمين، لذا سنقيس في هذا التمرين مدى قوة هذا التجانف.

يُعَدّ المسح السكاني الحالي Current Population Survey -أو CPS اختصارًا- جهدًا مشتركًا بين مكتب إحصاءات العمل ومكتب التعداد لدراسة الدخل والمتغيرات ذات الصلة، كما أنّ البيانات التي جُمعَت في عام 2013 متاحة في census.gov.

حمّلنا ملف hinc06.xls وهو جدول بيانات إكسل يحتوي على معلومات حول دخل الأسر المعيشية، ومن ثم حولناه إلى hinc06.csv وهو ملف من النوع CSV يمكنك إيجاده في مستودع هذا الكتاب، كما ستجد hinc2.py الذي يقرأ الملف السابق ويحوِّل بياناته.

تتخذ مجموعة البيانات شكل سلسلة مجالات الدخل وعدد المستجيبين الموجودين في كل مجال، إذ يشمل المجال الأدنى المستجيبين الذين أفادوا بأن دخل الأسر المعيشية في السنة أقل من 5000 دولارًا أمريكيًا، في حين يشمل المجال الأعلى المستجيبين الذين يكسبون 250000 دولارًا أمريكيًا أو أكثر.

لتقدير المتوسط والإحصائيات الأخرى الخاصة من هذه البيانات علينا وضع بعض الافتراضات بما يخص الحدود الدنيا والعليا وبما يخص توزيع القيم في كل مجال.

يزوِّدنا hinc2.py بالتابع InterpolateSample الذي ينمذج البيانات بإحدى الطرق المتاحة، حيث يأخذ إطار بيانات DataFrame مع عمود، وincome الذي يحتوي القيمة العليا لكل مجال، وfreq الذي يحوي عدد المستجيبين في كل إطار، وlog_upper وهي القيمة العليا المفترضة على المجال الأعلى ويُعبَّر عنها كما يلي: log10 دولارًا -أي نحسب اللوغاريتم العشري للقيمة بالدولار-.

تمثِّل القيمة الافتراضية log_upper=6.0‎ الافتراض الذي يقول أن الدخل الأعلى ضمن المستجيبين هو 10‎⁶‎ أي مليون دولار.

اقتباس

توضيح: log10(10‎⁶)=6.0).

يولّد InterpolateSample عيّنةً وهميةً pseudo-sample، أي عيّنةً من مداخيل (جمع دخل) الأسر المعيشية تحتوي على عدد المستجيبين نفسه الموجود في كل مجال البيانات الفعلية، كما تفترض العيّنة الوهمية أن جميع المداخيل في كل مجال تبعد عن بعضها مسافات متساوية على مقياس log10. احسب الوسيط والمتوسط والتجانف وتجانف بيرسون للعيّنة الناتجة، وما هي نسبة الأسر المعيشية التي يكون دخلها الخاضع للضريبة أقل من المتوسط؟ وكيف تعتمد النتائج على الحد الأعلى upper bound المفترَض؟

ترجمة -وبتصرف- للفصل Chapter 6 Probability density functions analysis من كتاب Think Stats: Exploratory Data Analysis in Python.