تناولنا في المقالات السابقة كل متغير على حدة وسنناقش العلاقات بين المتغيرات في هذا الفصل، حيث نقول عن متغيرين أنهما مرتبطان إذا استطعت استنباط معلومات عن أحدهما لمجرّد علمك بالمتغير الآخر، إذ يُعَدّ الطول والوزن مثلًا متغيرَين مرتبطَين، فعادةً ما يكون الأشخاص الأطول هم الأكثر وزنًا من غيرهم، لكنها بالطبع ليست علاقةً مثاليةً، إذ يوجد بعض الأشخاص الذين لا يتمتعون بطول كبير لكنّ وزنهم مرتفع، كما يوجد بعض الأشخاص النحيلين والطوال، لكن إذا حاولت تخمين وزن شخص ما، فستكون إجابتك أكثر دقةً إذا علمت طوله.
يمكنك الحصول على الشيفرة الخاصة بهذا المقال في scatter.py في مستودع ThinkStats2 على GitHub.
مخططات الانتشار Scatter plots
تتمثل أسهل طريقة للتحقق مما إذا كان هناك علاقةً بين متغيرَين في إنشاء مخطط انتشار scatter plot، لكن رسم مخطط انتشار جيّد ليس بالمهمة السهلة.
سنرسم مخطط الأوزان مقابل الأطوال للمستجيبين في نظام مراقبة عوامل المخاطر السلوكية BRFSS على أساس مثال على ذلك، كما يمكنك الاطلاع على قسم التوزيع اللوغاريتمي الطبيعي في مقال نمذجة التوزيعات Modelling distributions في بايثون.
إليك الشيفرة التي تقرأ ملف البيانات وتستخرج الطول والوزن:
df = brfss.ReadBrfss(nrows=None) sample = thinkstats2.SampleRows(df, 5000) heights, weights = sample.htm3, sample.wtkg2
يختار التابع SampleRows مجموعةً جزئيةً عشوائيةً من البيانات كما يلي:
def SampleRows(df, nrows, replace=False): indices = np.random.choice(df.index, nrows, replace=replace) sample = df.loc[indices] return sample
يشير df إلى إطار البيانات DataFrame، في حين يشير nrows إلى عدد الأسطر المختارة، كما يُعَدّ replace متغيرًا بوليانيًا يخبرنا عما إذا كانت عملية أخذ العيّنات sampling ستكون مع الاستبدال أم لا، أي إذا كان بالإمكان اختيار الأسطر نفسها أكثر من مرة.
تزوِّدنا thinkplot بالتابع Scatter الذي ينشئ مخططات انتشار، وفيما يلي الشيفرة الموافقة:
thinkplot.Scatter(heights, weights) thinkplot.Show(xlabel='Height (cm)', ylabel='Weight (kg)', axis=[140, 210, 20, 200])
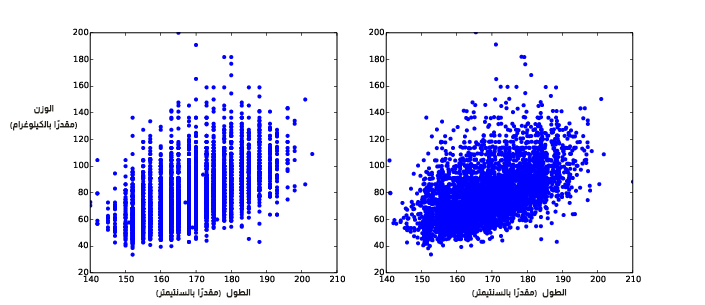
تظهر النتيجة الموجودة في الشكل التالي من الجهة اليسرى شكل العلاقة، وكما هو متوقع فإنّ الأشخاص الذين يتمتعون بطول عالٍ يميلون لأن يكونوا أكثر وزنًا.
يوضِّح الشكل السابق مخططات الانتشار للأوزان مقابل الأطوال للمستجيبين BRFSS، مع العلم أنه غير عشوائي في الجهة اليسرى وعشوائي في الجهة اليمنى.
لا يُعَدّ هذا أفضل تمثيل للبيانات لأنها محزَّمة ضمن أعمدة، وتكمن المشكلة في كون الأطوال مُقرّبة إلى أقرب بوصة inch ثم حُوِّلت إلى سنتيمترات، وبعدها قُرِّبت مرةً أخرى، وبالتالي ققد ضاعت بعض المعلومات بسبب العمليات السابقة.
لا يمكننا استرجاع المعلومات المفقودة في الواقع، إلّا أنه يمكننا تقليل الأثر على مخططات الانتشار عن طريق عشوائية (أو قلقلة jittering) البيانات، أي إضافة ضجيج عشوائي عليها لعكس أثر التقريب.
بما أنه طُبِّقَت عملية تقريب لأقرب بوصة على هذه القيم، فمن المحتمل أن تكون بعيدةً عن القيم الأصلية بمقدار 0.5 بوصة أو 1.3 سنتيمتر، وكذلك الأمر بالنسبة للأوزان التي يمكن أن تكون بعيدةً عن القيم الأصلية بمقدار 0.5 كيلوغرامًا.
heights = thinkstats2.Jitter(heights, 1.3) weights = thinkstats2.Jitter(weights, 0.5)
إليك تنفيذ التابع Jitter:
def Jitter(values, jitter=0.5): n = len(values) return np.random.uniform(-jitter, +jitter, n) + values
يمكن أن تنتمي القيم إلى أي تسلسل لكن ستكون النتيجة مصفوفة NumPy حتمًا.
يُظهر الشكل السابق في الجهة اليمنى النتيجة، حيث تقلل العشوائية jittering الأثر المرئي للتقريب ويوضِّح شكل العلاقة، لكن من المهم الانتباه إلى وجوب اللجوء إلى قلقلة (عشوائية) البيانات في حال كنت تريد عرضها فقط، كما يجب الابتعاد عن استخدام البيانات العشواء (المُقلقلة) من أجل التحليل، ولكن مع ذلك فلا يُعَدّ التذبذب أفضل طريقة لتمثيل البيانات، حيث يوجد العديد من النقاط المتداخلة التي تخفي البيانات في الأجزاء الكثيفة من الشكل وتعطي تركيزًا غير متناسب على القيم الشاذة، ويُدعى هذا التأثير بالإشباع saturation.
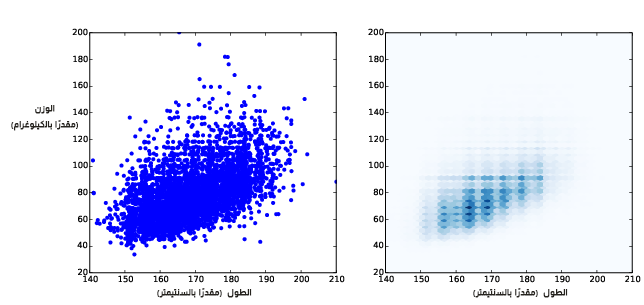
يوضِّح الشكل السابق مخطط الانتشار مع عشوائية وشفافية في الجهة اليسرى، ومخطط هيكسبين في الجهة اليمنى.
يمكننا حل هذه المشكلة باستخدام المعامِل alpha الذي يجعل النقاط شفافةً إلى حد ما، وتكون التعليمة الموافقة كما يلي:
thinkplot.Scatter(heights, weights, alpha=0.2)
يُظهِر الشكل السابق في الجهة اليسرى النتيجة، حيث تبدو نقاط البيانات المتداخلة أقتم من غيرها، أي يتناسب القتامة darkness مع الكثافة.
نرى في هذا المخطط تفصيلِين اثنين لم يظهرا سابقًا، حيث يكون التفصيل الأول هو عناقيد عمودية عند أطوال مختلفة، والتفصيل الثاني هو خط أفقي قريب من الوزن 90 كيلوغرام أو 200 رطل.
بما أن هذه البيانات تستند إلى تقارير ذاتية بالأرطال، فمن المرجَّح أن بعض المستجيبين قد طبقوا عملية تقريب على القيم. عادةً ما تكون الشفافية مناسبةً لمجموعات البيانات متوسطة الحجم، إلا أنّ هذا الشكل لا يُظهر سوى أول 5000 سجل في BRFSS من أصل 414509 سجل.
يُعَدّ مخطط هيكسبين hexbin plot أحد الخيارات المطروحة للتعامل مع مجموعات البيانات الأكبر حجمًا، فهو يقسم المخطط graph إلى صناديق سداسية، ويلوِّن كل صندوق بلون مختلف حسب عدد نقاط البيانات الموجودة فيه، كما توفِّر thinkplot التابع HexBin:
thinkplot.HexBin(heights, weights)
يُظهر الشكل السابق في الجهة اليمنى النتيجة، وتتمثل إحدى ميّزات مخطط هيكسبين في توضيح شكل العلاقة جيدًا، كما أنه فعّال في حالة مجموعات البيانات الكبيرة بالنسبة للزمن ولحجم الملف الذي يولده، إلّا أنه لا يُظهر القيم الشاذة.
استعرضنا هذا المثال لهدف أساسي ألا وهو توضيح عدم سهولة إنشاء مخطط انتشار يوضِّح العلاقات دون ظهور عناصر مضلّلة.
توصيف العلاقات
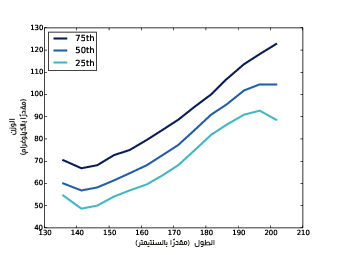
تُعطينا مخططات الانتشار انطباعًا عامًا عن العلاقة بين المتغيرات، إلّا أنه يوجد أنواع أخرى من المخططات التي تزودنا بمعلومات أكثر تفصيلًا عن طبيعة العلاقة، إذ يمكننا مثلًا فرز أو تصنيف متغير واحد ورسم مئين percentile المتغير الآخر.
تزوّدنا مكتبتي نمباي NumPy وبانداز pandas بدوال لتصنيف البيانات binning data كما يلي:
df = df.dropna(subset=['htm3', 'wtkg2']) bins = np.arange(135, 210, 5) indices = np.digitize(df.htm3, bins) groups = df.groupby(indices)
تحذف dropna الأسطر التي تحوي قيمة nan -أي ليس عددًا- في أيّ عمود مُدرَج، وتنشئ الدالة arange مصفوفة نمباي NumPy تحوي صناديق bins من 135 إلى 210 دون احتساب القيمة 210 بفارق 5 بين الصندوق والآخر، كما تحسب digitize فهرس الصندوق الذي يحوي كل قيمة في df.htm3، وتكون النتيجة مصفوفة نمباي NumPy من فهارس الأعداد الصحيحة، بحيث تكون فهارس القيم التي تقل عن أصغر صندوق هي 0، في حين تكون فهارس القيم التي تزيد عن أعلى صندوق هي len(bins).
يوضِّح الشكل السابق قيم المئين للوزن بمجال صناديق الأطوال. يُعيد تابع من إطار البيانات groupby كائن GroupBy وهو يُستخدَم في حلقة for؛ أما التابع groups فهو يمر بالترتيب على أسماء المجموعات في أُطُر البيانات التي تمثّلها، أي يمكننا مثلًا طباعة عدد الأسطر في كل مجموعة بالصورة التالية:
for i, group in groups: print(i, len(group))
يمكننا الآن حساب متوسط الطول لكل مجموعة بالإضافة إلى دالة التوزيع التراكمي للوزن:
heights = [group.htm3.mean() for i, group in groups] cdfs = [thinkstats2.Cdf(group.wtkg2) for i, group in groups]
يمكننا أخيرًا رسم قيم المئين للوزن مقابل الطول كما يلي:
for percent in [75, 50, 25]: weights = [cdf.Percentile(percent) for cdf in cdfs] label = '%dth' % percent thinkplot.Plot(heights, weights, label=label)
يُظهر الشكل السابق النتيجة، حيث تكون العلاقة بين المتغيرات من 140 إلى 200 سنتيمتر خطيّةً تقريبًا، حيث يحوي هذا المجال أكثر من نسبة 99% من البيانات، لذا ليس علينا القلق بشأن القيم المتطرفة.
الارتباط Correlation
الارتباط هو إحصائيّة هدفها تحديد قوة العلاقة بين متغيرَين، لكن في أغلب الأحيان تختلف واحدات قياس الارتباط بين المتغيرات التي نرغب بموازنتها، مما يخلق لنا تحديًا يواجهنا عند قياس الارتباط، وفي الواقع يكون مصدر هذه المتغيرات غالبًا توزيعات مختلفة حتى عندما تمتلك واحدت القياس نفسها.
فيما يلي بعض الحلول الشائعة لهذه المشاكل:
- حوِّل كل قيمة إلى درجة معيارية standard score التي هي عدد الانحرافات المعيارية عن المتوسط، حيث ينتج عن هذا التحويل "معامل ارتباط بيرسون الناتج عن العزوم".
- حوِّل كل قيمة إلى رتبتها rank التي هي الفهرس الخاص بها في القائمة المرتبة من القيم، حيث ينتج عن هذا التحويل مُعامل ارتباط سبيرمان Spearman rank correlation coefficient.
إذا كانت X سلسلةً series من n قيمة وكل قيمة فيها هي xi، فسيمكننا تحويلها إلى درجاتها المعيارية عن طريق طرح المتوسط منها والتقسيم على الانحراف المعياري، بحيث تكون المعادلة بالصورة: zi=(xi-μ)/σ ، مع العلم أنّ البسط هو انحراف المسافة عن المتوسط، وتؤدي القسمة على σ إلى تقييس الانحراف standardizes the deviation، وبالتالي تكون قيم Z بلا أبعاد -أي ليس لها واحدات قياس- ويكون متوسط توزيعها مساوويًا للصفر وتباينه مساويًا للواحد.
إذا كان توزيع قيم X طبيعيًا، فسيكون توزيع قيم Z طبيعيًا أيضًا، لكن إذا كان X متجانفًا skewed أو يحوي قيمًا شاذةً، فسيكون Z مثل X، وفي هذه الحالات يكون استخدام رتب المئين percentile ranks أكثر متانةً، لكن إذا حسبنا متغيرًا جديدًا هو R بحيث يكون ri رتبة xi، فسيكون توزيع R موحَّدًا uniform من 1 إلى n بغض النظر عن ماهية توزيع X.
التغاير Covariance
يُعَدّ التغاير مقياسًا لمَيل المتغيرين إلى الاختلاف معًا بحيث إذا كان لدينا سلسلتين X وY، فسيكون انحرافهما عن المتوسط كما يلي:
- dxi=xi-x̄
- dyi=yi-ȳ
بحيث تكون x̄ متوسط عيّنة X وȳ هي متوسط عيّنة Y، وإذا كانت العيّنتان X وY متغايرتان معًا، فسيملك انحرافهما الإشارة ذاتها.
إن ضربنا انحرافي العيّنتين ببعضهما، فسيكون الناتج موجبًا في حال كان لهما الإشارة ذاتها، في حين سيكون سالبًا إذا كان لهما إشارة متعاكسة، لذا يمكننا القول أنّ جمع النواتج يعطي قياسًا لميل العيّنتين للتغاير معًا.
يكون التغاير هو متوسط هذه النواتج:
| Cov(X,Y) = |
|
∑dxi dyi |
حيث يكون n طول السلسلتين ويجب أن يكون لهما الطول نفسه.
إذا درستَ الجبر الخطي، لا بد أنّك تدرك أن Cov هي حاصل الضرب القياسي dot product للانحرافات مقسومًا على طولها، لذا يكون التغاير في حده الأقصى إذا كان المتجهان متطابقَين تمامًا، و0 إذا كانا متعامدين، وسالبًا إذا أشارا إلى اتجاهين متعاكسين.
تزوِّدنا thinkstats2 بالتابع np.dot لتنفيذ Cov تنفيذًا فعالًا، وإليك الشيفرة الموافقة لذلك:
def Cov(xs, ys, meanx=None, meany=None): xs = np.asarray(xs) ys = np.asarray(ys) if meanx is None: meanx = np.mean(xs) if meany is None: meany = np.mean(ys) cov = np.dot(xs-meanx, ys-meany) / len(xs) return cov
يحسب Cov في الحالة الافتراضية الانحرافات من متوسطات العيّنة، أو بإمكانك تزويده بالمتوسطات المعلومة.
إذا كانتا xs وys تسلسلي بايثون، فسيحوِّلهما التابع np.asarray إلى مصفوفتي نمباي NumPy، وبطبيعة الحال لا يغيّر np.asarray شيئًا إذا كانتا xs وys مصفوفتي نمباي NumPy.
تقصّدنا أن يكون تنفيذ التغاير هذا بسيطًا لأنّ هدفنا هو الشرح فحسب، كما توفر كل من نمباي NumPy وبانداز pandas أيضًا تنفيذات للتغاير لكن كلاهما يطبِّق تصحيحًا لأحجام العينات الصغيرة التي لم نحوِّلها بعد، كما تُعيد np.cov مصفوفة التغاير covariance matrix التي تكفينا الآن.
ارتباط بيرسون Pearson’s correlation
يُعَدّ التغاير مفيدًا في بعض الحسابات، ولكن نادرًا ما يتم وضعه في الإحصائيات الموجزة لأنه من الصعب تفسيره، فهو يعاني من بعض المشاكل منها أنّ واحدة قياسه هي ناتج واحدات X و Y. فمثلًا، يكون تغاير الطول والوزن في BRFSS هو 113 كيلوغرام-سنتيمترات على الرغم أنها ليست منطقية تمامًا.
يمكن حل هذه المشكلة بعدة طرق منها تقسيم الانحرافات على الانحراف المعياري التي تحقق درجات معيارية وتحسب ناتج درجات معيارية كما يلي:
| pi = |
|
|
يكون SX وSY الانحرافَين المعياريَين لكل من X وY، كما يكون متوسط هذه النواتج كما يلي:
| ρ = |
|
∑pi |
يمكننا إعادة كتابة ρ عن طريق أخذSX وSY في الحسبان لينتج لدينا المعادلة التالية:
| ρ = |
|
سميت هذه القيمة بارتباط بيرسون Pearson’s correlation تيمّنًا بكارل بيرسون عالم الإحصاء الرائد، وفي الواقع فمن السهل حسابه وتفسيره أيضًا لأنّ الدرجات المعيارية وρ بلا أبعاد.
إليك التنفيذ في thinkstats2:
def Corr(xs, ys): xs = np.asarray(xs) ys = np.asarray(ys) meanx, varx = MeanVar(xs) meany, vary = MeanVar(ys) corr = Cov(xs, ys, meanx, meany) / math.sqrt(varx * vary) return corr
يحسب MeanVar المتوسط والتباين بصورة فعّالة أكثر من الاستدعاء المنفصل للتابعين np.mean وnp.var.
دائمًا ما يكون ارتباط بيرسون بين القيمتين 1- و 1+ متضمنًا هاتين القيمتين، وإذا كان ρ موجبًا فنقول أنّ الارتباط موجب ويعني هذا أنه إذا كانت قيمة أحد المتغيرَين عالية، فستكون قيمة الآخر عاليةً أيضًا؛ أما إذا كان ρ سالبًا فنقول أنّ الارتباط سالب ويعني هذا أنه إذا كانت قيمة أحد المتغيرَين عالية، فستكون قيمة الآخر منخفضةً.
يشير حجم ρ إلى قوة الارتباط، حيث إذا كانت تساوي 1 أو 1- فسيكون المتغيرين مرتبطَين تمامًا، مما يعني أنه إذا كنت تعرف أحد المتغيرين فسيصبح بإمكانك تنبؤ الآخر بصورة صحيحة.
على الرغم من أن معظم الارتباطات في العالم الحقيقي غير مثالية إلا أنها مفيدة، كما أنّ الارتباط بين الطول والوزن هو 0.51 والذي يُعَدّ ارتباطًا قويًا موازنةً بالمتغيرات المماثلة المتعلقة بالإنسان.
العلاقات اللاخطية Nonlinear relationships
قد نعتقد أنه لا يوجد علاقة بين المتغيرات إذا كان مُعامِل ارتباط بيرسون يقارب الصفر، إلا أنّ هذا ليس صحيحًا، حيث يقيس ارتباط بيرسون العلاقات الخطية فقط، وفي حال وجود علاقة لاخطية فلا يقيس ρ قوتها قياسًا صحيحًا.
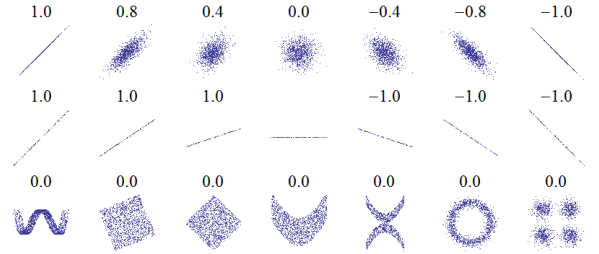
يوضِّح الشكل السابق أمثلةً عن مجموعات البيانات مع مجال متنوع من الارتباطات فيما بينها، ومصدر هذا الشكل من صفحة Correlation، حيث يُظهِر مخططات الانتشار ومعامِلات الارتباطات لعدة مجموعات بيانات مبنيّة بعناية.
يُظهِر الصف العلوي العلاقات الخطية مع مجال من الارتباطات، علمًا أنه يمكنك استخدام هذا الصف لمعرفة كيف تبدو القيم المختلفة لـ ρ؛ أمّا الصف الثاني فيُظهر ارتباطات مثاليّة مع مجال متنوع من قيم الميل، مما يشير إلى أنّ الارتباط لا علاقة له بالميل -وسنتحدث عن تقدير الميل قريبًا-، كما يُظهِر الصف الثالث متغيرات مرتبطة ارتباطًا واضحًا، ولكن معامِل الارتباط هو 0 نظرًا لكَون العلاقة لاخطيةً.
يمكننا القول أنّ المغزى من هذه القصة هو أنه عليك الاطلاع على مخطط انتشار بياناتك قبل حساب معامِل الارتباط دون الانتباه لأي شيء.
معامِل ارتباط سبيرمان حسب الرتب
يؤدي مُعامِل بيرسون عمله جيّدًا إن كانت العلاقات بين المتغيرات خطية وإذا كانت المتغيرات طبيعيةً إلى حد ما، إلا أنه ليس متينًا في حال وجود قيم شاذة.
يعَدّ معامِل ارتباط سبيرمان حسب الرتب Spearman’s rank correlation بديلًا يخفف من تأثير القيم الشاذة والتوزيعات المتجانفة skewed distributions، إذ يمكننا حساب ارتباط سبيرمان عن طريق حساب رتبة كل قيمة والتي هي فهرس القيمة في العيّنة المرتّبة. فمثلًا، لدينا فتكون رتبة القيمة 5 في العيّنة [7, 5, 2, 1] هي 3 لأن ترتيبها في القائمة المرتبة هو الثالث، ومن ثم نحسب ارتباط بيرسون لهذه الرُتب.
تزودنا thinkstats2 بدالة تحسب معامِل ارتباط سبيرمان للرتب كما يلي:
def SpearmanCorr(xs, ys): xranks = pandas.Series(xs).rank() yranks = pandas.Series(ys).rank() return Corr(xranks, yranks)
حوَّلنا الوسائط arguments إلى كائنات سلسلة بانداز pandas Series لكي نستطيع استخدَام rank وهي تحسب رتبة كل قيمة وتُعيد سلسلةً، ومن ثم استخدمنا Corr لحساب ارتباط الرتب.
كما يمكننا أيضًا استخدام Series.corr مباشرةً ومن ثم تحديد تابع سبيرمان كما يلي:
def SpearmanCorr(xs, ys): xs = pandas.Series(xs) ys = pandas.Series(ys) return xs.corr(ys, method='spearman')
مع العلم أن معامِل ارتباط سبيرمان للرتب لبيانات BRFSS هي 0.54، وهي أعلى بقليل من ارتباط بيرسون المساوية لـ 0.51، إذ يوجد هناك عدة أسباب وراء هذا الفرق منها:
- إذا كانت العلاقة غير خطية فعادةً ما يقلل ارتباط بيرسون من قوة العلاقة.
- يمكن أن يتأثر ارتباط بيرسون -في أيّ اتجاه- إذا كان أحد التوزيعين متجانفًا أو يحتوي على قيم متطرفة، حيث تُعَدّ معامِل ارتباط سبيرمان للرتب أكثر متانةً من ارتباط بيرسون.
نعلم أنه في مثال BRFSS يكون توزيع الأوزان لوغاريتميًا طبيعيًا تقريبًا، أي أنه في حال كان التحويل لوغاريتميًّا فهو يقارب توزيعًا طبيعيًا لا تجانف فيه، كما يمكن أيضًا إلغاء أثر التجانف عن طريق حساب ارتباط بيرسون بتطبيق لوغاريتم على الوزن والطول، أي كما يلي:
thinkstats2.Corr(df.htm3, np.log(df.wtkg2)))
تكون النتيجة هي 0.53 وهي قريبة من معامِل ارتباط سبيرمان التي تقدر قيمتها بـ 0.54، أي أنها تفترض أن التجانف في توزيع الأوزان يفسّر أغلب الفروق بين ارتباط بيرسون وارتباط سبيرمان.
الارتباط والسببية
إذا كان المتغيران A وB مرتبطين فسيكون لدينا ثلاثة تفسيرات وهي أنّ A تسبب B أو B تسبب A أو مجموعة أخرى من العوامل تسبب كلاً من A وB، وتدعى هذه التفسيرات بالعلاقات السببية causal relationships.
لا يُميِّز الارتباط لوحده بين هذه التفسيرات، أي أنها لا تعطينا فكرة عن أيّ منها هو الصحيح، وغالبًا ما تُلخَّص هذه القاعدة بما يلي: "الارتباط لا يقتضي السببية" وهو قول بليغ لدرجة أنّ له صفحة ويكيبيديا خاصة به.
إذًا ماذا يمكنك أن تفعل لكي تقدِّم دليلًا على السببيّة؟
- استخدِم زمنًا: إذا أتى المتغير A قبل B فيعني هذا أنّ A سبّب B وليس العكس -وهذا على الأقل حسب فهمنا الشائع للسببية-، حيث يساعدنا ترتيب الأحداث في استنتاج اتجاه السببية، لكنه لا يستبعد احتمال أن يتسبب شيء آخر في حدوث كل من A وB.
- استخدِم عشوائيةً: إذا قسمّتَ عينةً كبيرةً إلى مجموعتين عشوائيًا وحسبت متوسط أيّ متغير تقريبًا فستتوقع أن الفرق سيكون صغيرًا، وإذا كانت المجموعات متطابقةً تقريبًا في جميع المتغيرات ما عدا متغير واحد، فسيمكنك عندئذ استبعاد العلاقات الزائفة، وهذه الطريقة مناسبة حتى لو لم تعلم ما هي المتغيرات ذات الصلة، لكن من الأفضل أن تكون على علم بهذا لأنك تستطيع عندها التحقق فيما إذا كانت المجموعات متطابقةً أم لا.
كانت هذه الأفكار هي الدافع وراء ما يُعرف بالتجربة العشوائية المنتظمة randomized controlled trial، التي يتم فيها إسناد المشاركِين إلى مجموعتين -أو أكثر-: مجموعة العلاج treatment group التي تتلقى علاجًا أو تدخّلًا من نوع ما مثل دواء جديد، ومجموعة الموازنة أو المجموعة المرجعية control group التي لا تتلقى أيّ علاج أو تتلقى علاجًا أثره معروف مسبقًا.
تُعَدّ التجربة المنتظمة التي تستخدم عينات عشوائية الطريقة الأكثر موثوقية لإثبات العلاقة السببية، وهي أساس الطب القائم على العلم انظر إلى صفحة الويكيبيديا.
لكن لسوء الحظ، فإن التجارب العشوائية المنتظمة ليست ممكنةً إلا في العلوم المختبرية والطب وعدد قليل من التخصصات الأخرى، حيث نادرًا ما تحدث في العلوم الاجتماعية لأنها مستحيلة أو غير أخلاقية.
يتمثَّل أحد البدائل في البحث عن تجربة طبيعية natural experiment، حيث تتلقى مجموعات متشابهة علاجات مختلفة، وأحد مخاطر التجارب الطبيعية هو أنّ المجموعات قد تكون مختلفةً بطرق غير واضحة لنا، ويمكنك قراءة المزيد عن هذا الموضوع هنا.
يمكننا في بعض الأحيان استنتاج العلاقات السببية باستخدام تحليل الانحدار regression analysis، وهو موضوع الفصل الحادي عشر.
تمارين
يوجد حل هذا التمرين في chap07soln.py في مستودع ThinkStats2 على GitHub.
التمرين الأول
استخدِم بيانات المسح الوطني لنمو الأسرة من أجل إنشاء مخطط انتشار لأوزان الولادات مقابل عمر الأم، ومن ثم ارسم قيم مئين أوزان الولادات مقابل عمر الأم، واحسب مُعامِل ارتباط بيرسون ومُعامِل ارتباط سبيرمان، وكيف تصف العلاقة بين هذه المتغيرات؟
ترجمة -وبتصرف- للفصل Chapter 7 Relationships between variables analysis من كتاب Think Stats: Exploratory Data Analysis in Python.












أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.