فلنعد الآن إلى الدوال ونرى أمرها بتمعّن وتعمّق أكثر. سنتكلم أولًا عن التعاود (Rescursion).
لو كنت ذا علم بالبرمجة فالأغلب أنّك تعرف ما هذا التعاود ويمكنك تخطّي هذا الفصل.
يُعدّ التعاود (Rescursion) نمطًا برمجيًا نستعمله حين يمكن تقسيم المهمة الكبيرة جدًا إلى مهام أبسط منها متشابهة، أو حين يمكن تبسيط المهمة الواحدة إلى عملية بعضها بسيط وآخر يتشابه بين بعضه، أو نستعمله (كما سنرى قريبًا) للتعامل مع أنواعٍ محدّدة من بنى البيانات.
يمكن للدالة حين تحاول إجراء مهمّة ما نداءَ دوال أخرى. أحيانًا يمكن أن تنادي تلك الدالة نفسها ثانيةً. هذا ما ندعوه بالتعاود.
نهجان في التطوير
لنبدأ بما هو أبسط. لنكتب دالة pow(x, n) ترفع x إلى الأسّ الطبيعي n. بعبارة أخرى، تضرب x بنفسه n مرّة.
pow(2, 2) = 4 pow(2, 3) = 8 pow(2, 4) = 16
يمكننا تنفيذ هذه الدالة بطريقتين اثنتين.
-
التفكير بالتكرار: حلقة
for:
function pow(x, n) { let result = 1; // نضرب الناتج في x - n مرّة داخل الحلقة for (let i = 0; i < n; i++) { result *= x; } return result; } alert( pow(2, 3) ); // 8
- التفكير بالتعاود: تبسيط المهمة ونداء «الذات»:
function pow(x, n) { if (n == 1) { return x; } else { return x * pow(x, n - 1); } } alert( pow(2, 3) ); // 8
لاحظ كيف أنّ تلك الشيفرة التعاودية مختلفة جذريًا عن سابقتها.
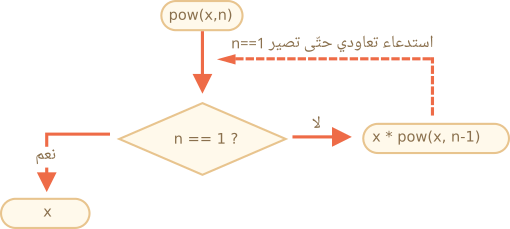
حين تُستدعى pow(x, n) تنقسم عملية التنفيذ إلى فرعين:
if n==1 = x
/
pow(x, n) =
\
else = x * pow(x, n - 1)
-
حين
n == 1، نرى كل شيء كالعادة. نسمّي تلك الحالة بأساس التعاود، لأنها تُعطينا الناتج البديهي مباشرة:pow(x, 1)تساويx. -
عدى تلك فيمكننا تمثيل
pow(x, n)على أنهاx * pow(x, n - 1). يمكنك رياضيًا كتابةx<sup>n</sup> = x * x<sup>n-1</sup>. نسمّي هذه خطوة تعاودية: فنعدّل مهمة الأس الكبيرة لتصير عملية أبسط (الضرب فيx) ونستعمل استدعاءً أبسط لمهمة الأس (powولكنnأقل). في الخطوات اللاحقة تصير أبسط وأبسط إلى أن تصلnإلى1.
يمكن أيضًا أن نقول بأن pow تستدعي نفسها تعاوديًا حتى تكون n == 1.
فمثلًا كي نحسب قيمة pow(2, 4) على التعاود إجراء هذه المهام:
1. pow(2, 4) = 2 * pow(2, 3) 2. pow(2, 3) = 2 * pow(2, 2) 3. pow(2, 2) = 2 * pow(2, 1) 4. pow(2, 1) = 2
للتلخيص، يبسّط التعاود استدعاء الدالة إلى استدعاءً آخر أبسط، وبعدها أبسط، وأبسط، وأبسط، حتّى يظهر الناتج ويصير معلومًا.
غالبًا ما تكون شيفرة التعاود أقصر عادةً ما يكون الحل باستعمال التعاود أقصر من التكرار بالحلقات.
يمكننا هنا مثلًا إعادة كتابة نفس الشيفرة ولكن باستعمال المُعامل الشرطي ? بدل if لتصير pow(x, n) أقصر أكثر وتبقى مقروءةً لنا:
function pow(x, n) { return (n == 1) ? x : (x * pow(x, n - 1)); }
يُسمّى أقصى عدد من الاستدعاءات المتداخلة (بما في ذلك أول استدعاء) بعمق التعاود (Rescursion Depth). في حالتنا هنا سيكون هذا العمق n.
يحدّ محرّك جافاسكربت من أقصى عمق تعاودي ممكن. يمكن أن نقول بأنّ 10000 هو الحدّ الذي يمكننا الاعتماد عليه (ولو أنّ بعض المحرّكات ترفع هذا الحدّ أكثر). أجل، هناك تحسينات تلقائية تحاول رفع هذا الحدّ («تحسينات نهاية الاستدعاء») ولكنّها ليست مدعومة في كلّ مكان ولا تعمل إلّا على الحالات البسيطة.
يقصّر هذا من تطبيقات استعمال التعاود، ولكنّه مع ذلك مستعمل بشدة، إذ هناك مهام كثيرة لو استعملت عليها التعاود لأعطتك شيفرة أقصر وأسهل للصيانة.
سياق التنفيذ والمكدس
لنرى الآن كيف يعمل التعاود أصلًا، ولذلك لا بدّ من أن نرى ما خلف كواليس الدوال هذه.
تُخزّن المعلومات حول عملية تنفيذ الدالة (حين تعمل) في سياقها التنفيذي (execution context). يُعدّ سياق التنفيذ بنيةَ بيانات داخلية تحوي التفاصيل التي تخصّ عملية تنفيذ الدالة: إلى أين وصلت الآن؟ ما المتغيرات الحالية؟ ما قيمة this (لا نستعملها هنا) وتفاصيل أخرى داخلية. لكلّ استدعاء دالة سياق تنفيذي واحد مرتبط بها.
حين تستدعي الدالة دوال أخرى متداخلة، يحدث:
- تتوقف الدالة الحالية مؤقتًا.
- يُحفظ سياق التنفيذ المرتبط بها في بنية بيانات خاصّة تسمى مكدس سياق التنفيذ execution context stack.
- يتنفّذ الاستدعاء المتداخل.
- ما إن ينتهي، يجلب المحرّك التنفيذ القديم ذاك من المكدس، وتواصل الدالة الخارجية عملها حيث توقفت.
لنرى ما يحدث أثناء استدعاء pow(2, 3).
pow(2, 3)
يخزّن سياق التنفيذ (في بداية استدعاء pow(2, 3)) المتغيرات هذه: x = 2, n = 3 وأنّ سير التنفيذ هو في السطر رقم 1 من الدالة.
يمكن أن نرسمه هكذا:
- السياق: { x: 2, n: 3, عند السطر 1 } pow(2, 3)
هذا ما يجري حين يبدأ تنفيذ الدالة. بعد أن يصير الشرط n == 1 خطأً، ينتقل سير التنفيذ إلى الفرع الثاني من الإفادة if:
function pow(x, n) { if (n == 1) { return x; } else { return x * pow(x, n - 1); } } alert( pow(2, 3) );
ما زالت المتغيرات كما هي، ولكن السطر تغيّر. بذلك يصير السياق الآن:
- السياق: { x: 2, n: 3, عند السطر 5 } pow(2, 3)
علينا لحساب x * pow(x, n - 1) استدعاء pow فرعيًا بالوُسطاء الجديدة pow(2, 2).
pow(2, 2)
كي يحدث الاستدعاء المتداخل، يتذكّر محرّك جافاسكربت سياق التنفيذ الحالي داخل مكدس سياق التنفيذ.
هنا نستدعي ذات الدالة pow، ولكن ذلك لا يهم إذ أنّ العملية هي ذاتها لكلّ الدوال:
- «يتذكّر المحرّك» السياقَ الحالي أعلى المكدس.
- يَصنع سياقًا جديدًا للاستدعاء الفرعي.
- متى انتهى الاستدعاء الفرعي يُطرح (pop) السياق السابق من المكدس ويتواصل التنفيذ.
هذا مكدس السياق حين ندخل الاستدعاء الفرعي pow(2, 2):
- السياق: { x: 2, n: 2, عند السطر 1 } pow(2, 2)
- السياق: { x: 2, n: 3, عند السطر 5 } pow(2, 3)
سياق التنفيذ الحالي والجديد هو الأعلى (بالخط الثخين) وأسفله السياقات التي تذكّرها المحرّك سابقًا.
حين ننتهي من الاستدعاء الفرعي يمكننا بسهولة بالغة مواصلة السياق السابق، إذ أنّ متغيراته ومكان توقف الشيفرة محفوظان بالضبط في السياق.
ملاحظة: نرى في الصورة أنّا استعملنا كلمة «سطر» إذ ليس في المثال إلّا استدعاءً فرعيًا واحدًا في السطر، ولكن يمكن أن تحتوي الشيفرات ذات السطر الواحد (بصفة عامة) على أكثر من استدعاءً فرعيًا، هكذا: pow(…) + pow(…) + somethingElse(…).
لذا سنكون أدقّ لو قلنا بأن عملية التنفيذ تتواصل «بعد الاستدعاء الفرعي مباشرةً».
pow(2, 1)
تتكرّر العملية: يُصنع استدعاء فرعي جديد في السطر 5 بالوسطاء الجديدة x=2 و n=1.
صنعنا سياقًا جديدًا، إذًا ندفع (push) الأخير أعلى المكدس:
- السياق: { x: 2, n: 1, عند السطر 1 } pow(2, 1)
- السياق: { x: 2, n: 2, عند السطر 5 } pow(2, 2)
- السياق: { x: 2, n: 3, عند السطر 5 } pow(2, 3)
الآن هناك سياقين اثنين قديمين، وواحد يعمل للاستدعاء pow(2, 1).
المخرج
نرى الشرط n == 1 صحيحًا أثناء تنفيذ الاستدعاء pow(2, 1) (عكس ما سبقه من مرّات)، إذًا فالفرع الأول من إفادة if سيعمل هنا:
function pow(x, n) { if (n == 1) { return x; } else { return x * pow(x, n - 1); } }
لا استدعاءات متداخلة من هنا، بذلك تنتهي الدالة وتُعيد 2.
وحين تنتهي الدالة لا يكون هناك حاجة لسياق التنفيذ فيُزال من الذاكرة، وبعدها يرجع السياق السابق أعلى المكدس:
- السياق: { x: 2, n: 2, عند السطر 5 } pow(2, 2)
- السياق: { x: 2, n: 3, عند السطر 5 } pow(2, 3)
يتواصل تنفيذ الاستدعاء pow(2, 2)، وفيه ناتج الاستدعاء الفرعي pow(2, 1) لذا يُنهي أيضًا تنفيذ x * pow(x, n - 1) فيُعيد 4.
بعدها يستعيد المحرّك السياقَ السابق:
- السياق: { x: 2, n: 3, عند السطر 5 } pow(2, 3)
وحين ينتهي، يكون عندنا ناتج pow(2, 3) = 8.
عمق التعاود في هذه الحالة هو: 3.
كما نرى في الصور أعلاه فعمق التعاود يساوي أقصى عدد من السياقات في المكدس.
لكن اعلم بأنّ السياقات تطلب الذاكرة. في حالتنا هنا نرفع العدد للأسّ n، وبذلك نحتاج ما يكفي من ذاكرة تسع لتخزين n سياق لكل القيم الأصغر من n.
خوارزميات الحلقات والتكرار أفضل من حيث استعمال الذاكرة:
function pow(x, n) { let result = 1; for (let i = 0; i < n; i++) { result *= x; } return result; }
تستعمل دالة pow المتكرّرة سياقًا واحدًا تغيّر فيه المتغيران i وresult أثناء عملها، كما وأنّ احتياجاتها للذاكرة قليلة وثابتة ولا تعتمد على قيمة n.
يمكن كتابة التعاودات أيًا كانت بصيغة الحلقات، وغالبًا ما تكون تلك الحلقات أفضل أداءً.
…ولكن أحيانًا ما تكون إعادة الكتابة تلك تافهة وبلا قيمة حقيقية خصوصًا حين تستعمل الدالة استدعاءاتَ دوال تعاودية تختلف حسب شروط معيّنة، أو أن تدمج الدالة نتائج الاستدعاءات أو حين يصير تفريع الدالة أصعب أكثر فأكثر. حينها سيكون ذلك التحسين من المحرّك بلا داعٍ ولا حاجة لبذل كل ذلك المجهود له.
هكذا يعطينا التعاود شيفرة أقصر سهلة الفهم ويمكننا دعمها بلا عناء. لا نحتاج إلى هذا «التحسين» في كلّ مكان؛ ما نريد هو فقط شيفرة جيدة، ولهذا نستعمل التعاود.
مسح الأشجار تعاوديًا
مسح الأشجار تعاوديًا Recursive Traversal هو تطبيق آخر عن روعة التعاود.
لنقل بأنّ لدينا شركة ويمكن أن نمثّل بنية موظّفيها في هذا الكائن:
let company = { sales: [{ name: 'John', salary: 1000 }, { name: 'Alice', salary: 600 }], development: { sites: [{ name: 'Peter', salary: 2000 }, { name: 'Alex', salary: 1800 }], internals: [{ name: 'Jack', salary: 1300 }] } };
أي أنّ في الشركة أقسام عدّة.
-
يمكن أن يحتوي كل قسم على مصفوفة من العاملين. فمثلًا لقسم المبيعات
salesعاملين اثنين: John وAlice. -
أو أن ينقسم القسم إلى أقسام فرعية، مثل قسم التطوير
developmentله فرعان: تطوير المواقعsitesوالبرمجيات الداخليةinternals. ولكلّ من الفرعين موظفين منفصلين. -
يمكن أيضًا أن يكبُر القسم الفرعي ويصير فروع من القسم الفرعي (أي «فِرَق»).
مثلًا قسم المبيعات
sitesسيتطوّر ويتحسّن وينقسم مستقبلًا إلى فرعينsiteAوsiteB. وبعدها ربما (لو عمل فريق التسويق بجدّ) ينقسم أكثر أيضًا. طبعًا هذا تخيّل فقط وليس في الصورة تلك.
الآن، ماذا لو أردنا دالة تعطينا مجموع كل الرواتب؟ كيف السبيل؟
لو جرّبنا بالتكرار فسيكون أمرًا عسيرًا إذ أنّ البنية ليست ببسيطة. أول فكرة على البال هي حلقة for تمرّ على الشركة company وداخلها حلقات فرعية على الأقسام بالمستوى الأول. ولكن هكذا سنحتاج حلقات فرعية متداخلة أيضًا لتمرّ على الموظفين في الأقسام بالمستوى الثاني مثل قسم sites… وبعدها حلقات أخرى داخل تلك فوقها للأقسام بالمستوى الثالث إن عمل فريق التسويق كما يجب… لو وضعنا 3-4 من هذه الحلقات الفرعية المتداخلة في شيفرة لتعمل جولة مسح على كائن واحد، فستنتج لنا شيفرة قبيحة حقًا.
لنجرّب التعاود الآن.
كما رأينا، حين تُلاقي الدالة قسمًا عليها جمع رواتبه، تواجه حالتين اثنتين:
- إمّا يكون قسمًا «بسيطًا» فيه مصفوفة من الناس، وهكذا تجمع رواتبهم في حلقة بسيطة.
-
أو تجد كائنًا فيه
Nمن الأقسام الفرعية، حينها تصنعNمن الاستدعاءات المتعاودة لتحصي مجموع كلّ قسم فرعي وتدمج النتائج كلها.
الحالة الأولى هي أساس التعاود، أي عملنا العادي حين نستلم مصفوفة.
الحالة الثانية (حين نرى كائنًا) هي خطوة في التعاود. يمكن تقسيم تلك المهمة المعقّدة إلى مهام فرعية لكلّ قسم. ربّما تنقسم تلك المهام الفرعية ثانيةً، ولكنّها عاجلًا أم آجلًا ستنتهي بالحالة (1) لا محالة.
ربّما… يكون أسهل لو قرأت الخوارزمية من الشيفرة ذاتها:
// الكائن كما هو، ضغطناه لألا نُطيل القصة فقط let company = { sales: [{name: 'John', salary: 1000}, {name: 'Alice', salary: 600 }], development: { sites: [{name: 'Peter', salary: 2000}, {name: 'Alex', salary: 1800 }], internals: [{name: 'Jack', salary: 1300}] } }; // الدالة التي ستنفّذ هذا العمل function sumSalaries(department) { if (Array.isArray(department)) { // حالة (1) return department.reduce((prev, current) => prev + current.salary, 0); // نجمع عناصر المصفوفة } else { // حالة (2) let sum = 0; for (let subdep of Object.values(department)) { // نستدعي الأقسام الفرعية تعاوديًا، ونجمع النتائج sum += sumSalaries(subdep); } return sum; } } alert(sumSalaries(company)); // 6700
الشيفرة قصيرة وسهل فهمها (كما هو أملي). هنا تظهر قوّة التعاود، فسيعمل على أيّ مستوى من الأقسام الفرعية المتداخلة.
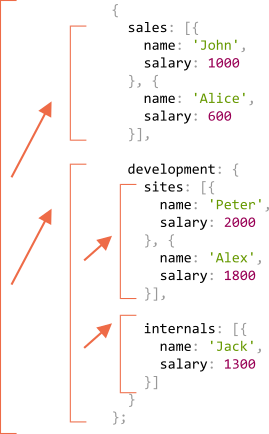
إليك رسمة توضّح الاستدعاءات:
الفكرة بسيطة للغاية: لو كان كائنًا {...}، نستعمل الاستدعاءات الفرعية، ولو كانت مصفوفات [...] هي آخر «أوراق» شجرة التعاود، فتعطينا الناتج مباشرةً.
لاحظ كيف أنّ الشيفرة تستعمل مزايا ذكيّة ناقشناها سابقًا:
التابِع arr.reduce في الفصل «توابِع المصفوفات» لنجمع الرواتب.
-
الحلقة
for(val of Object.values(obj))للمرور على قيم الكائن إذ يُعيد التابِعObject.valuesمصفوفة بالقيم.
بنى التعاود
بنية البيانات التعاودية (أيّ التي يحدّد أساسها التعاود) هي بنية تكرّر نفسها على أجزاء منفصلة.
رأينا لتوّنا مثالًا عن هذه البنية: بنية الشركة أعلاه.
القسم في الشركة هو إمّا:
- مصفوفة من الناس.
- أو كائنًا فيه أقسام أخرى.
لو كنت مطوّر وِب فالأمثلة التي تعرفها وتُدركها هي مستندات HTML وXML.
ففي مستندات HTML، يمكن أن يحتوي وسم HTML على قائمة من:
- أجزاء من نصوص.
- تعليقات HTML.
- وسوم HTML أخرى (أي ما يمكن أن يحتوي على أجزاء من نصوص أو تعليقات أو وسوم أخرى وهكذا).
وهذا ما نسمّيه بالبنى التعاوديّة.
لنفهم التعاود أكثر سنشرح بنية تعاود أخرى تسمّى «القوائم المترابطة» (Linked List). يمكن أن تكون هذه القوائم أحيانًا بديلًا أفضل موازنةً بالمصفوفات.
القوائم المترابطة
لنقل بأنّا نريد تخزين قائمة كائنات مرتّبة.
ستصنع مصفوفة كالعادة:
let arr = [obj1, obj2, obj3];
ولكن… هناك مشكلة تخصّ المصفوفات. عمليات «حذف العنصر» و«إدراج العنصر» مُكلفة. فمثلًا على عملية arr.unshift(obj) إعادة ترقيم كلّ العناصر للكائن الجديد obj، ولو كانت المصفوفة كبيرة فستأخذ العملية وقتًا طويلًا. الأمر نفسه ينطبق لعملية arr.shift().
التعديلات على بنية البيانات (التي لا تحتاج إلى إعادة الترقيم بالجملة) هي تلك التي تؤثّر على نهاية المصفوفة: arr.push/pop. لذا يمكن أن تكون المصفوفة بطيئة حقًا لو كانت الطوابير طويلة حين نعمل مع المصفوفات من عناصرها الأولى.
يمكننا عوض ذلك استعمال بنية بيانات أخرى لو أردنا إدخال البيانات وحذفها سريعًا. تُدعى هذه البنية بالقائمة المترابطة.
يُعرّف عنصر القائمة المترابطة تعاوديًا على أنّه كائن فيه:
-
قيمة
value. -
خاصية «التالي»
nextتُشير إلى عنصر القائمة المترابطة التالي أو إلىnullلو كانت هذه نهاية القائمة.
مثال:
let list = { value: 1, next: { value: 2, next: { value: 3, next: { value: 4, next: null } } } };
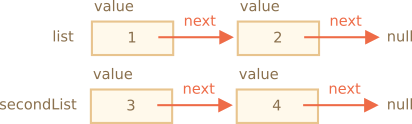
إليك التمثيل البصري لهذه القائمة:
هذه شيفرة أخرى لنصنع القائمة:
let list = { value: 1 }; list.next = { value: 2 }; list.next.next = { value: 3 }; list.next.next.next = { value: 4 }; list.next.next.next.next = null;
هنا نرى بوضوح أكثر كيف أنّ هناك كائنات متعدّدة لكلّ منها خاصية value وأخرى next تُشير إلى العنصر بقرب «هذا». متغيّر list هو أول الكائنات في السلسلة وبهذا لو اتّبعنا إشارات next بدءًا منها سنصل إلى أيّ عنصر آخر نريد.
يمكننا قسمة القائمة إلى أجزاء عدّة ودمجها لاحقًا لو أردنا:
let secondList = list.next.next; list.next.next = null;
للدمج:
list.next.next = secondList;
وطبعًا يمكننا إدخال العناصر إلى أي مكان وإزالتها من أي مكان.
فمثلًا لو أردنا إضافة قيمة جديدة للبداية فعلينا تحديث رأس القائمة:
let list = { value: 1 }; list.next = { value: 2 }; list.next.next = { value: 3 }; list.next.next.next = { value: 4 }; // نُضيف قيمة جديدة إلى بداية القائمة list = { value: "new item", next: list };
ولنُزيل قيمة من المنتصف نعدّل خاصية next للكائن الذي يسبق الجديد:
list.next = list.next.next;
هكذا أجبرنا list.next بأن «تقفز» فوق 1 لتصل 2، بهذا استثنينا القيمة 1 من السلسلة. وطالما أنّها ليست مخزّنة في أيّ مكان آخر فستُزال من الذاكرة تلقائيًا.
وعلى عكس المصفوفات فلسنا هنا نُعيد الترقيم بالجملة، أي أنّ إعادة ترتيب العناصر أسهل.
بالطبع فالقوائم ليست أفضل من المصفوفات دومًا وإلا فاستعملناها هي دومًا وما احتجنا المصفوفات أبدًا.
السلبية الأساس هي أنّ الوصول إلى العنصر حسب رقمه ليس سهلًا كما في المصفوفات حيث نستعمل الإشارة المباشرة arr[n]. ولكن في القوائم علينا البدء من العنصر الأول والانتقال N مرّة عبر next لنصل إلى العنصر بالرقم N.
…ولكننا لا نحتاج دومًا إلى هذه العمليات فمثلًا حين نريد طابورًا أو حتّى طابورًا متعدّد الطرفين فيجب أن نستعمل بنية مرتّبة تتيح بإضافة/إزالة العناصر من الجهتين بسرعة فائقة، وليس بالضروري أن نعرف ما في وسطها.
يمكننا تحسين القوائم هكذا:
-
إضافة الخاصية
prevمع الخاصيةnextللإشارة إلى العنصر السابق، لننتقل وراءً بسهولة أكبر. -
إضافة متغيّر بالاسم
tailيُشير إلى آخر عنصر من القائمة (وتحديثه متى أضفنا/أزلنا عناصر من النهاية). - …يمكن أن تتغيّر بنية البيانات حسب متطلباتنا واحتياجاتنا.
ملخص
المصطلحات:
-
التعاود* هو مصطلح برمجي يعني استدعاء دالة من داخلها. يمكن استعمال الدوال التعاودية لحلّ المهام المختلفة بطرق ذكية نظيفة.
حين تستدعي الدالة نفسها نسمّي ذلك خطوة تعاود. تُعدّ وُسطاء الدالة التي تبسّط المهمّة إلى أقصى درجة بحيث لا تستدعي الدالة أيّ شيء بعدها - تُعدّ أساس التعاود.
-
بنية البيانات التعاودية هي أيّة بنية بيانات تُحدّد نفسها بنفسها.
فمثلًا يمكن تعريف القائمة المترابطة على أنّها بنية بيانات تحتوي على كائن يُشير إلى قائمة (أو يُشير إلى null).
list = { value, next -> list }
تُعدّ الأشجار مثل شجرة عناصر HTML أو شجرة الأقسام في هذا الفصل كائنات تعاودية بطبعها، فهي تتفرّع ولكلّ فرع فروع أخرى.
يمكن استعمال الدوال التعاودية للمرور فيها كما رأينا في مثال
sumSalary.
يمكن إعادة كتابة أيّ دالة تعاودية لتصير دالة تستعمل التكرار، وغالبًا ما نفعل هذا لتحسين أداء الدوال. ولكن هناك مهام عديدة يكون الحلّ التعاودي سريعًا كفايةً وأسهل كتابةً ودعمًا.
تمارين
اجمع كلّ الأعداد إلى أن تصل للممرّر
الأهمية: 5
اكتب الدالة sumTo(n) التي تجمع الأعداد 1 + 2 + ... + n.
مثال:
sumTo(1) = 1 sumTo(2) = 2 + 1 = 3 sumTo(3) = 3 + 2 + 1 = 6 sumTo(4) = 4 + 3 + 2 + 1 = 10 ... sumTo(100) = 100 + 99 + ... + 2 + 1 = 5050
اكتب 3 شيفرات:
- واحدة باستعمال حلقة for.
-
واحدة باستعمال التعاود، إذ أنّ
sumTo(n) = n + sumTo(n-1)طالماn > 1. - واحدة باستعمال المتتاليات الحسابية.
مثال عن الناتج:
function sumTo(n) { /*... شيفرتك هنا ... */ } alert( sumTo(100) ); // 5050
ملاحظة: أيّ الشيفرات أسرع من الأخرى؟ وأيها أبطأ؟ ولماذا؟
ملاحظة أخرى: هل يمكن أن نستعمل التعاود لحساب sumTo(100000)؟
الحل
الحلّ باستعمال الحلقة:
function sumTo(n) { let sum = 0; for (let i = 1; i <= n; i++) { sum += i; } return sum; } alert( sumTo(100) );
الحلّ باستعمال التعاود:
function sumTo(n) { if (n == 1) return 1; return n + sumTo(n - 1); } alert( sumTo(100) );
الحلّ باستعمال المعادلة sumTo(n) = n*(n+1)/2:
function sumTo(n) { return n * (n + 1) / 2; } alert( sumTo(100) );
عن الملاحظة: بالطبع فالمعادلة هي أسرع الحلول فلا تستعمل إلا ثلاث عمليات لكلّ عدد n. الرياضيات إلى جانبنا هنا!
الشيفرة باستعمال الحلقة تأتي في المرتبة الثانية من ناحية السرعة. لو تلاحظ فنحن هنا نجمع الأعداد نفسها في الشيفرتين التعاودية والحلقية، إلّا أنّ التعاودية فيها استدعاءات متداخلة أكثر وإدارةً لمكدس التنفيذ، هذا ما يستهلك موارد أكثر فتصير الشيفرة أبطأ.
عن الملاحظة الأخرى: تدعم بعض المحرّكات «تحسين نهاية الاستدعاء» (tail call optimization)، ويعني أنّه لو كان الاستدعاء التعاودي هو آخر ما في الدالة (مثلما في الدالة sumTo أعلاه)، فلن تواصل الدالة الخارجية عملية التنفيذ كي لا يتذكّر المحرّك سياقها التنفيذي. يتيح هذا للمحرّك إزالة قضية الذاكرة بذلك يكون ممكنًا عدّ sumTo(100000). ولكن، لو لم يدعم محرّك جافاسكربت هذا النوع من التحسين (وأغلبها لا تدعم) فستواجه الخطأ: تخطّيت أكبر حجم في المكدس، إذ يُفرض -عادةً- حدّ على إجمالي حجم المكدس.
احسب المضروب
الأهمية: 4
المضروب هو عدد طبيعي مضروب بِ «العدد ناقصًا واحد» وثمّ بِ «العدد ناقصًا اثنين» وهكذا إلى أن نصل إلى 1. نكتب مضروب n بهذا الشكل: n!
يمكننا كتابة تعريف المضروب هكذا:
n! = n * (n - 1) * (n - 2) * ...*1
قيم المضاريب لأكثر من n:
1! = 1 2! = 2 * 1 = 2 3! = 3 * 2 * 1 = 6 4! = 4 * 3 * 2 * 1 = 24 5! = 5 * 4 * 3 * 2 * 1 = 120
مهمّتك هي كتابة الدالة factorial(n) لتحسب n! باستعمال الاستدعاءات التعاودية.
alert( factorial(5) ); // 120
ملاحظة وفائدة: يمكنك كتابة n! هكذا n * (n-1)! مثلًا: 3! = 3*2! = 3*2*1! = 6
الحل
حسب التعريف فيمكن كتابة المضروب n! هكذا n * (n-1)!.
أي أنّه يمكننا حساب ناتج factorial(n) على أنّه n مضروبًا بناتج factorial(n-1). ويمكن أن ينخفض استدعاء n-1 أنزل وأنزل إلى أن يصل 1.
function factorial(n) { return (n != 1) ? n * factorial(n - 1) : 1; } alert( factorial(5) ); // 120
القيمة الأساس للتعاود هي 1. يمكننا أن نجعل 0 هي الأساس ولكنّ ذلك لا يهم، ليست إلا خطوة تعاود أخرى:
function factorial(n) { return n ? n * factorial(n - 1) : 1; } alert( factorial(5) ); // 120
أعداد فيبوناتشي
الأهمية: 5
لمتتالية فيبوناتشي الصيغة F<sub>n</sub> = F<sub>n-1</sub> + F<sub>n-2</sub>. أي أنّ العدد التالي هو مجموع العددين الذين سبقاه.
أوّل عددين هما 1، وبعدها 2(1+1) ثمّ 3(1+2) ثمّ 5(2+3) وهكذا: 1, 1, 2, 3, 5, 8, 13, 21....
ترتبط أعداد فيبوناتشي بالنسبة الذهبية وبظواهر طبيعية أخرى عديدة حولنا من كلّ مكان.
اكتب الدالة fib(n) لتُعيد عدد فيبوناتش n-th.
مثال لطريقة عملها:
function fib(n) { /* شيفرتك هنا */ } alert(fib(3)); // 2 alert(fib(7)); // 13 alert(fib(77)); // 5527939700884757
ملاحظة: يجب أن تعمل الدالة بسرعة. يجب ألا يأخذ استعداء fib(77) أكثر من جزء من الثانية.
الحل
أوّل حلّ نفكّر به هو الحلّ بالتعاود.
أعداد فيبوناتشي تعاودية حسب تعريفها:
function fib(n) { return n <= 1 ? n : fib(n - 1) + fib(n - 2); } alert( fib(3) ); // 2 alert( fib(7) ); // 13 // fib(77); // سيكون استدعاءً أبطأ من السلحفاة
…ولكن لو كانت قيمة n كبيرة فسيكون بطيئًا جدًا. يمكن أن يعلّق الاستدعاء fib(77) محرّك جافاسكربت لفترة من الوقت بينما يستهلك موارد المعالج كاملةً.
يعزو ذلك إلى أنّ الدالة تؤدّي استدعاءات فرعية كثيرة، وتُعيد تقدير (evaluate) القيم ذاتها مرارًا وتكرارًا.
لنرى مثلًا جزءًا من حسابات fib(5):
... fib(5) = fib(4) + fib(3) fib(4) = fib(3) + fib(2) ...
يمكننا أن نرى هنا بأنّ قيمة fib(3) مفيدة للاستدعائين fib(5) وfib(4). لذا فستُستدعى fib(3) وتُقدّر قيمتها مرتين كاملتين منفصلتين عن بعضهما البعض.
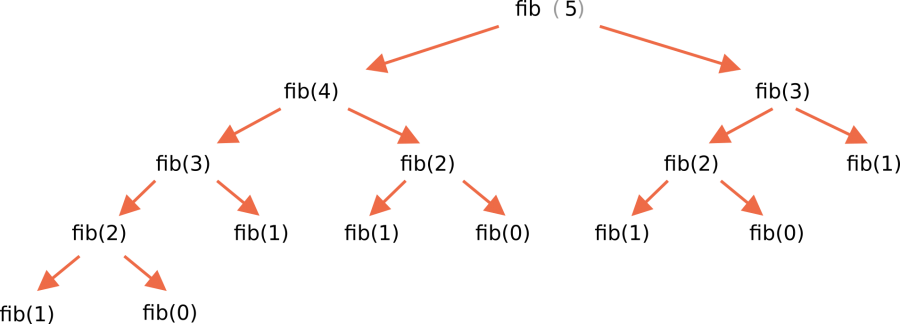
إليك شجرة التعاود كاملةً:
نرى بوضوح كيف أنّ fib(3) تُقدّر مرتين اثنتين وfib(2) تُقدّر ثلاث مرات. إجمالي الحسابات يزداد أسرع مما تزداد قيمة n، ما يجعل الحسابات مهولة حين نصل n=77.
يمكننا تحسين أداء الشيفرة بتذكّر القيم التي قدّرنا ناتجها قبل الآن: لو حسبنا قيمة fib(3) مثلًا، فيمكننا إعادة استعمالها في أيّ حسابات مستقبلية.
أو، يمكن أن نترك التعاود كله ونحاول استعمال خوارزمية مختلفة جذريًا تعتمد على الحلقات.
فبدلًا من أن نبدأ بِ n وننطلق نحو أسفل، يمكن أن نصنع حلقة تبدأ من 1 و2 ثمّ تسجّل ناتج ذلك على أنّه fib(3)، وناتج القيمتين السابقتين على أنّه fib(4) وهكذا دواليك إلى أن تصل إلى القيمة المطلوبة. هكذا لا نتذكّر في كلّ خطوة إلى قيمتين سابقتين فقط.
إليك خطوات الخوارزمية الجديدة هذه بالتفصيل الممل.
البداية:
// a = fib(1)، b = fib(2)، هذه القيم حسب التعريف رقم 1 let a = 1, b = 1; // نأخذ c = fib(3) ليكون مجموعها let c = a + b; /* لدينا الآن fib(1) و fib(2) و fib(3) a b c 1, 1, 2 */
الآن نريد معرفة fib(4) = fib(2) + fib(3).
لنحرّك ما في المتغيّرات إلى الجانب: a,b سيكونان fib(2),fib(3) وc سيكون مجموعهما:
a = b; // now a = fib(2) b = c; // now b = fib(3) c = a + b; // c = fib(4) /* الآن لدينا المتتابعة: a b c 1, 1, 2, 3 */
الخطوة التالية تعطينا عددًا آخر في السلسلة:
a = b; // الآن صار a = fib(3) b = c; // الآن صار b = fib(4) c = a + b; // c = fib(5) /* الآن لدينا المتتابعة (أضفنا عددًا آخر): a b c 1, 1, 2, 3, 5 */
…وهكذا إلى أن نصل إلى القيمة المطلوبة. وهذا أسرع بكثير من التعاود وليس فيه أيّة حسابات متكرّرة.
الشيفرة كاملةً:
function fib(n) { let a = 1; let b = 1; for (let i = 3; i <= n; i++) { let c = a + b; a = b; b = c; } return b; } alert( fib(3) ); // 2 alert( fib(7) ); // 13 alert( fib(77) ); // 5527939700884757
تبدأ الحلقة بالقيمة i=3 إذ أنّ قيمتا المتتابعة الأولى والثانية مكتوبتان داخل المتغيّران a=1 و b=1.
يُدعى هذا الأسلوب بالبرمجة الديناميكية من أسفل إلى أعلى.
طباعة قائمة مترابطة
لنقل بأنّ أمامنا القائمة المترابطة هذه:
let list = { value: 1, next: { value: 2, next: { value: 3, next: { value: 4, next: null } } } };
اكتب الدالة printList(list) لتطبع لنا عناصر القائمة واحدةً واحدة.
اصنع نسختين من الحل: واحدة باستعمال الحلقات وواحدة باستعمال التعاود.
أيّ الحلّين أفضل؟ بالتعاود أو بدون؟
الحل
نسخة الحلقات
هذا الحلّ باستعمال الحلقات:
let list = { value: 1, next: { value: 2, next: { value: 3, next: { value: 4, next: null } } } }; function printList(list) { let tmp = list; while (tmp) { alert(tmp.value); tmp = tmp.next; } } printList(list);
لاحظ كيف استعملنا المتغير المؤقت tmp للمرور على عناصر القائمة. يمكننا نظريًا استعمال مُعامل الدالة list بدل ذلك:
function printList(list) { while(list) { // (*) alert(list.value); list = list.next; } }
ولكن… سنندم على ذلك لاحقًا إذ قد نحتاج إلى توسيع عمل الدالة وإجراء عملية أخرى غير هذه على القائمة، ولو بدّلنا list فلن نقدر على ذلك حتمًا.
وعلى سيرة الحديث عن تسمية المتغيرات «كما ينبغي»، فهنا تُعدّ القائمةُ list ذاتَ القائمة، أي العنصر الأوّل من تلك القائمة، ويجب أن يبقى الاسم كما هو هكذا، مقروءًا وواضحًا.
بينما لا يعدو دور tmp إلّا أداةً لمسح القائمة، تمامًا مثل i في حلقات for.
نسخة التعاود
مفهوم النسخة التعاودية من الدالة printList(list) بسيط: علينا -كي نطبع قائمةً- طباعةَ العنصر الحالي list وتكرار ذلك على كلّ list.next:
let list = { value: 1, next: { value: 2, next: { value: 3, next: { value: 4, next: null } } } }; function printList(list) { alert(list.value); // نطبع العنصر الحالي if (list.next) { printList(list.next); // ذات الحركة لكلّ عنصر باقٍ في القائمة } } printList(list);
أمّا الآن، فأيّ النسختين أفضل؟
نظريًا تُعدّ نسخة الحلقات أفضل أداءً. صحيح أنّ الاثنتين عملهما واحد إلّا أن الحلقات لا تستهلك الموارد بتداخل استدعاءات الدوال.
ولكن لو نظرنا للجهة الأخرى من الكأس فالنسخة التعاودية أقصر وأسهل فهمًا أحيانًا.
طباعة قائمة مترابطة بالعكس
الأهمية: 5
اطبع القائمة المترابطة من التمرين السابق، ولكن بعكس ترتيب العناصر.
اصنع نسختين من الحل: واحدة باستعمال الحلقات وواحدة باستعمال التعاود.
الحل
نسخة التعاود
هنا توجد خدعة في فكرة التعاود، إذ علينا أوّلًا طباعة الباقي من القائمة وبعدها طباعة القائمة الحالية:
let list = { value: 1, next: { value: 2, next: { value: 3, next: { value: 4, next: null } } } }; function printReverseList(list) { if (list.next) { printReverseList(list.next); } alert(list.value); } printReverseList(list);
نسخة الحلقات
نسخة الحلقات هنا أكثر تعقيدًا (بقليل) عن سابقتها.
ما من طريقة لنأخذ آخر قيمة في قائمتنا list، ولا يمكننا أن «نعود» فيها.
لذا يمكننا أوّلًا المرور على العناصر بالترتيب المباشر وحِفظها في مصفوفة، بعدها طباعة ما حفظناه بالعكس:
let list = { value: 1, next: { value: 2, next: { value: 3, next: { value: 4, next: null } } } }; function printReverseList(list) { let arr = []; let tmp = list; while (tmp) { arr.push(tmp.value); tmp = tmp.next; } for (let i = arr.length - 1; i >= 0; i--) { alert( arr[i] ); } } printReverseList(list);
لاحظ كيف أنّ الحل باستعمال التعاود هو بالضبط كما باستعمال الحلقات، إذ يتبع القائمة ويحفظ العناصر في سلسلة من الاستدعاءات المتداخلة (في مكدس سياق التنفيذ)، وبعدها يطبع القيم.
ترجمة -وبتصرف- للفصل Recursion and stack من كتاب The JavaScript language















أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.