تَعرَّضنا بالقسم الفرعي 3.8.5 للمصفوفات ثنائية البعد (two-dimensional arrays)، ولكننا لم نَستخدِمها بالقدر الكافي منذ ذلك الحين. تَملُك المصفوفات ثنائية البعد نوعًا أيضًا مثل int[][] أو String[][] بزوجين من الأقواس المربعة. تُرتَّب عناصر المصفوفات ثنائية البعد ضِمْن مجموعة من الصفوف والأعمدة بحيث يُخصِّص العامل new كُلًا من عدد تلك الصفوف والأعمدة كالتالي:
int[][] A; A = new int[3][4];
تُنشِئ تلك التَعليمَة مصفوفة ثنائية البعد مُكوَّنة من 12 عنصر مُرتَّبين ضِمْن 3 صفوف و 4 أعمدة. يَتَوفَّر أيضًا مُهيِئ (initializers) للمصفوفات ثنائية البعد. فمثلًا، تُنشِئ التَعْليمَة التالية مصفوفة 3x4:
int[][] A = { { 1, 0, 12, -1 }, { 7, -3, 2, 5 }, { -5, -2, 2, -9 } };
يَتَكوَّن مُهيِئ المصفوفات ثنائية البعد من عدة صفوف مفصولة بفواصل (comma) ومُضمَّنة داخل أقواس. بالمثل، كل صف عبارة عن قائمة من القيم مفصولة بفواصل ومُضمَّنة داخل أقواس. إلى جانب ذلك، تَتَوفَّر قيم مُصنَّفة النوع (literals) لتَمثيِل المصفوفات ثنائية البعد لها نفس قواعد الصيغة (syntax)، ويُمكِن اِستخدَامها بأي مكان وليس فقط تَعْليمَات التّصرِيح (declarations). اُنظر المثال التالي:
A = new int[][] { { 1, 0, 12, -1 }, { 7, -3, 2, 5 }, { -5, -2, 2, -9 } };
في الواقع، يُمكِنك أن تُطبِق نفس الأمر على المصفوفات ثلاثية البعد ورباعية البعد..إلخ، ولكنها غَيْر شائعة الاِستخدَام في العموم.
حقيقة المصفوفات ثنائية البعد (two-dimensional arrays)
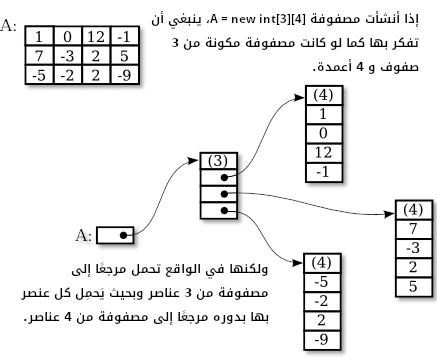
قبل أن نتعمق أكثر من ذلك، هنالك مفاجأة صغيرة! لا تَملُك الجافا مصفوفات ثنائية البعد (two-dimensional arrays) بصورة فعلية. تَحتلّ العناصر بمصفوفة فعلية ثنائية البُعد مَواضِعًا مُتصِلة من الذاكرة، ولكن هذا ليس صحيحًا بالجافا. في الحقيقة، تَكشِف الصيغة (syntax) المُستخدَمة لتمثيل أنواع المصفوفة ذلك: بِفرض وجود النوع BaseType، ينبغي إذًا أن نَكُون قادرين على إنشاء النوع BaseType[]، وهو ما يَعنِي "مصفوفة من النوع BaseType". إذا اِستخدَمنا النوع int[] ذاته كنوع أساسي للمصفوفة، فإننا نَحصُل على النوع int[][] الذي يُمثِل "مصفوفة من النوع int[]" أو "مصفوفة من مصفوفة من النوع int ". بمصفوفة ثنائية البعد من النوع int[][]، تَكُون العناصر نفسها مُتْغيِّرات من النوع int[]. ولمّا كان أي مُتْغيِّر من النوع int[] بدوره قادرًا على حَمْل مؤشر (pointer) إلى مصفوفة من النوع int. يُمكِننا إذًا أن نقول أن أي مصفوفة ثنائية البعد هي في الواقع عبارة عن مصفوفة من المؤشرات (pointers) بحيث يُشيِر كل مؤشر منها بدوره إلى مصفوفة أحادية البعد (one-dimensional array). تُمثِل المصفوفات أحادية البعد إذًا صفوفًا (rows) ضِمْن المصفوفة ثنائية البعد (two-dimensional). تُبيِّن الصورة التالية مصفوفة مُكوَّنة من 3 صفوف و 4 أعمدة:
غالبًا ما نتجاهل تلك الحقيقة، ونُفكِر بالمصفوفة ثنائية البعد كما لو كانت شبكة (grid). ولكننا سنحتاج أحيانًا لأن نتذكَّر أن كل صف ضِمْن تلك الشبكة هو مصفوفة بحد ذاته. يُمكننا في الواقع أن نُشيِر إلى تلك المصفوفات باِستخدَام A[0] و A[1] و A[2] أي أن كل صف هو قيمة من النوع int[] يُمكِننا أن نُمرِّرها حتى إلى برنامج فرعي (subroutine) يَستقبِل مُعاملًا (parameter) من النوع int[] على سبيل المثال.
يترتَّب على التفكير بمصفوفة ثنائية البعد A على أنها مصفوفة من المصفوفات عدة نتائج: أولًا، يُساوِي A.length عدد الصفوف (rows) ضِمْن المصفوفة، وهو ما يَتضِح معناه عند التفكير بها بتلك الطريقة. ثانيًا، إذا كانت A تَملُك الشكل المعتاد للمصفوفات ثنائية البعد، فسيَكُون عدد الأعمدة بالمصفوفة A هو نفسه عدد العناصر بالصف الأول أي A[0].length. لاحِظ مع ذلك أنه لا توجد قاعدة تَنصّ على ضرورة أن تَكُون جميع الصفوف ضِمْن مصفوفة ثنائية البعد بنفس الطول حيث يُعدّ كل صف بمثابة مصفوفة مُنفصِلة أحادية البعد، ويُمكِن لها إذًا أن تَملٌك طولًا مختلفًا. في الواقع، قد يَكُون صف معين ضِمْن مصفوفة فارغًا (null). اُنظر التَعْليمَة التالية على سبيل المثال:
A = new int[3][];
لا يَتَضمَّن التعريف السابق عددًا داخل الأقواس الثانية، ولهذا فإنه يُنشِئ مصفوفة مُكوَّنة من ثلاثة عناصر جميعها فارغة (null) أي أنه يُوفِّر مساحة لثلاثة صفوف (rows)، ولكنه لا يُنشِئ تلك الصفوف بشكل فعليّ. يُمكِنك أن تُنشِئ الصفوف A[0] و A[1] و A[2] بشكل منفصل.
كمثال آخر، لنُفكِر بمصفوفة مُتماثِلة M -المصفوفة المتماثلة (symmetric) عبارة عن مصفوفة ثنائية البعد يَتساوَى عدد صفوفها مع عدد أعمدتها كما تَتَساوَى قيم M[j] و M[j] لجميع قيم i و j-، نحتاج لتَخْزِين قيم M[j] التي تُحقِّق الشَّرط i >= j أي يُمكِننا أن نُخزِّن البيانات بمصفوفة مُثلثة (triangular array) كالتالي:
يُمكِننا أن نُنشِئ مصفوفة مثلثية (triangular array) إذا أنشأنا كل صف على حدى. تُنشِئ الشيفرة التالية مصفوفة مثلثية 7x7 من النوع double:
double[][] matrix = new double[7][]; // لم ننشئ الصفوف بعد for (int i = 0; i < 7; i++) { // انشئ الصف i بحيث يحتوي على i+1 من العناصر matrix[i] = new double[i+1]; }
إذا أردنا أن نَجلب قيمة matrix بالمَوضِع (i,j)، وكان i < j، فإنه ينبغي أن نَجلب قيمة matrix[j]، ويَنطبِق الأمر نفسه على ضَبْط قيم تلك المصفوفة. تُعرِّف الشيفرة التالية صَنْفًا لتمثيل المصفوفات المُتماثِلة (symmetric matrices):
public class SymmetricMatrix { private double[][] matrix; // مصفوفة مثلثية لحمل البيانات public SymmetricMatrix(int n) { matrix = new double[n][]; for (int i = 0; i < n; i++) matrix[i] = new double[i+1]; } public double get( int row, int col ) { if (row >= col) return matrix[row][col]; else return matrix[col][row]; } public void set( int row, int col, double value ) { if (row >= col) matrix[row][col] = value; else matrix[col][row] = value; } public int size() { return matrix.length; // يمثل عدد الصفوف } } // end class SymmetricMatrix
يُمكِنك أن تجد تعريف الصَنْف بالأعلى داخل الملف SymmetricMatrix.java كما يَحتوِي الملف TestSymmetricMatrix.java على برنامج صغير لاختبار الصَنْف.
بالمناسبة، لا تستطيع الدالة (function) القياسية Arrays.copyOf() أن تُنشِئ نسخة كاملة من مصفوفة ثنائية البعد (2d array) ضِمْن خطوة واحدة، وإنما ينبغي أن تَفعَل ذلك لكل صف (row) ضِمْن المصفوفة على حدى. نستطيع إذًا كتابة الشيفرة التالية لنسخ مصفوفة ثنائية البعد من الأعداد الصحيحة:
int[][] B = new int[A.length][]; // B و A لديهم نفس عدد الصفوف for (int i = 0; i < A.length; i++) { B[i] = Arrays.copyOf(A[i], A[i].length)); // انسخ الصف i }
لعبة الحياة (Game of Life)
كمثال آخر على معالجة المصفوفات ثنائية البعد، سنَفْحَص مثال مشهور آخر: لعبة الحياة (Game of Life) الذي اخترعها عالم الرياضيات جون هورتون كونواي (John Horton Conway) بعام 1970. لا تُعدّ لعبة الحياة (Game of Life) لعبة بحق، فهي تُمثِل آلة أوتوماتيكية ثنائية البعد. يَعنِي ذلك أنها مُكوَّنة من شبكة (grid) من الخلايا (cells) تَتَغيَّر محتوياتها بمرور الوقت وفقًا لقواعد محدَّدة. يُمكِن لأي خلية أن تَكُون بحالة من اثنين: "حية (alive)" أو "ميتة (dead)". سنَستخدِم مصفوفة ثنائية البعد لتَمثيِل تلك الشبكة بحيث يُمثِل كل عنصر بالمصفوفة حالة خلية واحدة ضِمْن الشبكة. ستُهيِئ اللعبة شبكة (grid) مبدئية بحيث تَكُون جميع خلاياها إما "حية" أو "ميتة". بَعْد ذلك، ستتطوَّر الشبكة وفقًا لسِلسِلة من الخطوات. ستُحدَّد حالة خلايا الشبكة بكل خطوة وفقًا لحالة خلاياها بالخطوة السابقة ووفقًا لعدد من القواعد البسيطة: ستَفحَص كل خلية بالشبكة الخلايا المجاورة لها (أفقيًا ورأسيًا وقطريًا)، وتَحسِب عدد الخلايا الحية ثم تُحدَّد حالة الخلية بالخطوة التالية وفقًا للقواعد التالية:
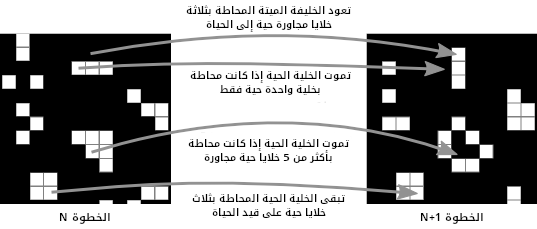
- في حالة كانت الخلية "حية" بالخطوة الحالية، وكانت أيضًا مُحاطَة بعدد 2 أو 3 خلايا حية، فإنها ستَبقَى حية بالخطوة التالية أما إذا لم تَكُن مُحاطَة بذلك العدد، فإنها ستموت. (أي تَموُت الخلية الحية نتيجة للوحدة إذا كانت مُحاطة بعدد أقل من خليتين حيتين أو نتيجة للازدحام إذا كانت مُحاطَة بأكثر من 3 خلايا حية).
- في حالة كانت الخلية "ميتة" بالخطوة الحالية، وكانت أيضًا مُحاطَة بثلاث خلايا حية، فإنها تتحوَّل لتُصبِح حية بالخطوة التالية أما إذا لم تَكُن مُحاطَة بذلك العدد، فإنها ستَبقَى ميتة. (أي يَنتُج عن وجود ثلاثة خلايا حية خلية حية جديدة).
تُظهِر الصورة التالية شكل شبكة الخلايا قَبْل تطبيق قواعد اللعبة وبَعْدها. تُطبَق القواعد على كل خلية بالشبكة، وتُبيِّن الصورة كيفية تطبيقها على أربعة خلايا:
تُعدّ لعبة الحياة (Game of Life) شيقة حيث تَعرِض الكثير من الأنماط المفاجئة (اُنظر بصفحة ويكيبيديا الخاصة باللعبة). نحن هنا مُهتمين فقط بكتابة برنامج لمحاكاة تلك اللعبة. يُمكِنك أن تَطلِع على شيفرة البرنامج بالكامل بالملف Life.java. تَظهَر رقعة الحياة كشبكة من المربعات بحيث تَكون المربعات الميتة سوداء اللون أما المربعات الحية فتَكُون بيضاء اللون. (سيَستخدِم البرنامج الصنف MosaicCanvas.java من القسم 4.7 لتَمثيِل تلك الشبكة، لذلك ستحتاج إلى إضافة ذلك الملف لتَصرِيف [compile] البرنامج وتَشْغِيله). يُمكِننا أن نملئ رقعة الحياة بخلايا حية وميتة عشوائيًا أو قد نَستخدِم الفأرة لضَبطها. يُوفِّر البرنامج الزر "Step" المسئول عن تحديد حالة الشبكة بَعْد خطوة واحدة فقط" بالإضافة إلى الزر "Start" المسئول عن تَشْغِيل تلك الخطوات بهيئة تحريكة (animation).
سنَفْحَص العمليات المُتعلِقة بمعالجة المصفوفات (array processing) اللازمة لتّنفِيذ برنامج لعبة الحياة (Game of Life). أولًا، يُمكِن لأي خلية أن تَكُون حية أو ميتة، لذلك سنَستخدِم بطبيعة الحال مصفوفة ثنائية البعد من النوع boolean[][] لتمثيل حالة جميع الخلايا، وليَكُن اسم تلك المصفوفة هو alive. ستُساوِي قيمة أي عنصر alive[r][c] القيمة true إذا كانت الخلية برقم الصف r ورقم العمود c حية. سنَستخدِم أيضًا نفس قيمة الثابت GRID_SIZE لتمثيل عدد الصفوف والأعمدة بتلك المصفوفة. يُمكِننا إذًا أن نَستخدِم حَلْقة التَكْرار for المُتداخلة (nested) التالية لمَلْئ قيم تلك المصفوفة المُمثِلة لشبكة الحياة بقيم عشوائية:
for (int r = 0; r < GRID_SIZE; r++) { for (int c = 0; c < GRID_SIZE; c++) { // اضبط الخلية لتكون حية بنسبة احتمال تساوي 25% alive[r][c] = (Math.random() < 0.25); } }
يُعيد التعبير Math.random() < 0.25 القيمة true أو false، والتي يُمكِننا أن نُسنِدها (assign) إلى عنصر مصفوفة من النوع boolean. سنَستخدِم تلك المصفوفة لضَبْط لون كل خلية بالشاشة. نظرًا لأننا سنَرسِم شبكة الخلايا على شاشة من الصَنْف MosaicCanvas، فإننا سنَستخدِم واجهة برمجة التطبيقات (ِAPI) الخاصة بذلك الصنف لضَبْط ألوانها. ونظرًا لأن الصَنْف MosaicCanvas هو المسئول عن الرسم الفعليّ، سيَكُون برنامج لعبة الحياة مسئولًا فقط عن ضَبْط الألوان باِستخدَام واجهة برمجة التطبيقات الخاصة بالصَنْف. سنُعرِّف ذلك بتابع اسمه showBoard()، والذي ينبغي أن يُستدعَى بكل مرة تَتَغيَّر فيها رقعة الحياة. سنَستخدِم مجددًا حَلْقة تَكْرار for مُتداخِلة لضَبْط لون كل مربع بالشبكة كالتالي:
for (int r = 0; r < GRID_SIZE; r++) { for (int c = 0; c < GRID_SIZE; c++) { if (alive[r][c]) display.setColor(r,c,Color.WHITE); else display.setColor(r,c,null); // اعرض لون الخلفية بالأسود } }
بالطبع، يُعدّ حساب الحالة الجديدة لشبكة الخلايا بَعْد تطبيق قواعد اللعبة على حالتها الحالية هو الجزء الأكثر تشويقًا من البرنامج. لمّا كانت القواعد ستُطبَق على كل خلية على حدى، فإننا سنحتاج إلى اِستخدَام حَلْقة تَكْرار for مُتداخِلة للمرور عبر جميع خلايا الشبكة، ولكن ستَكُون المعالجة أكثر تعقيدًا هذه المرة. لاحظ أنه لا يُمكِننا أن نُجرِي أي تغييرات على قيم المصفوفة أثناء معالجتها؛ لأننا سنحتاج إلى معرفة الحالة القديمة لخلية معينة أثناء معالجة خلاياها المجاورة. سيَستخدِم البرنامج مصفوفة آخرى للاحتفاظ بالحالة الجديدة أثناء المعالجة، وعندما ننتهي من معالجة جميع الخلايا ضِمْن الشبكة، يُمكننا أن نَستخدِم المصفوفة الجديدة بدلًا من القديمة. يُمكِننا كتابة الخوارزمية (algorithm) بالشيفرة الوهمية (pseudocode) كالتالي:
let newboard be a new boolean[][] array for each row r: for each column c: Let N be the number of neighbors of cell (r,c) in the alive array if ((N is 3) or (N is 2 and alive[r][c])) newboard[r][c] = true; else newboard[r][c] = false; alive = newboard
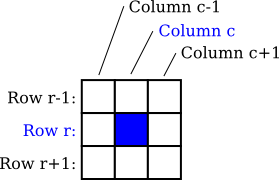
سيُشيِر alive عند انتهاء المعالجة إلى مصفوفة جديدة، وهو أمر لا ينبغي أن نقلق بشأنه طالما كانت محتويات المصفوفة الجديدة مُمثِلة للحالة الجديدة لشبكة الخلايا أما المصفوفة القديمة فسيُحرِّرها كانس المُهملات (garabage collector). قد لا يَكون اختبار ما إذا كان newboard[r][c] مُتحقِقًا أم لا واضحًا بما فيه الكفاية، ولكنه يُنفِّذ القواعد بشكل سليم. سنحتاج أيضًا لحِسَاب عدد الخلايا المجاورة. إذا كان لدينا خلية بالصف r والعمود c، ولم تَكُن تلك الخلية واقعة على حافة الرقعة، فإن الخلايا المجاورة لتلك الخلية هي كالتالي:
لاحِظ أن رقم الصف فوق الصف r يُساوِي r-1 أما الصف أسفله فهو r+1. يَنطبِق نفس الأمر على الأعمدة. ينبغي إذًا أن نَفْحَص القيم alive[r-1][c-1] و alive[r-1][c] و alive[r-1][c+1] و alive[r][c-1] و alive[r][c+1] و alive[r+1][c-1] و alive[r+1][c] و alive[r+1][c+1]، ونَعِد منها تلكم المُحتوية على القيمة true. اِحرِص على فهم كيفية عمل فهارس المصفوفة.
في المقابل، ستواجهنا مشكلة إذا كانت الخلية وَاقِعة على إحدى حواف الشبكة. في تلك الحالة، لا تَكُون بعض العناصر ضِمْن القائمة السابقة موجودة، وستَتَسبَّب محاولة الاشارة إليها إلى حدوث اِعترَاض (exception). لكي نَتَجنَّب حُدوث ذلك، ينبغي أن نُعامِل الخلايا الواقعة على الحواف بطريقة مختلفة. يُمكِننا مثلًا أن نَفْحَص ما إذا كان عنصر المصفوفة موجودًا قبل محاولة الإشارة إليه. في تلك الحالة، يُمكِننا مثلًا أن نَكْتُب شيفرة حساب عدد الخلايا المجاورة الحية كالتالي:
if (r-1 >= 0 && c-1 >= 0 && alive[r-1][c-1]) N++; // خلية بالموضع (r-1,c-1) موجودة وحية if (r-1 >= 0 && alive[r-1][c]) N++; // خلية بالموضع (r-1,c) موجودة وحية if (r-1 >= 0 && c+1 <= GRID_SIZE && alive[r-1][c+1]) N++; // خلية بالموضع (r-1,c+1) موجودة وحية // إلخ
سنتجنَّب بذلك كل الاعتراضات (exceptions). اِستخدَمنا في الواقع حلًا آخر شائع الاِستخدَام بألعاب الحاسوب ثنائية البعد. سنَتَظاهَر كما لو أن الحافة اليسرى للرقعة مُرتبطِة بالحافة اليمنى وكما لو أن الحافة العلوية مُرتبطِة بالحافة السفلية. بالنسبة لخلية برقم الصف 0 على سبيل المثال، فإن الصف أعلاها هو الصف الأخير أي بالرقم GRID_SIZE-1. سنَستخدِم أيضًا مُتْغيِّرات لتمثيل المَواضِع above و below و left و right الخاصة بخلية معينة. اُنظر شيفرة التابع المسئولة عن حساب الحالة الجديدة للرقعة، والتي ستَجِد أنها أبسط كثيرًا:
private void doFrame() { // احسب الحالة الجديدة لرقعة لعبة الحياة boolean[][] newboard = new boolean[GRID_SIZE][GRID_SIZE]; for ( int r = 0; r < GRID_SIZE; r++ ) { // تعد الصفوف أعلى وأسفل الصف r int above, below; // تعد الأعمدة على يمين ويسار العمود c int left, right; above = r > 0 ? r-1 : GRID_SIZE-1; // (for "?:" see Subsection 2.5.5) below = r < GRID_SIZE-1 ? r+1 : 0; for ( int c = 0; c < GRID_SIZE; c++ ) { left = c > 0 ? c-1 : GRID_SIZE-1; right = c < GRID_SIZE-1 ? c+1 : 0; int n = 0; // عدد الخلايا الحية المجاورة if (alive[above][left]) n++; if (alive[above][c]) n++; if (alive[above][right]) n++; if (alive[r][left]) n++; if (alive[r][right]) n++; if (alive[below][left]) n++; if (alive[below][c]) n++; if (alive[below][right]) n++; if (n == 3 || (alive[r][c] && n == 2)) newboard[r][c] = true; else newboard[r][c] = false; } } alive = newboard; }
يُمكِنك الإطلاع على شيفرة البرنامج بالملف Life.java، وأن تُجرِبه. لا تنسى أنك ستحتاج إلى اِستخدَام الملف MosaicCanvas.java أيضًا.
لعبة داما (Checkers)
سنَفْحَص الآن مثالًا أكثر واقعية لاستخدام المصفوفات ثنائية البعد. يُعدّ هذا البرنامج هو الأطول حتى الآن حيث يَتَكوَّن من 745 سطر. يَسمَح ذلك البرنامج للمُستخدمين بلعب مباراة داما (checkers). تتكوَّن لعبة الداما من رقعة مُكوَّنة من 8 صفوف و8 أعمدة. سنعتمد على المثال الذي كتبناه بالقسم الفرعي 6.5.1. سنُسمِي اللاعبين بأسماء "أحمر" و "أسود" وفقًا للون قطع الداما الخاصة بهما. لن نشرح قواعد لعبة الداما هنا، ولربما تستطيع أن تتعلَّمها بينما تُجرِّب البرنامج.
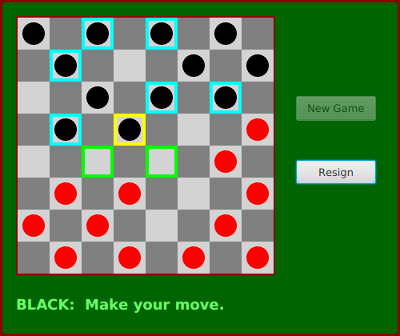
يستطيع اللاعب أن يَتحرَك بالنَقْر على القطعة التي يريد أن يُحرِكها ثُمَّ بالنَقْر على المربع الفارغ الذي يريد أن يَنقِل إليه تلك القطعة. سيَرسِم البرنامج بأي لحظة إطارًا حول المربعات التي يستطيع اللاعب أن يَنقُر عليها بلون أفتح قليلًا كنوع من المساعدة. على سبيل المثال، سيُحَاط المربع المُتضمِّن للقطعة التي اختارها المُستخدِم للحركة بإطار أصفر اللون بينما ستُحَاط القطع الآخرى التي بإمكانه تَحرِيكها بإطار أزرق سماوي. إذا كان المُستخدِم قد اختار قطعة بالفعل لتَحرِيكها، فستُحَاط جميع المربعات الفارغة التي يستطيع أن يُحرِك إليها تلك القطعة بإطار أخضر اللون. ستَتبِع اللعبة قاعدة تَنُص على أنه إذا كان اللاعب الحالي قادرًا على القفز (jump) على إحدى قطع الخصم، فإنه لابُدّ أن يَقفِز. عندما تُصبِح إحدى القطع "قطعة ملك" أي بَعْد وصولها إلى الحافة الأخرى من الرقعة، سيَرسِم البرنامج حرف "K" أبيض كبير على تلك القطعة. تَعرِض الصورة التالية لقطة شاشة مبكرة من اللعبة، والتي تُظهِر اللاعب الأسود وقد اختار القطعة الموجودة بالمربع ذو الإطار الأصفر للحركة. يستطيع اللاعب الآن أن يَنقُر على إحدى المربعات المُحاطَة بإطار أخضر لكي يُكمِل تلك الحركة أو قد يَنقُر على إحدى المربعات المُحاطَة بإطار أزرق سماوي ليختار قطعة آخرى لتَحرِيكها.
سنَمُر عبر جزءًا من شيفرة ذلك المثال، ولكن يُمكِنك الاطلاع على الشيفرة بالكامل بالملف Checkers.java. قد يَكُون البرنامج طويلا ومعقدًا، ولكنه بقليل من الدراسة، ستَتَمكَّن من فهم جميع التقنيات المُستخدَمة به. يُعدّ البرنامج مثالًا جيدًا على البرمجة كائنية التوجه (object-oriented) المُعتمدِة على كُلًا من الأحداث (event-driven) والحالات (state-based).
سنُخزِّن بيانات قطع الرقعة بمصفوفة ثنائية البعد (two-dimensional array). نظرًا لأن البرنامج مُعقَد نوعًا ما، سنُقسِّمه إلى عدة أصناف. إلى جانب الصَنْف الأساسي، سنُعرِّف بعض الأصناف المُتداخِلة (nested) الآخرى منها الصَنْف CheckersData المُستخدَم لمعالجة بيانات الرقعة. لا يُعدّ ذلك الصَنْف مسئولًا مباشرًا عن أي جزء من الرسوم (graphics) أو مُعالجة الأحداث (event-handling)، ولكنه يُوفِّر التوابع (methods) التي يُمكِننا أن نستدعيها بأصناف آخرى لأغراض معالجة الرسوم والأحداث (events). سنناقش ذلك الصَنْف قليلًا.
يَحتوِي الصَنْف CheckersData على مُتْغيِّر نُسخة (instance variables) اسمه هو board من النوع int[][]. تُضبَط قيمة ذلك المُتْغيِّر إلى new int[8][8] لتُمثِل شبكة 8x8 من الأعداد الصحيحة (integers). تُستخدَم ثوابت (constants) لتعريف القيم المُحتمَل تَخْزِينها بمربع برقعة شطرنج (checkboard):
static final int EMPTY = 0, // يمثل مربعًا فارغًا RED = 1, // قطعة حمراء عادية RED_KING = 2, // قطعة ملك حمراء BLACK = 3, // قطعة سوداء عادية BLACK_KING = 4; // قطعة ملك سوداء
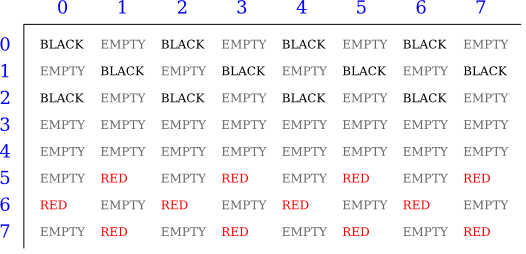
سنَستخدِم أيضًا الثابتين RED و BLACK بالبرنامج لتَمثيِل لاعبي المباراة. عندما تبدأ المباراة، ستُضبَط قيم المصفوفة لتمثيل الحالة المبدئية للرقعة، وستبدو كالتالي:
يُمكِن لأي قطعة سوداء عادية أن تتحرك لأسفل الشبكة فقط أي لابُدّ أن يكون رقم الصف للمربع الذي ستنتقل إليه أكبر من رقم الصف للمربع القادمة منه. بالمقابل، تستطيع أي قطعة حمراء عادية أن تَتَحرك لأعلى الشبكة فقط. يُمكِن للملوك بأي من اللونين الحركة بكلا الاتجاهين.
لابُدّ أن ينتبه الصَنْف CheckersData لأي تَغييرات ينبغي إجراؤها على هياكل البيانات (data structures) عندما يُحرِك أحد اللاعبين قطعة معينة بالرقعة. في الواقع، يُعرِّف الصَنْف تابع النسخة makeMove() المُخصَّص لذلك الغرض. عندما يُحرِك لاعب قطعة من مربع إلى آخر، سيُعدِّل التابع قيمة عنصرين ضِمْن المصفوفة. بالإضافة إلى ذلك، إذا كانت الحركة عبارة عن قفزة (jump)، ستُحذَف القطعة التي كانت موجودة بالمربع المقفوز إليه من الرقعة. يستطيع التابع أن يُحدِّد ما إذا كانت حركة معينة عبارة عن قفزة أم لا بِفْحَص ما إذا كان المربع الذي تَحرَكت إليه القطعة يَبعُد بمقدار صفين عن المربع الذي بدأت منه. إلى جانب ما سبق، تُصبِح القطعة الحمراء RED التي تتحرك إلى الصف 0 أو القطعة السوداء Black التي تتحرك إلى الصف 7 بمثابة قطعة ملك (king). سنَضَع جميع ما سبق ببرنامج فرعي (subroutine)، وبالتالي، لن يضطّر باقي البرنامج للقلق بشأن أي من تلك التفاصيل السابقة. يُمكِنه فقط أن يَستدعِي التابع makeMove():
void makeMove(int fromRow, int fromCol, int toRow, int toCol) { board[toRow][toCol] = board[fromRow][fromCol]; // حرك القطعة board[fromRow][fromCol] = EMPTY; // المربع الذي تحركت منه أصبح فارغًا if (fromRow - toRow == 2 || fromRow - toRow == -2) { // الحركة كانت قفزة لذلك احذف القطعة المقفوز إليها من الرقعة int jumpRow = (fromRow + toRow) / 2; // صف القطعة المقفوز إليها int jumpCol = (fromCol + toCol) / 2; // عمود القطعة المقفوز إليها board[jumpRow][jumpCol] = EMPTY; } if (toRow == 0 && board[toRow][toCol] == RED) board[toRow][toCol] = RED_KING; // تصبح القطعة الحمراء ملك if (toRow == 7 && board[toRow][toCol] == BLACK) board[toRow][toCol] = BLACK_KING; // تصبح القطعة السوداء ملك } // end makeMove()
ينبغي أن يَسمَح الصَنْف CheckersData بالعثور على جميع الحركات الصالحة بالرقعة. سنستخدم كائنًا ينتمي للصَنْف التالي لتمثيل الحركة داخل لعبة داما:
private static class CheckersMove { int fromRow, fromCol; // موضع القطعة المطلوب تحريكها int toRow, toCol; // المربع الذي انتقلت إليه القطعة CheckersMove(int r1, int c1, int r2, int c2) { // اضبط قيم متغيرات النسخة fromRow = r1; fromCol = c1; toRow = r2; toCol = c2; } boolean isJump() { // اختبر ما إذا كانت الحركة عبارة عن قفزة // بالقفزة، تتحرك القطعة مسافة صفين return (fromRow - toRow == 2 || fromRow - toRow == -2); } } // end class CheckersMove.
يُعرِّف الصَنْف CheckersData تابع نسخة (instance method) للعثور على جميع الحركات المتاحة حاليًا لكل لاعب. يُعدّ ذلك التابع بمثابة دالة (function) تُعيِد مصفوفة من النوع CheckersMove[] تحتوي على جميع الحركات المتاحة مُمثَلة بهيئة كائنات من النوع CheckersMove. يُمكِننا إذًا كتابة توصيف التابع كالتالي:
CheckersMove[] getLegalMoves(int player)
يُمكِننا كتابة خوارزمية التابع بالشيفرة الوهمية (pseudocode) كالتالي:
// ابدأ بقائمة فارغة من الحركات Start with an empty list of moves // ابحث عن أي قفزات صالحة و أضفها إلى القائمة Find any legal jumps and add them to the list // إذا لم يكن هناك أي قفزات صالحة if there are no jumps: // ابحث عن الحركات العادية الأخرى و أضفها إلى القائمة Find any other legal moves and add them to the list // إذا كانت القائمة فارغة if the list is empty: return null else: return the list
الآن، ما هو المقصود بالقائمة (list)؟ في الواقع، ينبغي أن نُعيد الحركات المسموح بها ضِمْن مصفوفة، ولكن لأن المصفوفات ثابتة الحجم، لا يُمكِننا أن نُنشِئها حتى نَعرِف عدد الحركات، وهو في الواقع ما لا يُمكِننا معرفته حتى نَصِل إلى نهاية التابع أي بَعْد أن نَكُون قد أنشأنا القائمة بالفعل! أحد الحلول إذًا هو اِستخدَام مصفوفة ديناميكية من النوع ArrayList بدلًا من مصفوفة عادية لكي تَحمِل الحركات بينما نَجِدها. يَستخدِم البرنامج بالأسفل كائنًا من النوع ArrayList<CheckersMove> لكي يُمكِّن القائمة من حَمْل كائنات من الصَنْف CheckersMove فقط. بينما نُضيِف الحركات إلى تلك القائمة، سيزداد حجمها بما يتناسب مع عدد الحركات. يُمكِننا أن نُنشِئ المصفوفة المطلوبة ونَنسَخ البيانات إليها بنهاية التابع. اُنظر الشيفرة الوهمية التالية:
// أنشئ قائمة moves فارغة للحركات Let "moves" be an empty ArrayList<CheckersMove> // ابحث عن القفزات المسموح بها و أضفها إلى القائمة Find any legal jumps and add them to moves // إذا كان عدد الحركات ما يزال يساوي 0 if moves.size() is 0: // There are no legal jumps! // ابحث عن الحركات العادية الصالحة و أضفها إلى القائمة Find any other legal moves and add them to moves // إذا لم يكن عدد الحركات يساوي 0 if moves.size() is 0: // There are no legal moves at all! return null else: // عرف مصفوفة moveArray من النوع CheckersMoves // طولها يساوي moves.size() Let moveArray be an array of CheckersMoves of length moves.size() // انسخ محتويات المصفوفة moves إلى moveArray Copy the contents of moves into moveArray return moveArray
علينا الآن أن نُحدِّد الحركات والقفزات المسموح بها. تَتَوفَّر المعلومات التي نحتاج إليها بالمصفوفة board، ولكن يَلزَمنا بعض العمل لاِستخراجها. لابُدّ أن نَفْحَص جميع المواضع بالمصفوفة ونَعثُر على القطع التي تنتمي للاعب الحالي. بَعْد ذلك، ينبغي أن نَفْحَص المربعات التي يُمكِن لكل قطعة أن تنتقل إليها، ونُحدِّد ما إذا كانت تلك الحركة صالحة أم لا. إذا كنا نبحث عن القفزات المسموح بها، فينبغي أن نَفْحَص المربعات التي تَبعُد بمسافة صفين وعمودين من كل قطعة. يُمكِننا إذًا أن نُوسِّع سطر الخوارزمية "اِبحَث عن القفزات المسموح بها ثم أَضِفها إلى الحركات" كالتالي:
// لكل صف بالرقعة For each row of the board: // لكل عمود بالرقعة For each column of the board: // إذا كانت إحدى قطع اللاعبين بذلك المكان if one of the player's pieces is at this location: // إذا كان من الممكن القفز إلى الموضع row+2,column+2 if it is legal to jump to row + 2, column + 2 // أضف تلك الحركة إلى moves add this move to moves // إذا كان من الممكن القفز إلى الموضع row-2,column+2 if it is legal to jump to row - 2, column + 2 add this move to moves // إذا كان من الممكن القفز إلى الموضع row+2,column-2 if it is legal to jump to row + 2, column - 2 add this move to moves // إذا كان من الممكن القفز إلى الموضع row-2,column-2 if it is legal to jump to row - 2, column - 2 add this move to moves
ينبغي أن نُوسِّع السطر "ابحث عن الحركات الصالحة الآخرى وأضفها إلى قائمة الحركات" بنفس الطريقة باستثناء أن علينا الآن فَحْص المربعات الأربعة التي تَبعُد مسافة صف واحد وعمود واحد من كل قطعة. لاحِظ أن اختبار ما إذا كان لاعب معين يستطيع أن يُحرِك قطعة من مربع معين إلى مربع آخر ليس بالأمر السهل. لابُدّ أن يَكُون المربع الذي ينتقل إليه اللاعب موجودًا بالرقعة، كما ينبغي أن يَكُون فارغًا. علاوة على ذلك، تستطيع القطع الحمراء والسوداء العادية أن تَتَحرَك باتجاه واحد. سنَستخدِم التابع (method) التالي لفْحَص ما إذا كان لاعب معين قادر على القيام بتحريك مربع:
private boolean canMove(int player, int r1, int c1, int r2, int c2) { if (r2 < 0 || r2 >= 8 || c2 < 0 || c2 >= 8) return false; // (r2,c2) خارج الرقعة if (board[r2][c2] != EMPTY) return false; // (r2,c2) يحتوي بالفعل على قطعة if (player == RED) { if (board[r1][c1] == RED && r2 > r1) return false; // القطع الحمراء العادية يمكنها أن تتحرك للأسفل فقط return true; // الحركة صالحة } else { if (board[r1][c1] == BLACK && r2 < r1) return false; // القطع السوداء العادية يمكنها أن تتحرك للأعلى فقط return true; // الحركة صالحة } } // end canMove()
يَستدعِى التابع getLegalMoves() التابع canMove() المُعرَّف بالأعلى ليَفْحَص ما إذا كانت حركة مُحتمَلة لقطعة معينة صالحة فعليًا أم لا. سنُعرِّف تابعًا مشابهًا لفَحْص ما إذا كانت قفزة (jump) معينة صالحة أم لا. في تلك الحالة، سنُمرِّر للتابع كُلًا من مربع القطعة والمربع الذي يُحتمَل أن تَنتقِل إليه وكذلك المربع الواقع بين هذين المربعين أي ذلك الذي سيَقفِز اللاعب فوقه. لابُدّ أن يَحتوِي المربع المقفوز إليه على إحدى قطع الخصم. يُمكننا تَوصِيف ذلك التابع كالتالي:
private boolean canJump(int player, int r1, int c1, int r2, int c2, int r3, int c3) { . . .
ينبغي الآن أن تَكُون قادرًا على فِهم شيفرة التابع getLegalMoves() بالكامل. يَدمِج ذلك التابع عدة مواضيع معًا: المصفوفات أحادية البعد (one-dimensional) والمصفوفات الديناميكية ArrayLists والمصفوفات ثنائية البعد (two-dimensional):
CheckersMove[] getLegalMoves(int player) { if (player != RED && player != BLACK) return null; // لن يحدث هذا ببرنامج سليم int playerKing; // The constant for a King belonging to the player. if (player == RED) playerKing = RED_KING; else playerKing = BLACK_KING; ArrayList<CheckersMove> moves = new ArrayList<CheckersMove>(); // ستخزن الحركة ضمن القائمة // تحقق من جميع القفزات الممكنة for (int row = 0; row < 8; row++) { for (int col = 0; col < 8; col++) { if (board[row][col] == player || board[row][col] == playerKing) { if (canJump(player, row, col, row+1, col+1, row+2, col+2)) moves.add(new CheckersMove(row, col, row+2, col+2)); if (canJump(player, row, col, row-1, col+1, row-2, col+2)) moves.add(new CheckersMove(row, col, row-2, col+2)); if (canJump(player, row, col, row+1, col-1, row+2, col-2)) moves.add(new CheckersMove(row, col, row+2, col-2)); if (canJump(player, row, col, row-1, col-1, row-2, col-2)) moves.add(new CheckersMove(row, col, row-2, col-2)); } } } // إذا وجدت أي قفزات ممكنة، فلابد أن يقفز اللاعب. لذلك لن نضيف أي // حركات عادية. أما إذا لم تجد أي قفزات، ابحث عن أي حركات عادية if (moves.size() == 0) { for (int row = 0; row < 8; row++) { for (int col = 0; col < 8; col++) { if (board[row][col] == player || board[row][col] == playerKing) { if (canMove(player,row,col,row+1,col+1)) moves.add(new CheckersMove(row,col,row+1,col+1)); if (canMove(player,row,col,row-1,col+1)) moves.add(new CheckersMove(row,col,row-1,col+1)); if (canMove(player,row,col,row+1,col-1)) moves.add(new CheckersMove(row,col,row+1,col-1)); if (canMove(player,row,col,row-1,col-1)) moves.add(new CheckersMove(row,col,row-1,col-1)); } } } } // إذا لم تجد أي حركات صالحة، أعد فراغا if (moves.size() == 0) return null; else { // انشئ مصفوفة وأضف إليها الحركات المسموح بها CheckersMove[] moveArray = new CheckersMove[moves.size()]; for (int i = 0; i < moves.size(); i++) moveArray[i] = moves.get(i); return moveArray; } } // end getLegalMoves
يُعدّ برنامج الداما مُعقدًا نوعًا ما، ويحتاج إلى الكثير من التصميم الجيد لتَقْرِير الأصناف (classes) والكائنات (classes) المُستخدمَة، وكذلك لتَقرِير التوابع (methods) التي ينبغي كتابتها، وكذلك لتقرير الخوارزميات (algorithms) التي ينبغي لتلك التوابع اِستخدَامها. يُمكِنك الاطلاع على شيفرة البرنامج بالكامل بالملف Checkers.java.
ترجمة -بتصرّف- للقسم Section 5: Two-dimensional Arrays من فصل Chapter 7: Arrays and ArrayLists من كتاب Introduction to Programming Using Java.














أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.