البحث والترتيب في المصفوفات Array في جافا

تُعدّ عمليتي البحث (searching) والترتيب (sorting) أكثر الأساليب شيوعًا لمعالجة المصفوفات. يُشير البحث (searching) هنا إلى محاولة العثور على عنصر بمواصفات معينة ضِمْن مصفوفة بينما يُشير الترتيب (sorting) إلى إعادة ترتيب عناصر المصفوفة ترتيبًا تصاعديًا أو تنازليًا. عادةً ما يَعتمِد المقصود بالترتيب التصاعدي والتنازلي على السياق المُستخدَم به الترتيب. في الواقع، تُوفِّر الجافا تُوفِّر بعض التوابع المَبنية مُسْبَقّا (built-in methods) الخاصة بعمليات البحث والترتيب -كما رأينا بالقسم الفرعي 7.2.2-، ومع ذلك ينبغي أن تَكُون على اطلاع ومعرفة بالخوارزميات (algorithms) التي تَستخدِمها تلك التوابع. ولهذا، سنَتعلَّم بعضًا من تلك الخوارزميات بهذا القسم.

عادةً ما يُناقَش البحث (searching) والترتيب (sorting) نظريًا باِستخدَام مصفوفة من الأعداد. ولكن من الناحية العملية، هناك أمور أكثر تشويقًا بكثير. فمثلًا، قد تَكُون المصفوفة عبارة عن قائمة بريدية بحيث يَكُون كل عنصر بها عبارة عن كائن (object) يَحتوِي على اسم وعنوان. إذا كان لدينا اسم شخص معين، يُمكِننا العثور على عنوانه، وهو ما يُعدّ مثالًا على عملية البحث (searching)؛ لأنك ببساطة تَبحَث عن كائن ضِمْن مصفوفة بالاعتماد على اسم الشخص. سيَكُون من المفيد أيضًا لو تَمَكَّنا من ترتيب المصفوفات وفقًا لمعيار معين مثل أن نُرتِّب المصفوفة السابقة بحيث تَكُون الأسماء مُرتَّبة ترتيبًا أبجديًا أو قد نُرتِّبها وفقًا للرقم البريدي.

سنُعمِّم الآن المثال السابق إلى تصور مُجرَّد بعض الشئ: لنتخيل أن لدينا مصفوفة تَحتوِي على عدة كائنات (objects)، وأننا نرغب بالبحث داخل تلك المصفوفة أو نرغب بترتيبها بالاعتماد على احدى مُتْغيِّرات النُسخ (instance variables) المُعرَّفة بتلك الكائنات. سنلجأ إلى اِستخدَام بعض المصطلحات الشائعة بقواعد البيانات (databases). سنُطلِق اسم "تسجيل (record)" على كل كائن ضِمْن المصفوفة بينما سنُطلِق اسم "الحقول (fields)" على مُتْغيِّرات النُسخ المُعرَّفة بتلك الكائنات. نستطيع الآن أن نُعيِد صياغة مثال القائمة البريدية إلى ما يلي: يَتَكوَّن كل تسجيل (record) من اسم وعنوان. قد تَتَكوَّن حقول التسجيل من الاسم الأول والأخير والعنوان والمدينة والدولة والرقم البريدي. ينبغي أن نختار إحدى تلك الحقول لتُصبِح "مفتاحًا (key)" لكي نَتَمكَّن من إجراء عمليتي البحث والترتيب. وفقًا لهذا التصور، سيُمثِل البحث محاولة العثور على تسجيل بالمصفوفة بحيث يَحتوِي مفتاحه على قيمة معينة بينما سيُمثِل الترتيب (sorting) تَبديِل مواضع تسجيلات المصفوفة إلى أن تُصبِح مفاتيحها (keys) مُرتَّبة ترتيبًا تصاعديًا أو تنازليًا.

البحث (Searching)

هناك خوارزمية واضحة للبحث عن عنصر معين داخل مصفوفة: افحص كل عنصر بالمصفوفة بالترتيب، واختبر ما إذا كانت قيمة ذلك العنصر هي نفسها القيمة التي تبحث عنها. إذا كان كذلك، فقد انتهت عملية البحث إذًا. أما إذا لم تعثر عليه بعد فحص جميع عناصر المصفوفة، فهو إذًا غير موجود بها. يُمكننا كتابة برنامج فرعي لتنفيذ تلك الخوارزمية (algorithm) بسهولة. بفرض أن المصفوفة التي تريد البحث بها عبارة عن مصفوفة من النوع int[]‎، يبحث التابع (method) التالي عن قيمة عددية ضمن مصفوفة. سيعيد التابع فهرس (index) العنصر بالمصفوفة إذا عثر عليه بينما سيعيد -1 إذا لم يعثر عليه كإشارة أن العدد الصحيح غير موجود:

static int find(int[] A, int N) {

   for (int index = 0; index < A.length; index++) {
      if ( A[index] == N ) 
          // ‫عثرنا على N بهذا الفهرس
         return index;  
   }

    // ‫إذا وصلنا إلى هنا، فإن N غير موجودة بأي مكان ضمن المصفوفة 
    // أعد القيمة -1

   return -1;

}

يُطلَق على طريقة البحث السابقة اسم البحث الخطي (linear search). إذا لم يَكُن لدينا أي معلومة عن كيفية ترتيب العناصر ضِمْن المصفوفة، فإنها تُمثِل الخيار الأفضل. في المقابل، إذا كنا على علم بكَوْن عناصر المصفوفة مُرتَّبة تصاعديًا أو تنازليًا، يُمكِننا إذًا أن نستغل تلك الحقيقة، ونَستخدِم خوارزميات أسرع. إذا كانت عناصر مصفوفة معينة مرتبة، يُقال عليها أنها "مصفوفة مرتبة (sorted)". يَستغرق ترتيب عناصر مصفوفة بعض الوقت بالطبع، ولكن إذا كانت المصفوفة مرتبة بالفعل، فيُمكننا إذًا أن نستغل تلك الحقيقة.

يُعدّ البحث الثنائي (binary search) أحد الطرائق المُتاحة للبحث عن عنصر ضِمْن مصفوفة مُرتَّبة (sorted). على الرغم من أن تّنْفِيذه (implement) ليس سهلًا تمامًا، فإن فكرته بسيطة: إذا كنت تَبحَث عن عنصر ضِمْن قائمة مُرتَّبة، يُمكِنك أن تَستبعِد نُصف العناصر ضِمْن القائمة بِفَحْص عنصر واحد فقط. على سبيل المثال، لنَفْترِض أننا نبحث عن العدد 42 ضِمْن مصفوفة مُرتَّبة مُكوَّنة من 1000 عدد صحيح، ولنَفْترِض أن المصفوفة مُرتَّبة ترتيبًا تصاعديًا، ولنَفْترِض أننا فَحصَنا العنصر الموجود بالفهرس 500، ووجدنا أن قيمته تُساوِي 93. لمّا كان العدد 42 أقل من 93، ولمّا كانت العناصر بالمصفوفة مُرتَّبة ترتيبًا تصاعديًا، يُمكِننا إذًا أن نَستنتج أنه في حالة كان العدد 42 موجودًا بتلك المصفوفة من الأساس، فإنه لابُدّ وأنه يَقَع بمَوضِع فهرسه أقل من 500. يُمكِننا إذًا أن نَستبِعد جميع العناصر الموجودة بمَواضِع فهرسها أكبر من 500؛ فهي بالضرورة أكبر من أو تُساوِي 93.

الخطوة التالية ببساطة هي فَحْص قيمة العنصر بالمَوْضِع 250. إذا كان العدد بذلك المَوْضِع يُساوِي -21 مثلًا، يُمكِننا إذًا أن نَستبعِد جميع العناصر قَبل المَوْضِع 250، ونُقصِر بحثنا على المَواضِع من 251 إلى 499. سيُقصِر الاختبار التالي بحثنا إلى 125 مَوضِع فقط ثُمَّ إلى 62. سيَتَبقَّى مَوضِع واحد فقط بعد 10 خطوات. تُعدّ تلك الطريقة أفضل كثيرًا من فَحْص كل عنصر ضِمْن المصفوفة. فمثلًا، إذا كانت المصفوفة تَحتوِي على مليون عنصر، ستَستغرِق خوارزمية البحث الثنائي 20 خطوة فقط للبحث بكامل المصفوفة. في العموم، يُساوِي عدد الخطوات اللازمة للبحث بأي مصفوفة لوغاريتم عدد العناصر بتلك المصفوفة بالنسبة للأساس 2.

لكي نَتَمكَّن من تَحْوِيل خوارزمية البحث الثنائي (binary search) إلى برنامج فرعي (subroutine) يَبحَث عن عنصر N ضِمْن مصفوفة A، ينبغي أن نَحتفِظ بنطاق المَوْاضِع التي يُحتمَل أن تَحتوِي على N بحيث نَستبعِد منها تدريجيًا المزيد من الاحتمالات، ونُقلِّل من حجم النطاق. سنَفْحَص دائمًا العنصر الموجود بمنتصف النطاق. إذا كانت قيمته أكبر من N، يُمكِننا إذًا أن نَستبعِد النصف الثاني من النطاق أما إذا كانت قيمته أقل من N، يُمكِننا أن نَستبعِد النصف الأول. أما إذا كانت قيمته تُساوي N، فإن البحث يَكُون قد انتهى. إذا لم يَتبقَّى أية عناصر، فإن العدد N غَيْر موجود إذًا بالمصفوفة. اُنظر شيفرة البرنامج الفرعي (subroutine):

/**
 * Precondition:  A must be sorted into increasing order.
 * Postcondition: If N is in the array, then the return value, i,
 *    satisfies A[i] == N.  If N is not in the array, then the
 *    return value is -1.
 */
static int binarySearch(int[] A, int N) {

    int lowestPossibleLoc = 0;
    int highestPossibleLoc = A.length - 1;

    while (highestPossibleLoc >= lowestPossibleLoc) {
       int middle = (lowestPossibleLoc + highestPossibleLoc) / 2;
       if (A[middle] == N) {
           // ‫عثرنا على N بهذا الفهرس
          return middle;
       }
       else if (A[middle] > N) {
           // ‫استبعد المواضع الأكبر من أو تساوي middle
          highestPossibleLoc = middle - 1;
       }
       else {
           // ‫استبعد المواضع الأقل من أو تساوي middle
          lowestPossibleLoc = middle + 1;   
       }
    }

    // ‫إذا وصلنا إلى هنا فإن highestPossibleLoc < LowestPossibleLoc
    // ‫أي أن N غير موجود بالمصفوفة.
    // أعد القيمة -1 لكي تشير إلى عدم وجود‫ N بالمصفوفة

    return -1;

}

القوائم الارتباطية (Association Lists)

تُعدّ القوائم الارتباطية (association lists) مثل القاموس (dictionary) واحدة من أشهر التطبيقات على البحث (searching). يَربُط القاموس (dictionary) مجموعة من التعريفات مع مجموعة من الكلمات. يُمكِنك مثلًا أن تَستخدِم كلمة معينة لمعرفة تَعرِيفها. قد تُفكِر بالقاموس على أنه قائمة من الأزواج (pairs) على الهيئة (w,d) حيث تُمثِل w كلمة معينة بينما d هي تعريف تلك الكلمة. بالمثل، تَتَكوَّن القوائم الارتباطية (association list) من قائمة من الأزواج (k,v) حيث تُمثِل k مفتاحًا (key) معينًا بينما تُمثِل v القيمة (value) المرتبطة بذلك المفتاح. لا يُمكِن لزوجين (pairs) ضِمْن قائمة معينة أن يَملُكا نفس قيمة المفتاح (key). عادةً ما نُطبِق عمليتين أساسيتين على القوائم الارتباطية: أولًا، إذا كان لديك مفتاح معين k، يُمكِنك أن تَجلُب القيمة v المُرتبِطة به إن وجدت. ثانيًا، يُمكِننا أن نُضيِف زوجًا جديدًا (k,v) إلى قائمة ارتباطية (association list). لاحِظ أنه في حالة إضافة زوج (pair) إلى قائمة، وكانت تلك القائمة تَحتوِي على زوج له نفس المفتاح، فإن القيمة الجديدة المضافة تَحلّ محلّ القديمة. يُطلق عادةً على تلك العمليتين اسم الجَلْب (get) والإضافة (put).

يُشاع اِستخدَام القوائم الارتباطية (association lists) في العموم بعلوم الحاسوب (computer science). على سبيل المثال، لابُدّ أن يَحتفِظ المُصرِّف (compiler) بمَوضِع الذاكرة (memory location) الخاص بكل مُْتْغيِّر. يستطيع المُصرِّف إذًا أن يَستخدِم قائمة ارتباطية بحيث يُمثِل كل مفتاح (key) بها اسمًا لمُتْغيِّر بينما تُمثِل قيمة (value) ذلك المفتاح عنوانه بالذاكرة. مثال آخر هو القوائم البريدية إذا كان العنوان مَربُوطًا باسم ضِمْن تلك القائمة. فمثلًا، يَربُط دليل الهاتف كل اسم برقم هاتف. سنَفْحَص فيما يَلي نُسخة مُبسَطة من ذلك المثال.

يُمكِننا أن نُمثِل عناصر دليل الهاتف بالقائمة الارتباطية (association list) بهيئة كائنات تنتمي إلى الصَنْف التالي:

class PhoneEntry {
   String name;
   String phoneNum;
}

تَتَكوَّن البيانات الموجودة بدليل الهاتف من مصفوفة من النوع PhoneEntry[]‎ بالإضافة إلى مُتْغيِّر من النوع العددي الصحيح (integer) للاحتفاظ بعدد المُدْخَلات المُخزَّنة فعليًا بذلك الدليل. يُمكِننا أيضًا أن نَستخدِم تقنية المصفوفات الديناميكية (dynamic arrays) -اُنظر القسم الفرعي 7.2.4- لكي نَتجنَّب وَضْع حد أقصى عشوائي على عدد المُدْخَلات التي يُمكِن لدليل الهاتف أن يَحتوِيه أو قد نَستخدِم النوع ArrayList. ينبغي أن يَحتوِي الصَنْف PhoneDirectory على توابع نسخ (instance methods) لتّنْفِيذ (implement) كلًا من عمليتي الجَلْب (get) والإضافة (put). تُمثِل الشيفرة التالية تعريفًا (definition) بسيطًا لذلك الصَنْف:

public class PhoneDirectory {

   private static class PhoneEntry {
      String name;     // الاسم
      String number;   // رقم الهاتف
   }

   private PhoneEntry[] data;  // مصفوفة لحمل أزواج مكونة من أسماء وأرقام هاتف
   private int dataCount;      // عدد الأزواج ضمن المصفوفة

   /**
    * Constructor creates an initially empty directory.
    */
   public PhoneDirectory() {
      data = new PhoneEntry[1];
      dataCount = 0;
   }

   private int find( String name ) {
      for (int i = 0; i < dataCount; i++) {
         if (data[i].name.equals(name))
            return i;  // الاسم موجود بالموضع‫ i
      }
      return -1;  // الاسم غير موجود بالمصفوفة
   }

   /**
    * @return The phone number associated with the name; if the name does
    *    not occur in the phone directory, then the return value is null.
    */
   public String getNumber( String name ) {
      int position = find(name);
      if (position == -1)
         return null;   // لا يوجد بيانات لذلك الاسم
      else
         return data[position].number;
   }

   public void putNumber( String name, String number ) {
      if (name == null || number == null)
         throw new IllegalArgumentException("name and number cannot be null");
      int i = find(name);
      if (i >= 0) {
          // ‫الاسم موجود بالفعل بالموضع i بالمصفوفة 
          // استبدل العدد الجديد بالعدد القديم بذلك الموضع
         data[i].number = number;
      }
      else {
          // أضف زوج جديد مكون من اسم وعدد إلى المصفوفة
          // إذا كانت المصفوفة ممتلئة، أنشئ مصفوفة جديدة أكبر
         if (dataCount == data.length) {
            data = Arrays.copyOf( data, 2*data.length );
         }
         PhoneEntry newEntry = new PhoneEntry();  // أنشئ زوجا جديدا
         newEntry.name = name;
         newEntry.number = number;
         data[dataCount] = newEntry;   // أضف الزوج الجديد إلى المصفوفة
         dataCount++;
      }
   }

} // end class PhoneDirectory

يُعرِّف الصَنْف تابع النسخة find()‎. يَستخدِم ذلك التابع أسلوب البحث الخطي (linear search) للعثور على مَوْضِع اسم معين بالمصفوفة المُكوَّنة من أزواج من الأسماء والأرقام. يَعتمِد كُلًا من التابعين getNumber()‎ و putNumber()‎ على التابع find()‎. لاحِظ أن التابع putNumber(name,number)‎ يَفحَص أولًا ما إذا كان الاسم موجودًا بدليل الهاتف أم لا. إذا كان موجودًا، فإنه فقط يُغيِّر الرقم المُرتبِط بذلك الاسم أما إذا لم يَكُن موجودًا، فإنه يُنشِئ مُدخلًا جديدًا ويُضيفه إلى المصفوفة.

قد نُضيِف الكثير من التحسينات بالطبع على الصَنْف المعرَّف بالأعلى. فمثلًا، قد نَستخدِم البحث الثنائي (binary search) بالتابع getNumber()‎ بدلًا من البحث الخطي، ولكن يَتَطلَّب ذلك أن تَكُون الأسماء المُخزَّنة بقائمة المُدْخَلات مُرتَّبة ترتيبًا أبجديًا، وهو ليس أمرًا صعبًا كما ستَرَى بالقسم الفرعي التالي.

عادةً ما يُطلَق اسم الخارطة (maps) على القوائم الارتباطية (association lists)، وتُوفِّر الجافا صَنْفًا قياسيًا ذو معاملات غَيْر محددة النوع (parameterized) اسمه هو Map كتنفيذ (implementation) لها. تستطيع أن تَستخدِم ذلك الصَنْف لكي تُنشِئ قوائمًا ارتباطية مُكوَّنة من مفاتيح (keys) وقيم (values) من أي نوع. يُعدّ ذلك التنفيذ (implementation) أكفأ بكثير من أي شيء قد تَفعَلُه باِستخدَام مصفوفات بسيطة. سنَتعرَّض بالفصل العاشر لذلك الصَنْف.

الترتيب بالإدراج (Insertion Sort)

اتضح لنا الآن الحاجة إلى ترتيب المصفوفات. في الواقع، تَتَوفَّر الكثير من الخوارزميات المُخصَّصة لذلك الغرض، منها خوارزمية الترتيب بالإدراج (insertion sort). تُعدّ تلك الخوارزمية واحدة من أسهل الطرائق لترتيب مصفوفة، كما يُمكِننا أن نُطبِقها للإبقاء على المصفوفة مُرتَّبة بينما نُضيِف إليها عناصر جديدة. لنَفْحَص المثال التالي أولًا:

لنَفْترِض أن لدينا قائمة مُرتَّبة ونريد إضافة عنصر جديد إليها. إذا كنا نريد التأكُّد من أنها ستظلّ مُرتَّبة، ينبغي أن نُضيِف ذلك العنصر بمَوْضِعه الصحيح بحيث تأتي قبله جميع العناصر الأصغر بينما تَحِلّ بَعْده جميع العناصر الأكبر. يَعنِي ذلك تَحرِيك جميع العناصر الأكبر بمقدار خانة واحدة لترك مساحة للعنصر الجديد.

static void insert(int[] A, int itemsInArray, int newItem) {

   int loc = itemsInArray - 1;  // ابدأ من نهاية المصفوفة

    // ‫حرك العناصر الأكبر من newItem للأعلى بمقدار مسافة واحدة
    // وتوقف عندما تقابل عنصر أصغر أو عندما تصل إلى بداية المصفوفة

   while (loc >= 0 && A[loc] > newItem) {
      A[loc + 1] = A[loc];  // Bump item from A[loc] up to loc+1.
      loc = loc - 1;        // انتقل إلى الموضع التالي
   }

    // ‫ضع newItem بآخر موضع فارغ
   A[loc + 1] = newItem;  

}

يُمكِننا أن نَمِد ذلك إلى تابع للترتيب (sorting) بأخذ جميع العناصر الموجودة بمصفوفة غَيْر مُرتَّبة (unsorted) ثم اضافتها تدريجيًا واحدًا تلو الآخر إلى مصفوفة آخرى مع الإبقاء عليها مُرتَّبة. نستطيع أن نَستخدِم البرنامج insert بالأعلى أثناء كل عملية إدراج (insertion) لعنصر جديد. ملحوظة: بالخوارزمية الفعليّة، لا نأخُذ جميع العناصر من المصفوفة، ولكننا فقط نتذكَّر الأجزاء المُرتَّبة منها:

static void insertionSort(int[] A) {
    // ‫رتب المصفوفة A ترتيبًا تصاعديا

   int itemsSorted; // عدد العناصر المُرتَّبة إلى الآن

   for (itemsSorted = 1; itemsSorted < A.length; itemsSorted++) {
       // ‫افترض أن العناصر A[0]‎ و A[1]‎ .. إلخ
       // ‫مرتبة بالفعل. أضف A[itemsSorted]‎ إلى الجزء المرتب من 
       // القائمة

      int temp = A[itemsSorted];  // العنصر المطلوب إضافته
      int loc = itemsSorted - 1;  // ابدأ بنهاية القائمة

      while (loc >= 0 && A[loc] > temp) {
         A[loc + 1] = A[loc]; // Bump item from A[loc] up to loc+1.
         loc = loc - 1;       // Go on to next location.
      }

       // ‫ضع temp بآخر موضع فارغ
      A[loc + 1] = temp; 
   }
}

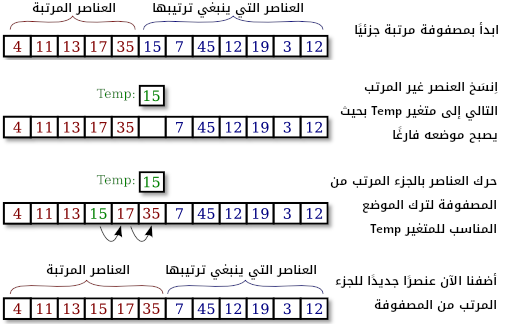
تُوضِح الصورة التالية مرحلة واحدة من عملية الترتيب بالإدراج (insertion sort) حيث تُبيِّن ما يحدث أثناء تّنفِيذ تَكْرار واحد من الحلقة for بالأعلى بالتحديد عندما يَكُون عدد العناصر ضِمْن المصفوفة itemsSorted مُساوِيًا للقيمة 5:

الترتيب الانتقائي (Selection Sort)

تَستخدِم خوارزمية ترتيب (sorting) آخرى فكرة العُثور على أكبر عنصر ضِمْن القائمة، وتَحرِيكه إلى نهايتها حيث ينبغي أن يتواجد إذا كنا نريد ترتيبها ترتيبًا تصاعديًا. بمُجرَّد تَحرِيك أكبر عنصر بالقائمة إلى مَوْضِعه الصحيح، يُمكِننا أن نُطبِق نفس الفكرة على العناصر المُتبقَاة أي أن نَعثُر على العنصر الأكبر التالي، ونُحرِكه إلى المَوْضِع قبل الأخير، وهكذا. يُطلَق اسم "الترتيب الانتقائي (selection sort)" على تلك الخوارزمية (algorithm). يُمكِننا كتابتها كما يلي:

static void selectionSort(int[] A) {
    // رتب المصفوفة A ترتيبا تصاعديا باستخدام الترتيب الانتقائي

   for (int lastPlace = A.length-1; lastPlace > 0; lastPlace--) {
      int maxLoc = 0;  // موضع أكبر عنصر إلى الآن

      for (int j = 1; j <= lastPlace; j++) {
         if (A[j] > A[maxLoc]) {
             // ‫لأن A[j]‎ أكبر من أكبر قيمة رأيناها إلى الآن، فإن j هو
             // الموضع الجديد لأكبر قيمة وجدناها إلى الآن
            maxLoc = j;  
         }
      }

      int temp = A[maxLoc];  // Swap largest item with A[lastPlace].
      A[maxLoc] = A[lastPlace];
      A[lastPlace] = temp;

   }  // end of for loop

}

يَستخدِم الصَنْف Hand الذي كتبناه بالقسم الفرعي 5.4.1 نسخة مختلفة قليلًا من الترتيب الانتقائي (selection sort). يُعرِّف الصَنْف Hand مُتْغيِّرًا من النوع ArrayList<Card>‎ لتَمثيِل اليد (hand) يحتوي بطبيعة الحال على كائنات من النوع Card. يَحتوِي أي كائن من النوع Card على توابع النسخ getSuit()‎ و getValue()‎، والتي يُمكِننا أن نَستخدِمها لمَعرِفة كُلًا من قيمة ورقة اللعب ورمزها (suit). يُنشِئ التابع (method) المسئول عن عملية الترتيب (sorting) قائمة جديدة، بحيث يَختار ورق اللعب من القائمة القديمة تدريجيًا وبترتيب مُتصاعِد ثم يُحرِكها من القائمة القديمة إلى الجديدة. يَستخدِم التابع (method) القائمة الجديدة بالنهاية لتمثيل اليد بدلًا من القديمة. قد لا يَكُون ذلك هو الأسلوب الأكفأ لإنجاز الأمر، ولكن نظرًا لأن عدد ورق اللعب ضِمْن أي يد (hand) عادةً ما يَكون صغيرًا، فإنه لا يُمثِل مشكلة كبيرة. اُنظر شيفرة ترتيب (sorting) ورق اللعب:

public void sortBySuit() {
   ArrayList<Card> newHand = new ArrayList<Card>();
   while (hand.size() > 0) {
      int pos = 0;  // موضع البطاقة الأقل
      Card c = hand.get(0);  // البطاقة الأقل
      for (int i = 1; i < hand.size(); i++) {
         Card c1 = hand.get(i);
         if ( c1.getSuit() < c.getSuit() ||
              (c1.getSuit() == c.getSuit() && c1.getValue() < c.getValue()) ) {
            pos = i;  // Update the minimal card and location.
            c = c1;
         }
      }
      hand.remove(pos);  // احذف ورقة اللعب من اليد الأصلية
      newHand.add(c);    // أضف ورقة اللعب إلى اليد الجديدة
   }
   hand = newHand;
}

لاحِظ أن موازنة العناصر ضِمْن قائمة ليست دائمًا ببساطة اِستخدَام < كالمثال بالأعلى. في هذه الحالة، تُعدّ ورقة لعب معينة أصغر من ورقة لعب آخرى إذا كان رمز (suit) الأولى أقل من رمز الثانية أو أن يَكُونا متساويين بشرط أن تَكُون قيمة ورقة اللعب الثانية أقل من قيمة الأولى. يتأكَّد الجزء الثاني من الاختبار من ترتيب ورق اللعب بنفس الرمز ترتيبًا صحيحًا بحسب قيمته.

يُمثِل ترتيب قائمة من النوع String مشكلة مشابهة؛ فالعامل < غَيْر مُعرَّف للسَلاسِل النصية. في المقابل، يُعرِّف الصنف String التابع compareTo. إذا كان str1 و str2 من النوع String، يُمكِننا كتابة ما يلي:

str1.compareTo(str2)

يُعيِد التابع السابق قيمة من النوع int تُساوِي 0 إذا كان str1 يُساوِي str2 أو قيمة أقل من 0 عندما يأتي str1 قبل str2 أو أكبر من 0 عندما يأتي str1 بَعْد str2. تستطيع مثلًا أن تختبر ما إذا كان str1 يَسبِق str2 أو يُساويه باِستخدَام الاختبار التالي:

if ( str1.compareTo(str2) <= 0 )

يُقصَد بكلمات مثل "يَسبِق" أو "يَتبَع" -عند اِستخدَامها مع السَلاسِل النصية (string)- ترتيبها وفقًا للترتيب المعجمي (lexicographic ordering)، والذي يَعتمِد على قيمة اليونيكود (Unicode) للمحارف (characters) المُكوِّنة للسِلسِلة النصية (strings). يَختلِف الترتيب المعجمي (lexicographic ordering) عن الترتيب الأبجدي (alphabetical) حتى بالنسبة للكلمات المُكوَّنة من أحرف أبجدية فقط؛ لأن جميع الأحرف بحالتها الكبيرة (upper case) تَسبِق جميع الأحرف بحالتها الصغيرة (lower case). في المقابل، يُعدّ الترتيب الأبجدي والمعجمي للكلمات المُقتصِرة على 26 حرف بحالتها الصغيرة فقط أو الكبيرة فقط هو نفسه. يُحوِّل التابع str1.compareToIgnoreCase(str2)‎ أحرف سِلسِلتين نصيتين (strings) إلى الحالة الصغيرة (lowercsae) أولًا قبل موازنتهما.

يتناسب كُلًا من الترتيب الانتقائي (selection sort) والترتيب بالادراج (insertion sort) مع المصفوفات الصغيرة المُكوَّنة من مئات قليلة من العناصر. أما بالنسبة للمصفوفات الكبيرة، فتَتَوفَّر خوارزميات آخرى أكثر تعقيدًا ولكنها أسرع بكثير. هذه الخوارزميات أسرع بكثير ربما بنفس الكيفية التي يُعدّ بها البحث الثنائي (binary search) أسرع من البحث الخطي (linear search). يَعتمِد التابع القياسي Arrays.sort على الخوارزميات السريعة. سنَتعرَّض لإحدى تلك الخوارزميات بالفصل التاسع.

الترتيب العشوائي (unsorting)

يُعدّ الترتيب العشوائي لعناصر مصفوفة مشكلة أقل شيوعًا ولكنها شيقة. قد نحتاجها مثلًا لخَلْط مجموعة ورق لعب ضِمْن برنامج. تَتًوفَّر خوارزمية شبيهة بالترتيب الانتقائي (selection sort)، فبدلًا من تَحرِيك أكبر عنصر بالمصفوفة إلى نهايتها، سنختار عنصرًا عشوائيًا ونُحرِكه إلى نهايتها. يَخلِط البرنامج الفرعي (subroutine) التالي عناصر مصفوفة من النوع int:

/**
 * Postcondition:  The items in A have been rearranged into a random order.
 */
static void shuffle(int[] A) {
   for (int lastPlace = A.length-1; lastPlace > 0; lastPlace--) {
       // ‫اختر موضعا عشوائيًا بين 0 و 1 و... حتى lastPlace
      int randLoc = (int)(Math.random()*(lastPlace+1));
       // ‫بدل العناصر بالموضعين randLoc و lastPlace
      int temp = A[randLoc];
      A[randLoc] = A[lastPlace];
      A[lastPlace] = temp;
   }
}