تُعدّ مسألة تقييم نماذج تعلم الآلة، أي حساب مجموعة من مقاييس تقييم الأداء والتي تُبرهن على وصول النموذج المُتعلم إلى درجة جيدة من التعلم وبحيث يُمكن الاعتماد عليه واستخدامه في مسألة ما، أمرًا أساسيًا في مسائل تعلم الآلة.
تسمح هذه المقاييس، في نهاية المطاف، بالمقارنة بين مختلف نماذج التعلم المُمكن استخدامها (والتي يولد كل منها باستخدام خوارزمية ما معينة)، مما يسمح باختيار الأنسب منها.
نعرض في هذه المقالة مجموعة المقاييس الأكثر استخدامًا لتقييم نماذج تعلم التصنيف classification وتقييم نماذج الانحدار regression ومن ثم نعرض كيفية المقارنة بين عدة نماذج تعلم ممكنة واختيار الأفضل منها.
مقاييس تقييم نماذج تعلم التصنيف
تهدف نماذج تعلم التصنيف إلى بناء مُصنف يُمكن استخدامه لتصنيف غرض ما إلى صف مُعين مثلًا ليكن لدينا مسألة تعلم تصنيف صورة إلى كلب أو قط، وبفرض أن لدينا عشرة صور لها قيم الصفوف التالية (كلب أم قط):
Actual values = ['cat', 'dog', 'cat', 'dog', 'cat', 'cat', 'dog', 'cat, 'dog', 'cat']
وبفرض أن نموذج تصنيف أعطى التصنيفات التالية لنفس الصور (ندعوها عادًة تنبؤ نموذج التعلم):
Predicted values = ['cat', 'cat', 'cat', 'dog', 'cat', 'cat', 'dog', 'dog', 'dog', 'dog']
من الواضح أن نموذج التصنيف أصاب في بعض الحالات وأخطأ في البعض الآخر. والسؤال المطروح هنا بشكل أساسي: ما كفاءة (تقييم) هذا النموذج؟
مصفوفة الارتباك confusion matrix
وهي عبارة عن جدول يُستخدم لبيان كفاءة نموذج تعلم التصنيف، إذ يعرض عدد حالات الصواب والخطأ المُمكنة المختلفة.
يُبين الجدول التالي مثلًا الحالات المختلفة في المثال السابق (ندعو، للتبسيط، صف الكلب بالموجب وصف القط بالسالب):
| تنبؤ نموذج التصنيف | القيمة الحقيقية: كلب (موجب) | القيمة الحقيقية: قط (سالب) |
|---|---|---|
| كلب (موجب) | 3 | 1 |
| قط (سالب) | 2 | 4 |
يُبين الجدول السابق أن نموذج التعلم أصاب في 3 حالات (الحقيقة: كلب / التنبؤ: كلب) + 4 حالات (الحقيقة: قط / التنبؤ: قط) = 7 حالات.
وأخطأ في حالتين (الحقيقة: كلب / التنبؤ: قط) + حالة (الحقيقة: قط / التنبؤ: كلب) = 3 حالات.
| تنبؤ نموذج التصنيف | القيمة الحقيقية: (موجب) | القيمة الحقيقية: (سالب) |
|---|---|---|
| موجب | عدد الحالات الصحيحة الموجبة | عدد الحالات الخاطئة الموجبة |
| سالب | عدد الحالات الخاطئة السالبة | عدد الحالات الصحيحة السالبة |
الحالات الصحيحة الموجبة True Positive
الحالات الصحيحة الموجبة True Positive وتختصر إلى TP وهي الحالات التي يكون من أجلها تنبؤ النموذج موجب والقيمة الحقيقة موجب (تنبؤ صحيح).
الحالات الصحيحة السالبة True Negative
الحالات الصحيحة السالبة True Negative وتختصر إلى TN وهي الحالات التي يكون من أجلها تنبؤ النموذج سالب والقيمة الحقيقة سالب (تنبؤ صحيح).
الحالات الخاطئة الموجبة False Positive (FP)
الحالات الخاطئة الموجبة False Positive وتختصر إلى FP وهي الحالات التي يكون من أجلها تنبؤ النموذج موجب والقيمة الحقيقة سالب (تنبؤ خاطئ).
الحالات الخاطئة السالبة False Negative (FN)
الحالات الخاطئة السالبة False Negative وتختصر إلى FN وهي الحالات التي يكون من أجلها تنبؤ النموذج سالب والقيمة الحقيقة موجب (تنبؤ خاطئ).
مقياس الصحة Accuracy
مقياس الصحة Accuracy وهو نسبة التصنيفات الصحيحة من العدد الكلي للأمثلة:
????????= (??+??)/(??+??+??+??) * 100
تكون الصحة في مثالنا السابق:
????????= (3+4)/10 * 100 = 70%
مقياس الدقة Precision
مقياس الدقة Precision هو نسبة التصنيفات الصحيحة للأمثلة الموجبة على العدد الكلي للأمثلة التي صُنّفت موجبة:
?????????= ??/(??+??) * 100
تكون الدقة في مثالنا السابق:
?????????= 3/(3+1) * 100 = 75%
مقياس الاستذكار Recall
مقياس الاستذكار Recall هو نسبة التصنيفات الصحيحة للأمثلة الموجبة على العدد الكلي للأمثلة الموجبة (يُدعى هذا المقياس أيضًا بالحساسية Sensitivity أو نسبة الموجب الصحيح True Positive Rate):
??????= ??/(??+??) * 100
يكون الاستذكار في مثالنا السابق:
??????= 3/(3+2) * 100 = 60%
المقياس F1
المقياس F1 وهو مقياس يوازن بين الدقة والاستذكار في قيمة واحدة:
?1−?????= (2∗?????????∗??????)/(?????????+??????)
يكون F1 في مثالنا السابق:
?1−?????= (2∗75∗60)/(75+60) = 66.66%
الخصوصية Specificity
الخصوصية Specificity هو نسبة التصنيفات الخاطئة للأمثلة الموجبة على العدد الكلي للأمثلة السالبة (يُدعى هذا المقياس أيضًا بنسبة الموجب الخاطئ False Positive Rate):
???= ??/(??+??) * 100
تكون الخصوصية في مثالنا السابق:
???= 1/(1+4) * 100 = 20%
حساب مقاييس الأداء في بايثون
توفر المكتبة sklearn.metrics في بايثون إمكانية حساب كل المقاييس السابقة، كما تُبين الشيفرة البرمجية التالية:
# تقييم نماذج التصنيف from sklearn.metrics import confusion_matrix from sklearn.metrics import accuracy_score from sklearn.metrics import precision_score from sklearn.metrics import recall_score from sklearn.metrics import f1_score # الصفوف actual = ['cat', 'dog', 'cat', 'dog', 'cat', 'cat', 'dog', 'cat', 'dog', 'cat'] # التنيؤ predicted = ['cat', 'cat', 'cat', 'dog', 'cat', 'cat', 'dog', 'dog', 'dog', 'dog'] # مصفوفة الارتباك cf_matrix = confusion_matrix(actual , predicted, labels=["dog", "cat"] ) print ('Confusion Matrix :') print (cf_matrix) # مقاييس الأداء print ('Accuracy Score :{:.2f}'.format(accuracy_score(actual, predicted)*100)) print ('Precision Score :{:.2f}'.format(precision_score(actual, predicted, pos_label='dog')*100)) print ('Recall Score :{:.2f}'.format(recall_score(actual, predicted, pos_label='dog')*100)) print ('F1 Score :{:.2f}'.format(f1_score(actual, predicted, pos_label='dog')*100)) print ('Specificity :{:.2f}'.format(cf_matrix[0,1]/(cf_matrix[0,1]+cf_matrix[1,1])*100))
نستخدم في الشيفرة السابقة كل من الدوال التالية والتي يكون لها معاملين هما قائمة القيم الحقيقية وقائمة قيم التنبؤ:
| الوصف | الدالة |
|---|---|
| حساب مصفوفة الارتباك | confusion_matrix |
| حساب الصحة | accuracy_score |
| حساب الدقة | precision_score |
| حساب الاستذكار | recall_score |
| حساب F1 | f1_score |
تكون نتائج مثالنا:
Confusion Matrix : [[3 1] [2 4]] Accuracy Score :70.00 Precision Score :60.00 Recall Score :75.00 F1 Score :66.67
يُمكن أيضًا رسم مصفوفة الارتباك باستخدام المكتبة seaborn كما يلي:
import seaborn as sns sns.heatmap(cf_matrix, annot=True)
مما يُظهر الشكل التالي:
خصائص المُستقبل التشغيلية ROC
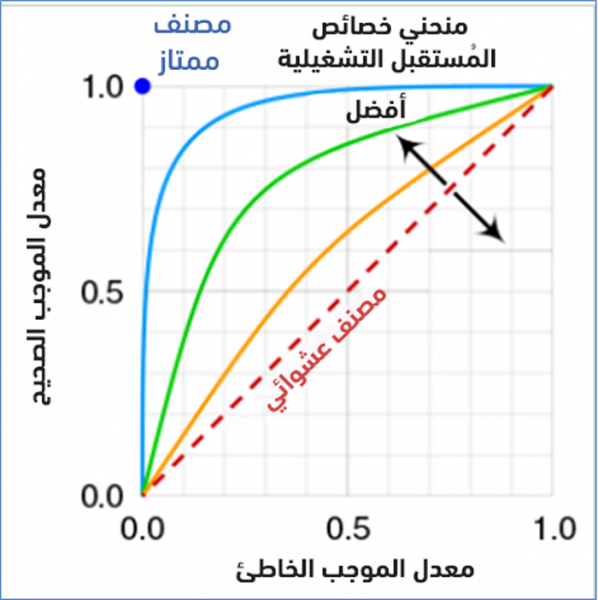
خصائص المُستقبل التشغيلية ROC -اختصار Receiver Operating Characteristic- هو منحني يُبين كفاءة نموذج التصنيف في قدرته على الفصل بين الصفوف الموجبة والسالبة.
كي يكون نموذج تصنيف ممتازًا، يجب أن يصل إلى الزاوية العليا اليسارية أي أن تكون نسبة الصفوف الموجبة الصحيحة (الاستذكار) TPR أقرب للواحد، ونسبة الصفوف الموجبة الخاطئة (الخصوصية) FPR أقرب للصفر.
يُبين الشكل التالي منحنيات ROC مختلفة ممكنة. كلما اقتربنا من أعلى اليسار كان المُصنّف أفضل:
المساحة تحت المنحني AUC
كلما كانت المساحة AUC -اختصار Area Under the Curve- تحت منحني ROC أكبر (أقرب من الواحد)، كان المُصنّف أفضل (لأن ذلك يعني أن المنحني أقرب للأعلى يسارًا).
يُمكن رسم منحني ROC في بايثون وحساب المساحة تحت المنحني AUC كما تُبين الشيفرة البرمجية التالية لمثالنا السابق:
# مكتبة الترميز from sklearn.preprocessing import LabelEncoder # الصفوف actual = ['cat', 'dog', 'cat', 'dog', 'cat', 'cat', 'dog', 'cat', 'dog', 'cat'] # التنيؤ predicted = ['cat', 'cat', 'cat', 'dog', 'cat', 'cat', 'dog', 'dog', 'dog', 'dog'] # ترميز الصفوف le = LabelEncoder() # ترميز الصفوف كأرقام actual=le.fit_transform(actual) # ترميز التنبؤ كأرقام predicted = le.fit_transform(predicted) # مكتبة المقاييس اللازمة from sklearn import metrics # مكتبة الرسم import matplotlib.pyplot as plt # حساب المقاييس fpr, tpr, _ = metrics.roc_curve(actual, predicted) auc = metrics.roc_auc_score(actual, predicted) # رسم المنحني plt.plot(fpr,tpr,label="AUC="+str(auc)) plt.ylabel('True Positive Rate') plt.xlabel('False Positive Rate') plt.legend(loc=4) plt.show()
لاحظ استخدام الصف LabelEncoder من المكتبة sklearn.preprocessing لترميز الصفوف كأرقام.
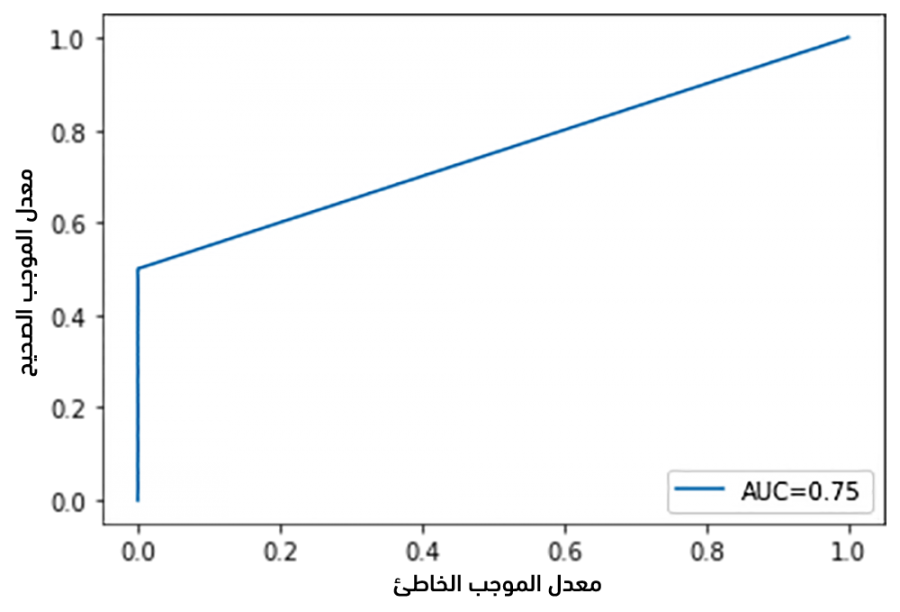
يكون الإظهار:
لاحظ أن المساحة تحت المنحني تُساوي إلى 0.75 مما يعني أن المُصنف جيد نسبيًا.
تقييم نماذج الانحدار
نُذكّر أولًا بأن الهدف من نماذج الانحدار هو التنبؤ بقيمة رقمية y انطلاقًا من قيمة (أو مجموعة من القيم) x.
ليكن لدينا مثلًا جدول بيانات التدريب التالي والذي يُعطي عدد الأعطال لآلة وفق عمر الآلة بالسنوات:
| Failures | Age |
|---|---|
| 15 | 10 |
| 30 | 20 |
| 40 | 40 |
| 55 | 50 |
| 75 | 70 |
| 90 | 90 |
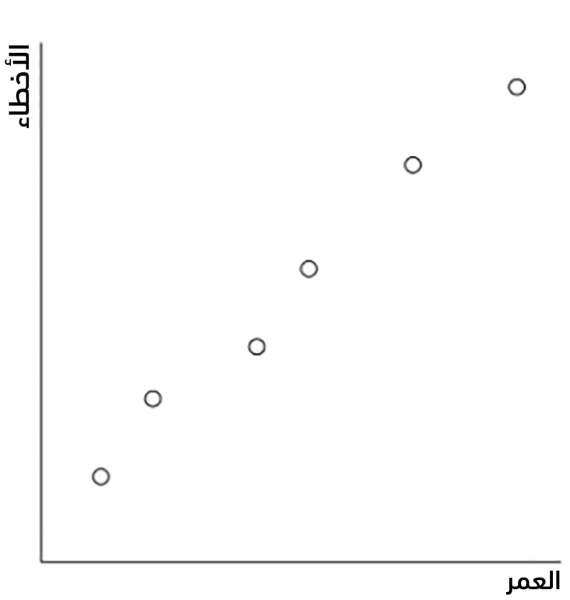
يُبين الشكل التالي هذه النقاط على محور العمر Age والأعطال Failures:
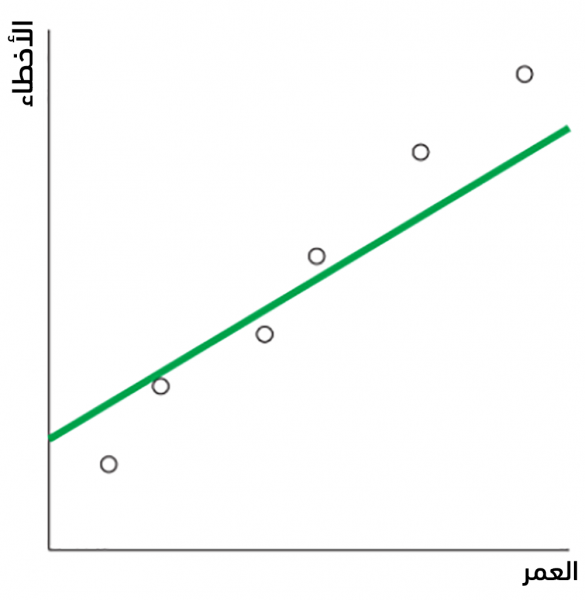
يُعدّ الانحدار الخطي linear regression من أكثر أنواع الانحدار استخدامًا نظرًا لبساطته في كل من التعلم والتنبؤ، فيُمكن مثلًا أن يتلائم fit الانحدار الخطي مع البيانات السابقة ليولد المستقيم التالي:
يُمكن حساب التنبؤ Predictions لكل من قيم الجدول السابق باستخدام معادلة المستقيم الناتجة عن نموذج الانحدار، مما يُعطي:
| Failures | Age | Predictions |
|---|---|---|
| 15 | 10 | 26 |
| 30 | 20 | 32 |
| 40 | 40 | 44 |
| 55 | 50 | 50 |
| 75 | 70 | 62 |
| 90 | 90 | 74 |
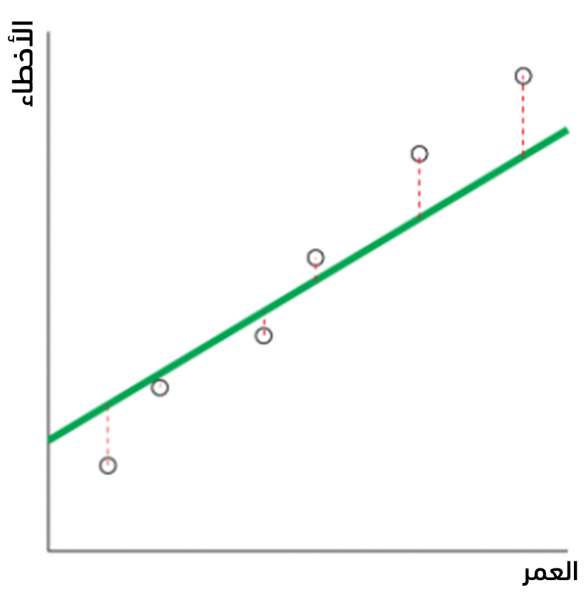
يُمكن الآن قياس مدى ملائمة المستقيم للبيانات بحساب المسافة بين النقاط الأساسية والمستقيم، وذلك بحساب الأخطاء Errors الحاصلة أي الفروقات بين القيم الأساسية و قيم التنبؤ، كما يُبين الجدول التالي:
| Errors | Predictions | Failures | Age |
|---|---|---|---|
| 11 | 26 | 15 | 10 |
| 2 | 32 | 30 | 20 |
| 4 | 44 | 40 | 40 |
| -5 | 50 | 55 | 50 |
| -13 | 62 | 75 | 70 |
| -16 | 74 | 90 | 90 |
يُبين الشكل التالي هذه الفروقات أيضًا:
تُستخدم المقاييس التالية لتقييم أداء الانحدار:
- الجذر التربيعي لمتوسطات مربعات الأخطاء Root Mean Square Error (ويختصر إلى RMSE)
- متوسط الأخطاء بالقيمة المطلقة Mean Absolute Error (ويختصر إلى MAE)
الجذر التربيعي لمتوسطات مربعات الأخطاء RMSE
تُستخدم عملية التربيع أولًا للتخلص من الإشارة السالبة للأخطاء:
| Errors2 | Errors | Predictions | Failutres | Age |
|---|---|---|---|---|
| 121 | 11 | 26 | 15 | 10 |
| 4 | 2 | 32 | 30 | 20 |
| 16 | 4 | 44 | 40 | 40 |
| 25 | -5 | 50 | 55 | 50 |
| 169 | -13 | 62 | 75 | 70 |
| 256 | -16 | 74 | 90 | 90 |
ومن ثم نحسب متوسط مربعات الأخطاء، مما يُعطي 89.5. وأخيًرا نجذر المتوسط السابق فيكون الناتج 9.9 قيمة المقياس RMSE أي الجذر التربيعي لمتوسطات مربعات الأخطاء Root Mean Square Error.
بالطبع، كلما كان هذا العدد صغيرًا فهذا يعني أن الملائمة أفضل (الحالة المثالية هي الصفر).
متوسط الأخطاء بالقيمة المطلقة MAE
| \Errors\ | Errors | Predictions | Failutres | Age |
|---|---|---|---|---|
| 11 | 11 | 26 | 15 | 10 |
| 2 | 2 | 32 | 30 | 20 |
| 4 | 4 | 44 | 40 | 40 |
| 5 | -5 | 50 | 55 | 50 |
| 13 | -13 | 62 | 75 | 70 |
| 16 | -16 | 74 | 90 | 90 |
ومن ثم نحسب المتوسط الحسابي لها، مما يُعطي: 8.5 في مثالنا وهو مقياس MAE أي متوسط الأخطاء بالقيمة المطلقة Mean Absolute Error.
يُمكن حساب هذه المقاييس في بايثون باستخدام الدوال الموافقة من المكتبة sklearn.metrics، كما تُبين الشيفرة البرمجية التالية والتي نستخدم فيها بيانات مثالنا السابق:
from sklearn.metrics import mean_absolute_error from sklearn.metrics import mean_squared_error from math import sqrt y_true = [15, 30, 40, 55, 75, 90] y_pred = [26, 32, 44, 50, 62, 74] print ('MAE :{:.2f}'.format(mean_absolute_error(y_true, y_pred))) print ('RMSE :{:.2f}'.format(sqrt(mean_squared_error (y_true, y_pred))))
يكون الناتج:
RMSE :9.92 MAE :8.50
تقييم نماذج التعلم باستخدام طريقة التقسيم العشوائي Hold-out method
لبناء نموذج مُتعلم، يجب توفير مجموعة من البيانات dataset لتنفيذ خوارزمية التعلم عليها أولًا، ومن ثم تقييم نموذج التعلم الناتج.
يجب لتقييم نموذج التعلم، بشكل حيادي، أن نمرر له مجموعة من البيانات التي لم يرها خلال تدريبه وذلك تفاديًا لحصولنا على مقاييس تقييم ممتازة مزيفة نتيجة وقوع نموذج التعلم في مطب مشكلة فرط التخصيص overfitting، أي أن النموذج تعلم بشكل جيد على الأمثلة المُمره له فقط، وهو غير قادر على تعميم التعلم ليتعامل مع أمثلة جديدة بشكل جيد.
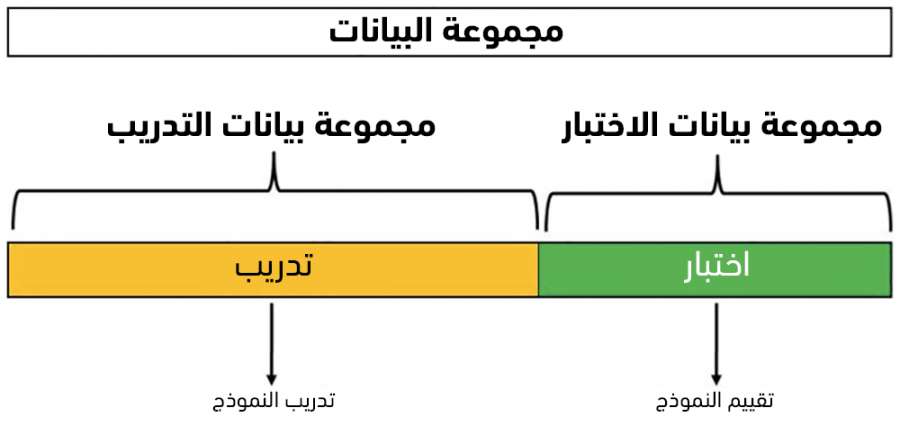
تُعدّ طريقة التقسيم العشوائي من أبسط الطرق المستخدمة لتقييم نماذج التعلم والتي تُقسّم البيانات المتاحة إلى قسمين بشكل عشوائي: ندعو القسم الأول ببيانات التدريب training data (عادًة حوالي 80% من البيانات)، والقسم الآخر المتبقي (حوالي 20%) ببينات الاختبار testing data.
نعمد إلى تدريب وبناء نموذج التعلم باستخدام بيانات التدريب فقط، ومن ثم تقييم النموذج الناتج باستخدام بيانات الاختبار.
توفر المكتبة sklearn في بايثون كل ما يلزم للقيام بذلك كما تٌبين الشيفرة البرمجية التالية والتي نبني فيها نموذج تصنيف باستخدام مُصنّف بايز Bayes وذلك على مجموعة بيانات تصنيف أزهار السوسن iris المتاحة من المكتبة نفسها.
# مجموعة بيانات # أزهار السوسن from sklearn.datasets import load_iris # مكتبة تقسيم البيانات إلى تدريب واختبار from sklearn.model_selection import train_test_split # مكتبة مُصنف بايز from sklearn.naive_bayes import GaussianNB # مكتبات مقاييس التقييم from sklearn.metrics import accuracy_score from sklearn.metrics import precision_score from sklearn.metrics import recall_score from sklearn.metrics import f1_score # تحميل البيانات X, y = load_iris(return_X_y=True) # تقسيم البيانات إلى تدريب و اختبار X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) # بناء مصنف بايز gnb = GaussianNB() # الملائمة على بيانات التدريب # والتنبؤ على بيانات الاختبار y_pred = gnb.fit(X_train, y_train).predict(X_test) # حساب مقاييس التقييم # بمقارنة بيانات الاختبار # مع تنبؤ المصنف print ('Accuracy Score :{:.2f}'.format(accuracy_score(y_test, y_pred)*100)) print ('Precision Score :{:.2f}'.format(precision_score(y_test, y_pred, average='macro')*100)) print ('Recall Score ::{:.2f}'.format(recall_score(y_test, y_pred, average='macro')*100)) print ('F1 Score ::{:.2f}'.format(f1_score(y_test, y_pred, average='macro')*100))
لاحظ أن الدالة train_test_split والتي نُمرر لها كل من:
- X: مصفوفة ثنائية يكون كل عنصر فيها مصفوفة من 4 عناصر (طول وعرض كل من السبال والبتلات لزهرة السوسن).
- y: مصفوفة أحادية (تصنيف الزهرة الموافق)
- test_size: النسبة المئوية لبيانات الاختبار من البيانات الكليه (20% افتراضيًا)
تُعيد:
- X_train: بيانات التدريب المختارة عشوائيًا من X.
- X_test: بيانات الاختبار المختارة عشوائيًا من X.
- y_train: صفوف بيانات التدريب.
- y_test: صفوف بيانات الاختبار.
يُمكن تنفيذ الشيفرة لمعاينة قيم مقاييس الأداء:
Accuracy Score :93.33 Precision Score :92.59 Recall Score :93.94 F1 Score :92.50
يجب الانتباه إلى أن هذه القيم هي قيم استرشادية، بمعنى أنها ستختلف عند كل تنفيذ للشيفرة البرمجية إذ أن حسابها يعتمد في كل مرة على مجموعة مختلفة من بيانات الاختبار (إذ أن هذه البيانات تُختار كل مرة بشكل عشوائي) مثلًا يُعطي تنفيذ ثاني لنفس الشيفرة السابقة النتائج التالية:
Accuracy Score :90.00 Precision Score :92.31 Recall Score :92.86 F1 Score :91.65
تقييم نماذج التعلم باستخدام طريقة التقييم المتقاطع Cross Validation method
تهدف هذه الطريقة بشكل أساسي إلى استخدام كل البيانات للتدريب (بخلاف الطريقة السابقة والتي تستخدم قسمًا منها فقط)، كما أن قيم مقاييس التقييم ستكون نفسها من أجل كل تنفيذ للشيفرة (بخلاف الطريقة السابقة كما عرضنا أعلاه).
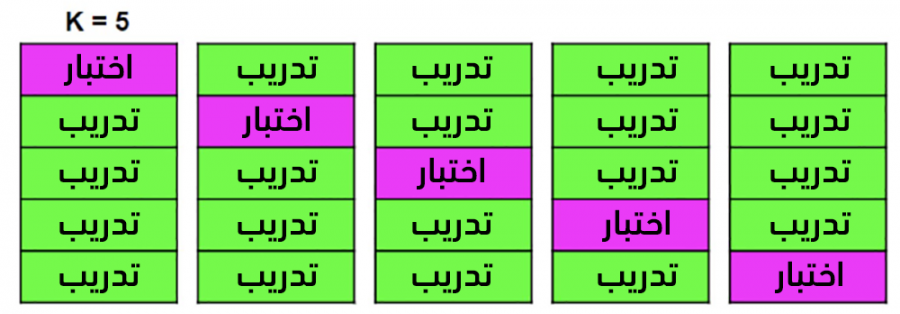
عوضًا عن تقسيم البيانات إلى بيانات للتدريب وبيانات للاختبار (التقييم) مما يُخفّض من البيانات التي يُمكن لنا استخدامها للتدريب، نستخدم التقويم المتقاطع مع عدد محدّد من الحاويات K-Fold.
تُقسم بيانات التدريب إلى عدد K من الحاويات ومن ثم نقوم بتكرار ما يلي K مرة: في كل مرة i نقوم بتدريب النموذج مع بيانات K-1 حاوية (كل الحاويات ما عدا الحاوية i) ومن ثم تقييمه مع بيانات الحاوية i. في النهاية، يكون مقياس الأداء النهائي هو متوسط مقياس التقييم لكل التكرارات (i:1..K).
توفر المكتبة sklearn في بايثون الدالة cross_val_score لتنفيذ التقييم المتقاطع مع تحديد عدد الحاويات المطلوب، كما تُبين الشيفرة البرمجية التالية والتي نحسب فيها مقياس الدقة مثلًا:
# مجموعة بيانات # أزهار السوسن from sklearn.datasets import load_iris # مكتبة تقسيم البيانات إلى تدريب واختبار from sklearn.model_selection import train_test_split # مكتبة مُصنف بايز from sklearn.naive_bayes import GaussianNB # مكتبة التقييم المتقاطع from sklearn.model_selection import cross_val_score # مكتبات مقاييس التقييم from sklearn.metrics import accuracy_score from sklearn.metrics import precision_score from sklearn.metrics import recall_score from sklearn.metrics import f1_score # تحميل البيانات X, y = load_iris(return_X_y=True) # تقسيم البيانات إلى تدريب و اختبار X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) # بناء مصنف بايز gnb = GaussianNB() # حساب مقياس الصحة scores = cross_val_score(gnb, X, y, cv=5, scoring="accuracy") print(scores) # حساب المتوسط meanScore = scores.mean() print(meanScore * 100)
يكون ناتج التنفيذ (في كل مرة):
[0.93333333 0.96666667 0.93333333 0.93333333 1. ] 95.33333333333334
اختيار نموذج التعلم الأفضل
يُمكن استخدام طريقة التقويم المتقاطع السابقة لتقييم مجموعة من نماذج التعلم. نُعرّف في الشيفرة البرمجية التالية الدالة cv_comparison_classification والتي نُمرر لها مجموعة من نماذج التعلم models والبيانات كلها (X,y) وعدد الحاويات cv، وتُعيد هذه الدالة إطار بيانات يُظهر مقياس الدقة لكل نموذج.
تدور حلقة for في الدالة على النماذج المُمرره، وتستدعي من أجل كل نموذج دالة التقويم المتقاطع من المكتبة sklearn.model والتي تُعيد قائمة بقيم مقياس الصحة (كل عنصر في القائمة هو قيمة مقياس الصحة من أجل حاوية اختبار ما).
نحسب متوسط mean القائمة السابقة، ونضيف عمودًا جديدًا إلى إطار البيانات يكون اسمه اسم النموذج والقيمة في الخلية الموافقة للسطر الوحيد في إطار البيانات (والمفهرس بـ Accuracy) قيمة مقياس الصحة.
# مكتبة أطر البيانات import pandas as pd # مكتبة التقييم المتقاطع from sklearn.model_selection import cross_val_score # دالة لمقارنة مجموعة من النماذج def cv_comparison_classification(models, X, y, cv): # تهيئة إطار بيانات لمقاييس التقييم cv_df = pd.DataFrame() # الدوران على النماذج # تطبيق التقييم المتقاطع for model in models: # حساب مقياس الصحة لكل حاوية acc = cross_val_score(model, X, y,scoring='accuracy', cv=cv) # حساب متوسط الصحة للنموذج acc_avg = round(acc.mean(), 4) # كتابة النتيجة في إطار البيانات cv_df[str(model)] = [ acc_avg] cv_df.index = ['Accuracy'] return cv_df
نستدعي في الشيفرة البرمجية التالية الدالة السابقة للمقارنة بين ثلاثة نماذج للتصنيف: مصنف بايز GaussianNB ومصنف أشجار القرار DecisionTreeClassifier ومصنف أقرب الجيران KNeighborsClassifier.
نستخدم بيانات تصنيف أزهار السوسن المتاحة من sklearn.datasets لتنفيذ نماذج التعلم عليها.
# مجموعة بيانات # أزهار السوسن from sklearn.datasets import load_iris # مصنف بايز from sklearn.naive_bayes import GaussianNB # مصنف شجرة القرار from sklearn.tree import DecisionTreeClassifier # مصنف أقرب الجيران from sklearn.neighbors import KNeighborsClassifier # تحميل البيانات X, y = load_iris (return_X_y=True) # إنشاء متغيرات النماذج mlr_g = GaussianNB() mlr_d = DecisionTreeClassifier() mlr_k = KNeighborsClassifier() # وضع النماذج في قائمة models = [mlr_g, mlr_d, mlr_k] # استدعاء دالة المقارنة comp_df = cv_comparison_classification(models, X, y, 4) # إظهار إطار البيانات للمقارنه print(comp_df)
يُظهر تنفيذ الشيفرة السابقة إطار البيانات التالي والذي يسمح لنا بمعاينة مقياس الصحة لكل نموذج مما يسمح لنا باختيار الأنسب منها:
الخلاصة
عرضنا في هذه المقالة مقاييس تقييم نماذج التعلم المختلفة وكيفية اختيار النموذج الأفضل منها لمسألة معينة.
يُمكن تجربة جميع أمثلة المقالة من موقع Google Colab من الرابط أو من الملف المرفق.
الملف المرفق eval.zip.















أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.