يعد باي تورش PyTorch أحد أشهر أطر عمل التعلم العميق Deep Learning، فهو الخيار الأول للباحثين في هذا المجال، وتزداد باستمرار أعداد الشركات ومراكز الأبحاث التي تتبنى استخدامه نظرًا لمرونته الكبيرة التي تساعد على تنفيذ الأفكار المختلفة.
سنتعرف في هذه المقالة على مفاهيم أساسية في إطار عمل باي تورش PyTorch مثل مفهوم التفاضل التلقائي automatic differentiation، ومفهوم المخططات الرسومية الحسابية computation graphs، وكيفية تحقيق الاستفادة العظمى من المكتبات والأدوات التي يوفرها باي تورش واستخدامها لتطبيق هذه المفاهيم.
المتطلبات السابقة
يتطلب فهم هذه المقالة توفر الإلمام بالمواضيع التالية:
- معرفة بأساسيات الذكاء الاصطناعي والتعلم العميق
- فهم قاعدة التسلسل chain rule، وهي صيغة رياضية مستخدمة في تدريب نماذج التعلم العميق
- تنزيل إطار عمل باي تورش على الجهاز المحلي لتجربة الأكواد والأمثلة العملية
التفاضل التلقائي Automatic Differentiation
قبل مناقشة الهياكل الأساسية المستخدمة في باي تورش، سنوضح بداية مفهوم التفاضل التلقائي automatic differentiation -أو autograd اختصارًا- ودوره في التعلم العميق، فعملية حساب المشتقات أساسية في مجال التعلم العميق لدورها في تحسين أداء الشبكات العصبية. لكن تعقيدها يتزايد مع تعقيد النماذج، لذا طُورت تقنيات متقدمة مثل التفاضل التلقائي للتعامل مع هذا الأمر بكفاءة عالية.
تعمل هذه التقنية -كما سنشرح لاحقًا- على إنشاء رسم بياني حسابي يتتبع العلاقات بين المتغيرات، مما يسمح بحساب المشتقات بشكل تلقائي ودقيق عبر طبقات الشبكة العصبية. حيث تحتوي الشبكات العصبية على ملايين المعاملات والأوزان التي تحتاج لتعلمها من خلال التدريب، وخلال عملية التدريب سنحتاج لحساب المشتقات Derivatives لمعرفة كيفية تحديث هذه المعاملات بما يضمن تحسين أداء النموذج.
فالتفاضل التلقائي هو العمود الفقري لإطار عمل باي تورش PyTorch ولجميع مكتبات وأطر التعلم العميق، ويساعدنا محرك التفاضل التلقائي المدمج في باي تورش PyTorch والمعروف أيضًا بمحرك Autograd في فهم آلية عمل التفاضل التلقائي والأساس الذي بنيت عليه أطر عمل الذكاء الاصطناعي.
تمتلك معماريات الشبكات العصبية ملايين المعاملات parameters القابلة للتعلم، وتمر عملية تدريب أي شبكة عصبية بمرحلتين وهما:
- مرحلة الانتشار الأمامي Forward pass التي تحسب قيمة الخسارة باستخدام دالة خسارة loss function
- مرحلة الانتشار الخلفي Backward pass التي يحسب قيم التدرجات gradients لتحديث المعاملات القابلة للتعلم
يكون الانتشار الأمامي forward pass في غاية البساطة، فالمخرجات للطبقة الحالية هي مدخلات الطبقة التالية ويستمر هذا النمط في التكرار، ولكن الانتشار الخلفي backward pass أكثر تعقيدًا من الناحية الحسابية، فهو يتطلب استخدام قاعدة السلسلة التفاضلية chain rule من أجل حساب التدرجات بالنسبة لمعاملات دالة الخسارة loss function، بمعنى أبسط تُخبرنا التدرجات بكيفية تعديل الأوزان والمعاملات في الشبكة العصبية لتقليل الخسارة.
اقتباسالتدرج gradient ∇ هو رمز لعملية رياضية تفاضلية مثل حرف d المستخدم في عملية التفاضل أو ∂ المستخدم للتفاضل الجزئي، ويختلف في كونه يجري تفاضل متجه vector مكون من عدة عناصر، حيث نشتق كل عنصر في هذه المتجه بالنسبة للبعد أو المحور الذي يمثله، وبالتالي دخل هذه العملية متجه وخرجها متجه.
مثال بسيط
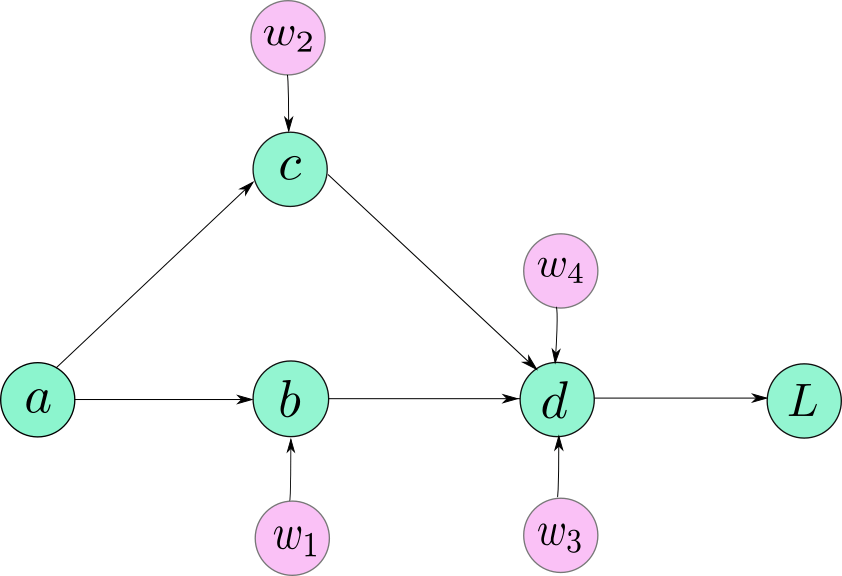
لنلقِ النظر على شبكة عصبية في غاية البساطة، تتكون من 5 عصبونات أو عقد neurons، وتعرض هذه الصورة الشبكة العصبية التي نتحدث عنها.
تصف المعادلات التالية هذه الشبكة العصبية البسيطة:
لنحسب التدرجات التصحيحية لكل معامل قابل للتعلم w:
حُسِبَت جميع هذه التدرجات gradients باستخدام قاعدة السلسلة chain rule، ويمكن أن نلاحظ أن جميع التدرجات الفردية في الجانب الأيمن من المعادلة يمكن حسابها بشكل مباشر بما أن البسط هو دالة ضمنية لتلك الموجودة في المقام.
المخططات البيانية الحسابية Computation Graphs
يمكن أن نحسب التدرجات gradients لشبكتنا العصبية يدويًا لأنها شبكة بسيطة للغاية، ولكن ماذا لو أردنا إجراء حسابات لشبكة تتكون من 152 طبقة، أو شبكة تمتلك عددًا كبيرًا من التفرعات. يتطلب تصميم برنامج لبناء الشبكات العصبية الاصطناعية ANN إيجاد طريقة تمكننا من حساب التدرج التصحيحي gradient بسهولة لمختلف المعماريات التي يمكن تكونيها، فنحن لا نريد أن ينشغل المطور بالتعامل اليدوي مع عملية حساب التدرج gradient عند حدوث أي تغيير في تصميم الشبكة.
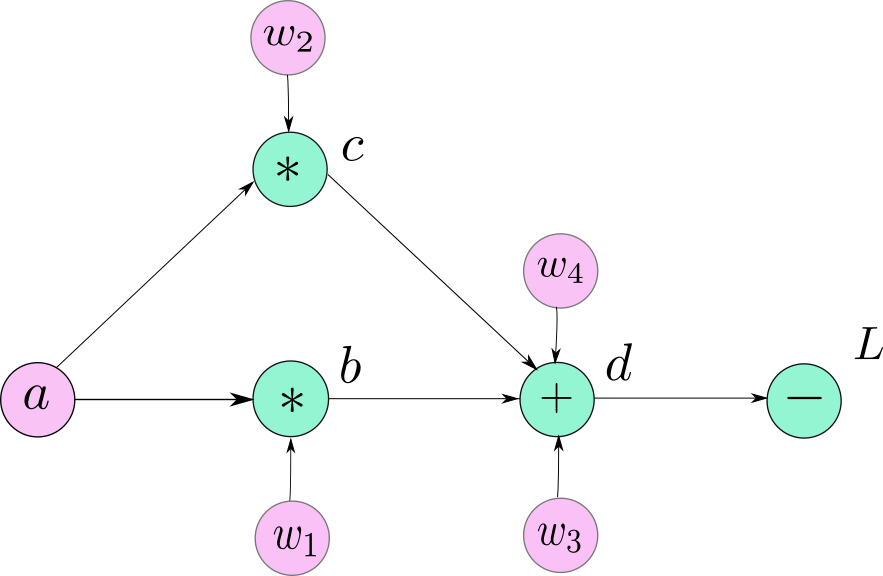
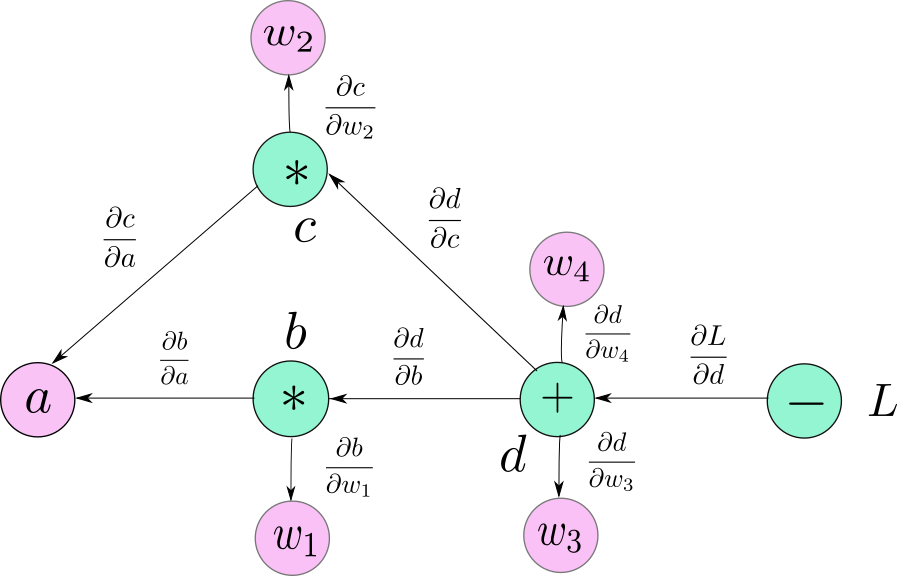
يمكننا تحقيق هذا المبدأ باستخدام هيكل بيانات يسمى المخطط البياني الحسابي computation graph، وتتشابه هذه البنية في الشكل مع الرسم التوضيحي للشبكة العصبية البسيطة، مع وجود بعض الاختلافات، حيث أن العقد nodes في المخطط الحسابي هي معاملات operators وهي معاملات حسابية في أغلب الحالات كالجمع والطرح والضرب والقسمة، عدا في حالة واحدة حيث نحتاج لتعريف معامل operator يعبر عن عملية إنشاء المستخدم لمتغير مخصص.
نلاحظ في الصورة التالية أننا رمزنا للمتغيرات الطرفية leaf variables بالرموز التالية a, w1, w2, w3, w4 من أجل التوضيح وسهولة التعامل، ولكنها ليست جزءًا أصيلًا من المخطط الرسومي graph، فما تمثله هو الحالة الخاصة التي ينشئ فيها المستخدم المتغيرات الخاصة به.
أنشئت المتغيرات التالية b,c,d كنتيجة للعمليات الحسابية، بينما تكون المتغيرات a,w1,w2,w3,w4 معرّفة ومدخلة بواسطة المستخدم، وبما أنها ليست متغيرات ناتجة أن أي عملية حسابية، فسنرمز للعقد التي تعبر عنها باسم المتغير الذي أنشأه المستخدم. وهذا ينطبق على كل العقد الطرفية leaf nodes في المخطط الحسابي.
حساب التدرجات Gradients
بعد التعرف على بعض المفاهيم الأساسية، لنتعرف الآن على آلية حساب التدرجات gradients باستخدام المخطط الحسابي computation graph، يمكن اعتبار كل عقدة node في المخطط -باستثناء العقد الطرفية- دالة تستقبل مدخلات وتعالجها وتدفع بالمخرجات لتنتشر خلال المخطط.
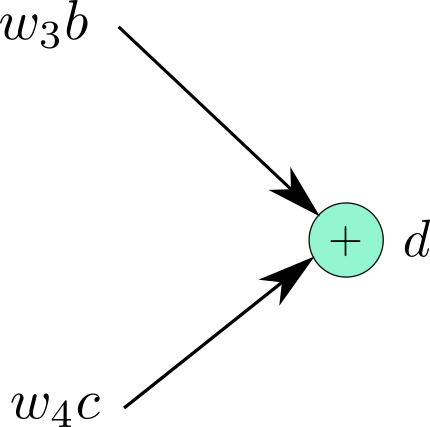
لنلقِ نظرة على العقدة التي تخرج المتغير d بعد معالجة المدخلات w4×c و w3×b، يمكننا التعبير عنها كدالة على النحو التالي:
حيث تعبر d عن مخرجات الدالة f(x,y)=x+y.
يمكننا الآن وببساطة حساب التدرجات gradients للدالة f بالنسبة لمدخلاتها، وفق المعادلة التالية:
بعد حساب التدرجات gradients سنعمل على وسم الأسهم في الاتجاه المعاكس لها بقيمة التدرج الخاص بها، كما في الصورة التالية:
توضح الصورة التالية المخطط الحسابي كاملًا بعد أن طبقنا هذه على الخطوات عند كل العقد:
تاليًا، سنصف الخوارزمية التي تحسب القيمة المشتقة عند أي عقدة في المخطط الحسابي بالنسبة لدالة الخسارة L. لنقل أننا نريد حساب الاشتقاق التالي :
سنتبع أولًا كل المسارات الممكنة من d إلى w4 وفي حالتنا هناك مسار واحد يصل بين المتغيرين، ثم سنضرب قيم الحواف أو الوصلات edges الواقعة على هذا المسار. يمكن أن نلاحظ أن حاصل الضرب الناتج هو نفسه الذي حصلنا عليه عند استخدام قاعدة السلسلة chain rule، وإذا كان هناك أكثر من مسار يربط المتغير بدالة الخسارة L نضرب الوصلات في كل مسار ثم نجمع حاصل الضرب من كل مسار، كما في المثال التالي:
حساب التفاضل التلقائي في PyTorch Autograd
بعد أن تعرفنا بشكل مفصل على ماهية المخطط الحسابي computational graph، لنستكشف الآن آلية تطبيق المخطط الحسابي في باي تورش PyTorch بشكل آلي، سنستخدم هيكل بيانات يسمى التنسور أو المُوتِر Tensor وهو أساسي في باي تورش PyTorch، حيث يشبه نوعًا ما مصفوفات مكتبة نمباي NumPy arrays، ولكن على النقيض من نمباي NumPy، فإن التنسورات tensors مصممة للاستفادة من قدرات الحوسبة الفائقة على التوزاي التي توفرها وحدات المعالجة الرسومية GPUs، ويتشابه الكود وقواعد كتابته مع تلك الموجودة في نمباي NumPy.
للنشئ tensor من 3 صفوف و 5 اعمدة، ونهيأه بقيم عشوائية كما يلي:
In [1]: import torch In [2]: tsr = torch.Tensor(3,5) In [3]: tsr Out[3]: tensor([[ 0.0000e+00, 0.0000e+00, 8.4452e-29, -1.0842e-19, 1.2413e-35], [ 1.4013e-45, 1.2416e-35, 1.4013e-45, 2.3331e-35, 1.4013e-45], [ 1.0108e-36, 1.4013e-45, 8.3641e-37, 1.4013e-45, 1.0040e-36]])
لنضمن قيام باي تورش PyTorch بإنشاء مخطط حسابي للموترات tensor الذي عرفناه، ينبغي علينا ضبط قيمة المتغير requires_grad إلى True، فبدون هذه الخطوة سيكون الموتر مجرد هيكل بيانات تقليدي كالذي توفره مكتبة نمباي NumPy يمكن استخدامه للعمليات الجبر الخطي السريعة.
قد يكون استخدام باي تورش لإنشاء موترات أمرًا مربكًا في البداية، حيث توجد عدة طرق لإنشاء الموترات tensors، فتسمح بعض الطرق بتمرير تعريف المتغير requires_grad بشكل صريح في الدالة المُنشأة، وطرقًا أخرى تجعلنا نضبط هذا المتغير يدويًا بعد إنشاء الموتر tensor.
t1 = torch.randn((3,3), requires_grad = True) t2 = torch.FloatTensor(3,3) # لا تسمح هذه الدالة بضبط هذا المتغير وقت الإنشاء # لكن يمكن ضبطه بعد الإنشاء t2.requires_grad = True
تحدد الخاصية requires_grad فيما إذا كان على باي تورش تتتبع العمليات الرياضية التي تنفذ على الموتر حتى يتمكن لاحقًا من حساب التدرجات gradients أثناء الانتشار الخلفي، فإذا كانت قيمته True يجري تتبع العمليات وحساب التدرجات لاحقًا، وفي حال كانت False لن يكون هناك تتبع للعمليات، ولن تحسب التدرجات.
وعند إنشاء موتر tensor كنتيجة لعملية على موتر آخر يضبط هذه الخاصية بالقيمة True فإن الموتر الناتج سيمتلكها أيضًا، فيلزم على الأقل أن يكون أحد الموترات tensors الداخلة في العملية قد فعّل هذه الخاصية أثناء إنشائه لتنتشر من خلال الموتر الناتج عن هذه العملية حتى إن لما تكن مفعلة في باقي الموترات.
كما يمتلك كل موتر tensor خاصية تسمى grad_fn ، والتي تشير إلى إلى معامل رياضي operator يقوم بإنشاء المتغير، وحينما تكون خاصية requires_grad غير مفعلة False فتكون grad_fn قيمتها None.
سنجد في مثال d=f(w3b,w4c)، أن دالة التدرج grad function ستكون هي عملية الجمع، حيث تجمع الدالة f المدخلات معًا، وستكون عملية الجمع عقدة في المخطط الحسابي الذي يخرج d، وفي حالة كون العقدة طرفية أي متغير معرف بواسطة المستخدم فستكون دالة التدرج الخاصة به grad_fn=None.
import torch a = torch.randn((3,3), requires_grad = True) w1 = torch.randn((3,3), requires_grad = True) w2 = torch.randn((3,3), requires_grad = True) w3 = torch.randn((3,3), requires_grad = True) w4 = torch.randn((3,3), requires_grad = True) b = w1*a c = w2*a d = w3*b + w4*c L = 10 - d print("The grad fn for a is", a.grad_fn) print("The grad fn for d is", d.grad_fn)
ينتج تشغيل هذا الكود الخرج التالي:
The grad fn for a is None The grad fn for d is <AddBackward0 object at 0x1033afe48>
دوال الصنف Autograd.Function
تُنفَّذ جميع العمليات الحسابية في باي تورش PyTorch من خلال الصنف البرمجي torch.nn.Autograd.Function، الذي يشكل جزءًا أساسيًا من آلية التفاضل التلقائي. يعتمد هذا الصنف على دالتين رئيسيتين: الأولى هي دالة الانتشار الأمامي backward والتي تحسب المخرجات بناءً على المدخلات السابقة، مما يمثل العملية الحسابية التي تجريها الطبقة أثناء تمرير البيانات عبر النموذج. أما الدالة الثانية فهي دالة الانتشار الخلفي backward التي تتولى حساب التدرجات من خلال استقبالها من الطبقات التالية في الشبكة.
يمكن ملاحظة أن اتجاه انتشار التدرجات gradients يكون عكسيًا، أي من المخرجات نحو المدخلات، وليس العكس. هذا يعني أن التدرجات القادمة من الدالة f تنتقل من الطبقات الأخيرة في النموذج إلى الطبقات الأولى. وتعدّل الأوزان في كل طبقة بناءً على مدى تأثيرها على الخطأ النهائي. يتم ذلك عن طريق ضرب التدرج القادم من الطبقة التالية في التدرج المحلي الخاص بتلك الطبقة، مما يساعد على حساب مقدار التغيير اللازم لكل وزن حتى تتحسن دقة النموذج.
وبالتالي، تتلقى كل طبقة معلومات من الطبقة التي تليها حول كيفية تغيير أوزانها لتقليل الخطأ، ويستمر هذا التدفق العكسي حتى تصل التحديثات إلى أول طبقة في النموذج. هذا هو جوهر عملية الانتشار الخلفي التي تتيح للنموذج التعلم من الأخطاء وتحسين أدائه بمرور الوقت.
مثال عملي
لنفهم الأمر بمثال عملي لنفرض أن لدينا دالة حسابية بسيطة تمثل جزءًا من شبكة عصبيةd = f(w3b , w4c)
d هنا هي موتر tensor، ودالة التدرج grad_fn هي <ThAddBackward> وهي عملية جميع بسيطة حيث أن الدالة التي أنشئت d تجمع المدخلات، وتتلقى دالة الانتشار الأمامي forward مدخلات دالة التدرج grad_fn حيث تتلقى w3b و w4c وتجمع المدخلات في دالة التدرج، ثم تتدفق النتيجة للأمام بعد أن تحفظ في الموتر d.
وتتلقى دالة التراجع backward الخاصة بالدالة <ThAddBackward> التدرجات الداخلة incoming gradient من الطبقات التالية لها كمدخلات أي الطبقات التي على يمين الطبقة الحالية، ما نحاول حسابه هو الاشتقاق الجزئي لدالة الخسارة L بالنسبة للمتغير d والتي تتكون من كل القيم الموجودة على الوصلات edges التي تربط بين L و d، ويمكن الوصول لقيم التدرجات gradients بالنسبة للمتغير d حيث تخزن في grad وهو خاصية للموتر، فتصل لها من خلال d.grad.
نحسب بعد هذا التدرجات المحلية local gradients، أي التفاضل الجزئي للمتغير d أس الدالة التي تجمع بالنسبة للمدخلات w4c ومرة أخرى بالنسبة للمدخل w3b. تُضرب التدرجات gradients القادمة من الطبقات التالية مع التدرجات المحسوبة محليًا بواسطة دالة التراجع، ومن ثم ترسل التدرجات لتنتشر تراجعيًا ناحية المدخلات محفزة تفاعلًا متسلسلًا، تشغّل فيه دالة التراجع لحساب تدرجات الدالة grad_fn المرتبطة بالمدخلات السابقة.
نوضح الأمر بمثال، تقوم دالة التراجع backward المرتبطة بالدالة <ThAddBackward> الخاصة بالمتغير d بتحفيز دالة التراجع للمدخلات grad_fn والتي بدورها تحفز دالة التراجع للمدخل w4c، لاحظ أن w4c هو موتر انتقالي أي أنه مُنشَأ لحفظ ناتج العملية الوسيطة ودالة التدرجات gradient الخاصة به هي <ThMulBackward>، وحينما تستدعي هذه دالة التراجع backward لحساب عملية التدرجات gradients يمرر لها تدرج الاشتقاق الجزئي لدالة الخسارة L بالنسبة إلى المتغير d مضروبة في الاشتقاق الجزئي للمتغير d بالنسبة للمتغير w4c، وتوضح الصورة التالية المعادلة المعبرة عن هذه العملية:
ويحين الدور الآن على المتغير w4c، فتصبح المعادلة المكتوبة في الأعلى هي المدخلات لهذه العقدة في عملية الانتشار التراجعي لحساب التدرجات gradients، كما كان الأمر في الخطوة الثالثة بالنسبة للمتغير d حيث كانت المدخلات هي الاشتقاق الجزئي لدالة الخسارة بالنسبة للمتغير d.
لنطبق الأمر من خلال خوارزمية تحسب عملية الانتشار الخلفي باستخدام المخطط الحسابي computation graph، هذا ليس التطبيق الكامل لهذه الدالة ولكنه مثال توضيحي بسيط.
def backward(self, incoming_gradients): # اضبط قيمة التدرج للموتر الحالي self.Tensor.grad = incoming_gradients # حلقة تكرارية لتنفيذ الانتشار التراجعي للتدرجات for inp in self.inputs: if inp.grad_fn is not None: # احسب التدفقات القادمة تجاه المُدخل الحالي # Compute new incoming gradients for the input new_incoming_gradients = incoming_gradients * local_grad(self.Tensor, inp) # استدعِ دالة التراجع بشكل تعاودي # Recursively call inp.grad_fn.backward(new_incoming_gradients)
نجد في هذا الكود أن self.Tensor هو موتر Tensor منشئ بواسطة Autograd.Function، والتي كانت في مثالنا d، وقد شرحنا سابقًا مفهوم التدرجات القادمة incoming gradients والتدرجات المحلية local gradients.
لنحسب المشتقات في الشبكة العصبية، سنحتاج لاستدعاء دالة التراجع backward وتطبيقها على Tensor الذي يمثل الخسارة loss، ونستمر في الرجوع للخلف backtrack خلال المخطط الحسابي بداية من العقدة التي تمثل دالة التدرج grad_fn الخاصة بدالة الخسارة.
وشرحنا سابقًا أن دالة التراجع backward تستدعى بشكل تعاودي recursive، فأثناء تتبع أثر التفرعات خلال الشبكة الحسابية نستدعي هذه الدالة، والتي بدورها تستدعي نفسها عندما تتراجع للمستوى السابق وهكذا حتى نصل لحالة التوقف الأساسية base case وهي العقد الطرفية leaf node والتي تكون دالة التدرج grad_fn فيه عديمة القيمة None.
ننبه لأن باي تورش PyTorch يعطي خطأ Error عندما نحاول استدعاء دالة التراجع backward وتطبيقها على موتر تتكون عناصره من متجهات متعددة القيم vector-valued Tensor، ويعني هذا أن دالة التراجع backward تعمل على موترات تحتوي قيمًا رقمية أحادية scalers.
import torch a = torch.randn((3,3), requires_grad = True) w1 = torch.randn((3,3), requires_grad = True) w2 = torch.randn((3,3), requires_grad = True) w3 = torch.randn((3,3), requires_grad = True) w4 = torch.randn((3,3), requires_grad = True) b = w1*a c = w2*a d = w3*b + w4*c L = (10 - d) L.backward()
سوف يعطي تشغيل هذا الكود الخطأ التالي:
RuntimeError: grad can be implicitly created only for scalar outputs
يرجع سبب هذا الخطأ لكون قيم التدرجات gradient قابلة لأن تحسب بالنسبة لقيم رقمية أحادية scalers، السبب هو طريقة تعريف التدرج gradient definition، حيث لا يمكنها أن تفاضل متجهًا بالنسبة لمتجه آخر، ولتحقيق ذلك نستخدم عملية رياضية مختلفة تسمى Jacobian وهي خارج نطاق اهتمامنا في هذا المقال.
تكمن المشكلة في توقع دالة التراجع بأن تكون المخرجات قيمة واحدة أو رقم واحد وليست متجهًا. يمكننا تجاوز هذه المشكلة بطريقتين، حيث يمكننا إجراء تعديل بسيط على الكود السابق بضبط قيمة L لتكون مجموع كل الأخطاء، سوف يحل هذا مشكلتنا.
import torch a = torch.randn((3,3), requires_grad = True) w1 = torch.randn((3,3), requires_grad = True) w2 = torch.randn((3,3), requires_grad = True) w3 = torch.randn((3,3), requires_grad = True) w4 = torch.randn((3,3), requires_grad = True) b = w1*a c = w2*a d = w3*b + w4*c # L = (10 - d) استبدلنا هذا # بهذا L = (10 -d).sum() L.backward()
يمكننا الوصول للتدرجات الآن بكل سهولة من خلال استدعاء خاصية grad الموجودة في الموتر Tensor.
لنشرح الطريقة الثانية مفترضين أننا نحتاج -لأي سبب من الأسباب- لاستخدام دالة backward على دالة متجهة vector function، يمكننا تجاوز الخطأ بتمرير موتر torch.ones للدالة بأبعاد مطابقة للموتر الذي نحاول تمريره لدالة التراجع.
# L.backward() استبدل L.backward(torch.ones(L.shape))
ويمكن أن نلاحظ أننا مررنا لدالة backward التدرجات القادمة incoming gradients من مدخلاتها، وبهذا جعلنا الدالة تتلقى التدرجات gradients على هيئة موترات مليئة بالواحد Tensor of ones بنفس أبعاد L، مما يجعلها قابلة للانتشار الخلفيbackward propagation بشكل مبسط.
تمكننا هذه الطريقة من الحصول على تدرجات gradients أي موتر Tensor، وتحديث الأوزان والمعاملات من خلال خوارزمية التحسين التي نفضلها.
w1 = w1 - learning_rate * w1.grad
أبرز الاختلافات بين باي تورش PyTorch و تنسورفلو Tensorflow المخططات الحسابية
ينشئ باي تورش PyTorch مخططات حسابية ديناميكية Dynamic Computation Graph أي أنها تولد بشكل مرن تلقائيًا عند الحاجة، واستخدام دالة الانتشار الأمامي forward هو المحفز لإنشاء المتغيرات التي سنستخدمها لاحقًا في خطوة الانتشار الخلفي، وبالتالي قبل استدعاء دالة الانتشار الأمامي forward لن توجد أي عقدة تحمل موتر بخاصية دالة التدرج grad_fn.
# لا يوجد أي شبكة حسابية حتى الآن، فهنا نعرف مجرد عقدة طرفية a = torch.randn((3,3), requires_grad = True) # ينطبق نفس الأمر هنا، مجرد تعريفنا لموتر w1 = torch.randn((3,3), requires_grad = True) # هنا يتم إنشاء شبكة حسابية بها دالة ضرب سيتم استخدامها لحساب التدرجات b = w1*a #Graph with node `mulBackward` is created.
أنشئت الشبكة الحسابية هنا كنتيجة لتشغيل دالة الانتشار الأمامي forward الخاصة بعدة موترات tensors، وفقط عند استدعائها تُخصّص مساحات تخزينية ومتغيرات وسيطة لتحتفظ بالقيم الانتقالية التي ستستخدم في حساب التدرجات gradient لاحقًا عندما تستدعى دالة التراجع backward ، وتُحرّر المساحات التخزينية المخصصة فور الانتهاء من حساب التدرجات gradients في العقد غير الطرفية، وعندما تستدعى دالة الانتشار الأمامي forward على نفس المجموعة من الموترات Tensors، يعاد استخدام المساحات التخزينية للعقد الطرفية من التشغيل السابق للشبكة، بينما تنشأ وتخصص من جديد تلك المساحات الانتقالية أو الوسيطة عند وصول دالة الانتشار الأمامي لها.
إن حاولنا استدعاء دالة التراجع backward أكثر من مرة على عقد غير طرفية non-leaf nodes، سنحصل على الخطأ التالي:
RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.
يرجع هذا الخطأ لتحرير المساحات التخزينية التي أنشئت سابقًا للعقد غير الطرفية عند استدعاء دالة backward ، فلا يوجد طريق تنتشر فيه خلفيًا من خلاله عند استدعاء الدالة مرة أخرى، الأمر أشبه بعبور جسر من الحبال ثم قطع الحبال، للعبور مجددًا سنحتاج لإنشاءها من جديد، ولكن يمكنك أن نلغي هذا التأثير بضبط خاصية متاحة في دالة backward وهي retain_graph لتكون True.
loss.backward(retain_graph = True)
عند تفعيل هذه الخاصية سنتمكن من استخدام التراجع الخلفي backpropagation على نفس المخطط الحسابي، حيث ستتراكم التدرجات gradients، أي في المرة القادمة التي ننفذ فيها التراجع الخلفي ستضاف قيم التدرجات إلى تلك الموجودة سابقًا والمخزنة من الدورة السابقة.
يناقض هذا طريقة عمل المخططات الحسابية الثابتة Static Computation Graphs التي يستخدمها تنسورفلو TensorFlow، حيث يعرف المخطط الحسابي قبل تشغيل البرنامج. ويجري تشغيله عن طريق إدخال القيم المعرفة مسبقًا.
تسمح المخططات الحسابية الديناميكية dynamic graph بالتغيير في معمارية المخطط أثناء التشغيل، حيث يتم إنشاء المخطط فقط عند تشغيل جزء محدد من الكود. ويعني هذا أيضًا أن المخطط يمكن أن يعاد تعريفه أثناء تشغيل البرنامج، وكما وضحنا فهذا غير ممكن في المخطط الثابت حيث يعرف المخطط وينشأ قبل تشغيل البرنامج.
ويسهل تقفي أثر الأخطاء والمشاكل التي قد تحدث مع المخططات الديناميكية المرنة حيث يمكننا معرفة مصدر الخطأ، فلن نستطيع إكمال الانتشار إن وجدنا مشكلة بجزء معين، على النقيض من المخططات الثابتة حيث يتم الانتشار في مسارات معرفة مسبقًا.
| وجه المقارنة | مخطط حسابي ديناميكي | مخطط حسابي ثابت |
|---|---|---|
| إطار العمل | باي تورش PyTorch | تنسورفلو TensorFlow |
| تعريف المخطط | وقت التشغيل | قبل التشغيل |
| طريقة التشغيل | يؤجل التشغيل حتى البناء الكامل للمخطط الرسومي | يتم التشغيل بشكل متزامن مع بناء المخطط الرسومي |
| المرونة | مرن للغاية، يمكن تغير المعمارية وقت التشغيل | أقل مرونة، فنحتاج لإعادة بناء المخطط عند كل تعديل |
| الأداء | أبطء نسبيًا، حيث تفسر كل عملية على حدة وقد يوجد تكرار | أسرع حيث يتم تحسين المخطط قبل تشغيله وتفادي التكرار |
| التحسين | مساحة محدودة للتحسين، حيث تنفذ جميع العمليات فورًا | مع معرفتنا بهيكل المخطط كاملًا يمكن تطبيق خوارزميات تحسن ترتيبه وطريقة تشغيله بسهولة |
| كفاءة التخزين | أقل كفاءة، فكل عملية يحجز لها مساحة مخصوصة حتى وإن كانت مكررة. | أكثر كفاءة، فيعاد استخدام المتغيرات المتكررة. |
| اكتشاف المشاكل وحل الأخطاء | أسهل | أصعب |
| المعماريات المناسبة | مناسب للغاية للمعماريات المرنة، مثل الشبكات العصبية التكرارية RNN، التي تتعامل مع متسلسلات من المدخلات مثل الجمل، ومرونة باي تورش تمكننا من التعامل مع حجم جمل متغير. | أنسب للمعماريات الثابتة، مثل الشبكات العصبية الالتفافية CNN |
| مجال الاستخدام | المجال البحثي، وتطوير المعماريات الجديدة، ولكنه قد لا يكون محسنًا بما يكفي لبيئات التشغيل | يشيع استخدامه في بيئات التشغيل وعملية الاستدلال، حيث تكون الشبكة محسنة بدرجة فائقة وقابلة للنقل والتشغيل في بيئات مختلفة. |
ملاحظات إضافية
لنتعرف الآن على بعض الملاحظات والطرق التي يمكن أن نستخدمها لتغيير سلوك المخطط الحسابي في باي تورش PyTorch.
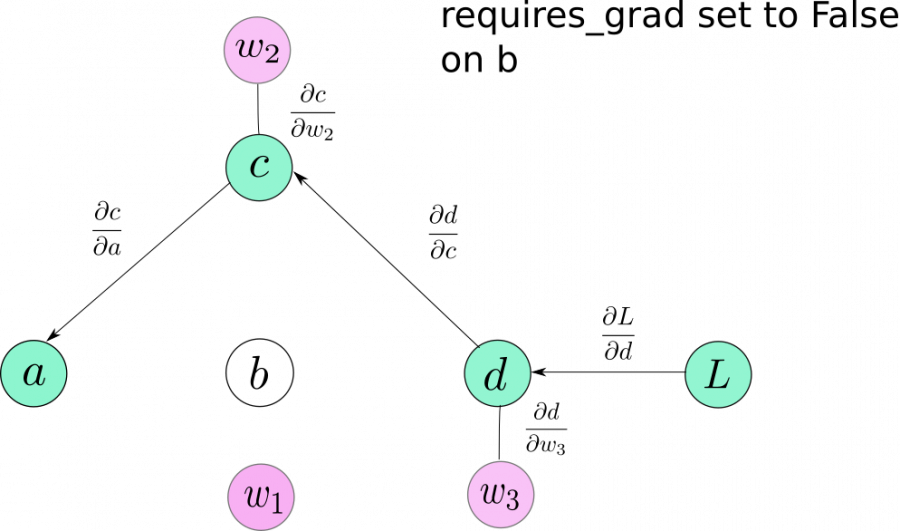
الخاصية requires_grad
تكون هذه الخاصية المتعلقة بالموترات Tensors في غاية الأهمية، عندما تريد أن تجمد بعض الطبقات في الشبكة العصبية ولا تريد أن يتم تدريبها، حيث يمكنك ببساطة أن تجعل قيمة هذه الخاصية False، وبالتالي لن تكون هذه الموترات داخلة في عملية حساب التدرجات gradients.
ولن تنتشر لهم أي تدرجات gradients نتيجة لإيقاف هذه الخاصية، ولا للطبقات التي تعتمد عليها، ونلاحظ أن هذه الخاصية في الأصل قابلة للانتشار فعند تنفيذ عملية على موترات أحدها مفعل به هذه الخاصية، فسيكون الموتر الناتج يحمل هذه الخاصية مفعلة True.
الخاصية torch.no_grad
نحتاج أحيانًا إلى تخزين بعض المدخلات والمتغيرات الانتقالية مؤقتًا أثناء حساب التدرجات gradients، لنستخدمهم في خطوات قادمة لحساب شيء آخر، فمثلًا تدرج المتغير b=w1*a بالنسبة لمدخلاته w1 و a يساوي w1 و a فنحتاج تخزين هذه المتغيرات لاستخدامها لاحقًا في حساب التدرجات أثناء الانتشار الخلفي، ولهذا أثر ثقيل على استخدام الذاكرة.
والاستدلال بحد ذاته لا يتطلب منا إعادة حساب التدرجات gradients، وبالتالي لسنا بحاجة لتخزينها بشكل دائم، في الواقع نحن لانحتاج أن ننشئ المخطط الحسابي وقت الاستدلال حيث سيؤدي هذا لهدر الذاكرة.
يقدم باي تورش PyTorch حلًا لهذه المشكلة، من خلال مدير السياق context manager، المسمى torch.no_grad والذي يعطل عملية حساب التدرجات gradients في أي سياق يتطلب تحديث أوزان النموذج أو ربما تقييمه، ويوفر هذا الكثير من الذاكرة، حيث لا ننشئ المتغيرات الوسيطة ولا المخطط الحسابي.
with torch.no_grad: كود الاستدلال هنا
الخاتمة
تعرفنا في مقال اليوم على آلية عمل التفاضل التلقائي ومحرك التفاصل المستخدم في باي تورش PyTorch والمسمى Autograd، والذي يجعل من التعامل مع باي تورش PyTorch أسهل وأبسط، بعد فهم هذه الأساسيات يمكن التعمق في فهم النماذج المعقدة، وكيف يمكن بناؤها بواسطة باي تورش.
ترجمة وبتصرف لمقال PyTorch 101, Understanding Graphs, Automatic Differentiation and Autograd لصاحبه Ayoosh Kathuria


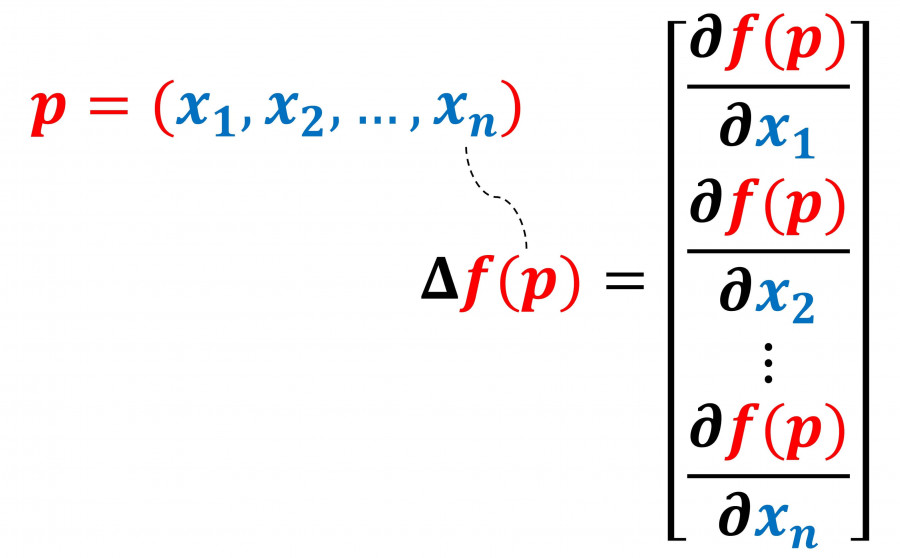
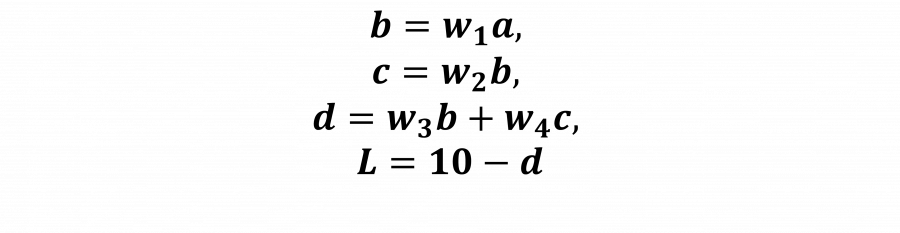

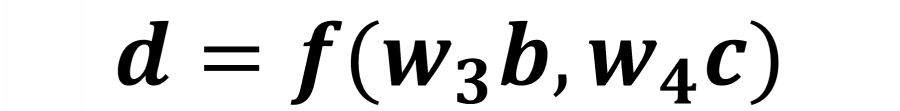



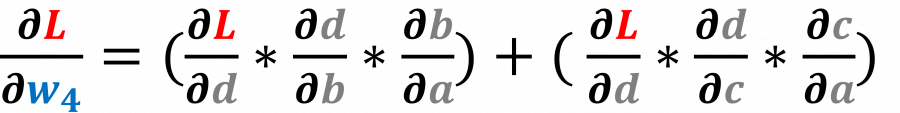
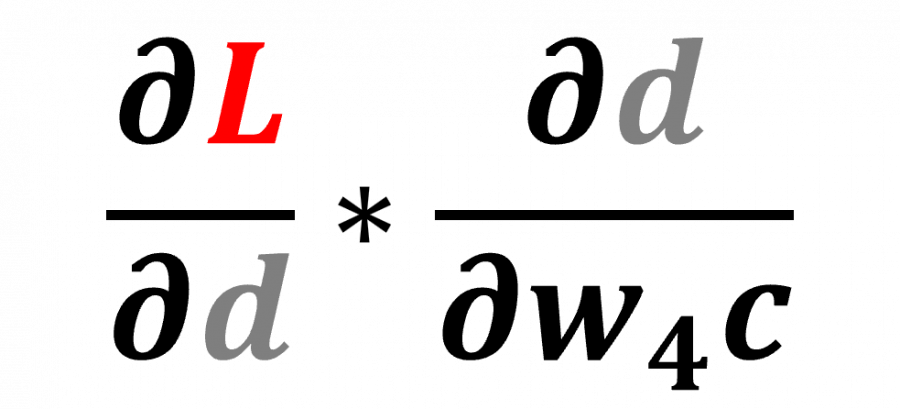











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.