تستعرض هذه المقالة بعض الخوارزميات المتعلقة بالمتتاليات الرياضية، مثل خوارزمية أطول متتالية جزئية مشتركة، وخوارزمية أطول متتالية متزايدة، وخوارزمية الحيد الزمني الديناميكي.
أطول متتالية جزئية مشتركة Longest Common Subsequence
سوف نعرّف بعض المصطلحات الأساسية أولًا:
المتتالية الجزئية Subsequence: في الرياضيات، المتتالية الجزئية هي متتالية مشتقة من متتالية أخرى، بحيث يمكن الحصول عليها بحذف بعض عناصر المتتالية الضامّة دون المساس بترتيب عناصرها.
لتكن ABC سلسلة نصية، سنحصل عند حذف حرف واحد أو أكثر من هذه السلسلة النصية على متتالية جزئية من هذه السلسلة النصية، لذا فإنّ السلاسل النصية { A - B - C - AB - AC - BC - ABC …إلخ} كلها متتاليات جزئية من ABC، بل حتى السلسلة الفارغة (الناتجة عن إزالة جميع الأحرف) تُعدّ أيضًا متتالية جزئية.
وهناك طريقة سهلة لاستخراج المتتاليات الجزئية من سلسلة نصية، بالمرور على كل حرف من حروف السلسلة النصية، وأمامك خياران، إمّا أن تأخذه أو تتركه، ومهما كانت خياراتك ستكون المتتالية المؤلّفة من الحروف التي أخذتها متتالية جزئية، كذلك إن كان طول السلسلة النصية يساوي n، فيمكن أن نستخرج منها 2n متتالية جزئية.
أطول متتالية جزئية مشتركة longest Common Subsequence: لتكن س و ش سلسلتين نصيتين، ولتكن ج المجموعة المؤلفة من كل المتتاليات الجزئية في س، ولتكن ح المجموعة المؤلفة من جميع المتتاليات الجزئية في ش. هناك على الأقل متتالية جزئية واحدة مشتركة بين هاتين المجموعتين، وهي المتتالية الفارغة، لأنّ المتتالية الفارغة تُعدّ دائما متتالية جزئية من كل المتتاليات.
أطول متتالية جزئية مشتركة LCS بين السلسلتين النصيتين س و ش هي أطول عنصر مشترك بين المجموعتين ج و ح، فمثلًا: المتتاليات الجزئية المشتركة بين السلسلتين النصيتين HELLOM وHMLD هي H و HL و HM، والسلسلة النصية HLL هي الأطول من بين كل هذه المتتاليات، لذا فهي أطول متتالية جزئية مشتركة بين HMLD و HELLOM.
هناك عدّة طرق للعثور على أطول متتالية جزئية مشتركة، منها الطريقة العنيفة وطريقة البرمجة الديناميكية.
الطريقة العنيفة: يمكننا إنشاء جميع المتتاليات الجزئية للسلسلتين النصيتين ثم نوازن بينها لنخرج بالمتتاليات الجزئية المشتركة بينهما، ثم سنحاول العثور على أطول عنصر / متتالية مشتركة. بما أننا قد رأينا أنّ هناك 2n متتالية جزئية لكل سلسلة نصية طولها n، فنحن نعلم أننا سنستغرق أعوامًا من أجل حل المشكلة إن كانت n أكبر من 20، وبناءً على ذلك فهي غير عملية، وهناك طريقة أفضل لإيجاد أطول متتالية جزئية مشتركة، وهي البرمجة الديناميكية.
طريقة البرمجة الديناميكية: لنفترض أنّ لدينا سلسلتين نصيتين abcdaf و acbcf نرمز لهما بالرمزين s1 و s2، وأطول متتالية جزئية مشتركة بين هاتين السلسلتين النصيتين هي abcf، وطولها يساوي 4. بما أن المتتاليات الجزئية لا يشترط أن تكون متواصلة، فيمكن إنشاء المتتالية abcf عبر تجاهل da في s1 و c في s2. والآن، كيف نعرف هذا باستخدام البرمجة الديناميكية؟
سنبدأ بإنشاء جدول (مصفوفة ثنائية الأبعاد) تحتوي جميع أحرف s1 في أحد صفوفها، وتحتوي جميع أحرف s2 في أحد أعمدتها، ونفهرس الجدول انطلاقًا من 0، ونضع الأحرف في المصفوفة ابتداءً من الفهرس 1، وسيبدو الجدول كما يلي:
0 1 2 3 4 5 6 +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | | chʳ | | a | b | c | d | a | f | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 0 | | | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 1 | a | | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 2 | c | | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 3 | b | | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 4 | c | | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 5 | f | | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+
تمثل كل خانة Table[i][j] من خانات الجدول طول أطول متتالية جزئية مشتركة بين السلسلتين النصيتين t1 و t2، حيث تساوي t1 سابقة السلسلة النصية s1 التي تبدأ من بدايتها وحتى الحرف رقم j، وتساوي t2 سابقة السلسلة النصية s2 التي تبدأ من بدايتها وحتى الحرف رقم i. على سبيل المثال: تمثّل الخانة Table[2][3] طول أطول متتالية جزئية مشتركة بين ac و abc.
يمثّل العمود رقم 0 المتتالية الجزئية الفارغة من s1، وبالمثل فإن الصفّ رقم 0 يمثّل المتتالية الجزئية الفارغة من s2. إذا أخذنا متتالية جزئية فارغة من سلسلة نصية وحاولنا مطابقتها بسلسلة نصية أخرى، فسيساوي طول المتتالية الجزئية المشتركة 0 مهما كان طول السلسلة النصية الفرعية الثانية، لهذا نملأ خانات الصف الأوّل والعمود الأوّل بالقيمة 0، ونحصل على:
0 1 2 3 4 5 6 +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | | chʳ | | a | b | c | d | a | f | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 1 | a | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 2 | c | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 3 | b | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 4 | c | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 5 | f | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+
نريد الآن ملء الخانة Table[1][1]، إن كان لدينا سلسلتين نصيتين a و a أخرى، ما هي أطول متتالية جزئية مشتركة يمكننا الحصول عليها هنا؟
نحن نعلم أنّ طول أطول متتالية جزئية مشتركة بين السلسلة النصية a و a هو 1، فنذهب الآن إلى Table[1][2] التي تمثّل طول أطول متتالية جزئية مشتركة بين ab و a، والتي تساوي 1، وكما ترى فإن جميع قيم الصف رقم 1 تساوي القيمة 1، وذلك لأنه يحتوي على طول أطول متتالية جزئية مشتركة بين a والسلاسل abcd و abcda و abcdaf.
سيبدو الجدول كما يلي:
0 1 2 3 4 5 6 +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | | chʳ | | a | b | c | d | a | f | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 1 | a | 0 | 1 | 1 | 1 | 1 | 1 | 1 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 2 | c | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 3 | b | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 4 | c | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 5 | f | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+
نذهب الآن إلى الصف رقم 2 الذي يتضمن الحرف c. تحتوي الخانة Table[2][1] طول أكبر متتالية جزئية مشتركة بين السلسلتين النصيتين ac و a والذي يساوي 1، وقد حصلنا على هذه القيمة من القيمة الموجودة في الصف الأعلى، ذلك أنّه إذا كان الحرفان s1 [2] و s2 [1] غير متساويين فلا بدّ أن يساوي طول أكبر متتالية جزئية مشتركة الحد الأقصى لقيمة LCS (أطول متتالية جزئية مشتركة) الموجودة في الأعلى أو على اليسار.
إن أخذنا قيمة LCS الموجودة في الأعلى فذلك يعني أنّنا تجاهلنا الحرف الحالي في السلسلة النصية s2، وبالمثل إن أخذنا قيمة LCS الموجودة على اليسار فذلك يعني أنّنا تجاهلنا الحرف الحالي في s1.
نحصل على هذا الجدول:
0 1 2 3 4 5 6
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| | chʳ | | a | b | c | d | a | f |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| 1 | a | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| 2 | c | 0 | 1 | | | | | |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| 3 | b | 0 | | | | | | |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| 4 | c | 0 | | | | | | |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
| 5 | f | 0 | | | | | | |
+-----+-----+-----+-----+-----+-----+-----+-----+-----+
هذه صيغة الحالة الأولى:
if s2[i] is not equal to s1[j] Table[i][j] = max(Table[i-1][j], Table[i][j-1] endif
ننتقل الآن إلى Table[2][2] التي تحوي طول أطول متتالية جزئية مشتركة بين ab و ac. بما أن الحرفين الأخيرين من هاتين السلسلتين مختلفان (c و b)، فسنَأخذ الحدّ الأقصى الموجود في الأعلى أو على اليسار، وهو 1 في هذه الحالة.
ثم بعد ذلك ننتقل إلى Table[2][3] والتي تحتوي طول أكبر متتالية جزئية مشتركة بين abc و ac، ستتساوى القيمتان الحاليتان في كل من الصف والعمود هذه المرة، لذا فإن طول المتتالية الجزئية المشتركة الأطول يساوي قيمة LCS القصوى الحالية + 1.
ولكي تحصل على قيمة LCS القصوى الحالية عليك أن تتحقق من القيمة القطرية diagonal value، والتي تمثل أفضل تطابق بين ab و a، ومن هذه الحالة نضيف محرفًا من محارف s1 وآخر من s2، وقد وجدنا أنّهما متساويين -أي s1 و s2-، لذا سيزيد طول أكبر متتالية جزئية مشتركة حتمًا. نضع القيمة 1 + 1 = 2 في الخانة Table[2][3] لنحصل على:
0 1 2 3 4 5 6 +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | | chʳ | | a | b | c | d | a | f | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 1 | a | 0 | 1 | 1 | 1 | 1 | 1 | 1 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 2 | c | 0 | 1 | 1 | 2 | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 3 | b | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 4 | c | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 5 | f | 0 | | | | | | | +-----+-----+-----+-----+-----+-----+-----+-----+-----+
هذه صيغتنا الثانية:
if s2[i] equals to s1[j] Table[i][j] = Table[i-1][j-1] + 1 endif
لقد عرّفنا كلا الحالتين، سنملأ الآن الجدول كله باستخدام هاتين الصيغتين، وسيبدو بعد أن نتمّ ملأه كما يلي:
0 1 2 3 4 5 6 +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | | chʳ | | a | b | c | d | a | f | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 1 | a | 0 | 1 | 1 | 1 | 1 | 1 | 1 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 2 | c | 0 | 1 | 1 | 2 | 2 | 2 | 2 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 3 | b | 0 | 1 | 2 | 2 | 2 | 2 | 2 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 4 | c | 0 | 1 | 2 | 3 | 3 | 3 | 3 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+ | 5 | f | 0 | 1 | 2 | 3 | 3 | 3 | 4 | +-----+-----+-----+-----+-----+-----+-----+-----+-----+
نستنتج من الجدول أنّ طول أكبر متتالية جزئية مشتركة بين s1 و s2 هو Table[5][6] = 4. لاحظ أنّ 5 و 6 هما طولا s2 و s1 على التوالي.
انظر المثال التوضيحي التالي:
Procedure LCSlength(s1, s2): Table[0][0] = 0 for i from 1 to s1.length Table[0][i] = 0 endfor for i from 1 to s2.length Table[i][0] = 0 endfor for i from 1 to s2.length for j from 1 to s1.length if s2[i] equals to s1[j] Table[i][j] = Table[i-1][j-1] + 1 else Table[i][j] = max(Table[i-1][j], Table[i][j-1]) endif endfor endfor Return Table[s2.length][s1.length]
التعقيد الزمني لهذه الخوارزمية يساوي O(mn)، حيث يمثّل m و n طولي السلسلتين النصيتين.
ها قد عرفنا طول أكبر متتالية جزئية مشتركة، فكيف نستخرج هذه المتتالية الجزئية؟
من أجل معرفة أطول متتالية جزئية مشتركة، سننشئ مكدسًا لتخزين محارفها، وسنبدأ من الزاوية اليمنى السفلى باحثين عن المصدر الذي أتت منه القيمة، فإذا كانت القيمة قادمة من القطر diagonal -أي إذا كانت Table[i][j] - 1 = Table[i-1][j-1]- فسندفع إمّا [i]s2 أو s1 [j] (كلاهما متساويان) إلى المكدّس ثمّ نتحرك قُطريًا.
أمّا إذا كانت القيمة آتية من الأعلى -أي إن كانت Table[i][j] = Table[i-1][j]- فإننا ننتقل إلى الأعلى، وإذا كانت القيمة آتية من اليسار، أي إن كانت Table[i][j] = Table[i][j-1]، فإننا ننتقل إلى اليسار.
ينتهي بحثنا عندما نصل إلى العمود الموجود في الأعلى أو في أقصى اليسار، وننزع القيم المخزّنة في المكدّس ثمّ نطبعها.
انظر المثال التوضيحي:
Procedure PrintLCS(LCSlength, s1, s2)
temp := LCSlength
S = stack()
i := s2.length
j := s1.length
while i is not equal to 0 and j is not equal to 0
if Table[i-1][j-1] == Table[i][j] - 1 and s1[j]==s2[i]
S.push(s1[j]) //or S.push(s2[i])
i := i - 1
j := j - 1
else if Table[i-1][j] == Table[i][j]
i := i-1
else
j := j-1
endif
endwhile
while S is not empty
print(S.pop)
endwhile
ملاحظة: إذا كان كلّ من Table[i-1][j] و Table[i][j-1] يساويان Table[i][j]، ولم يكن Table[i-1][j-1] مساويًا للقيمة Table[i][j] - 1، فذلك يعني أنّه قد تكون هناك أكثر من متتالية جزئية مشتركة طولى (أي كل واحدة منها تعدّ أطول متتالية جزئية مشتركة)، ولا يأخذ المثال التوضيحي المذكور آنفًا هذا الأمر في الحسبان. إن أردت العثور على جميع المتتاليات الجزئية المشتركة القصوية، فسيكون عليك استخدام العوديّة.
التعقيد الزمني لهذه الخوارزمية هو: O (max (m, n)).
أطول متتالية جزئية متزايدة Longest Increasing Subsequence
أطول متتالية جزئية متزايدة، هي أطول متتالية جزئية عناصرها مرتبة تصاعديًا أو تنازليًا.
تُستخدم خوارزميات حساب أطول متتالية جزئية متزايدة في العديد من التطبيقات مثل أنظمة إدارة الإصدارات Git وغيرها، وفيما يلي وصفٌ مبسّط للخوارزمية التي تعتمدها أنظمة إدارة الإصدارات للموازنة بين ملفّين يمثّلان إصدارين مختلفين من الملف نفسه:
- ابحث عن الأسطر المشتركة في كلا الملفين.
- خذ كل هذه الأسطر من الملف الأوّل ثم رتّبها بحسب ظهورها في الملف الثاني.
- اعثر على أطول متتالية جزئية متزايدة LIS للمتتالية الناتجة (باستخدام خوارزمية ترتيب الصبر patience sorting). ستحصل على أطول متتالية متطابقة من الأسطر، والتي تمثّل التقابلات بين السطور المشتركة في الملفّين.
- كرّر الخوارزمية عوديًا على كل مجال من الأسطر بين السطور المُتطابقة.
لننظر الآن في مثال بسيط على مشكلة أطول متتالية جزئية متزايدة:
مدخلات المشكلة هي متتالية من الأعداد الصحيحة المختلفة a1,a2,...,an.، ونريد أن نجد أطول متتالية جزئية متزايدة. إذا كانت المدخلات تُساوي 7,3,8,4,2,6 مثلًا، فإنّ أطول متتالية جزئية متزايدة فيها هي 3,4,6.
أسهل طريقة للحصول على أطول متتالية جزئية متزايدة هي ترتيب عناصر المدخلات ترتيبًا تزايديًا ثمّ تطبيق خوارزمية LCS على التسلسلات الأصلية والمرتّبة، غير أنّه إذا ألقيت نظرة سريعة على المصفوفة الناتجة، فستلاحظ أنّ العديد من قيمها متساوية إذ تحتوي المصفوفة الكثير من العناصر المكرّرة، هذا يعني أنّه يمكن حل مشكلة LIS بالبرمجة الديناميكية باستخدام مصفوفة من بعد واحد.
المثال التوضيحي:
-
صِف مصفوفة القيم التي نريد حسابها: لكل
1 <= i <= n، ليكن A (i) طول أكبر متتالية جزئية متزايدة في المتتالية المؤلفة من أوّل i عنصر في المدخلات. لاحظ أنّ طول أكبر متتالية جزئية متزايدة في المدخلات (بالكامل) يحقق العبارةmax{A(i)|1 ≤ i ≤ n}، أي أنّه:-
إن كان طول أكبر متتالية جزئية متزايدة في المدخلات هو
L، فإنّه يوجد عددkيحقّقA(k) = L، و لكل1 =< n >= jلدينا:L > A(j).
-
إن كان طول أكبر متتالية جزئية متزايدة في المدخلات هو
- نحسب قيم A (i) عوديًا على النحو التالي:
For 1 <= i <= n, A(i) = 1 + max { A(j)|1 ≤ j < i and input(j) < input(i) }
- احسب قيم A باستخدام الصيغة السابقة.
- ابحث عن الحل الأمثل.
يستخدم البرنامج التالي A لحساب الحل الأمثل، ويحسب الجزء الأول منه قيمة m حيث تساوي A (m) طول متتالية جزئية متزايدة مثلى في المدخلات، فيما يحاول الجزء الثاني العثور على متتالية جزئية متزايدة مثلى.
سنطبع المتتالية بترتيب عكسي لجعلها أوضَح. يستغرق هذا البرنامج O (n)، وتستغرق الخوارزمية إجمالًا O (n ^ 2).
الجزء الأول:
m ← 1 for i : 2..n if A(i) > A(m) then m ← i end if end for
الجزء الثاني:
put a while A(m) > 1 do i ← m−1 while not(ai < am and A(i) = A(m)−1) do i ← i−1 end while m ← i put a end while
الحل العودي، المنظور الأول:
LIS(A[1..n]): if (n = 0) then return 0 m = LIS(A[1..(n − 1)]) B is subsequence of A[1..(n − 1)] with only elements less than a[n] (* let h be size of B, h ≤ n-1 *) m = max(m, 1 + LIS(B[1..h])) Output m
التعقيد الزمني للمنظور الأول: O(n*2^n).
المنظور الثاني:
LIS(A[1..n], x): if (n = 0) then return 0 m = LIS(A[1..(n − 1)], x) if (A[n] < x) then m = max(m, 1 + LIS(A[1..(n − 1)], A[n])) Output m MAIN(A[1..n]): return LIS(A[1..n], ∞)
التعقيد الزمني للمنظور الثاني: O(n^2).
المنظور الثالث:
LIS(A[1..n]): if (n = 0) return 0 m = 1 for i = 1 to n − 1 do if (A[i] < A[n]) then m = max(m, 1 + LIS(A[1..i])) return m MAIN(A[1..n]): return LIS(A[1..i])
التعقيد الزمني للمنظور الثالث: O(n^2).
الخوارزمية التكرارية Iterative Algorithm: تحسب هذه الخوارزمية القيم بطريقة متكررة من أسفل إلى أعلى.
LIS(A[1..n]): Array L[1..n] (* L[i] = value of LIS ending(A[1..i]) *) for i = 1 to n do L[i] = 1 for j = 1 to i − 1 do if (A[j] < A[i]) do L[i] = max(L[i], 1 + L[j]) return L MAIN(A[1..n]): L = LIS(A[1..n]) return the maximum value in L
التعقيد الزمني للمنظور التكراري: O(n^2).
المساحة الإضافية: O(n).
على سبيل المثال، لو كانت المدخلات تساوي:
{0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}
فستكون أطول متتالية جزئية متزايدة في المدخلات هي: {0, 2, 6, 9, 11, 15}.
الحيد الزمني الديناميكي Dynamic Time Warping
خوارزمية الحيد الزمني الديناميكي Dynamic Time Warping -أو DTW اختصارًا- هي خوارزمية لقياس مدى التشابه بين متتاليتين زمنيتين قد تختلفان في السرعة، فمثلًا يمكن رصد أوجه التشابه في مشية شخصين باستخدام خوارزمية DTW حتى لو كان أحدهما يمشي أسرع من الآخر، أو كان هناك تسارع وتباطؤ أثناء المراقبة.
وتُستخدم هذه الخوارزمية لمطابقة مقطع صوتي قياسي مع مقطع صوتي لشخص آخر، حتى لو كان ذلك الشخص يتحدث أسرع من صوت العينة القياسية المسجّلة أو أبطأ منها. تُطبَّق خوارزمية DTW على التسلسلات الزمنية لبيانات الفيديو والصوت والرسومات، أو أيّ نوع من البيانات ما دام يمكن تحويلها إلى متتالية خطية.
تحاول هذه الخوارزمية إيجاد التطابق الأمثل بين متتاليتين زمنيتين مع الأخذ بالحسبان قيودًا معيّنة، فمثلًا لنفترض أنّ لدينا متتاليتين صوتيتين Sample و Test، ونريد أن نتحقق من تطابق هاتين المتتاليتين الزمنيتين. يشير مصطلح متتالية صوتية هنا إلى الإشارة الرقمية للصوت، وقد تُمثَّل بسعة الصوت amplitude أو تردّده frequency. لنفترض أنّ:
Sample = {1, 2, 3, 5, 5, 5, 6} Test = {1, 1, 2, 2, 3, 5}
نريد العثور على أمثل تطابق بين هاتين المتتاليتين، نبدأ بتعريف دالة المسافة d (x، y)، حيث تمثل x و y النقطتين اللتان نودّ حِساب المسافة الفاصلة بينهما. تكون صيغة حساب المسافة كما يلي:
d(x, y) = |x - y| // القيمة المطلقة للفرق
ننشئ الآن مصفوفة ثنائية الأبعاد Table باستخدام قيم المتتاليتين Sample و Test، وسنحسب المسافات بين كل نقطة في Sample وكل نقطة في Test ونبحث عن أفضل تطابق بينهما.
+------+------+------+------+------+------+------+------+ | | 0 | 1 | 1 | 2 | 2 | 3 | 5 | +------+------+------+------+------+------+------+------+ | 0 | | | | | | | | +------+------+------+------+------+------+------+------+ | 1 | | | | | | | | +------+------+------+------+------+------+------+------+ | 2 | | | | | | | | +------+------+------+------+------+------+------+------+ | 3 | | | | | | | | +------+------+------+------+------+------+------+------+ | 5 | | | | | | | | +------+------+------+------+------+------+------+------+ | 5 | | | | | | | | +------+------+------+------+------+------+------+------+ | 5 | | | | | | | | +------+------+------+------+------+------+------+------+ | 6 | | | | | | | | +------+------+------+------+------+------+------+------+
تحتوي كل خانة Table[i][j] من خانات الجدول المسافة المثلى بين المتتاليتين الزمنيتين الجزئيتين t1 و t2، حيث تساوي t1 المتتالية الجزئية من Test التي تبدأ من بدايتها وحتى العنصر رقم j، وتساوي t2 المتتالية الجزئية من Sample التي تبدأ من بدايتها وحتى العنصر رقم i.
إذا لم نأخذ أيّ قيمة من Sample في الصف الأول فستكون المسافة بينها وبين Test لا نهائية، لذا نضع ما لا نهاية في الصف الأول، وكذلك نفعل مع العمود الأول لأنّنا إن لم نأخذ أيّ قيمة من Test فستكون المسافة بينها وبين Sample لا نهائية كذلك، والمسافة بين 0 و 0 تساوي 0.
نحصل على ما يلي:
+------+------+------+------+------+------+------+------+ | | 0 | 1 | 1 | 2 | 2 | 3 | 5 | +------+------+------+------+------+------+------+------+ | 0 | 0 | in | inf | inf | inf | inf | inf | +------+------+------+------+------+------+------+------+ | 1 | inf | | | | | | | +------+------+------+------+------+------+------+------+ | 2 | inf | | | | | | | +------+------+------+------+------+------+------+------+ | 3 | inf | | | | | | | +------+------+------+------+------+------+------+------+ | 5 | inf | | | | | | | +------+------+------+------+------+------+------+------+ | 5 | inf | | | | | | | +------+------+------+------+------+------+------+------+ | 5 | inf | | | | | | | +------+------+------+------+------+------+------+------+ | 6 | inf | | | | | | | +------+------+------+------+------+------+------+------+
سنحسب في كل خطوة المسافة بين النقاط الحالية ثمّ نضيفها إلى الحد الأدنى للمسافة التي وجدناها حتى الآن، وسينتج عن هذا المسافة المثلى بين المتتاليتين الجزئيتين t1 و t2 (انظر تعريفيهمَا في الأعلى). هذه هي الصيغة التي سنعمل بها:
Table[i][j] := d(i, j) + min(Table[i-1][j], Table[i-1][j-1], Table[i][j-1])
يكون لدينا في البداية d(1, 1) = 0، كما تحتوي الخانة Table[0][0] القيمةَ الصغرى، لذا نضع Table[1][1] = 0 + 0 = 0. لدينا في الحالة الثانية d(1, 2) = 0، وتحتوي الخانة Table[1][1] القيمةَ الصغرى، لذا نضع Table[1][2] = 0 + 0 = 0. نستمر على هذا المنوال إلى أن نملأ الجدول، الذي سيبدو بعد الانتهاء كما يلي:
+------+------+------+------+------+------+------+------+ | | 0 | 1 | 1 | 2 | 2 | 3 | 5 | +------+------+------+------+------+------+------+------+ | 0 | 0 | inf | inf | inf | inf | inf | inf | +------+------+------+------+------+------+------+------+ | 1 | inf | 0 | 0 | 1 | 2 | 4 | 8 | +------+------+------+------+------+------+------+------+ | 2 | inf | 1 | 1 | 0 | 0 | 1 | 4 | +------+------+------+------+------+------+------+------+ | 3 | inf | 3 | 3 | 1 | 1 | 0 | 2 | +------+------+------+------+------+------+------+------+ | 5 | inf | 7 | 7 | 4 | 4 | 2 | 0 | +------+------+------+------+------+------+------+------+ | 5 | inf | 11 | 11 | 7 | 7 | 4 | 0 | +------+------+------+------+------+------+------+------+ | 5 | inf | 15 | 15 | 10 | 10 | 6 | 0 | +------+------+------+------+------+------+------+------+ | 6 | inf | 20 | 20 | 14 | 14 | 9 | 1 | +------+------+------+------+------+------+------+------+
تمثل قيمة الخانة Table[7][6] المسافة القصوى بين المتتاليتين Sample و Test، وتشير القيمة 1 هنا إلى أنّ المسافة القصوى بين Sample و Sample تساوي 1.
الآن إذا ارتددنا من النقطة الأخيرة وحتى نقطة البداية (0 , 0) فسنحصل على خط طويل يتحرك أفقيًا وعموديًا وقطريًا. هذا مثال توضيحي لعملية الارتداد:
if Table[i-1][j-1] <= Table[i-1][j] and Table[i-1][j-1] <= Table[i][j-1] i := i - 1 j := j - 1 else if Table[i-1][j] <= Table[i-1][j-1] and Table[i-1][j] <= Table[i][j-1] i := i - 1 else j := j - 1 end if
نواصل على هذا المنوال حتى نصل إلى النقطة (0 , 0)، واعلم أن كل حركة لها معنى خاص:
- تمثل الحركة الأفقية حذفًا، وهذا يعني أنّ المتتالية Test قد تسرّعت أثناء هذه المدة.
- تمثل الحركة الرأسية إدراجًا، وهذا يعني تباطؤ المتتالية Test أثناء هذه المدة.
- تمثل الخطوة القطرية تطابقًا، أي أنّ Test تتطابق مع Sample أثناء هذه المدة.
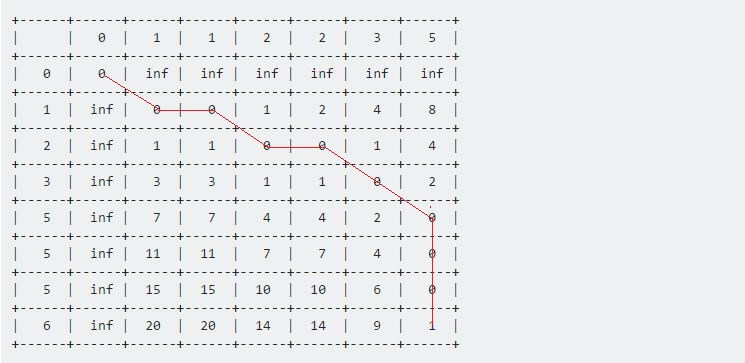
انظر المثال التوضيحي التالي:
Procedure DTW(Sample, Test): n := Sample.length m := Test.length Create Table[n + 1][m + 1] for i from 1 to n Table[i][0] := infinity end for for i from 1 to m Table[0][i] := infinity end for Table[0][0] := 0 for i from 1 to n for j from 1 to m Table[i][j] := d(Sample[i], Test[j]) + minimum(Table[i-1][j-1], // مطابقة Table[i][j-1], // إدراج Table[i-1][j]) // حذف end for end for Return Table[n + 1][m + 1]
يمكن أيضًا أن نضيف قيودًا محلية، كأن نشترط أنّه إذا تطابقت Sample[i] مع Test[j]، فيجب أن لا تكون قيمة |i - j| أكبر من w (معامل نافذة - window parameter).
التعقيد: التعقيد الزمني لخوارزمية DTW هو O (m * n)، حيث يمثل كلّ من m و n طولي المتتاليتين. ويجدر التنويه إلى أنّ هناك تقنيات أخرى أسرع لحساب DTW مثل: PrunedDTW و SparseDTW و FastDTW.
ترجمة -بتصرّف- للفصول 47 و 48 و 54 من كتاب Algorithms Notes for Professionals.













أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.