دوال التوزيع التراكمي Cumulative distribution functions

يمكنك الحصول على الشيفرة الخاصة توجد بهذا المقال في cumulative.py في مستودع ThinkStats2 على GitHub.

حدود دوال الكتلة الاحتمالية

تؤدي دوال الكتلة الاحتمالية probability mass functions -أو PMFs اختصارًا- وظيفتها بصورة جيدة عندما يكون عدد القيم صغيرًا، لكن كلما ازداد عدد القيم، أصبح الاحتمال المرتبط بكل قيمة أصغر ويزداد أثر الضجيج العشوائيّ.

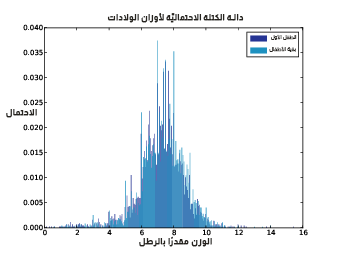
قد نرغب بدراسة توزيع أوزان الأطفال الخدّج في بيانات المسح الوطني لنمو الأسرة NSFG على سبيل المثال، حيث يسجِّل المتغير totalwgt_lb وزن الطفل عند ولادته مقدرًا بالرطل، ويُظهر الشكل التالي دالة الكتلة الاحتمالية لأوزان الأطفال الأوائل والأطفال الآخرين -أي جميع الأطفال الذين يولدون بعد الطفل الأول للأم ذاتها- عند الولادة.

يوضِّح الشكل السابق دالة الكتلة الاحتمالية لأوزان المواليد، كما يظهر هذا الشكل وجود حدود على دوال الكتلة الاحتمالية، إلا أنه لا يمكن موازنتها بصريًا.

تشبه هذه التوزيعات عمومًا شكل الجرس كما هو الحال في التوزيع الطبيعي normal distribution مع توضُّع الكثير من القيم بالقرب من المتوسط mean، وتوضُّع قلة قليلة من القيم في كلا الطرفين -أي أعلى وأخفض من المتوسط بكثير-، ولكن يصعب تفسير بعض هذه أجزاء هذا الشكل، إذ توجد العديد من القمم -الارتفاعات- والانخفاضات بالإضافة إلى بعض الفروقات الواضحة بين التوزيعات، إلا أنه من الصعب معرفة إن كانت هذه الميزات ذات معنى، ومن الصعب أيضًا رؤية الأنماط العامة، مثل ما هو برأيك التوزيع الذي يحتوي على المتوسط الأعلى؟

يمكن تخفيف هذه المشاكل عن طريق تصنيف binning البيانات وهي تقسيم مجالات القيم إلى مجالات غير متداخلة بالإضافة إلى حساب عدد القيم في كل مجال مصنَّف bin.

قد تكون عملية تصنيف مفيدة، إلا أنّ الحصول على الحجم الصحيح للمجالات المصنَّفة ليس بالأمر السهل، فإذا كان حجمها كبيرًا بما يكفي لتخفيف الضجيج، فستتسبب في تنعيم معلومات مفيدة.

تُعَدّ دوال التوزيع التراكمي cumulative distribution functions -أو CDF اختصارًا- حلًا بديلًا يجنبنا هذه المشاكل، وسيكون هذا المفهوم موضوع دراسة المقال الحالي.

سنستهل حديثنا بشرح مفهوم المئين percentiles قبل البدء بشرح دوال التوزيع التراكمي CDFs.

المئين percentiles

إذا خضعت لامتحان موحد سابقًا، فمن المرجح أن تكون تلقيت نتيجتك على صورة مجموع صافي ورتبة مئين percentile rank، وتكون رتبة المئين في سياقنا هذا هي نسبة الأشخاص الذين حصلوا على مجموع أقل من المجموع الذي حصلت عليه أو مجموع يساويه، فإذا كنت في رتبة المئين التسعين، فهذا يعني أنّ أداءك في الامتحان كان بمستوى أو أفضل من تسعين بالمئة ممن خضعوا لهذا الامتحان.

إليك طريقة حساب رتبة المئين لقيمة معيّنة (ويمثلها المتغيّر your_score) بالنسبة للقيم في متسلسلة sequence التي تحوي الدرجات scores:

def PercentileRank(scores, your_score):
    count = 0
    for score in scores:
        if score <= your_score:
            count += 1

    percentile_rank = 100.0 * count / len(scores)
    return percentile_rank

إذا كانت الدرجات في متسلسلة على سبيل المثال هي 55 و66 و77 و88 و99، وكانت نتيجتك هي 88، فستكون رتبة المئين هي 80 والتي تحصل عليها عن طريق المعادلة التالية: 100‎ * 4 / 5.

فإذا كانت لديك قيمة معيّنة ،فسيكون حساب رتبة المئين سهل للغاية، إلا أنّ العملية العكسية أصعب بقليل، فإذا أُعطيت رتية مئين وتريد إيجاد القيمة الموافقة لها فسيكون أحد الخيارات المتاحة لديك هي ترتيب القيم، ومن ثم البحث عن القيمة التي تريدها كما في هذه الشيفرة التالية:

def Percentile(scores, percentile_rank):
    scores.sort()
    for score in scores:
        if PercentileRank(scores, score) >= percentile_rank:
            return score

نتيجة هذا الحساب هي المئين percentile، فالمئين الخمسين مثلًا هو القيمة ذات رتبة المئين percentile rank الخمسين، ويكون المئين الخمسين في توزيع درجات الامتحان هو 77.

لا يُعَدّ تنفيذ دالة Percentile في الشيفرة السابقة فعالًا، إلا أنه توجد طريقة أفضل، وهي استخدام رتبة المئين percentile rank من أجل حساب فهرس المئين الموافق كما يلي:

def Percentile2(scores, percentile_rank):
    scores.sort()
    index = percentile_rank * (len(scores)-1) // 100
    return scores[index]

قد يكون التمييز بين "المئين" percentile و"رتبة المئين" percentile rank أمرًا محيّرًا خاصةً أن الناس لا يستخدِمون المصطلحات بدقة دائمًا، ويمكننا القول باختصار تأخذ الدالة PercentileRank قيمة على أساس وسيط لها وتحسب رتبة المئين percentile rank لها في مجموعة من القيم؛ أما الدالة Percentile فهي تأخذ ترتيبًا مئيني وتحسب القيمة الموافقة له.

دوال التوزيع التراكمي

والآن بعد شرح مفهومي المئين ورتبة المئين أصبحنا جاهزين لتناول موضوع دالة التوزيع التراكمي Cumulative distribution function -أو CDF اختصارًا-، وهي دالة تحوِّل القيمة إلى ترتيب مئين percentile rank.

تُعَدّ دالة التوزيع التراكمي دالةً لـ x، بحيث تكون x هي أيّ قيمة موجودة في التوزيع، ولتقييم دالة التوزيع التراكمي CDF(‎x‎)‎ لقيمة محدَّدة x علينا حساب نسبة القيم الموجودة في التوزيع والتي هي أقل أو تساوي القيمة x.

لدينا فيما يلي الدالة التي تأخذ وسيطين هما sample وهو متسلسلة sequence وx القيمة التي لدينا:

def EvalCdf(sample, x):
    count = 0.0
    for value in sample:
        if value <= x:
            count += 1

    prob = count / len(sample)
    return prob

تشبه هذه الدالة دالة PercentileRank إلى حد التطابق تقريبًا، إلا أنّ الفرق الوحيد هو أنّ نتيجة دالة EvalCdf احتمالية في المجال 0-1، في حين تكون نتيجة PercentileRank هي رتبة مئين في المجال 0-100.

لنستعرض مثالًا عن الفكرة السابقة، حيث لدينا عيّنة تحوي القيم [5, 3, 2, 2, 1]، وإليك قيم من دالة التوزيع التراكمي الخاصة بهذه العيّنة:

CDF(0)=0
CDF(1)=0.2
CDF(2)=0.6
CDF(3)=0.8
CDF(4)=0.8
CDF(5)=1

يمكننا تخمين دالة التوزيع التراكمي لأيّ قيمة للمتغير x، أي ليس فقط للقيم الموجودة في العيّنة، فإذا كانت قيمة x أقل من أصغر قيمة موجودة في العيّنة، فإن دالة التوزيع التراكميّ هي 0 أي CDF(x)=0؛ أما إذا كانت قيمتها أعلى من أكبر قيمة، فستساوي دالة التوزيع التراكمي للمتغيّر x الواحد أي CDF(x)=1.

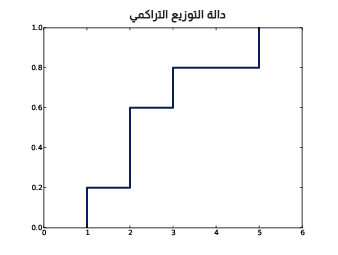
يوضِّح الشكل التالي مثالًا عن دالة توزيع تراكمي CDF.

يُعَدّ الشكل السابق تمثيلًا رسوميًا لدالة التوزيع التراكمي هذه، كما تُعَدّ دالة التوزيع التراكمي الخاصة بعيّنة دالة خطوة step function.

تمثيل دوال التوزيع التراكمي

تزوّدنا مكتبة thinkstats2 بصنف class يدعى Cdf ويمثِّل دوال التوزيع التراكمي، وفيما يلي التوابع الأساسية التي يزودنا بها صنف Cdf:

(x)Prob: بفرض لدينا قيمة x، فإن هذا التابع يحسب الاحتمال p=CDF(x)
(p)Value: بفرض أنه لدينا قيمة احتمال p، فسيحسب هذا التابع القيمة الموافقة x، أي أنّها دالة التوزيع التراكمي العكسية inverse CDF للاحتمال p.

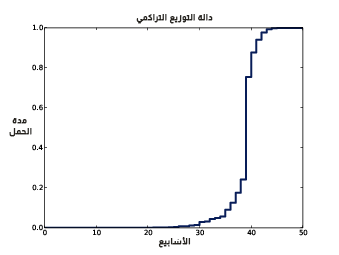
يوضِّح الشكل التالي دالة التوزيع التراكمي لمدة الحمل.

يمكن أن يأخذ باني Cdf قائمةً list من القيم على أساس وسيط أو سلسلة بانداز pandas Series، أو Hist، أو Pmf، أو Cdf آخر.

تمثِّل الشيفرة التالية Cdf لتوزيع احتمالي لمدة الحمل في المسح الوطني لنمو الأسرة:

    live, firsts, others = first.MakeFrames()
    cdf = thinkstats2.Cdf(live.prglngth, label='prglngth')

يزوّدنا thinkplot بدالة تدعى Cdf ترسم دوال التوزيع التراكمي على صورة أسطر:

   thinkplot.Cdf(cdf)
    thinkplot.Show(xlabel='weeks', ylabel='CDF')

يُظهر الشكل السابق النتيجة، وإحدى طرق قراءة دالة توزيع تراكمي هي المئينات. فمثلًا، يبدو أنّ 10% من حالات الحمل استمرت فترةً تقل عن 36 أسبوع، بينما لم تتعدى 90% من الحالات مدة 41 أسبوع.

تزوّدنا دالة التوزيع التراكمي بتمثيل رسومي لشكل التوزيع، وتكون القيم الشائعة -التي تظهر عادةً- على شكل أجزاء حادة أو رأسية من دالة التوزيع التراكمي، حيث يكون المنوال mode في هذا المثال وضوحًا 39 أسبوع، كما يوجد عدد قليل من القيم أقل من 30 أسبوع، لذا تكون دالة التوزيع التراكمي في هذا المجال منبسطة flat

اقتباس

توضيح: الدالة المنبسطة هي دالة منتظمة smooth مستقرها ومنطلقها مجموعة الأعداد الحقيقية ، إلا أنّ جميع مشتقاتها تختفي عند نقطة معيّنة من مجموعة الأعداد الحقيقية .

إنّ التعوّد على دوال التوزيع التراكميّ ليس بالمهمة السهلة، فهي تحتاج إلى وقت طويل، لكن حالما تصبح مألوفةً بالنسبة لك ستجد أنها تزودنا بمعلومات أكثر من دوال الكتلة الاحتمالية PMFs وبوضوح أكبر منها أيضًا.

موازنة دوال التوزيع التراكمي

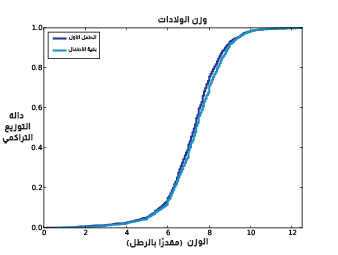
تتجلى فائدة دوال التوزيع التراكمي بصورة خاصة في موازنة التوزيعات. فمثلًا، إليك الشيفرة التي ترسم دالة التوزيع التراكمي لأوزان الأطفال الأوائل والأطفال الآخرين عند الولادة:

   first_cdf = thinkstats2.Cdf(firsts.totalwgt_lb, label='first')
    other_cdf = thinkstats2.Cdf(others.totalwgt_lb, label='other')

    thinkplot.PrePlot(2)
    thinkplot.Cdfs([first_cdf, other_cdf])
    thinkplot.Show(xlabel='weight (pounds)', ylabel='CDF')

يوضِّح الشكل السابق دالة التوزيع التراكمي لأوزان الأطفال الأوائل وبقية الأطفال، كما يُظهر النتيجة، ويمكن أن نلاحظ بالموازنة مع الشكل الأول في هذا المقال أن شكل التوزيعات والفرق بينهما تظهر بوضوح أكبر في الشكل السابق، كما نلاحظ أيضًا أن التوزيع يُظهر أنّ وزن الأطفال الأوائل أخف، بالإضافة إلى وجود تباين أكبر فوق المتوسط mean.

الإحصائيات المبنية على أساس المئين

يصبح حساب المئينات ورتبة المئين عمليةً سهلةً عند حساب دالة التوزيع التراكمي، ويزوّدنا الصنف Cdf بالتابعين التاليين:

PercentileRank(x)‎: يحسب هذا التابع رتبة المئين لقيمة معيّنة x بالشكل: 100 CDF(x)
Percentile(p)‎: يحسب هذا التابع القيمة الموافقة x لرتبة مئين p وهي تساوي Value(p/100)‎.

يمكن استخدام التابع Percentile لحساب إحصائية موجزة مبينة على أساس المئين. فالمئين الخمسين مثلًا هو القيمة التي تقسم التوزيع إلى النصف، ويُعرف أيضًا باسم الوسيط median الذي يُعَدّ مقياسًا للنزعة المركزية لتوزيع معيّن مثل المتوسط mean.

توجد في الواقع عدة تعريفات لمفهوم "الوسيط" ولكل منها خصائص مختلفة عن الآخر، إلا أنه من السهل حسابه عن طريق Percentile(50) وهي طريقة فعالة وبسيطة.

يُعدّ الانحراف الربيعي interquartile range -أو IQR اختصارًا- إحصائيةً مبنيةً على أساس المئين، وهو مقياس للانتشار في توزيع معيّن، أي أنّ الانحراف الربيعي هو الفرق بين المئين الخامس والسبعين والمئين الخامس والعشرين.

يُستخدَم المئين عمومًا لتلخيص شكل التوزيع، فغالبًا ما يكون توزيع الدخل مثلًا على صورة نقاط التجزيء الخمسية quintiles أي مقسومة عند المئينات العشرين والأربعين والستين والثمانين؛ أما التوزيعات الأخرى فتُقسم إلى 10 نقاط أعشارية deciles.

يُدعى هذا النوع من الإحصائيات التي تمثل النقاط التي تبعد عن بعضها مسافات متساوية في دالة توزيع تراكمي نقاط التجزيء quantiles، ويمكنك زيارة الرابط لمزيد من المعلومات.

الأعداد العشوائية

لنفترض أننا اخترنا عيّنةً عشوائيةً من مجموعة الولادات الحية وننظر إلى رتبة المئين لأوزان الأطفال عند الولادة، ومن ثم لنفترض أننا حسبنا دالة التوزيع التراكمي لرتب المئين، برأيك كيف سيبدو التوزيع؟

إليك كيفية حسابه، لكن في البداية يجب إنشاء دالة التوزيع التراكمي Cdf لأوزان الولادات:

    weights = live.totalwgt_lb
    cdf = thinkstats2.Cdf(weights, label='totalwgt_lb')

ومن ثم نولِّد عيّنةً ونحسب رتبة المئين لكل قيمة في العيّنة:

    sample = np.random.choice(weights, 100, replace=True)
    ranks = [cdf.PercentileRank(x) for x in sample]

بحيث تكون sample عيّنةً عشوائيةً لأوزان 100 ولادة مُختارة مع الاستبدال replacement، أي أنّه يمكن اختيار القيمة نفسها أكثر من مرة، وكذلك تكون ranks قائمةً list من رتب المئين.

يمكننا الآن إنشاء ورسم دالة التوزيع التراكمي لرتب المئين:

   rank_cdf = thinkstats2.Cdf(ranks)
    thinkplot.Cdf(rank_cdf)
    thinkplot.Show(xlabel='percentile rank', ylabel='CDF')

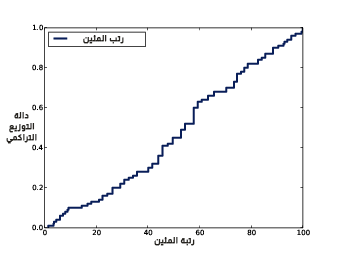
الشكل 4.5.png

يوضَّح الشكل السابق دالة التوزيع التراكمي لرتب المئين لعينة عشوائية من أوزان الولادات، كما يُظهر النتيجة، بحيث تكون دالة التوزيع التراكمي خطًا مستقيمًا أي أنّ التوزيع موحَّد.

قد لا يكون هذا الخرج واضحًا إلا أنّه نتج بسبب طريقة تعريف دالة التوزيع التراكمي، حيث يُظهر هذا الشكل أن 10% من العيّنة هي تحت المئين العاشر، و20% من العيّنة تحت رتبة المئين العشرين، وهكذا، كما كنا متوقعين.

لذا يكون توزيع رتب المئين موحَّدًا بعض النظر عن شكل دالة التوزيع التراكمي، وتُعَدّ هذه الخاصية مفيدةً لأنها أساس لخوارزمية بسيطة وفعالة تولِّد أعداد عشوائية في حال وجود دالة توزيع تراكمي، وذلك عن طريق اتباع الطريقة التالية:

اختر رتبة مئين بصورة موحَّدة من المجال 0-100.
استخدِم Cdf.Percentile من أجل إيجاد القيمة الموجودة في التوزيع والتي توافق رتبة المئين التي اخترتها.

يزوّدنا Cdf بتنفيذ لهذه الخوارزمية ويدعى Random:

# class Cdf:
    def Random(self):
        return self.Percentile(random.uniform(0, 100))

كما يزودنا Cdf بـ Sample التي تأخذ عددًا صحيحًا n، وتُعيد قائمةً عدد عناصرها n وقيمها مُختارة عشوائيًا من Cdf.

موازنة رتب المئين

تفيد رُتب المئين percentile ranks في موازنة المقاييس في مجموعات مختلفة، إذ يُجمع الأشخاص الذين يشاركون في سباقات الركض مثلًا حسب العمر والجنس عادةً، كما يمكنك تحويل وقت السباق إلى رُتب مئين لموازنة الأشخاص في المجموعات العمرية المختلفة.

شارك آلان بي داوني Allen B. Downey في سباق جيمس جويس رامبل بطول مسار 10 كيلومتر في ديدهام في ماساتشوستس منذ عدة سنوات، وكان في ترتيب 97 من أصل 1633، أي تغلّب على أو تعادل مع 1633 عدّاء، وهذا يعني أنّ رتبة المئين الخاصة به في الملعب كانت 94%.

يمكننا عمومًا حساب رتبة المئين باستخدام الموقع وحجم الملعب:

def PositionToPercentile(position, field_size):
    beat = field_size - position + 1
    percentile = 100.0 * beat / field_size
    return percentile

كانت مرتبته 26 من أصل 256 في فئته العمرية التي كان يُشار إليها بـ M4049، والتي تعني ذّكر male بين عمري 40 و49، وبالتالي كانت رتبة المئين الخاصة بي في فئته العمرية هي 90%، وإذا لم يتوقف عن الركض بعد 10 سنوات -وهو يأمل ذلك-، فسيصبح في فئة M5059.

لنفترض الآن أنّ رتبة المئين الخاصة به في الفئة العمرية هذه لم تتغير، كم سأكون أبطأ حينها؟ يمكننا الإجابة عن هذا السؤال عن طريق تحويل رتبة المئين في الفئة M4049 إلى موقع في الفئة M5059، وإليك الشيفرة التي تعبر عن ذلك:

def PercentileToPosition(percentile, field_size):
    beat = percentile * field_size / 100.0
    position = field_size - beat + 1
    return position

كان هناك 171 شخصًا في الفئة M5059، لذا يجب أن يكون في المكان السابع عشر أو الثامن عشر ليكون لديه رتبة المئين نفسها، كما أنّ زمن انتهاء العدّاء رقم 17 في الفئة M5059 كان 46:05، أي يجب أن يصل بهذا الوقت لكي يحافظ على رتبة المئين.

تمارين

يمكنك البدء بـ chap04ex.ipynb من أجل التمارين التالية، علمًا أنّ الحل الخاص بنا موجود في ملف chap04soln.ipynb في مستودع ThinkStats2 على GitHub حيث ستجد كل الشيفرات والملفات المطلوبة.

تمرين 1

كم كان وزنك عندما ولدت؟ إذا لم يكن لديك الجواب فبإمكانك الاتصال بوالدتك أو أحد آخر يملك الجواب، وباستخدام بيانات المسح الوطني لنمو الأسرة لكل الولادات الحية؛ احسب توزيع أوزان الولادات، ومن ثم استخدمه لحساب رتبة المئين الخاصة بك.

إذا كنت الطفل الأول في عائلتك، فاحسب رتبة المئين الخاصة بك في توزيع الأطفال الأوائل، وإلا فاستخدم توزيع الأطفال الآخرين. وإذا كنت في المئين التسعين أو أكثر، فاتصل بوالدتك واعتذر إليها.

تمرين 2

من المفترض أن تكون الأعداد التي تولِّدها random.random موحَّدةً بين 0 و1، أي يجب أن يكون لكل قيمة في المجالالاحتمال نفسه.

ولِّد 1000 عدد باستخدام الدالة random.random وارسم دالة الكتلة الاحتمالية ودالة التوزيع التراكمي لها. هل وجدت أنّ التوزيع موحَّد؟

المفاهيم الأساسية

رتبة المئين percentile rank: تشير إلى النسبة المئوية للقيم الموجودة في توزيع معيّن والتي تساوي قيمة محدَّدة أو أصغر منها.
المئين percentile: القيمة المرتبطة برتبة مئين معطاة.
دالة التوزيع التراكمي cumulative distribution function -أو CDF اختصارًا-: دالة تحوِّل القيم إلى احتمالاتها التراكمية، حيث أنّ CDF(x) هو نسبة القيم من العيّنة التي إما تساوي x أو أصغر منها.
دالة التوزيع التراكمي العكسية inverse CDF: دالة تحوِّل الاحتمال التراكمي p إلى القيمة الموافقة له.
الوسيط median: وهو المئين الخمسون -أي 50th percentile-، وغالبًا ما يُستخدَم على أساس مقياس للنزعة المركزيّة central tendency.
الانحراف الربيعي interquartile range: الفرق بين المئين الخامس والسبعين 75th percentile والمئين الخامس والعشرين 25th percentile، ويُستخدَم على أساس مقياس للانتشار.
نقطة التجزيء quantile: متسلسلة من القيم التي توافق الترتيبات المئينة التي تبعد عن بعضها مسافات متساوية، فنقاط التجزيء لتوزيع ما هي المئين رقم 25 والمئين رقم 50 والمئين رقم 75.
الاستبدال replacement: خاصية من خواص عملية اختيار العيّنات sampling، حيث يشير المصطلح "مع استبدال" إلى أنه يمكن استخدام القيمة نفسها أكثر من مرة، كما يشير مصطلح "بدون استبدال" إلى أنه حالما تُختار القيمة فإنها تُحذَف من المجموعة السكانية.