التوزيعات الإحصائية في بايثون

سنتعرف في هذا المقال على التوزيعات الإحصائية في بايثون.

المدرجات التكرارية Histograms

يُعَدّ توزيع المتغير من أفضل الطرق المستخدمة لوصف متغير Variable، وهو إعطاء تقرير عن القيم Values الموجودة في مجموعة البيانات Dataset وعدد مرات ظهور هذه القيمة، كما يُعَدّ المدرَّج التكراري histogram التمثيل الأكثر شيوعًا، وهو عبارة عن مدرَّج بياني يُظهر تردد frequency كل قيمة، حيث يشير التردد في هذا السياق إلى عدد مرات ظهور كل قيمة.

يُعَدّ القاموس Dictionary طريقةً فعالةً لحساب الترددات في لغة بايثون، فإذا كان لدينا تسلسل t من القيم كما يلي:

hist = {}
for x in t:
    hist[x] = hist.get(x, 0) + 1

تكون النتيجة قاموسًا يربط بين القيم وتردداتها، كما يمكنك استخدام الصنف Counter المعرَّف في وحدة collections بدلًا من ذلك، أي كما يلي:

from collections import Counter
counter = Counter(t)

تكون النتيجة هنا كائن Counter وهو صنف فرعي من القاموس dictionary.

يوجد خيار آخر وهو استخدام تابع pandas المعروف باسم value_counts والذي رأيناه في المقال السابق، ولكن أنشأنا هنا صنفًا باسم Hist يمثِّل المدرَّجات التكرارية ويزودنا بالتوابع التي ستعمل على تلك المدرَّجات.

تمثيل المدرجات التكرارية

يقبل الباني Hist تسلسلًا sequence أو قاموسًا dictionary أو سلسلة pandas أو كائن Hist آخر، كما يمكنك تهيئة وتمثيل كائن Hist كما يلي:

>>> import thinkstats2
>>> hist = thinkstats2.Hist([1, 2, 2, 3, 5])
>>> hist
Hist({1: 1, 2: 2, 3: 1, 5: 1})

توفِّر كائنات Hist التابع Freq الذي يقبل قيمةً على أساس وسيط ويُعيد ترددها، كما يلي:

>>> hist.Freq(2)
2

يفعل عامِل القوس المربع bracket operator الشيء ذاته:

>>> hist[2]
2

يكون التردد 0 عند البحث عن قيمة غير موجودة، أي:

>>> hist.Freq(4)
0

يُعيد التابع Values قائمةً غير مرتَّبة بالقيم الموجودة في Hist.

>>> hist.Values()
[1, 5, 3, 2]

ويمكن استخدام الدالة المبنية مسبقًا sorted للمرور على القيم بالترتيب:

for val in sorted(hist.Values()):
    print(val, hist.Freq(val))

أو استخدم items للمرور على أزواج القيم وتردداتها، كما يلي:

for val, freq in hist.Items():
     print(val, freq)

الرسم البياني للمدرجات التكرارية

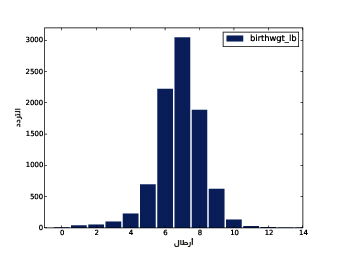
الشكل 2.1.jpg

يُظهِر الشكل السابق المدرَّج التكراري لوزن الولادات بالرطل.

أُنشئت لهذه السلسلة تحديدًا وحدة باسم thinkplot.py توفِّر دوالًا لرسم المدرَّجات التكرارية، وكائنات أخرى مُعرَّفة في الوحدة thinkstats2.py، وهي مبنية على pyplot الذي هو جزء من حزمة matplotlib.

جرّب الشيفرة التالية لرسم hist باستخدام thinkplot:

>>> import thinkplot
>>> thinkplot.Hist(hist)
>>> thinkplot.Show(xlabel='value', ylabel='frequency')

يمكنك قراءة توثيق thinkplot من الموقع .

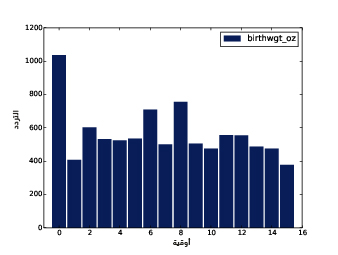
الشكل 2.2.jpg

يُظهِر الشكل السابق المدرَّج التكراري لوزن الولادات بالأوقية.

متغيرات المسح الوطني لنمو الأسرة NSFG

توجد شيفرة هذا المقال في ملف first.py، ويُفضَّل اكتشاف المتغيرات المخطَّط لاستخدامها واحدًا تلو الآخر عند البدء بالعمل مع مجموعة بيانات جديدة، وأفضل طريقة للبدء هي إلقاء نظرة على المدرَّجات االتكرارية.

حوّلنا agepreg في القسم 1.6 من سنتي-سنوات centiyears إلى سنوات years، كما دمجنا birthwgt_lb وbirthwgt_oz في كمية واحدة وهي totalwgt_lb.

سنستخدِم في هذا القسم تلك المتغيرات لإظهار بعض ميزات المدرَّجات التكرارية.

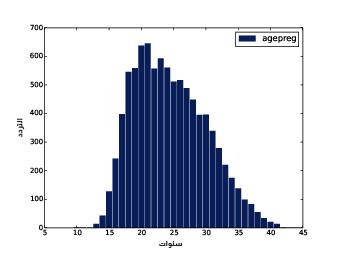
الشكل 2.3.jpg

يُظهر الشكل السابق المدرَّج التكراري لعمر الأم في نهاية الحمل.

سنبدأ بقراءة البيانات ونحدِّد سجلات الولادات الحية كما يلي:

    preg = nsfg.ReadFemPreg()
    live = preg[preg.outcome == 1]

يُعَدّ التعبير الموجود بين القوسين الهلاليَين سلسلةً بوليانيةً تُحدِّد الأسطر من إطار البيانات وتُعيد إطار بيانات جديد.

سنرسم مدرَّجًا تكراريًا لـ birthwgt_lb للولادات الحية كما يلي:

    hist = thinkstats2.Hist(live.birthwgt_lb, label='birthwgt_lb')
    thinkplot.Hist(hist)
    thinkplot.Show(xlabel='pounds', ylabel='frequency')

ستُزال قيم nan -أي ليس عددًا- عندما يكون الوسيط الممرَّر إلى المدرَّج التكراري Hist سلسلة بانداز pandas؛ أما label فهي سلسلة نصية تظهر في العنوان التفسيري عندما يُرسم Hist.

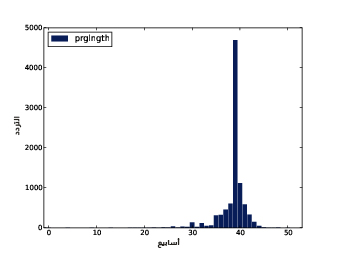
الشكل 2.4.jpg

يُظهِر الشكل السابق المدرَّج التكراري لمدة الحمل مقاسةً بالأسابيع.

يوضِّح الشكل الأول النتيجة، حيث تكون القيمة الأكثر شيوعًا والتي تدعى المنوال mode هي 7 أرطال، إذ يشبه التوزيع الجرس تقريبًا، وهو شكل التوزيع الطبيعي normal distribution الذي يسمى أيضًا بالتوزيع الغاوسي Gaussian distribution، ولكن على عكس التوزيع الطبيعي الحقيقي؛ يكون هذا التوزيع غير متناظر، حيث يملك ذيلًا tail يمتد من إلى اليسار أكثر من اليمين، ويوضِّح الشكل الثاني المدرَّج التكراري الخاص بالمتغير birthwgt_oz، وهو وزن الولادة بالأوقية، كما نتوقَّع أن يكون هذا التوزيع موحّدًا uniform، أي ستمتلك جميع القيم التردد نفسه نظريًا، إلا أنه في الواقع ستكون القيمة 0 أكثر شيوعًا من القيم الأخرى، في حين تكون القيمتان 1 و15 أقل شيوعًا، وذلك ربما لأن المستجيبين قرّبوا أوزان المواليد إلى أقرب قيمة صحيحة؛ أما الشكل الثالث فيوضّح المدرَّج التكراري الخاص بالمتغير agepreg، وهو عمر الأم في نهاية الحمل، ويكون المنوال هنا هو 21 سنة، كما يكون التوزيع على صورة جرس تقريبًا، ولكن هنا سيمتد الذيل إلى اليمين أكثر من اليسار، حيث أن معظم الأمهات في العشرينات من عمرهن وقليل منهن في الثلاثينات. يوضِّح الشكل الرابع المدرَّج التكراري الخاص بالمتغير prglngth، وهو مدة الحمل مقاسةً بالأسابيع، إذ تكون القيمة الأكثر شيوعًا هي 39 أسبوعًا، كما يكون الذيل الأيسر أطول من الأيمن، أي أن ولادة الأطفال باكرًا هي أمر شائع، لكن من النادر استمرار الحمل أكثر من 43 أسبوعًا، وإلا فسيتدخل الأطباء غالبًا.

القيم الشاذة Outliers

يمكننا تحديد القيم الأكثر تكرارًا وتحديد شكل التوزيع بسهولة عن طريق النظر إلى المدرَّجات التكرارية، إلا أن القيم النادرة الوجود لا تظهر دائمًا، كما يُستحسَن التحقق من وجود قيم شاذة، أي القيم المتطرفة التي يمكن أن تكون أخطاءً في القياس والتسجيل، أو تكون تقاريرًا دقيقةً ناتجةً عن أحداث نادرة.

توفِّر Hist تابعَين باسم Largest وSmallest، حيث يأخذان عددًا صحيحًا n، ويُعيدان أكبر أو أصغر n قيمة من المدرَّج التكراري كما يلي:

    for weeks, freq in hist.Smallest(10):
        print(weeks, freq)

تكون القيم العشرة القليلة في قائمة مدة حمل الولادات الحية هي [22, 21, 20, 19, 18, 17, 13, 9, 4, 0]، حيث أن القيم التي تقل عن 10 أسابيع بالتأكيد خاطئة، والتفسير الأكثر احتمالًا هو عدم ترميز الخرج بصورة صحيحة.

القيم التي تزيد عن 30 أسبوعًا صحيحة غالبًا؛ أمّا القيم التي تتراوح بين 10 و30 أسبوع، فمن الصعب التأكّد من صحتها، فقد تكون بعض القيم خاطئة، ولكن تمثِّل بعضها أطفالًا خُدّج. وتكون القيم العليا بالنسبة للطرف الآخر من المجال هي:

weeks  count
43     148
44     46
45     10
46     1
47     1
48     7
50     2

يقترح معظم الأطباء الولادة المحفَّزة إذا تجاوزت مدة الحمل 42 أسبوعًا، لذا ستكون بعض القيم التي تمثل مدةً طويلةً مدهشة، إذ تبدو مدة 50 أسبوع مستبعَدة طبيًا.

تعتمد أفضل طريقة لمعالجة القيم الشاذة على "معرفة النطاق"، أي معلومات عن مصدر البيانات ومعنى هذه البيانات، كما تعتمد على التحليل الذي نخطط لإجرائه.

السؤال الذي دعانا للبحث في هذا المثال هو ما إن كان الأطفال الأوائل يولدون باكرًا -أم متأخرًا-، وعندما يطرح أحدهم هذا السؤال، فهو مهتم بحالات الحمل المكتملة غالبًا، لذا سنركِّز في هذا التحليل على حالات الحمل التي استمرت لأكثر من 27 أسبوعًا.

الأطفال الأوائل First babies

أصبح بإمكاننا الآن موازنة توزيعات مدة حمل الأطفال الأوائل وغيرهم.

قُسِّم إطار البيانات للولادات الحية باستخدام birthord، ومن ثم حساب مدرَّجهم التكراري، أي كما يلي:

    firsts = live[live.birthord == 1]
    others = live[live.birthord != 1]

    first_hist = thinkstats2.Hist(firsts.prglngth, label='first')
    other_hist = thinkstats2.Hist(others.prglngth, label='other')

ثم رسمنا مدرَّجهم التكراري على المحاور نفسها:

    width = 0.45
    thinkplot.PrePlot(2)
    thinkplot.Hist(first_hist, align='right', width=width)
    thinkplot.Hist(other_hist, align='left', width=width)
    thinkplot.Show(xlabel='weeks', ylabel='frequency',
                   xlim=[27, 46])

تأخذ الدالة thinkplot.PrePlot عدد المدرَّجات التكرارية التي ستُرسم، حيث تُستخدم هذه المعلومة من أجل اختيار تجميعة مناسبة من الألوان.

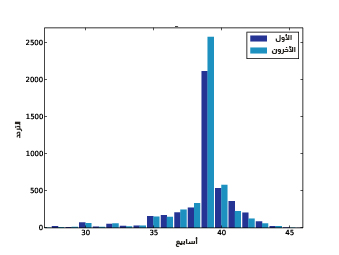
الشكل 2.5.jpg

يُظهِر الشكل السابق مدرَّجًا تكراريًا لمدة الحمل.

تحاذي الدالة thinkplot.Hist القيم عادةًّ إلى الوسط أي باعتماد 'align='center، لذا يتوضّع كل شريط فوق قيمته، كما تُستخدَم 'align='right و'align='left لوضع الأشرطة المقابِلة على جانبي القيمة. وقد وضعنا width=0.45 ليكون عرض الشريط 0.45، أي سيكون العرض الكلي للشريطَين هو 0.9 مع ترك بعض الفراغ بين كل زوج، وأخيرًا ضبطنا المحاور لإظهار البيانات الموجودة بين 27 و46 أسبوعًا فقط، حيث سيعرض الشكل السابق النتيجة.

اقتباس

تُعَدّ المدرَّجات التكرارية مفيدةً لأنّ القيم الأكثر تكرارًا تظهر فيها بصورة واضحة وعلى الفور، ولكنها ليست الخيار الأفضل لموازنة توزيعين.

كان عدد "الأطفال الأوائل" في هذا المثال أقل من عدد "الأطفال الآخرين"، لذا تعود بعض الفروق الواضحة بين المدرَّجين التكراريَين إلى أحجام العينة، حيث سنعالِج هذه المشكلة في المقال القادم باستخدام دوال الكتلة الاحتمالية.

تلخيص التوزيعات

يُعَدّ المدرَّج التكراري وصفًا كاملًا لتوزيع عينة ما، حيث أنه يمكننا إعادة بناء قيم العينة من خلال المدرَّج التكراري وحده، إلا أنه لا يمكننا معرفة ترتيب القيم.

إذا كانت تفاصيل التوزيع هامة، فقد يكون من الضروري تمثيل مدرَّج تكراري، ولكن يمكننا تلخيص التوزيع غالبًا من خلال بعض الإحصائيات الوصفية، وتكون بعض الخصائص التي قد نرغب في تقديم تقرير عنها:

النزعة المركزية central tendency: هل تميل القيم للتجمُّع حول نقطة معيّنة؟
المنوالات modes: هل يوجد أكثر من تجمُّع؟
الانتشارspread: ما مقدار التباين variability الموجود في القيم؟
الذيول tails: ما مدى سرعة انخفاض الاحتمالات عندما نبتعد عن المنوال؟
القيم الشاذة outliers: هل توجد قيم متطرِّفة بعيدة عن المنوالات؟

تُدعى الإحصائيات المصمَّمة للإجابة عن مثل هذه الأسئلة إحصائيات موجزة summary statistics، وأكثر الإحصائيات الموجزة شيوعًا هي المتوسط mean والتي تهدف إلى وصف النزعة المركزية للتوزيع.

إن كانت لديك عيّنة تحوي n قيمة x_i فإنّ المتوسط x̄ هو مجموع القيم مقسومًا على عددها، وبمعنى آخر:

x =

∑

x_i

تُستخدم عادةً الكلمتان المتوسط mean والمتوسط الحسابي average على سبيل الترادف، وقد يعتقد البعض أنهما تعنيان الشيء ذاته على الرغم من وجود فرق بينهما وهو:

متوسط العينة هو الإحصائية الموجزة التي تُحسَب بالمعادلة السابقة.
المتوسط الحسابي هو أحد الإحصائيات الموجزة التي قد تختارها لوصف النزعة المركزية.

يُمثّل المتوسط وصفًا جيدًا لمجموعة من القيم في بعض الأحيان. فمثلًا، تملك حبات التفاح جميعها الوزن نفسه تقريبًا -والتي تُباع في المتاجر الكبرى-، فإذا اشترينا ست تفاحات وكان الوزن الكلي هو 3 أرطال، فسيكون قولنا "تَزِن كل تفاحة نصف رطل" موجزًا منطقيًا.

لكن القرع أكثر تنوّعًا، فبفرض أننا زرعنا عدة أنواع في الحديقة وحصدنا في يوم من الأيام 3 حبات قرع للزينة بحيث تَزِن كل حبة رطلًا واحدًا، وحبتي قرع للفطيرة بحيث تَزِن كل منها 3 أرطال، وحبة واحدة من نوع آتلانتيك جيانت Atlantic Giant تَزن 591 رطلًا. سيكون متوسط mean هذه العينة هو 100 رطل، لكن من الخطأ القول أنّ المتوسط الحسابي average هو 100 رطل، وبالتالي لا يوجد في هذا المثال متوسط حسابي ذو معنى لأنه لا يوجد قرع مثالي.

التباين variance

إذا لم يكن هناك عددًا واحدًا يُلخِّص أوزان القرع، فسيمكننا فعل ذلك باستخدام عددين هما المتوسط mean والتباين variance.

التباين هو إحصائية موجزة تهدف إلى وصف التباين أو انتشار التوزيع.، وتكون الصيغة الرياضية لتباين مجموعة من القيم كما يلي:

S² =

∑

(x_i − x)²

يُسمّى(x<sub>i</sub>-x̄) "الانحراف عن المتوسط"، لذا سيكون التباين هو متوسط مربع الانحراف، ويكون الجذر التربيعي للتباين هو الانحراف المعياري S.

إذا كانت لديك خبرة سابقة في المجال، فربما صادفت صيغةً للتباين تحوي n − 1 في المقام بدلًا من n، إذ تُستخدَم هذه الإحصائية لتقدير التباين في إحصاء السكان باستخدام عينة.

تزوِّدنا بنى بيانات البانداز pandas بتوابع لحساب المتوسط والتباين والانحراف المعياري كما يلي:

    mean = live.prglngth.mean()
    var = live.prglngth.var()
    std = live.prglngth.std()

يكون متوسط مدة الحمل بالنسبة للولادات الحية 38.6 أسبوعًا، وانحرافه المعياري 2.7 أسبوعًا، أي علينا أن نتوقع الانحرافات بمقدار بين أسبوعين وثلاثة أسابيع وهي أمر شائع، وبذلك يكون تباين مدة الحمل هو 7.3، وهو أمر يَصعُب تفسيره، خاصةً أنّ الوحدات هي مربع الأسابيع، ويُعَدّ التباين مفيدًا في بعض العمليات الحسابية لكنه ليس إحصائية موجزة جيدة.

حجم الأثر

حجم الأثر هو إحصائية موجزة تهدف إلى وصف حجم الأثر، إذ لن تتوقع ما هو قادم، فإذا أردنا وصف الفرق بين مجموعتين مثلًا، فسيكون أحد الخيارات الشائعة هو حساب الفرق بين المتوسطات.

متوسط الحمل للأطفال الأوائل هو 38.601 ويكون لبقية الأطفال 38.523، وبالتالي يكون الفرق بينهما هو 0.078 أسبوع أي حوالي 13 ساعة، كما يكون الفارق هو 0.2% على أساس جزء من مدة الحمل الطبيعي.

إذا افترضنا أنّ هذا التقدير دقيقًا، فلن يكون لهذا الفارق أيّ عواقب عملية، ومن غير المحتمل واقعيًا ملاحظة أحد أيّ اختلاف على الإطلاق بدون مراقبة عدد كبير من حالات الحمل.

هناك طريقة أخرى لتوضيح حجم الأثر، وهي موازنة الفرق بين المجموعات مع التباين داخل المجموعات، حيث يهدف معامل كوهن د Cohen's d إلى فعل ذلك، ويُعرَّف بالصورة التالية:

S² =

∑

(x_i − x)²

يكون x̄-1 وx̄-2 متوسطي المجموعتين وs هي "الانحراف المعياري المجمَّع"، كما تكون شيفرة البايثون لحساب Cohen's d بالصورة التالية:

def CohenEffectSize(group1, group2):
    diff = group1.mean() - group2.mean()

    var1 = group1.var()
    var2 = group2.var()
    n1, n2 = len(group1), len(group2)

    pooled_var = (n1 * var1 + n2 * var2) / (n1 + n2)
    d = diff / math.sqrt(pooled_var)
    return d

يكون الفرق بين المتوسطات في هذا المثال هو 0.029 انحرافًا معياريًا الذي هو صغير جدًا، ولتوضيح ذلك بمثال آخر، سيكون الفرق في الطول بين النساء والرجال هو 1.7 انحرافًا معياريًّا، كما يمكنك الإطلاع هنا.

التقارير الخاصة بالنتائج

رأينا عدة طرق لوصف الفرق في مدة الحمل بين الأطفال الأوائل وبقية الأطفال، فكيف يمكننا إعطاء تقارير بهذه النتائج؟

تعتمد الإجابة على مَن يطرح السؤال، فقد يكون أحد العلماء مثلًا مهتمًا بأيّ تأثير حقيقي مهما كان صغيرًا؛ أما الطبيب فقد يكون مهتمًا بالتأثيرات ذات الأهمية السريرية فقط، أي أن الفروق التي تؤثِّر على القرارات العلاجية للمريض، هي حين قد تهتم المرأة الحامل بالنتائج التي تخصُّها مثل احتمالية الولادة الباكرة أو المتأخرة.

كما تعتمد طريقة تقديم تقارير بالنتائج على أهدافك، فإذا كنت تحاول إثبات أهمية تأثير معيَّن، فقد تختار إحصائية موجزة تشدِّد على الفروقات؛ أما إذا كنت تحاول طمأنة مريض، فقد تختار إحصائيةً موجزة تضع الفروقات في السياق.

يجب أن تأخذ قراراتك أخلاقيات المهنة بالحسبان، ولا بأس بأن تكون مُقنعًا، إذ عليك تصميم تقارير إحصائية وتقارير رسومية تروي القصة بوضوح، كما عليك بذل جهدك لجعل تقاريرك صادقة، وتعترف بالقيود والأمور التي ليست مؤكَّدة.

تمارين

التمرين الأول

افترض أنه قد طُلب منك تلخيص ما تعلَّمته حول ما إذا كان الأطفال الأوائل يولدون متأخرين أم لا بناءً على النتائج الواردة في هذا المقال.

ما هي الإحصائية الموجزة التي ستستخدِمها إن أردت عرض نتائجك في أخبار المساء؟ وما هي الإحصائية الموجزة التي ستستخدِمها إذا أردت طمأنة أم حامل قلقة حيال هذا الأمر؟

تخيَّل أنك سيسل آدامز Cecil Adams وهو مؤلف كتاب The Straight Dope الموجود هنا، وكانت مهمتك هي الإجابة عن هذا السؤال: "هل يولد الأطفال الأوائل متأخرين؟".

اكتب فقرةً تستخدِم النتائج الموجودة في هذا المقال للإجابة عن السؤال بكل وضوح ودقة وشفافية.

التمرين الثاني

يجب أن تجد في المستودع repository الذي حمَّلته، ملفًا باسم chap02ex.ipynb افتحه أولًا.

لقد مُلئت بعض الخلايا وعليك تنفيذها؛ أما الخلايا الأخرى فستزوِّدك بتعليمات حول التمارين، لذلك اتبع التعليمات واملأ الإجابات.

اقتباس

ملاحظة حل هذا التمرين موجود في chap02soln.ipynb.

ستجد في المستودع repository الذي حمَّلته ملفًا باسم chap02ex.py، حيث يمكنك استخدام هذا الملف على أساس نقطة انطلاق للتمارين اللاحقة.

اقتباس

ملاحظة: حل هذا التمرين موجود في chap02soln.py.

التمرين الثالث

يكون منوال التوزيع هو القيمة الأكثر تكرارًا، كما يمكنك الاطلاع على Mode_(statistics).

اكتب دالةً اسمها Mode بحيث تأخذ مدرَّجًا تكراريًا Hist وتُعيد القيمة الأكثر تكرارًا، واكتب دالةً اسمها AllModes تُعيد قائمةً من أزواج القيم وتردداتها مرتَّبةً تنازليًا حسب التردد.

التمرين الرابع

ابحث فيما إن كان وزن الأطفال الأوائل عادةً أخف وزنًا أو أثقل من البقية بالاعتماد على المتغيرtotalwgt_lb، واحسب Cohen’s d لقياس مقدار الفرق بين المجموعات، وكيف يمكن موازنتها مع الاختلاف في مدة الحمل؟

المفاهيم الأساسية

التوزيع distribution: القيم التي تظهر في العينة وتردد كل منها.
المدرَّج التكراري histogram: تحويل القيم إلى ترددات، أو رسم بياني يُظهِر هذا التحويل.
التردد frequency: عدد المرات ظهور قيمة معيَّنة في العينة.
المنوال mode: القيمة الأكثر تكرارًا في العينة أو إحدى القيم التي تملك أكبر تكرار.
التوزيع الطبيعي normal distribution: معالجة مثالية للتوزيع الذي يشبه الجرس، أو ما يُعرَف بالتوزيع الغاوسي.
التوزيع الموحَّد uniform distribution: هو التوزيع الذي يكون فيه التردد نفسه لكل القيم.
الذيل tail: جزء من التوزيع الموجود في نهاية الطرف المرتفع ونهاية الطرف المنخفض.
النزعة المركزية central tendency: صفة لعينة أو السكان، هي قيمة متوسطة أو نموذجية بديهيًا.
القيمة الشاذة outlier: قيمة بعيدة عن النزعة المركزية.
الانتشار spread: مقياس لكيفية انتشار القيم في التوزيع.
إحصائية موجزة summary statistic: إحصائية تُحدِّد بعض جوانب التوزيع مثل النزعة المركزية أو الانتشار.
التباين variance: إحصائية موجزة تُستخدَم غالبًا لقياس الانتشار.
الانحراف المعياري standard deviation: هو الجذر التربيعي للتباين، ويستخدم أيضًا على أساس مقياس للانتشار.
حجم الأثر effect size: إحصائية موجزة تهدف إلى تحديد حجم التأثير، مثل الفرق بين المجموعات.
أهمية سريرية clinically significant: نتيجة مهمة من الناحية العملية مثل الفرق بين المجموعات.