جافاسكربت متقدمة منحنى بيزيه وأهميته في الرسوميات وصناعة الحركات في جافاسكربت

تستخدم منحنيات بيزيه Bezier curves في رسوميات الحاسوب لإنشاء الأشكال والرسوم المتحركة المعتمدة على أوراق التنسيق المتتالية CSS وغيرها. هذه المنحنيات بسيطة وتستحق الدراسة، وبعدها ستكون مرتاحًا عند التعامل مع الرسوميات الشعاعية vector graphics والرسوم المتحركة المتقدمة.

نقاط التحكم

يحدد منحني بيزيه بواسطة مجموعة من النقاط الحاكمة، وقد يكون عددها 2 أو 3 أو 4 أو أكثر، لاحظ مثلًا منحنيًا من نقطتين:

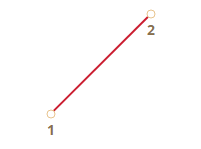
والمنحني التالي محدد بثلاث نقاط:

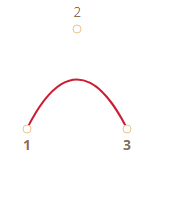
وهذا بأربع نقاط:

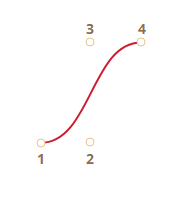
لو تمعنت في هذه المنحنيات، فيمكنك أن تلاحظ التالي:

1. لا تنتمي النقاط بالضرورة إلى المنحني وهذا أمر طبيعي، وستفهم ذلك عندما سنشرح طريقة بنائه لاحقًا.
2. درجة المنحني curve order تساوي عدد النقاط ناقصًا واحدًا، فالمنحني المؤلف من نقطتين هو خط مستقيم من الدرجة الأولى، والمنحني المؤلف من ثلاث نقاط هو منحن تربيعي، أي قطع مكافئ، وهكذا.
3. ينحصر المنحني ضمن المضلع المحدّب convex hull الذي تشكله النقاط الحاكمة:

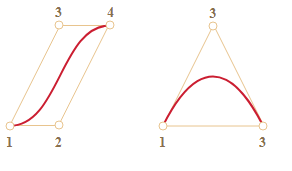
سنتمكن من أَمثَلة اختبارات التداخل في رسوميات الحاسوب اعتمادًا على الخاصية الأخيرة، فلن تتداخل المنحنيات إن لم تتداخل المضلعات المحدبة، وبالتالي ستعطي دراسة تداخل المضلعات المحدبة جوابًا سريعًا لتداخل المنحنيات، بالإضافة إلى أنّ دراسة تداخل المضلعات أسهل لأنّ أشكالها مثل المثلث والمربع، تُعَد مفهومة موازنةً بالمنحنيات.

تكمن الفائدة الرئيسية لاستخدام منحني بيزيه في تغيير شكل المنحني بمجرد تحريك النقاط الحاكمة. لاحظ المنحني الذي تولده الشيفرة التالية، واستخدم الفأرة لتحريك النقاط الحاكمة وراقب تغير المنحني:

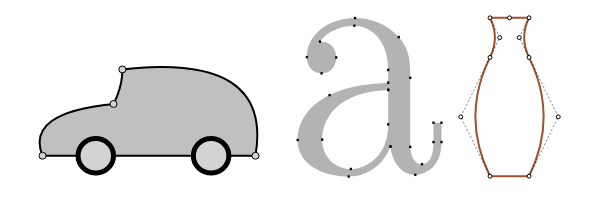
ستتمكن بعد التمرن قليلًا من رسم المنحني المطلوب بمجرد تحريك النقاط الحاكمة، ويمكنك عمليًا الحصول على أي شكل تريده بوصل عدة منحنيات، إليك بعض الأمثلة:

خوارزمية دي كاستلجو De Casteljau

يمكننا استخدام صيغة رياضية لرسم منحنيات بيزيه، وهذا ما سنشرحه لاحقًا، لأنّ خوارزمية دي كاستلجو De Casteljau’s algorithm التي نسبت لمخترعها، تتطابق مع التعريف الرياضي، وتساعدنا على تمييز طريقة إنشاء المنحنيات بصريًا.

سنرى أولًا مثالًا لمنحن من ثلاث نقاط حاكمة، لاحظ أنه يمكنك تحريك النقاط 1 و 2 و 3 بالفأرة، ثم انقر زر التشغيل الأخضر.

خوازمية دي كاستلجو لبناء منحني بيزيه من ثلاث نقاط

1. ارسم النقاط الثلاث، والتي تمثلها النقاط 1 و2 و3 في المثال السابق.
2. صل بين النقاط السابقة باتجاه واحد 3 → 2 → 1، وهي الخطوط البنية في المثال السابق.
3. يأخذ المعامل t قيمه بين "0" و"1"، وقد استخدمنا في مثالنا النموذجي السابق خطوةً مقدارها "0.05"، أي تتحرك حلقة التنفيذ وفق الآتي: 0 ثم 0.05 ثم 0.1 ثم 0.15 وهكذا.

لكل قيمة من قيم t:

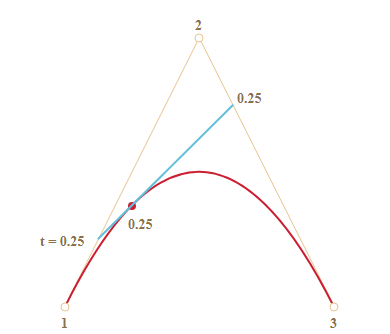
• نأخذ على كل خط بني بين نقطتين متتاليتين نقطةً تبعد عن بدايته مسافةً تتناسب مع t، وطالما أن هناك خطان، فسنحصل على نقطتين، وستكون كلتا النقطتين في بداية الخط عندما يكون t=0 مثلًا، كما ستبعد النقطة الأولى عن بداية الخط مسافةً تعادل 25% من طوله عندما تكون t=0.25، وهكذا.
• نصل بين النقطتين المتشكلتين، والخط الواصل في المثال التالي باللون الأزرق.

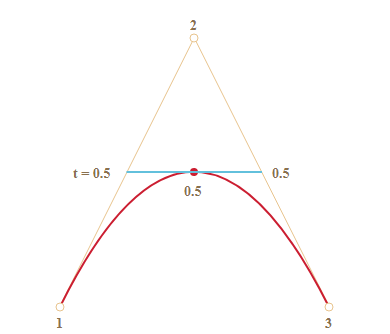
t=0.25	t=0.5

4. خذ على الخط الأزرق السابق نقطةً تبعد عن طرفه مقدارًا يتناسب مع t، ستكون النقطة في نهاية الربع الأخير من الخط من أجل t=0.25، وستكون في منتصف الخط من أجل t=0.5، وهي النقطة الحمراء في الشكل السابق.
5. عندما تتحول t بين 0 و1 ستضيف كل قيمة لهذا المعامل نقطةً من نقاط المنحني، وتمثل هذه المجموعة من النقاط منحني بيزيه.

نتبع الأسلوب ذاته بالنسبة لمنحنى مكون من أربع نقاط حاكمة.

الخوارزمية المتبعة لأربع نقاط هي:

• صل بين النقاط الحاكمة 1 إلى 2، و2 إلى 3، و3 إلى 4، وستحصل على ثلاثة خطوط بنية.
• لكل قيمة للمعامل t بين 0 و1:
• نأخذ نقاطًا على الخطوط الثلاثة تتناسب مع t كما فعلنا سابقًا، وبوصل هذه النقاط الثلاثة المتشكلة سنحصل على خطين جديدين، باللون الأخضر مثلًا.
• نأخذ على الخطين الأخضرين نقاطًا متناسبةً مع t، وعندها سنصل بين النقطتين المتشكلتين فنحصل على خط واحد، وليكن باللون الأزرق.
• نأخذ على الخط الأزرق نقطةً تبعد عن أحد طرفي الخط مسافةً متناسبةً مع t، فنحصل على نقطة حمراء واحدة تمثل أحد نقاط منحني بيزيه.
• تمثل النقاط الحمراء كلها المنحني الكامل.

إن الخوارزمية السابقية تعاودية، أي قادرة على إعادة نفسها، لذلك يمكن تعميمها إلى N نقطة حاكمة:

1. نصل بين النقاط فنحصل على N-1 خطًا.
2. لكل قيمة للمعامل t بين 0 و1 نأخذ على كل خط نقطةً تبعد عن طرف الخط مسافةً متناسبةً مع t، ونصل بين هذه النقاط فنحصل على N-2 خطًا.
3. نكرر الخطوة 2 حتى نحصل على نقطة واحدة تمثل إحدى نقاط منحني بيزيه.
4. تشكل جميع النقاط الناتجة في الخطوة 3 منحني بيزيه.

شغّل الرسوميات التالية ولاحظ شكل المنحني:

• منحن يبدو مثل الخط البياني للدالة y=1/t.

• نقاط حاكمة بشكل Zig-zag تبدو جيدةً أيضًا:

• يمكن رسم حلقة:

• يمكن رسم منحني بيزيه غير أملس أيضًا:

تابع الأمثلة الحية السابقة لترى كيف يُبنى المنحني، إذا وجدت شيئًا مبهمًا في وصف الخوارزمية.

يمكن استخدام العدد الذي نريده من النقاط الحاكمة لرسم منحني بيزيه من أي درجة، ما دامت الخوارزمية تعاوديةً، لكن يفضل عمليًا استخدام عدد قليل من النقاط -عادةً 2 أو 3 نقاط-، ثم نربط بين عدة منحنيات بسيطة إذا أردنا شكلًا أكثر تعقيدًا.

اقتباس

كيف ترسم منحنيًا من خلال مجموعة محددة من النقاط؟ لتحديد منحني بيزيه لا بدّ من استخدام نقاط حاكمة، وكما رأينا، لا تنتمي النقاط الحاكمة بالضرورة إلى المنحني عدا النقطتان الأولى والأخيرة. ينبغي علينا أحيانًا تنفيذ مهمة أخرى، فلرسم منحن يمر عبر عدة نقاط جميعها على منحن أملس واحد، فلا بدّ من تنفيذ مهمة تُدعى الاستيفاء interpolation، لكننا لن نغطي ذلك الآن. توجد صيغ رياضية لرسم منحنيات كهذه مثل كثير حدود لاغرانج Lagrange polynomial، لكن ما نستخدمه في عالم رسوميات الحاسب هو الاستيفاء القِطَعي spline interpolation لبناء منحنيات ملساء تصل بين عدة نقاط.

الصيغ الرياضية

يمكن توصيف منحني بيزيه باستخدام صيغة رياضية، وكما رأينا فلا حاجة لمعرفة هذه الصيغة. يرسم المستخدمون المنحني بمجرد تحريك النقاط بالفأرة، لكن إذا أردت استخدام الرياضيات فلك هذا.

لنفترض أنّ إحداثيي نقطة حاكمة هو Pi. ستكون النقطة الأولى (P1 = (x1, y1، والثانية (P2 = (x2, y2، وهكذا حتى آخر نقطة (Pi = (xi, yi، ويمكن أن نصف منحني بيزيه بمعادلة متغيرها t يأخذ قيمه بين 0 و1.

• صيغة منحن يمر بنقطتين هي:

• صيغة منحن يمر من 3 نقاط هي:

• صيغة منحن يمر من 4 نقاط هي:

• إنّ المعادلات السابقة هي معادلات شعاعية، أي يمكننا وضع الإحداثيين x وy بدلًا من P، فمن أجل المنحني المار من ثلاث نقاط مثلًا ستصبح الصيغة بدلالة x وy هي:

• ينبغي تعويض القيم x1, y1, x2, y2, x3, y3 في المعادلات وكتابة الصيغة بدلالة المتغير t، فلو فرضنا أنّ إحداثيات النقاط الحاكمة الثلاثة هي: (0,0) و(0.5, 1) و(1, 0)،فستصبح قيمة إحداثيي النقطة المقابلة من منحني بيزيه:

سنحصل على إحداثيي نقطة جديدة (x,y) من نقاط منحني بيزيه كلما تغيرت قيمة t بين 0 و1.

خلاصة

تُحدَّد منحنيات بيزيه بثلاث نقاط حاكمة، ويمكن رسمها بأسلوبين كما رأينا:

• باستخدام عملية رسومية: أي خوارزمية دي كاستلجو.
• باستخدام صيغة رياضية.

من الصفات الجيدة لمنحنيات بيزيه:

• إمكانية رسم منحنيات ملساء عبر تحريك النقاط الحاكمة باستخدام الفأرة.
• إمكانية رسم أشكال أكثر تعقيدًا بوصل عدة منحنيات بيزيه معًا.

استخدامات منحنيات بيزيه:

• في رسوميات الحاسوب والنمذجة ومحررات الرسوميات الشعاعية، كما توصف بها أنواع خطوط الكتابة.
• في تطوير تطبيقات الويب، من خلال الرسم ضمن لوحات وفي الملفات بتنسيق SVG، وقد كتبت الأمثلة النموذجية السابقة بتنسيق SVG، وهي عمليًا مستند SVG مفرد أُعطي نقاطًا مختلفةً مثل معاملات، ويمكن فتح هذه النماذج في نوافذ منفصلة والاطلاع على الشيفرة المصدرية: demo.svg.
• في الرسوميات المتحركة لوصف مسارها وسرعتها.

ترجمة -وبتصرف- للفصل Bezier curve من سلسلة The Modern JavaScript Tutorial.

اقرأ أيضًا

• المقال السابق: كائنا localStorage وsessionStorage لتخزين بيانات الويب في جافاسكربت
• أساسيات منحنى بيزيه Bezier Curve في سكريبوس
• تأثيرات الانتقال والحركة في CSS