يُستخدم تحويل فورييه المتقطع Discrete Fourier Transforms أو DFT بشكليه الحقيقي والمركّب لتحليل ترددات الإشارات المتقطعة والدورية.
تحويل فورييه السريع Fast Fourier Transform أو FFT هو تطبيق خاص لتحويل فورييه المتقطع DFT، يتميّز بالسرعة ويناسب وحدات المعالجة المركزية الحديثة.
تحويل فورييه السريع من الأساس 2
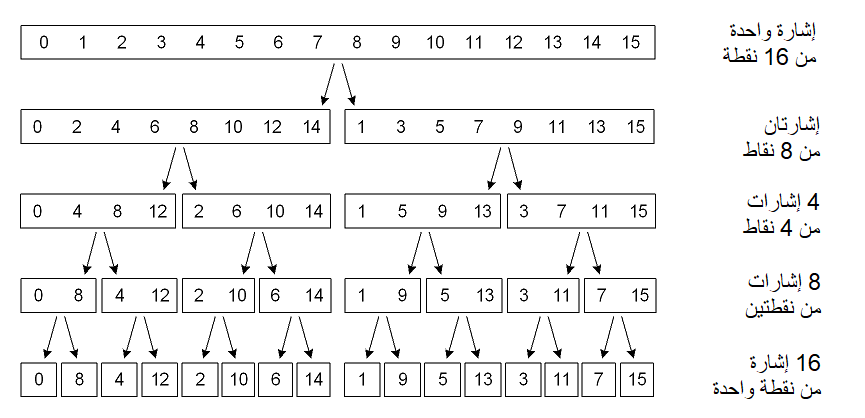
لعلّ أبسط طرق حساب تحويل فورييه السريع FFT وأشهرها هي خوارزمية التعشير الزمني من الأساس 2 أي Radix-2 Decimation in Time، وينبني عمل هذه الخوارزمية على تفكيك إشارة معيّنة ذات نطاق زمني مؤلف من N نقطة إلى N إشارة أحادية (أي ذات نطاق زمني مؤلف من نقطة واحدة).
يمكن تفكيك الإشارة -أو التعشير الزمني decimation in time- عن طريق عكس بتّات المؤشّرات في مصفوفة بيانات النطاق الزمني، فإن كانت الإشارة مؤلفة من ستة عشر نقطة مثلًا، فستُبدّل العينة 1 (ترميزها الثنائي 0001) بالعينة 8 (ترميزها الثنائي 1000)، وتبديل العينة 2 (0010) بـ 4 (0100) وهكذا دواليك. يمكن إجراء مبادلة العينات Sample swapping باستخدام تقنية عكس البتات bit reverse، بيْد أنّ ذلك سيحدّ إمكانية استخدام خوارزمية Radix 2 FFT على الإشارات التي يمكن كتابة أطوالها وفق الصيغة N = 2 ^ M.
تتطابق قيم الإشارات الأحادية داخل النطاق الزمني time domain مع قيمها في نطاق التردد frequency domain، لهذا لا تتطلب هذه المصفوفة المؤلّفة من نقاط النطاق الزمني المفكّكة أيّ تحويل لتصبح مصفوفة لترددات النطاق. بيْد أنّه يجب إعادة بناء النقاط الفردية، وعددها N كما تعلم ، إلى طيف ترددات مؤلف من N نقطة N-point frequency spectra. تُعدّ طريقة الفراشة أفضل طريقة لإعادة بناء طيف الترددات.
تتجنّب خوارزمية تحويل فورييه السريع الحسابات الزائدة التي يُجريها تحويل فورييه المتقطع DFT، وذلك عبر استغلال التواتر الدوري periodicity لـ Wn ^ R. تستغرق عملية إعادة البناء الطيفي عدد log2 (N) مرحلة من مراحل حسابات الفراشة لتُعيد قيمة X [K]؛ أي بيانات نطاق التردد وفق الشكل الجبري.
ولكي نحول الإحداثيات الجبرية إلى إحداثيات قطبية فإننا نحسب القيمة المطلقة التي تساوي: √(Re^2 + Im^2)، حيث يمثّل Re الجزء الحقيقي من العدد المركب، ويمثّل Im الجزء التخيلي. سيكون علينا إيضًا حساب وسيط العدد المركّب عبر الصيغة: tan-1 (Im / Re).
حيث:
- N: عدد النقاط في تحويل فورييه السريع
- R: قيمة WN الحالية، وتعتمد على قيمة N و المرحلة الحالية من تحويل فورييه السريع وقيمة حسابات الفراشة في هذه المرحلة.
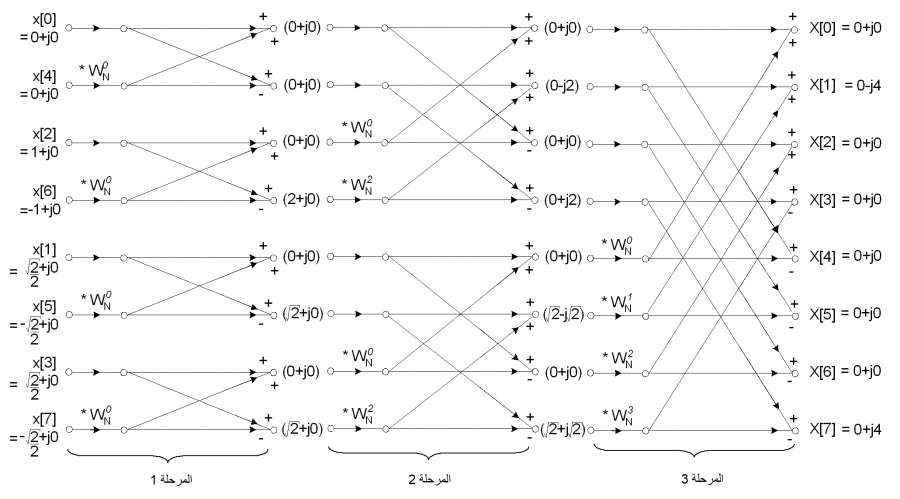
يمثل الرسم البياني التالي مخطّط الفراشة لخوارزمية فورييه السريع الثُمانِي من الأساس 2 - أي eight point Radix 2 FFT- ولاحظ أن الإشارات المُدخلة رُتَِبت وفقًا لقيم التعشير الزمني المشار إليه سابقًا.
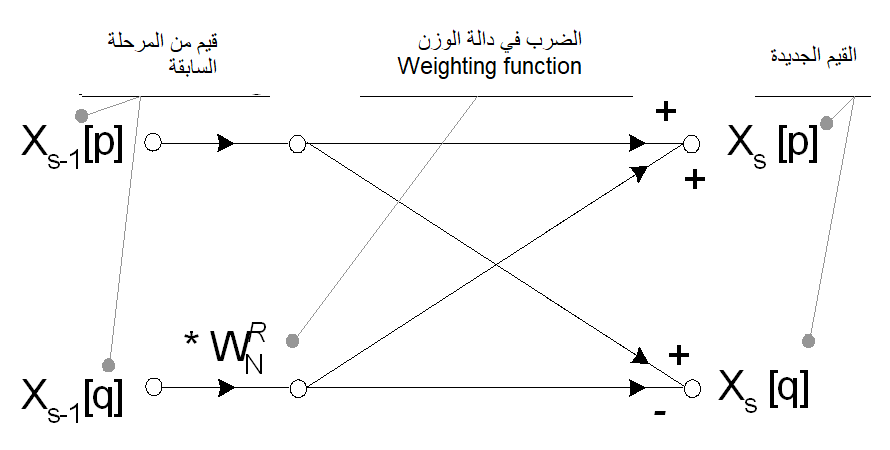
يأخذ تحويل فورييه السريع أعدادًا مركّبة ويعيد أعدادًا مركّبة، فإن أردت تمرير إشارات حقيقية (أي تنتمي لمجموعة الأعداد الحقيقية R)، فيجب أن تعيّن الجزء التخيلي على القيمة 0، وتعطي للجزء الحقيقي قيمة الإشارة المُمرَّرة، أي x [n]. يمكن تحديد قيم Wn ^ R المستخدمة خلال أطوار إعادة البناء باستخدام معادلة أسّية موزونة exponential weighting equation.
تُحدَِّد قيمة R (القوة الأسية الموزونة) المرحلة الحالية في عملية إعادة البناء الطيفية ومرحلة حسابات الفراشة.
هذه شيفرة مكتوبة بلغة C / C++ لحساب تحويل فورييه السريع من الأساس 2. تعمل هذه الشيفرة مهما كان الحجم N، شرط أن يكون N قوة للعدد 2. هذه الطريقة أبطأ 3 مرات تقريبًا من أسرع تقديم لتحويل فورييه السريع، ولكنّها تقنية واعدة ويمكن تحسينها مستقبلًا، كما أنّها مناسبة لتعليم أساسيات خوارزمية تحويل فورييه السريع.
#include <math.h> #define PI 3.1415926535897932384626433832795 // PI قيمة #define TWOPI 6.283185307179586476925286766559 // 2*PI قيمة // معامل التحويل من Degrees إلى Radians #define Deg2Rad 0.017453292519943295769236907684886 // معامل التحويل من Radians إلى Degrees #define Rad2Deg 57.295779513082320876798154814105 / #define log10_2 0.30102999566398119521373889472449 // Log10 of 2 #define log10_2_INV 3.3219280948873623478703194294948 // 1/Log10(2) // بنية لتمثيل الأعداد المركبة struct complex { public: double Re, Im; }; // تعيد true إن كان N قوة للعدد 2 bool isPwrTwo(int N, int *M) { // تمثل M عدد المراحل التي يجب إجراؤها، 2^M = N *M = (int)ceil(log10((double)N) * log10_2_INV); int NN = (int)pow(2.0, *M); // تحقق من أنّ N قوة للعدد 2 if ((NN != N) || (NN == 0)) return false; return true; } void rad2FFT(int N, complex *x, complex *DFT) { int M = 0; // تحقق من أنّه قوة للعدد 2، وإن كان خلاف ذلك فأنهِ البرنامج if (!isPwrTwo(N, &M)) throw "Rad2FFT(): N must be a power of 2 for Radix FFT"; // متغيرات صحيحة // لتخزين المسافة في الذاكرة بين حسابات الفراشة int BSep; // لتخزين المسافة بين الطرفين المتقابلين في حسابات الفراشة int BWidth; // المتماثلة التي ستُستخدم في هذه المرحلة Wn عدد قيم P يمثل المتغير int P; // في حلقة التكرار لإجراء كل الحسابات في هذه المرحلة j يُستخدم int j; // رقم المرحلة الحالية في تحليل فورييه السريع stage يمثل المتغير // في المجموعة M هناك int stage = 1; // الخاصة بالقيمة العليا DFT يمثَّل فهرس مصفوفة // في كل عملية من حسابات الفراشة int HiIndex; // يُستخدم في قلب القناع البتي unsigned int iaddr; // يُستخدم في التعشير الزمني int ii; int MM1 = M - 1; unsigned int i; int l; unsigned int nMax = (unsigned int)N; // يمثل TwoPi_N ثابتة لتخزين مدّة الحسابات = 2*PI / N double TwoPi_N = TWOPI / (double)N; double TwoPi_NP; // أعداد مركبة complex WN; // يمثل دالة الوزن الأسية وفق الشكل a + jb complex TEMP; // يُستخدم لتخزين نتائج حسابات الفراشة complex *pDFT = DFT; // مؤشر يشير إلى العنصر الأول في مصفوفة DFT complex *pLo; // مؤشّر يشير إلى lo / hi في حسابات الفراشة complex *pHi; complex *pX; // x[n] مؤشر إلى for (i = 0; i < nMax; i++, DFT++) { // حساب قيمة x[n] انطلاقا من العنوان *x والفهرس i pX = x + i; // DFT[n] إعادة تعيين عنوان جديد لـ ii = 0; iaddr = i; for (l = 0; l < M; l++) // ii وتخزين الناتج في i قلب بتات { if (iaddr & 0x01) // تحديد البتة الأقل أهمية ii += (1 << (MM1 - l)); iaddr >>= 1; operations for speed increase if (!iaddr) break; } DFT = pDFT + ii; DFT->Re = pX->Re; DFT->Im = pX->Im; // العدد التخيلي يساوي 0 دائما } for (stage = 1; stage <= M; stage++) { //تقسيم حسابات الفراشة إلى 2^stage BSep = (int)(pow(2, stage)); // قيم Wn المتماثلة في هذه المرحلة = N/Bsep P = N / BSep; // عرض المرحلة الحالية في حسابات الفراشة // (المسافة بين النقاط المتقابلة) BWidth = BSep / 2; TwoPi_NP = TwoPi_N*P; for (j = 0; j < BWidth; j++) { //حفظ الحسابات إن كان R = 0، حيث WN^0 = (1 + j0) if (j != 0) { //WN.Re = cos(TwoPi_NP*j) // (حساب Wn (الجزء الحقيقي والتخيلي WN.Re = cos(TwoPi_N*P*j); WN.Im = -sin(TwoPi_N*P*j); } for (HiIndex = j; HiIndex < N; HiIndex += BSep) { pHi = pDFT + HiIndex; // التأشير إلى القيمة العليا pLo = pHi + BWidth; // التأشير إلى القيمة السفلى if (j != 0) { //CMult(pLo, &WN, &TEMP); TEMP.Re = (pLo->Re * WN.Re) - (pLo->Im * WN.Im); TEMP.Im = (pLo->Re * WN.Im) + (pLo->Im * WN.Re); //CSub (pHi, &TEMP, pLo); pLo->Re = pHi->Re - TEMP.Re; pLo->Im = pHi->Im - TEMP.Im; //CAdd (pHi, &TEMP, pHi); pHi->Re = (pHi->Re + TEMP.Re); pHi->Im = (pHi->Im + TEMP.Im); } else { TEMP.Re = pLo->Re; TEMP.Im = pLo->Im; //CSub (pHi, &TEMP, pLo); pLo->Re = pHi->Re - TEMP.Re; pLo->Im = pHi->Im - TEMP.Im; //CAdd (pHi, &TEMP, pHi); pHi->Re = (pHi->Re + TEMP.Re); pHi->Im = (pHi->Im + TEMP.Im); } } } } pLo = 0; pHi = 0; pDFT = 0; DFT = 0; pX = 0; }
تحويل فورييه السريع المعكوس من الأساس 2
يمكن الحصول على تحويل فورييه المعكوس عبر تعديل ناتج تحويل فورييه السريع العادي، ويمكن تحويل البيانات في نطاق الترددات frequency domain إلى النطاق الزمني time domain بالطريقة التالية:
- اعثر على مرافق العدد المركب لبيانات نطاق الترددات.
- طبّق تحويل فورييه السريع العادي على مرافق بيانات نطاق التردّد conjugated frequency domain data.
- اقسم كل مخرجات نتيجة تحويل فورييه السريع على N للحصول على القيمة الصحيحة للنطاق الزمني.
- احسب مرافق العدد المركب للعنصر الناتج عبر عكس المكوّن التخيلي لبيانات النطاق الزمني لجميع قيم n.
ملاحظة: تُعدّ كل من بيانات نطاق التردد وبيانات النطاق الزمني متغيّراتٍ مركبة، وعادة ما يساوي المكونّ التخيلي للنطاق الزمني للإشارة التي تعقُب تحويل فورييه السريع المعكوس القيمة 0، وإلا فستُعد خطأ تقريبيًا وتُتجاهل. وإنّ زيادة دِقة المتغيرات من 32 بتّة عشرية 32-bit float إلى 64 بتّة مزدوجة 64-bit double أو إلى 128 بتّة مزدوجة سيقلّص أخطاء التقريب الناتجة عن تعاقب عدّة تحويلات فورييه سريعة.
هذا تطبيق مكتوب بلغة C / C++:
#include <math.h> #define PI 3.1415926535897932384626433832795 #define TWOPI 6.283185307179586476925286766559 #define Deg2Rad 0.017453292519943295769236907684886 #define Rad2Deg 57.295779513082320876798154814105 #define log10_2 0.30102999566398119521373889472449 // Log10 of 2 #define log10_2_INV 3.3219280948873623478703194294948 // 1/Log10(2) // بنية لتمثل الأعداد المركبة struct complex { public: double Re, Im; }; void rad2InverseFFT(int N, complex *x, complex *DFT) { // تمثل M عدد المراحل التي يجب إجراؤها، 2^M = N double Mx = (log10((double)N) / log10((double)2)); int a = (int)(ceil(pow(2.0, Mx))); int status = 0; if (a != N) { x = 0; DFT = 0; throw "rad2InverseFFT(): N must be a power of 2 for Radix 2 Inverse FFT"; } complex *pDFT = DFT; complex *pX = x; double NN = 1 / (double)N; // تعديل معامل تحويل فورييه السريع المعكوس for (int i = 0; i < N; i++, DFT++) DFT->Im *= -1; // حساب مرافق التردد الطيفي DFT = pDFT; rad2FFT(N, DFT, x); // حساب تحويل فورييه السريع العادي int i; complex* x; for ( i = 0, x = pX; i < N; i++, x++){ x->Re *= NN; // تقسيم النطاق الزمني على N لتصحيح السعة x->Im *= -1; // ImX تغيير إشارة } }
ترجمة -بتصرّف- للفصل 55 من كتاب Algorithms Notes for Professionals.
اقرأ أيضًا
- المقال السابق: خوارزميات للتعامل مع المصفوفات matrix algorithms
- المرجع الشامل إلى: تعلم الخوارزميات للمبتدئين
- خوارزميات البحث في النصوص
- أمثلة عن أنواع الخوارزميات
- خوارزميات الترتيب وأشهرها

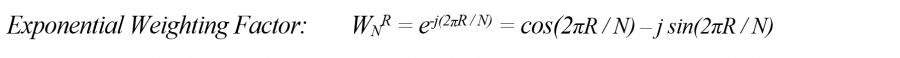









أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.