تمثل الأشجار نوعًا فرعيًا لهيكل أعم من هياكل البياناتٍ التخطيطية التفرعية Node-Edge Graph Data Structure كالآتي:
والشجرة هي مخطط يحقق الشرطين التاليين:
- غير حلقي acyclic: أي لا يحتوي أيّ دورات cycles أو حلقات loops.
- متصل: أي يمكن الوصول إلى كل عقدة من عقد المخطط عبر مسار معيّن.
وهيكل الشجرة شائع جدًا في علوم الحاسوب، إذ يُستخدم لنمذجة العديد من هياكل البيانات الخوارزمية المختلفة، مثل الأشجار الثنائية العادية والأشجار الحمراء-السوداء red-black trees، وأشجار B وأشجار AB وأشجار 23 وأشجار الكومة Heap وكذلك أشجار Trie.
وتكون الشجرة جِذريةً Rooted Tree في حال:
- اختيار خلية واحدة لتكون جذرًا للشجرة.
- صباغة Painting الجذر في أعلى الشجرة.
-
إنشاء طبقة سفلية lower layer لكل خلية في المخطط تبعًا للمسافة بينها وبين الجذر، فكلما كانت المسافة أكبر، كانت الخلية أسفل كما في الصورة التوضيحية أعلاه. ويرمز عادةً للأشجار بالرمز
T.
الأشجار اللانهائية anary tree
نُمثّل الأشجار اللانهائية -أي الأشجار التي يمكن أن يتفرّع عدد لانهائي من الفروع من عقدها- على هيئة أشجار ثنائية binary tree، وهي أشجار يتفرع عن كل عقدة منها فرعان فقط، ويُعَد الفرع الثاني منهما شقيقًا Sibling، لاحظ أنه إذا كانت الشجرة ثنائيةً، فسينشئ التمثيل عُقدًا إضافية.
ثم نكرر بعد ذلك على الأشقاء، ومن ثم على الفروع، وبما أن أغلب الأشجار ضحلة (أي لها مستويات تفرع هرمي قليلة، رغم إمكانية كثرة الفروع للمستوى الواحد)، فإن هذا ينتج عنه شيفرة ذات كفاءة عالية، لاحظ أن هذا عكس هرمية البشر، إذ يكون لنا مستويات كثيرة جدًا في هرمية الآباء وأولاد قليلون لكل مستوى موازنةً بأولئك الآباء.
من الممكن حفظ المؤشرات الخلفية للسماح للشجرة أن ترتقي، لكن تلك المؤشرات صعبة في معالجتها وصيانتها. لاحظ أنه عادةً ما يكون لدينا دالة واحدة للاستدعاء على الجذر، ودالة تكرارية recursive مع معامِلات إضافية، وفي هذا المثال فهي عمق الشجرة، انظر:
struct node { struct node *next; struct node *child; std::string data; } void printtree_r(struct node *node, int depth) { int i; while(node) { if(node->child) { for(i=0;i<depth*3;i++) printf(" "); printf("{\n"): printtree_r(node->child, depth +1); for(i=0;i<depth*3;i++) printf(" "); printf("{\n"): for(i=0;i<depth*3;i++) printf(" "); printf("%s\n", node->data.c_str()); node = node->next; } } } void printtree(node *root) { printree_r(root, 0); }
التحقق من تساوي شجرتين ثنائيتين
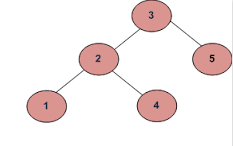
انظر الشجرتين التاليتين:
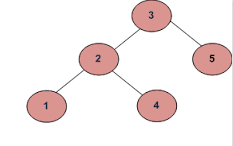
هاتان الشجرتين متساويتان، على خلاف الشجرتين التاليتين:
وفيما يلي شيفرة عامة زائفة pseudo code للتحقق من تساوي شجرتين:
boolean sameTree(node root1, node root2){ if(root1 == NULL && root2 == NULL) return true; if(root1 == NULL || root2 == NULL) return false; if(root1->data == root2->data && sameTree(root1->left,root2->left) && sameTree(root1->right, root2->right)) return true; }
أشجار البحث الثنائية Binary Search Trees
الأشجار الثنائية هي الأشجار التي يتفرّع عن كلّ عقدة منها ابنان على الأكثر، وشجرة البحث الثنائية Binary search tree أو BST اختصارًا هي شجرة ثنائية عناصرها مُرتّبة ترتيبًا خاصًا، إذ تكون جميع القيم الموجودة في الشجيرة أو الفرع sub tree الأيسر أصغر من القيم في الشجَيرة اليمنى.
إدراج عنصر في شجرة بحث ثنائية Python
رسم يوضح كيفية إدراج عنصر في الشجرة
هذا تنفيذ بسيط لكيفية إدراج عنصر في شجرة بحث ثنائية مكتوب بلغة Python.
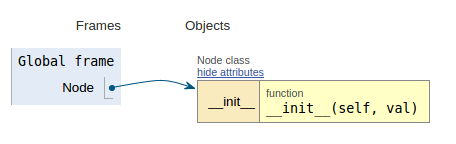
class Node: def __init__(self, val): self.l_child = None self.r_child = None self.data = val
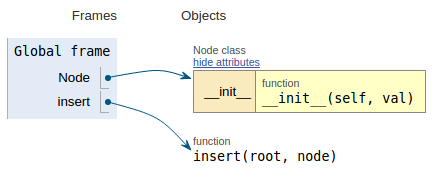
def insert(root, node): if root is None: root = node else: if root.data > node.data: if root.l_child is None: root.l_child = node else: insert(root.l_child, node) else: if root.r_child is None: root.r_child = node else: insert(root.r_child, node)
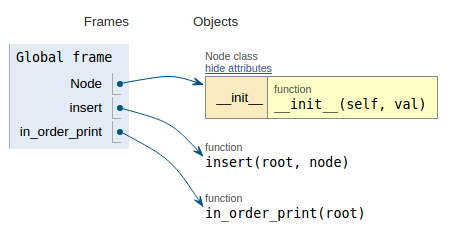
def in_order_print(root): if not root: return in_order_print(root.l_child) print root.data in_order_print(root.r_child)
def pre_order_print(root): if not root: return print root.data pre_order_print(root.l_child) pre_order_print(root.r_child)
حذف عنصر من شجرة بحث ثنائية C++
قبل أن نبدأ، نريد أن التذكير بمفهوم شجرة البحث الثنائية BST، وهي التي يتفرّع عن كل عقدة منها عقدتان كحد أقصى (ابن أيمن وأيسر)، حيث تحتوي الشجيرة اليسرى المتفرّعة عن عقدة ما على مفتاح قيمته أصغر من أو تساوي مفتاحَ العقدة الأصلية. وتحتوي الشجيرة اليمنى للعقدة على مفتاح أكبر من مفتاح العقدة الأصلية.
سنناقش في هذه الفقرة كيفية حذف عقدة من شجرة بحث ثنائية مع الحفاظ على الخاصية أعلاه.
هناك ثلاث حالات يجب مراعاتها عند حذف العقدة، هي الآتية:
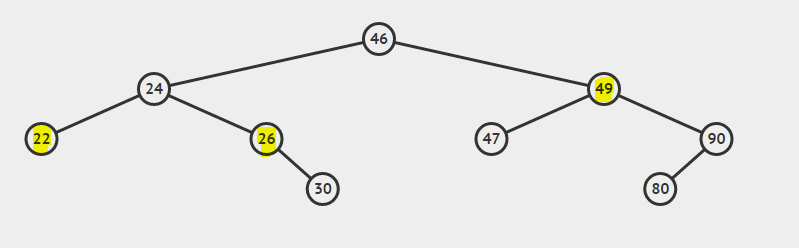
- الحالة 1: العقدة المراد حذفها هي ورقة أو عقدة طرفية leaf node، مثل العقدة ذات القيمة 22.
- الحالة 2: العقدة المراد حذفها لها ابن واحد، مثل العقدة ذات القيمة 26.
- الحالة 3: العقدة المراد حذفها لها ابنان، مثل العقدة ذات القيمة 49.
شرح الحالات
-
عندما تكون العقدة المراد حذفها ورقةً، فما عليك سوى حذف العقدة وتعيين المؤشر الفارغ
nullptrإلى العقدة الأصلية. - عندما تحتوي العقدة المراد حذفها على ابن واحد فقط، انسخ قيمة الابن إلى قيمة العقدة ثمّ احذف الابن (ستُحوّل إلى الحالة 1).
- عندما يكون للعقدة المراد حذفها ابنان، فيمكن نسخ القيمة الأصغر من شجيرتها اليمنى إلى العقدة، بعدها يمكن حذف القيمة الدنيا من الشجيرة اليمنى للعقدة، حيث ستُحوَّل إلى الحالة 2.
اقتباسملاحظة: يمكن أن يحتوي الحد الأدنى في الشجيرة اليمنى على ابن واحد على الأكثر، والذي سيكون الابن الأيمن، إذ أنّه في حال كان لها ابن آخر أيسر، فذلك يعني أنّها ليست القيمة الأدنى أو لا تستوفي خاصية أشجار البحث الثنائية BST.
انظر المثال التالي على حذف عنصر من شجرة بحث ثنائية:
struct node { int data; node *left, *right; }; node* delete_node(node *root, int data) { if(root == nullptr) return root; else if(data < root->data) root->left = delete_node(root->left, data); else if(data > root->data) root->right = delete_node(root->right, data); else { if(root->left == nullptr && root->right == nullptr) // الحالة 1 { free(root); root = nullptr; } else if(root->left == nullptr) // الحالة 2 { node* temp = root; root= root->right; free(temp); } else if(root->right == nullptr) // الحالة 2 { node* temp = root; root = root->left; free(temp); } else // الحالة 3 { node* temp = root->right; while(temp->left != nullptr) temp = temp->left; root->data = temp->data; root->right = delete_node(root->right, temp->data); } } return root; }
التعقيد الزمني للشيفرة أعلاه هو O(h)، حيث تمثّل h ارتفاع الشجرة.
أدنى سلف مشترك في شجرة بحث ثنائية
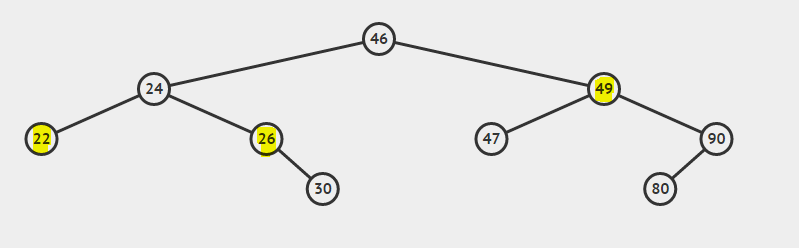
انظر شجرة البحث الثنائية التالية:
- أدنى سلف مشترك Lowest common ancestor لـ 22 و26 هو 24.
- أدنى سلف مشترك لـ 26 و49 هو 46.
- أدنى سلف مشترك لـ 22 و24 هو 24.
تُستغل الخاصية المميّزة لأشجار البحث الثنائية للعثور على السلف الأدنى للعقد، فيما يلي شيفرة عامة للعثور على السلف المشترك الأدنى:
lowestCommonAncestor(root,node1, node2){ if(root == NULL) return NULL; else if(node1->data == root->data || node2->data== root->data) return root; else if((node1->data <= root->data && node2->data > root->data) || (node2->data <= root->data && node1->data > root->data)){ return root; } else if(root->data > max(node1->data,node2->data)){ return lowestCommonAncestor(root->left, node1, node2); } else { return lowestCommonAncestor(root->right, node1, node2); } }
شجرة البحث الثنائية Python
انظر إلى شيفرة البايثون التالية:
class Node(object): def __init__(self, val): self.l_child = None self.r_child = None self.val = val class BinarySearchTree(object): def insert(self, root, node): if root is None: return node if root.val < node.val: root.r_child = self.insert(root.r_child, node) else: root.l_child = self.insert(root.l_child, node) return root def in_order_place(self, root): if not root: return None else: self.in_order_place(root.l_child) print root.val self.in_order_place(root.r_child) def pre_order_place(self, root): if not root: return None else: print root.val self.pre_order_place(root.l_child) self.pre_order_place(root.r_child) def post_order_place(self, root): if not root: return None else: self.post_order_place(root.l_child) self.post_order_place(root.r_child) print root.val
هذه شيفرة لإنشاء عقدة جديدة وإدراج البيانات فيها:
r = Node(3) node = BinarySearchTree() nodeList = [1, 8, 5, 12, 14, 6, 15, 7, 16, 8] for nd in nodeList: node.insert(r, Node(nd)) print "------In order ---------" print (node.in_order_place(r)) print "------Pre order ---------" print (node.pre_order_place(r)) print "------Post order ---------" print (node.post_order_place(r))
التحقق مما إذا كانت الشجرة شجرة بحث ثنائية أم لا
تكون شجرةٌ ثنائيةٌ ما "شجرةَ بحث ثنائية" إذا كانت تستوفي أيًّا من الشروط التالية:
- إن كانت فارغة.
- لا تتفرع منها أيّ شجيرات.
- لكلّ عقدة x في الشجرة، يجب أن تكون جميع المفاتيح (إن وجدت) في الشجيرة اليسرى أصغر من مفتاح x، أي key(x)، ويتعيّن أن تكون جميع المفاتيح (إذا وجدت) في الشجيرة اليمنى أكبر من key(x).
الخوارزمية التكرارية التالية تتحقق من الشروط أعلاه:
is_BST(root): if root == NULL: return true
تحقق من القيم في الشجيرة اليسرى:
if root->left != NULL: max_key_in_left = find_max_key(root->left) if max_key_in_left > root->key: return false
تحقق من القيم في الشجيرة اليمنى:
if root->right != NULL: min_key_in_right = find_min_key(root->right) if min_key_in_right < root->key: return false return is_BST(root->left) && is_BST(root->right)
رغم صحة الخوارزمية أعلاه إلا أنها تفتقر إلى الكفاءة، لأنّها تمر على كلّ عقدة عدّة مرات، ولتقليل عدد مرّات زيارة كل عقدة يجب أن نتذكر القيم الدنيا والقصوى الممكنة للمفاتيح في الشجيرة التي نزورها.
سنستخدم هذه الفكرة لتطوير خوازمية أكثر فعالية.
ولفعل هذا، نرمز للقيمة الدنيا الممكنة لأيّ مفتاح K_MIN، والقيمة القصوى بالرمز K_MAX. فإن بدأتَ من جذر الشجرة يكون نطاق قيم الشجرة هو [ K_MIN ،K_MAX]. وإذا كان x هو مفتاح عقدة الجذر فسيكون نطاق القيم في الشجيرة اليسرى هو [K_MIN,x)(x,K_MAX].
s_BST(root, min, max):
if root == NULL:
return true
// هل مفتاح العقدة الحالية خارج النطاق؟
if root->key < min || root->key > max:
return false
// التحقق مما إذا كانت الشجيرتان اليسرى واليمنى أشجارَ بحث ثنائية
return is_BST(root->left,min,root->key-1) && is_BST(root->right,root->key+1,max)وستُستَدعى في البداية على النحو التالي:
is_BST(my_tree_root,KEY_MIN,KEY_MAX)هناك منظور آخر لحل الأمر، وهو الاجتياز المُرتّب inorder traversal للشجرة الثنائية -انظر أدناه-، فإذا نتج عن ذلك الاجتياز المُرتب تسلسلٌ مرتّب من المفاتيح، فستكون الشجرة شجرة بحث ثنائية. وللتحقق ممّا إذا كان التسلسل الناتج مُرتّبًا أم لا، فعليك تخزين قيمة العقدة المُزارة سابقًا، ثمّ موازنتها بالعقدة الحالية.
النظر في ما إن كانت شجرة ما تحقق شرط أشجار البحث الثنائية
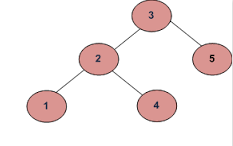
انظر المثال التالي: إن كانت المدخلات كما يلي:
فإن الخرج سيكون خاطئًا false، وعليه لا تكون هذه شجرة بحث ثنائية، ذلك أنّ 4 في الشجيرة اليسرى أكبر من قيمة الجذر 3. انظر الآن مثالًا على شجرة أخرى:
النتيجة ستكون صحيحة وتكون شجرة بحث ثنائية.
اجتيازات الأشجار الثنائية Binary Tree traversals
زيارة عقدة لشجرة ثنائية بترتيب معيّن يُسمّى اجتيازَا أو عبورًا traversal، وهناك عدة أنواع من الاجتياز سنستعرض في هذه الفقرة بعضها.
الاجتياز بالمستويات: التطبيق
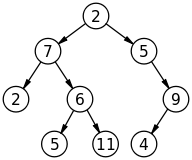
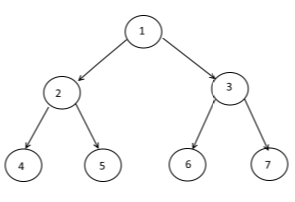
انظر الشجرة التالية:
يكون الاجتياز بالمستويات على الترتيب التالي:
1 2 3 4 5 6 7 مع طبع بيانات العُقَد مستوىً بمستوى، انظر:
include<iostream>
#include<queue>
#include<malloc.h>
using namespace std;
struct node{
int data;
node *left;
node *right;
};
void levelOrder(struct node *root){
if(root == NULL) return;
queue<node *> Q;
Q.push(root);
while(!Q.empty()){
struct node* curr = Q.front();
cout<< curr->data <<" ";
if(curr->left != NULL) Q.push(curr-> left);
if(curr->right != NULL) Q.push(curr-> right);
Q.pop();
}
}
struct node* newNode(int data)
{
struct node* node = (struct node*)
malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
int main(){
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
printf("Level Order traversal of binary tree is \n");
levelOrder(root);
return 0;
}تُستخدم الصفوف Queues -وهو نوع من البيانات- لتحقيق الهدف أعلاه.
الاجتياز التنازلي والتصاعدي والمرتب
انظر الشجرة الثنائية التالية:
- الاجتياز التنازلي Pre-order traversal: يبدأ هذا النوع باجتياز العقدة، ثم الشجيرة اليسرى للعقدة، ثمّ الشجيرة اليمنى لها. ويكون الاجتياز التنازلي بالترتيب التالي:
1 2 4 5 3 6 7- الاجتياز المُرتّب In-order traversal: هو اجتياز الشجيرة اليسرى للعقدة، ثمّ العقدة نفسها، ثم الشجيرة اليمنى للعقدة. يكون الاجتياز المُرتّب بالترتيب التالي:
4 2 5 1 6 3 7 - الاجتياز التصاعدي Post-order traversal: هو اجتياز الشجيرة اليسرى للعقدة، ثم الشجيرة اليمنى، ثمّ العقدة، ويكون الاجتياز التصاعدي بالترتيب التالي:
4 5 2 6 7 3 1العثور على أدنَى سلف مشترك لشجرة ثنائية
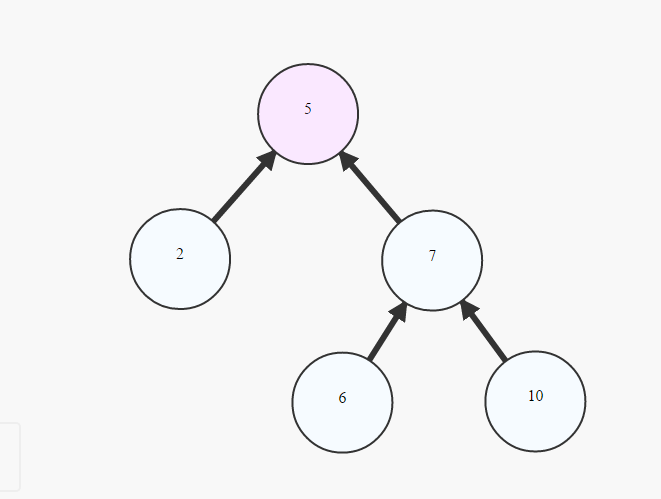
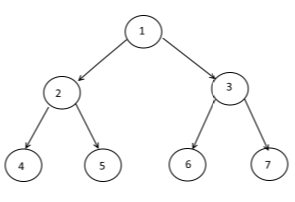
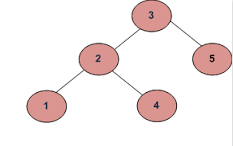
السلف المشترك الأدنى للعقدتين n1 وn2 هو أدنى عقدة في الشجرة يكون كلّ من n1 وn2 أحفادًا لها. انظر الشجرة التالية:
- أدنى سلف مشترك للعقدتين ذواتي القيمتين 1 و4 هو 2.
- أدنى سلف مشترك للعقدتين ذواتي القيمتين 1 و5 هو 3.
- أدنى سلف مشترك للعقدتين ذواتي القيمتين 2 و4 هو 4.
- أدنى سلف مشترك للعقدتين ذواتي القيمتين 1 و2 هو 2.
ترجمة -بتصرّف- للفصول من 4 إلى 8 من كتاب Algorithms Notes for Professionals
اقرأ أيضًا
- المقالة السابقة: ترميز Big-O
- المرجع الشامل إلى: تعلم الخوارزميات للمبتدئين
- تعقيد الخوارزميات Algorithms Complexity
- مدخل إلى الخوارزميات
- دليل شامل عن تحليل تعقيد الخوارزمية
- النسخة الكاملة من كتاب مدخل إلى الذكاء الاصطناعي وتعلم الآلة

















أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.