خوارزمية ديكسترا Dijkstra’s Algorithm

تُعرف خوارزمية ديكسترا بخوارزمية أقصر مسار أحادي المصدر single-source shortest path algorithm، وتُستخدم للعثور على أقصر المسارات بين العقد في مخطط، وقد ابتُكرت هذه الخوارزمية على يد إدجستر ديكسترا Edsger W. Dijkstra -النطق من الهولندية- عام 1956، ونُشِرت بعدها بثلاث سنوات.

يمكننا العثور على أقصر مسار باستخدام خوارزمية البحث بالوُسع أو العرض أولًا Breadth First Search اختصارًا BFS. وتعمل هذه الخوارزمية جيدًا لكنّها محدودة، إذ تفترض أنّ تكلفة cost اجتياز كل مسار لا تتغيّر، أي أنّ أوزان جميع الأضلاع متساوية. تساعدنا خوارزمية ديكسترا على العثور على أقصر مسار حتى لو كانت تكاليف المسارات مختلفة.

سنتعلّم في البداية كيفية تعديل خوارزمية BFS لكتابة خوارزمية Dijkstra، ثم سنضيف طابور الأولويات priority queue لجعلها خوارزمية Dijkstra كاملة.

لنفترض أنّ المسافة بين كل عقدة وبين المصدر مُخزّنة في مصفوفة d[]‎‎، حيث تمثّل d[3]‎‎ مثلًا الوقت اللازم للوصول إلى العقدة 3 من المصدر، وإذا لم نعرف المسافة فسنضع قيمة ما لا نهاية inﬁnity في d[3]‎‎. لنفترض أن cost مصفوفة تخزّن التكاليف، بحيث تحتوي cost[‎u][v]‎‎ على كلفة مجموع أوزان الأضلاع التي تؤلف المسار u-v، أي أنّ الانتقال من العقدة u إلى العقدة v يتطلب تكلفة cost[‎u][v]‎‎.

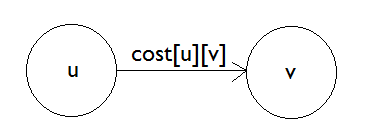
قبل أن نواصل، سنوضّح مفهوم تخفيف الضلع Edge Relaxation.

لنفترض أنّك تحتاج 10 دقائق للانتقال من منزلك (المصدر) إلى المكان A، بينما يستغرق الانتقال إلى المكان B حوالي 25 دقيقة. سيكون لدينا إذًا الآتي:

d[A] = 10
d[B] = 25

لنفترض الآن أنّك تحتاج 7 دقائق للانتقال من A إلى B، هذا يعني أنّ:

cost[A][B] = 7

يمكننا الذهاب إلى B عبر الانتقال من المصدر (منزلك) إلى A، ثمّ من A إلى B، وسيستغرق هذا 10 + 7 = 17 دقيقة بدلًا من 25 دقيقة:

d[A] + cost[A][B] < d[B]

نحدّث الجدول على النحو التالي:

d[B] = d[A] + cost[A][B]

يسمّى هذا تخفيفًا relaxation، إذ نذهب من u إلى v، فإذا وجدنا أنّ < d[‎u] + cost[‎u][v] < d[v]‎‎، فسنحدّث المصفوفة بالقيمة d[v] = d[‎u] + cost[‎u][v]‎‎.

لم نكن بحاجة إلى زيارة أيّ عقدة مرتين في خوارزمية البحث بالوُسع أولًا BFS، فقد اكتفينا بالتحقّق ممّا إذا تمّت زيارة العقدة أم لا، فإن لم تُزَر، فسنضع العقدة في الطابور ثمّ نحددها على أنّها "تمت زيارتها"، بعدها نزيد المسافة بمقدار 1؛ أما في خوارزمية Dijkstra، فإننا نضع العقدة في الطابور، لكن بدلًا من تحديثها وتحديدها على أنّها مُزارة، فسنخفّف الضلع الجديد relax أو نحدّثه.

انظر المثال التالي:

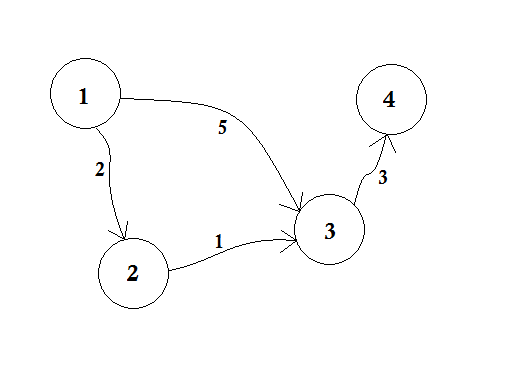
لنفترض أنّ العقدة 1 هي المصدر، إذًا:

d[1] = 0
d[2] = d[3] = d[4] = infinity (or a large value)

لقد عيّنا قيم d [2]‎‎ وd [3]‎‎ وd [4]‎‎ إلى ما لا نهاية لأنّنا لا نعرف المسافة بعد،‎‎‎‎ أمّا مسافة المصدر فتُساوي 0 بالطبع. سننتقل الآن إلى العُقد الأخرى انطلاقًا من المصدر، وإذا كانت هناك حاجة لتحديثها فسنضيفها إلى الطابور. لنقل على سبيل المثال أنّنا سنجتاز الضلع 1-2، وبما أن d[1] + 2 < d[2]‎‎، فسنضع d[2] = 2، وبالمثل نجتاز الضلع 1-3، وتبعًا لذلك نكتب d [3] = 5.

يمكن أن ترى بوضوح أنّ 5 ليست أقصر مسافة يمكننا عبورها للذهاب إلى العقدة 3، لذا فإنّ اجتياز العقدة مرّةً واحدةً فقط كما في خوارزمية BFS، ليس صالحًا هنا. ويمكننا إضافة التحديث d [3] = d [2] + 1 = 3 إذا انتقلنا من العقدة 2 إلى العقدة 3 باستخدام الضلع 2-3. وكما ترى، فمن الممكن تحديث العقدة الواحدة عدّة مرات.

قد تسأل عن عدد المرات التي يمكن أن نفعل فيها ذلك، والإجابة هنا هي أن الحد الأقصى لعدد مرات تحديث العقدة هو الدرجة الداخلية in-degree لتلك العقدة.

فيما يلي شيفرة عامّة لزيارة أيّ عقدة عدّة مرات، هذه الشيفرة هي تعديل لخوارزمية BFS:

procedure BFSmodified(G, source):
Q = queue()
distance[] = infinity
Q.enqueue(source)
distance[source]=0
while Q is not empty
    u <- Q.pop()
   for all edges from u to v in G.adjacentEdges(v) do
        if distance[u] + cost[u][v] < distance[v]
            distance[v] = distance[u] + cost[u][v]
        end if
  end for
end while
Return distance

يمكن استخدام هذا للعثور على أقصر مسار إلى جميع العقدة انطلاقًا من المصدر، ولا يُعد تعقيد هذه الشيفرة جيدًا، ذلك أننا في خوارزمية BFS نتبّع طريقة أوّل من يأتي هو أوّل من يُخدم "ﬁrst come, ﬁrst serve" عندما تنتقل من العقدة 1 إلى أي عقدة أخرى.

فمثلًا، نحن ذهبنا إلى العقدة 3 من المصدر قبل معالجة العقدة 2، وعليه سنحدّث العقدة 4 إذا ذهبنا إلى العقدة 3 من المصدر، وذلك لأنّ 5 + 3 = 8. وعندما نحدّث العقدة 3 مرّةً أخرى من العقدة 2، فسيكون علينا تحديث العقدة 4 بالقيمة 3 + 3 = 6 مرّةً أخرى، وعليه تكون العقدة 4 قد حُدِّثَت مرتين.

وقد اقترح Dijkstra طريقة أخرى بدلًا من طريقة أوّل من يأتي أوّل من يُخدَم، فإذا حدّثنا العُقَد الأقرب أولًا سنستطيع إجراء عدد أقل من التحديثات، وإذا كنا قد عالجنا العقدة 2 من قبل، فإنّ العقدة 3 ستكون قد حُدِّثت كذلك من قبل، وسنحصل على أقصر مسافة بسهولة بعد تحديث العقدة 4 وفقًا لذلك.

الفكرة هنا هي أن نختار أقرب عقدة إلى المصدر من الطابور، لذلك سنستخدم طابور أولويات Priority Queue، وعندما ننزع عنصرًا من الطابور، سنحصل على أقرب عقدة u من المصدر عبر التحقق من قيمة d[‎u]‎‎.

انظر الشيفرة التوضيحية التالية:

procedure dijkstra(G, source):
Q = priority_queue()
distance[] = infinity
Q.enqueue(source)
distance[source] = 0
while Q is not empty
    u <- nodes in Q with minimum distance[]
    remove u from the Q
   for all edges from u to v in G.adjacentEdges(v) do
         if distance[u] + cost[u][v] < distance[v]
            distance[v] = distance[u] + cost[u][v]
            Q.enqueue(v)
        end if
    end for
end while
Return distance

تعيد الشيفرة التوضيحية مسافةَ جميعِ العقد الأخرى من المصدر، فإذا أردنا معرفة مسافة عقدة v، فيمكننا ببساطة إعادة القيمة الناتجة عن أخذ v من الطابور.

السؤال الآن هو: هل تعمل خوارزمية ديكسترا حال وجود ضلع سالب negative edge؟ إذا كانت هناك دورة سالبة فستحدث حلقة لا نهائية، وذلك لأنها ستستمر في تخفيض التكلفة إلى الأبد، ولن تعمل خوارزمية ديكسترا حتى لو كان لدينا ضلع سالب إلا إذا عدنا مباشرةً بعد أخذ الهدف من الطابور، لكن لن تكون الخوارزمية حينئذ خوارزميةَ Dijkstra، وسنحتاج إلى خوارزمية بيلمن فورد Bellman-Ford لمعالجة الأضلاع أو الدورات السالبة.

يتساوى تعقيد خوارزمية BFS مع O(log(V+E))‎‎، حيث يمثّل V عدد العقد، ويمثّل E عدد الأضلاع، والتعقيد مقارب لهذه القيمة فيما يخصّ خوارزمية Dijkstra، لكنّ ترتيب طابور الأولويات يأخذ O (logV)‎‎، لذا فإنّ التعقيد الكلي يساوي: O (V log (V) + E‎‎)‎‎.

المثال أدناه هو تطبيق بلغة جافا لخوارزمية Dijkstra باستخدام مصفوفة التجاور:

import java.util.*;
import java.lang.*;
import java.io.*;
class ShortestPath
{
   static final int V=9;
   int minDistance(int dist[], Boolean sptSet[])
   {
int min = Integer.MAX_VALUE, min_index=-1;
       for (int v = 0; v < V; v++)
           if (sptSet[v] == false && dist[v] <= min)
           {
               min = dist[v];
               min_index = v;
           }
       return min_index;
   }
   void printSolution(int dist[], int n)
   {
       System.out.println("Vertex Distance from Source");
       for (int i = 0; i < V; i++)
           System.out.println(i+" \t\t "+dist[i]);
   }
   void dijkstra(int graph[][], int src)
   {
       Boolean sptSet[] = new Boolean[V];
       for (int i = 0; i < V; i++)
       {
           dist[i] = Integer.MAX_VALUE;
           sptSet[i] = false;
       }
       dist[src] = 0;
       for (int count = 0; count < V-1; count++)
       {
           int u = minDistance(dist, sptSet);
           sptSet[u] = true;
           for (int v = 0; v < V; v++)
               if (!sptSet[v] && graph[u][v]!=0 &&
                       dist[u] != Integer.MAX_VALUE &&
                       dist[u]+graph[u][v] < dist[v])
                   dist[v] = dist[u] + graph[u][v];
       }
       printSolution(dist, V);
   }
   public static void main (String[] args)
   {
   int graph[][] = new int[][]{{0, 4, 0, 0, 0, 0, 0, 8, 0},
                               {4, 0, 8, 0, 0, 0, 0, 11, 0},
                               {0, 8, 0, 7, 0, 4, 0, 0, 2},
                               {0, 0, 7, 0, 9, 14, 0, 0, 0},
                               {0, 0, 0, 9, 0, 10, 0, 0, 0},
                               {0, 0, 4, 14, 10, 0, 2, 0, 0},
                               {0, 0, 0, 0, 0, 2, 0, 1, 6},
                               {8, 11, 0, 0, 0, 0, 1, 0, 7},
                               {0, 0, 2, 0, 0, 0, 6, 7, 0}
                               };
       ShortestPath t = new ShortestPath();
t.dijkstra(graph, 0);
   }
}

هذا هو الخرج المتوقّع:

Vertex   Distance from Source
0                0
1                4
2                12
3                19
4                21
5                11
6                9
7                8
8                14