تطبيقات الخوارزميات الشرهة

هذه المقالة هي تتمة للمقالة السابقة، وفيها تجد عددًا من التطبيقات الحقيقية للخوارزميات الشَرِهَة لحل بعض المشاكل، مثل تقليل التأخير وجدولة الوظائف وإدارة ذاكرة التخزين المؤقت.

التخزين المؤقت غير المتصل Offline Caching

تنشأ مشكلة التخزين المؤقت caching بسبب محدودية مساحة التخزين، فمثلًا لنفرض أن ذاكرةَ تخزينٍ مؤقتة ولتكن C، تحتوي على عدد k من الصفحات، ونريد معالجة سلسلة من العناصر عددها m عنصر، هنا يجب تخزين هذه العناصر في الذاكرة المؤقتة قبل معالجتها.

لا شك أنه لن توجد مشكلة إن كانت ‎m<=k‎، إذ سنضع جميع العناصر في ذاكرة التخزين المؤقت، ولكن في العادة تكون ‎m>>k‎.

نقول أنّ طلبيّةً ما مقبولة في ذاكرة التخزين المؤقت cache hit إذا كان العنصر موجودًا في ذاكرة التخزين المؤقت فعليًا، وإلا سنقول أنّها مُفوَّتة عن ذاكرة التخزين المؤقت cache miss. سيكون علينا في مثل هذه الحالة إحضار العنصر المطلوب إلى ذاكرة التخزين المؤقت وإخراج عنصر آخر، وذلك بفرض أنّ ذاكرة التخزين المؤقت ممتلئة، وهدفنا هو تصميم جدول إخلاء eviction schedule يقلّل قدر الإمكان من عدد عمليات الإخلاء الضرورية.

هناك عدة استراتيجيات شَرِهَة لحلّ هذه المشكلة، من بينها:

أول داخل، أول خارج First in, ﬁrst out أو FIFO: تُخلى أقدم صفحة.
آخر داخل، أوّل خارج Last in, ﬁrst out أو LIFO: تُخلى أحدث صفحة.
خروج الأبكر وصولًا Last recent out أو اختصارا LRU: إخلاء الصفحة التي تمّ الدخول إليها في أبكر وقت.
الأقل طلبًا Least frequently requested أو LFU: إخلاء الصفحة التي طُلِبت أقل عدد من المرات.
أطول مسافة أمامية Longest forward distance أو LFD: إخلاء الصفحة التي ستُطلَب في أبعد مسافة في المستقبل.

اقتباس

تنبيه: في الأمثلة التالية، سنُخلى الصفحة ذات الفهرس الأصغر في حال كان بالإمكان إخلاء أكثر من صفحة واحدة.

مثال FIFO

لنفترض أنّ حجم ذاكرة التخزين المؤقت هو ‎k=3‎، وأنّ ذاكرة التخزين المؤقت الأولية تحتوي ‎a,b,c‎، وأنّ هناك قائمةً من الطلبيات هي على النحو الآتي:

‎a,a,d,e,b,b,a,c,f,d,e,a,f,b,e,c‎

الطلب	a	a	d	e	b	b	a	c	f	d	e	a	f	b	e	c
المخزن المؤقت 1	a	a	d	d	d	d	a	a	a	d	d	d	f	f	f	c
المخزن المؤقت 2	b	b	b	e	e	e	e	c	c	c	e	e	e	b	b	b
المخزن المؤقت 3	c	c	c	c	b	b	b	b	f	f	f	a	a	a	e	e
الحالات المفوَّتة			x	x	x		x	x	x	x	x	x	x	x	x	x

فوّتنا ثلاثة عشرة عنصرًا من ذاكرة التخزين المؤقت من بين ستة عشر طلبية، وهو أمر لا يبدو جيدًا، لذلك من الأحسن أن نجرّب استراتيجيةً أخرى.

مثال LFD

لنفترض أنّ حجم ذاكرة التخزين المؤقت هو ‎k=3‎، وأنّ ذاكرة التخزين المؤقت الأولية تحتوي ‎a,b,c‎؛ أما الطلبيات فهي:

الطلب	a	a	d	e	b	b	a	c	f	d	e	a	f	b	e	c
المخزن المؤقت 1	a	a	d	e	e	e	e	e	e	e	e	e	e	e	e	c
المخزن المؤقت 2	b	b	b	b	b	b	a	a	a	a	a	a	f	f	f	f
المخزن المؤقت 3	c	c	c	c	c	c	c	c	f	d	d	d	d	b	b	b
الحالات المفوَّتة			x	x			x		x	x			x	x		x

فوّتنا ثمانيةً هذه المرة، وهذا أفضل بكثير.

تمرين

جرّب استراتيجيات LIFO وLFU وRFU على المثال، وانظر إلى ما يحدث.

يتكون البرنامج التوضيحي التالي (مكتوب بلغة C++‎) من جزأين، حيث أن الأول هو هيكل البرنامج، ويحلّ المشكلة اعتمادًا على استراتيجية الشَرِههَ المختارة:

#include <iostream>
#include <memory>
using namespace std;
const int cacheSize     = 3;
const int requestLength = 16;
const char request[]    = {'a','a','d','e','b','b','a','c','f','d','e','a','f','b','e','c'};
char cache[]            = {'a','b','c'};
// for reset
char originalCache[]    = {'a','b','c'};
class Strategy {
public:
   Strategy(std::string name) : strategyName(name) {}
   virtual ~Strategy() = default;
   // احسب موضع التخزين المؤقت الذي ينبغي  أن يُستخدم
   virtual int apply(int requestIndex)     = 0;
   // حدّث المعلومات التي تحتاجها الاستراتيجية
   virtual void update(int cachePlace, int requestIndex, bool cacheMiss)    = 0;
   const std::string strategyName;
};
bool updateCache(int requestIndex, Strategy* strategy)
{
   // حدد مكان وضع الطلب
   int cachePlace = strategy->apply(requestIndex);
   // تحقق مما إذا قُبِل التخزين المؤقت أم لا
   bool isMiss = request[requestIndex] != cache[cachePlace];
   // تحديث الاستراتيجية - مثلا: إعادة حساب المسافات
   strategy->update(cachePlace, requestIndex, isMiss);
   //الكتابة في ذاكرة التخزين المؤقت
   cache[cachePlace] = request[requestIndex];
   return isMiss;
}
int main()
{
   Strategy* selectedStrategy[] = { new FIFO, new LIFO, new LRU, new LFU, new LFD };
   for (int strat=0; strat < 5; ++strat)
   {
       //إعادة تعيين المخزن المؤقت 
       for (int i=0; i < cacheSize; ++i) cache[i] = originalCache[i];
       cout <<"\nStrategy: " << selectedStrategy[strat]->strategyName << endl;
       cout << "\nCache initial: (";
       for (int i=0; i < cacheSize-1; ++i) cout << cache[i] << ",";
       cout << cache[cacheSize-1] << ")\n\n";
       cout << "Request\t";
       for (int i=0; i < cacheSize; ++i) cout << "cache " << i << "\t";
       cout << "cache miss" << endl;
       int cntMisses = 0;
       for(int i=0; i<requestLength; ++i)
       {
           bool isMiss = updateCache(i, selectedStrategy[strat]);
           if (isMiss) ++cntMisses;
           cout << "  " << request[i] << "\t";
           for (int l=0; l < cacheSize; ++l) cout << "  " << cache[l] << "\t";
           cout << (isMiss ? "x" : "") << endl;
       }
       cout<< "\nTotal cache misses: " << cntMisses << endl;
   }
   for(int i=0; i<5; ++i) delete selectedStrategy[i];
}

الفكرة الأساسية بسيطة، حيث نستدعي الاستراتيجية مرتين لكل طلب:

التطبيق apply: يجب أن تخبر الاستراتيجية المستدعي بالصفحة التي يجب استخدامها.
التحديث update: بعد أن يستخدم المستدعي المساحة، يخبر الإستراتيجية ما إذا تمّ تفويته أم لا. ثمّ تستطيع الاستراتيجية حينها تحديث بياناتها الداخلية. فمثلًا، على الاستراتيجية LFU تحديث تردّد القبول hit frequency لصفحات ذاكرة التخزين المؤقت، بينما تعيد استراتيجية LFD حساب مسافات صفحات ذاكرة التخزين المؤقت.

نقدّم الآن تطبيقات للاستراتيجيات الخمس:

FIFO

class FIFO : public Strategy {
public:
   FIFO() : Strategy("FIFO")
   {
       for (int i=0; i<cacheSize; ++i) age[i] = 0;
   }
   int apply(int requestIndex) override
   {
       int oldest = 0;
       for(int i=0; i<cacheSize; ++i)
       {
           if(cache[i] == request[requestIndex])
               return i;
           else if(age[i] > age[oldest])
               oldest = i;
       }
       return oldest;
   }
   void update(int cachePos, int requestIndex, bool cacheMiss) override
   {
       // لم يتغير أي شيء، لسنا بحاجة إلى تحديث الصفحات
if(!cacheMiss)
           return;
       // كل الصفحات القديمة تُصبح أقدم، والجديدة تحصل على القيمة 0
       for(int i=0; i<cacheSize; ++i)
       {
           if(i != cachePos)
               age[i]++;
           else
               age[i] = 0;
       }
   }
private:
   int age[cacheSize];
};

لا تحتاج FIFO إلا إلى المعلومات المتعلقة بطول الصفحة في ذاكرة التخزين المؤقت (نسبة إلى الصفحات الأخرى)، لذا فهي تكتفي بانتظار حدوث فوات miss، ثم تجعل الصفحات التي لم تُخلى أقدم.

بالنسبة للمثال أعلاه، فسيكون الحل كالتالي:

Strategy: FIFO
Cache initial: (a,b,c)
Request          cache 0        cache 1        cache 2    cache miss
  a                  a              b              c    
  a                  a              b              c    
  d                  d              b              c              x
  e                  d              e              c              x
  b                  d              e              b              x
  b                  d              e              b    
  a                  a              e              b              x
  c                  a              c              b              x
  f                  a              c              f              x
  d                  d              c              f              x
  e                  d              e              f              x
  a                  d              e              a              x
  f                  f              e              a              x
  b                  f              b              a              x
  e                  f              b              e              x
  c                  c              b              e              x
Total cache misses: 13 العدد الإجمالي للفوات

وهذا يكافئ الحل أعلاه.

LIFO

class LIFO : public Strategy {
public:
   LIFO() : Strategy("LIFO")
   {
       for (int i=0; i<cacheSize; ++i) age[i] = 0;
   }
   int apply(int requestIndex) override
   {
       int newest = 0;
for(int i=0; i<cacheSize; ++i)
       {
           if(cache[i] == request[requestIndex])
               return i;
           else if(age[i] < age[newest])
               newest = i;
       }
       return newest;
   }
   void update(int cachePos, int requestIndex, bool cacheMiss) override
   {
       // لم يتغير شيء، لا نحتاج إلى تحديث الصفحات
       if(!cacheMiss)
           return;
       // كل الصفحات القديمة تُصبح أقدم، والصفحة الجديدة تحصل على القيمة 0
       for(int i=0; i<cacheSize; ++i)
       {
           if(i != cachePos)
               age[i]++;
           else
               age[i] = 0;
       }
   }
private:
   int age[cacheSize];
};

تقديم LIFO مشابه إلى حد ما لتقديم FIFO، بيْد أنّنا نخلي الصفحة الأحدث وليس الأقدم. ستكون نتائج البرنامج كالتالي:

Strategy: LIFO
Cache initial: (a,b,c)
Request            cache 0       cache 1    cache 2    cache miss
 a                   a              b          c   
 a                   a              b          c   
 d                   d              b          c          x
 e                   e              b          c          x
 b                   e              b          c   
 b                   e              b          c   
 a                   a              b          c          x
 c                   a              b          c   
 f                   f              b          c          x
 d                   d              b          c          x
 e                   e              b          c          x
 a                   a              b          c          x
 f                   f              b          c          x
 b                   f              b          c   
 e                   e              b          c          x
 c                   e              b          c   

Total cache misses: 9 العدد الإجمالي لحالات الفوات

LRU، سنستخدم كلمة oldest في المثال أدناه للإشارة إلى طول فترة "عدم" الاستخدام.

class LRU : public Strategy {
public:
   LRU() : Strategy("LRU")
   {
       for (int i=0; i<cacheSize; ++i) age[i] = 0;
   }

        int apply(int requestIndex) override
   {
       int oldest = 0;
       for(int i=0; i<cacheSize; ++i)
       {
           if(cache[i] == request[requestIndex])
               return i;
           else if(age[i] > age[oldest])
               oldest = i;
       }
       return oldest;
   }
   void update(int cachePos, int requestIndex, bool cacheMiss) override
   {
       // الصفحات القديمة تصبح أقدم، والصفحة الجديدة تأخذ القيمة 0
       for(int i=0; i<cacheSize; ++i)
       {
           if(i != cachePos)
               age[i]++;
           else
               age[i] = 0;
       }
   }
private:
   int age[cacheSize];
};

في حالة LRU، فإن الاستراتيجية مستقلة عن صفحة ذاكرة التخزين المؤقت، إذ أنّ تركيزها ينصبّ على الصفحة الأخيرة فقط.

نتائج البرنامج هي:

Strategy: LRU
Cache initial: (a,b,c)
Request            cache 0        cache 1         cache 2    cache miss
  a                   a              b              c    
  a                   a              b              c    
  d                   a              d              c              x
  e                   a              d              e              x
  b                   b              d              e              x
  b                   b              d              e    
  a                   b              a              e              x
  c                   b              a              c              x
  f                   f              a              c              x
  d                   f              d              c              x
  e                   f              d              e              x
  a                   a              d              e              x
  f                   a              f              e              x
  b                   a              f              b              x
  e                   e              f              b              x
  c                   e              c              b              x
Total cache misses: 13 العدد الإجمالي لحالات الفوات

LFU:

class LFU : public Strategy {
public:
   LFU() : Strategy("LFU")
   {
       for (int i=0; i<cacheSize; ++i) requestFrequency[i] = 0;
   }
   int apply(int requestIndex) override
   {
       int least = 0;
       for(int i=0; i<cacheSize; ++i)
       {
           if(cache[i] == request[requestIndex])
               return i;
           else if(requestFrequency[i] < requestFrequency[least])
               least = i;
       }
       return least;
   }
   void update(int cachePos, int requestIndex, bool cacheMiss) override
   {
       if(cacheMiss)
           requestFrequency[cachePos] = 1;
       else
           ++requestFrequency[cachePos];
   }
private:
   // ما هو تردد استخدام الصفحة
   int requestFrequency[cacheSize];
};

تُخلي LFU الصفحة الأقل استخدامًا، لذا تعتمد استراتيجية التحديث على عدد مرّات الوصول إلى الصفحات. وبالطبع، يُصفَّر العدّاد بعد الإخلاء، وهذه نتائج البرنامج:

Strategy: LFU
Cache initial: (a,b,c)
Request          cache 0         cache 1        cache 2    cache miss
  a                  a              b              c    
  a                  a              b              c    
  d                  a              d              c              x
  e                  a              d              e              x
  b                  a              b              e              x
  b                  a              b              e    
  a                  a              b              e    
  c                  a              b              c              x
  f                  a              b              f              x
  d                  a              b              d              x
  e                  a              b              e              x
  a                  a              b              e    
  f                  a              b              f              x
  b                  a              b              f    
  e                  a              b              e              x
  c                  a              b              c              x
Total cache misses: 10

LFD:

class LFD : public Strategy {
public:
   LFD() : Strategy("LFD")
   {
       // الحساب المُسبق للاستخدام اللاحق قبل تلبية الطلبات
       for (int i=0; i<cacheSize; ++i) nextUse[i] = calcNextUse(-1, cache[i]);
   }
   int apply(int requestIndex) override
   {
       int latest = 0;
       for(int i=0; i<cacheSize; ++i)
       {
           if(cache[i] == request[requestIndex])
               return i;
           else if(nextUse[i] > nextUse[latest])
               latest = i;
       }
       return latest;
   }
   void update(int cachePos, int requestIndex, bool cacheMiss) override
   {
           nextUse[cachePos] = calcNextUse(requestIndex, cache[cachePos]);
   }
private:
   int calcNextUse(int requestPosition, char pageItem)
   {
       for(int i = requestPosition+1; i < requestLength; ++i)
       {
           if (request[i] == pageItem)
               return i;
       }
       return requestLength + 1;
   }
   // الاستخدام اللاحق للصفحة
   int nextUse[cacheSize];
};

تختلف استراتيجية LFD عن جميع ما قبلها، فهي الاستراتيجية الوحيدة التي تستخدم الطلبات المستقبلية لاتخاذ القرار بخصوص الصفحة التي ينبغي أن تُخلى. يَستخدم التطبيق دالة ‎calcNextUse‎ للحصول على الصفحة التي يكون استخدَامها التالي هو الأبعد في المستقبل.

الحل الذي يعطيه البرنامج يساوي الحل اليدوي الذي وجدناه أعلاه:

Strategy: LFD
Cache initial: (a,b,c)
Request            cache 0       cache 1       cache 2       cache miss
  a                  a              b              c    
  a                  a              b              c    
  d                  a              b              d              x
  e                  a              b              e              x
  b                  a              b              e    
  b                  a              b              e    
  a                  a              b              e    
  c                  a              c              e              x
  f                  a              f              e              x
  d                  a              d              e              x
  e                  a              d              e    
  a                  a              d              e    
  f                  f              d              e              x
  b                  b              d              e              x
  e                  b              d              e    
  c                  c              d              e              x
Total cache misses: 8

استراتيجية LFD الشَرِهَة هي الاستراتيجية المثلى من بين الاستراتيجيات الخمس المقدمة، لكن هناك مشكلة كبيرة، فهي حل مثالي غير متصل optimal oﬄine solution، أي أنّها تتطلب قراءة جميع عناصر الطابور مرّةً واحدة؛ لكن عند التطبيق، سيكون التخزين المؤقت غالبًا مشكلة متصلة online، أي لا يمكنك أن تعرف من العناصر غير السابقة وحدها، وهذا يعني أنّ هذه الاستراتيجية غير مجدية لأننا لا نستطيع معرفة الموعد القادم الذي سنحتاج فيه إلى عنصر معيّن؛ أما الاستراتيجيات الأربع الأخرى فهي متصلة أيضًا. وبالنسبة للمشاكل المتصلة online، سنحتاج إلى منظور مختلف.

جهاز التذاكر

لنفترض أنّ لدينا جهاز تذاكر يصرّف المبالغ بقطع نقدية تحمل القيم 1 و2 و5 و10 و20. يمكن النظر إلى عملية الصرف مثل سلسلة من القطع النقدية التي تتساقط حتى يُستوفى المبلغ الصحيح، ونقول أنّ الصرف مثالي حين يكون عدد القطع النقدية أقل ما يمكن بالنسبة إلى قيمته.

وإذا كانت ‎M‎ توجد بين ‎[1,50]‎ وتمثّل سعر التذكرة ‎T‎، و العدد ‎P‎ الموجود بين ‎[1,50]‎ يمثل المبلغ المالي المدفوع مقابل التذكرة ‎T‎، حيث ‎P >= M‎؛ فإننا نكتب ‎D=P-M‎، ونعرّف الفائدة beneﬁt لخطوة معيّنة على أنّها الفرق بين ‎D‎ و‎D-c‎، حيث تمثّل‎c‎ القطعة النقدية التي أضافها الجهاز في هذه الخطوة.

انظر إلى الخوارزمية الشَرِهَة التوضيحية لإجراء عملية الصرف:

الخطوة 1: إذا كانت ‎D > 20‎، أضف القطعة 20، وعيّن ‎D = D - 20‎.
الخطوة 2: إذا كانت ‎D > 10‎، أضف القطعة 10 وعيّن ‎D = D - 10‎.
الخطوة 3: إذا كانت ‎D > 5‎، أضف القطعة 5 وعيّن ‎D = D - 5‎.
الخطوة 4: إذا كانت ‎D > 2‎، أضف القطعة 2 وعيّن ‎D = D - 2‎.
الخطوة 5: إذا كانت ‎D > 1‎، أضف القطعة 1 وعيّن ‎D = D - 1‎.

بعد ذلك سيكون مجموع جميع العملات مساويًا القيمة ‎D‎. هذه الخوارزمية شَرِهَة لأنّها تبحث بعد كل خطوة وبعد كل تكرار عن تعظيم الفائدة.

والآن، لنكتب برنامج التذكرة بلغة C++‎‎‎:

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
// اقرأ قيم بعض القطع النقدية، ورتّبها تنازليا
// احذف النسخ مع ضمان أن تكون القطعة 1 موجودة بينها
std::vector<unsigned int> readInCoinValues();
int main()
{
   std::vector<unsigned int> coinValues;   //  مصفوفة القطع النقدية تنازليا  
   int ticketPrice;                        // في المثال M
   int paidMoney;                          // في المثال P

   // ولِّد قيم القطع النقدية
   coinValues = readInCoinValues();

   cout << "ticket price: ";
   cin >> ticketPrice;

   cout << "money paid: ";
   cin >> paidMoney;

   if(paidMoney <= ticketPrice)
   {
       cout << "No exchange money" << endl;
       return 1;
   }

   int diffValue = paidMoney - ticketPrice;

   // هنا تبدأ الخوارزمية الشَرِهَة.
   // نحفظ عدد القطع النقدية التي علينا إعطاؤها
   std::vector<unsigned int> coinCount;

   for(auto coinValue  = coinValues.begin();
            coinValue != coinValues.end(); ++coinValue)
   {
       int countCoins = 0;

       while (diffValue >= *coinValue)
       {
           diffValue -= *coinValue;
           countCoins++;
       }

       coinCount.push_back(countCoins);
   }

   // اطبع النتائج
   cout << "the difference " << paidMoney - ticketPrice
        << " is paid with: " << endl;
for(unsigned int i=0; i < coinValues.size(); ++i)
   {
       if(coinCount[i] > 0)
           cout << coinCount[i] << " coins with value "
                << coinValues[i] << endl;
   }

   return 0;
}
std::vector<unsigned int> readInCoinValues()
{
   // قيم القطع النقدية
   std::vector<unsigned int> coinValues;

   // تحقق من أنّ 1 موجود في المتجهة
   coinValues.push_back(1);
   // اقرأ قيم القطع النقدية، لاحظ أن خطأ المعالجة يهمَل.
   while(true)
   {
       int coinValue;

       cout << "Coin value (<1 to stop): ";
       cin >> coinValue;

       if(coinValue > 0)
           coinValues.push_back(coinValue);

       else
           break;
   }

   // رتب القيم
   sort(coinValues.begin(), coinValues.end(), std::greater<int>());

   // امح النسخ التي لها القيمة نفسها
   auto last = std::unique(coinValues.begin(), coinValues.end());
   coinValues.erase(last, coinValues.end());

   // اطبع المصفوفة
   cout << "Coin values: ";

   for(auto i : coinValues)
       cout << i << " ";

   cout << endl;

   return coinValues;
}

لاحظ أننا لم نضع أيّ فحص للمدخلات من أجل إبقاء المثال بسيطًا، وهنا سيكون خرج المثال كما يلي:

Coin value (<1 to stop): 2
Coin value (<1 to stop): 4
Coin value (<1 to stop): 7
Coin value (<1 to stop): 9
Coin value (<1 to stop): 14
Coin value (<1 to stop): 4
Coin value (<1 to stop): 0
Coin values: 14 9 7 4 2 1
ticket price: 34
money paid: 67
the difference 33 is paid with:
2 coins with value 14
1 coins with value 4
1 coins with value 1

إن كانت قيمة القطعة النقدية تساوي ‎1‎، فستنتهي الخوارزمية، لأن:

D تنخفض مع كل خطوة.
لا يمكن أن تكون D موجبةً وأصغر من أصغر عملة (‎1‎) في نفس الوقت.

هذه الخوارزمية فيها ثغرتان:

إذا كانت ‎C‎ هي أكبر قطعة نقدية، فسيكون وقت التشغيل كثير الحدود polynomial طالما أنّ ‎D/C‎ كثيرة الحدود أيضًا، ذلك أن تمثيل ‎D‎ يستخدم بتَّات ‎log D‎ وحسب؛ أمّا وقت التشغيل، فهو على الأقل خطيٌ في ‎D/C‎
تختار خوَارزميتنا الخيار المحلي الأمثل في كل خطوة، لكنّ هذا لا يعني أنّ الحل الذي تقدمه الخوارزمية هو الحل الأمثل العام.

انظر إلى المثال التوضيحي التالي: لنفترض أنّ القطع النقدية هي ‎1,3,4‎، وأنّ ‎D=6‎. من الواضح أنّ الحل الأمثل هو قطعتان نقديتان من فئة ‎3‎، ولكنّ الخوارزمية الشَرِهَة ستختار ‎4‎ في الخطوة الأولى، لذا سيكون عليها أن تختار ‎1‎ في الخطوتين الثانية والثالثة، وعليه فهي لا تعطينا الحل الأمثل. قد يكون استخدام البرمجة الديناميكية لإيجاد الحل الأمثل هو الأفضل في هذه الحالة.

جدولة الوظائف

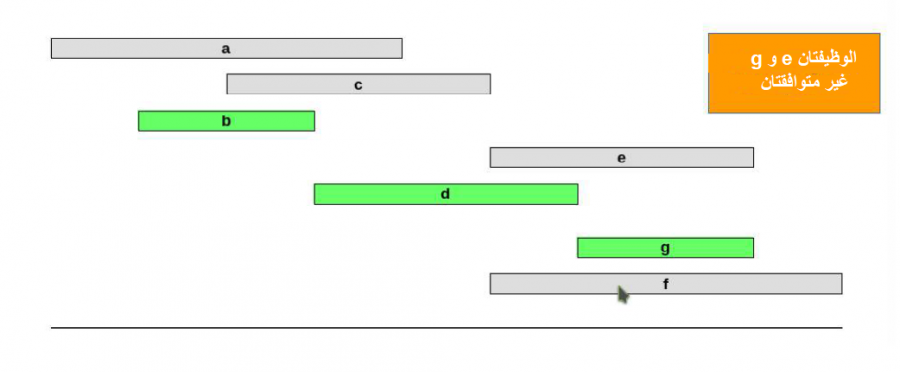
لنفترض أنّ لدينا مجموعةً من الوظائف ‎J={a,b,c,d,e,f,g}‎. إذا كانت j التي تنتمي إلى ‎J‎ هي وظيفة تبدأ عند ‎sj‎ وتنتهي عند ‎fj‎، فسنقول عندئذ أنّ وظيفتين متوافقتان إذا لم تتدَاخلا overlap. انظر الصورة التالية:

والهدف هنا هو العثور على أكبر مجموعة من الوظائف المتوافقة مع بعضها بعضًا، وهناك عدة أوجه شَرِهَة لحل هذه المشكلة:

أبكر وقت بداية: خذ الوظائف وفق ترتيب تصاعدي لقيم ‎sj‎.
أبكر وقت انتهاء: خذ الوظائف وفق ترتيب تصاعدي لـ ‎fj‎.
أقصر مدة: خذ الوظائف وفق ترتيب تصاعدي لـ ‎fj-sj‎.
أقل تعارض: لكل وظيفة ‎j‎، احسب عدد الوظائف المتعارضة معها (‎cj‎).

السؤال الآن هو: أيّ وجه أفضل؟ من الواضح أنّ منظور أبكر وقت بداية غير صالح كما يوضّح المثال المضاد التالي:

كذلك فإن منظور أقصر مدة ليس مثاليًا:

وقد يبدو أنّ منظور أقل تعارض هو الأمثل، غير أن المثال المضاد التالي ينفي ذلك:

إذًا الحل المتبقي هو أبكر وقت انتهاء. انظر شيفرته التوضيحية:

رتّب الوظائف بحسب وقت الانتهاء ‎f1<=f2<=...<=fn‎.
لتكن ‎A‎ مجموعةً فارغة.
من ‎j=1‎ إلى ‎n‎، إذا كان ‎j‎ متوافقًا مع جميع الوظائف في ‎A‎، ضع ‎A=A+{j}‎.
ستكون A هي أكبر مجموعة تضمّ وظائفًا متوافقة.

أو نفس الأمر مكتوبًا في برنامج بلغة C++‎:

#include <iostream>
#include <utility>
#include <tuple>
#include <vector>
#include <algorithm>
const int jobCnt = 10;
// أوقات بداية الوظائف
const int startTimes[] = { 2, 3, 1, 4, 3, 2, 6, 7, 8, 9};
// أوقات انتهاء الوظائف
const int endTimes[]   = { 4, 4, 3, 5, 5, 5, 8, 9, 9, 10};
using namespace std;
int main()
{
   vector<pair<int,int>> jobs;

   for(int i=0; i<jobCnt; ++i)
       jobs.push_back(make_pair(startTimes[i], endTimes[i]));

   // المرحلة الأولى: الترتيب
   sort(jobs.begin(), jobs.end(),[](pair<int,int> p1, pair<int,int> p2)
                                    { return p1.second < p2.second; });

   // A المرحلة الثانية: المجموعة الفارغة
   vector<int> A;

   // المرحلة الثالثة
   for(int i=0; i<jobCnt; ++i)
   {
       auto job = jobs[i];
       bool isCompatible = true;

       for(auto jobIndex : A)
       {
           // A تحقق مما إذا كانت الوظيفة الحالية غير متوافقة مع الوظيفة من
           if(job.second >= jobs[jobIndex].first &&
              job.first  <= jobs[jobIndex].second)
           {
               isCompatible = false;
               break;
           }
       }

       if(isCompatible)
           A.push_back(i);
   }

   // A المرحلة الرابعة: طباعة
   cout << "Compatible: ";

   for(auto i : A)
       cout << "(" << jobs[i].first << "," << jobs[i].second << ") ";
   cout << endl;

   return 0;
}

خرج هذا المثال سيكون:

Compatible: (1,3) (4,5) (6,8) (9,10)

تعقيد هذا التطبيق يساوي ‎Θ (n ^ 2)‎‎، لكن هناك تطبيق آخر من التعقيد ‎Θ (n log n)‎‎ (انظر مثال جافا أدناه). أصبحت لدينا الآن خوارزمية شَرِهَة لحل مشكلة الجدولة الزمنية، ولكن أهي مُثلى؟

اقتباس

خاصية: خوارزمية أبكر وقت انتهاء الشَرِهَة هي خوارزميةٌ مُثلى.

لنفترض أنّ هذه الخوارزمية الشَرِهَة ليست مثلى، وأن ‎i1,i2,...,ik‎ تشير إلى مجموعة من الوظائف التي اختارتها الخوارزمية الشَرِهَة، ولتكن ‎j1,j2,...,jm‎ تشير إلى مجموعة الوظائف في الحل الأمثل، وليكن ‎r‎ هو العدد الأكبر الذي يحقق ‎i1=j1,i2=j2,...,ir=jr‎.

الوظيفة ‎i(r+1)‎ موجودة وتنتهي قبل الوظيفة ‎j(r+1)‎ (أبكر وقت انتهاء)، لكن هذا يعني أنّ الوظيفة الآتية ستكون أيضًا حلًّا أمثلَ، ولكلّ ‎k‎ من المجال ‎[1,(r+1)]‎، سيكون لدينا ‎jk=ik‎، مما يناقض فرضية أنّ ‎r‎ هو العدد الأكبر. وهذا يُتمّ البرهان.

‎j1,j2,...,jr,i(r+1),j(r+2),...,jm‎

يوضّح المثال التالي أنّ هناك العديد من الاستراتيجيات الشَرِهَة الممكنة في الغالب، ولكن ليست كلها تجد الحل الأمثل العام، بل قد لا تجده أي منها.

فيما يلي برنامج Java تعقيده ‎Θ (n log n) ‎‎‎.

import java.util.Arrays;
import java.util.Comparator;
class Job
{
   int start, finish, profit;
   Job(int start, int finish, int profit)
   {
       this.start = start;
       this.finish = finish;
       this.profit = profit;
   }
}
class JobComparator implements Comparator<Job>
{
   public int compare(Job a, Job b)
   {
       return a.finish < b.finish ? -1 : a.finish == b.finish ? 0 : 1;
   }
}
public class WeightedIntervalScheduling
{
   static public int binarySearch(Job jobs[], int index)
   {
       int lo = 0, hi = index - 1;
       while (lo <= hi)
       {
           int mid = (lo + hi) / 2;
           if (jobs[mid].finish <= jobs[index].start)
           {
               if (jobs[mid + 1].finish <= jobs[index].start)
                   lo = mid + 1;
               else
                   return mid;
           }
           else
               hi = mid - 1;
       }
       return -1;
   }
   static public int schedule(Job jobs[])
   {
       Arrays.sort(jobs, new JobComparator());
       int n = jobs.length;
       int table[] = new int[n];
       table[0] = jobs[0].profit;
       for (int i=1; i<n; i++)
       {
           int inclProf = jobs[i].profit;
           int l = binarySearch(jobs, i);
           if (l != -1)
               inclProf += table[l];
           table[i] = Math.max(inclProf, table[i-1]);

       }
       return table[n-1];
   }
   public static void main(String[] args)
   {
       Job jobs[] = {new Job(1, 2, 50), new Job(3, 5, 20),
                   new Job(6, 19, 100), new Job(2, 100, 200)};
       System.out.println("Optimal profit is " + schedule(jobs));
   }
}

الخرج المتوقع هو:

Optimal profit is 250

تقليل التأخير Minimizing Lateness

هناك العديد من المشاكل التي تقلل التأخير، ولنفترض هنا أنّ لدينا مصدرًا وحيدًا يمكنه معالجة مهمّة واحدة فقط في كل مرّة، والوظيفة ‎j‎ تتطلب ‎tj‎ وحدة وقت من زمن المعالجة، وتبدأ عند التوقيت ‎dj‎، فإن بدأت ‎j‎ في الوقت ‎sj‎، فستنتهي عند الوقت fj ‎=‎ sj ‎+‎ tj.

نعرّف التأخير lateness بالصيغة التالية: ‎L=max{ 0 ,fj-dh}‎، لكل وظيفة j، والهدف هو تقليل أقصى تأخير لـ L.

	1	2	3	4	5	6
`tj`	3	2	1	4	3	2
`dj`	6	8	9	9	10	11

الوظيفة	3	2	2	5	5	5	4	4	4	4	1	1	1	6	6
الوقت	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
`Lj`	8-		5-			4-				1			7		4

من الواضح أنّ الحل ‎L=7‎ ليس الأمثل. لهذا من الأفضل أن نلقي نظرةً على بعض الاستراتيجيات الشَرِهَة:

أقصر وقت معالجة أولاً: نُجدول المهام وفق ترتيب تصاعدي لوقت المعالجة j`.
أبكر موعد نهائي أولًا: جدولة المهام وفق ترتيب تصاعدي للمواعيد النهائية ‎dj‎.
أقصر مُهلة Smallest slack: جدولة المهام وفق ترتيب تصاعدي للمهلة ‎dj-tj‎.

من الواضح أنّ منظور أقصر وقت معالجة أولًا ليس الأمثل، هذا المثال المضاد يبيّن ذلك:

	1	2
`tj`	1	5
`dj`	10	5

كذلك فإن منظور أقصر مهلة لديه مشاكل مشابهة كما يبيّن المثال التالي:

	1	2
`tj`	1	5
`dj`	3	5

والإستراتيجية الأخيرة تبدو صالحة، انظر هذه الشيفرة التوضيحية لها:

رتّب ‎n‎ وظيفةً بحسب المواعيد النهائية، بحيث تكون ‎d1<=d2<=...<=dn‎.
عيّن ‎‎t=0.
من ‎j=1‎ إلى ‎n‎:
- عيّن المهمة ‎j‎ للفاصل الزمني ‎[t,t+tj]‎.
- عيّن ‎sj=t‎ و‎fj=t+tj‎.
- عيّن ‎t=t+tj‎.
أعِد المجالات ‎[s1,f1],[s2,f2],...,[sn,fn]‎.

هذا تطبيق بلغة C++‎:

#include <iostream>
#include <utility>
#include <tuple>
#include <vector>
#include <algorithm>
const int jobCnt = 10;
// أوقات بداية الوظائف
const int processTimes[] = { 2, 3, 1, 4, 3, 2, 3, 5, 2, 1};
// أوقات انتهاء الوظائف
const int dueTimes[] = { 4, 7, 9, 13, 8, 17, 9, 11, 22, 25};
using namespace std;
int main()
{
    vector<pair<int,int>> jobs;

 for(int i=0; i<jobCnt; ++i)
        jobs.push_back(make_pair(processTimes[i], dueTimes[i]));

 // المرحلة الأولى: الترتيب
    sort(jobs.begin(), jobs.end(),[](pair<int,int> p1, pair<int,int> p2)
 { return p1.second < p2.second; });

 // t=0 المرحلة الثانية: تعيين
 int t = 0;

 // المرحلة الثالثة
    vector<pair<int,int>> jobIntervals;

 for(int i=0; i<jobCnt; ++i)
 {
        jobIntervals.push_back(make_pair(t,t+jobs[i].first));
        t += jobs[i].first;
 }

 // المرحلة الرابعة: طباعة المجالات
 cout << "Intervals:\n" << endl;

 int lateness = 0;

 for(int i=0; i<jobCnt; ++i)
 {
 auto pair = jobIntervals[i];

        lateness = max(lateness, pair.second-jobs[i].second);
 cout << "(" << pair.first << "," << pair.second << ") "
 << "Lateness: " << pair.second-jobs[i].second << std::endl;
 }

 cout << "\nmaximal lateness is " << lateness << endl;
 return 0;
}

والخرج الناتج لهذا البرنامج هو:

Intervals:
(0,2)   Lateness:-2
(2,5)   Lateness:-2
(5,8)   Lateness: 0
(8,9)   Lateness: 0
(9,12)  Lateness: 3
(12,17) Lateness: 6
(17,21) Lateness: 8
(21,23) Lateness: 6
(23,25) Lateness: 3
(25,26) Lateness: 1
maximal lateness is 8

الظاهر هنا أنّ وقت تشغيل هذه الخوارزمية هو ‎‎Θ(n log n)‎‎، لأنّ الترتيب هو العملية الغالبة في هذه الخوارزمية. سنحاول الآن إثبات أنّ هذه الخوارزمية مُثلى، وهذا يستلزم ألا يكون في الجدول الزمني وقت خامل idle time أو غير مُستخدم. وهو أمر يتحقق في منظور أبكر موعد نهائي أولًا.

لنفترض أنّ الوظائف مُرقّمة بحيث تكون ‎d1<=d2<=...<=dn‎. نقول أن تقليبات جدول ما inversion of a schedule هي أزواج من الوظائف ‎i‎ و‎j‎، بحيث تكون ‎i<j‎، وتكون j مُجدولةً قبل ‎i‎. من الواضح أنّ منظور أبكر وقت نهائي أولًا ليس لها تقليبات، وإن كان الجدول يحتوي تقليبة، فهذا يعني أنّه يحتوي زوجًا من الوظائف المقلوبة والمُجدولة بالتتابع.

اقتباس

خاصية: يؤدي تبديل وظيفتين متجاورتين adjacent ومقلوبتين inverted إلى تقليل عدد التقليبات بمقدار واحد دون أن يزيد الحد الأقصى لوقت التأخير.

إذا كانت ‎L‎ هي قيمة التأخير قبل التبديل، و‎M‎ هو التأخير بعد التبديل، فستكون ‎Lk=Mk‎ لكل ‎k != i,j.‎، نظرًا لأنّ تبديل وظيفتين متجاورتين لا ينقل الوظائف الأخرى من مواقعها.

من الواضح أنّ ‎Mi<=Li‎ لأنّ الوظيفة ‎i‎ جُدوِلَت في وقت أبكر، أما إذا تأخرت الوظيفة ‎j‎ فيمكن أن نستنتج من التعريف أنّ:

       Mj = fi-dj    من التعريف 
       <= fi-di    ( j و i لأنّه يمكن مبادلة) 
       <= Li

هذا يعني أنّ التأخير بعد المبادلة سيكون أقل أو يساوي التأخير قبل المبادلة، وهذا يُتمّ البرهان.

اقتباس

خاصية: الجدول الزمني S الناتج عن منظور أبكر وقت نهائي أولًا هو الجدول الأمثل.

لنفترض أنّ ‎S*‎ هو الجدول الأمثل وأنّ له أقل عدد ممكن من التقليبات. يمكن أن نفترض أنّ ‎S*‎ ليس فيه وقت شاغر، إذ لو كانت لـ ‎S*‎ أي تقليبات، فسيكون لدينا ‎S=S*‎، وهذا يتمّ البرهان؛ أمّا إن احتوى ‎S*‎ على تقلِيبة فستكون له تقلِيبة مجاورة adjacent inversion. الخاصية الأخيرة تنصّ على أنّنا نستطيع تبديل التقليبات المتجاورة وتقليل عدد التقليبات دون زيادة التأخير، وهذا يتناقض مع تعريف ‎S*‎.

هناك الكثير من التطبيقات لمشكلة تقليل التأخير ومشكلة الحد الأدنى المشابهة لها minimum makespan problem، وهي المشكلة التي تحاول تقليل وقت انتهاء الوظائف. والمعتاد أنه لا تكون لديك آلة واحدة فقط، بل العديد من الآلات التي يمكنها القيام بالمهام نفسها بمعدّلات مختلفة. يمكن أن تتحول هذه المشكلة بسرعة إلى مشكلة من الصنف NP-complete.

يظهر هنا سؤال مثير للاهتمام إن نظرنا إلى المشكلة المتصلة online، حيث تكون لدينا كل المهام والبيانات، لكن في صورة متصلة online، حيث تظهر المهام أثناء التنفيذ.

ترجمة -بتصرّف- للفصل 18 من كتاب Algorithms Notes for Professionals.