نستعرض في هذه المقالة أمثلةً على مجموعة من الخوارزميات، مثل خوارزمية الأعداد الكاتالانية وخوارزمية بريزنهام لرسم المستقيمات، وخوارزميات إدارة ذاكرة التخزين المؤقت، إضافة إلى بعض الخوارزميات متعددة الخيوط.
خوارزمية رسم المستقيمات
تُرسم المستقيمات على شاشة الحاسوب بِمدِّ نقاط متتابعة ومتقاربة على طول المسار الذي يمرّ منه المستقيم بين النقطتين اللتين تحدّدان طرفي المستقيم، وسنستعرض في هذه الفقرة إحدى أفضل الخوارزميات التي يستخدمها المبرمجون لحساب إحداثيات هذه النقاط وهي خوارزمية بريزنهام لرسم المستقيمات، التي هي عبارة عن خوارزمية لرسم الخطوط بفعالية ودقّة، طورها جاك إيلتون بريزنهام Jack E. Bresenham، وهي دقيقة وسريعة لأنها تتم بإجراء عمليات على الأعداد الصحيحة فقطـ، وهي تسع أيضًا رسم الدوائر والمنحنيات الأخرى.
وفي خوارزمية بريزنهام، لنقل أنّ ميل المستقيم الذي نريد رسمه هو m.
- إن كان |m|<1:
- إما تُزاد قيمة الإحداثية x.
- أو تُزاد قيمتا الإحداثيتان x و y معًا باستخدام معامل قرار decision parameter خاصّ.
- إن كان |m|<1:
- إما أن تُزاد قيمة y.
- أو تُزاد قيمتا x و y معا باستخدام معامل قرار خاصّ.
والآن، نستعرض خطوات الخوارزمية اعتمادًا على ميل المستقيم المراد رسمه.
الحالة الأولى: | m | <1
- أدخِل طرفي المستقيم (x1، y1) و (x2، y2).
- ارسم النقطة الأولى (x1، y1).
-
احسب القيمتين:
- Delx = | x2 – x1 | .
- Dely = | y2 – y1 | .
-
احسب معامل القرار الأولي عبر الصيغة التالية:
- P = 2 * dely – delx
- لكل I من 0 إلى delx:
-
إذا كان p <0، فسيكون:
- X1 = x1 + 1.
- ارسم (x1، y1).
- P = p + 2dely.
-
وإلا:
- X1 = x1 + 1.
- Y1 = y1 + 1.
- ارسم (x1، y1).
- P = p + 2dely – 2 * delx.
- نهاية عبارة إن.
- نهاية عبارة لكل.
- النهاية.
فيما يلي شيفرة الخوارزمية، وهي برنامج مكتوب بلغة C لتطبيق خوارزمية بريزنهام في حالة | m | <1:
#include<stdio.h> #include<conio.h> #include<graphics.h> #include<math.h> int main() { int gdriver=DETECT,gmode; int x1,y1,x2,y2,delx,dely,p,i; initgraph(&gdriver,&gmode,"c:\\TC\\BGI"); printf("Enter the intial points: "); scanf("%d",&x1); scanf("%d",&y1); printf("Enter the end points: "); scanf("%d",&x2); scanf("%d",&y2); putpixel(x1,y1,RED); delx=fabs(x2-x1); dely=fabs(y2-y1); p=(2*dely)-delx; for(i=0;i<delx;i++){ if(p<0) { x1=x1+1; putpixel(x1,y1,RED); p=p+(2*dely); } else { x1=x1+1; y1=y1+1; putpixel(x1,y1,RED); p=p+(2*dely)-(2*delx); } } getch(); closegraph(); return 0; }
الحالة الثانية: | m | > 1:
- أدخل طرفي المستقيم (x1، y1) و (x2، y2).
- ارسم النقطة الأولى (x1، y1).
-
احسب القيمتين:
- Delx = | x2 – x1 | .
- Dely = | y2 – y1 | .
-
احسب معامل القرار الأول عبر الصيغة التالية:
- P = 2 * dely – delx.
- لكل I من 0 إلى delx:
-
إذا كان p <0 فسيكون:
- Y1 = y1 + 1.
- ارسم (x1، y1).
- P = p + delx.
-
وإلا:
- X1 = x1 + 1.
- Y1 = y1 + 1.
- ارسم (x1، y1)
- P = p + 2delx – 2 * dely.
- نهاية عبارة إن.
- نهاية عبارة لكل.
- النهاية.
انظر إلى الشيفرة أدناه، وهي برنامج مكتوب بلغة C لتطبيق خوارزمية بريزنهام في حالة | m | > 1:
#include<stdio.h> #include<conio.h> #include<graphics.h> #include<math.h> int main() { int gdriver=DETECT,gmode; int x1,y1,x2,y2,delx,dely,p,i; initgraph(&gdriver,&gmode,"c:\\TC\\BGI"); printf("Enter the intial points: "); scanf("%d",&x1); scanf("%d",&y1); printf("Enter the end points: "); scanf("%d",&x2); scanf("%d",&y2); putpixel(x1,y1,RED); delx=fabs(x2-x1); dely=fabs(y2-y1); p=(2*delx)-dely; for(i=0;i<delx;i++){ if(p<0) { y1=y1+1; putpixel(x1,y1,RED); p=p+(2*delx); } else { x1=x1+1; y1=y1+1; putpixel(x1,y1,RED); p=p+(2*delx)-(2*dely); } } getch(); closegraph(); return 0; }
خوارزمية الأعداد الكاتالانية
خوارزمية الأعداد الكاتالانية Catalan Number Algorithm هي إحدى خوارزميات البرمجة الديناميكية، وتشكل الأعداد الكاتلانية في الرياضيات التوافقية combinatorial mathematics سلسلةً من الأعداد الطبيعية التي تظهر في العديد من المسائل العددية المختلفة، وخاصةً المقادير التي تُعرّف بطريقة تكرارية، كما تظهر في مشاكل عدّ الأشجار. ويمكن استخدام خوارزمية الأعداد الكاتالانية لحساب مقادير مثل:
- عدد الطرق التي يمكن تكديس القطع النقدية بها في صف سفلي يتكون من n قطعة نقدية متتالية في المستوى، بحيث لا يُسمح بوضع أي قطعة نقدية على جانبي القطع النقدية السفلية، كما يجب أن تكون كل قطعة نقدية فوق قطعنين نقديتين أُخريين، الجواب هو العدد الكتالاني رقم n.
- عدد التعابير التي تحتوي على n زوج من الأقواس الهلالية، والتي تطابق بعضها البعض تطابقًا صحيحًا هو العدد الكتالاني رقم n.
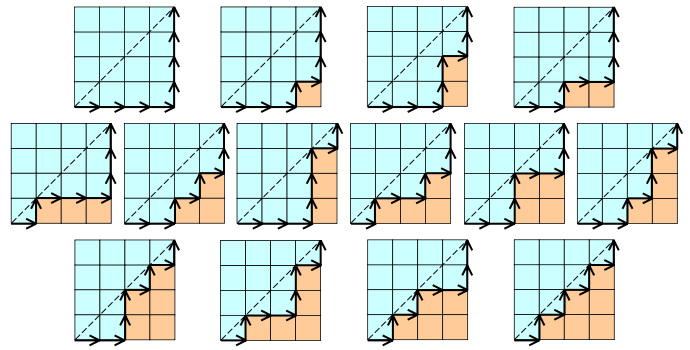
- عدد الطرق الممكنة لقطع مضلّع محدّب ذو n+2 وجهًا n+2-sided convex polygon في مستوى ما إلى مثلثات عبر ربط الحروف ذات الخطوط المستقيمة غير المتقاطعة هو العدد الكاتالاني رقم n.
يُحصَل على العدد الكاتالاني رقم n مباشرةً عبر المعادلة التالية التي تستخدم المعاملات الثنائية.
إليك مثال على عدد كاتالاني:
- n = 4
-
المساحة الإضافية =
O(n). -
تعقيد الوقت =
O(n^2).
الخوارزميات متعددة الخيوط Multithreaded Algorithms
سنستعرض في هذه الفقرة أمثلة على بعض الخوارزميات متعددة الخيوط.
مثال عن ضرب المصفوفة المربعة Square matrix multiplication:
multiply-square-matrix-parallel(A, B) n = A.lines C = Matrix(n,n) //n*n إنشاء مصفوفة من الحجم parallel for i = 1 to n parallel for j = 1 to n C[i][j] = 0 pour k = 1 to n C[i][j] = C[i][j] + A[i][k]*B[k][j] return C
مثال عن خوارزمية ضرب مصفوفة ومتجه متعددة الخيوط:
matrix-vector(A,x) n = A.lines y = Vector(n) //create a new vector of length n parallel for i = 1 to n y[i] = 0 parallel for i = 1 to n for j = 1 to n y[i] = y[i] + A[i][j]*x[j] return y
خوارزمية دمج وترتيب متعددة الخيوط
لتكن A وB مصفوفتان، وليكن p و r فهرسان للمصفوفة A، سنحاول ترتيب المصفوفة الجزئية A [p..r]. وسنملأ المصفوفة B عند ترتيب المصفوفة الجزئية.
في الشيفرة التالية، ترتب الدالة p-merge-sort (A، p، r، B، s) عناصر A [p..r] وتضعها في B [s..s + rp].
p-merge-sort(A,p,r,B,s) n = r-p+1 if n==1 B[s] = A[p] else T = new Array(n) //create a new array T of size n q = floor((p+r)/2)) q_prime = q-p+1 spawn p-merge-sort(A,p,q,T,1) p-merge-sort(A,q+1,r,T,q_prime+1) sync p-merge(T,1,q_prime,q_prime+1,n,B,s)
في الشيفرة أدناه، تجري الدالة المساعدة p-merge عملية الدمج بالتوازي، وتفترض هذه الدالة أنّ المصفوفتين الجزئيتين المراد دمجهما موجودتان في المصفوفة نفسها، ولكنّها لا تفترض أنهما متجاورتان في المصفوفة، لذا علينا تزويدها بالفهارس p1 وr1 p2 وr2.
p-merge(T,p1,r1,p2,r2,A,p3) n1 = r1-p1+1 n2 = r2-p2+1 if n1<n2 // n1>=n2 التحقق من أنّ permute p1 and p2 permute r1 and r2 permute n1 and n2 if n1==0 // كلاهما فارغ؟ return else q1 = floor((p1+r1)/2) q2 = dichotomic-search(T[q1],T,p2,r2) q3 = p3 + (q1-p1) + (q2-p2) A[q3] = T[q1] spawn p-merge(T,p1,q1-1,p2,q2-1,A,p3) p-merge(T,q1+1,r1,q2,r2,A,q3+1) sync
الشيفرة أدناه تمثل دالة البحث الانقسامي المساعِدة auxillary function dichotomic-search، ويكون x فيها هو المفتاح المراد البحث عنه في المصفوفة الفرعية T [p..r].
dichotomic-search(x,T,p,r) inf = p sup = max(p,r+1) while inf<sup half = floor((inf+sup)/2) if x<=T[half] sup = half else inf = half+1 return sup
خوارزمية KMP
خوارزمية KMP هي خوارزمية لمطابقة الأنماط، إذ تبحث عن مواضع ظهور كلمةٍ ما W في سلسلة نصية S.
ومبدأ هذه الخوارزمية أنّه في كلّ مرة نرصد فيها عدم تطابق، فإنّنا سنكون على علم ببعض الحروف الموجودة في النص والتي ستكون مطابقة في الخطوة القادمة. سنستغل هذه المعلومة لتجنب مطابَقة الحروف التي نعلم بأنّها ستكون متطابقة بأي حال. ولا يتجاوز تعقيد هذه الخوارزمية O (n) في أسوأ الحالات.
سنأخذ مثالًا على هذا النوع من الخوارزميات؛ تتألف هذه الخوارزمية من خطوتين:
-
الخطوة الأولى: التجهيز
-
نعالج النمط معالجةً مسبقة، وننشئ مصفوفة مساعدة
lps []تُستخدم لتخطي المحارف أثناء المطابقة. -
تشير
lps[]هنا إلى أطول سابقة ملائمة proper prefix تكون لاحقة suffix أيضًا. نقصد بالسابقة المناسبة أيّ سابقة تبدأ بها السلسلة النصية المبحوث عنها، شرط ألا تحتوي كامل السلسلة النصية. مثلاً، سوابق "ABC" الملائمة هي "" و "A" و "AB"، أما اللواحق الخاصة بهذه السلسلة النصية فهي: "" و "C" و "BC" و "ABC".
-
نعالج النمط معالجةً مسبقة، وننشئ مصفوفة مساعدة
- الخطوة الثانية: البحث
-
نستمر في مطابقة المحارف txt و pat [j]، ونستمر في زيادة
iوjطالما تطابقpat [j]وtxt. -
عندما نرصد عدم تطابق فإننا نعلم أنّ الأحرف
pat[0..j-1]تتطابق معtxt [i-j +1… i-1]. ونعلم أيضًا أنّlps[j-1]يساوي تعداد محارفpat[0 … j-1]التي هي سوابق ملائمة ولواحق على حدّ سواء، لهذا لا نحتاج إلى مطابقة أحرفlps [j-1]معtxt [ij… i-1]، لأنّنا نعلم سلفًا أنّها مُتطابقة.
فيما يلي تطبيق على ذلك بلغة جافا:
public class KMP { public static void main(String[] args) { // TODO Auto-generated method stub String str = "abcabdabc"; String pattern = "abc"; KMP obj = new KMP(); System.out.println(obj.patternExistKMP(str.toCharArray(), pattern.toCharArray())); } public int[] computeLPS(char[] str){ int lps[] = new int[str.length]; lps[0] = 0; int j = 0; for(int i =1;i<str.length;i++){ if(str[j] == str[i]){ lps[i] = j+1; j++; i++; }else{ if(j!=0){ j = lps[j-1]; }else{ lps[i] = j+1; i++; } } } return lps; } public boolean patternExistKMP(char[] text,char[] pat){ int[] lps = computeLPS(pat); int i=0,j=0; while(i<text.length && j<pat.length){ if(text[i] == pat[j]){ i++; j++; }else{ if(j!=0){ j = lps[j-1]; }else{ i++; } } } if(j==pat.length) return true; return false; } }
خوارزمية مسافة التعديل الديناميكية Edit Distance Dynamic Algorithm
بيان المشكلة: إذا أُعطيت سلسلتين نصيتين str1 و str2، فما هو العدد الأدنى للعمليات التي يمكن إجراؤها على str1 لتحويلها إلى str2. علمًا بأنّ العمليات الممكنة هي:
- الإدراج Insert.
- الحذف Remove.
- الاستبدال Replace.
إليك مثال:
- إن كانت str1 = "geek" و str2 = "gesek" فالجواب هو 1، لأنّنا نحتاج فقط إلى إدراج الحرف s في السلسلة النصية str1.
- إن كانت str1 = "march" و str2 = "cart" فالجواب هو 3، لأنّنا نحتاج إلى 3 عمليات هي وضع c مكان m، ثمّ حذف c، ثمّ وضع t مكان h.
ولحل هذه المشكلة، سنستخدم المصفوفة dp[n+1] [m+1] ثنائية الأبعاد، حيث يمثّل n طول السلسلة النصية الأولى، و m طول السلسلة النصية الثانية. على سبيل المثال، إذا كانت str1 تساوي "azcef" و str2 تساوي "abcdef"، فستكون المصفوفة من البعدين dp [6] [7]، وستُخزّن الإجابة النهائية في الموضع dp [5] [6].
(a) (b) (c) (d) (e) (f) +---+---+---+---+---+---+---+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | +---+---+---+---+---+---+---+ (a) | 1 | | | | | | | +---+---+---+---+---+---+---+ (z) | 2 | | | | | | | +---+---+---+---+---+---+---+ (c) | 3 | | | | | | | +---+---+---+---+---+---+---+ (e) | 4 | | | | | | | +---+---+---+---+---+---+---+ (f) | 5 | | | | | | | +---+---+---+---+---+---+---+
بالنسبة للفهرس dp [1] [1]، ليس علينا فعل شيء لتحويل a إلى a لأنّهما متساويان، لذا نضع 0 هناك.
وبالنسبة للفهرس dp [1] [2]، ما الذي علينا أن نفعله لتحويل a إلى ab؟ سنحتاج إلى عملية واحدة، وهي إدراج الحرف b. ستبدو المصفوفة كما يلي بعد التكرار الأول:
(a) (b) (c) (d) (e) (f) +---+---+---+---+---+---+---+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | +---+---+---+---+---+---+---+ (a) | 1 | 0 | 1 | 2 | 3 | 4 | 5 | +---+---+---+---+---+---+---+ (z) | 2 | | | | | | | +---+---+---+---+---+---+---+ (c) | 3 | | | | | | | +---+---+---+---+---+---+---+ (e) | 4 | | | | | | | +---+---+---+---+---+---+---+ (f) | 5 | | | | | | | +---+---+---+---+---+---+---+
بالنسبة للفهرس dp [2] [1]، لأجل تحويل az إلى a، نحتاج إلى إزالة z، ومن ثم نضع 1 في dp [2] [1]. أما بالنسبة لـ dp [2] [2]، نحتاج إلى استبدال z بـ b، ومن ثم نضع 1 في dp [2] [2].
هكذا ستبدو المصفوفة الآن:
(a) (b) (c) (d) (e) (f) +---+---+---+---+---+---+---+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | +---+---+---+---+---+---+---+ (a) | 1 | 0 | 1 | 2 | 3 | 4 | 5 | +---+---+---+---+---+---+---+ (z) | 2 | 1 | 1 | 2 | 3 | 4 | 5 | +---+---+---+---+---+---+---+ (c) | 3 | | | | | | | +---+---+---+---+---+---+---+ (e) | 4 | | | | | | | +---+---+---+---+---+---+---+ (f) | 5 | | | | | | | +---+---+---+---+---+---+---+
نستمر في إعادة العملية إلى أن نحوّل السلسلة النصية الأولى إلى الثانية ("azcef" ← "abcdef")، وستبدو المصفوفة النهائية هكذا:
(a) (b) (c) (d) (e) (f) +---+---+---+---+---+---+---+ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | +---+---+---+---+---+---+---+ (a) | 1 | 0 | 1 | 2 | 3 | 4 | 5 | +---+---+---+---+---+---+---+ (z) | 2 | 1 | 1 | 2 | 3 | 4 | 5 | +---+---+---+---+---+---+---+ (c) | 3 | 2 | 2 | 1 | 2 | 3 | 4 | +---+---+---+---+---+---+---+ (e) | 4 | 3 | 3 | 2 | 2 | 2 | 3 | +---+---+---+---+---+---+---+ (f) | 5 | 4 | 4 | 2 | 3 | 3 | 3 | +---+---+---+---+---+---+---+
هذه هي الصيغة العامة لتحديث المصفوفة:
if characters are same dp[i][j] = dp[i-1][j-1]; // الحرفان متطابقان else dp[i][j] = 1 + Min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])
هذا تطبيق مكتوب بلغة جافا:
public int getMinConversions(String str1, String str2){ int dp[][] = new int[str1.length()+1][str2.length()+1]; for(int i=0;i<=str1.length();i++){ for(int j=0;j<=str2.length();j++){ if(i==0) dp[i][j] = j; else if(j==0) dp[i][j] = i; else if(str1.charAt(i-1) == str2.charAt(j-1)) dp[i][j] = dp[i-1][j-1]; else{ dp[i][j] = 1 + Math.min(dp[i-1][j], Math.min(dp[i][j-1], dp[i-1][j-1])); } } } return dp[str1.length()][str2.length()]; }
التعقيد الزمني لهذه الخوارزمية هو O(n^2).
الخوارزميات المتصلة Online algorithms
تنشأ مشكلة التخزين المؤقت caching من محدودية مساحة التخزين، وسنفترض أنّ ذاكرة التخزين المؤقت C تحتوي على k صفحة، ونحن نريد معالجة سلسلة من طلبات الصفحات عددها m طلب، ويجب تخزينها في ذاكرة التخزين المؤقت قبل معالجتها.
إذا كانت m<=k فلن تكون هناك مشكلة إذ سنضع جميع العناصر في ذاكرة التخزين المؤقت، ولكن في العادة تكون m>>k.
تكون طلبيّة ما مقبولة في ذاكرة التخزين المؤقت (نقول أنها cache hit) إذا كان العنصر موجودًا في ذاكرة التخزين المؤقت بالفعل، وإلا نقول أنّها مُفوَّتة من ذاكرة التخزين المؤقت cache miss، وفي مثل هذه الحالة سيكون علينا إحضار العنصر المطلوب إلى ذاكرة التخزين المؤقت وإخراج عنصر آخر وذلك على افتراض أنّ ذاكرة التخزين المؤقت ممتلئة. إن الهدف هنا هو تصميم جدول إخلاء eviction schedule يقلّل عدد عمليات الإخلاء الضرورية قدر الإمكان.
هناك العديد من الاستراتيجيات الممكنة لحلّ هذه المشكلة، منها:
- من دخل أولًا، يخرج أولًا First in, first out أو FIFO: تُخلى أقدم صفحة.
- من دخل آخرًا، يخرج أولًا Last in, first out أو LIFO: تُخلى أحدث صفحة.
- الأقل استخدامًا مؤخرًا LRU: تخلى الصفحة التي كان آخر وصول لها هو الأبكر.
-
الأقل طلبًا LFU: تخلى الصفحة التي طُلِبت أقل عدد من المرّات.
- أطول مسافة أمامية LFD: تخلى الصفحة التي لن تُطلَب إلا بعد أطول مدة.
- التفريغ عند الامتلاء FWF: مسح ذاكرة التخزين المؤقت كاملة بمجرد حدوث فوات في ذاكرة التخزين المؤقت.
هناك طريقتان للتعامل مع هذه المشكلة:
- الطريقة غير المتصلة offline: يكون فيها تسلسل الطلبات معروف منذ البدء.
- الطريقة المتصلة online: يكون تسلسل الطلبات غير معروف مسبقًا.
وقبل أن نواصل، سنقدم بعض التعاريف الرياضية المساعدة.
-
التعريف 1: نقول أنّ المشكلة
Πهي مشكلة تحسين optimization problem إن كانت تتألف من مجموعة من الحالاتΣΠ، بحيث يكون لكل حالةσ∈ΣΠمجموعة من الحلول ودالة تقييمf σ: Ζσ → ℜ≥ 0تعطي قيمة حقيقية موجبة لكلّ حل من تلك الحلول، ونرمز لقيمة الحل الأمثل (optimal solution) من بين كل حلول الحالة σ بالرمز OPT (σ).
ولكل خوارزمية A، يشير الرمز A (σ) إلى حل الخوارزمية A للمشكلة Π في الحالة σ، بينما يساوي التعبير wA (σ) = fσ (A (σ)) قيمة الخوارزمية.
-
التعريف 2: نقول أنّ خوارزمية متصلة A لمشكلة تصغير
Πminimization problem لديها معدل تنافسي competetive ratio قيمته r ≥ 1 إذا كان هناك ثابتτ∈ℜيحقّق:
wA(σ) = fσ(A(σ)) ≤ r ⋅ OPT(σ) + τ
لكل الحالات σ∈ΣΠ، نقول أنّ الخَوارزمية A خوارزمية متصلة ذات r تنافسية r-competitive online algorithm إن كان لدينا:
wA(σ) ≤ r ⋅ OPT(σ)
لكل عنصر σ∈ΣΠ، نقول أنّ A خوارزمية متصلة ذات r تنافسية قطعًا strictly r-competitive online algorithm.
- تعريف 3: نقول أنّ خوارزمية A خوارزمية واسمة Marking Algorithm فقط إذا لم تكن تُخلي أيّ صفحة موسومة من ذاكرة التخزين المؤقت، مما يعني أنّ الصفحات التي تُستخدم أثناء أيّ مرحلة لن تُخلى.
خاصية 1.3: الخوارِزميتان LRU -الأقل استخدامًا مؤخرًا Least recently used، أي إخلاء الصفحة التي لم يُدخل إليها منذ أطول مدة-، و FWF -التفريغ عند الملء Flush when full، وتعني مسح ذاكرة التخزين المؤقت بمجرد وقوع فوات في ذاكرة التخزين المؤقت cache miss- هما خوارِزميتان واسمَتان.
اقتباسبرهان: في بداية كل مرحلة (ما عدا المرحلة الأولى) يكون هناك فوات في خوارزمية FWF ، كما تُمسَح ذاكرة التخزين المؤقت. هذا يعني أنّه ستكون لدينا عدد k صفحة فارغة. وفي كل مرحلة، ستُطلب k صفحة مختلفة على الأكثر، لذا لا بدّ أن يكون هناك إخلاء خلال هذه المرحلة. وعليه فإنّ FWF هي خوارزمية واسمة.
دعنا نفترض أن LRU ليست خوارزميةًواسمة، إذًا ستكون هناك حالة σ، بحيث تخلي الخوازرمية LRU صفحة x موسومة marked page في المرحلة i. وإن كان σt هو الطلب في المرحلة i حيث أُخلِيت الصفحة x، وبما أن صفحة x موسومة، فلا بدّ أن يكون هناك طلب سابق σt* للصفحة x في المرحلة نفسها، لذا تكون t * <t
بعد t* ، ستكون x هي الصفحة الأحدث في ذاكرة التخزين المؤقت، لذا ينبغي أن يطلب التسلسل σt*+1,...,σt على الأقل k صفحة مختلفة عن x، وذلك لأجل إخلائها عند الوقت t. هذا يعني أنّ المرحلة i قد طلبت على الأقل k +1 صفحة مختلفة، وهذا يتعارض مع تعريف المرحلة. وعليه نستنتج أنّ LRU خوارزمية واسمة.
خاصية 1.4: كل الخوارزميات الواسمة هي خوارزميات ذات k تنافسية قطعًا.
اقتباسبرهان: إذا كانت
σحالة من مشكلة التصفيح paging problem، و هي عدد مراحلσ، وإذا كانت l = 1، فستكون كل الخوارزميات الواسمة مُثلى ولا يمكن للخوارزمية غير المتصلة offline algorithm المثلى أن تكون أفضل.
إذا افترضنا أنّ l ≥ 2، فستكون تكلفة جميع الخوارزميات الواسمة للحالة σ أصغر من l ⋅ k، لأنه لا يمكن للخوارزمية الواسمة أن تخلي في كل مرحلة أكثر من k صفحة دون إخلاء صفحة واحدة واسمة على الأقل.
سنحاول الآن أن نبيّن أنّ الخوارزمية غير المتصلة المثلى optimal offline algorithm تخلي على الأقل k + l-2 صفحةً في الحالة σ، حيث تُخلي k في المرحلة الأولى، إضافةً إلى صفحة واحدة على الأقل في كل مرحلة تالية خلال المرحلة الأخيرة:
نعرّف الآن l - 2 تسلسلًا فرعيًا منفصلا للحالة σ، يبدأ التسلسلi ∈ {1,…,l-2} في الموضع الثاني من المرحلة i + 1 وينتهي عند الموضع الأول للمرحلة i + 2. لتكن x الصفحة الأولى من المرحلة i +1، في بداية التسلسل i توجد صفحة x، إضافةً إلى k-1 صفحة مختلفة على الأكثر في ذاكرة التخزين المؤقت الخاصة بالخوارزميات غير المتصلة المثلى.
هناك k صفحة مطلوبة في التسلسل i مختلفة عن x، لذا يتوجّب على الخوارزمية غير المتصلة المثلى إخلاء صفحة واحدة على الأقل في كل تسلسل. وبما أن ذاكرة التخزين المؤقت في المرحلة الأولى فارغة، فإنّ الخوارزمية غير المتصلة المثلى تجري k عملية إخلاء خلال المرحلة الأولى. وهذا يبيّن أنّ:
wA(σ) ≤ l⋅k ≤ (k+l-2)k ≤ OPT(σ) ⋅ k
خاصية 1.5: الخوارزمِيتان LRU و FWF خوارِزميتان ذواتا k تنافسية قطعا.
لتكن A خوارزمية متصلة، إذا لم تكن هناك أيّ ثابتة r بحيث تكون هذه الخوارزمية ذات r تنافسية، نقول أنّ A غير تنافسية not competitive.
خاصية 1.6: الخوارزميتان LFU و LIFO غير تنافُسيتان.
اقتباسبرهان: لتكن l ≥ 2 ثابتة، و k ≥ 2 حجم ذاكرة التخزين المؤقت، سنرقّم صفحات ذاكرة التخزين المؤقت كما يلي 1، …، k +1. انظر التسلسل التالي:
الصفحة الأولى مطلوبة عدد l مرّة، وكذلك الصفحة 2، وهكذا دواليك، وفي النهاية سيكون لدينا (l-1) طلبًا للصفحة k و k +1.
تملأ الخوارِزميتان LFU و LIFO صفحات المخزن المؤقت بـالصفحات من 1 إلى k، وعند طلب الصفحة k +1 تُخلى الصفحة k، والعكس صحيح. هذا يعني أنّ كل طلب من التسلسل (k,k+1)l-1 يخلي صفحة واحدة.
أيضًا، هناك مرات فوات قدرها k-1 فواتًا في ذاكرة التخزين المؤقت cache misses في أول استخدام للصفحات من 1 إلى (k-1)، وهذا يعني أنّ الخوارزميتَين LFU و LIFO تخليان k-1 +2 (l-1) صفحة بالضبط.
سنحاول الآن أن نثبت أنّه لكل ثابتة τ∈ℜ، ولكل ثابتة r ≤ 1، يوجد l يحقق:
والذي يساوي:
لتحقيق هذه المتراجحة، يكفي أن تختار عدد I كبيرًا بما يكفي.
نستنتج من كل هذا أنّ الخوارزميتَين LFU و LIFO غير تنافسيتَين.
خاصية 1.7: لكل r <k، لا توجد أيّ خوارزمية حتمية متصلة ذات r تنافسية لحل مشكلة التصفيح r-competetive deterministic online algorithm for paging.
المنظور غير المتصل Offline Approach
قبل المواصلة، راجع مقالة تطبيقات خوارزميات الشَّرِهة، وراجع فقرة التخزين المؤقت غير المتصل والاستراتيجيات الخمس المستخدمة فيها.
لقد وسّعنا برنامج المثال بإضافة استراتيجية FWF:
class FWF : public Strategy { public: FWF() : Strategy("FWF") { } int apply(int requestIndex) override { for(int i=0; i<cacheSize; ++i) { if(cache[i] == request[requestIndex]) return i; // بعد أول صفحة فارغة، يجب أن تكون كل الصفحات الأخرى فارغة else if(cache[i] == emptyPage) return i; } // لا صفحات حرة return 0; } void update(int cachePos, int requestIndex, bool cacheMiss) override { // لا صفحات حرة -> فوات -> مسح المخزن المؤقت if(cacheMiss && cachePos == 0) { for(int i = 1; i < cacheSize; ++i) cache[i] = emptyPage; } } };
يمكنك تحميل الشيفرة المصدرية كاملة من pastebin.
إذا أعدنا استخدام المثال، فسنحصل على النتيجة التالية:
Strategy: FWF Cache initial: (a,b,c) Request cache 0 cache 1 cache 2 cache miss a a b c a a b c d d X X x e d e X b d e b b d e b a a X X x c a c X f a c f d d X X x e d e X a d e a f f X X x b f b X e f b e c c X X x Total cache misses: 5
على الرغم من أنّ خوارزمية LFD مثلى، إلا أنّ خوارزمية FWF تتميّز بأنّ عدد الفوات فيها أقل، غير أن الهدف الرئيسي هو تقليل عدد عمليات الإخلاء إلى الحد الأدنى، وفي خوارزمية FWF تحدث 5 حالات فوات، مما يعني أنّه ستكون هناك 15 عملية إخلاء، ما يجعلها الخيار الأسوء.
المنظور المتصل Online Approach
نريد الآن أن نبحث عن حل لمشكلة التصفيح المتصل online problem of paging، نحن نعلم أنّه لا يمكن لأيّ خوارزمية متصلة أن تكون أفضل من الخوارزمية غير المتصلة المثلى، لأنّه في الخوارزمية غير المتصلة تكون سلسلة الطلبات معروفة منذ البداية، وذلك على خلاف الخوارزميات المتصلة التي لا تعرف مسبقًا إلا الطلبات السابقة وليس اللاحقة، لهذا فإنّ الخوارزميات غير المتصلة لديها دائما معلومات أكثر موازنةً بالخوارزميات المتصلة، ما يجعلها أكثر كفاءة.
سنحتاج إلى بعض التعريفات الدقيقة قبل أن نواصل:
-
التعريف 1: نقول أنّ المشكلة
Πهي مشكلة تحسين optimization problem إن كانت تتألف من مجموعة من الحالاتΣΠ. بحيث يكون لكل حالةσ∈ΣΠمجموعة من الحلول، ودالة تقييمf σ: Ζσ → ℜ≥ 0تعطي قيمة حقيقية موجبة لكلّ حل من تلك الحلول. نرمز للحل الأمثل optimal solution من بين كل حلول الحالة σ بالرمز OPT (σ).
لكل خوارزمية A، يشير الرمز A (σ) إلى حل الخوارزمية A للمشكلة Π في الحالة σ، فيما يساوي التعبير wA (σ) = fσ (A (σ)) قيمة الخوارزمية.
-
التعريف 2: نقول أنّ خوارزمية متصلة A لمشكلة تصغير Π
minimization problemلديها معدل تنافسي competetive ratio قيمته r ≥ 1 إذا كان هناك عددτ∈ℜثابت يحقّق:
wA(σ) = fσ(A(σ)) ≤ r ⋅ OPT(σ) + τ
لكل الحالات σ∈ΣΠ، نقول أنّ الخَوارزمية A خوارزمية r-تكرارية متصلة r-competitive online algorithm إن كان لدينا:
wA(σ) ≤ r ⋅ OPT(σ)
لكل عنصر σ∈ΣΠ، نقول أنّ A خوارزمية متصلة تنافسية قطعا strictly r-competitive online algorithm.
لذا فإن السؤال هو مدى تنافسية خوارزميتنا المتصلة موازنةً بالخوارزمية غير المتصلة المثلى. وصف كل من آلان بورودين Allan Borodin وران الينيف Ran El-Yaniv في كتابهما الشهير خوارزميةَ التصفيح المتصل بالتعبير الطريف التالي:
اقتباسهناك خصم شرير يعرِف خوارِزميتك والخوارزمية غير المتصلة المثلى. ويحاول في كل خطوة أن يطلب صفحةً تكون أسوأ ما يكون لك، وفي الوقت نفسه تكون أفضل ما يكون للخوارزمية غير المتصلة. والعامل التنافسي competitive factor لخوارزميتك هو مؤشر على مدى سوء خَوارزميتك موازنةً بخوارزمية الخصم المثلى غير المتصلة.
إذا أردت أن تكون مكان الخصم، فيمكنك تجربة لعبة الخصم (حاول التغلب على استراتيجيات التصفيح).
الخوارزميات الواسمة Marking Algorithms
بدلاً من تحليل كل الخوارزميات على حدة، سنحلّل عائلةً خاصةً من الخوارزميات المتصلة الخاصة بمشكلة التصفيح تسمّى خوارزميات الوسم أو الخوارزميات الواسمة marking algorithms.
تعريف: نقول أنّ خوارزمية A خوارزمية واسمةً، فقط إذا لم تكن تُخلي أيّ صفحة موسومة من ذاكرة التخزين المؤقت، مما يعني أنّ الصفحات التي تُستخدم أثناء أيّ مرحلة لن تُخلى.
لتكن σ=(σ1,...,σp) حالة من المشكلة، و k حجم ذاكرة التخزين المؤقت، فعندئذ يمكن تقسيم σ إلى مراحل:
-
المرحلة 1 هي أقصى تتابع لـ
σمن البداية حتى أقصى k صفحة مختلفة مطلوبة. -
المرحلة i ≥ 2 هي أقصى تتابع لـ
σمن نهاية المرحلة i-1 حتى أقصى k صفحة مختلفة مطلوبة
على سبيل المثال: في الحالة k = 3، نحصل على:
تتذكّر الخوارزميات الواسمة (ضمنيًا أو صراحة) ما إذا كانت الصفحة موسومةً أم لا، وتكون كل الصفحات غير موسومة في بداية كل مرحلة، وتوسم الصفحة بمجرد أن تُطلب أثناء مرحلة ما.
خاصية 1.3: الخوارِزميتان LRU (وتعني الأقل استخدامًا مؤخرًا - Least recently used، أي إخلاء الصفحة التي لم يُدخل إليها منذ أطول مدة)، و FWF (أي التفريغ عند الملء - Flush when full، وتعني مسح ذاكرة التخزين المؤقت بمجرد وقوع فوات في ذاكرة التخزين المؤقت cache miss) هما خوارِزميتان واسمَتان marking algorithm.
اقتباسبرهان: في بداية كل مرحلة (ما عدا المرحلة الأولى) يكون هناك فوات في خوارزمية FWF ، كما تُمسَح ذاكرة التخزين المؤقت، هذا يعني أنّه ستكون لدينا k صفحة فارغة. وفي كل مرحلة، ستُطلب k صفحة مختلفة على الأكثر، لذلك لا بدّ أن يكون هناك إخلاء خلال هذه المرحلة. وبالتالي فإنّ FWF هي خوارزمية واسمة.
لنفترض أنّ LRU ليست خوارزميةً واسمة، إذًا ستكون هناك حالة σ بحيث تخلي الخوازرمية LRU صفحة x موسومة marked page في المرحلة i. ليكن *σt هو الطلب في المرحلة i، حيث أُخلِيت الصفحة x، عندئذ وبما أن الصفحة x موسومة، فلا بدّ أن يكون هناك طلب سابق *σt للصفحة x في المرحلة نفسها، لذلك فإنّ t * <t.
بعد * t، ستكون x هي الصفحة الأحدث في ذاكرة التخزين المؤقت، لذلك ينبغي أن يطلب التسلسل σt*+1,...,σt على الأقل k صفحة مختلفة عن x لأجل إخلائها عند الوقت t، وهذا يعني أنّ المرحلة i قد طلبت على الأقل k +1 صفحة مختلفة، مما يتعارض مع تعريف المرحلة، وعليه نستنتج أنّ LRU خوارزمية واسمة.
خاصية 1.4: كل الخوارزميات الواسمة هي خوارزميات ذات k تنافسية قطعًا.
اقتباس: لتكن
σحالة من مشكلة التصفيح paging problem، و l عدد مراحلσ. إذا كانت l = 1، ستكون كل الخوارزميات الواسمة مُثلى، ولا يمكن للخوارزمية غير المتصلة offline algorithm المثلى أن تكون أفضل.
إذا افترضنا أنّ l ≥ 2، فستكون تكلفة جميع الخوارزميات الواسمة للحالة σ أصغر من l ⋅ k، لأنه لا يمكن للخوارزمية الواسمة أن تخلي في كل مرحلة أكثر من k صفحة دون إخلاء صفحة واحدة واسمة على الأقل.
سنحاول الآن أن نبيّن أنّ الخوارزمية غير المتصلة المثلى optimal offline algorithm تخلي على الأقل k + l-2 صفحة في الحالة σ، حيث تُخلي k في المرحلة الأولى، إضافةً إلى صفحة واحدة على الأقل في كل مرحلة تالية عدا المرحلة الأخيرة.
نعرّف الآن l - 2 تسلسلًا فرعيًا منفصلا للحالة σ، يبدأ التسلسل i ∈ {1,…,l-2} في الموضع الثاني من المرحلة i + 1 وينتهي عند الموضع الأول للمرحلة i + 2. لتكن x الصفحة الأولى من المرحلة i +1. في بداية التسلسل i توجد صفحة x، إضافةً إلى k-1 صفحة مختلفة على الأكثر في ذاكرة التخزين المؤقت الخاصة بالخوارزميات غير المتصلة المثلى.
في التسلسل i، هناك عدد k صفحة مطلوبة مختلفة عن x، لذا يتوجّب على الخوارزمية غير المتصلة المثلى إخلاء صفحة واحدة على الأقل في كل تسلسل. وبما أن ذاكرة التخزين المؤقت في المرحلة الأولى فارغة، فإنّ الخوارزمية غير المتصلة المثلى تجري k عملية إخلاء خلال المرحلة الأولى، وهذا يبيّن أنّ:
wA(σ) ≤ l⋅k ≤ (k+l-2)k ≤ OPT(σ) ⋅ k
خاصية 1.5: الخوارزميتان LRU و FWF خوارزميتان ذواتا k تنافسية قطعًا.
- تمرين: أثبت أنّ خوارزمية FIFO ليست خوارزميةً واسمة، وإنّما خوارزمية ذات k تنافسية قطعًا.
- لتكن A خوارزمية متصلة، إذا لم تكن هناك أيّ ثابتة r بحيث تكون هذه الخوارزمية ذات r تنافسية، نقول أنّ A غير تنافسية not competitive.
خاصية 1.6: الخوارزميتان LFU و LIFO غير تنافُسيتان.
اقتباس
برهان: لتكن l ≥ 2 ثابتة، و k ≥ 2 هو حجم ذاكرة التخزين المؤقت، سنرقّم صفحات ذاكرة التخزين المؤقت كما يلي 1، …، k +1. انظر التسلسل التالي:
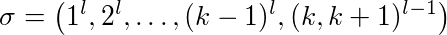
الصفحة الأولى مطلوبة عدد l مرّة، وكذلك الصفحة 2، وهكذا دواليك. في النهاية، سيكون هناك (l-1) طلبًا للصفحة k و k +1.
تملأ الخوارِزميتان LFU وLIFO صفحات المخزن المؤقت بـالصفحات من 1 إلى k، وتُخلى الصفحة k عند طلب الصفحة k +1، والعكس صحيح. هذا يعني أنّ كل طلب من التسلسل (k,k+1)l-1 يخلي صفحة واحدة.
أيضًا، هناك عدد k-1 فواتًا في ذاكرة التخزين المؤقت cache misses في أول استخدام للصفحات من 1 إلى (k-1)، وهذا يعني أنّ الخوارزميتَين LFU و LIFO تخليان k-1 +2 (l-1) صفحة بالضبط.
الآن، سنحاول أن نثبت أنّه لكل ثابتة τ∈ℜ، ولكل ثابتة r ≤ 1، يوجد l يحقق:
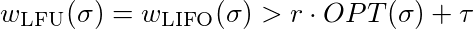
والذي يساوي:

لتحقيق هذه المتراجحة، يكفي أن تختار عدد I كبيرًا بما يكفي، من ذلك نستنتج أنّ الخوارزميتَين LFU و LIFO غير تنافسيتَين.
خاصية 1.7: لكل r <k، لا توجد أيّ خوارزمية حتمية متصلة ذات r تنافسية لحل مشكلة التصفيح r-competetive deterministic online algorithm for paging.
برهان هذه الخاصية طويل نوعًا ما ويستند إلى فكرة أنّ LFD هي خوارزمية مثلى.
السؤال الآن هو: هل هناك منظور أفضل؟ للإجابة على هذا السؤال سيكون علينا أن نتجاوز المنظور الحتمي deterministic approach ونستخدم المقاربات العشوائية في خوَارزميتنا، وهو أمر سنعود إليه لاحقًا في هذه السلسلة.
ترجمة -بتصرّف- للفصول 21 و 23 و 24 و25 و26 و27 من كتاب Algorithms Notes for Professionals.
اقرأ أيضًا
- المقال التالي: خوارزميات الترتيب وأشهرها
- المقال السابق: خوارزميات تحليل المسارات في الأشجار
- مدخل إلى الخوارزميات
- تعلم بايثون
- تعلم PHP

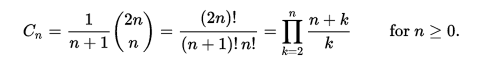
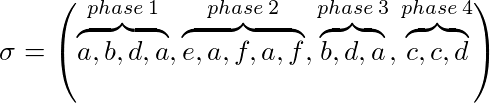











أفضل التعليقات
لا توجد أية تعليقات بعد
انضم إلى النقاش
يمكنك أن تنشر الآن وتسجل لاحقًا. إذا كان لديك حساب، فسجل الدخول الآن لتنشر باسم حسابك.